西北师大附中高一物理奥赛教案第六节驻波
普通物理学-机械波-2-6-驻波

2– 6 驻 波
第2章 机械波
当波从波密介质垂直入射到波疏介质, 被反射
到波密介质时形成波腹。入射波与反射波在此处的 相位时时相同,即反射波在分界处不产生相机械波
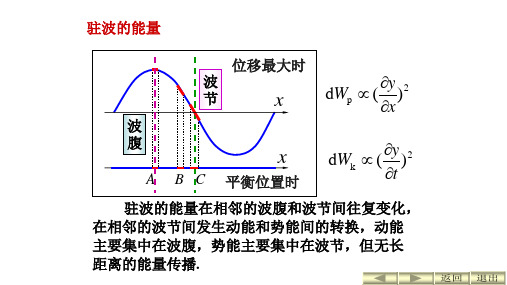
四、驻波的能量
位移最大时
波 节
x
dWp
(y )2 x
波
腹
x
A B C 平衡位置时
第2章 机械波
2)相邻两波节之间质点振动同相位,任一波节
π 两侧振动相位相反,在波节处产生 的相位跃变 。
(与行波不同,无相位的传播)。
y 2Acos2π x cos2π t
例 x 为波节
4
y
2
2
o
x
cos2π x 0, x ,
44
y 2Acos 2π x cos 2π t
(4)驻波中驻波中各质点同时达到各自的最大位移,同时经 过各自的平衡位置,因此我们称驻波各质点作同步振动。
(5)没有振动状态或相位的逐点传播,即没有“跑动”的波 形,也没有能量的传播。
2– 6 驻 波
驻波的形成
第2章 机械波
2– 6 驻 波
第2章 机械波
二、驻波方程
正向
y1
A c os2π
(t
x
)
负向
y2
A c os2π
(t
x)
y y1 y2
Acos2π (t x ) Acos2π (t x )
2 Acos2π x cos2π t
驻波的振幅 与位置有关
各质点都在作同 频率的简谐运动
2– 6 驻 波
第2章 机械波
讨论 ➢ 1)振幅
驻波方程 y
高二物理竞赛课件:驻波的能量
须是波节,弦上形成驻波的条件(称为简正模式):
Ln
( n=1,2,3)
2
驻波波长和简正模频率:
2L , nu (基频, 二次谐频)
n
2L
返回 退出
*若弦的一端固定,一端自由,简正模:
Ln
24
(2n 1)u
4L
返回 退出
例 如图二胡弦长 l 0.3 m ,张力 T 9.4N . 密度 3.810 4 kg m . 求弦所发的声音的基频和谐频.
π] 3
(m)
为了在此弦线上形成驻波,并且在x= 0处为一
波节,此弦上还应有一简谐波,求其表达式。
解: 反向波:
y2
0.02 cos[2π( t 0.02
x) 20
]
合成波:
y y1 y2
0.04 cos[1 ( 2x π )]cos[1 ( 4πt π )]
2 20
3
2 0.02
x l 2 时,y1 = Acos t,
A c os t
l 2u
1
Acost
1
l
2u
返回 退出
x l 2 时,y2 = Acos t,
A c os t
l 2u
2
Acos(t
)
2
l
2u
右行波、左行波表达式:
y1
A cos
t
x u
l 2u
y2
A c os t
x u
l 2u
返回 退出
入射波与反射波 在反射点同相
波腹
光波:光密 到 光疏
固定端反射 半波反射
波疏 波密界面反射 光波:光疏 到 光密
入射波与反射波 在反射点反相
5驻波

1
•如果 •如果
2
2u2 1u1 2u2 1u1
界面处出现半波损失;则介
质1称为波疏媒质,介质2称为波密媒质。 界面处不出现半波损失;则介 质1称为波密媒质,介质2称为波疏媒质。
2.相位突变
界面处为波节时,反射波相位突变了,相当半 个波长的波程----半波损失。
11
五、弦线上驻波形成条件
§ 5.6
驻波
1
一、驻波
1.驻波的产生 驻波是两列振幅、频率和传播速率都相同的相干 波在同一直线上沿相反方向传播时波的叠加而形成的现 象。(由于其波动看起来处于静止状态,与行波相对称 为驻波。) 当一列波遇到障碍时产生的反射波与入射波叠加 可产生驻波----波形不传播。
2
二 、驻波方程
t x 正行波(入射波) y1 A cos2 T t x 负行波(反射波) y2 A cos2 T
合成波 由三角公式:
y y1 y2
cosα+cosβ=2cos[(α+β)/2]cos[ (α-β)/2]
t x t x y A cos2 A cos2 T T
t 2 A cos 2 cos 2 T
4.波节、波腹位置 ①.波节位置
波腹
x 0
2 A cos 2
2
x
(2k 1)2x (2k 1)
4
( k 0,1,2)
5
/2
波节
②.相邻波节距离
波腹
x (2k 1)
4
x k1 x k [2( k 1) 1] (2k 1) 4 4 2 x cos 2 1 ③.波腹位置
高三高中物理竞赛驻波和多普勒效应(无答案)

驻波和多普勒效应1、驻波频率相同、振幅相等、振动方向一致、传播方向相反的两列简谐波互相叠加,便形成驻波。
设坐标原点的振动方程为t A y ωcos =,则满足上述条件的两列简谐波的波动方程分别为:)2cos(1x t A y λπω-= )2cos(2x t A y λπω+=叠加所得的合成波的方程为:t x A y y y ωλπcos )2cos(221⋅=+=式中)2cos(2x A λπ是此合成波的振幅,它与x 有关。
振幅最大处称为波腹,振幅最小处称为波节。
波腹的位置为:)(2z k kx ∈=λ波节的位置为:2)21(λ+=k x 相邻两波腹(或波节)之间的间距为2λ。
不同时刻驻波的波形图如图所示,其中实线表示t=0,T ,2T ,…时的波形,点线表示T t 21=,T 23,…时的波形;点画线表示T t 81=,T 89,…时的波形。
2、多普勒效应由于波源和观察者之间有相对运动,使观察者接受到的频率f R 与波源的振动频率f s 不同,这种现象称为多普勒效应。
相互远离时,频率变低;相互接近时,频率变高。
利用声波的多普勒效应可以测定流体的流速、潜艇的速度,还可以用来报警和监测车速。
在医学上,利用超声波的多普勒效应对心脏跳动情况进行诊断,如做超声心动,多普勒血流仪等。
(1)三种情况:(波源频率为s f ,波的频率为f ,观察者接受到的波频率为R f ) ① 相对于媒质,波源不动,观察者以速度v R ,向着或远离波源运动。
如右图所示。
f uv u f u v u v u f RR RR +=+=+=/λ(式中u 为波速);因为此时波源的频率就是波的频率,所以s RR f uv u f +=因此观察者向着波源运动时,接受到的频率大于波源的频率;当观察者远离静止波源运动时,接受到的频率小于波源的频率。
② 相对于媒质,观察者不动,波源以速度v s 向着观察者运动。
波源运动时,波的频率不再等于波源的频率。
公开课驻波ppt课件

(1)波腹: 令
cos( 2 x ) 1
2 x k ,
(k 0,1,2,)
求出的 x 即为波腹的位置。
(2)波节: 令 cos( 2 x )=0
2 x (2K 1) ,
2
(k 0,1,2,)
求出的 x 即为波节的位置。
势能主要集中在波节附近。 驻波的能量在相邻的波腹和波节间不断地
进行动能与势能的相互转换,而不向外传播。9
四. 半 波 损 失
当波从波疏媒质垂直入 射到波密媒质界面上反射 时,在反射点,形成波节 (固定端)。即反射波在
分界处较入射波产生了
的相位跃变(即有半波损 失)。
当波从波密媒质垂直入 射到波疏媒质界面上反射 时,在反射点,形成波腹 (自由端)。即无半波损 失)。
处位相突变 ,设反射波的强度不变,试写出
反射波的波动方程。
设:y反 0.01cos[4t+ x+] (SI)
2x 3 10 3
2 3 10
取 2 3
y反 0.01cos[4t+ x+2 3] (SI) 13
第五节 驻
波
一、 驻波的产生
振幅相同的两列相干波,在同一直线上
沿相反方向传播,叠加后所形成的波叫
驻波(驻波是一种特殊的干涉现象)
横驻波演示
波节
波腹
波腹是干涉极大值位置;波节是干涉极小值位置。
纵驻波演示 1
二、 驻 波方 程
负向: 正向:
y1
A cos(t
2
x
1)
y2
A cos(t
AB
o
10.7--驻波

10.7 驻波教学目的1.知道驻波现象及什么是波节、波腹,驻波是一种特殊的干涉现象.2.理解驻波的形成过程,理解驻波与行波的区别,理解空气柱共鸣的条件.引入新课一列波在向前传播的途中遇到障碍物或者两种介质的分界面时,会发生反射,如果反射波和原来向前传播的波相互叠加,会发生什么现象呢?一、驻波1、驻波的演示:如课本图10-31所示,把弦线的一端A固定在电磁打点计时器的振针上,另一端跨过定滑轮拴一个砝码盘,盘上放砝码,将弦线拉平.在靠近定滑轮的B处,用一个尖劈把弦线支起来.接通电磁打点计时器的电源,振针振动时,有一列波向定滑轮的一侧传播,并在B处发生反射.改变尖劈的位置,来调节AB的长度,当尖劈调到某适当位置时,可以看到,弦线会分段振动起来.2、几个概念:①波节——弦线上有些点始终是静止不动的,这些点叫做波节.波腹——在波节和波节之间的那段弦线上,各质点以相同的频率、相同的步调振动,但振幅不同,振幅最大的那些点叫做波腹.在相邻的两段弦线上,质点的振动方向是相反的.相邻的两个波节(或波腹)之间的距离等于半个波长,即等于λ/2.②驻波——波形虽然随时间而改变,但是不向任何方向移动,这种现象叫做驻波.波形不传播,是媒质质元的一种集体振动形态。
"驻"字的第一层含义。
行波——驻波跟前面讲过的波形向前传播的那种波显然是不同的,相对于驻波来说波形向前传播的那种波叫行波.③驻波与行波的区别A物理意义不同:驻波是两列波的特殊干涉现象,行波是一列波在介质中的传播.B质点振动不同:相邻波节间质点运动方向一致.波节两侧质点振动方向总相反.C波形不同:波形向前传播的是行波,波形不向任何方向传播的是驻波.3、驻波的形成两列振幅相同的相干波在同一直线上沿相反方向传播时形成的叠加波。
①两列沿相反方向传播的振幅相同、频率相同的波叠加,形成驻波.②振幅相同、频率相同波的叠加.三、驻波的特点课本10-33中用虚线表示两列沿相反方向传播的振幅相同、频率相同波的叠加,用实线表示这两列波叠加后形成的合成波.图中画出了每隔T/8周期波形的变化情况.由图可以看出,合成波在波节的位置(图中的“·”表示),位移始终为零.在两波节之间,各质点以相同的步调在振动,两波节之间的中点振幅最大,就是波腹(图中用“+”表示).驻波不是振动状态的传播,也没有能量的传播。
教学PPT:2-5 驻波[16页]
•週期、波長及 振幅均相同的兩 個正弦波(紅色 及綠色)相向行 進,疊加後產生 的藍色駐波。
駐波
•當兩個波長、週期及振幅均相同的正弦波 ,在同一弦線反向行進疊加後,弦線上會 產生波節和波腹。
•在疊加區域,節點的位置都固定不動,看 起來合成波形並未前進或後退,彷彿穩定 地駐留在該處,所以稱之為駐波 (standing wave)。
輪
BFµ,,懸其掛中質F量及為µ
4.0kg 的重物,AB 間恰好是 5.0m。 分別為繩之張力及線密度,則當時
起振器的振動頻率為若干?(g=9.8 m/s2)
範例2-6
概念Байду номын сангаас
1. 弦兩端固定形成駐波時,駐波波長與弦長關係為 n‧λ2 =L
2. 波速、頻率及波長的關係。 策略 1. 由題意知弦線長度為波長的 2 倍,如下圖所示。
•駐波波長λ與弦長L 之關係為
即 λ=2nL(=2L、L、23 L、12 L、……),而駐波之最長波 長為 λ=2L。
•兩端固定的弦線產生駐波,經多重曝光所得的照 片。(由於拍攝角度的關係,有些圖的波節間距 看似不同)
•兩端固定形成駐波的三種情形,其中最上方部分
的波長最長,且λ=2L。
一端固定一端為自由端的駐波
高中選修物理(上)
2-5 駐 波
連續週期波在弦線中傳播
•利用疊加原理,可以了解兩個行進波在同 一條弦線上交會時所形成的合成波形。
•如果是兩個連續的週期波在同一條弦線中 傳播,可以發現有些點在任何時刻都不會 發生位移,而有一些點的振幅最大,且位 於相鄰兩個不振動之 N 點的中點。
•這些不振動的點(N 點)稱為波節或節點 ,振幅最大的點(A 點)稱為波腹或腹點 。
高二物理竞赛课件:驻波
1. 驻波的产生 振幅、频率、波速都相同的两列相干波,在同一
直线上沿相反方向传播时叠加而形成的一种特殊的干 涉现象.
驻波的特点:媒质中各质点都作稳定的振动, 波形并没有传播。
y 2A
t=0
0
x
驻
t = T/ 8
0
x
波 t = T/4
0
x
的
t = 3T/8
0
形
成
t = T/2
0
x x
2A
振动范围
用旋转矢量法,可得同样结果。
y
y1
y2
Acos( t
2
x)
Acos( t
2
x)
由图可见
A合
2Acos 2
x
合 0
故得驻波方程:
2 x y
A
A2 • A1
y
y1
y2
2Acos 2
x cost
正向波与反向波的位相差 2 2 x 4 x
讨论: 驻波方程 y 2Acos 2 x cos t
●振幅 2 A cos 2 x 随 x 而异,与时间无关。
(a)
波2腹x :振k幅的最各大点的;点振。幅对值应最于大| c为o2sA2.
波腹的位置:
x
k
,
k 0,1, 2,
x | 1 即
波腹其实就是 干涉相长点.
3,...
2
(b) 波节:振幅为零的点。
对应于 | cos 2 x | 0 即
波节 波腹
4 x 3 4, cos 2 x 0,
y 2A cos 2 x cos(t )
• 相邻波节之间的质点振动位相相同, 速度方向相同,
西北师大附中高一物理奥赛教案动量和能量
专题:动量与牛顿运动定律、功能关系综合应用专题 例题1:下面是一个物理演示实验,它显示:图中自由下落的物体A 和B 经反弹后,B 能上升到比初始位置高得多的地方。
A 是某种材料做成的实心球,质量m 1=0.28kg ,在其顶部的凹坑中插着质量m 2=0.10kg 的木棍B 。
B 只是松松地插在凹坑中,其下端与坑底之间有小空隙,将此装置从A 下端离地板的高度H=1.25m 处由静止释放。
实验中,A 触地后在极短的时间内反弹,且其速度大小不变;接着木棍B 脱离A 开始上升,而球A 恰好停留在地板上。
求木棍B 上升的高度,重力加速度g=10m/s 2。
解析:根据题意,A 碰地板后,反弹速度的大小等于它下落到地面时速度的大小: v 1 =gH 2A 刚反弹后,速度向上,立刻与下落的B 碰撞,碰前B 的速度: v 2 =gH 2 由题意,碰后A 速度为0,以v '2表示B 上升的速度,根据动量守恒: 112222m v m v m v '-=令h 表示B 上升的高度,有: h = g v 22'2 由以上各式并代入数据得 h = 4.05m 。
例题2:如图所示,水平轨道AB 与竖直面内的半径为R=2.5m 的光滑半圆轨道BC 相切于B 点,C 点为半圆轨道的最高点。
可以看成质点的质量分别为m 1、m 2的两滑块静止在水平轨道上的A 点,已知m 2=2m 1,两滑块与水平轨道间的动摩擦因数μ=0.2,A 、B 间的距离S=11m ,两滑块靠少许塑胶炸药粘在一起。
若给两滑块水平向左的初速度v 0,滑块恰好能够通过半圆轨道的最高点C ,且当滑块通过C 点时,塑胶炸药突然爆炸使两滑块分开,爆炸后滑块m 2沿直径CB 做自由落体运动。
(g=10m/s 2)。
求:1(1)两滑块获得的初速度v 0的大小。
(2)滑块m 1在水平面上的落点距B 点的距离。
解析:⑴在AB 段,对m 1、m 2整体,据动能定理,有-202122121)(21)(21)(v m m v m m gs m m B +-+=+μ 在BC 段,m 1、m 2整体机械能守恒,即R g m m v m m v m m C B 2)()(21)(2121221221⋅+++=+ 其中,gR v C =解方程组,得90=v (m/s )⑵在C 处爆炸时,m 1、m 2系统动量守恒,即1121)(v m v m m C =+,得1531==C v v (m/s )此后,m 1平抛,有t v x 1= 及 2212gt R =解方程组,得15=x (m ) 例题3:如图所示,一对杂技演员(都视为质点)乘秋千(秋千绳处于水平位置)从A 点由静止出发绕O 点下摆,当摆到最低点B 时,女演员在极短时间内将男演员沿水平方向推出,然后自已刚好能回到高处A 。
高一物理北师大版《波动与声学》教案
高一物理北师大版《波动与声学》教案第一部分:引言在高中物理教学中,波动与声学是一门重要的课程内容。
它涉及到波的性质、传播、干涉等方面的知识,对学生的学习有着深远的影响。
为了提高教学质量,本教案以北师大版《波动与声学》为参考教材,结合学生的学习水平和特点,全面而系统地设计了教学内容和教学方法,旨在帮助学生更好地理解和掌握波动与声学相关知识。
第二部分:教学目标1. 理解波的概念,掌握波的传播规律。
2. 掌握波的分类和特性,能够准确区分各种波。
3. 理解波的干涉和衍射现象,能够解释其产生的原理。
4. 学会利用波动和声学的知识解决实际问题。
第三部分:教学内容1. 第一章:波的基本概念和传播规律a. 波的定义和分类b. 波的传播方式和传播规律c. 波长、频率和波速的关系2. 第二章:波的特性a. 纵波和横波的特点和传播规律b. 波的波动方向和振动方向的关系c. 波的能量传递和波的强度3. 第三章:波的干涉和衍射a. 干涉现象的产生原理和条件b. 干涉的类型和干涉条纹的特点c. 衍射现象的产生原理和条件d. 衍射的特点和衍射图样的分析4. 第四章:声波的产生和传播a. 声波的产生和传播方式b. 声波的传播速度和传播介质c. 声波的特性和声强的计算第四部分:教学方法1. 情景模拟:通过实例或故事情景模拟,引发学生兴趣,激发学习的主动性。
2. 实验探究:设计与波动与声学相关的实验,让学生亲自动手操作,体验到波的传播和干涉衍射现象,提高他们的实践能力和科学思维能力。
3. 多媒体辅助:利用多媒体教学手段,呈现生动的图像和动画,帮助学生更直观地理解和记忆波动与声学知识。
4. 小组合作:组织学生进行小组合作学习,通过合作探讨、讨论和交流,共同解决问题,培养他们的合作与沟通能力。
第五部分:教学评价1. 课堂反馈:通过课堂讨论、回答问题和小组展示等方式,检查学生对教学内容的理解情况。
2. 实验报告:要求学生进行实验,并撰写实验报告,评估他们的实验设计和实验结果分析的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材分析:
驻波是一种常见的现象,弦振动产生的驻波和空气柱振动产生的驻波,在国外教
材中多加以介绍,我国高中教材多年没有这一内容,但为了使学生对波的认识更全面,
新大纲列入了这一内容,但本节教材属于选学内容,所以教学时让学生对这一现象有
个最初步的了解即可,不宜作过高的要求。
本节教学时,要做好课本的演示实验。
实验一:弦上的驻波演示,利用已有的打点计时器、长木板、定滑轮和砝码即可
完成。准备演示实验时要细心调整好弦线的长度,以取得最佳效果。
实验二:演示空气柱内的驻波时,所用粗玻璃管长度可根据所用音叉的频率(波长)
算出,使它能至少有1.5个波长为好。
课题 第六节:驻波
教学目标 知识目标:
1、知道驻波现象,知道波腹和波节; 2、知道驻波是怎样产生的;
3、知道驻波是一种特殊的干涉现象。
能力目标:
通过空气柱内驻波的教学,使学生学会测声波波长和波速的方法。
德育目标:
课型 新授课
课时 1课时
重点 驻波现象、波腹和波节的教学。
难点 对驻波是怎样产生的教学。
教学方法 讲练法、实验法。
教具 打点计时器、带有定滑轮的木板、砝码、弦线、音叉、玻璃管、水。
教 学 过 程
讲解驻波如何产生时,只要让学生知道:它是由两列在同一直线上向相反方向传
播的行波叠加而成的,但叠加后介质的运动状态却不传播,故名“驻波”就可以了。
引入课题
一个乐队中有弦乐器和管乐器,它们为什么会发声呢?学了本节课的知识你就明
白了。
板书: 第六节 驻波
新课教学
一、驻波
演示实验:P59页实验,
把弦线的一端A固定在电磁打点计时器的振针上,另一端跨过定滑轮拴一个砝码
盘,盘上放砝码,将弦线拉平。在靠近定滑轮的B处,用一个尖劈把弦线支起来。接
通打点计时器的电源,振针振动时,有一列波向定滑轮的一侧传播,并在B处发生反
射。改变尖劈的位置,来调节AB的长度,把尖劈调到某适当位置时,可以看到:弦
线会分段振动起来。
结合实验现象和模拟图教师总结,在弦线上形成的波:
1、波节:有一些点始终静止不动,这些点称为波节。
2、波腹:在波节和波节之间,各质点以相同的频率、相同的步调振动,但振幅不
同,两波节之间的中点振幅最大,称为波腹。
二、驻波的产生过程
1、分析弦上驻波的产生过程:在弦上A处激发的波沿弦线传到B上被反射,反
射回来的波与入射波叠加后,波形虽然随时间改变,但是不向任何方向传播,产生了
驻波。
2、总结驻波的产生条件
入射波和反射波——频率相同;入射波和反射波——方向相反;入射波和反射波
——振幅相同。
所以产生驻波的条件是:两列沿相反方向传播的振幅相同,频率相同的波叠加时,
形成驻波。
3、模拟驻波的产生过程(P60图10——26)
用两种不同颜色的线表示两列沿相反方向传播的振幅相同,频率相同的点,用黑
实线表示这两列波叠加后形成的合成波。
当慢慢向上提起玻璃管的过程中,当管内空气柱达到一定长度时,可以听到空气
柱发出较强的声音。
对现象的解释:之所以听到空气柱发出较强的声音,是因为从音叉发出并进入玻
璃管的声波和经水面反射回来的反射波相互叠加,在空气柱内产生驻波,且玻璃管开
口处为波腹,水面处为波节,所以在管口处发出较强的声音。
学生讨论:当空气柱的长度满足什么条件时,分别发出第一声、第二声、……较
强的声音?
叙述讨论结果:
在这个实验中,如果测出空气柱的长度L,就可以测出声波的波长λ。如果已知
音叉的频率f,还可以测出声波的速度v=fλ。
总结:空气柱内的驻波可看作空气柱的一种振动模式,即音叉和空气柱发生了
共鸣,所以,只要设法激起空气柱的振动(如吹奏),就能使空气柱产生驻波,并在周
围空气中发出声波,这就是管乐器发声的原理。
巩固练习
1、叙述行波与驻波的区别。
2、为什么说驻波是一种特殊的干涉现象?
3、设计一个测定声波波长的实验。
参考答案:
1、驻波和行波的区别:
(1)物理意义不同:驻波是两列波的特殊干涉现象;行波是一列波在介质中的传
播。
(2)质点的振动情况不同:在行波中各个质点做振幅相同的简谐振动;在驻波中
各个质点做振幅不同的简谐振动,处于波腹位置的质点振幅最大,处于波节位置的质
点振幅等于零,其他一些质点的振幅也不相同。
(3)波形不同:行波波形经过一段时间,波形向前平移;驻波的波形并不随时间
发生平移,只是各自的振动位移发生变化而已。
2、驻波是一种特殊的干涉现象。
(1)波源特殊:驻波是由频率相同,振幅相同,而传播方向相反的两列波叠加而
成的。
(2)波形特殊:驻波的波形并不随时间发生平移,只是各自的振动位移发生变化
而已,是一个停驻不前的波。
3、实验装置如图所示:把正在振动的音叉放在玻璃管口的上方,同时使左面的储
水容器慢慢下降,待听到很响的共鸣声音时,若玻璃管中的水面恰好降到A处,说
明这时管内空气柱的固有频率和音叉的频率相同,使空气柱产生了共振现象,这是第
一次共鸣,此时从音叉发出并进入玻璃管中的声波和经水面反射回来的反射波叠加形
成驻。
课堂小结
1、两列频率相同、振幅相同、传播方向相反的波叠加而成的波叫驻波;
2、振幅最大的哪些点叫波腹,始终静止不动的那些点叫波节;
3、驻波是由波节分成的分段振动,在两个波节之间的同一个分段的所有质点都
以相同频率、相同的步调振动,但振幅不同,在相邻的两个分段上,质点的振动方向
相反。
布置作业
教学后记
