家庭作业:比和比例
小升初数学常考十大内容比和比例

小升初数学常考十大内容-比和比例小升初数学常考十大内容比和比例1 、比和比例的意义比的意义是:两个数相除又叫做两个数的比,比例的意义是:表示两个比相等的式子叫做比例。
比例是比的结果,比是比例的基础。
他们都是衡量数量关系的一种工具。
比和比例,是小学数学中的一个重要内容,也是学习更多数学知识的重要基础.有了“比”和“比例”这两个概念和表达方式,对于处理倍数、分数等问题,要方便灵活得多. 比和比例的相关知识在生活中用非常广泛,我们在以后还要进行更广泛更深入的学习。
因此,要为以后的学习打下坚实的基础。
2、比和比例的基本类型及解法(一)比和比例的分配最基本的比例问题是求比或比值,从已知一些比或者其他数量关系,求出新的比.例1、甲、乙、丙三人同去商场购物,甲花钱数的乙花钱数的,乙花钱数的等于丙花钱数的,结果丙比甲多花93元,问他们三人共花了多少钱?解、根据比例与乘法的关系甲数×=乙数×即:甲数:乙数=:=2:3乙数×=丙数×即:乙数:丙数=:=16:21连比后是甲∶乙∶丙=(2×16)∶(3×16)∶(3×21 )=32∶48∶63.三人共花了93÷(63-32)×(32+48+63)=429(元)答:甲、乙、丙三人共花了429元.下面我们转向求比的另一问题,即“比的分配”问题,当一个数量被分成若干个数量,如果知道这些数量之比,我们就能求出这些数量.例2一个分数,分子与分母之和是100.如果分子加23,分母加32,新的分数约分后是,原来的分数是多少?解:新的分数,分子与分母之和是(10+23+32),而分子与分母之比2∶3.因此分子=(100+23+32)×=62分母=(100+23+32)×=93原来分数是=答:原来分数是例3加工一个零件,甲需3分钟,乙需3.5分钟,丙需4分钟,现有1825个零件要加工,为尽早完成任务,甲、乙、丙应各加工多少个?所需时间是多少?解:三人同时加工,并且同一时间完成任务,所用时间最少,要同时完成,应根据工作效率之比,按比例分配工作量.三人工作效率之比是::=28:24:21他们分别需要完成的工作量是甲完成1825×=700(个)乙完成1825×=600(个)丙完成1825×=525(个)所需时间是700×3=2100分钟)=35小时 .答:甲、乙、丙分别完成700个,600个,525个零件,需要35小时.(二)比的变化已知两个数量的比,当这两个数量发生增减变化后,当然比也发生变化.通过变化的描述,如何求出原来的两个数量呢?.例4、有一些球,其中红球占,当再放入8个红球后,红球占总球数的,问现在共有多少球?解:其他球的数量没有改变.增加8个红球后,红球与其他球数量之比是5∶(14-5)=5∶9.在没有球增加时,红球与其他球数量之比是1∶(3-1)=1∶2=4.5∶9.因此8个红球是5-4.5=0.5(份).现在总球数是8÷0.5×(5+9)=224(个)答:现在共有球224个.本题的特点是两个数量中,有一个数量没有变.把1∶2写成4.5∶9,就是充分利用这一特点.本题也可以列出如下方程求解:(x+8)∶2x=5∶9.例5 张家与李家的收入钱数之比是8∶5,开支的钱数之比是8∶3,结果张家结余240元,李家结余270元.问每家各收入多少元?解一:我们采用“假设”方法求解.如果他们开支的钱数之比也是8∶5,那么结余的钱数之比也应是8∶5.张家结余240元,李家应结余x元.有240∶x=8∶5,x=150(元).实际上李家结余270元,比150元多120元.这就是8∶5中5份与8∶3中3份的差,每份是120÷(5-3)=60.(元).因此可求出张家:开支60×8=480(元),收入480+240=720(元)李家:开支60×3=180(元),收入180+270=450(元)答:张家收入720元,李家收入450元.解二:设张家收入是8份,李家收入是5份.张家开支的3倍与李家开支的8倍的钱一样多.我们画出一个示意图:张家开支的3倍是(8份-240)×3.李家开支的8倍是(5份-270)×8.从图上可以看出5×8-8×3=16份,相当于270×8-240×3=1440(元).因此每份是1440÷16=90(元).张家收入是90×8=720(元),李家收入是90×5=450(元).本题也可以列出比例式:(8x-240)∶(5x-270)=8∶3.例6 小明和小强原有的图画纸之比是4∶3,小明又买来15张.小强用掉了8张,现有的图画纸之比是5∶2.问原来两人各有多少张图画纸?解一:充分利用已知数据的特殊性.4+3=7,5+2=7,15-8=7.原来总数分成7份,变化后总数仍分成7份,总数多了7张,因此,新的1份=原来1份+1原来4份,新的5份,5-4=1,因此新的1份有15-1×4=11(张).小明原有图画纸11×5-15=40(张),小强原有图画纸11×2+8=30(张).答:原来小明有40张,小强有30张图画纸.解二:我们也可采用“假设”方法.先要将两个比中的前项化成同一个数(实际上就是通分)4∶3=20∶155∶2=20∶8.假设小强也买来15×=(张),那么变化后的比仍是20:15 但现在是20∶8,因此这个比的每一份是()÷(15-8)=小明现有20×=55(张),原有55-15=40(张)小强现有8×=22(张),原有22+8=30(张)“假设”这一思路是很有用的,希望大家能很好掌握,灵活运用.从课外的角度,我们更应启发小同学善于思考,去找灵巧的解法,这就要充分利用数据的特殊性.因此我们总是先讲述灵巧的解法,利于心算,促进思维.(三)比例的其他问题比例关系可以用比表示,也可以用分数表示,例如,甲比乙的多7,这里必须用分数来说,而不能用比.实际上它还是隐含着比例关系:(甲-7)∶乙= 2∶3.因此,有些分数问题,就是比例问题. .例7、有两堆棋子, A堆有黑子 350个和白子500个, B堆有黑子400个和白子100个,为了使A堆中黑子占A堆的,B堆中黑子占,要从B堆中拿到 A堆黑子、白子各多少个?解:要B堆中黑子占,即黑子与白子之比是3:1,先从B堆中拿出黑子100个,使余下黑子与白子之比是(40-100)∶100=3∶1.再要从 B堆拿出黑子与白子到A堆,拿出的黑子与白子数目也要保持3∶1的比.现在 A堆已有黑子 350+ 100= 450个),与已有白子500个,相差50个黑子,占就是两种棋子一样多,从B堆再拿出黑子与白子,要相差50个,又要符合3∶1这个比,要拿出白子数是50÷(3-1)=25(个).再要拿出黑子数是 25×3= 75(个).答:从B堆拿出黑子 175个,白子25个.例8 张、王、李三人共有108元,张用了自己钱数的,王用了自己钱数的,李用了自己钱数的,各买了一支相同的钢笔,问张和李剩下的钱共有多少元?解:设钢笔的价格是1.张有的钱数是1÷=王有的钱数是1÷=李有的钱数是1÷=这样就可以求出,钢笔价格是108÷(++)=108÷=24(元)张剩下的钱数是24×(-1)=16(元)李剩下的钱数24×(-1)=12(元)16+12=28(元)答:张、李两人剩下的钱共28元.。
比和比例问题经典例题

比和比例问题经典例题比和比例问题知识要点及解题技巧内容:比、按比例分配、正比例、反比例。
1、两个数相除又叫两个数的比。
比的前项和后项同时乘以{或除以)相同的数(零除外),比值不变,即比的基本性质。
2、表示两个比相等的式子叫比例。
在比例中,两个外项的积等于两个内项的积。
y3、正比例数量关系:=k(一定),则x与y成正比例。
x4、反比例数量关系:x×y=k(一定),则x与y成反比例。
解题技巧:1、解答按比例分配应用题。
关键要确定分配总量和分配的比。
对于隐含的分配总量和分配比要仔细分析,正确确定。
2、在解一般的比例应用题时,第一步要找出与问题有关的两种相关数量。
并且确定它们之间的关系。
第二步要找出两种量的对应关系,并设未知数为x,第三步尹根据正、反比例的意义列出比例式。
第四步解比例,求出x的值。
最后检验,写出答案。
3、比例应用题常常与比的知识、分数应用题、工程问题及几何图形交织在一起。
数量关系比较复杂。
解题时应先理清关系再正确地列出比例式解答。
典型例题24例1:甲数是乙数的,乙数是丙数的的,甲乙丙三个数的比是:35( ):( ):( )。
3例2:两数差相当于被减数的,减数与差的比是( ):( )。
4例3:一个圆柱和一个圆锥,体积比是2:3,高的比是5:6,它们的地面积的比是多少,例4:一块合金,铜与锌的比是2:3,现在加入同120克,锌40克,可得合金560克,求新合金中铜与锌的比。
例5:甲乙两包糖的重量比是4:1,如从甲包取出10克放入乙包后,甲乙两包糖的重量比变为7:5,那么两包糖的重量的总和是多少, 例6:有三批货物共值152元,这三批货物的重量比为2:4:3,单价比为6:5:2,第三批货物值多万元, 例7:甲乙两班原有人数比为5:4,若从甲班调出9人到乙班,那么乙班与甲班人数之比为5:4,两班原来各有多少人,例8:某俱乐部男、女会员人数之比是3:2,分为甲乙丙三组,已知甲、乙、丙三组的人数比是10:8:7,甲组中男女会员的人数比是3:1,乙组中男女会员的人数比是5:3,求丙组中男女会员人数之比。
比和比例总结讲解+例题解析

比和比例总结讲解+例题解析比和比例是数学中常见的概念,在实际生活中也有很多应用。
本文将对比和比例的概念进行总结讲解,并提供一些例题解析。
一、比的概念比是两个数或物品在数量、大小、质量等方面的关系,用冒号(:)表示。
如2:3表示第一个数是第二个数的2/3。
二、比例的概念比例是两个或多个比之间的关系,用等号(=)表示。
如2:3=4:6表示前者的比是后者的比的相等关系。
三、比例的性质1.比例的交换律:a:b=c:d等于c:d=a:b。
2.比例的比例律:a:b=c:d, b:e=f:g,则a:e=c:g。
3.比例的倍数律:a:b=c:d,则ka:kb=kc:kd。
4.比例的倒数律:a:b=c:d,则b:a=d:c。
四、比例的应用1.求未知量在已知两个量的比例和其中一个量的值的情况下,可以求出另一个量的值。
如已知2:3=4:x,可以用比例的性质,将比例转化为等式,解出未知数x=6。
2.比例的分配在已知两个量的比例和其中一个量的值的情况下,可以求出另一个量在这个比例下的值。
如已知2:3=4:x,已知x=6,则2:3=4:6,可以求出x在这个比例下的值为9。
五、例题解析例题1:已知a:b=3:4,b:c=5:6,求a:b:c的大小关系。
解:由已知可得a:b=3:4,b:c=5:6,则a:b:c=3:4:6,即a:b:c=1:4/3:2。
例题2:已知a:b=4:5,c:b=6:7,求a:c的大小关系。
解:将两个比例的两个已知量对应相乘,得到a:c=24:35,即a:c=4:5/7。
总结:比和比例是数学中的基础概念,掌握了比例的性质和应用方法,可以在实际生活中解决一些问题。
五年级下册比与比例

五年级下册比与比例在五年级下册的数学学习中,“比与比例”可是一个重要的知识点。
它就像一把神奇的钥匙,能帮助我们解决很多生活中的数学问题。
首先,咱们来聊聊“比”。
比是什么呢?简单来说,比就是两个数相除的关系。
比如说,咱们班男生有 20 人,女生有 15 人,那男生人数和女生人数的比就是 20∶15。
这里的“∶”就是比号,读的时候要读作“比”。
比有前项和后项,就像除法里的被除数和除数一样。
在 20∶15 这个比中,20 是前项,15 是后项。
而且,比的前项除以后项所得的商,我们叫做比值。
还是刚才那个例子,20∶15 的比值就是20÷15 =4/3 。
比有很多有趣的性质。
比如,比的前项和后项同时乘或除以一个相同的数(0 除外),比值不变。
这就好像我们把一个分数的分子和分母同时扩大或缩小相同的倍数,分数的大小不变一样。
接着,咱们再来说说比例。
比例啊,就是表示两个比相等的式子。
比如 2∶3 = 4∶6,这就是一个比例。
在比例中,组成比例的四个数,叫做比例的项。
两端的两项叫做比例的外项,中间的两项叫做比例的内项。
比例也有它的性质,那就是在一个比例中,两个外项的积等于两个内项的积。
比如说在 2∶3 = 4∶6 这个比例中,2×6 = 12,3×4 = 12,是不是很神奇?学习比和比例能帮助我们解决很多实际问题呢!比如说,我们在调配饮料的时候,如果知道了某种饮料中各种成分的比例,就能算出需要多少材料来调配出一定量的饮料。
再比如,在地图上,我们常常会看到比例尺。
比例尺就是图上距离与实际距离的比。
通过比例尺,我们可以算出地图上的距离对应的实际距离是多少,也能算出实际距离在地图上应该画多长。
还有在按比例分配问题中,比如学校要把一批图书按照班级人数的比例分给各个班级。
如果知道了总图书数量和各班的人数,我们就能算出每个班级能分到多少本书。
总之,“比与比例”虽然看起来有点复杂,但只要我们认真学习,多做练习,就能熟练掌握它,并用它来解决更多的数学问题,让我们的数学学习变得更加有趣和有用!在学习比与比例的过程中,同学们可能会遇到一些容易混淆的地方。
比和比例——学生版
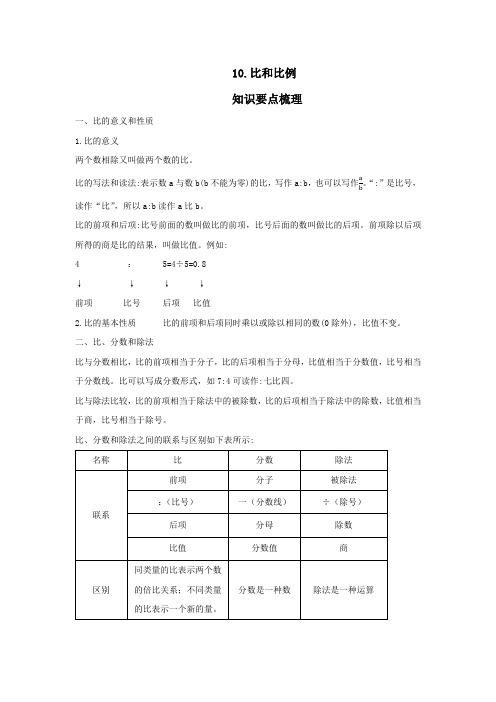
10.比和比例 知识要点梳理 一、比的意义和性质 1.比的意义 两个数相除又叫做两个数的比。 比的写法和读法:表示数a与数b(b不能为零)的比,写作a:b,也可以写作ab。“:”是比号,读作“比”,所以a:b读作a比b。 比的前项和后项:比号前面的数叫做比的前项,比号后面的数叫做比的后项。前项除以后项所得的商是比的结果,叫做比值。例如: 4 : 5=4÷5=0.8 ↓ ↓ ↓ ↓ 前项 比号 后项 比值 2.比的基本性质 比的前项和后项同时乘以或除以相同的数(0除外),比值不变。 二、比、分数和除法 比与分数相比,比的前项相当于分子,比的后项相当于分母,比值相当于分数值,比号相当于分数线。比可以写成分数形式,如7:4可读作:七比四。 比与除法比较,比的前项相当于除法中的被除数,比的后项相当于除法中的除数,比值相当于商,比号相当于除号。 比、分数和除法之间的联系与区别如下表所示: 名称 比 分数 除法
联系 前项 分子 被除法 :(比号) 一(分数线) ÷(除号) 后项 分母 除数 比值 分数值 商
区别 同类量的比表示两个数的倍比关系;不同类量的比表示一个新的量。 分数是一种数 除法是一种运算 三、求比值与化简比 1.求比值 前项除以后项所得的商是比的结果,叫比值。 同类量的比,其比值没有单位名称;不同类量的比,其比值有单位名称。例如: 100千米:5时=20千米/时 2.化简比 比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。 把两个数的比化成最简整数比的,称为化简比或比的化简。 四、比例的意义和性质 1.比例的意义 表示两个比相等的式子叫做比例。组成比便的四个数,叫做比例的项,两端的两项叫做比例配外项,中间的两项叫做比例的内项。例如:
2.比例的基本性质 在比例单,两个外项的积等于两个内项的积,这叫做比例的基本性质。 例如:15:60=12:48可得:60×12=15×48 如果把比例写成分数形式,等号两边的分子和分母分别交叉相乘,所得的积相等。 五、比和比例的区别 名称 比 比例 意义 两个数的比表示两个数相除 表示两个比相等的式子
小升初-比和比例

比和比例知识集结知识精讲比和比例知识讲解一、比的读法、写法及各部分名称1.读法:几比几,如15:10读作15比10.2.写法:把“比”字用比号代替.如15比10 记作15:10或1510.3.各部分名称:比的前项:在两个数的比中,比号前面的数叫做比的前项.比的后项:在两个数的比中,比号后面的数叫做比的后项.比值:比的前项除以后项所得的商.二、比与分数、除法的关系1.联系:比的前项相当于分数的分子、除法中的被除数;比号相当于分数的分数线、除法中的除号;比的后项相当于分数的分母、除法中的除数;比值相当于分数的分数值、除法中的商.2.区别:比是一种关系,分数是一种数,除法是一种运算.三、比的性质比的前项和后项同时乘或除以相同的数(0除外),比值不变.这叫做比的基本性质.四、求比值和化简比1.求两个数的比值,就是用比的前项除以比的后项,它的结果是一个数值,这个数值可以是整数,也可以是小数或分数.2.求比值和化简比的方法:把两个数的比化成最简单的整数比.(1)整数比化简方法:把比的前项和后项同时除以它们的最大公因数.(2)分数比化简方法:把比的前项和后项同时乘它们的分母的最小公倍数,变成整数比,再进行化简;利用求比值的方法也可化简分数比,但结果必须写成比的形式.(3)小数比化简方法:先把比的前项和后项的小数点同时向右移动相同位数,完成整数比,再进行化简.五、比例的意义及基本性质比例的意义:表示两个比相等的式子,叫做比例.组成比例的四个数,叫做比例的项.组成比例两端的两项叫做外项,中间的两项叫做内项.比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质.如:4:5=16:20⇔4×20=5×16六、正比例和反比例的意义1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:yx=k(一定).2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的乘积(一定),反比例的关系可以表示为:xy=k(一定).七、解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项.求比例中的未知项,叫做解比例.一般来说,求比例的未知项有以下两种情况:八、比的应用1.按比例分配问题的解题方法:(1)把比看作分得的份数,用先求出每一份的方法来解答.解题步骤:a.求出总份数;b.求出每一份是多少;c.求出各部分相应的具体数量.(2)转化成份数乘法来解答.解题步骤:a.先根据比求出总份数;b.再求出各部分量占总量的几分之几;c.求出各部分的数量.2.按比例分配问题常用解题方法的应用:(1)已知一个数量的各部分的比和其中某一部分的量,求另外几个部分量;(2)已知两个量或几个量的比和其中两个量的差,求总量.九、辨识成正比例的量和成反比例的量1.成正比例的量:(1)“变化方向”相同,一种量扩大或缩小,另一种量也扩大或缩小.(2)相对应的两个数的比值(商)一定.(3)关系式:yx=k(一定).2.成反比例的量:(1)“变化方向”相反,一种量扩大或缩小,另一种量反而缩小或扩大.(2)相对应的两个数的乘积一定.(3)关系式:xy=k(一定).3.判断方法:关键是看着两种相关量中相对应的两个数是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例.例题精讲比和比例例1.甲数是乙数的3倍,甲与甲、乙两数和的比是()A.1:3 B.3:1 C.3:4 D.4:1例2.如图,空白部分与阴影部分面积的比是()A.1:2 B.1:4 C.1:3 D.无法确定例3.下面两个比不能组成比例的是()A.10:12=35:42 B.20:10=60:20C.:12:8 D.0.6:0.2:例4.两个变量X和Y,当X∙Y=45时,X和Y是()A.成正比例量B.成反比例量C.不成比例量例5.某班女生人数与男生人数的比是4:5,最近又转进1名女生,这时女生人数是男生人数的,现在全班有学生()A.30人B.25人C.45人D.55人例6.下面4个关系式中,x和y成反比例关系的是()A.(x+1)y=6 B.x 3C.3x=5y(x、y均不为零)D.x-y=0例7.20:________÷40=____%=___折。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴氏精品堂学校成渝总校 ——唐老师
第 1 页 共 1 页
家庭作业:比和比例强化训练
一、填空题
1、0.75:32化成最简整数比是( )。
2、在10001的图纸上,一个正方形的面积为16平方厘米,它的实际面积是( )平方米。
3、一个比例式,两个外项的和是37,差是13,比值是65,这个比例式可以是( )。
4、星期天,小丽看一本书用了2小时15分,小红同样一本书用了2.15小时,小丽和小红看书用的时
间比是( )。
5、在一个比例式中。两个外项都质数,它们的积是22,一个内项是这个积的101,这个比例式可以是
( )。
6、两地相距80千米,画在比例尺是1:400000的地图上,应画( )厘米。
7、一杯糖水,糖与水的比是1:4,喝去21杯糖水后,又用水加满,这时糖与水的比是( )。
8、已知一个比例的两个外项分别是3和41,组成比例的两个比的比值是21,这个比例是( )。
9、甲、乙、丙三个数的平均数是15,甲、乙、丙三个数的比是2:3:4,甲数是( )。
10、一个比例的两个内项互为倒数,一个外项是81,另一个外项是( )。
11、圆柱的高一定,圆柱的底面积与体积( )比例。
12、东风小学六年级人数是五年级人数的98,五年级与六年级人数的比是( )。
13、学校购到一批书,按2:3:5借给四、五、六三个年级。四年级借到这批书的( )%。
14、一个机器零件长2米,在设计图上这个零件长4厘米,这幅设计图的比例尺是( )。
15、把(5平方米):(50平方分米)化成最简整数比是( ),它们的比值是( )。
16、甲数除以乙数的商是1.5,甲数与乙数的最简整数比是( )。
17、若图上距离的2厘米表示实际距离的80千米,则这幅图的比例尺是( )。
18、甲、乙两地之间的距离是120千米,在比例尺是30000001的地图上,这段距离应该画( )厘米。
19、在比例尺是2001的平面图上,量得教室的长是4.5厘米,教室的实际长是( )米。
20、在六年级达标课上,六(2)班的达标人数与未达标人数的比是24:1,这个班学生的达标率是( )。
21、请你写出一个比例,使它的两个外项互为倒数:( )。
22、把一个比化成最简整数比是3:2,这个比有可能是( )。
23、在一幅云南地图上,要把实际距离224千米用线段5.6厘米表示出来,请你计算这幅地图的比例尺
戴氏精品堂学校成渝总校 ——唐老师
第 2 页 共 2 页
是( )。
24、在一个比例式中,两个外项都是质数,它们的积是39,一个内项是这个积的20%,这个比例式可以
是( )。
25、甲、乙两地的实际距离是360千米,在一幅地图上量得它们之间的距离是7.2厘米,这幅地图的比
例尺是( )。
26、一个长方形操场,长110米,宽90米。把它画在比例尺是10001的图纸上,长画( )厘米,
宽画( )厘米。
27、写一个能与31:41组成比例的比( )。
28、=5,与成( )比例;y=8x,表示x和y成 比例;6=7,与成( )比例。
29、在一个比例里,两个外项互为倒数,一个内项是最小的质数,另一个内项是( )。
30、如果a×5=b×8,那么a:b=( )。
31、三个数的平均数是40,三个数的比是1:2:3,最大数是( )。
32、甲数的53等于乙数的41,甲乙两个数的最简整数比是( )。
33、在含盐10%的500克盐水中,再加入50克盐,这时盐与盐水的比是( )。
34、把132与它的倒数的比化成最简整数比是( ),比值是( )。
35、甲数的43等于乙数的52,(甲乙两数都不为0)甲数和乙数的比是( )。
36、甲、乙两地之间的距离是120千米,在比例尺是30000001的地图上,这段距离应该画( )厘米。
37、4分:31时的比值是( ),最简整数比是( )。
38、把103:0.75化成最简单的整数比是( ),比值是( )。
39、一个比例的两个内项互为倒数,一个外项是314,另一个外项是( )。
40、141:0.75化成最简单的整数比是( ),比值是( )。
42、如果ab与cd互为倒数,那么a、b、c、d这四个数写成比例是( )。
43、甲数与乙数的比是5:8,甲数比乙数少( )%,乙数比甲数多( )( )。
二、判断题
1、因为甲数:乙数=25:23,所以甲数=25,乙数=23。 ( )
2、车轮的直径一定,车轮转动的周数和所行路程成正比例。 ( )
戴氏精品堂学校成渝总校 ——唐老师
第 3 页 共 3 页
3、从学校到文化宫,甲用9分钟,乙用10分钟,甲和乙每分钟行的路程比是9:10。( )
4、山羊和绵羊头数的比是4:5,表示山羊比绵羊少41。 ( )
5、长方形的长和宽成反比例。 ( )
6、长方形的面积一定,长方形的长和宽成反比例。 ( )
7、长方体的体积一定,底面积和高成反比例。 ( )
三、选择题
1、一块长方形的周长是28米,它的长和宽的比是4:3,这块地的面积是( )平方米。
A、192 B、48 C、28
2、一个圆柱和一个圆锥体积相等,已知圆锥体和圆柱的高的比是9:1,圆柱体底面积和圆锥体底面积
的比是( )。
A、9:1 B、3:1 C、6:1
3、一幅地图的比例尺是1:100000。下面说法不正确的是( )。
A、图上1厘米的距离相当于地面实际距离的100000米
B、把实际距离缩小100000倍后,再画在图纸上。 C、图上距离相当于实际的1000001。
4、做一批零件,甲需要4小时,乙需要3小时,甲与乙的速度比是( )。
A、4:3 B、5:4 C、3:4
5、互为倒数的两个数( )。
A、成正比例 B、成反比例 C、不成比例
6、下列各组比能与51:61组成比例的是( )。
A、5:6 B、6:5 C、61:51
7、一个圆的直径与周长的比是( )。
A、1:2 B、1: C、2:
8、一批产品,合格产品与不合格产品的比是4:1,这批产品的不合格率是( )
A、25% B、20% C、10%
9、在同一个圆里,周长与直径( )。
A、成正比例 B、成反比例C、不成比例
10、一个三角形内角度数的比是7:2:1,这个三角形是( )。
A、钝角三角形 B、锐角三角形 C、直角三角形
11、一条长5米的线段画在比例尺是1:100的图中,要比画在比例尺只是1:1000的图中( )。
戴氏精品堂学校成渝总校 ——唐老师
第 4 页 共 4 页
A、长 B、短 C、一样长
12、表示与成正比例关系的式子是( )。
A、=6 B、=6 C、=+6
13、在一幅云南地图上用4厘米的线段表示实际距离160千米,这幅地图的比例尺是( )。
A、401 B、40000001 C、4000001
14、路程一定,速度和时间( )。
A、成正比例 B、成反比例 C、不成比例
15、的5倍与的3倍的比是1:2,那么与的比是( )。
A、3:10 B、10:3 C、3:5
16、在比例尺是1:1000000的地图上,图上距离为10厘米的两地,实际距离是( )千米。
A、100000 B、100 C、1000 D、10000
17、在含糖25%的糖水中,糖与水的比是( )。
A、1:4 B、3:1 C、1:3
18、两个圆的直径比是1:2,周长比是( )。
A、1:2 B、1:4 C、1:8
19、距离一定,时间和速度( )
A、不成比例 B、成正比例 C、成反比例
四、求未知数
752.125= 44125:=: 6.5:=3.25:4 :=:411018
1
6328.0:=: 951527:=: 25324=:
55.03:=:
156194:=: 12343:=: :=:4151103 156194:=:
