第三章_线性疲劳累积损伤理论 PPT
第3章疲劳强度1

kσ = 1 + q(α σ 1), kτ = 1 + q(ατ 1)
1)降低应力集中,提高疲劳强度的措施: )降低应力集中,提高疲劳强度的措施: 减缓尺寸突变、增大过渡圆角半径、增加卸载结构等 减缓尺寸突变、增大过渡圆角半径、增加卸载结构等. 2)对应力集中的敏感与零件的材料和硬度有关: )对应力集中的敏感与零件的材料和硬度有关: 钢的强度极限愈高,敏感系数q值愈大, 钢的强度极限愈高,敏感系数q值愈大,对应力集中愈敏感 3)若在同一截面上同时有几个应力集中源,采用其中最大 )若在同一截面上同时有几个应力集中源, 有效应力集中系数进行计算。 有效应力集中系数进行计算。
低周循环疲劳区: 低周循环疲劳区: N<103(104) 高周循环疲劳区: 高周循环疲劳区: N>=103(104)
0
σrN 有限寿命区 低周循环
σ
无限寿命区
高周循环
1
σr
1).10 (10 ) ≤ N < N 0
3 4
10(10
)
No
疲劳曲线
N
图 3.2
疲劳极限随N的增加而降低。 疲劳极限随N的增加而降低。
3.4.2 许用疲劳极限应力图 许用疲劳极限应力图(零件) 许用疲劳极限应力图(零件) 工作点C( 必须落在安全区内。 工作点 (σm,σa)必须落在安全区内。
注意:综合影响系数只对极限应力幅有影响; 注意:综合影响系数只对极限应力幅有影响; 寿命系数对极限平均应力和极限应力幅都有影响
σ σ
简化疲 劳极限 曲线
a a a
a
]
(3.11)
式中 ψ σ ,ψ τ 为等效系数
σ ae ,τ ae 当量对称循环变应力
Miner疲劳理论

Miner疲劳理论
Miner -Palmgren 理论
1)构造⼀个疲劳累积损伤理论, 不论它有效与否, 必须定量地回答三个问题:
a .⼀个载荷循环对材料或结构造成多⼤损伤;
b.多个载荷循环时损伤是如何累加的;
c .失效时临界损伤有多⼤。
对这三个问题的不同回答, 构成了不同的确定性疲劳累积损伤理论。
2) Miner 理论对三个问题的回答
a .⼀个循环造成的
损伤为
式中N 是对应于当前载荷⽔平的疲劳寿命。
损伤为
b.等幅载荷下n 个循环造成的
个循环造成的损伤为
c .临界疲劳损伤DCR 。
若是常幅循环载荷, 显
得到
然当循环载荷次数n 等于其疲劳寿命N 时, 发⽣疲劳破坏, 即n =N , 由式(3)
Miner 理论简评。
Miner 理论可以认为是线性损伤、线性累积循环⽐理论, 其成功之处在于⼤量的实验结果(特别是随机谱试验)显⽰临界疲劳损伤DCR的均值确实接近于1 , 在⼯程上因简便⽽得到⼴泛的应⽤, 其他确定性的⽅法则需要进⾏⼤量试验来拟合众多参数, 精度并不⽐Miner 理论更好。
Miner 理论的主要不⾜是:a.损伤与载荷状态⽆关;b .累积损伤与载荷次序⽆关;c .不能考虑载荷间的相互作⽤。
钢结构疲劳计算.ppt

(6-7)
23.03.2019
3
例 6-9 一焊接箱形钢梁,在跨中截面受到Fmin=10 kN和 Fmax =100 kN 的常幅交变荷载作用,跨中截面对其水平形心轴z
的惯性矩 Iz=68.5×10-6 m4。该梁由手工焊接而成,属4类构件,
若欲使构件在服役期限内,能承受2×106次交变荷载作用。试 校核其疲劳强度。
No Image
(2)
设想有常幅Dse作用Sni次,使构件产生疲劳破坏,有
No Image
(3)
23.03.2019
式中,Dse为等效应力幅。
8
把(2)式代入(1)式,
No Image
得
No Image
(4)
将(4)式代入(3)式,得
No Image
(6-9)
式中,分子中的ni 为应力水平为Dsi 时的实际循环次数,分母 中的Sni为预期使用寿命。疲劳强度条件为
No Image
(6-8)
9
23.03.2019
第六章完
23.03.2019
4
解:1. 计算跨中截面危险点(a点)的应力幅
No Image
No Image
2. 确定[Ds ],并校核疲劳强度
No Image
从表中查得 C =2.18×1012,b =3,
No Image
显然
23.03.2019
No Image
5
Ⅱ. 变幅疲劳(应力幅不是常量,如图)
若以最大应力幅按常幅疲劳 计算,过于保守。当应力谱已知 时,可用线性累积损伤法则,将 变幅疲劳折算成常幅疲劳。
Ds
Dsk Dsi Ds1 Nk Ni N1
疲劳载荷及分析理论 谱 寿命 设计 累积损伤

第3章疲劳载荷及分析理论 (1)3.1 疲劳载荷谱 (1)3.1.1 疲劳载荷谱及其编谱 (1)3.1.2 统计分析方法 (2)3.2 疲劳累积损伤理论 (3)3.2.1 概述 (3)3.2.2 线性累积损伤理论 (4)3.3起重机疲劳计算常用方法 (5)3.3.1 应力比法 (6)3.3.2 应力幅法 (6)3.4 疲劳寿命设计方法 (7)3.4.1无限寿命设计 (7)3.4.2 安全寿命设计 (8)3.4.3 损伤容限设计 (8)3.4.4 概率疲劳设计 (9)3.4 小结 (10)第3章疲劳载荷及分析理论疲劳载荷谱(fatigue load spectrum)是建立疲劳设计方法的基础。
根据研究对象的不同,施加在对象上的疲劳载荷也是不同的,所以在应用时要依据某种统计分析方法和理论进行分析。
3.1 疲劳载荷谱3.1.1 疲劳载荷谱及其编谱载荷分为静载荷和动载荷两大类。
动载荷又分为周期载荷、非周期载荷和冲击载荷。
周期载荷和非周期载荷可统称为疲劳载荷。
在很多情况下,作用在结构或机械上的载荷是随时间变化的,这种加载过程称为载荷—时间历程。
由于随机载荷的不确定性,这种谱无法直接使用,必须对其进行统计处理。
处理后的载荷—时间—历程称为载荷谱。
载荷谱是具有统计特性的图形,它能本质地反映零件的载荷变化情况[]。
为了估算结构的使用寿命和进行疲劳可靠性分析,以及为最后设计阶段所必需的全尺寸结构和零部件疲劳试验,都必须有反映真实工作状态的疲劳载荷谱。
实测的应力—时间历程包含了外加载荷和结构的动态响应的影响,它不仅受结构系统的影响,而且也受应力—时间历程的观测部位的影响。
将实测的载荷—时间历程处理成具有代表性的典型载荷谱的过程称为编谱。
编谱的重要一环,是用统计理论来处理所获得的实测子样[]。
3.1.2 统计分析方法对于随机载荷,统计分析方法主要有两类:计数法和功率谱法[]。
由于产生疲劳损伤的主要原因是循环次数和应力幅值,因此在编谱时首先必须遵循某一等效损伤原则,将随机的应力—时间历程简化为一系列不同幅值的全循环和半循环,这一简化的过程叫做计数法。
连续损伤力学 ppt课件

损伤-断裂全过程通常可分为两阶段:第1阶段是 损伤的起始、损伤场的形成与发展,直到断裂起始; 第2阶段是断裂发展过程直到固体(结构)完全破坏。 对固体的破坏而言,前一阶段称为断裂潜伏阶段,后 一阶段称为断裂发展阶段。下面主要讨论第1阶段的 损伤发生和损伤场的发展,直到断裂起始。
设应力是位置r和时间t的函数,即:
PPT课件 10
Kachanov方程(6)等价于下列用损伤度表示脆性 损伤演变过程:
A(
1
)n
(7)
(a)恒载荷情况 对于均匀拉伸杆受恒载荷,由于脆性材料的变形 很小,因则恒载荷意味着恒应力,设σ =σ0 。积分式 (6),利用初始条件:t=0时,ψ=1,有:
得到ψ-t关系:
tc (1 c )t f
n1
(11)
12
PPT课件
(b)连续变化载荷情况 设均匀拉伸杆受连续载荷,应力是时间的函数, 即σ =σ(t) 。Kachanov方程写为:
(t ) n A[ ]
(12)
利用式(9)的结果,设想脆断时间是应力的连 续函数,即:
t f t n 1 A
1 n 1
注意到,在y=h0处, σ =σmax ,有ψ =ψmin 。当 ψmin(h0)=0时,在y=h0处发生断裂。因此,由上式 可以导出断裂起始时间:
M nm t fi n 1 A n h0 I0
n 1
例2 等矩形截面梁受一般弯曲 设弯矩M=M(x),x是沿梁长度方向的坐标,有 20 PPT课件 应力场:
s
多级载荷下的断裂时间为:
t tk
f k 1
s
(2)非均匀损伤场 如果弹性固体受应力场是均匀的,如等截面的受 拉杆,其损伤从理论上说也是均匀的。加载过程中, 损伤场将均匀增强,直到发生瞬时破坏。
线性累计疲劳理论计算公式

线性累计疲劳理论计算公式疲劳是指在一定条件下,物体在受到交变应力作用下,经历了一段时间后,出现了疲劳破坏的现象。
疲劳破坏是由于物体在受到交变应力作用下,出现了微小裂纹,并且这些微小裂纹随着应力的作用不断扩展,最终导致了物体的破坏。
在工程实践中,疲劳破坏是一种非常常见的破坏形式,因此对于疲劳的研究和预测显得尤为重要。
线性累计疲劳理论是一种常用的疲劳寿命预测方法,它是基于线性累积损伤理论和极限疲劳强度的概念而建立的。
线性累计疲劳理论认为,当物体受到的应力是交变应力时,物体的疲劳寿命是由应力的幅值和循环次数共同决定的。
因此,线性累计疲劳理论可以用一个简单的公式来描述,即疲劳寿命N与应力幅值S和循环次数Nf之间的关系。
线性累计疲劳理论计算公式可以用如下的公式表示:N = k (S^m) Nf^(-a)。
其中,N表示疲劳寿命,k是一个常数,S表示应力幅值,m和a是实验确定的常数,Nf表示循环次数。
这个公式表明了疲劳寿命N和应力幅值S以及循环次数Nf之间的关系。
根据这个公式,我们可以通过实验测定应力幅值和循环次数,然后利用公式计算出疲劳寿命。
这样,我们就可以在不断的应力作用下,预测物体的疲劳寿命,从而及时进行维护和修理,避免疲劳破坏的发生。
在工程实践中,线性累计疲劳理论计算公式是非常有用的。
通过这个公式,我们可以对材料和结构的疲劳寿命进行预测,从而指导工程设计和使用。
例如,在飞机、汽车、桥梁等工程中,对于金属材料和焊接接头的疲劳寿命进行预测是非常重要的。
通过线性累计疲劳理论计算公式,我们可以对这些材料和结构的疲劳寿命进行预测,从而保证它们的安全可靠性。
除了对材料和结构的疲劳寿命进行预测外,线性累计疲劳理论计算公式还可以用于疲劳寿命的评估和比较。
通过对不同材料和结构的疲劳寿命进行计算和比较,我们可以选择最适合的材料和结构,从而提高工程的安全性和可靠性。
当然,线性累计疲劳理论计算公式也有一定的局限性。
首先,该公式是基于线性累积损伤理论和极限疲劳强度的假设而建立的,因此在某些情况下可能存在一定的误差。
机械设计(2.6.1)--规律性非稳定变应力下零件的强度计算
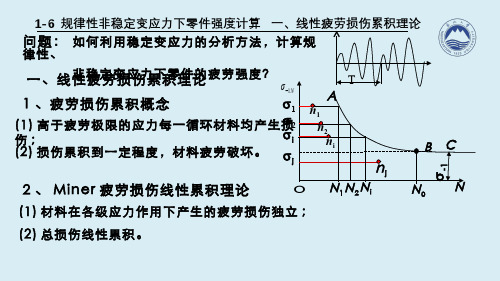
一、线性疲劳损伤累积理论1、疲劳损伤累积概念问题: 如何利用稳定变应力的分析方法,计算规律性、非稳定变应力下零件的疲劳强度?(1)高于疲劳极限的应力每一循环材料均产生损伤;1-6 规律性非稳定变应力下零件强度计算 一、线性疲劳损伤累积理论(1)材料在各级应力作用下产生的疲劳损伤独立;(2)总损伤线性累积。
2、Miner 疲劳损伤线性累积理论Nσ1-σj σiσ2σ1n1OABC σ-1N 2N 1N iN 0n 2n i n jNT(2)损伤累积到一定程度,材料疲劳破坏。
1-6 规律性非稳定变应力下零件强度计算 一、线性疲劳损伤累积理论%100,累积总损伤率达方程:材料破坏时Miner 1 i1=∑=N n ini 注:(1) σi <σ-1 的影响不计(2) 非对称循环变应力折算成当量对称循环变应力处理ma i σψσσσ+=Nσ1-σjσi σ2σ1n 1OA BCσ-1N 2N 1N iN 0n 2n in jN1N N mm -=σσ二、规律性非稳定变应力下材料疲劳强度计算(r=-1) 1、等效循环次数N v 与条件疲劳限σ-1N vσi 对应的 N i :mii N N )( 10σσ-=代入Miner 方程:(损伤极限状态)1101i 1==∑-==∑mni mii ini N n N n σσm mii ni N n 101 -=<∑σσmv m m i i n i m N N n 101111)( -=<=∑σσσσσ力最大值长的当量对称循环变应数值较大、作用时间较注:-1 σ损伤等效:未损伤状态:N σ1-σjσiσ2σ1n1OA BC σ-1N 2N 1N i N 0n 2n in jNN v 01N N mm -=σσ2、安全系数计算[]S S Nv≥=-11σσ循环变应力应力幅材料(试件)当量对称-1σ111m a σψσσσ+=111---==σσσmvN Nv N N K mii n i v n N )(11σσ=∑=对应N v 条件疲劳极限:等效循环次数N v :N σ1-σjσiσ2σ1n1OA BC σ-1N 2N 1N i N 0n2n in jNN v三、规律性非稳定应力下零件疲劳强度计算 []S K K S m a c N ad c Nv ≥+'==--1111)(1σψσσσσσσm vNN N K '='0寿命系数:miai adiK σψσσσσ+=等效应力幅:)( )( 111'不计等效循环次数:c adi m ad adi i ni v n N -=≤∑=σσσσ零件安全系数:非稳定问题的处理思路:对称化、稳定化。
疲劳分析.ppt

Stress Life Analysis
PAT 318 Course Notes
Introduction to MSC/FATIGUE
部件S-N曲线
Component S-N curves
• 在某些情形如结构或特征存在点焊等需要修 正材料S-N曲线(但通常是较困难的)
For some components or features, especially structural joints such as welds, there are so many things modifying the behaviour of the base material that there is little point in applying corrections to a material S-N curve
Notched Shaft
Log (fatigue life)
缺口试样
Some of Wohler’s data for rotating bending tests
Copyright © 1999 MacNeal Schwendler Corporation
Lec 16-7
Stress Life Analysis
设计寿命下的疲劳强度
determination of a fatigue strength at a specified life
通过改变材料或表面处理提高抗疲劳能力
demonstration of improved fatigue resistance from a material or surface treatment
• 在MSC/FATIGUE SN分析中有限元弹性计算结果可直接 利用(无塑性修正)
