圆专项练习4(配完整解析)
高考数学复习圆的方程专项练习(附解析)

高考数学复习圆的方程专项练习(附解析)圆的标准方程(x-a)+(y-b)=r中,有三个参数a、b、r,只要求出a、b、r,这时圆的方程就被确定。
以下是圆的方程专题练习,请考生查缺补漏。
一、填空题1.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是________.[解析] 设圆心C(a,b)(a0,b0),由题意得b=1.又圆心C到直线4x-3y=0的距离d==1,解得a=2或a=-(舍).因此该圆的标准方程为(x-2)2+(y-1)2=1.[答案] (x-2)2+(y-1)2=12.(2021南京质检)已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为________.[解析] 因为点P关于直线x+y-1=0的对称点也在圆上,该直线过圆心,即圆心满足方程x+y-1=0,因此-+1-1=0,解得a=0,因此圆心坐标为(0,1).[答案] (0,1)3.已知圆心在直线y=-4x上,且圆与直线l:x+y-1=0相切于点P(3,-2),则该圆的方程是________.[解析] 过切点且与x+y-1=0垂直的直线为y+2=x-3,与y=-4x联立可求得圆心为(1,-4).半径r=2,所求圆的方程为(x-1)2+(y+4)2=8.[答案] (x-1)2+(y+4)2=84.(2021江苏常州模拟)已知实数x,y满足x2+y2-4x+6y+12=0,则|2x-y |的最小值为________.[解析] x2+y2-4x+6y+12=0配方得(x-2)2+(y+3)2=1,令x=2+cos ,y=-3+sin ,则|2x-y|=|4+2cos +3-sin |=|7-sin (-7-(tan =2).[答案] 7-5.已知圆x2+y2+4x-8y+1=0关于直线2ax-by+8=0(a0,b0)对称,则+的最小值是________.[解析] 由圆的对称性可得,直线2ax-by+8=0必过圆心(-2,4),因此a+b =2.因此+=+=++52+5=9,由=,则a2=4b2,又由a+b=2,故当且仅当a=,b =时取等号.[答案] 96.(2021南京市、盐都市高三模拟)在平面直角坐标系xOy中,若圆x2 +(y-1)2=4上存在A,B两点关于点P(1,2)成中心对称,则直线AB的方程为________.[解析] 由题意得圆心与P点连线垂直于AB,因此kOP==1,kAB=-1,而直线AB过P点,因此直线AB的方程为y-2=-(x-1),即x+y-3=0.[答案] x+y-3=07.(2021泰州质检)若a,且方程x2+y2+ax+2ay+2a2+a-1=0表示圆,则a =________.[解析] 要使方程x2+y2+ax+2ay+2a2+a-1=0表示圆,则a2+(2a)2-4(2a2 +a-1)0,解得-20)关于直线x+y+2=0对称.(1)求圆C的方程;(2)设Q为圆C上的一个动点,求的最小值.[解] (1)设圆心C(a,b),由题意得解得则圆C的方程为x2+y2=r2,将点P的坐标代入得r2=2,故圆C的方程为x2+y2=2.(2)设Q(x,y),则x2+y2=2,=(x-1,y-1)(x+2,y+2)=x2+y2+x+y-4=x+y-2.令x=cos ,y=sin ,=x+y-2=(sin +cos )-2=2sin-2,因此的最小值为-4.10.已知圆的圆心为坐标原点,且通过点(-1,).(1)求圆的方程;(2)若直线l1:x-y+b=0与此圆有且只有一个公共点,求b的值;(3)求直线l2:x-y+2=0被此圆截得的弦长.[解] (1)已知圆心为(0,0),半径r==2,因此圆的方程为x2+y2=4.(2)由已知得l1与圆相切,则圆心(0,0)到l1的距离等于半径2,即=2,解得b=4.(3)l2与圆x2+y2=4相交,圆心(0,0)到l2的距离d==,所截弦长l=2=2= 2.一样说来,“教师”概念之形成经历了十分漫长的历史。
中考数学专项训练-圆(含解析)

中考数学专项训练-圆附参考答案1.(2015•贵阳)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O 于点D,连接OD交BC于点E,∠B=30°,FO=2.(1)求AC的长度;(2)求图中阴影部分的面积.(计算结果保留根号)2.(2015•丹东)如图,AB是⊙O的直径,=,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.(1)若OA=CD=2,求阴影部分的面积;(2)求证:DE=DM.3.(2015•青海)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.(1)求证:AM=AC;(2)若AC=3,求MC的长.4.(2015•庆阳)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.(1)求证:FE⊥AB;(2)当EF=6,=时,求DE的长.5.(2015•呼伦贝尔)如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)求证:AB=AC;(2)若PC=2,求⊙O的半径及线段PB的长.6.(2015•天水)如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:(1)AC•PD=AP•BC;(2)PE=PD.7.(2015•贵港)如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O 的切线BM与AO的延长线相交于点M,连接AC,CM.(1)若AB=4,求的长;(结果保留π)(2)求证:四边形ABMC是菱形.8.(2015•柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O 相交于点E,连接AE,BE.(1)求证:AB=AC;(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.9.(2015•鞍山)⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.(1)求证:BE⊥CE;(2)若BC=,⊙O的半径为,求线段CD的长度.10.(2015•黔西南州)如图,点O在∠APB的平分线上,⊙O与PA相切于点C.(1)求证:直线PB与⊙O相切;(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.11.(2015•鄂尔多斯)如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.(1)求证:CF是⊙O的切线.(2)设⊙O的半径为2,且AC=CE,求AM的长.12.(2015•铁岭)如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.(1)求证:AE是⊙O的切线;(2)若BD=AD=4,求阴影部分的面积.13.(2015•贺州)如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.(1)求证:DC是⊙O的切线;(2)若OE=cm,AC=2cm,求DC的长(结果保留根号).14.(2015•抚顺)如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.(1)求证:CF与⊙O相切;(2)若AD=2,F为AE的中点,求AB的长.15.(2015•赤峰)如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是圆O的切线.(2)若PB=6,DB=8,求⊙O的半径.1.【解答】解:(1)∵OF⊥AB,∴∠BOF=90°,∵∠B=30°,FO=2,∴OB=6,AB=2OB=12,又∵AB为⊙O的直径,∴∠ACB=90°,∴AC=AB=6;(2)∵由(1)可知,AB=12,∴AO=6,即AC=AO,在Rt△ACF和Rt△AOF中,∴Rt△ACF≌Rt△AOF,∴∠FAO=∠FAC=30°,∴∠DOB=60°,过点D作DG⊥AB于点G,∵OD=6,∴DG=3,∴S△ACF+S△OFD=S△AOD=×6×3=9,即阴影部分的面积是9.2.【解答】(1)解:如图,连接OD,∵CD是⊙O切线,∴OD⊥CD,∵OA=CD=2,OA=OD,∴OD=CD=2,∴△OCD为等腰直角三角形,∴∠DOC=∠C=45°,∴S阴影=S△OCD﹣S扇OBD=﹣=4﹣π;(2)证明:如图,连接AD,∵AB是⊙O直径,∴∠ADB=∠ADM=90°,∴ED=BD,∠MAD=∠BAD,在△AMD和△ABD中,,∴△AMD≌△ABD,∴DM=BD,∴DE=DM.3.【解答】(1)证明:连接OA,∵AM是⊙O的切线,∴∠OAM=90°,∵∠B=60°,∴∠AOC=120°,∵OA=OC,∴∠OCA=∠OAC=30°,∴∠AOM=60°,∴∠M=30°,∴∠OCA=∠M,∴AM=AC;(2)作AG⊥CM于G,∵∠OCA=30°,AC=3,∴AG=,由勾股定理的,CG=,则MC=2CG=3.4.【解答】(1)证明:连接AD、OD,∵AC为⊙O的直径,∴∠ADC=90°,又∵AB=AC,∴CD=DB,又CO=AO,∴OD∥AB,∵FD是⊙O的切线,∴OD⊥EF,∴FE⊥AB;(2)∵=,∴=,∵OD∥AB,∴==,又EF=6,∴DE=9.5.【解答】证明:(1)如图1,连接OB.∵AB切⊙O于B,OA⊥AC,∴∠OBA=∠OAC=90°,∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,∵OP=OB,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠ACP=∠ABC,∴AB=AC;(2)如图2,延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5﹣r,则AB2=OA2﹣OB2=52﹣r2,AC2=PC2﹣PA2=(2)2﹣(5﹣r)2,∴52﹣r2=(2)2﹣(5﹣r)2,解得:r=3,∴AB=AC=4,∵PD是直径,∴∠PBD=90°=∠PAC,又∵∠DPB=∠CPA,∴△DPB∽△CPA,∴=,∴=,解得:PB=.∴⊙O的半径为3,线段PB的长为.6.【解答】解:(1)∵AB是⊙O的直径,BC是切线,∴AB⊥BC,∵DE⊥AB,∴DE∥BC,∴△AEP∽△ABC,∴=…①,又∵AD∥OC,∴∠DAE=∠COB,∴△AED∽△OBC,∴===…②,由①②,可得ED=2EP,∴PE=PD.∴AB⊥BC,∵DE⊥AB,∴DE∥BC,∴△AEP∽△ABC,∴,∵PE=PD,∴,∴AC•PD=AP•BC.7.【解答】(1)解:∵OA=OB,E为AB的中点,∴∠AOE=∠BOE,OE⊥AB,∵OE⊥AB,E为OD中点,∴OE=OD=OA,∴在Rt△AOE中,∠OAB=30°,∠AOE=60°,∠AOB=120°,设OA=x,则OE=x,AE=x,∵AB=4,∴AB=2AE=x=4,解得:x=4,则的长l==;(2)证明:由(1)得∠OAB=∠OBA=30°,∠BOM=∠COM=60°,∠AMB=30°,∴∠BAM=∠BMA=30°,∴AB=BM,∵BM为圆O的切线,∴OB⊥BM,在△COM和△BOM中,,∴△COM≌△BOM(SAS),∴CM=BM,∠CMO=∠BMO=30°,∴CM=AB,∠CMO=∠MAB,∴CM∥AB,∴四边形ABMC为菱形.【解答】证明:(1)∵AD与△ABC的外接圆⊙O恰好相切于点A,∴∠ABE=∠DAE,又∠EAC=∠EBC,∴∠DAC=∠ABC,∵AD∥BC,∴∠DAC=∠ACB,∴∠ABC=∠ACB,∴AB=AC;(2)作AF⊥CD于F,∵四边形ABCE是圆内接四边形,∴∠ABC=∠AEF,又∠ABC=∠ACB,∴∠AEF=∠ACB,又∠AEB=∠ACB,∴∠AEH=∠AEF,在△AEH和△AEF中,,∴△AEH≌△AEF,∴EH=EF,∴CE+EH=CF,在△ABH和△ACF中,,∴△ABH≌△ACF,∴BH=CF=CE+EH.9.【解答】(1)证明:连接OB,OD,在△BOD和△BOA中,∴△BOD≌△BOA(SSS),∴∠DBO=∠ABO,又∵∠CDB=∠A,∠OBA=∠A,∴∠DBO=∠CDB,∴OB∥DE,∴∠E+∠EBO=180°,∵BE为⊙O的切线,∴OB⊥BE,∴∠EBO=90°,∴∠E=90°,∴BE⊥CE;(2)解:在Rt△ABC中,∵AC=2OA=5,BC=,∴AB==2,∴BD=BA=2,∵∠ABC=∠E=90°,∠BAC=∠BDE,∴△ABC∽△DEB,∴==,∴DE=4,BE=2,在Rt△BCE中,CE==1,∴CD=DE﹣CE=3.10.【解答】(1)证明:连接OC,作OD⊥PB于D点.∵⊙O与PA相切于点C,∴OC⊥PA.∵点O在∠APB的平分线上,OC⊥PA,OD⊥PB,∴OD=OC.∴直线PB与⊙O相切;(2)解:设PO交⊙O于F,连接CF.∵OC=3,PC=4,∴PO=5,PE=8.∵⊙O与PA相切于点C,∴∠PCF=∠E.又∵∠CPF=∠EPC,∴△PCF∽△PEC,∴CF:CE=PC:PE=4:8=1:2.∵EF是直径,∴∠ECF=90°.设CF=x,则EC=2x.则x2+(2x)2=62,解得x=.则EC=2x=.11.【解答】(1)证明:连接OC,如图,∵⊙O是△ABC的外接圆,圆心O在AB上,∴AB是⊙O的直径,∴∠ACB=90°,又∵∠B=2∠A,∴∠B=60°,∠A=30°,∵EM⊥AB,∴∠EMB=90°,在Rt△EMB中,∠B=60°,∴∠E=30°,又∵EF=FC,∴∠ECF=∠E=30°,又∵∠ECA=90°,∴∠FCA=60°,∵OA=OC,∴∠OCA=∠A=30°,∴∠FCO=∠FCA+∠ACO=90°,∴OC⊥CF,∴FC是⊙O的切线;(2)解:在Rt△ABC中,∵∠ACB=90°,∠A=30°,AB=4,∴BC=AB=2,AC=BC=2,∵AC=CE,∴CE=2,∴BE=BC+CE=2+2,在Rt△BEM中,∠BME=90°,∠E=30°∴BM=BE=1+,∴AM=AB﹣BM=4﹣1﹣=3﹣.12.【解答】解:(1)∵AB=AC,AD是BC边上的中线,∴∠ODB=90°,在△BOD和△EOA中,,∴△BOD≌△EOA,∴∠OAE=∠ODB=90°,∴AE是⊙O的切线;(2)∵∠ODB=90°,BD=OD,∴∠BOD=45°,∴∠AOE=45°,则阴影部分的面积=×4×4﹣=8﹣2π.13.【解答】(1)证明:连接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠BAD,∴∠DAC=∠OAC,∴∠DAC=∠OCA,∴AD∥OC,∴∠ADC=∠OCF,∵AD⊥DC,∴∠ADC=90°,∴∠OCF=90°,∴OC⊥CD,∵OC为半径,∴CD是⊙O的切线.(2)∵OE⊥AC,∴AE=AC=cm,在Rt△AOE中,AO===4cm,由(1)得∠OAC=∠CAD,∠ADC=∠AEO=90°,∴△AOE∽△ACD,∴,即,∴DC=cm.14.【解答】(1)证明:如图所示:连接OF、OC,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠ADC=90°,∵E为BC边中点,AO=DO,∴AO=AD,EC=BC,∴AO=EC,AO∥EC,∴四边形OAEC是平行四边形,∴AE∥OC,∴∠DOC=∠OAF,∠FOC=∠OFA,∵OA=OF,∴∠OAF=∠OFA,∴∠DOC=∠FOC,∵在△ODC和△OFC中,∴△ODC≌△OFC(SAS),∴∠OFC=∠ODC=90°,∴OF⊥CF,∴CF与⊙O相切;(2)解:如图所示:连接DE,∵AO=DO,AF=EF,AD=2,∴DE=20F=2,∵E是BC的中点,∴EC=1,在Rt△DCE中,由勾股定理得:DC===,∴AB=CD=.15.【解答】(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,∴∠OBP=∠E=90°,∵OB为圆的半径,∴PB为圆O的切线;(2)解:在Rt△PBD中,PB=6,DB=8,根据勾股定理得:PD==10,∵PD与PB都为圆的切线,∴PC=PB=6,∴DC=PD﹣PC=10﹣6=4,在Rt△CDO中,设OC=r,则有DO=8﹣r,根据勾股定理得:(8﹣r)2=r2+42,解得:r=3,则圆的半径为3.。
中考数学《圆》专项训练及答案解析

中考数学《圆》专项训练及答案解析1.(2018•鞍山)如图,四边形ABCD内接于⊙O,AC与BD为对角线,∠BCA=∠BAD,过点A 作AE∥BC交CD的延长线于点E.(1)求证:EC=AC.(2)若cos∠ADB=,BC=10,求DE的长.解:(1)证明:∵BC∥AE,∴∠ACB=∠EAC,∵∠ACB=∠BAD,∴∠EAC=∠BAD,∴∠EAD=∠CAB,∵∠ADE+∠ADC=180°,∠ADC+∠ABC=180°,∴∠ADE=∠ABC,∵∠EAD+∠ADE+∠E=180°,∠BAC+∠ABC+∠ACB=180°,∴∠E=∠ACB=∠EAC,∴CE=CA.(2)解:设AE交⊙O于M,连接DM,作MH⊥DE于H.∵∠EAD=∠CAB,∴=,∴DM=BC=10,∵∠MDE+∠MDC=180°,∠MDC+∠MAC=180°,∴∠MDE=∠CAM,∵∠E=∠CAE,∴∠E=∠MDE,∴MD=ME=10,∵MH⊥DE,∴EH=DH,∵∠ADB=∠ACB=∠BAD=∠E,∴cos∠E==,∴EH=4,∴DE=2EH=8.2.(2018•河池)如图,⊙O的直径为AB,点C在⊙O上,点D,E分别在AB,AC的延长线上,DE⊥AE,垂足为E,∠A=∠CDE.(1)求证:CD是⊙O的切线;(2)若AB=4,BD=3,求CD的长.(1)证明:连接OC,∵DE⊥AE,∴∠E=90°,∴∠EDC+∠ECD=90°,∵∠A=∠CDE,∴∠A+∠DCE=90°,∵OC=OA,∴∠A=∠ACO,∴∠ACO+∠DCE=90°,∴∠OCD=90°,∴OC⊥CD,∴CD是⊙O的切线;(2)解:∵AB=4,BD=3,∴OC=OB=AB=2,∴OD=2+3=5,∴CD===.3.(2018•朝阳)如图,AB是⊙O的直径,AC是⊙O的弦,OD⊥AB,OD与AC的延长线交于点D,点E在OD上,且CE=DE.(1)求证:直线CE是⊙O的切线;(2)若OA=,AC=3,求CD的长.(1)证明:连接OC,∵OD⊥AB,∴∠AOD=90°,∴∠D+∠A=90°,∵OA=OC,∴∠A=∠ACO,∵CE=DE,∴∠ECD=∠D,∵∠ACO+∠DCE=90°,∴∠OCE=90°,∴OC⊥AD,∴直线CE是⊙O的切线;(2)解:连接BC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠AOD=∠ACB,∵∠A=∠A,∴△ABC∽△ADO,∴,∴=,∴AD=8,∴CD=AD﹣AC=5.4.(2018•安丘市)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,交AC于点E,AC的反向延长线交⊙O于点F.(1)求证:DE是⊙O的切线;(2)若DE+EA=8,⊙O的半径为10,求△OAF的面积.(1)证明:∵OB =OD ,∴∠ABC =∠ODB ,∵AB =AC ,∴∠ABC =∠ACB ,∴∠ODB =∠ACB ,∴OD ∥AC .∵DE ⊥AC ,OD 是半径,∴DE ⊥OD ,∴DE 是⊙O 的切线;(2)解:如图,过点O 作OH ⊥AF 于点H ,则∠ODE =∠DEH =∠OHE =90°,∴四边形ODEH 是矩形,∴OD =EH ,OH =DE .设AH =x .∵DE +AE =8,OD =10,∴AE =10﹣x ,OH =DE =8﹣(10﹣x )=x ﹣2,在Rt △AOH 中,由勾股定理知:AH 2+OH 2=OA 2,即x 2+(x ﹣2)2=102,解得x 1=8,x 2=﹣6(不合题意,舍去).∴AH =8,OH =6,∵OH ⊥AF ,∴AH =FH =AF ,∴AF =2AH =2×8=16∴△OAF 的面积=×16×6=48.5.(2018•营口)如图,△ABC内接于⊙O,AB是⊙O的直径,弦CD与AB交于点E,连接AD,过点A作直线MN,使∠MAC=∠ADC.(1)求证:直线MN是⊙O的切线.(2)若sin∠ADC=,AB=8,AE=3,求DE的长.(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠B+∠BAC=90°,∵∠B=∠D,∠MAC=∠ADC,∴∠B=∠MAC,∴∠MAC+∠CAB=90°,∴∠BAM=90°,∴AB⊥MN,∴直线MN是⊙O的切线;(2)解:连接OC,过E作EH⊥OC于H,∵sin∠ADC=,∴∠D=30°,∴∠B=∠D=30°,∴∠AOC=60°,∵AB=8,∴AO=BO=4,∵AE=3,∴OE=1,BE=5,∵∠EHO=90°,∴OH=,EH=,∴CH=,∴CE==,∵弦CD与AB交于点E,由相交弦定理得,AE•BE=CE•DE,∴DE===.6.(2018•丹东)如图,直线AD经过⊙O上的点A,△ABC为⊙O的内接三角形,并且∠CAD =∠B.(1)判断直线AD与⊙O的位置关系,并说明理由;(2)若∠CAD=30°,⊙O的半径为1,求图中阴影部分的面积.(结果保留π)解:(1)直线AD与⊙O的位置关系是相切,理由是:作直径AE,连接CE,∵AE为直径,∴∠ACE=90°,∴∠E+∠EAC=90°,∵∠B=∠DAC,∠B=∠E,∴∠E=∠DAC,∴∠EAC+∠DAC=90°,即OA⊥AD,∵OA过O,∴直线AD与⊙O的位置关系是相切;(2)连接OC,过O作OF⊥AC于F,则∠OFA=90,∵∠CAD=30°,∠DAO=90°,∴∠OAC=60°,∵OC=OA=1,∴△OAC是等边三角形,∴AC=OA=1,∠AOC=60°,∵OA=OC,OF⊥AC,∴AF=FC=,由勾股定理得:OF==,∴阴影部分的面积为﹣=﹣.7.(2018•无锡)如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,点O在边AB 上.过点A、D的圆的圆心O在边AB上,它与边AB交于另一点E.(1)试判断BC与圆O的位置关系,并说明理由;(2)若AC=6,sin B=,求AD的长.解:(1)BC与圆O相切,理由如下:如图,连接OD∵OA=OD∴∠ODA=∠OAD,∵AD平分∠CAB∴∠CAD=∠DAO∴∠CAD=∠ODA∴DO∥AC∵AC⊥CD∴OD⊥BC,且D在圆O上,∴BC与圆O相切(2)在Rt△ABC中,∵AC=6,sin B=,∴AB=10,BC=8在Rt△BDO中,sin B===,∴30=8DO∴DO==AO∴BO=AB﹣AO=∴BD==5∴CD=BC﹣BD=3在Rt△ACD中,AD===38.(2019•邵阳县一模)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.(1)求证:CB平分∠ACE;(2)若BE=3,CE=4,求⊙O的半径.(1)证明:如图1,连接OB,∵AB是⊙0的切线,∴OB⊥AB,∵CE丄AB,∴OB∥CE,∴∠1=∠3,∵OB=OC,∴∠1=∠2∴∠2=∠3,∴CB平分∠ACE;(2)如图2,连接BD,∵CE丄AB,∴∠E=90°,∴BC===5,∵CD是⊙O的直径,∴∠DBC=90°,∴∠E=∠DBC,∴△DBC∽△CBE,∴,∴BC2=CD•CE,∴CD==,∴OC==,∴⊙O的半径=.9.(2018•鄂尔多斯)如图,⊙O是△ABC的外接圆,AC是直径,弦BD=BA,EB⊥DC,交DC 的延长线于点E.(1)求证:BE是⊙O的切线;(2)当sin∠BCE=,AB=3时,求AD的长.解:(1)证明:连结OB,OD,在△ABO和△DBO中,,∴△ABO≌△DBO(SSS),∴∠DBO=∠ABO,∵∠ABO=∠OAB=∠BDC,∴∠DBO=∠BDC,∴OB∥ED,∵BE⊥ED,∴EB⊥BO,∴BE是⊙O的切线;(2)∵AC是直径,∴∠ABC=90°,∵BE⊥DE,∴∠E=90°,∴∠OBC+∠CBE=∠BAC+∠ACB=90°,∴∠BAC=∠EBC,∴∠ACB=∠BCE,∵sin∠BCE=,∴sin∠ACB=,∵AB=3,∴AC=4,∵∠BDE=∠BAC,∴sin∠DBE=,∵BD=AB=3,∴DE=,∴BE==,∵∠CBE=∠BAC=∠BDC,∠E=∠E,∴△BDE∽△CBE,∴=,∴CE=,∴CD=,∴AD==.10.(2018•铁岭)如图,四边形ABCD中,连接AC,AC=AD,以AC为直径的⊙O过点B,交CD于点E,过点E作EF⊥AD于点F.(1)求证:EF是⊙O的切线;(2)若∠BAC=∠DAC=30°,BC=2,求的长.(结果保留π)(1)证明:设圆心为O,连接OE,AE,∵AC为⊙O的直径,∴∠AEC=90°,∴∠AED=90°,∵AC=AD,∴∠CAE=∠DAE,∵EF⊥AD,∴∠AFE=90°,∴∠EAF+∠AEF=∠AEF+∠DEF=90°,∴∠EAF=∠DEF,∵OA=OE,∴∠OAE=∠OEA,∴∠OEA=∠DEF,∴∠OEA+∠AEF=90°,∴∠OEF=90°,∴EF是⊙O的切线;(2)解:连接OB,∵∠BAC=30°,∴∠BOC=60°,∵OB=OC,∴△OBC是等边三角形,∴OB=BC=2,∵∠CAD=30°,∴∠CAE=CAD=15°,∴∠COE=2∠CAE=30°,∴∠BOE=90°,∴的长==π.11.(2018•本溪)如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.(1)判断直线DF与⊙O的位置关系,并说明理由;(2)当∠A=30°,CF=时,求⊙O的半径.解:(1)结论:DF是⊙O的切线.理由:作OG⊥DF于G.连接OE.∵BD=DC,BO=OA,∴OD∥AC,∴∠ODG=∠DFC,∵∠OGD=∠DCF=90°,OD=DF,∴△OGD≌△DCF(AAS),∴OG=CD,∵AC是⊙O的切线,∴OE⊥AC,∴∠AEO=∠C=90°,∴OE∥BC,∵OD∥CE,∴四边形CDOE是平行四边形,∴CD=OE,∴OG=OE,∴DF是⊙O的切线.(2)∵FA,FD是⊙O的切线,∴FG=FE,设FG=FE=x,∵△OGD≌△DCF(AAS),∴DG=CF=,∴OD=DF=+x,∵AC=2OD,CE=OD,∴AE=EC=OD=+x,∵∠A=30°,∴CD=OE=,在Rt△DCF中,∵DF2=CD2+CF2,∴(+x)2=()2+()2,解得x=﹣或﹣﹣(舍弃),∴OE==1.方法二:设半径是r,則DF=OD=√3r,在三角形DCF中,由勾股定理得,r=1.12.(2018•辽阳)如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.(1)求证:EM是⊙O的切线;(2)若∠A=∠E,BC=,求阴影部分的面积.(结果保留π和根号).解:(1)连接OC,∵OF⊥AB,∴∠AOF=90°,∴∠A+∠AFO+90°=180°,∵∠ACE+∠AFO=180°,∴∠ACE=90°+∠A,∵OA=OC,∴∠A=∠ACO,∴∠ACE=90°+∠ACO=∠ACO+∠OCE,∴∠OCE=90°,∴OC⊥CE,∴EM是⊙O的切线;(2)∵A B是⊙O的直径,∴∠A CB=90°,∴∠ACO+∠BCO=∠BCE+∠BCO=90°,∴∠ACO=∠BCE,∵∠A=∠E,∴∠A=∠ACO=∠BCE=∠E,∴∠ABC=∠BCO+∠E=2∠A,∴∠A=30°,∴∠BOC=60°,∴△BOC是等边三角形,∴OB=BC=,∴阴影部分的面积=﹣××=﹣.13.(2018•广元)如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F 是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=P.(1)求证:PA是⊙O的切线;(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C 为顶点的三角形与△BFM相似,求DH的长度.(1)证明:如图1中,作PH⊥FM于H.∵PD⊥AC,∴∠PHM=∠CDM=90°,∵∠PMH=∠DMC,∴∠C=∠MPH,∵∠C=∠FPM,∴∠HPF=∠HPM,∵∠HFP+∠HPF=90°,∠HMP+∠HPM=90°,∴∠PFH=∠PMH,∵OF=OC,∴∠C=∠OFC,∵∠C+∠CDM=∠C+∠PMF=∠C+∠PFH=90°,∴∠OFC+∠PFC=90°,∴∠OFP=90°,∴直线PA是⊙O的切线.(2)解:如图1中,∵∠A=30°,∠AFO=90°,∴∠AOF=60°,∵∠AOF=∠OFC+∠OCF,∠OFC=∠OCF,∴∠C=30°,∵⊙O的半径为4,DM=1,∴OA=2OF=8,CD=DM=,∴OD=OC﹣CD=4﹣,∴AD=OA+OD=8+4﹣=12﹣,在Rt△ADP中,DP=AD•tan30°=(12﹣)×=4﹣1,∴PM=PD﹣DM=4﹣2.(3)如图2中,由(2)可知:BF=BC=4,FC=BF=4,CM=2DM=2,CD=,∴FM=FC﹣CM=4﹣2,①当△CDH∽△BFM时,=,∴=,∴DH=②当△CDH∽△MFB时,=,∴=,∴DH=,∵DN==,∴DH<DN,符合题意,综上所述,满足条件的DH的值为或.14.(2018•济南)如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.解:(1)方法一:如图1,连接AD.∵BA是⊙O直径,∴∠BDA=90°.∵=,∴∠BAD=∠C=60°.∴∠ABD=90°﹣∠BAD=90°﹣60°=30°.方法二:如图2,连接DA、OD,则∠BOD=2∠C=2×60°=120°.∵OB=OD,∴∠OBD=∠ODB=(180°﹣120°)=30°.即∠ABD=30°.(2)如图1,∵AP是⊙O的切线,∴∠BAP=90°.在Rt△BAD中,∵∠ABD=30°,∴DA=BA=×6=3.∴BD=DA=3.在Rt△BAP中,∵cos∠ABD=,∴cos30°==.∴BP=4.∴PD=BP﹣BD=4﹣3=.15.(2018•毕节市)如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.(1)求证:EG是⊙O的切线;(2)若tan C=,AC=8,求⊙O的半径.证明(1)如图:连接OE,BE∵∠ABG=2∠C,∠ABG=∠C+∠A∴∠C=∠A∴BC=AB,∵BC是直径∴∠CEB=90°,且AB=BC∴CE=AE,且CO=OB∴OE∥AB∵GE⊥AB∴EG⊥OE,且OE是半径∴EG是⊙O的切线(2)∵AC=8,∴CE=AE=4∵tan∠C==∴BE=2∴BC==2∴CO=即⊙O半径为16.(2018•巴彦淖尔)如图,AB为⊙O的直径,C,G是⊙O上两点,过点C的直线CD⊥BG 于点D,交BA的延长线于点E,连接BC,交OD于点F,且BC平分∠ABD.(1)求证:CD是⊙O的切线;(2)若=,求∠E的度数;(3)连结AD,在(2)的条件下,若CD=2,求AD的长.证明:(1)连接OC,∵OC=OB,BC平分∠ABD,∴∠OCB=∠OBC,∠OBC=∠DBC,∴∠DBC=∠OCB,∴OC∥BD,∴∠BDC=∠ECO,∵CD⊥BD,∴∠BDC=90°,∴∠ECO=90°,∵OC是⊙O的半径,∴CD是⊙O的切线;(2)由(1)知,OC∥BD,∴∠OCF=∠DBF,∠COF=∠BDF,∴△OCF∽△DBD,∴,∵=,∴,∵OC∥BD,∴△EOC∽△EDB,∴,∴,设OE=2a,EB=3a,∴OB=a,∴OC=a,∵∠OCE=90°,OC=OE,∴∠E=30°;(3)∵∠E=30°,∠BDE=90°,BC平分∠DBE,∴∠EBD=60°,∠OBC=∠DBC=30°,∵CD=2,∴BC=4,BD=6,∵,∴OC=4,作DM⊥AB于点M,∴∠DBM=90°,∵BD=6,∠DBM=60°,∴BM=3,DM=3,∵OC=4,∴AB=8,∴AM=5,∵∠DMA=90°,DM=3,∴AD==.17.(2018•德阳)如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.(1)求证:DH=DB;(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.①求证:EF为圆O的切线;②求DF的长.解:(1)证明:连接HB,∵点H是△ABC的内心,∴∠DAC=∠DAB,∠ABH=∠CBH,∵∠DBC=∠DAC,∴∠DHB=∠DAB+∠ABH=∠DAC+∠CBH,∵∠DBH=∠DBC+∠CBH,∴∠DHB=∠DBH,∴DH=DB;(2)①连接OD,∵∠DOB=2∠DAB=∠BAC∴OD∥AC,∵AC⊥BC,BC∥EF,∴AC⊥EF,∴OD⊥EF,∵点D在⊙O上,∴EF是⊙O的切线;②过点D作DG⊥AB于G,∵∠EAD=∠DAB,∴DE=DG,∵DC=DB,∠CED=∠DGB=90°,∴△CDE≌△BDG,∴GB=CE=1,在Rt△ADB中,DG⊥AB,∴∠DAB=∠BDG,∵∠DBG=∠ABD,∴△DBG∽△ABD,∴,∴DB2=AB•BG=5×1=5,∴DB=,DG=2,∴ED=2,∵H是内心,∴AE=AG=4,∵DO∥AE,∴△OFD∽△AFE,∴,∴,∴DF=.。
最新圆的专项培优练习题及答案
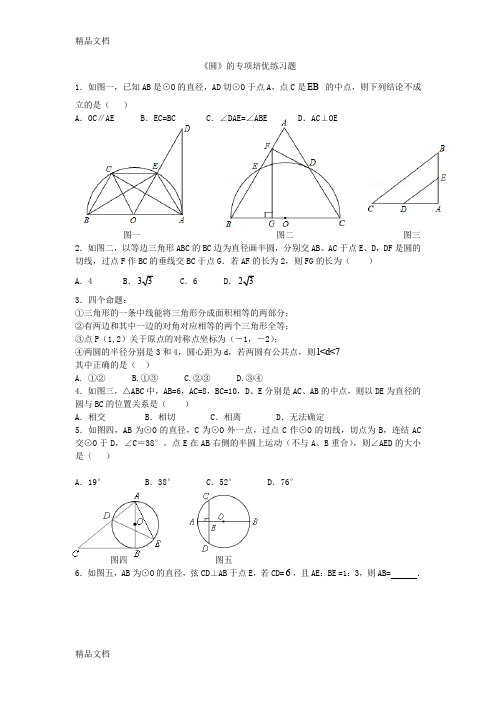
《圆》的专项培优练习题1.如图一,已知AB是⊙O的直径,AD切⊙O于点A,点C是EB的中点,则下列结论不成立的是()A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE图一图二图三2.如图二,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为()A.4 B.C.6 D.3.四个命题:①三角形的一条中线能将三角形分成面积相等的两部分;②有两边和其中一边的对角对应相等的两个三角形全等;③点P(1,2)关于原点的对称点坐标为(-1,-2);④两圆的半径分别是3和4,圆心距为d,若两圆有公共点,则1<d<7其中正确的是()A. ①②B.①③C.②③D.③④4.如图三,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是()A.相交 B.相切 C.相离 D.无法确定5.如图四,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC 交⊙O于D,∠C=38°。
点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是()A.19° B.38° C.52° D.76°图四图五6.如图五,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE =1:3,则AB= .7.已知AB是⊙O的直径,AD⊥l于点D.(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.8.如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P 作AB的垂线交BC的延长线于点Q。
在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD 与⊙O的位置关系,并说明理由。
高中数学必修二第四章圆与方程解答题专项练习附答案 教师版

﹣4),
∴r=
t
t =2
∴所求圆的方程为(x﹣1)2+(y+4)2=8;
(2)解:当 CP⊥AB,即 P 为 AB 中点时,弦长 AB 最小
CP=
t
t
.
弦长 AB 的最小值为 2
.
第 3 页 共 36 页
【解析】【分析】(1)首先利用切点坐标和切线方程,求出过该切点的半径所在直线的方程,然后将所
求方程与圆心所在直线方程联立,求出圆心坐标,再利用两点间距离公式求出半径,进而求出圆的标准方
垂直的弦长最短,∵圆心 C 点坐标为(3,4),∴
, ∴所求直线的斜率 k=1,代入点斜
式方程,得 y﹣5=x﹣2,即 x﹣y+3=0.∴P 点的弦中,弦长最短的弦所在的直线方程为 x﹣y+3=0.(Ⅱ) 当直线垂直 x 轴时,即 x=5,圆心 C 到直线的距离为 2,此时直线 x=5 与圆 C 相切,当直线不垂直 x 轴时,
C 到直线的距离等于半径,能求出切线方程.
6.已知圆 C 的圆心在直线 4x+y=0 上,且与直线 x+y﹣1=0 相切于点 P(3,﹣2).
(1)求圆 C 的方程;
(2)过圆内一点 P(2,﹣3)的直线 l 与圆交于 A、B 两点,求弦长 AB 的最小值.
【答案】 (1)解:过切点且与 l:x+y﹣1=0 垂直的直线为 y=x﹣5,与 y=﹣4x 联立可求得圆心为 C(1,
【答案】 (1)解:由圆的方程的要求可得,22+42-4m>0,∴m<5
(2)解:圆心(1,2),半径
线,
因为圆和直线相切,所以有
t
线 ,所以 线
【解析】【分析】(1) 由圆的方程判定方法求出实数 线 的取值范围。
圆的专项训练解析附答案

【详解】
∵四边形ABCD是矩形,
∴∠B=90°,
∵ , ,
∴BC=8,
连接OA、OB、OC、过点O作OH⊥AB,OE⊥BC,OF⊥AC,
【详解】
解:连接CO并延长交⊙O于点D,连接AD,
由CD是⊙O的直径,可得∠CAD=90°,
∵∠B和∠D所对的弧都为弧AC,
∴∠B=∠D,即sinB=sinD= ,
∵半径AO=5,
∴CD=10,
∴ ,
∴AC=4,
故选:C.
【点睛】
本题考查了同弧所对的圆周角相等,以及三角函数的内容,注意到直径所对的圆周角是直角是解题的关键.
4.如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A.4.5B.4C.3D.2
【答案】B
【解析】
【分析】连接AI、BI,因为三角形的内心是角平分线的交点,所以AI是∠CAB的平分线,由平行的性质和等角对等边可得:AD=DI,同理BE=EI,所以图中阴影部分的周长就是边AB的长.
【解析】
【分析】
根据侧面展开图的弧长等于圆锥的底面周长,即可求得底面周长,进而即可求得底面的半径长.
【详解】
圆锥的底面周长是:π;
设圆锥的底面半径是r,则2πr=π.
解得:r= .
故选B.
【点睛】
本题考查了圆锥的计算,正确理解理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
小学数学《圆》提升练习(含解析)
完美的图形—圆1、从树木的年轮,我们可以清楚地看出树木的生长年龄,如果一棵20年树龄的红杉树的树干直径是23厘米,你知道这棵红杉树的半径平均每年增加多少厘米吗?解析:20年树龄的树干直径是23厘米,我们可以根据在同一个圆中直径是半径的2倍关系求出半径,然后再求出平均每年半径增加的厘米数。
解答:23÷2÷20=0.575(厘米)答:这棵红杉树的半径平均每年增加0.575厘米。
2、将两个大小相同的圆形铁片平放在桌面上,一个固定不动,另一个沿着不动铁片的边缘滚动,则滚动铁片的圆心转一周后所形成的圆的半径是铁片半径的几倍?若圆形铁片的半径是1厘米,则形成的大圆的半径是多少厘米?解析:由图知,两个圆形铁片大小相同,滚动铁片的圆心转一周后所形成的圆就是虚线画的圆,虚线的圆的半径是铁片半径的2倍,如果圆形铁片的半径是1厘米,则形成的大圆的半径就是2个铁片半径,也就是2厘米。
解答:滚动铁片的圆心转一周后所形成的圆的半径是铁片半径的2倍,若圆形铁片的半径是1厘米,则形成的大圆的半径是2厘米。
3、在一张边长是2厘米的正方形纸上画一个最大的扇形。
解析:扇形是由两条半径和圆上的一段弧线组成的,在边长是2厘米的正方形中画出一个最大的扇形,需要考虑扇形的圆心角要最大,因此需要把正方形的一个顶点为圆心,边长为半径作弧,这样就可以找到最大的扇形。
解答:4、下面扇形的圆心角各是多少度?解析:因为一个周角是360°,12圆的圆心角就是360°的一半,也就是180°;14圆的圆心角就是360°的14,也就是90°;15圆的圆心角就是360°的15,也就是72°。
解答: 180° 90° 72°5、下图中大圆的直径是6厘米,小圆的直径是4厘米,你知道阴影部分的宽是多少吗?解析:根据题意可知大圆的直径是6厘米,则半径就是3厘米;小圆的直径是4厘米,则半径就是2厘米。
高中数学必修二第四章圆与方程专项练习题附答案 教师版
A. 1
B.
C. 2
D. 3
【答案】 B
【解析】【解答】切线长的最小值是当直线 y=x+1 上的点与圆心距离最小时取得,
圆心(3,0)到直线的距离为
t
晦
,
圆的半径为 1,故切线长的最小值为
故答案为:B
【分析】根据题意先求圆心到直线的距离,此时切线长最小,由勾股定理不难求解切线长的最小值.
10.设直线 t
高中数学必修二第四章圆与方程专项练习题附答案
一、单选题(共 40 题;共 80 分)
1.圆
t
关于直线 t 䁜 晦 对称,则 䁜 的值是( )
A.
B.
【答案】B
C.
D.
【解析】【解答】解:因为圆
t
所以圆心(1,1)在直线 t 䁜 晦 上,得 䁜
故答案为:B.
关于直线 t 䁜 晦 对称,
晦
6.已知圆
t晦
,圆 晦 t
动点, 为 轴上的动点,则
的最小值为( )
A.
B.
C.
【答案】 A
【解析】【解答】如图所示,两圆为内含关系,
t,
分别是圆 , 上的 D.
第 2 页 共 18 页
将 关于 轴对称为
′,
连结
′ 交圆于 ′ , ,
交 轴于 ,连
交圆 于 ,
此时
最小,
最小值为 ′ .
和圆 t t 相交或相切,
可得
,即
,
∵
∴解得
故实数 a 的取值范围是
。
故答案为:B
【分析】由题意可得,圆
t
和圆 t t 相交或相切,两圆圆心距大于等于两圆
3 专项训练(四) 圆中的动态问题
图3
上一页 主页 下一页
③如图 4,当⊙P 与 DB 所在直线相切时,
PM 即⊙P 的半径.在 Rt△DAB 中,
由勾股定理可得 BD= AB2+AD2= 22+42=2 5.
∵∠ABD=∠PBM,∠DAB=∠PMB=90°,
∴△DAB∽△PMB,故PAMD=DBPB,
设⊙P 的半径为 R,则R4=32+5R,解得 R=6 5+12,
上一页 主页 下一页
解:(1)如图 1,当 t=21=2(秒)时, PC∥BD;
图1
上一页 主页 下一页
(2)当 t=136÷1=136(秒)时,PC⊥BC; (3)⊙P 与△BCD 的边相切分三种情况. ①如图 2,当⊙P 与 DC 所在直线相切时,由题可得 PO=PM=CO=4, ∴t=41=4(秒);
上一页 主页 下一页
图1 图3
图2
图4
上一页 主页 下一页
解:(1)RP 与 RQ 的数量关系为相等.如图 1,连接 OQ. ∵RQ 为⊙O 的切线, ∴∠OQR=∠OQB+∠PQR=90°. 又∵OB=OQ,OA⊥OB,∴∠OQB=∠OBQ, ∠OBQ+∠BPO=90°,∴∠PQR=∠BPO.
图2
上一页 主页 下一页
②如图 3,当⊙P 与 BC 所在直线相切时, PM 即⊙P 的半径. 在 Rt△BOC 中, 由勾股定理得 BC= BO2+CO2=5. 又∵∠CBO=∠PBM,∠PMB=∠COB=90°, ∴△BCO∽△BPM,故PCMO=BBCP. 设⊙P 的半径为 R,则R4=3+5 R,解得 R=12, ∴t=112=12(秒);
图1
图2
上一页 主页 下一页
3.【易错】如图,在坐标系 xOy 中,已知 D(-5, 4)、B(-3,0),过 D 点分别作 DA、DC 垂直于 x 轴、
最新初中数学圆的专项训练解析附答案
最新初中数学圆的专项训练解析附答案 一、选择题 1.“直角”在几何学中无处不在,下列作图作出的AOB不一定...是直角的是( )
A. B.
C. D.
【答案】C 【解析】 【分析】 根据作图痕迹,分别探究各选项所做的几何图形问题可解. 【详解】 解:选项A中,做出了点A关于直线BC的对称点,则AOB是直角. 选项B中,AO为BC边上的高,则AOB是直角. 选项D中,AOB是直径AB作对的圆周角,故AOB是直角. 故应选C 【点睛】 本题考查了尺规作图的相关知识,根据基本作图得到的结论,应用于几何证明是解题关键.
2.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,
则∠C的度数是( )
A.25° B.27.5° C.30° D.35° 【答案】D 【解析】 分析:直接利用三角形外角的性质以及邻补角的关系得出∠B以及∠ODC度数,再利用圆周角定理以及三角形内角和定理得出答案. 详解:∵∠A=60°,∠ADC=85°, ∴∠B=85°-60°=25°,∠CDO=95°, ∴∠AOC=2∠B=50°, ∴∠C=180°-95°-50°=35° 故选D. 点睛:此题主要考查了圆周角定理以及三角形内角和定理等知识,正确得出∠AOC度数是解题关键.
3.如图,正方形ABCD内接于⊙O,AB=22,则»AB的长是( )
A.π B.32π C.2π D.12π 【答案】A 【解析】 【分析】连接OA、OB,求出∠AOB=90°,根据勾股定理求出AO,根据弧长公式求出即可. 【详解】连接OA、OB,
∵正方形ABCD内接于⊙O, ∴AB=BC=DC=AD, ∴»»»»ABBCCDDA,
∴∠AOB=14×360°=90°, 在Rt△AOB中,由勾股定理得:2AO2=(22)2, 解得:AO=2,
∴»AB的长为902180´=π, 故选A. 【点睛】本题考查了弧长公式和正方形的性质,求出∠AOB的度数和OA的长是解此题的关键. 4.如图,AB是Oe的直径,C是Oe上一点(A、B除外),132AOD,则C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(共16页) 圆专项练习4(配完整解析) 1.如图,直线PO交⊙O于A,B两点,直径AB=10,弦AC∥PM.点M是的中点, (1)求证:直线PM是⊙O的切线; (2)若BC=4,求PO的长.
【解答】(1)证明:连接OM交AC于N,如图所示: ∵点M是的中点, ∴OM⊥AC,AN=CN, ∵AC∥PM, ∴PM⊥OM, ∴直线PM是⊙O的切线; (2)解:∵OA=OB,AN=CN, ∴ON是△ABC的中位线,
∴ON=BC=2, ∵AB=10, ∴OM=OA=AB=5, ∵AC∥PM, ∴△OAN∽△OPM,
∴,即, 解得:PO=12.5.
2.如图,某窗户由矩形和弓形组成,已知弓形的跨度AB=6m,弓形的高EF=2m,现设计安装玻璃,请帮工程师求出所在圆O的半径. 第2页(共16页)
【解答】解:∵弓形的跨度AB=6m,EF为弓形的高, ∴OE⊥AB于F,
∴AF=AB=3m,
∵所在圆O的半径为r,弓形的高EF=2m, ∴AO=r,OF=r﹣2, 在Rt△AOF中,由勾股定理可知:AO2=AF2+OF2, 即r2=32+(r﹣2)2,
解得r=(m).
答:所在圆O的半径为m. 3.如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(2,2),B(1,0),C(3,1). (1)画出△ABC关于x轴对称的图形△A1B1C1; (2)画出将△ABC绕原点O按逆时针方向旋转90°所得作的△A2B2C2,并求出C2的坐标;
(3)在旋转过程中,点A经过的路径为弧,那么的长为 π ;
(4)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
【解答】解:(1)如图,△A1B1C1为所作; (2)如图,△A2B2C2为所作,并求出C2的坐标为(﹣1,3); 第3页(共16页)
(3)OA==2, 在旋转过程中,点A经过的路径为弧,那么的长==π; (4)△A1B1C1与△A2B2C2成中心对称,对称中心的坐标为(,). 故答案为π. 4.汽车正在行驶可车轮突然陷入无盖井,骑车人正在快速前行却因突然出现在面前的凸起井盖被摔伤,夜间出门时被一个没有井盖的窖井吞噬…全国各地因为井盖缺失而造成事故的情形不绝于耳,井盖吞人事件更是频频发生,为了保障市民的人身安全,合肥市政部门开始更换质量更好的井盖(如图所示).小明想知道井盖的半径,在⊙O上,取了三个点A、B、C,测量出AB=AC=50,BC=80,请你帮助小明求出井盖的半径,写出计算过程.
【解答】解:如图所示:连接AO,交BC于点D,连接CO, ∵AB=AC=50,BC=80, ∴AO⊥BC,BD=DC=40,
∴AD==30, ∴设CO=x,则DO=x﹣30, 故DO2+DC2=CO2, 即(x﹣30)2+402=x2,
解得:x=,
答:井盖的半径为. 第4页(共16页)
5.已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,∠AOC的度数为60°,连接PB. (1)求BC的长; (2)求证:PB是⊙O的切线.
【解答】(1)解:如图,连接OB. ∵AB⊥OC,∠AOC=60°, ∴∠OAB=30°, ∵OB=OA, ∴∠OBA=∠OAB=30°, ∴∠BOC=60°, ∵OB=OC, ∴△OBC的等边三角形, ∴BC=OC. 又OC=2, ∴BC=2;
(2)证明:由(1)知,△OBC的等边三角形,则∠COB=60°,BC=OC. ∵OC=CP, ∴BC=PC, ∴∠P=∠CBP. 又∵∠OCB=60°,∠OCB=2∠P, ∴∠P=30°, ∴∠OBP=90°,即OB⊥PB. 又∵OB是半径, ∴PB是⊙O的切线. 第5页(共16页)
6.如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE. (1)求证:DE是⊙O的切线; (2)若CD=,∠ACB=30°,求OE的长.
【解答】(1)证明:连接OD、BD, ∵AB是⊙O直径, ∴∠ADB=90°, ∴BD⊥AC, ∵AB=BC, ∴D为AC中点, ∵OA=OB, ∴OD∥BC, ∵DE⊥BC, ∴DE⊥OD, ∵OD为半径, ∴DE是⊙O的切线;
(2)解:∵CD=,∠ACB=30°, ∴cos30°=, ∴BC=2, ∴BD=BC=1, ∵AB=BC, ∴∠A=∠C=30°, ∵BD=1, ∴AB=2BD=2, ∴OD=1, 在Rt△CDB中,由三角形面积公式得:BC×DE=BD×CD, 1×=2DE,
DE=,
在Rt△ODE中,由勾股定理得:OE==. 第6页(共16页)
7.如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E. (1)求证:E为BC的中点; (2)若BC=8,DE=3,求AB的长度.
【解答】解:(1)∵AB是半圆O的直径, ∴∠C=90°, ∵OD∥AC, ∴∠OEB=∠C=90°, ∴OD⊥BC, ∴BE=CE, ∴E为BC的中点;
(2)设圆的半径为x,则OB=OD=x,OE=x﹣3, ∵BE=BC=4, 在Rt△BOE中,OB2=BE2+OE2, ∴x2=42+(x﹣3)2,解得x=,
∴AB=2x=. 8.如图,已知点I是△ABC的内心,AI交BC于D,交外接圆O于E,求证: (1)IE=EC; (2)IE2=ED•EA.
【解答】解:(1)如图所示;连接IC. 第7页(共16页)
∵点I是△ABC的内心, ∴∠ACI=∠BCI,∠BAE=∠CAE. 又∵∠BAE=∠BCE, ∴∠CAE=∠BCE. ∴∠CAE+∠ACI=∠ICB+∠BCE. ∴∠EIC=∠ICE. ∴IE=EC. (2)由(1)可知:∠CAE=∠BCE. 又∵∠AEC=∠DEC, ∴△DCE∽△CAE.
∴. ∴CE2=DE•EA. ∵IE=EC, ∴IE2=DE•EA. 9.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD. (1)求证:△COD是等边三角形; (2)当α=150°时,试判断△AOD的形状,并说明理由.
【解答】(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC, ∴∠OCD=60°,CO=CD, ∴△OCD是等边三角形;
(2)解:△AOD为直角三角形. 理由:∵△COD是等边三角形. ∴∠ODC=60°, ∵将△BOC绕点C按顺时针方向旋转60°得△ADC, 第8页(共16页)
∴∠ADC=∠BOC=α, ∴∠ADC=∠BOC=150°, ∴∠ADO=∠ADC﹣∠CDO=150°﹣60°=90°,于是△AOD是直角三角形.
10.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0). ①画出△ABC关于x轴对称的△A1B1C1,写出B1点的坐标; ②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,写出B2点的坐标.
【解答】解:①如图所示,△A1B1C1即为△ABC关于x轴对称的图形, B1点的坐标是(1,0);
②如图所示,△A2B2C2即为△ABC绕原点O按逆时针旋转90°的三角形, B2点的坐标是(0,1).
11.如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线 第9页(共16页)
上,且∠CBF=∠CAB. (1)求证:直线BF是⊙O的切线; (2)若AB=5,sin∠CBF=,求BC和BF的长.
【解答】(1)证明:连接AE, ∵AB是⊙O的直径, ∴∠AEB=90°, ∴∠1+∠2=90°. ∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB, ∴∠1=∠CBF ∴∠CBF+∠2=90° 即∠ABF=90° ∵AB是⊙O的直径, ∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G. ∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=, ∵在Rt△AEB中,∠AEB=90°,AB=5, ∴BE=AB•sin∠1=, ∵AB=AC,∠AEB=90°, ∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE==2,
∴sin∠2===,cos∠2===, 在Rt△CBG中,可求得GC=4,GB=2, ∴AG=3, ∵GC∥BF, ∴△AGC∽△ABF,
