40.圆的对称性学案.doc
圆的对称性教案

§3.2 圆的对称性(第二课时)主备教师:王娇 参加教师: 授课日期: 教学目标:圆的旋转不变性,圆心角、弧、弦之间相等关系定理证明及应用.教学重点:圆心角、弧、弦之间关系定理的证明及应用.教学难点:“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.教学方法:指导探索法.教学过程:一、温故互查 :轴对称图形 中心对称图形二、设问导学:(1)圆是轴对称图形吗?(2)圆是中心对称图形吗?学生自己解决(3了解圆心角的定义BAO如图所示,∠AOB 的顶点在圆心,像这样顶点在圆心的角叫做圆心角. 师生共同讨论课本70页做一做的问题,并思考提出的问题在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.如果在同圆或等圆这个前提下,将题设和结论中任何一项交换一下,结论正确吗?师生共同讨论 得出结论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.例1 :如图,AB ,DE 是⊙O 的直径,C 是⊙O 的一点,且 AD CE ,BE 与CE的大小有什么关系?为什么?例2.如图,在⊙O 中,AB 、CD 是两条弦,OE ⊥AB ,OF ⊥CD ,垂足分别为EF .(1)如果∠AOB=∠COD ,那么OE 与OF 的大小有什么关系?为什么?(2)如果OE=OF ,那么 AB 与 CD 的大小有什么关系?AB 与CD 的大小有什么关系?•为什么?∠AOB 与∠COD 呢? OB AC ED F三、自学检测1.下列命题中,正确的有( )A .圆只有一条对称轴B .圆的对称轴不止一条,但只有有限条C .圆有无数条对称轴,每条直径都是它的对称轴D .圆有无数条对称轴,经过圆心的每条直线都是它的对称轴2.下列说法中,正确的是( )A .等弦所对的弧相等B .等弧所对的弦相等C .圆心角相等,所对的弦相等D .弦相等所对的圆心角相等 3.下列命题中,不正确的是( )A .圆是轴对称图形B .圆是中心对称图形C .圆既是轴对称图形,又是中心对称图形D .以上都不对四、巩固训练1、已知A,B 是⊙O 上的两点,∠AOB=1200,C 是的中点,试确定四边形OACB 的形状,并说明理由.2、课后习题第3题五、布置作业完成绩优学案六、教后反思。
《圆的对称性(1)》导学案_最新修正版

§5.2 圆的对称性(第一课时)学习目标:经历探索圆的对称性及圆心角、弧、弦之间关系的过程,理解圆的对称性及圆心角、弧、弦之间的相等关系.学习重点:圆心角、弧、弦之间关系定理.学习难点:“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.学习过程:一、举例:【例1】判断正误:(1)直径是圆的对称轴.(2)相等的圆心角所对的弧相等,所对的弦相等.【例2】已知A,B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,试确定四边形OACB的形状,并说明理由.【例3】如图,AB、CD、EF都是⊙O的直径,且∠1=∠2=∠3,弦AC、EB、DF是否相等?为什么?【例4】如图,弦DC、FE的延长线交于⊙O外一点P,直线PAB经过圆心O,请你根据现有圆形,添加一个适当的条件:,使∠1=∠2.二、课内练习:1、判断题(1)相等的圆心角所对弦相等()(2)相等的弦所对的弧相等()2、填空题⊙O中,弦AB的长恰等于半径,则弦AB所对圆心角是________度.3、选择题如图,O为两个同圆的圆心,大圆的弦AB交小圆于C、D两点,OE⊥AB,垂足为E,若AC=2.5 cm,ED=1.5 cm,OA=5 cm,则AB长度是___________.A、6 cmB、8 cmC、7 cmD、7.5 cm4、选择填空题如图2,过⊙O内一点P引两条弦AB、CD,使AB=CD,求证:OP平分∠BPD.证明:过O作OM⊥AB于M,ON⊥CD于N.A、OM⊥PBB、OM⊥ABC、ON⊥CDD、ON⊥PD【自我评价】1、本节课有困惑的题目是:2、本节课的学习收获是:。
小学数学《圆的对称性》教案

小学数学《圆的对称性》教案教学目标:1. 了解圆的对称轴和对称中心的概念。
2. 能通过画图判断圆是否有对称轴或者对称中心。
3. 能通过对称绘制图形。
教学重点:1. 圆的对称轴的概念和判断方法。
2. 圆的对称中心的概念和判断方法。
3. 对称绘制图形的方法。
教学难点:1. 对称绘制复杂图形。
2. 发现和利用圆的对称性质。
3. 培养学生观察、推理和绘图能力。
教学准备:1. 教师准备圆盘、圆规、铅笔等。
2. 学生准备笔、纸、橡皮等。
教学过程:一、导入新课1. 介绍圆的对称性质。
2. 引导学生回忆以前所学无线扭结的对称性质,进一步巩固学生对“对称”的理解。
二、讲授新课1. 圆的对称轴1)定义:将一个圆分成两个部分的直线叫做圆的对称轴。
2)判断方法:如果有一条直线让以它为对称轴对称的两个部分完全重合,那么这条直线就是圆的对称轴。
3)练习:教师出示一些图形,让学生判断圆的对称轴。
2. 圆的对称中心1)定义:它是圆上任意两点的中垂线的交点。
2)判断方法:圆上的任意两点的中垂线应相交于同一点上,这个点就是圆的对称中心。
3)练习:让学生结合图形,判断圆的对称中心。
3. 对称绘制图形1)定义:利用圆的对称性质进行绘制。
2)练习:让学生利用圆的对称中心和对称轴,画出不同的图形。
三、课堂练习1. 让学生在小组内练习对称绘制图形。
2. 教师出题,让学生分组展开竞赛。
四、作业布置1. 巩固课堂所学的内容,完成课后习题。
2. 要求学生在日常生活中,注意观察圆的对称性质。
五、课堂总结通过本节课的学习,学生掌握了圆的对称轴和对称中心的概念,能利用圆的对称性质进行对称绘制图形,这也为日常生活中的很多情况做好了准备。
圆的对称性学案
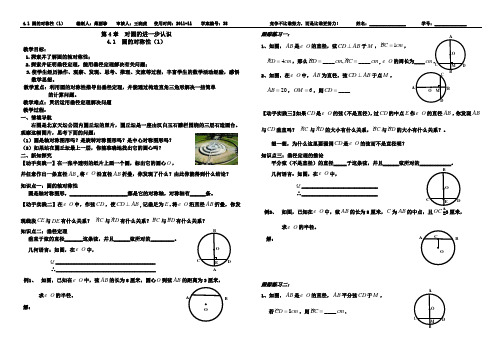
第4章 对圆的进一步认识4.1 圆的对称性(1)教学目标:1.探索并了解圆的轴对称性;2.探索并证明垂径定理,能用垂径定理解决有关问题;3.使学生经历操作、观察、发现、思考、推理、交流等过程,丰富学生的数学活动经验,感悟数学思想。
教学重点:利用圆的对称性推导出垂径定理,并能通过构造直角三角形解决一些简单的计算问题。
教学难点:灵活运用垂径定理解决问题 教学过程: 一、情境导航右图是北京天坛公园内圜丘坛的照片,圜丘坛是一座由汉白玉石雕栏围绕的三层石造圆台。
观察这幅图片,思考下面的问题:(1)圆是轴对称图形吗?是旋转对称图形吗?是中心对称图形吗? (2)如果站在圜丘坛最上一层,你能准确地找出它的圆心吗? 二、新知探究【动手实践一】在一张半透明的纸片上画一个圆,标出它的圆心O ,并任意作出一条直径A B ,将O 沿直径A B 折叠,你发现了什么?由此你能得到什么结论? 知识点一:圆的轴对称性圆是轴对称图形,______________________都是它的对称轴,对称轴有______条。
【动手实践二】在O 中,作弦C D ,使C D AB ⊥,记垂足为E .将O 沿直径A B 折叠,你发现线段C E 与D E 有什么关系? A C 与 A D 有什么关系? BC与 BD 有什么关系? 知识点二:垂径定理垂直于弦的直径_______这条弦,并且______弦所对的_________。
几何语言:如图,在O 中,______________________________________∴______________________________________例1、 如图,已知在O 中,弦A B 的长为8厘米,圆心O 到弦A B 的距离为3厘米,求O 的半径。
解:跟踪练习一:1、如图,A B 是O 的直径,弦C D AB ⊥于M , 1BCcm =, 4AD cm =,那么 ____,____BD cm AC cm ==,O 的周长为____cm .2、如图,在O 中,A B 为直径,弦C D AB ⊥于点M ,20A B =,6O M =,则____CD =【动手实践三】如果C D 是O 的弦(不是直径),过C D 的中点E 作O 的直径A B ,你发现A B 与C D 垂直吗? A C 与 A D 的大小有什么关系, BC与 BD 的大小有什么关系?。
圆的对称性 教案

圆的对称性教案教案标题:圆的对称性教案目标:1. 理解圆的对称性概念;2. 掌握圆的对称性特征及其应用;3. 培养学生观察、分析和解决问题的能力;4. 提高学生的几何思维能力和创造力。
教学重点:1. 圆的对称性概念;2. 圆的对称性特征;3. 圆的对称性应用。
教学难点:1. 理解圆的对称性特征;2. 运用圆的对称性解决问题。
教学准备:1. 教学投影仪或黑板;2. 圆规、直尺、铅笔等绘图工具;3. 圆形物体或图片。
教学过程:Step 1:导入新知1. 引入圆的对称性的概念,与学生一起回顾对称性的概念和常见形状的对称性特征。
2. 提问学生:你们知道圆是否具有对称性吗?为什么?Step 2:探究圆的对称性特征1. 展示一个圆形物体或图片,让学生观察,并讨论圆的对称性特征。
2. 引导学生发现圆的对称轴,并解释圆的对称性特征。
Step 3:巩固对称性特征1. 给学生分发练习题,让他们找出圆的对称轴并标出。
2. 学生互相交换练习题,检查答案并互相讨论。
Step 4:应用圆的对称性解决问题1. 引导学生思考如何利用圆的对称性解决实际问题。
2. 给学生提供一些实际问题,让他们运用圆的对称性进行解答。
Step 5:拓展活动1. 给学生展示一些具有圆对称性的艺术品或建筑物,让他们欣赏并分析其中的对称性特征。
2. 鼓励学生设计自己的圆对称艺术品或建筑物,并展示给同学们。
Step 6:总结与评价1. 与学生一起总结圆的对称性概念和特征。
2. 对学生的学习情况进行评价和反馈。
教学延伸:1. 鼓励学生探究其他形状的对称性特征,并与圆的对称性进行比较。
2. 给学生提供更复杂的圆对称性问题,培养他们的解决问题的能力。
教学资源:1. 圆形物体或图片;2. 练习题;3. 具有圆对称性的艺术品或建筑物图片。
教学评估:1. 教师观察学生在课堂上的参与情况;2. 学生完成的练习题和解答问题的能力;3. 学生设计的圆对称艺术品或建筑物的创造力和表现力。
圆的对称性(第一课时)导学案

圆的对称性(第一课时)导学案§3.2 圆的对称性(第一课时)导学学案【导入情景】我国古代石拱桥的杰出代表是举世闻名的河北省赵县的赵州桥(又称安济桥)该桥在隋朝大业初年(公元605年左右)为李春所创建,是一座空腹式的圆弧形石拱桥,赵州桥的设计构思和工艺的精巧,被誉为“国际历史土木工程的里程碑”。
赵州桥的主桥是圆弧形,它的跨度为37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?开始学习:回顾与思考:探究圆的对称性 1、什么是轴对称图形?OACB2、我们所学的圆是不是轴对称图形呢?如果是,它的对称轴是什么?它有多少对称轴?结论:圆是轴对称图形.它的对称轴可以是任意一条经过圆心的直线。
有无数条对称轴。
3、我们可以用什么方法验证上述发现?我们可用折叠的方法验证其对称性。
全面地认识圆 1、图中表示圆的直径的线段是表示圆的半径的线段是2、写出图中圆的弦的线段3、写出图中的圆弧线:优弧:(至少写2个)劣弧:(至少写2个) 4、(弦心距)过圆心O作OF⊥AB于F,OG⊥CD于G,则OF的长度表示的距离,则OG的长度表示的距离、CGEAFBD 探究活动:垂径定理 1.如图1,AB是圆的一条弦,作直径CD,使CD⊥AB,垂足为P: 请同学们将图1沿着直径CD对折,你能发现什么结论?C2.如图2,AB是圆的一条弦,作直径CD,使CD与AB相较于点P: 请同学们将图2沿着直径CD对折,还有上面结论吗?ADCBABD探究活动2:提炼新知识梳理归纳:AB是⊙的一条弦,作直径CD,使CD⊥AB,垂足为M.ACB CD是直径CD⊥AB垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.1、看看下列图形,能否使用垂径定理?为什么?D2、写出垂径定理的逆命题,并判断其真假。
EEE例题分析例1如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米AB求⊙O的半径。
例2如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
数学:3.2《圆的对称性》学案(1)(北师大版九年级下)
数学:3.2《圆的对称性》学案(1)(北师大版九年级下)学习目标:
经历探索圆的对称性及相关性质的过程.理解圆的对称性及相关知识.理解并掌握垂径定理.学习重点:
垂径定理及其应用.
学习难点:
垂径定理及其应用.
学习方法:
指导探索与自主探索相结合。
学习过程:
一、举例:
【例1】判断正误:
(1)直径是圆的对称轴.
3、已知:⊙O弦AB∥CD 求证:
⋂
=
⋂
BD AC
4、已知:⊙O半径为6cm,弦AB与直径CD垂直,且将CD分成1∶3两部分,求:弦AB的长.
5、已知:AB为⊙O的直径,CD为弦,CE⊥CD交AB于E DF⊥CD交AB于F求证:AE=BF
6、已知:△ABC内接于⊙O,边AB过圆心O,OE是BC的垂直平分线,交⊙O
于E、D两点,求证,
⋂
=
⋂
BC
2
1 AE
7、已知:AB为⊙O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连结OE,OF求证:⑴OE=OF ⑵ CE =DF
8、在⊙O中,弦AB∥EF,连结OE、OF交AB于C、D求证:AC=DB
9、已知如图等腰三角形ABC中,AB=AC,半径OB=5cm,圆心O到BC的距离为3cm,求ABC的长
10、已知:⊙O与⊙O'相交于P、Q,过P点作直线交⊙O于A,交⊙O'于B使OO'与AB平行求证: AB =2OO'
11、已知:AB为⊙O的直径,CD为弦,AE⊥CD于E,BF⊥CD于F求证:EC=DF。
圆的对称性
B '初三年级数学学案3.2圆的对称性学习目标:圆的旋转不变性,圆心角、弧、弦之间相等关系定理.学习重点:圆心角、弧、弦之间关系定理.学习难点:“圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明.一、导学过程:阅读教材 完成课前预习 【课前预习】 1:知识准备(1)圆是轴 图形,任何一条 所在直线都是它的对称轴. (2)圆是__________图形,对称中心为__________. 2:探究如图所示,∠AOB 的顶点在圆心,像这样顶点在圆心的角叫做 .请同学们按下列要求作图并回答问题: 如图所示的⊙O 中,分别作相等的圆心角∠AOB•和∠A•′OB•′将圆心角∠AOB 绕圆心O 旋转到∠A ′OB ′的位置,你能发现哪些等量关系?为什么?相等的弦: ;相等的弧: 理由:结论:在同圆或等圆中,相等的圆心角所对的 相等,所对的弦也 .表达式:同样,还可以得到:D在同圆或等圆中,如果两条弧相等,那么它们所对的 相等,•所对的弦也 .表达式:在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,•所对的 也相等.表达式:注:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也 。
二、【课堂活动】 活动1:预习反馈 活动2:典型例题例1.如图,在⊙O 中,弧AB=弧AC ,∠AOB=60 °,求证∠AOB=∠BOC=∠AOC活动3:随堂训练1、如图,AB ,CD 是⊙O 的两条弦。
(1)如果AB=CD ,那么 ,(2)如果弧AB=弧CD ,那么 , (3)如果∠AOB=∠COD ,那么 ,2、如图,AB 是⊙O 的直径,弧BC=弧CD=弧DE ,∠COD=35 °,求∠AOE 的度数。
活动4:课堂小结在同圆或等圆中,相等的圆心角所对的 相等,所对的弦也 . 在同圆或等圆中,如果两条弧相等,那么它们所对的 相等,•所对的弦也 .在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 ,•所对的 也相等.三、课后作业一、选择题.1.如果两个圆心角相等,那么( )A .这两个圆心角所对的弦相等;B .这两个圆心角所对的弧相等C .这两个圆心角所对的弦的弦心距相等;D .以上说法都不对2.在同圆中,圆心角∠AOB=2∠COD ,则两条弧AB 与CD 关系是( ) A .弧AB =2弧CD B .弧AB >2弧CD C .弧AB <2弧CD D .不能确定 3.如图5,⊙O 中,如果弧AB =2弧AC ,那么( ). A .AB=AC B .AB=AC C .AB<2AC D .AB>2AC(5) (6)二、填空题1.一条弦长恰好为半径长,则此弦所对的弧是半圆的_________.2.如图6,AB 和DE 是⊙O 的直径,弦AC ∥DE ,若弦BE=3,则弦CE=________. 三、解答题1.如图,在⊙O 中,C 、D 是直径AB 上两点,且AC=BD ,MC ⊥AB ,ND ⊥AB ,M 、N•在⊙O 上.(1)求证:弧AM =弧BN ;(2)若C 、D 分别为OA 、OB 中点,则弧AM=弧MN=弧NB 成立吗?2.如图以 ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若∠D=50°,求弧BE的度数和弧BF的度数.3.如图,∠AOB=90°,C、D是弧AB三等分点,AB分别交OC、OD于点E、F 求证:AE=BF=CD.。
圆的对称性教学设计
圆的对称性教学设计一、教学目标:1. 学生能够理解圆的对称性概念,并能应用到实际问题中。
2. 学生掌握圆的对称性性质,能够运用这一性质解决与圆的对称性有关的数学问题。
3. 学生培养观察、分析和推理的能力。
二、教学内容:1. 圆的对称轴及性质。
2. 圆内与圆对称的点的性质。
3. 与圆相关的对称图形的性质。
4. 运用圆的对称性解决实际问题。
三、教学过程:Step 1 引入(5分钟)引导学生回顾已学的相关知识,如什么是对称轴、什么是对称图形等,为圆的对称性的引入做铺垫。
Step 2 探究圆的对称轴及性质(15分钟)1. 要求学生将一张白纸剪成一个小圆形,然后用铅笔沿着圆形的边缘剪去一小段。
2. 让学生观察并描述剪下的小段。
3. 引导学生发现剪下的小段与原来的圆是否对称。
4. 引导学生找出圆的对称轴。
5. 通过多个小组的讨论,让学生总结出圆的对称轴的性质。
Step 3 圆内与圆对称的点的性质(20分钟)1. 让学生画一个半径为5cm的圆。
2. 让学生在圆内随便选取一个点,然后通过一条线将这个点与圆心连接。
3. 引导学生观察这条线段与圆的性质,并找出几个有关的点。
4. 让学生总结出这些点与圆的对称性质,并找出规律。
Step 4 与圆相关的对称图形的性质(20分钟)1. 让学生观察一些和圆有关的对称图形,如圆环、圆柱等。
2. 引导学生分析这些图形的性质,并总结出与圆的对称性有关的特点。
3. 让学生在小组内进行讨论,并展示自己的观察结果。
Step 5 运用圆的对称性解决实际问题(20分钟)1. 准备一些与圆的对称性有关的实际问题,如使用圆的对称性画出一幅有规律的图案等。
2. 让学生在小组内合作解决这些问题,并展示解决过程和答案。
Step 6 总结与拓展(10分钟)1. 让学生回顾本节课所学的内容,并复述圆的对称性的性质和应用。
2. 提出一些推广问题,引导学生进一步扩展和应用圆的对称性的知识。
四、教学评估:1. 在教学过程中,教师能通过观察学生的表现,评估学生对圆的对称性的理解程度。
圆的对称性教案
圆的对称性教案标题:圆的对称性教案教案概述:本教案旨在帮助学生了解圆的对称性,以及对称性在生活中的应用。
通过多种教学方法和活动,学生将能够理解圆的对称性的概念,并能够在实际生活中应用这一概念。
教学目标:1. 了解圆的对称性的概念。
2. 能够识别和描述圆的对称性。
3. 掌握圆的对称性在日常生活中的应用。
教具准备:1. 圆形的物体:球、扔子等。
2. 黑板或白板。
3. 教学PPT或投影仪。
教学步骤:引入活动:1. 引导学生观察身边的物体,询问他们有没有注意到某些物体具有对称性。
2. 让学生分享他们观察到的对称物体,并对他们进行讨论。
概念解释:1. 通过投影仪或黑板上的图片,解释圆的对称性概念。
强调圆在任何方向上都具有对称性。
2. 展示一些圆的图片,并与学生一起探讨这些图片是否具有对称性。
引导学生发现圆的任何一条直径都具有对称轴。
3. 让学生自己尝试画出一些圆,并找出其中的对称轴。
引导学生注意对称轴与圆心的关系。
活动一:探索圆的对称性1. 让学生分成小组,给每个小组发放一些圆形的物体。
2. 学生围坐在一起,观察自己手中的物体,并发现其中的对称轴。
3. 每个小组成员依次分享他们找到的对称轴。
4. 引导学生讨论这些物体是否在不同的方向上都具有对称性。
活动二:圆的对称性在生活中的应用1. 展示一些生活中常见的具有圆对称性的物体图片,如钟表、车轮等。
2. 让学生思考并讨论这些物体为什么需要具有对称性。
3. 分组活动:每个小组选择一个具有圆对称性的物体,并設計一则广告,展示这个物体的对称性在生活中的应用。
4. 让每个小组展示他们的广告,并进行讨论和评价。
总结:1. 回顾本堂课所学的内容,强调圆的对称性的重要性。
2. 确保学生理解并掌握了课程的目标,并解答他们的问题。
3. 鼓励学生在生活中寻找更多具有圆对称性的事物,并加深对圆对称性的理解。
教案评估:1. 监测学生在活动一中对圆的对称性的理解程度,以小组分享和讨论的形式评估。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青岛版九年级数学上册教学案 班级: 姓名:
课题 4.1圆的对称性(2) 课 型 新 授 总第( 40 ) 课时 主备人 马金勇
目标
1、了解圆的中心对称的性质。
2、探索并证明圆心角与其所对弧的关系定理,能运用它们解决有关实际问题。
重点 探索并证明圆心角有关定理,能运用它们解决有关实际问题。
预 习 内 容 批注
一、自主预习:
(一)前置补偿:垂径定理及其推论的内容是什么?
(二)预习新知·任务一: 圆的中心对称性:
圆是轴对称图形,__________________________都是对称轴,圆是
旋转对称图形,并且是中心对称图形,对称中心是_____,圆具有
旋转不变性,一个圆绕着它的_____旋转_____角度,都能够与原
来的图形_________.
·任务二:圆心角:
1、定义:顶点在_______的角叫做圆心角.
2、圆心角的度数和它所对的_____的度数_________.
3、把顶点在圆心的周角分成____等份时,每一份的圆心角是____度
的角,因为同圆中相等的________所对的弧相等,所以整个圆也被分
成_____等份,我们把每一份这样的弧叫做____度的弧.因此定义:
_________所对的弧,叫做1°的弧。
4、一个圆心角的度数和它所对的弧的度数有什么关系呢?
注意:(1)一定要弄清楚这里说的相等指的是“角与弧的度数”相
等,而不是“角与弧”相等,因为角于弧是两个不同的概念,不能
比较和度量.因此,只能写成∠AOB的度数=弧AB的度数,决不能写
成∠AOB =弧AB.
(2)度量一条弧有两个量:弧长和弧度.
弧长:即弧的长度,标志着弧“伸直” 以后的长短;
弧度:即弧的度数,标志着弧“弯曲”的程度.
·任务三:圆心角、弧、弦关系定理:
定理1: 。
定理2: 。
定理3: 。
【注意】正确理解和使用同心角、弧、弦三者关系
它们的关系可理解为:在同圆或等圆中,①圆心角_____,所对
的______相等,所对的______相等,三项“知一推二”,一项相
等,其余两项皆分别相等.这源于圆的旋转不变性,即:圆围绕
其圆心旋转任意角度,所得图形与原图形完全重合.
●
B
D E O A C
F
青岛版九年级数学上册教学案 班级: 姓名:
二、【互助探究】【例1】如图所示,AB是⊙O的弦,C,D是弦AB上两点,
且OC=OD,延长OC、OD,分别交⊙O于点E、F.试说明弧AE=弧BF.
【例2】如图,AB和CD是两条直径,弦CE∥AB,
求证:弧AD=弧AE
·任务四:圆心角与正多边形的关系:
1、如何画正多边形?
2、用直尺、圆规作一个证六边形?试一试。
三、巩固练习:
1、⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm.
则AB和CD的距离为( )
A.2cm B.14cm C.2cm或14cm D. 10cm或20cm
2、如图所示,在⊙O中,弦AB所对的劣弧为圆的13,
圆的半径为2cm,求AB的长.
四、系统总结:1、学到的知识
2、学到的方法
五、当堂 测评(10分) 得分:
1、如图,AB是⊙O的直径,M,N分别是OA,DB的中点,
CM⊥AB于M,DN⊥AB于N,求证:弧AC=弧BD.
2、如图所示,AB是⊙O的直径,AC为弦,OD∥BC,
交AC于D且OD=2cm,求BC的长.
预习困惑:
反思:
A D
O B C E
O
A C B
A B
C D
M O N
A
D
C
O
B
