奥数专题 圆的周长和面积
奥数圆的周长和面积

例:计算阴影部分的周长。
练一绦:计制月费于琦的周长,(,甲位「里米,例:现有两根圆木।横截面直径都是E分米।如果把它们用铁丝捆在一起, 两端各超一圈(接头不计),那之叵性卷多长的铁丝?求右图阴矍部分的周长;每个圆的半径都是E座外)例:求木图外圆的周长C 0(单位:介米)C©练一练:求右图阴导部介的周长。
例,如右图,已知正方先面积至EU三万厘米,求同的面积.络一练;二用右图口佐急剖分的向祖是对。
平E;里米,豆园的宜和ffl:已知右图中阴影部分的面积是如平方厘米।求圆环的面积0球一厘,右图口工行匹辿无::附面租是1QQ三内厘米,米明制部三、书面和舛有一个半圆形零件,周长是因.56厘米,求这个半是形零件的面一练一练;如右图,一个扇形的圆心角是90. ।它的周长是L4.照理米,求它的面积瓶一稣,L亘俎充邓小馆而和,1皇后:J里例;求出右图中正方形面积与圆的面积比c箫一练;石图圆多面租品91L干;:方云:那二正上出多百根品多少?如只王.6另体面引品平工月米,那么圆的面积是多少?I制:图中杷CD是边长为4米的正方形,分别以AB、EC、Oj、他为直径画半{圆,求这四举半圆孤所围成的阴影部分的面积。
练一练;图中三角形ABC是边长为6厘米的正三角形,求阴影部分的面积.例;计算阴影部郑的面积。
*~4L求下面各个图形中阴置言盼的面积(单位二厘米)2 .求下面各个图形中阴影言盼的面积(里位二厘米)朝工,计算下面图形中阴影部分的面积(单位:厘米,正方形边长外2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)朝4如图所示?三角形ABC 是直角三角形,AC 长4厘米,EC 长2厘米。
以AC.BC 为直径画半SL 两个半周的交点在AB 边上口求图中阴骂部分的面积口/C1IHZ 0在图中,正方形的边长是⑷厘米,求图中阴影部分的面积口,求右面各图形中阴舞部分的面积(单位二厘2、求右面各图形中阴膏部分的面积(单位二厘朝5h 求下面各图形中阴的E 分的面积(单位二厘米)在图的扇形中F正方形的面积是前平方厘米。
小升初奥数第十讲 圆的周长和面积

第十讲 圆的周长和面积【知识概述】圆的认识:圆中心的一点叫做圆心,圆心一般用字母“o ”表示;连接圆心和圆上任意一点的线段叫做半径,半径一般用字母“r ”表示;通过圆心并且两端都在圆上的线段叫做直径,直径一般用字母“d ”表示。
d圆心决定圆的位置, O r 半径决定圆的大小。
圆的特征:(1)在同圆或等圆中,半径的长度都相等,直径的长度都相等,直径长度是半径长度的2倍,用字母表示是:d =2r 或r =2d。
(2)圆是轴对称图形,圆有无数条对称轴。
圆的对称轴是直径所在的直线。
圆的周长:围成圆的曲线的长。
周长一般用字母“C ”表示,C=πd=2πr .圆周率:圆的周长和直径的比值,用字母π表示。
(π≈)圆的面积:圆所占平面的大小叫圆的面积,圆的面积一般用字母“S”表示, S =πr 2. 圆环的面积计算公式:S =πR2-πr2=π(R2-r2)扇形的面积公式: 360nr S n 360r S 22⨯=⨯=ππ或【典型例题】例1 求下面各圆的周长。
【学大名师】圆的周长是直径的π倍,是半径的2π倍。
解:(1) cm 3r = (2)d = 7dm84.18=(cm ) 98.21=(cm )例2 求下面各圆的面积。
(1)r = 4cm (2)d = 10dm (3)C = 18.84m【学大名师】圆的面积公式是2r S π=,要想求面积,要先求出半径。
解: (1)r=4cm24.501614.3414.32=⨯=⨯(平方厘米)(2)d=10dm10÷2=5(dm )5.782514.3514.32=⨯=⨯(2dm )(3)已知圆的周长,要先求出圆的半径,再利用2r S π=求面积。
C=18.84m3214.384.18=÷÷(m )26.28914.3314.32=⨯=⨯(2m )例3 小乌龟和小白兔又要比赛了,这一次小白兔沿大圆跑一圈,小乌龟沿两个小圆“∞”跑一圈,谁跑的路程长呢?好好想一想。
六年级奥数第12讲圆的周长与面积

学生课程讲义
有关圆的计算是指与圆有关的图形的周长和面积的计算,其中组合图形的面积是学习的重点。
在进行组合图形计算时,必须掌握有关概念、公式,要仔细观察、认真思考,看清组合图形是由哪几个基本图形组成的,看清题目的已知条件和问题,要注意找出图中的隐蔽条件与已知条件和问题的联系。
圆的周长:当一条线段绕着它的一个端点O,在平面上旋转一周时,它的另一个端点所画的封闭曲线叫做圆,端点O就是这个圆的圆心,这条封闭曲线的长度就是这个圆的周长,用C来表示,连接圆心到圆上任意一点的线段叫半径,一般用字母r来表示,通过圆并且两端都在圆上的
线段叫直径,用字母d表示,用
S
表示圆的面积,于是有下列公式
d=2r C=πd=2πr
S=πr2(其中π是圆周率,取π=3.14)
圆上两点间的部分叫做弧,这两点与圆心连接所得两条半径的夹角叫做圆心角,一般用n 表示圆心角的度数,用L表示弧长,则L=n
180
πr
圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形,则S=n
360πr2=1
2
Lr
【例1】计算图中阴影部分的面积。
(单位:
厘米)
【例2】求图中外圆的周长。
(单位:分米)
【例3】已知AC=AB,求图中阴影部分的周长。
小学五年级奥数 圆和扇形的周长与面积(二)

圆和扇形的周长与面积(二)本讲主线1. 不规则图形的求解4. 其他相关扇形:2. 差不变和等积变形弓形=扇形-△弯角=正方形-扇形.r2. 圆的面积:S=πr2谷子=弓形面积×23. 扇形:在圆的基础上×360120°5 5【例2】(★★★)板块一:不规则图形的常用解法求图中阴影部分的面积。
(π取3)如图, ABCD是正方形,且 FA=AD=DE=1,求阴影部分的面积。
(π取3.14 ) 45°45°20cm1【例4】(★★★)板块二:差不变和等积变形如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分【例3】(★★★☆)面积是多少?(圆周率取 3.14)DE 在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差。
(圆周率取3 )AC FB【例5】(★★★★)如图,矩形ABCD中,AB= 6厘米,BC= 4厘米,扇形ABE 半径AE =6厘米,扇形CBF 的半径CB= 4厘米,求阴影部分的面积。
(π取3)5. 圆中的直角三角形:顶点在圆上,并且经过圆心的三角形是直角三.C△ABC中,∠C=90°r B【超常大挑战】(★★★★)已知AB、AC、BC分别为3个半圆的直径. 请证明:阴影部分的面积=△ABC的面积. AB C 2知识大总结【今日讲题】1. 公式:圆=π×r2n扇形=圆×3602. 基本模型:弓形,弯角,谷子3. 不规则图形:割补、平移、旋转、对称4. 两个考点:⑴同加同减差不变⑵等积变形5. 一个模型:两个月亮换个三角A例1~超常大挑战【讲题心得】____________________________________________________________【家长评价】______________________________________________________________B C3。
六年级圆的周长奥数题

六年级圆的周长奥数题一、基础题型1. 一个圆的半径是3厘米,它的周长是多少厘米?- 解析:根据圆的周长公式C = 2π r(其中C表示周长,π通常取3.14,r为半径)。
当r = 3厘米时,C=2×3.14×3 = 18.84厘米。
2. 已知圆的直径是8分米,求这个圆的周长。
- 解析:因为圆的周长C=π d(d是直径),当d = 8分米时,C = 3.14×8=25.12分米。
3. 一个圆的半径扩大到原来的2倍,它的周长扩大到原来的几倍?- 解析:设原来圆的半径为r,则原来的周长C_1 = 2π r。
半径扩大2倍后变为2r,此时周长C_2=2π×(2r) = 4π r。
C_2div C_1=(4π r)div(2π r)=2,所以它的周长扩大到原来的2倍。
4. 有一个圆形花坛,半径是5米,在它的周围铺一条宽1米的小路,求小路的外沿周长是多少米?- 解析:小路的外沿半径为5 + 1=6米。
根据圆的周长公式C = 2π r,当r = 6米时,C=2×3.14×6 = 37.68米。
5. 一个半圆的直径是10厘米,求这个半圆的弧长(周长的一半)。
- 解析:圆的周长C=π d,半圆的弧长为(1)/(2)π d。
当d = 10厘米时,弧长=(1)/(2)×3.14×10 = 15.7厘米。
二、组合图形中的圆周长问题6. 正方形的边长为10厘米,在正方形内画一个最大的圆,求这个圆的周长。
- 解析:正方形内最大的圆的直径等于正方形的边长,即d = 10厘米。
根据圆的周长公式C=π d,C = 3.14×10 = 30.4厘米。
7. 长方形的长是12厘米,宽是8厘米,在长方形内画一个最大的半圆,求这个半圆的弧长。
- 解析:因为长方形的长是12厘米,宽是8厘米,所以这个半圆的直径最大为12厘米。
半圆的弧长=(1)/(2)π d=(1)/(2)×3.14×12 = 18.84厘米。
六年级奥数课程圆的知识
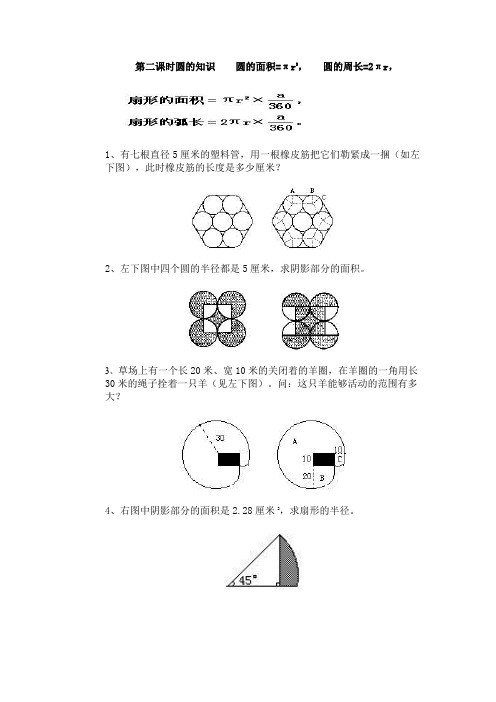
第二课时圆的知识圆的面积=πr2,圆的周长=2πr,
1、有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如左下图),此时橡皮筋的长度是多少厘米?
2、左下图中四个圆的半径都是5厘米,求阴影部分的面积。
3、草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?
4、右图中阴影部分的面积是2.28厘米2,求扇形的半径。
5、右图中的圆是以O 为圆心、径是10厘米的圆,求阴影部分的面积。
6、下页左上图中每个小圆的半径是1厘米,阴影部分的周长是多少厘米?
7、一只狗被拴在一个边长为3米的等边三角形建筑物的墙角上(见右上图),绳长是4米,求狗所能到的地方的总面积。
8、右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).
9、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π
10、下图池塘的周长251.2米,池塘周围(阴影)是一
条5米宽的水泥路,在路的外侧围一圈栏杆。
水泥路的面积是多少?栏杆长多少米?。
小学六年级奥数圆的周长和面积
圆的周长和面积一、填空:1、圆是平面上的一种()图形,围成圆的()的长叫做圆的周长。
在大大小小的圆中,它们的周长总是各自圆直径的()倍多一些,我们把这个固定的数叫做(),用字母()表示,它是一个()小数,在计算时,一般只取它的近似值()。
2、一个圆的直径扩大5倍,它的半径扩大()倍,它的周长扩大()倍,面积扩大()倍。
3、画一个周长12.56厘米的圆,圆规两脚间的距离是()厘米。
4、在一张长6厘米,宽4厘米的长方形纸片上画一个最大的圆,这个圆的半径是()厘米;如果画一个最大的半圆,这个圆的半径是()厘米,周长是(),面积是()。
5、()叫做圆的面积。
把圆沿着它的半径r分成若干等份,剪开后可以拼成一个近似的(),这个图形的长相当于圆周长的(),用字母表示是();宽相当于圆的(),用字母表示是()。
所以圆的面积S=( )×( ) =( )。
二、判断:1、圆的周长是这个圆的直径的3.14倍。
()2、小圆的圆周率比大圆的圆周率小。
()3、把一张圆形纸片对折若干次,所有折痕相交于圆心。
()4、圆的半径扩大3倍,它的直径就扩大6倍。
()5、半圆的周长等于圆周长的一半。
()6、经过一点可以画无数个圆。
()一、填空1、圆周率表示一个圆的()和()的倍数关系。
π约等于()。
2、在一个圆中,圆的周长是直径的()倍,是半径的()倍。
4、要画一个周长是31.4厘米的圆,圆规两角之间的距离是()厘米。
6、在一个正方形里面画一个最大的圆,这个圆的周长是6.28厘米,这正方形的面积是()平方厘米。
剩下的面积是()平方厘米。
7、大圆半径是3分米,小圆半径是2分米,小圆面积是大圆面积的()。
8、有大小两个圆,大圆直径是小圆半径的4倍,大圆周长是小圆的(),大圆面积是小圆的()。
9、用一根长12.56厘米的铁丝围成一个正方形,正方形的面积是()平方厘米;如果用这根铁丝围成一个圆,这个圆的面积是()平方厘米。
二、判断题(对的打√,错的打×)1,所有的直径都相等,所有的半径都相等. ()2,两端在圆上的线段,直径最长. ()3,经过圆心的线段就是直径. ()4,小圆的圆周率比大圆的圆周率小. ()5、圆的周长是6.28分米,那么半圆的周长是3.14分米。
六年级上册奥数题圆的面积
小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周,它的另一端在平面内画出一条封闭的曲线,这条封闭的曲线就是圆。
画圆时,固定的一点叫做圆心,从圆心到圆上任意一点的线段叫做圆的半径,在同一个圆中,所有的半径都相等。
通过圆心,并且两端在圆上的线段叫做直径。
在同一个圆中,所有的直径都相等,且等于半径的2倍。
圆心决定圆的位置,半径决定圆的大小。
任意一个圆,它的周长除以直径的商总是一个固定的数,这个数叫圆周率。
如果用C 表示圆周的长度,d 表示这个圆的直径,r 表示它的半径,π表示圆周率,就有C dπ=或2C r。
π是一个无限不循环小数,π=3.14159265358979323846…。
圆的周长:C=2πr 或C=πd,圆的面积:S=πr 2。
圆的周长和面积计算的基本方法是仔细观察,发现特点,找出内在的联系,常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计,把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米,钟面的面积是多少平方米?时针长2.7米,时针绕一圈时针尖端走过途径的长度是多少米?(得数保留一位小数)分析与解法:钟面的直径是5.8米这个条件是直接的,时针长指的是半径。
解:钟面的面积是:3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是:2×3.14×2.7≈17.0(米)。
例2、如图所示,试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法:本题有两问,一是比较阴影部分面积与大圆的面积;二是比较阴影部分周长与大圆的周长。
为了考虑问题方便,我们把图经过割补成图(1),在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解:先比较大圆面积与阴影部分的面积。
设大圆半径为r,则小圆半径为r,大圆面积为S 1=πr 2。
二年级奥数(圆形)-附答案
二年级奥数(圆形)-附答案题目一:计算圆的周长问题:一个圆形的周长是16厘米,求该圆的半径和面积。
答案:根据圆的周长公式可知,周长等于2πr(其中r为圆的半径),所以可以得到以下方程式:16 = 2πr求解上述方程式,解得r = 8/π 厘米。
接着,我们可以使用圆的面积公式计算圆的面积。
根据公式,圆的面积等于πr²,将半径代入计算可得:面积= π * (8/π)² = 64/π 平方厘米。
所以该圆的半径为8/π 厘米,面积为64/π 平方厘米。
题目二:计算扇形的面积问题:一个扇形的半径为10米,弧长为5米,求该扇形的面积。
答案:扇形的面积可以通过使用扇形面积公式来计算。
根据公式,扇形的面积等于弧长除以圆的周长乘以圆的面积。
首先,我们需要计算圆的周长,可以使用圆的周长公式计算:周长= 2πr = 2π * 10 = 20π 米。
然后,我们可以计算扇形的面积,将已知的半径和弧长代入公式:面积= (5 / 20π) * π * 10² = 10 平方米。
所以该扇形的面积为 10 平方米。
题目三:计算圆环的面积问题:一个圆环的外半径为12厘米,内半径为8厘米,求该圆环的面积。
答案:圆环的面积可以通过使用圆环面积公式来计算。
根据公式,圆环的面积等于外圆面积减去内圆面积。
首先,我们可以计算外圆的面积和内圆的面积,使用圆的面积公式:外圆面积= π * (12²) = 144π 平方厘米。
内圆面积= π * (8²) = 64π 平方厘米。
然后,我们可以计算圆环的面积,将已知的外圆面积和内圆面积相减:面积= 144π - 64π = 80π 平方厘米。
所以该圆环的面积为80π 平方厘米。
以上是二年级奥数圆形相关问题的答案。
希望对您有帮助!。
小学圆的面积奥数题100道及答案(完整版)
小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米,它的面积是多少平方厘米?答案:圆的面积= π×半径×半径,即3.14×3×3 = 28.26(平方厘米)题目2圆的直径是8 分米,求面积。
答案:半径= 8÷2 = 4 分米,面积= 3.14×4×4 = 50.24(平方分米)题目3一个圆的周长是18.84 米,求其面积。
答案:周长= 2×π×半径,所以半径= 18.84÷(2×3.14)= 3 米,面积= 3.14×3×3 = 28.26(平方米)题目4圆的面积是12.56 平方厘米,求半径。
答案:3.14×半径×半径= 12.56,半径×半径= 4,半径= 2 厘米题目5直径为10 厘米的圆,面积比半径为6 厘米的圆的面积小多少?答案:直径10 厘米的圆半径为5 厘米,面积为 3.14×5×5 = 78.5 平方厘米;半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米,小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍,面积扩大多少倍?答案:原来面积= π×半径×半径,半径扩大3 倍后,面积= π×(3×半径)×(3×半径)= 9×π×半径×半径,面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米,它们面积的和是多少?答案:面积分别为3.14×2×2 = 12.56 平方厘米,3.14×3×3 = 28.26 平方厘米,和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米,在里面画一个最大的正方形,正方形的面积是多少?答案:圆的半径= √(50.24÷3.14)= 4 分米,正方形的对角线是圆的直径为8 分米,正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米,面积增加了多少平方厘米?答案:原来面积= 3.14×4×4 = 50.24 平方厘米,新面积= 3.14×6×6 = 113.04 平方厘米,增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆,圆的面积是多少?答案:圆的直径= 8 厘米,半径= 4 厘米,面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米,求周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数专题 圆的周长和面积
1. 圆是平面上的曲线图形,它具有相对性。
2. 圆的周长=2r π=πd 圆的面积=2
r π
3. 计算圆的周长与面积常用割补法、旋转法、平移法等方法将不规则图形转化为规则图形求解。
在计算圆与其他平面图形组合而成的图形时,还可以用加减法,将不规则部分增加或减少一部分来求解。
4. 扇形是圆的一部分,它是由圆心角的两条半径和圆心角所对的弧围成的图形,其面积公式
02
0=360n S r π⨯扇形,弧长公式00
00
=2360360
n n L r d ππ⨯=⨯扇形。
一、 教材回顾
1.把一个边长是6分米的正方形铁皮加工成一个最大的圆,这个圆的周长是( )分米,面积是( )平方分米。
2.一种汽车的车轮直径是1米。
如果它每分钟转动400圈,那么它通过一座长2.512千米的大桥需要多少分钟?
3.两个大小不等的圆形仓库,小粮仓的底面周长是12.56米,它的占地面积是大粮仓的13。
大粮仓占地面积是多少平方米?
4. 求下面图形的周长。
(单位:厘米)
5. 已知圆的周长为
6.28厘米,求这个圆的面积是多少?
二、基础强化
例1如图,已知一个大圆中紧紧地排列着两个不同的小圆,并
且这三个圆的圆心恰好在直径上。
试比较外面的一个大圆的周
长与两个小圆的周长的和哪个长?为什么?
例2一个半圆的周长是10.28分米,这个半圆的的直径是多少厘米?
当堂模拟
1.如图,从点A到点C沿着大圆周走和沿着中小圆的圆周走,走的路程相同吗?
2. 画一个周长12.56厘米的圆,圆规两脚间的距离是()
厘米。
三、能力提升
例1求右图阴影部分的面积。
(单位:厘米)
例2 如图所示,两圆半径都是1厘米,且图中两个
阴影部分的面积相等。
求长方形ABO1O的面积。
你还有其他方法吗?
当堂模拟
1. 一个环形铁片,内圆直径是14厘米,外圆直径是18厘米,这个环形铁片的面积是多少?
2.下图正方形边长为8厘米,求中间阴影部分的面积。
四、走进名校
例1三角形的边长都为6厘米,现将三角形ABC沿着一条直线翻滚三次(如图),求A点经过的路程的长。
例2下面4个圆的半径都是10厘米,试求阴影部分的面积总和是多少平方厘米?( 取3)
当堂模拟
1.三角形的每边长都是3厘米,现将三角形ABC沿着一条直径翻滚763次(如下图所示翻滚
一次),求A点所经过的总路程。
2.求图中阴影部分的面积(单位:厘米)。
五、走进名校
例1在左图中三个圆的半径都是6厘米,三个圆两两相交于圆心,求阴影部分的面积。
例2左图中六个圆的半径相等,已知阴影部分的面积是80平方厘米,这六个圆面积之和是多少平方厘米?
当堂模拟
1.计算下面图形中阴影部分的面积(单位:厘米,半径为4)。
2.求下图中阴影部分与大圆的面积比。
六、分层检测(100分,我得了分)
A组(每题5分,共25分)
1、在一个圆形喷水池的周长是62.8米,绕着这个水池修一条宽2米的水泥路。
求路面的面积。
2、一个半圆形养鱼池,直径是4米,这个养鱼池的周长是多少米?占地面积是多少平方米?
3、一条漆包线长15.7米,正好在一个圆形线圈上绕满100圈,这个线圈的直径是多少?
4、如图,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是多少厘米?(保留两位小数)
5、一根长为6.28米的绳子可以绕直径1米的铁棍几圈?
B组(每题5分,共25分)
1.图中正方形边长为4厘米,求阴影部分的面积是多少平方厘米?
2.求下图中阴影部分的面积。
(单位:厘米)
4.求图中阴影部分的面积(单位:厘米)。
5.在下图中,两个阴影部分面积的和是多少?(单位:厘米)
C组(每题5分,共25分)
1.如图所示,AB=BC=8厘米,求阴影部分的面积。
2.下图中,长方形的宽为1厘米,以B点和C点为圆心,以宽为半径的扇形相交于G点,形成两个阴影部分。
已知两个阴影部分的面积相等,求长方形的长是多少厘米?
3.下图中,正方形边长6厘米,求阴影部分的面积。
4.如图所示,求图中阴影部分的面积(单位:厘米)。
5.一条直线上放着一个长方形1(如图),它的长与宽分别为4厘
90到达长方形2的位置,此时D点到米和3厘米,对角线长5厘米,让这个长方形绕顶点A顺时针旋转0
90到达长方形3的位置,此时C点到达了F点的位达了E点的位置。
再让长方形2绕顶点E顺时针旋转0
90到达长方形4的位置,此时B点到达了G点的位置。
再让长方置。
再让长方形3绕顶点E顺时针旋转0
90到达长方形5的位置,此时长方形1的A点到达了H点的位置。
求A点所走形4绕顶点E顺时针旋转0
过的总路程。
( 取3)
D组(每题5分,共25分)
1.如图所示,求阴影部分的面积(单位:厘米)
2.如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的
3.下图中,大圆的直径为4厘米,求阴影部分的面积。
4.在图中,正方形的边长是10厘米,求图中阴影部分的面积。
5.如图,半径为1厘米的圆,绕直角梯形滑动地滚动一周,求圆
心o所经过的总路程是多少?(其中AD=5厘米,BC=8厘米,AB=6厘米,
CD=8厘米)
圆与扇形拔尖部分
1.如图,一头羊被7米长的绳子拴在正五边形建筑物的一个顶点上,建筑物边长3米,周围都是草地,这头羊能吃到草的草地面积可达 _________平方米。
( =3)
2.已知:如图,在直角△ABC中,∠C=90°,AC=4,BC=3,以AC为直径作半圆,D为半圆弧的中点;连接BD,则线段BD把图形分成的两部分的面积之差(大减小)为.
D
C A
3.如下图,用木条钉一个边长6分米的等边三角形,平放在地面上,
再用硬纸片做一个半径1分米的圆形。
圆形纸片沿三角形外侧滚动一
周,圆经过的面积是多少平方分米(注:圆周率3.14)
4.图15-27中是一个半径为10厘米,中心角为135°的扇形,
D、E点是弧BC的三等分点,那么阴影部分的面积为多少平方
厘米?(π取3.14)
5.如图16-13所示,一块半径为2厘米的圆板,从平面上
标有1号位置起始,沿线段AB,BC,CD滚到2号位置。
如
果AB,BC,CD的长度都是20厘米,那么圆板经过区域的面
积是多少平方厘米?(取 3.14,保留两位小数)(角A,角
C,角D为直角)
6.如图16-14,将长方形ABCD绕顶点C顺时针旋转90度,若AB=4,BC=3,AC=5,求AD边扫过部分的面积(取3.14)
7.如图15-26,直角三角形的三条边长度为6、8、10,它的内部放了一个半圆。
图中阴影部分的面积是多少?
小升初单元模拟测试(每题10分,共100分)
姓名:班级:得分:
1.如图,两只蚂蚁同时从A点出发,要到达B点。
一只经大半圆向B点爬行,另一只经两个
小半圆周向B点爬行,如果它们速度相同,谁先到B点?
为什么?
2.求下图中阴影部分的面积。
(单位:厘米)
3.在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
4.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣
图形(如图)。
图中黑点是这些圆的圆心。
如果圆周率π=3.1416,
那么花瓣图形的的面积是多少平方厘米?
5.如图所示,圆O的直径AB与CD互相垂直,10
AB=厘米,以C为
圆心,CA为半径画弧,求图中阴影部分的面积。
6.在正方形ABCD中,AC=6厘米。
求阴影部分的面积。
7.如图所示,一个半径为1厘米的圆绕着一个直角三角形(各边长分别为3厘米、4厘米、
5厘米)滚动一周,求这个圆(圆心)所经过的总路程。
8.下图中,大圆的直径为8厘米,求阴影部分的面积。
9.如图,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等。
图中阴影部分的周长
是多少厘米?
10.如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径长都是1.求阴影部分
的面积。
