江苏省盐城中学2015届高三上学期12月月考试题数学 Word版含答案

合集下载

江苏省G4联盟(苏州中学、扬州中学、盐城2022-2023学年高三上学期12月联考数学试题

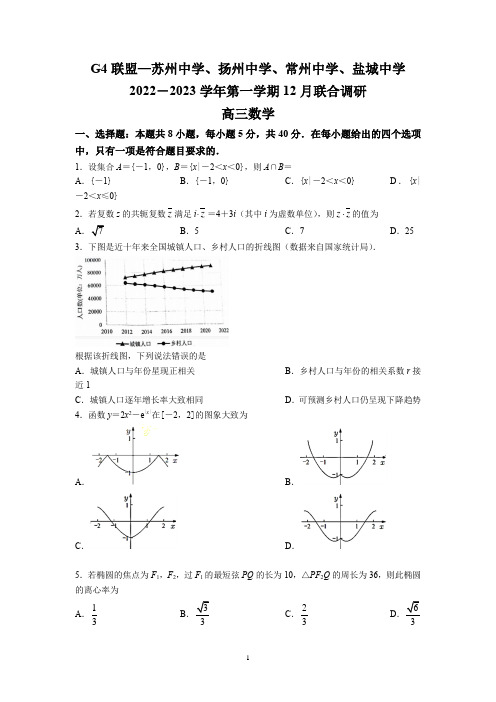
G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022－2023学年第一学期12月联合调研高三数学一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合A＝{－1，0}，B＝{x|－2＜x＜0}，则A∩B＝A．{－1} B．{－1，0} C．{x|－2＜x＜0} D．{x|－2＜x≤0}2．若复数z的共轭复数z满足i⋅z＝4＋3i（其中i为虚数单位），则z z⋅的值为A7B．5C．7D．25 3．下图是近十年来全国城镇人口、乡村人口的折线图（数据来自国家统计局）．根据该折线图，下列说法错误的是A．城镇人口与年份星现正相关B．乡村人口与年份的相关系数r接近1C．城镇人口逐年增长率大致相同D．可预测乡村人口仍呈现下降趋势4．函数y＝2x2－e|x|在[－2，2]的图象大致为A．B．C．D．5．若椭圆的焦点为F1，F2，过F1的最短弦PQ的长为10，△PF2Q的周长为36，则此椭圆的离心率为A．13B．33C．23D636．南宋时期，秦九韶就创立了精密测算雨量、雨雪的方法，他在《数学九章》载有“天池盆测雨”题，使用一个圆台形的天池盆接雨水．观察发现体积一半时的水深大于盆高的一半，体积一半时的水面面积大于盆高一半时的水面面积，若盆口半径为a ，盆地半径为b （0＜b ＜a ），根据如上事实，可以抽象出的不等关系为A 33322a ba b+<B 22a ba b+< C ．22222a b a b ++⎛⎫< ⎪⎝⎭D ．33322a b a b ++⎛⎫<⎪⎝⎭7．在数列{a n }中，()()111sin sin 10n n n n a a a a ++-⋅+=，则该数列项数的最大值为 A ．9B ．10C ．11D ．128．在△ABC 中，AB ＝4，BC ＝3，CA ＝2，点P 在该三角形的内切圆上运动，若AP mAB nAC =+（m ，n 为实数），则m ＋n 的最小值为A ．518B ．13C ．718D ．49二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知a ＞0，b ＞0，a ＋b ＝1，则 A ．114a b+≤B ．2222a b+≥C ．log 2a ＋log 2b ≤－2D ．1sin sin 2sin2a b +≤ 10．已知函数()x a a x f x e e --=+，()x a a x g x e e --=-，则 A ．函数y ＝g （x ）有且仅有一个零点B ．f ′（x ）＝g （x ）且g ′（x ）＝f （x ）C ．函数y ＝f （x ）g （x ）的图象是轴对称图形D ．函数()()g x y f x =在R 上单调递增11．乒乓球（tabletennis ），被称为中国的“国球”，是一种世界流行的球类体育项目，是推动外交的体育项目，被誉为“小球推动大球”．某次比赛采用五局三胜制，当参赛甲、乙两位中有一位赢得三局比赛时，就由该选手晋级而比赛结束．每局比赛皆须分出胜负，且每局比赛的胜负不受之前已赛结果影响．假设甲在任一局赢球的概率为p （0≤p ≤1），实际比赛局数的期望值记为f （p ），下列说法正确的是 A ．三局就结束比赛的概率为p 3＋（1－p ）3B ．f （p ）的常数项为3C ．1435f f ⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭D ．13328f ⎛⎫=⎪⎝⎭ 12．在四棱锥P －ABCD 中，底面ABCD 为正方形，P A ⊥底面ABCD ，P A ＝AB ＝1．G 为PC的中点，M 为平面PBD 上一点下列说法正确的是 A ．MG 的最小值为36B ．若MA ＋MG ＝1，则点M 的轨迹是椭圆C ．若156MA =M 的轨迹围成图形的面积为12π D ．存在点M ，使得直线BM 与CD 所成角为30°三、填空题：本题共4小题，每小题5分，共20分．13．在6x x ⎛- ⎝的展开式中，常数项为．14．如图，将绘有函数()sin 2f x M πϕ⎛⎫=+⎪⎝⎭（M ＞0，0＜φ＜π）部分图象的纸片沿x 轴折成直二面角，此时A ，B 10φ＝．15．我们利用“错位相减”的方法可求等比数列的前n 项和，进而可利用该法求数列{（2n －1）⋅3n }的前n 项和S n ，其操作步骤如下：由于S n ＝1×31＋3×32＋…＋（2n －1）⋅3n ，()23131333213n n S n +=⨯+⨯++-⋅，从而()()21232323213n n n S n +=--⨯++⨯+-⋅，所以()1133n n S n +=-⋅+，始比如上方法可求数列{n 2⋅3n }的前n 项和T n ，则2T n ＋3＝．16．已知函数f （x ）是定义在R 上的偶函数，且当x ≥0时，f （x ）＝2x ．若对任意x ∈[1，3]，不等式f （x ＋a ）≤f 2（x ）恒成立，则实数a 的取值范围是．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）在数列{a n }中，a ＝1，其前n 项和S n 满足2S n ＝（n ＋1）a n ，n ∈N *．（1）求数列{a n }的通项公式a n ；（2）若m 为正整数，记集合22n nn a a m a ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭≤的元素个数为b m ，求数列{b m }的前20项和．18．（本小题满分12分）在轴截面为正方形ABCD 的圆柱中，M ，N 分别为弧AD ，弧BC 的中点，且在平面ABCD 的两侧．（1）求证：四边形ANCM 是矩形；（2）求二面角B －MN －C 的余弦值．19．（本小题满分12分）文化月活动中，某班级在宣传栏贴出标语“学好数学好”，可以不同断句产生不同意思，“学/好数学/好”指要学好的数学，“学好/数学/好”强调数学学习的重要性，假设一段时间后，随机有N 个字脱落．（1）若N ＝3，用随机变量X 表示脱落的字中“学”的个数，求随机变量X 的分布列及期望；（2）若N ＝2，假设某同学检起后随机贴回，求标语恢复原样的概率． 20．（本小题满分12分）记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝1，c ＝2．（1）若2CD DB =，2AD CB ⋅=，求A ；（2）若23C B π-=，求△ABC 的面积． 21．（本小题满分12分）在平面直角坐标系xOy 中，已知点P 在抛物线C 1：y 2＝4x 上，圆C 2：（x －2）2＋y 2＝r 2（0＜r ＜2）．（1）若r ＝1，Q 为圆C 2上的动点，求线段PQ 长度的最小值；（2）若点P 的纵坐标为4，过P 的直线m ，n 与圆C 2相切，分别交抛物线C 1于A ，B （异于点P ），求证：直线AB 过定点． 22．（本小题满分12分）若对实数x 0，函数f （x ），g （x ）满足f （x 0）＝g （x 0）且f ′（x 0）＝g ′（x 0），则称()()()00,,f x x x F x g x x x <⎧⎪=⎨⎪⎩≥为“平滑函数”，x 0为该函数的“平滑点”．已知()323122x f x ax x x =-+，g （x ）＝bx ln x ．（1）若1是平滑函数F （x ）的“平滑点”，（ⅰ）求实数a ，b 的值；（ⅱ）若过点P （2，t ）可作三条不同的直线与函数y ＝F （x ）的图象相切，求实数t的取值范围；（2）对任意b ＞0，判断是否存在a ≥1，使得函数F （x ）存在正的“平滑点”，并说明理由．G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022-2023学年第一学期12月联合调研高三数学答案及其解析一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】A 2．【答案】D【解析】4334i z i z i ⋅=+⇒=-，所以25z z ⋅= 3．【答案】B【解析】因为乡村人口与年份望负线性相关关系，所以r 接近－1，故选B 4．【答案】D 5．【答案】C【解析】由题意得22245109436b b a a a ⎧⎧==⎪⇒⎨⎨=⎩⎪=⎩，所以226c a b =-=，故椭圆离心率为23c e a == 6．【答案】D 7．【答案】C 【解析】()()()()()()11112111cos cos sin sin sin 2n n n n n n n n n n n n n a a a a a a a a a a a a a +++++++--+--++⎡⎤⎡⎤⎣⎦⎣⎦-⋅+==-21sin 10n a =，所以{}2sin n a 为等差数列，公差为110，所以()2211sin sin 1110n a a n =+-⨯≤，所以110n -211sin 111a n -⇒≤≤≤，故选C 8．【答案】B【解析】()m n AP mAB nAC m n AB AC m n m n ⎛⎫=+=++⎪++⎝⎭，由P 在内切圆上，故APm n m n AB AC m n m n +=⎛⎫+ ⎪++⎝⎭，则11cos 16A =，所以BC 边上高为15h =圆半径15r =，故由平行线等比关系，可得213h r m n h -+=≥，故选B 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．【答案】BCD 【解析】选项A ，应该是114a b+≥，B ：22221a ba b+++≥，B 正确；C ：222log log 2log 22a ba b ++=-≤，C 正确；D ：1sin sin 2sincos 2sin 222a b a b a b +-+=⋅≤，D 正确；答案为BCD 10．【答案】ABD【解析】AB 正确，因为()f x 关于x a =轴对称，()g x 关于(),0a 中心对称，故()()f xg x 为中心对称图形，C 错误：而()()()()()220'g x f x q x f x B x ⎡⎤-=>⎢⎥∠⎣⎦或根据一般得分离常数变形可知D 正确；答案为：ABD 11．【答案】ABD 【解析】显然A 正确；()()()()()323131223343141151f p p p C p p C p p C p p ⎡⎤⎡⎤=+-+-+-+⨯-⎣⎦⎣⎦()03f =，13328f B ⎛⎫=⇒ ⎪⎝⎭，D 正确；求导或根据()f p 关于12对称，且p 越极端，越可能快结束，有11412352--≤，得1435f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，故答案为：ABD 12．【答案】ABC 【解析】A 选项判断：应用等体积法，可()()min min 11223MG AG =≥，A 正确； B 选项：因为面PBD 不与AG 垂直，也不平行，故轨迹不可能时圆，即为椭圆，B 正确； C 选项判断：设MH ⊥面PBD ，H ∈面PBD ，2151612MA HM =⇒=，故C 正确；D 选项判断：由于CD 与面PBD 夹角θ满足1sin 23θ=>，故[],6πθπθ∉-，D 错误；综上所述，答案为ABC三、填空题：本题共4小题，每小题5分，共20分．13．【答案】15【解析】展开式的通项为()()36621661rr rr Tr C x C x x --+⎛==- ⎝，当31602r -=，4r =时，为常数项15 14．【答案】56π【解析】如图，因为()f x 的周期为242T ππ==，所以22T CD ==，22TCD ==，所以22AB AC BC +22410M =+=解得3M =所以()32f x x πϕ⎛⎫=+ ⎪⎝⎭，所以()3032f ϕ==，1sin 2ϕ=，因为0ϕπ<<，所以6πϕ=或56π，又因为函数()f x 在y 轴右侧单调递减，所以56πϕ=． 15．【答案】()2113n n n +-+⋅【解析】2122213233n n T n =⨯+⨯+⋯+⋅① 222321313233n n T n +=⨯+⨯+⨯+⋅②②－①()()()222222322123123233133n n n T n n n +⎡⎤=-+-⋅+-⋅++--⋅+⋅⎣⎦()()3321333532133n n n n +=--⋅+⋅++-⋅+⋅()()212112333313n n n n n S n S n n n +++=---+⋅=-+⋅=-+⋅所以()212313n n T n n ++=-+⋅16．【答案】[]3,1-．【解析】()()()()[]2221,3f x a fx f x f x x +==⇒∀∈≤，[]23,1x a a +⇒∈-≤四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）解析：（1）()()()()()111212221212nn n n n n n n n n a S n a a S S n a na n n a na n n---=+⇒=-=+-⇒-=⇒=≥≥11111n n a a a n n -===⇒=- （2）2214222n n a n m m n m a n n ⎛⎫+⇒+⇒-+ ⎪⎝⎭≤≤≤，因为1422n n ⎛⎫+ ⎪⎝⎭≥，当且仅当2n =时成立，所以10b =，21b =，当3n ≥，35b =，47b =，59b =，611b =，…，2339b = 所以{}m b 的前20项和为()135739378+++++=．18．（本小题满分12分）【解析】（1）设轴截面正方形ABCD 边长为2a ，取弧BC 另一侧的中点Q ，则BC 与NQ 垂直平分，且2BC NQ a ==，所以四边形BNCQ 为正方形，2BQ NC a ==，因为M 为弧AD 中点，所以MQ AB ∥，四边形ABQM 为矩形，所以AM BQ ∥，所以AM CN ∥，所以四边形AMCN 为平行四边形，因为226AN AB BN a =+，2222MN MQ QN a =+=，所以22228AM AN MN a +==，所以AM ⊥AN ，所以四边形ANCM 为矩形；（2）由（1）知，226MB MC MQ QB a ==+=，2BN CN a ==，22MN a =，所以2MNB MNC π∠=∠=所以MNB MNC ∆∆≌，Rt △MBN 斜边MN 上的高626222a a h a==，作BP ⊥MN ，则CP ⊥MN ，∠BPC 即为二面角B -MN -C 的平面角，6BP CP ==，2BC a =，在△BPC 中，由余弦定理得222222341cos 233BP CP BC a a BPC BP CP a +--∠===-⨯，二面角B -MN -C 的余弦值为13- 19．（本小题满分12分）【解析】（1）随机变量X 的可能取值为0，1，2，12C()33351010C P X C ===，()1223356110C C P X C ===，()2123353210C C P X C ===，随机变量X 的分布列如下表：X 012P110 610 310随机变量X 的期望为()012 1.2101010E X =⨯+⨯+⨯= 法二：随机变量X 服从超几何分布X ～H （3，2，5），所以()26355E X =⨯= （2）设脱落一个“学”为事件A ，脱落一个“好”为事件B ，脱落一个“数”为事件C ，事件M 为脱落两个字M AA BB AB AC BC =++++，()2225110C P AA C ==，()2225110C P BB C ==，()112225410C C P AB C ⋅==，()112125210C C P AC C ⋅==，()112125210C C P BC C ⋅==，所以某同学捡起后随机贴回，标语恢复原样的概率为()()()()()()()11413125525P P AA P BB P AB P AC P BC =+⨯+++⨯=+⨯=，法二：掉下的两个字不同的概率为1020.810p -==，所以标语恢复原样的概率为()110.62p p -+=． 20．（本小题满分12分）解：（1）()112123333CD DB AD AB BD AB BC AB AC AB AB AC =⇒=+=+=+-=+ 所以()22212118112cos 233333333AD CB AB AC AB AC AB AC AB AC A ⎛⎫⋅=+-=--⋅=--⨯⨯=⇒⎪⎝⎭1cos 2A =，因为()0,A π∈，所以3A π=（2）法一：因为23C B π-=，所以562A C π=-，62AB π=-，因为2c b =，sin 2sinC B =，则5sin 2sin 6262A A ππ⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭化简整理得3tan 29A =，所以22tan332sin 141tan 2AA A ==+ 故面积为133sin 2S bc A == 法二：因为2sin 2sin c b C B =⇒=，因为23C B π-=，所以23sin 2sin sin 3B B B B π⎛⎫+=⇒=⎪⎝⎭①，联立22sin cos 1B B +=②解得3sin 27cos 27B B ⎧=⎪⎪⎨⎪=⎪⎩，所以3sin 2sin 7C B ==232C B ππ=+> 所以cos 0C <，则2cos 1sin 7C C =-=所以()33sin sin sin cos cos sin 14A B C B C B C =+=+=所以△ABC 的面积为133sin 214ABC S bc A ∆==． 21．（本小题满分12分）【解析】（1）设()2,2P t t ，则()222212411PQ PC t t --+-≥，当()0,0P ，Q 为2PC 线段与圆2C 的交点时，min 1PQ = （2）题意可知()4,4P ，过P 点直线()44y k x -=-与圆2C 相切， 2241k r k -=+，即()222416160r k k r --+-=，① 设直线AB 为：()()441m x n y -+-=，则与抛物线C 的交点方程可化为： ()()()()()()24844444(4)4y y m x n y x m x n y -+--+-=--+-⎡⎤⎡⎤⎣⎦⎣⎦，令44y z x -=-，则：()()2188440n z m n z m ++--=，② 题意有，①②方程同解，故有()()()[]()2233164164818444y r r m n m n -⎡⎤⎣=---+⨯=--+-⎦-，即：2111m n -=，故：直线AB 恒过()6,7-．22．（本小题满分12分）【解析】（1）（ⅰ）()21'332f x ax a =-+，()[]'1lng x b x =+，由题意可知10a -=，且532a b -=，故解得：1a =，12b =，（ⅱ）进一步()323,122ln ,12x x x x F x x x ⎧-+<⎪⎪=⎨⎪⎪⎩≥，过点()2,P t 作()F x 的切线，切点()(),x F x 满足方程：()()()2F x t F x x -=-，故题意等价于方程：()()()'2t F x F x x =--有3个不同根，()()()()'2p x F x F x x =--，()()()''2p x F x x =--，代入得1,2x ⎛⎫∈-∞ ⎪⎝⎭时，()p x 单调递减，1,22x ⎡⎫∈⎪⎢⎣⎭时，()p x 单调递增，[)2,x ∈+∞时，()p x 单调递减，故()13,2,ln 228t p x x ⎧⎫⎛⎫⎛⎫∈∈=-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ （2）题意等价于：0b ∀>，是否1a ∃≥，使得[]3223ln 221331ln 2x ax x bx x ax x b x ⎧-+=⎪⎪⎨⎪-+=+⎪⎩有解消a 有：()313212ln 122ln 1x x b x b x ---=-⇒=-，其中由0b >，可得23x e ⎛∈ ⎝，故题意进一步化简23x e ⎛∀∈ ⎝，是否1a ∃≥，使得()3ln 3122ln 1x x x a x x -+=-成立， 23x e ⎛⇔∀∈ ⎝，()23ln 3122ln 1x x x x x -+-≤是否恒成立设()()2243ln 231q x x x x x x =--+-，()()'83ln q x x x =-，故2,13x ⎛⎫∈ ⎪⎝⎭时，单调递减，(x e ∈，()q x 单调递增，故：()()10q x q =≥得证，即0b ∀>，31a ≥，使得()F x 存在的“平滑点”．。

2014-2015学年江苏省盐城中学高一(上)12月月考数学试卷

2014-2015学年江苏省盐城中学高一（上）12月月考数学试卷一、填空题（每题5分，共70分）1．（5分）（2014•上海模拟）设集合，则A∪B=_________2．（5分）的最小正周期为，其中ω＞0，则ω=_________．3．（5分）已知扇形的面积是4，扇形的圆心角的弧度数是2，则扇形的弧长是_________．4．（5分）计算lg8+lg125=_________．5．（5分）若函数f（x）是奇函数，且f（﹣1）=1，则f（1）=_________．6．（5分）若cos（π+α）=﹣，则sin（﹣α）=_________．7．（5分）函数f（x）=sin（2x﹣）在区间[0，]的值域_________．8．（5分）已知定义在R上的函数f（x）=2cos（x﹣），则函数的单调增区间是_________．9．（5分）已知函数y=sin（2x+）的图象为曲线C，函数y=sin（2x﹣）的图象为曲线C′，可将曲线C沿x轴向右至少平移_________个单位，得到曲线C′．10．（5分）（2008•虹口区二模）二次函数f（x）=2x2+bx+5，如实数p≠q，使f（p）=f（q），则f（p+q）=_________．11．（5分）已知函数f（x）=cos2x+4sinx，那么函数f（x）的值域是_________．12．（5分）定义在R上的函数f（x）满足f（x+y）=f（x）+f（y）+2xy（x，y∈R），f（1）=2，则（i）f（2）=_________；（ii）f（﹣2）=_________．13．（5分）已知函数f（x）=|sin（ωx+）|（ω＞0）在（π，π）上单调递减，则实数ω的取值范围是_________．14．（5分）设X={，，，，}，若集合G⊆X，定义G中所有元素之乘积为集合G的“积数”（单元素集合的“积数”是这个元素本身），则集合X的所有非空子集的“积数”的总和为_________．二．解答题（1）求tanα的值；（2）求的值．16．（14分）函数f（x）=Asin（ax+φ）（A＞0，ω＞0，|φ|＜），图象的一个最高点为（，2），图象两条相邻的对称轴之间的距离为．（1）求函数的解析式；（2）设α∈[0，π]，f（）=1，求α的值．17．（15分）已知f（x）是定义在R上的周期为3的函数，当x∈[0，3]时，f（x）=|x2﹣2x+|．（1）作出函数在区间[0，3）上的图象，并写出它的值域；（2）若函数y=f（x）﹣2m+在区间[﹣3，4]上有10个零点，求m的取值范围．18．（15分）已知奇函数f（x）的定义域为R，当x≥0，f（x）=（）x﹣1．（1）求函数f（x）的解析式，并判断函数在R上的单调性（不需证明，只需给出结论）；（2）对于函数f（x）是否存在实数m，使f（2m﹣mcosθ）+f（﹣1﹣sin2θ）＜f（0）对所有θ∈[0，]都成立？若存在，求出符合条件的所有实数m的范围；若不存在，说明理由．19．（16分）（2014•南通二模）为了净化空气，某科研单位根据实验得出，在一定范围内，每喷洒1个单位的净化剂，空气中释放的浓度y（单位：毫克/立方米）随着时间x（单位：天）变化的函数关系式近似为y=．若多次喷洒，则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和．由实验知，当空气中净化剂的浓度不低于4（毫克/立方米）时，它才能起到净化空气的作用．（1）若一次喷洒4个单位的净化剂，则净化时间可达几天？（2）若第一次喷洒2个单位的净化剂，6天后再喷洒a（1≤a≤4）个单位的药剂，要使接下来的4天中能够持续有效净化，试求a的最小值（精确到0.1，参考数据：取1.4）．20．（16分）已知函数f（x）=log2（4x+1）+kx（k∈R）是偶函数．（1）求k的值；（2）设函数，其中a＞0．若函数f（x）与g（x）的图象有且只有一个交点，求a 的取值范围．。

江苏省G4联盟(苏州中学、扬州中学、盐城中学、常州中学)22-23学年高三12月联考数学试题附答案

G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022－2023学年第一学期12月联合调研高三数学一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合A ＝{－1，0}，B ＝{x |－2＜x ＜0}，则A ∩B ＝ A ．{－1}B ．{－1，0}C ．{x |－2＜x ＜0}D ．{x |－2＜x ≤0}2．若复数z 的共轭复数z 满足i ⋅z ＝4＋3i （其中i 为虚数单位），则z z ⋅的值为AB ．5C ．7D ．253．下图是近十年来全国城镇人口、乡村人口的折线图（数据来自国家统计局）．根据该折线图，下列说法错误的是 A ．城镇人口与年份星现正相关B ．乡村人口与年份的相关系数r 接近1C ．城镇人口逐年增长率大致相同D ．可预测乡村人口仍呈现下降趋势4．函数y ＝2x 2－e |x |在[－2，2]的图象大致为A ．B ．C ．D ．5．若椭圆的焦点为F 1，F 2，过F 1的最短弦PQ 的长为10，△PF 2Q 的周长为36，则此椭圆的离心率为A ．13B ．3C ．23D ．36．南宋时期，秦九韶就创立了精密测算雨量、雨雪的方法，他在《数学九章》载有“天池盆测雨”题，使用一个圆台形的天池盆接雨水．观察发现体积一半时的水深大于盆高的一半，体积一半时的水面面积大于盆高一半时的水面面积，若盆口半径为a ，盆地半径为b （0＜b ＜a ），根据如上事实，可以抽象出的不等关系为A <B <C ．22222a b a b ++⎛⎫<⎪⎝⎭D ．33322a b a b ++⎛⎫<⎪⎝⎭7．在数列{a n }中，()()111sin sin 10n n n n a a a a ++-⋅+=，则该数列项数的最大值为 A ．9B ．10C ．11D ．128．在△ABC 中，AB ＝4，BC ＝3，CA ＝2，点P 在该三角形的内切圆上运动，若AP mAB nAC =+（m ，n 为实数），则m ＋n 的最小值为 A ．518B ．13C ．718D ．49二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知a ＞0，b ＞0，a ＋b ＝1，则A ．114a b+≤B ．22a b+≥C ．log 2a ＋log 2b ≤－2D ．1sin sin 2sin2a b +≤ 10．已知函数()x a a x f x e e --=+，()x a a x g x e e --=-，则 A ．函数y ＝g （x ）有且仅有一个零点B ．f ′（x ）＝g （x ）且g ′（x ）＝f （x ）C ．函数y ＝f （x ）g （x ）的图象是轴对称图形D ．函数()()g x y f x =在R 上单调递增 11．乒乓球（tabletennis ），被称为中国的“国球”，是一种世界流行的球类体育项目，是推动外交的体育项目，被誉为“小球推动大球”．某次比赛采用五局三胜制，当参赛甲、乙两位中有一位赢得三局比赛时，就由该选手晋级而比赛结束．每局比赛皆须分出胜负，且每局比赛的胜负不受之前已赛结果影响．假设甲在任一局赢球的概率为p （0≤p ≤1），实际比赛局数的期望值记为f （p ），下列说法正确的是 A ．三局就结束比赛的概率为p 3＋（1－p ）3B ．f （p ）的常数项为3C ．1435f f ⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭D ．13328f ⎛⎫=⎪⎝⎭ 12．在四棱锥P －ABCD 中，底面ABCD 为正方形，P A ⊥底面ABCD ，P A ＝AB ＝1．G 为PC 的中点，M 为平面PBD 上一点下列说法正确的是A ．MGB ．若MA ＋MG ＝1，则点M 的轨迹是椭圆C．若MA =M 的轨迹围成图形的面积为12π D ．存在点M ，使得直线BM 与CD 所成角为30°三、填空题：本题共4小题，每小题5分，共20分．13．在6x ⎛⎝的展开式中，常数项为．14．如图，将绘有函数()sin 2f x M πϕ⎛⎫=+⎪⎝⎭（M ＞0，0＜φ＜π）部分图象的纸片沿x 轴折成直二面角，此时A ，Bφ＝．15．我们利用“错位相减”的方法可求等比数列的前n 项和，进而可利用该法求数列{（2n －1）⋅3n }的前n 项和S n ，其操作步骤如下：由于S n ＝1×31＋3×32＋…＋（2n －1）⋅3n ，()23131333213n n S n +=⨯+⨯++-⋅，从而()()21232323213n n n S n +=--⨯++⨯+-⋅，所以()1133n n S n +=-⋅+，始比如上方法可求数列{n 2⋅3n }的前n 项和T n ，则2T n ＋3＝．16．已知函数f （x ）是定义在R 上的偶函数，且当x ≥0时，f （x ）＝2x ．若对任意x ∈[1，3]，不等式f （x ＋a ）≤f 2（x ）恒成立，则实数a 的取值范围是．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）在数列{a n }中，a ＝1，其前n 项和S n 满足2S n ＝（n ＋1）a n ，n ∈N *．（1）求数列{a n }的通项公式a n ；（2）若m 为正整数，记集合22n nn a a m a ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭≤的元素个数为b m ，求数列{b m }的前20项和． 18．（本小题满分12分）在轴截面为正方形ABCD 的圆柱中，M ，N 分别为弧AD ，弧BC 的中点，且在平面ABCD 的两侧．（1）求证：四边形ANCM 是矩形；（2）求二面角B －MN －C 的余弦值．19．（本小题满分12分）文化月活动中，某班级在宣传栏贴出标语“学好数学好”，可以不同断句产生不同意思，“学/好数学/好”指要学好的数学，“学好/数学/好”强调数学学习的重要性，假设一段时间后，随机有N 个字脱落．（1）若N ＝3，用随机变量X 表示脱落的字中“学”的个数，求随机变量X 的分布列及期望；（2）若N ＝2，假设某同学检起后随机贴回，求标语恢复原样的概率． 20．（本小题满分12分）记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝1，c ＝2．（1）若2CD DB =，2AD CB ⋅=，求A ；（2）若23C B π-=，求△ABC 的面积． 21．（本小题满分12分）在平面直角坐标系xOy 中，已知点P 在抛物线C 1：y 2＝4x 上，圆C 2：（x －2）2＋y 2＝r 2（0＜r ＜2）．（1）若r ＝1，Q 为圆C 2上的动点，求线段PQ 长度的最小值；（2）若点P 的纵坐标为4，过P 的直线m ，n 与圆C 2相切，分别交抛物线C 1于A ，B （异于点P ），求证：直线AB 过定点．22．（本小题满分12分）若对实数x 0，函数f （x ），g （x ）满足f （x 0）＝g （x 0）且f ′（x 0）＝g ′（x 0），则称()()()0,,f x x x F x g x x x <⎧⎪=⎨⎪⎩≥为“平滑函数”，x 0为该函数的“平滑点”．已知()323122x f x ax x x =-+，g （x ）＝bx ln x ．（1）若1是平滑函数F （x ）的“平滑点”，（ⅰ）求实数a ，b 的值；（ⅱ）若过点P （2，t ）可作三条不同的直线与函数y ＝F （x ）的图象相切，求实数t 的取值范围；（2）对任意b ＞0，判断是否存在a ≥1，使得函数F （x ）存在正的“平滑点”，并说明理由．G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022-2023学年第一学期12月联合调研高三数学答案及其解析一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】A 2．【答案】D【解析】4334i z i z i ⋅=+⇒=-，所以25z z ⋅= 3．【答案】B【解析】因为乡村人口与年份望负线性相关关系，所以r 接近－1，故选B 4．【答案】D 5．【答案】C【解析】由题意得22245109436b b a a a ⎧⎧==⎪⇒⎨⎨=⎩⎪=⎩，所以6c ==，故椭圆离心率为23c e a == 6．【答案】D 7．【答案】C【解析】()()()()()()11112111cos cos sin sin sin 2n n n n n n n n n n n n n a a a a a a a a a a a a a +++++++--+--++⎡⎤⎡⎤⎣⎦⎣⎦-⋅+==-21sin 10n a =，所以{}2sin n a 为等差数列，公差为110，所以()2211sin sin 1110n a a n =+-⨯≤，所以110n -211sin 111a n -⇒≤≤≤，故选C8．【答案】B【解析】()m n AP mAB nAC m n AB AC m n m n ⎛⎫=+=++⎪++⎝⎭，由P 在内切圆上，故APm n m n AB AC m n m n +=⎛⎫+⎪++⎝⎭，则11cos 16A =，所以BC 边上高为2h =6r =，故由平行线等比关系，可得213h r m n h -+=≥，故选B 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．【答案】BCD 【解析】选项A ，应该是114a b +≥，B ：22221a ba b+++≥，B 正确；C ：222log log 2log 22a b a b ++=-≤，C 正确；D ：1sin sin 2sin cos 2sin 222a b a b a b +-+=⋅≤，D 正确；答案为BCD 10．【答案】ABD【解析】AB 正确，因为()f x 关于x a =轴对称，()g x 关于(),0a 中心对称，故()()f x g x 为中心对称图形，C 错误：而()()()()()220'g x f x q x f x B x ⎡⎤-=>⎢⎥∠⎣⎦或根据一般得分离常数变形可知D 正确；答案为：ABD 11．【答案】ABD 【解析】显然A 正确；()()()()()323131223343141151f p p p C p p C p p C p p ⎡⎤⎡⎤=+-+-+-+⨯-⎣⎦⎣⎦()03f =，13328f B ⎛⎫=⇒ ⎪⎝⎭，D 正确；求导或根据()f p 关于12对称，且p 越极端，越可能快结束，有11412352--≤，得1435f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，故答案为：ABD 12．【答案】ABC 【解析】A 选项判断：应用等体积法，可()()min min 1122MG AG =≥A 正确；B 选项：因为面PBD 不与AG 垂直，也不平行，故轨迹不可能时圆，即为椭圆，B 正确；C 选项判断：设MH ⊥面PBD ，H ∈面PBD ，2112MA HM =⇒=，故C 正确； D 选项判断：由于CD 与面PBD 夹角θ满足1sin2θ=>，故[],6πθπθ∉-，D 错误；综上所述，答案为ABC三、填空题：本题共4小题，每小题5分，共20分．13．【答案】15【解析】展开式的通项为()()36621661rr r r Tr Cx C x --+⎛==- ⎝，当31602r -=，4r =时，为常数项15 14．【答案】56π【解析】如图，因为()f x 的周期为242T ππ==，所以22T CD ==，22TCD ==，所以AB ===解得M =所以()2f x x πϕ⎛⎫=+ ⎪⎝⎭，所以()0f ϕ==，1sin 2ϕ=，因为0ϕπ<<，所以6πϕ=或56π，又因为函数()f x 在y 轴右侧单调递减，所以56πϕ=． 15．【答案】()2113n n n +-+⋅【解析】2122213233n n T n =⨯+⨯+⋯+⋅① 222321313233n n T n +=⨯+⨯+⨯+⋅②②－①()()()222222322123123233133n n n T n n n +⎡⎤=-+-⋅+-⋅++--⋅+⋅⎣⎦()()3321333532133n n n n +=--⋅+⋅++-⋅+⋅()()212112333313n n n n n S n S n n n +++=---+⋅=-+⋅=-+⋅所以()212313n n T n n ++=-+⋅16．【答案】[]3,1-．【解析】()()()()[]2221,3f x a fx f x f x x +==⇒∀∈≤，[]23,1x a a +⇒∈-≤四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）解析：（1）()()()()()111212221212nn n n n n n n n n a S n a a S S n a na n n a na n n---=+⇒=-=+-⇒-=⇒=≥≥11111n n a a a n n -===⇒=-（2）2214222n n a n m m n m a n n ⎛⎫+⇒+⇒-+ ⎪⎝⎭≤≤≤，因为1422n n ⎛⎫+ ⎪⎝⎭≥，当且仅当2n =时成立，所以10b =，21b =，当3n ≥，35b =，47b =，59b =，611b =，…，2339b = 所以{}m b 的前20项和为()135739378+++++=．18．（本小题满分12分）【解析】（1）设轴截面正方形ABCD 边长为2a ，取弧BC 另一侧的中点Q ，则BC 与NQ 垂直平分，且2BC NQ a ==，所以四边形BNCQ为正方形，BQ NC ==，因为M 为弧AD 中点，所以MQ AB ∥，四边形ABQM 为矩形，所以AM BQ ∥，所以AM CN ∥，所以四边形AMCN 为平行四边形，因为AN ==，MN ==，所以22228AM AN MN a +==，所以AM ⊥AN ，所以四边形ANCM 为矩形；（2）由（1）知，MB MC ===，BN CN ==，MN =，所以2MNB MNC π∠=∠=所以MNB MNC ∆∆≌，Rt △MBN 斜边MN上的高2h a ==，作BP ⊥MN ，则CP ⊥MN ，∠BPC 即为二面角B -MN -C的平面角，2BP CP ==，2BC a =，在△BPC 中，由余弦定理得222222341cos 233BP CP BC a a BPC BP CP a +--∠===-⨯，二面角B -MN -C 的余弦值为13- 19．（本小题满分12分）【解析】（1）随机变量X 的可能取值为0，1，2，12C()33351010C P X C ===，()1223356110C C P X C ===，()2123353210C C P X C ===，随机变量X 的分布列如下表：随机变量X 的期望为()163012 1.2101010E X =⨯+⨯+⨯= 法二：随机变量X 服从超几何分布X ～H （3，2，5），所以()26355E X =⨯= （2）设脱落一个“学”为事件A ，脱落一个“好”为事件B ，脱落一个“数”为事件C ，事件M 为脱落两个字M AA BB AB AC BC =++++，()2225110C P AA C ==，()2225110C P BB C ==，()112225410C C P AB C ⋅==，()112125210C C P AC C ⋅==，()112125210C C P BC C ⋅==，所以某同学捡起后随机贴回，标语恢复原样的概率为()()()()()()()11413125525P P AA P BB P AB P AC P BC =+⨯+++⨯=+⨯=，法二：掉下的两个字不同的概率为1020.810p -==，所以标语恢复原样的概率为()110.62p p -+=． 20．（本小题满分12分）解：（1）()112123333CD DB AD AB BD AB BC AB AC AB AB AC =⇒=+=+=+-=+ 所以()22212118112cos 233333333AD CB AB AC AB AC AB AC AB AC A ⎛⎫⋅=+-=--⋅=--⨯⨯=⇒⎪⎝⎭1cos 2A =，因为()0,A π∈，所以3A π=（2）法一：因为23C B π-=，所以562A C π=-，62AB π=-，因为2c b =，sin 2sinC B =，则5sin 2sin 6262A A ππ⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭化简整理得tan 29A =，所以22tan2sin 1tan 2AA A ==+故面积为1sin 214S bc A == 法二：因为2sin 2sin c b C B =⇒=，因为23C B π-=，所以2sin 2sin sin 3B B B B π⎛⎫+=⇒=⎪⎝⎭①，联立22sin cos 1B B +=②解得sin cos B B ⎧=⎪⎪⎨⎪=⎪⎩，所以sin 2sin C B ==，232C B ππ=+> 所以cos 0C <，则cos C ==所以()sin sin sin cos cos sin 14A B C B C B C =+=+= 所以△ABC的面积为1sin 214ABC S bc A ∆==． 21．（本小题满分12分）【解析】（1）设()2,2P t t ，则211PQ PC -=≥，当()0,0P ，Q 为2PC 线段与圆2C 的交点时，min 1PQ =（2）题意可知()4,4P ，过P 点直线()44y k x -=-与圆2C 相切，r =，即()222416160r k k r --+-=，①设直线AB 为：()()441m x n y -+-=，则与抛物线C 的交点方程可化为：()()()()()()24844444(4)4y y m x n y x m x n y -+--+-=--+-⎡⎤⎡⎤⎣⎦⎣⎦，令44y z x -=-，则：()()2188440n z m n z m ++--=，② 题意有，①②方程同解，故有()()()[]()2233164164818444y r r m n m n -⎡⎤⎣=---+⨯=--+-⎦-，即：2111m n -=，故：直线AB 恒过()6,7-．22．（本小题满分12分）【解析】（1）（ⅰ）()21'332f x ax a =-+，()[]'1lng x b x =+，由题意可知10a -=，且532a b -=，故解得：1a =，12b =，（ⅱ）进一步()323,122ln ,12x x x x F x x x ⎧-+<⎪⎪=⎨⎪⎪⎩≥，过点()2,P t 作()F x 的切线，切点()(),x F x 满足方程：()()()2F x t F x x -=-，故题意等价于方程：()()()'2t F x F x x =--有3个不同根，()()()()'2p x F x F x x =--，()()()''2p x F x x =--，代入得1,2x ⎛⎫∈-∞ ⎪⎝⎭时， ()p x 单调递减，1,22x ⎡⎫∈⎪⎢⎣⎭时，()p x 单调递增，[)2,x ∈+∞时，()p x 单调递减，故()13,2,ln 228t p x x ⎧⎫⎛⎫⎛⎫∈∈=-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ （2）题意等价于：0b ∀>，是否1a ∃≥，使得[]3223ln 221331ln 2x ax x bx x ax x b x ⎧-+=⎪⎪⎨⎪-+=+⎪⎩有解消a 有：()313212ln 122ln 1x x b x b x ---=-⇒=-，其中由0b >，可得23x ⎛∈ ⎝，故题意进一步化简23x ⎛∀∈ ⎝，是否1a ∃≥，使得()3ln 3122ln 1x x x a x x -+=-成立，23x ⎛⇔∀∈ ⎝，()23ln 3122ln 1x x x x x -+-≤是否恒成立设()()2243ln 231q x x x x x x =--+-，()()'83ln q x x x =-，故2,13x ⎛⎫∈ ⎪⎝⎭时，单调递减，(x ∈，()q x 单调递增，故：()()10q x q =≥得证，即0b ∀>，31a ≥，使得()F x 存在的“平滑点”．。

江苏省盐城市2015届高三年级第一学期期中考试数学试题(20201222105708)

江苏省盐城市 2015 届高三年级第一学期期中考试数学试题(总分 160 分，考试时间 120 分钟 )一、填空题：本大题共14 小题，每题 5 分，计 70 分. 不需写出解答过程，请把答案写在答题纸的指定地点上 .1. 若会合A 0,1 ，会合 B 0, 1，则A B ▲.2b ,则2 2▲.．命题“若 a a b ”的否命题为3．函数f ( x) sin 2 x 的最小正周期为▲．4．若幂函数f (x) x ( Q) 的图象过点(2, 2)，则= ▲．25．若等比数列a n 知足 a2 3 ， a4 9 ，则 a6 ▲.6．若a,b均为单位向量，且 a (a 2b) ，则a, b的夹角大小为▲.7．若函数 f (x) 2x 1 m是奇函数，则 m ▲.2x 1．已知点 P 是函数f ( x) cos x(0 x ) 图象上一点，则曲线y f (x)在点 P 处的切线斜率的最小值83为▲.9．在等差数列 { a n} 中，S n是其前n项和，若S7=S5+4，则S9 S3= ▲.．在ABC 中，a,b,c 分别为角A,B,C的对边，若 a 4 ，10b 3 ， A 2B ，则 sin B = ▲.A DABC 中， AB=AC ，M 为 BC 中点，点 D 、 E11．如图，在等腰分别在边上，且 AD=1 EAB 、 AC D B， AE =3EC ，若B M C2第 11 题DME 90 ，则 cos A = ▲.12．若函数f ( x) x2 a x 2在(0, ) 上单一递加，则实数a的取值范围是▲.13. 设函数y x2 3 2n 1 x 2 4n 1 (n N * ) 的图象在 x 轴上截得的线段长为d n，记数列d n的前 n 项和为 S n ，若存在正整数n ，使得 log 2 m n218 建立，则实数 m 的最小值为▲.S n 1| x 3 2x 2 x | ( x 1)t R ，且 t0 ，使得 f (t)kt ”是假命题，14．已知函数 f ( x)ln x( x ，若命题“1)则实数 k 的取值范围是▲.二、解答题：本大题共 6 小题，计 90 分 .解答应写出必需的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定地区内 .15. (本小题满分 14 分 )已知函数 f ( x) sin x a cos x( 0) 知足 f (0) 3 ，且 f (x) 图象的相邻两条对称轴间的距离为 .（ 1 ）求 a 与的值；（ 2 ）若 f ( )1，(, ) ，求 cos( 5)的值.2 21216. (本小题满分 14 分 )设函数 y lg( x 24 x 3) 的定义域为 A ，函数 y2 , x (0, m) 的值域为 B .）当 m 2时，求 A B ；x 1（ 1（ 2 ）若“ xA ”是“ xB ”的必需不充足条件，务实数m 的取值范围 .17. (本小题满分 14 分 )设△ ABC 的面积为 S ，且 2S 3 AB AC 0 .（ 1 ）求角 A 的大小；（ 2 ）若 |BC|3 ，且角 B 不是最小角，求 S 的取值范围．18. ( 本小题满分 16 分 )如图是一块镀锌铁皮的边角料 ABCD ，此中 AB,CD,DA 都是线段，曲线段 BC 是抛物线的一部分，且点 B 是该抛物线的极点， BA 所在直线是该抛物线的对称轴. 经丈量， AB 2米， AD 3 米， AB AD ，点 C 到 AD, AB 的距离 CH, CR 1米．现要用这块边的长均为角料裁一个矩形 AEFG （此中点 F 在曲线段 BC 或线段 CD 上，点 E 在线段 AD 上，点G 在线段 AB 上） . 设 BG 的长为 x 米，矩形 AEFG 的面积为 S 平方米 . （1 ）将 S 表示为 x 的函数；（2 ）当 x 为多少米时， S 取得最大值，最大值是多少？DCHFEBG R A第18题19. (本小题满分 16 分 )设数列 a n 的前 n 项和为 S n ，且 S n 1 S n S n 1 3n 2 2(n 2,n N ) .（ 1 ）若 a n 是等差数列，求 a n 的通项公式；（ 2 ）若 a 11.① 当 a 21 时，试求 S 100 ；② 若数列 a n 为递加数列，且 S 3 k 225 ，试求知足条件的全部正整数 k 的值 .20. (本小题满分 16 分 )已知函数 f x e x ， g x xm ， m R .（ 1 ）若曲线 yf x 与直线 yg x 相切，务实数 m 的值；（ 2 ）记h x f x g x ，求 h x 在 0，1 上的最大值；（ 3 ）当 m0 时，试比较 e f x 2 与 g x 的大小 .盐城市 2015 届高三年级第一学期期中考试数学参照答案一、填空题：本大题共 14 小题，每题 5 分，计 70 分.1.0,1, 12. 若 ab , 则 2a2b3.4.1 5. 276. 7. 2238.3 9. 1210.5 11.1 12.[ 4,0]13. 1314. (1,1]235e二、解答题：本大题共6 小题，计 90 分 .解答应写出必需的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定地区内 . 15 ．解：（ 1 ）f (0)3 ， sin0 a cos03 ，解得 a3 ，2 分 f ( x) si n x3 c o sx2 si nx(， )4 分f ( x) 图象的相邻两条对称轴间的距离为 3，T22 ， | | 1，又0 ，因此 1 .6 分||（ 2 ）f ( )1， sin( ) 18 分，3 2(2 , )( , 5) 310236 666cos( 5 ) cos7cos 7cos(4 )1212 123cos( 5 ) cos cos sin sin4 2 6 .1412 x 23 4 3 41614x 3 01 x 3A (1,3)2y2 (0, m) y ( 2 1 ,2)B( 2,2)4x 1 (2,2)A Bmm 1m2 B (1,2) .632m 08“ xA ” “ xB ”B?A( 2 , 2) ? (1,3)102m 11121mm 1.14171ABCA, B, Ca,b, c2S 3AB AC2 1bc sin A 3bc cos A 0sin A3 cos A 022tan A 3 4 A(0, )A2 .632BC3a33b c2sin Bsin Csin3b 2sin B,c 2sin C8S1bcsin A3 sin B sinC3 sin Bsin(B)10233sin B( 3 cos B 131 cos2B3)3 122 sin B)3( sin 2B4)sin(2 B2 4264B( , ), 2B ( ,5)S (0, 3) .146 36 2 64181BBA x.2BC y 22px( p0)C (1,1)2 p 1DBC yx (0 x 1) .4yC (1,1),D (2,3) CDy 2x 1(1 x 2) .6GA2 xCHFEB G R A xSx (2 x),0 x1,8(2 x 1)(2x), 1 x2.1320x 1S x (2 x)2x 2x 213 12 3x2Sx 2 x 2S 0x102 2 x3x(0, 2)S0 S3x(2,1)S 0 Sx2 S max 4 6 123391x2S(2 x 1)(2 x)2( x5)2 94 8x5 9 14S max4894 6 x5 S max 9.168948AAD x191S nna 1 n(n 1) d d n 2 ( a 1d)n2 2 2S n 1 S n S n 1d( n 1)2(a 1d)(n 1) d n 2 (a 1 d )n d(n 1)2(a 1d)(n 1)22 2 222d(3n 22) 3(a 1d)n,222d (3n 22) 3(a 1d)n 3d n 23(a 1 d)n d 3n 2 222 2 23d 3, ad, d 2d 2,a 1a n 2n42 1 211S nan 2bn n2, n 3a 1d2S n 1 S nSn 13n 2 2(n 2)S nSn 1 S n 23(n 1)2 2 6a n a n1a n 26n 3(n 2)S100a 1 (a 2 a 3 a 4 ) ( a 5 a 6 a 7 )(a 98a99a 100)11(6 2 3 6 983) 33 10000 .82a 2 1.3a 2xS n1S n S n13n 2 2(n 2)S 1S 2 S 3 14 S 2 S 3 S 4 293a 1 2a 2 a 3 14 a 3 11 2x3a 1 3a 2 2a 3 a 4 29 a 4 x 410S nSn 1S n 2 3(n 1)22a nan 1an 26n 3(n 2)a n 1 a nan 16n 3(n 3)a n2an 16( n 3)a 5 a 2 6 x 6a na 1 a 2 a 3a 4 a 57 x 111233S 3ka 1 a 2 a 3 (a 4 a 5a 6 ) (a 7 a 8 a 9 )(a 3 k 2 a 3k 1 a 3k )S3k12 x1(6 43 6(3k 2) 3)( k 1)2S3k9k 2 x 3 22514x 9k2222( 7 ,11)k5 .163 3201f xe xg xx mP x 0 , y 0f xe x ex=1x 02 P0，1 gxx m m 1.42h xxm e x h xe x x m e xx (m 1) e x , x [0,1] .m 1 0 m 1hx 0hx0，1h xmaxh 1 1m e6m 11 1 m 2x0， m 1hx 0 h xxm 1,1 h x0 h xhm h 11 m e .(i)m 1 m ee m2h x max h 0 m1ee(ii)m1 m e1mh x maxh 1 1 m e8e1m 1 1m 2h x0hx0，1h xminh 0m .me1 m e mem .e h x maxh x max101e 1(3) 当 m 0 时， efx 2=e ex 2， g x x ，①当 x 0 时，明显 e f x 2 g x ；②当 x0 时， ln e f x 2=lne ex 2e x 2 ， ln g xln x ，x 21x记函数x =eln xe 2 eln x ，12 分则x =12e x1 e x2 1 ，可知x 在 0,+上单一递加，又由1 0，2 0 知，ex xx 在 0,+上有独一实根x 0 ，且 1 x 0 2 ，则x 0=e x21 0，即 e x 021 （），x 0x 0当 x 0, x 0 时， x 0 ， x 单一递减；当 x x 0，+ 时，x0 ， x 单一递加，因此xx 0 =e x 0 2 ln x 0 ，14 分联合（）式 ex 021 ，知 x 02 ln x 0 ，x 01x 0 2 2x 01 x 02因此 x x 0x 01x 2ln x 0 ，=2=x 0x 00 ，则 x =ex 0即 e x 2 ln x ，因此 e e x 2x .综上， e fx 2g x .16 分（说明：若学生找出两个函数 y e f x 2 与 yg x 图象的一条分隔线，如 y x 1 ，而后去证e fx 2x 1 与 x 1 g x ，且取等号的条件不一致，相同给分）。

江苏省盐城中学2015届高三上学期1月月考试题数学

江苏省盐城中学2015届高三上学期1月月考试题数学试卷说明：本场考试时间120分钟，总分160分．一、填空题：（本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上）1.已知集合{}1,0,1,2--=A ，集合{}1|2<=x x B ，则B A ⋂ = ▲ ． 2.已知复数32iiz -=+（i 为虚数单位），则||z 的值为 ▲ ． 3.从1,2,3,4,5这5个数中一次随机地取2个数,则所取2个数的和为5的概率是 ▲ ．4.阅读下面的流程图，若输入10=a ，6=b ，则输出的结果是 ▲ ．5.在ABC ∆中，33=a ，2=c ，150=B ，则b = ▲ ．6.已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的体积为 ▲ ．7.在等比数列{}n a 中，21=a ，164=a ，则=+⋅⋅⋅++n a a a 242 ▲ ． 8.函数a x f x+-=131)( （)0≠x ，则“1)1(=f ”是“函数)(x f 为奇函数”的 ▲ 条件．（用“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”填写） 9.已知,0,0,0>>>n y x ,1=+y nx yx 41+的最小值为,16则n 的值为 ▲ ． 10．在ABC ∆中，90=∠A ，1=AB ，2=AC ，设点Q P ,，满足λ=,)1(λ-=R ∈λ.若2-=⋅，则λ的值是 ▲ ．11.设)1,0(),0,1(B A ，直线,:ax y l =圆()1:22=+-y a x C .若圆C 既与线段AB 又与直线l 有公共点，则实数a 的取值范围是 ▲ ．12．若()x f 是定义在R 上的奇函数，当0≥x 时，()()⎩⎨⎧+∞∈--∈+=),1[,13)1,0[,1log 2x x x x x f ，则函数()()21-=x f x g 的所有零点之和为 ▲ ．13.如图，已知椭圆的中心在坐标原点，焦点21,F F 在x 轴上且焦距为c 2，21A A 为左右顶点，左准线l 与x 轴的交点为M ，图②1:6:112=F A MA ，若点p 在直线l 上运动，且离心率21<e ，则21tan PF F ∠的最大值为 ▲ ．14.若函数()ax x x f +=ln 存在与直线02=-y x 平行的切线，则实数a 的取值范围是 ▲ ．二、解答题：（本大题共6小题，计90分. 解答应写出必要的文字说明、证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15. （本小题14分）已知PA ⊥菱形ABCD 所在平面，点E 、F 分别为线段BC 、PA 的中点．（Ⅰ）求证：BD PC ⊥；（Ⅱ）求证：BF ∥平面PDE ．16. （本小题14分）已知ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，2=a ，向量)1,1(-=，)22sin sin ,cos (cos -=C B C B ，且⊥．（Ⅰ）求A ；（Ⅱ）当)127cos(sin C B -+π取得最大值时，求B 和b ．17. （本小题14分）如图①，一条宽为1km 的两平行河岸有三个工厂A 、B 、C ，工厂B 与A 、C 的直线距离都是2km ，BC 与河岸垂直，D 为垂足．现要在河岸AD 上修建一个供电站，并计划铺设地下电缆和水下电缆，从供电站向三个工厂供电．已知铺设地下电缆、水下电缆的费用分别为2万元/km 、4万元/km ．（Ⅰ）已知工厂A 与B 之间原来铺设有旧电缆（原线路不变），经改造后仍可使用，旧电缆的改造费用是0.5万元/km ．现决定将供电站建在点D 处，并通过改造旧电缆修建供电线路，试求该方案总施工费用的最小值；（Ⅱ）如图②，已知供电站建在河岸AD 的点E 处，且决定铺设电缆的线路为CE 、EA 、EB ，若)30(πθθ≤≤=∠DCE ，试用θ表示出总施最小工费用y （万元）的解析式,并求总施工费用y 的值．图①18. （本小题16分）若椭圆C 的方程为)0(12222>>=+b a by a x ，1F 、2F 是它的左、右焦点，椭圆C 过点)1,0(，且离心率为322=e ．（Ⅰ）求椭圆的方程；（Ⅱ）设椭圆的左右顶点为A 、B ，直线l 的方程为4=x ，P 是椭圆上任一点，直线PA 、PB 分别交直线l 于G 、H 21HF GF ⋅的值；（Ⅲ）过点)0,1(Q 任意作直线m （与x 轴不垂直）与椭圆C M 、N 两点，与y 轴交于R 点MQ RM λ=，NQ RN μ=．证明：μλ+为定值．19. （本小题16分）已知函数112)(22+-+=x a ax x f ，其中R a ∈．（Ⅰ）当1=a 时，求曲线)(x f y =在原点处的切线方程；（Ⅱ）求)(x f 的单调区间；（Ⅲ）若)(x f 在),0[+∞上存在最大值和最小值，求a 的取值范围．20. （本小题16分）已知无穷数列{}n a 的各项均为正整数，n S 为数列{}n a 的前n 项和．（Ⅰ）若数列{}n a 是等差数列，且对任意正整数n 都有()22n n S S =成立，求数列{}n a 的通项公式；（Ⅱ）对任意正整数n ，从集合12{,,,}n a a a 中不重复地任取若干个数，这些数之间经过加减运算后所得数的绝对值为互不相同的正整数，且这些正整数与12,,,n a a a 一起恰好是1至n S 全体正整数组成的集合．（ⅰ）求12,a a 的值；（ⅱ）求数列{}n a 的通项公式．）PA⊥平面，又ABCD是菱形，=，∴PA AC A．PD的中点G。

2024-2025学年江苏省盐城市高一上学期第二次月考(12月)数学检测试卷(含解析)

2024-2025学年江苏省盐城市高一上学期第二次月考（12月）数学检测试卷一、单选题（共8小题，每小题5分，共40分）1.命题p ：“0x ∀>，212x +≥”的否定为（）A.0x ∀>，212x +<．B.0x ∀≤，212x +<．C .00x ∃≤，0212x +≥．D.00x ∃>，0212x +<．2.cos 495 的值是（）A.12B.12-C.22D.22-3.下列函数中与函数y x =相等的函数是（）A.2y =B.y =C.y =D.2x y x=4.为提升学生学习双语的热情“G11•四市十一校”教学联盟计划在2025年4月举行“语文情境默写”､“英语读后续写”两项竞赛，我校计划派出20人的代表队，据了解其中擅长语文的有10名同学，擅长英语的有12名同学，两项都擅长的有5名同学，请问该代表队误选了几名均不擅长的同学？（）A .1B.2C.3D.55.设()2,01,0x a x f x x x x -+≤⎧⎪=⎨+>⎪⎩，若()0f 是()f x 的最小值，则实数a 的取值范围是（）A.(),1∞- B.(],1-∞ C.1,+∞D.[)1,+∞6.幂函数()()215m f x m m x+=--在()0,∞+上单调递减，则m 等于（）A.2- B.3 C.2-或3D.3-7.设0.40.6a =，0.60.4b =，0.40.4c =，则,,a b c 的大小关系是（）A.b c a >>B.c a b >>C.a b c>> D.a c b>>8.已知函数()()212log 3f x x =+，且()()2log 2f m f >，则实数m 的取值范围为（）A .()4,∞+ B.10,4⎛⎫⎪⎝⎭C.1,44⎛⎫⎪⎝⎭D.()10,4,4∞⎛⎫⋃+ ⎪⎝⎭二、多选题（共3小题，每小题6分，选对部分得部分分，选错不得分）9.下列说法中正确的是（）A.()π180rad -=-B.第一象限角都是锐角C.一个扇形半径扩大一倍，圆心角减小一半，则面积不变D.终边在直线y x =-上的角的集合是π|π4a k k α⎧⎫=-∈⎨⎬⎩⎭Z ，10.下列各组不等式中，同解的是（）A.21412xx x >-+与2412x x x >-+B.326x x ->+与()()22326x x ->+C.()()222log 2log 3x x >-与223x x >-D.()()()()23012x x x x --<++与()()()()23120x x x x --++<11.已知函数()[]()212,2f x x x =-+∈-，()[]()220,3g x x x x =-∈，则下列结论正确的是（）A.[]2,2x ∀∈-，()f x a <恒成立，则实数a 的取值范围是(),5-∞B.[]2,2x ∃∈-，()f x a <，则实数a 的取值范围是()3,-+∞C.[]0,3x ∃∈，()g x a =有解，则实数a 的取值范围是[]1,3-D.[]0,3t ∀∈，[]2,2x ∃∈-，使得()()f xg t =三、填空题（共2小题）12.“数摺聚清风，一捻生秋意”是宋朝朱翌描写折扇的诗句，折扇出人怀袖，扇面书画，扇骨雕琢，是文人雅士的宠物，所以有“怀袖雅物”的别号.当折扇所在扇形的圆心角为120 时，折扇的外观看上去是比较美观的，若该折扇的伞骨OB 长为40cm ，那么全部打开后的扇面弧AB 长为多少__________cm13.已知()2xxf x a a-=-+（0a >且1a ≠），若()23f =，则()2f -=______.14.国庆期间，一个小朋友买了一个体积为a 的彩色大气球，放在自己的房间内，由于气球密封不好，经过t 天后气球体积变为e kt V a -=.若经过15天后，气球体积变为原来的23，则至少经过__________天后，气球体积不超过原来的13（lg30.48,lg20.3≈≈，结果保留整数）.四、解答题（共5小题第15题13分，16，17题15分，18，19题17分）15.已知3sin 5α=-且α为第三象限角.（1）求cos α，tan α的值；（2）求()()()sin 2πcos 3ππsin sin π2αααα-++⎛⎫--- ⎪⎝⎭的值.16.已知集合111642xA x ⎧⎫⎪⎪⎛⎫=<≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭，{}623B x m x m =-≤≤+.（1）若1m =，求B A ð；（2）命题:p x A ∈，命题:q x B ∈，若p 是q 的充分不必要条件，求实数m 的取值范围.17.已知函数()f x 是定义在R 上的奇函数，且当0x ≤时，()22f x x x =--．（1）画出函数()y f x =的图象；（2）求函数()()f x x ∈R 的解析式（写出求解过程）．（3）求()y f x =，[]4,2x ∈-的值域．18.为了应对美国可能对华贸易的不当竞争，到2034年，某外贸玩具公司计划将生产成本控制在80万元，要比2024年下降20%，假设这期间每一年生产成本降低的百分比都相等，记2024年后第*()x x ∈N 年的成本支出为()f x 万元.（1）求2024年的生产成本为多少万元（2）求()f x 的解析式；（3）按此计划，到哪一年，可以将该工厂的成本控制在45万元以内？（参考数据：lg20.30,lg30.48≈≈，lg70.85≈）19.定义：若对定义域内任意x ，都有()()f x a f x +>（a 为正常数），则称函数()f x 为“a 距”增函数.（1）若()2f x x x =+，()1,x ∞∈-+，试判断()f x 是否为“1距”增函数，并说明理由；（2）若()312f x x x =-，∈是“a 距”增函数，求a 的取值范围；（3）若()22x k xf x +=，()1,x ∞∈-+，其中k ∈R ，是“2距”增函数，求k 的取值范围考试时间120分钟，总分1502024-2025学年江苏省盐城市高一上学期第二次月考（12月）数学检测试卷分命题：田家炳实验中学徐乐审核：李堡中学袁晨均唐洋中学王志钢一、单选题（共8小题，每小题5分，共40分）1. 命题p ：“0x ∀>，212x +≥”的否定为（）A. 0x ∀>，212x +<． B. 0x ∀≤，212x +<．C. 00x ∃≤，0212x +≥． D. 00x ∃>，0212x +<．【答案】D 【解析】【分析】利用全称命题的否定规则即可得到命题p 的否定【详解】命题p ：“0x ∀>，212x +≥”的否定为“00x ∃>，0212x +<”故选：D2. cos 495 的值是（）A.12B. 12-C.D. 【答案】D 【解析】【分析】由题意利用诱导公式求解即可.【详解】()()cos 495cos 360135cos135cos 9045sin 45=+==+=-= 故选：D .3. 下列函数中与函数y x =相等的函数是（）A. 2y =B. y =C. y =D. 2x y x=【答案】B【解析】【分析】化简各函数的解析式，根据函数的定义域、值域逐项判断可得答案..【详解】函数y x =的定义域为x ∈R ，值域为y ∈R ，对于A，函数2y x ==的定义域为{}|0x x ≥，故A 错误；对于B，函数y x ==，定义域为x ∈R ，故B 正确；对于C，函数y x ==的值域为{}|0y y ≥，故C 错误；对于D ，函数2x y x x==的定义域为{}|0x x ≠，故D 错误.故选：B.4. 为提升学生学习双语的热情“G11•四市十一校”教学联盟计划在2025年4月举行“语文情境默写”､“英语读后续写”两项竞赛，我校计划派出20人的代表队，据了解其中擅长语文的有10名同学，擅长英语的有12名同学，两项都擅长的有5名同学，请问该代表队误选了几名均不擅长的同学？（）A. 1 B. 2C. 3D. 5【答案】C 【解析】【分析】利用venn 图，结合集合的运算求解.【详解】设擅长语文的同学构成集合A ，擅长英语的同学构成集合B ，20人代表队构成全集U ，则()card 10A =，()card 12B =，()card 5A B ⋂=，()card 20U =，()()()()card card card card 1012517A B A B A B ∴⋃=+-⋂=+-=，()()card 20173U A B ∴⋃=-=ð，所以语文和英语均不擅长的同学人数为20173-=人.故选：C.5. 设()2,01,0x a x f x x x x -+≤⎧⎪=⎨+>⎪⎩，若()0f 是()f x 的最小值，则实数a 的取值范围是（）A. (),1∞-B. (],1-∞ C. (1,+∞)D. [)1,+∞【答案】B 【解析】【分析】根据分段函数分段求其最小值，再根据()0f 是()f x 的最小值可得答案.【详解】当0x >时，()12f x x x=+≥，当且仅当1x x =即1x =时等号成立，当0x ≤时，()2f x x a =-+为单调递减函数，所以()min 02=f a ，若()0f 是()f x 的最小值，则2a ≤2，解得1a ≤.故选：B.6. 幂函数()()215m f x m m x+=--在()0,∞+上单调递减，则m 等于（）A. 2-B. 3C. 2-或3D. 3-【答案】A 【解析】【分析】由已知可得2m =-或3m =，分别验证即可求解.【详解】因为()()215m f x m m x+=--为幂函数，所以251m m --=，解得2m =-或3m =，当2m =-时，()1f x x -=在()0,∞+上单调递减，符合题意，当3m =时，()4f x x =在()0,∞+上单调递增，不符合题意，所以2m =-.故选：A .7. 设0.40.6a =，0.60.4b =，0.40.4c =，则,,a b c 的大小关系是（）A. b c a >> B. c a b>> C. a b c>> D. a c b>>【答案】D 【解析】【分析】根据指数函数单调性，比较,b c ；根据幂函数单调性，比较,a c ，即可得出结果.【详解】因为指数函数0.4x y =是减函数，所以0.60.40.40.4<，即b c <；又因为幂函数0.4y x =是增函数，所以0.40.40.60.4>，即a c >，所以a c b >>.故选：D.8. 已知函数()()212log 3f x x =+，且()()2log 2f m f >，则实数m 的取值范围为（）A. ()4,∞+ B. 10,4⎛⎫ ⎪⎝⎭C. 1,44⎛⎫⎪⎝⎭D. ()10,4,4∞⎛⎫⋃+ ⎪⎝⎭【答案】C 【解析】【分析】根据函数()f x 的奇偶性、单调性可得答案.【详解】因为233x +≥，所以函数()()212log 3f x x =+的定义域为x ∈R ，关于原点对称，且()()()212log 3-=+=f x x f x ，所以()f x 偶函数，又0x ≥时，23+=u x 是单调递增函数，所以()()212log 3f x x =+是单调递减函数，根据对称性知0x <时，所以()()212log 3f x x =+是单调递增函数，由()()2log 2f m f >得2log 2<m ，解得144m <<.故选：C.二、多选题（共3小题，每小题6分，选对部分得部分分，选错不得分）9. 下列说法中正确的是（）A. ()π180rad -=-B. 第一象限角都是锐角C. 一个扇形半径扩大一倍，圆心角减小一半，则面积不变D. 终边在直线y x =-上的角的集合是π|π4a k k α⎧⎫=-∈⎨⎬⎩⎭Z ，【答案】AD 【解析】为【分析】根据弧度制、象限角、终边相同的角等知识对选项进行分析，从而确定正确答案.【详解】对于A ，()π180rad -=-，故A 正确；对于B ，300- 是第一象限角，但不是锐角，故B 错误；对于C ，设扇形半径为r ，圆心角为θ，则面积为2112S r θ=，若半径扩大一倍，圆心角减小一半，则面积()2221222S r r θθ=⨯⨯=，故C 错误；对于D ，终边在直线y x =-上的角的集合是π|π4a k k α⎧⎫=-∈⎨⎬⎩⎭Z ，，故D 正确.故选：AD.10. 下列各组不等式中，同解的是（）A.21412xx x >-+与2412x x x >-+B. 326x x ->+与()()22326x x ->+C. ()()222log 2log 3x x >-与223x x >-D. ()()()()23012x x x x --<++与()()()()23120x x x x --++<【答案】ABD 【解析】【分析】根据题意，对选项中的每对不等式进行分析、求解集，再判断它们的解集是否相同，即可求解.【详解】对于A ，因为()22412288x x x -+=-+≥，所以21412xx x >-+等价于2412x x x >-+，所以两个不等式的解集相同，故A 正确；对于B ，因为|x ―3|>|2x +6|，所以(x ―3)2>(2x +6)2，所以解集相同，故B 正确；对于C ，因为log 2(2x )>log 2(x 2―3)，所以2x >0x 2―3>02x >x 2―33x <<，解不等式223x x >-，得13x -<<，所以解集不同，故C 错误；对于D ，()()()()23012x x x x --<++等价于()()()()23120x x x x --++<，所以两个不等式的解集相同，故D 正确.故选：ABD .11. 已知函数()[]()212,2f x x x =-+∈-，()[]()220,3g x x x x =-∈，则下列结论正确的是（）A. []2,2x ∀∈-，()f x a <恒成立，则实数a 的取值范围是(),5-∞B. []2,2x ∃∈-，()f x a <，则实数a 的取值范围是()3,-+∞C. []0,3x ∃∈，()g x a =有解，则实数a 的取值范围是[]1,3-D. []0,3t ∀∈，[]2,2x ∃∈-，使得()()f x g t =【答案】BCD 【解析】【分析】求出()f x 、()g x 的值域，再根据恒成立问题或能成立问题逐项判断可得答案.【详解】当[]2,2x ∈-时，()[]3,5f x ∈-，当[]0,3x ∈时，()()[]222111,3g x x x x =-=--∈-，对于A ，[]2,2x ∀∈-，若()f x a <恒成立，则5a >，所以实数a 的取值范围是()5,∞+，故A 错误；对于B ，[]2,2x ∃∈-，若()f x a <，则3a >-，所以实数a 的取值范围是()3,∞-+，故B 正确；对于C ，[]0,3x ∃∈，()g x a =有解，则实数a 的取值范围是[]1,3-，故C 正确；对于D ，由于[]0,3t ∀∈，[]2,2x ∃∈-，使得()()f x g t =，等价于()g t 在[]0,3上的值域包含于()f x 在[]22-,上值域，显然[][]1,335-⊆-，的值域，故D 正确.故选：BCD.【点睛】关键点点睛：解题的关键点是求出函数值域后，转化为恒成立或能成立问题求参数.三、填空题（共2小题）12. “数摺聚清风，一捻生秋意”是宋朝朱翌描写折扇的诗句，折扇出人怀袖，扇面书画，扇骨雕琢，是文人的雅士的宠物，所以有“怀袖雅物”的别号.当折扇所在扇形的圆心角为120 时，折扇的外观看上去是比较美观的，若该折扇的伞骨OB 长为40cm ，那么全部打开后的扇面弧 AB 长为多少__________cm 【答案】80π3【解析】【分析】利用弧长公式进行求解.【详解】2π1203︒=，由弧长公式得2π80π4033⨯=cm.故答案：80π313. 已知()2x x f x a a-=-+（0a >且1a ≠），若()23f =，则()2f -=______.【答案】1【解析】【分析】根据解析式代入求值即可.【详解】因为()2x x f x a a -=-+，所以()22322f a a -=-+=，所以221a a --=，所以()()2222222121f aa a a ---=-+-=-+=-+=.故答案为：1.14. 国庆期间，一个小朋友买了一个体积为a 的彩色大气球，放在自己的房间内，由于气球密封不好，经过t 天后气球体积变为e kt V a -=.若经过15天后，气球体积变为原来的23，则至少经过__________天后，气球体积不超过原来的13（lg30.48,lg20.3≈≈，结果保留整数）.【答案】40【解析】【分析】依题意可得215ln 3k -=，设1t 天后体积变为原来的13，则11ln 3kt -=，两式相除，结合对数的为运算求出1t ，即可得解.【详解】由题意得，经过t 天后气球体积变为e kt V a -=，经过15天后，气球体积变为原来的23，即152e 3k a a -=，即152e 3k -=，则215ln 3k -=，设1t 天后体积变为原来的13，即11e 3kt a a -=，即11e 3kt -=，则11ln 3kt -=，两式相除可得12ln1531ln 3k kt -=-，即11322ln lg 152lg 2lg 30.30.4833log 0.375113lg 30.48ln lg 33t --====≈=--，所以140t ≈天，则至少经过40天后，气球体积不超过原来的13.故答案为：40四、解答题（共5小题第15题13分，16，17题15分，18，19题17分）15. 已知3sin 5α=-且α为第三象限角.（1）求cos α，tan α的值；（2）求()()()sin 2πcos 3ππsin sin π2αααα-++⎛⎫--- ⎪⎝⎭的值.【答案】（1）4cos 5α=-，3tan 4α= （2）7-【解析】【分析】（1）根据题意由同角三角函数的基本关系求解即可；（2）利用诱导公式化简，再代入求解即可.【小问1详解】因3sin 5α=-且α为第三象限角，所以4cos 5α==-，为sin 3tan cos 4ααα==；【小问2详解】()()()()()sin 2πcos 3πsin cos πsin cos πcos sin cos sin sin sin π2αααααααααααα-++-++--==--⎛⎫--- ⎪⎝⎭31tan 171tan 1434αα----===---.16. 已知集合111642x A x ⎧⎫⎪⎪⎛⎫=<≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭，{}623B x m x m =-≤≤+.（1）若1m =，求B A ð；（2）命题:p x A ∈，命题:q x B ∈，若p 是q 的充分不必要条件，求实数m 的取值范围.【答案】（1）[)[]5,42,5--= B A ð（2）1,22⎡⎤-⎢⎥⎣⎦【解析】【分析】（1）解指数不等式求出集合A ，再求B A ð；（2）由题意可得A 是B 的真子集，得到不等式组，求出答案.【小问1详解】集合{}11164242x A x A x x ⎧⎫⎪⎪⎛⎫=<≤==-≤<⎨⎬ ⎪⎝⎭⎪⎪⎩⎭，集合{}{}162355B x x x x =-≤≤+=-≤≤.则[)[]5,42,5B A =--⋃ð；【小问2详解】若p 是q 的充分不必要条件，则A 是B 的真子集，且A ≠∅，可得64232m m -≤-⎧⎨+≥⎩，解得122m -≤≤，所以实数m 的取值范围为1,22⎡⎤-⎢⎥⎣⎦.17. 已知函数()f x 是定义在R 上的奇函数，且当0x ≤时，()22f x x x =--．（1）画出函数()y f x =的图象；（2）求函数()()f x x ∈R 的解析式（写出求解过程）．（3）求()y f x =，[]4,2x ∈-的值域．【答案】（1）答案见解析（2）222,0()2,0x x x f x x x x ⎧->=⎨--≤⎩（3）[8,1]-【解析】【分析】（1）作出0x ≤时的图象（抛物线的一部分），再作出其关于原点对称的图象，即可得结论；（2）根据奇函数的定义求解析式；（3）由函数图象得函数的单调性，从而可得最大值和最小值，即得值域．【小问1详解】先作出0x ≤时的图象（抛物线的一部分），再作出其关于原点对称的图象：【小问2详解】()f x 是奇函数，0x >时，0x -<，22()()2()2f x x x x x -=---⨯-=-+，所以()2()2f x f x x x =--=-，所以222,0()2,0x x x f x x x x ⎧->=⎨--≤⎩；【小问3详解】由（1）可知()f x 在[4,1]--和[1,2]上是增函数，在[1,1]-上是减函数，(4)8f -=-，()11f -=，(11f =-），(2)0f =，因此最大值为1，最小值为8-，所以()f x 的值域为[8,1]-．18. 为了应对美国可能对华贸易的不当竞争，到2034年，某外贸玩具公司计划将生产成本控制在80万元，要比2024年下降20%，假设这期间每一年生产成本降低的百分比都相等，记2024年后第*()x x ∈N 年的成本支出为()f x 万元.（1）求2024年的生产成本为多少万元（2）求()f x 的解析式；（3）按此计划，到哪一年，可以将该工厂的成本控制在45万元以内？（参考数据：lg20.30,lg30.48≈≈，lg70.85≈）【答案】（1）100万元；（2）104()100()5x f x =⨯，*x ∈N ；（3）2058年.【解析】【分析】（1）利用给定关系列式计算得解.（2）由已知列出函数关系，再利用指数运算求出()f x .（3）利用对数函数单调性解不等式()45f x ≤.【小问1详解】设2024年的生产成本为a 万元，则(120%)80a ⋅-=，解得100a =（万元），所以2024年的生产成本为100万元.【小问2详解】设每一年生产成本降低的百分比都为(01)q q <<，则10100(1)80q -=，解得104(1)5q -=，所以1010104()100(1)100[(1)]100()5x x x f x q q =-=-=⨯，*x ∈N .【小问3详解】依题意，()45f x ≤，即104100(455x ⨯≤，则10445()5100x ≤，两边取对数得445lg lg 105100x ≤，解得lg 45210lg 4lg 5x -≥⨯-，而2lg 3lg 2120.480.3011010343lg 2130.301--⨯--⨯≈⨯=-⨯-，因此34x ≥，所以按此计划，到2058年，可以将该工厂的成本控制在45万元以内.19. 定义：若对定义域内任意x ，都有()()f x a f x +>（a 为正常数），则称函数()f x 为“a 距”增函数.（1）若()2f x x x =+，()1,x ∞∈-+，试判断()f x 是否为“1距”增函数，并说明理由；（2）若()312f x x x =-，x ∈R 是“a 距”增函数，求a 的取值范围；（3）若()22x k xf x +=，()1,x ∞∈-+，其中k ∈R ，是“2距”增函数，求k 的取值范围【答案】（1）()f x 为“1距”增函数，理由见解析（2）a >（3）()2,∞-+【解析】【分析】（1）根据定义检验即可；（2）由定义转化2213302x ax a ++->在x ∈R 上恒成立可得答案；（3）由条件结合定义分()1,0x ∈-、0x ≥讨论可得答案.【小问1详解】()f x 是否为“1距”增函数，理由如下，()()()2211132f x x x x x +=+++=++，()2f x x x =+，所以()()122f x f x x +-=+，当()1,x ∞∈-+时，()()1220f x f x x +-=+>，为所以()f x 为“1距”增函数；【小问2详解】若()312f x x x =-，x ∈R 是“a 距”增函数，则()()f x a f x +>，即()()331122x a x a x x +-+>-，可得2213302a x ax a ⎛⎫++-> ⎪⎝⎭，因为a 为正常数，所以2213302x ax a ++->在x ∈R 上恒成立，所以22191202a a ⎛⎫--< ⎪⎝⎭，解得a >【小问3详解】若()22x k x f x +=，()1,x ∞∈-+，其中k ∈R ，是“2距”增函数，则()()2f x f x +>，即()222222x k x x k x ++++>，可得()2222x k x x k x +++>+，当()1,0x ∈-时，可得()()2222x k x x kx +++>-，整理得()()1420x k ++>，所以420k +>，解得2k >-；当0x ≥时，可得()()2222x k x x kx +++>+，整理得4420x k ++>，所以420k +>，解得2k >-；综上，k 的取值范围为()2,∞-+.【点睛】方法点睛：“新定义”主要是指定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.。

江苏省盐城中学高三数学上学期开学试卷(含解析)

江苏省盐城中学2015届高三上学期开学数学试卷一、填空题（共14小题，每小题3分，满分42分）1．（3分）集合{﹣1，0，1}共有个真子集．2．（3分）若复数（1﹣i）（2i+m）是纯虚数，则实数m的值为．3．（3分）执行如图所示的程序框图，若输出的b的值为31，则图中判断框内①处应填的整数为．4．（3分）函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0）的部分图象如图所示，则f（0）=．5．（3分）已知圆锥的母线长为5cm，侧面积为15πcm2，则此圆锥的体积为cm3．6．（3分）从1，2，3，4，5这五个数中一次随机取两个数，则其中一个数是另一个的两倍的概率为．7．（3分）设椭圆+=1（m＞0，n＞0）的右焦点与抛物线y2=8x的焦点相同，离心率为，则此椭圆的短轴长为．8．（3分）如图，在△ABC中，AD⊥AB，，，则=．9．（3分）曲线y=和y=x2在它们的交点处的两条切线互相垂直，则a的值是．10．（3分）设f（x）=，若f（t）=f（）则t的范围．11．（3分）直线y=kx+3与圆（x﹣3）2+（y﹣2）2=4相交于M，N两点，若|MN|≥2，则k 的取值范围是．12．（3分）方程a x+x2=2（a＞0且a≠1）的解的个数为．13．（3分）若a，b∈R，且4≤a2+b2≤9，则a2﹣ab+b2的最小值是．14．（3分）无穷数列{a n}中，a1，a2，…，a m是首项为10，公差为﹣2的等差数列；a m+1，a m+2，…，a2m是首项为，公比为的等比数列（其中m≥3，m∈N*），并且对于任意的n∈N*，都有a n+2m=a n 成立．记数列{a n}的前n项和为S n，则使得S128m+5≥2013（m≥3，m∈N*）的m的取值集合为．二、解答题：15．在锐角△ABC中，已知内角A、B、C的对边分别为a、b、c．向量，，且向量、共线．（1）求角B的大小；（2）如果b=1，求△ABC的面积S△ABC的最大值．16．已知四边形ABCD是等腰梯形，AB=3，DC=1，∠BAD=45°，DE⊥AB（如图1）．现将△ADE 沿DE折起，使得AE⊥EB（如图2），连接AC，AB，设M是AB的中点．（1）求证：BC⊥平面AEC；（2）判断直线EM是否平行于平面ACD，并说明理由．17．已知A（﹣2，0）、B（2，0），点C、点D依次满足．（1）求点D的轨迹方程；（2）过点A作直线l交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为，且直线l与点D的轨迹相切，求该椭圆的方程．18．围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．（1）将修建围墙的总费用y表示成x的函数；（2）当x为何值时，修建此矩形场地围墙的总费用最小？并求出最小总费用．19．已知数列{a n}中，a2=1，前n项和为S n，且S n=．（1）求a1；（2）证明数列{a n}为等差数列，并写出其通项公式；（3）设lgb n=，试问是否存在正整数p，q（其中1＜p＜q），使b1，b p，b q成等比数列？若存在，求出所有满足条件的数组（p，q）；若不存在，说明理由．20．已知函数f（x）=λx2+λx，g（x）=λx+lnx，h（x）=f（x）+g（x），其中λ∈R，且λ≠0．（1）当λ=﹣1时，求函数g（x）的最大值；（2）求函数h（x）的单调区间；（3）设函数若对任意给定的非零实数x，存在非零实数t（t≠x），使得φ′（x）=φ′（t）成立，求实数λ的取值范围．江苏省盐城中学2015届高三上学期开学数学试卷参考答案与试题解析一、填空题（共14小题，每小题3分，满分42分）1．（3分）集合{﹣1，0，1}共有7个真子集．考点：子集与真子集．专题：规律型．分析：根据集合元素个数与集合真子集之间的关系即可得到结论．解答：解：∵集合{﹣1，0，1}含有3个元素，∴集合的真子集个数为23﹣1=8﹣1=7，故答案为：7．点评：本题主要考查集合关系的应用，含有n个元素的集合，其子集个数为2n，真子集的公式为2n﹣1个．2．（3分）若复数（1﹣i）（2i+m）是纯虚数，则实数m的值为﹣2．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：化简复数，由纯虚数的定义可得m的式子，可得m的值．解答：解：化简可得（1﹣i）（2i+m）=2i+m+2﹣mi=m+2+（2﹣m）i，由纯虚数的定义可得m+2=0，且2﹣m≠0解得m=﹣2故答案为：﹣2点评：本题考查纯虚数的定义，涉及复数的乘除运算，属基础题．3．（3分）执行如图所示的程序框图，若输出的b的值为31，则图中判断框内①处应填的整数为4．考点：程序框图．专题：算法和程序框图．分析：根据框图的流程依次计算程序运行的结果，直到输出的b的值为31，确定跳出循环的a值，从而确定判断框的条件．解答：解：由程序框图知：第一次循环b=2+1=3，a=2；第二次循环b=2×3+1=7，a=3；第三次循环b=2×7+1=15，a=4；第四次循环b=2×15+1=31，a=5．∵输出的b的值为31，∴跳出循环的a值为5，∴判断框内的条件是a≤4，故答案为：4．点评：本题考查了循环结构的程序框图，根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法．4．（3分）函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0）的部分图象如图所示，则f（0）=．考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：三角函数的图像与性质．分析：由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式，从而求得f（0）的值．解答：解：由函数的图象可得A=，•T=﹣=•，求得ω=2．再根据五点法作图可得2×+φ=π，∴φ=，故f（x）=sin（2x+），∴f（0）=sin=，故答案为：．点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，属于基础题．5．（3分）已知圆锥的母线长为5cm，侧面积为15πcm2，则此圆锥的体积为12πcm3．考点：棱柱、棱锥、棱台的体积．专题：计算题．分析：先求圆锥的底面半径，再求圆锥的高，然后求其体积．解答：解：已知圆锥的母线长为5cm，侧面积为15πcm2，所以圆锥的底面周长：6π底面半径是：3圆锥的高是：4此圆锥的体积为：故答案为：12π点评：本题考查圆锥的侧面积、体积，考查计算能力，是基础题．6．（3分）从1，2，3，4，5这五个数中一次随机取两个数，则其中一个数是另一个的两倍的概率为．考点：列举法计算基本事件数及事件发生的概率．专题：概率与统计．分析：根据题意，首先用列举法列举从1，2，3，4，5这五个数中一次随机取两个数的全部情况，可得其情况数目，进而可得其中一个数是另一个的两倍的情况数目，由古典概型的公式，计算可得答案解答：解：从1，2，3，4，5这五个数中一次随机取两个数，有（1，2），（1，3），（1，4），（1，5），（2，3），（2，4）（2，5），（3，4），（3，5），（4，5），共10种情况；其中其中一个数是另一个的两倍的有2种，即（1，2），（2，4），故其中一个数是另一个的两倍的概率为=，故答案为：点评：本题考查古典概型的计算，解本题时，用列举法，注意按一定的顺序，做到不重不漏．7．（3分）设椭圆+=1（m＞0，n＞0）的右焦点与抛物线y2=8x的焦点相同，离心率为，则此椭圆的短轴长为4．考点：椭圆的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：由题意可得：抛物线y2=8x的焦点（2， 0），可得c=2，利用离心率为，可得a=4，即可求出椭圆的短轴长．解答：解：由题意可得：抛物线y2=8x的焦点（2，0），∴c=2，∵离心率为，∴a=4，∴b==2，即n=2，∴椭圆的短轴长为4，故答案为：4．点评：本题主要考查椭圆的标准方程及性质，在研究和应用性质时必须将方程转化为标准方程再解．8．（3分）如图，在△ABC中，AD⊥AB，，，则=．考点：向量在几何中的应用．专题：平面向量及应用．分析：本题主要考查平面向量的基本运算与解三角形的基础知识，属于难题．解答：解：，∵，∴，∵，∴cos∠DAC=sin∠BAC，，在△ABC中，由正弦定理得变形得|AC|sin∠BAC=|BC|sinB，，=|BC|sinB==，故答案为．点评：近几年天津卷中总可以看到平面向量的身影，且均属于中等题或难题，应加强平面向量的基本运算的训练，尤其是与三角形综合的问题9．（3分）曲线y=和y=x2在它们的交点处的两条切线互相垂直，则a的值是a=．考点：曲线与方程；两条直线垂直的判定．专题：计算题．分析：先求出它们交点的横坐标，再求出它们的斜率表达式，由两条切线互相垂直、斜率之积等于﹣1，解出a的值．解答：解：曲线y=和y=x2的交点的横坐标是，它们的斜率分别是=﹣和 2x=2，∵切线互相垂直，∴﹣•2=﹣1，∴a=±，故答案为a=±．点评：本题考查曲线与方程、两条直线垂直的条件．10．（3分）设f（x）=，若f（t）=f（）则t的范围[2，3]∪{﹣}．考点：函数的值；分段函数的应用．专题：函数的性质及应用．分析：利用分段函数的性质求解．解答：解：∵f（x）=，f（t）=f（），∴当t≤﹣1时，t+2=，解得t=﹣，或t=（舍）；当﹣1＜t＜0时，2t+1=，无解；0＜t＜2时，2t+1=8，t=2，不成立；2≤t≤3时，f（t）=f（）=8，成立；t＞3时，8=2，解得t=3，不成立．综上所述，t的范围为：[2，3]∪{﹣}．故答案为：[2，3]∪{﹣}．点评：本题考查实数的取值范围的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．11．（3分）直线y=kx+3与圆（x﹣3）2+（y﹣2）2=4相交于M，N两点，若|MN|≥2，则k 的取值范围是[﹣，0]．考点：直线与圆的位置关系．专题：直线与圆．分析：由圆的方程找出圆心坐标与半径r，利用点到直线的距离公式表示出圆心到直线的距离d，利用垂径定理及勾股定理表示出弦长|MN|，列出关于k的不等式，求出不等式的解集即可得到k的范围．解答：解：由圆的方程得：圆心（3，2），半径r=2，∵圆心到直线y=kx+3的距离d=，|MN|≥2，∴2=2≥2，变形得：4﹣≥3，即8k2+6k≤0，解得：﹣≤k≤0，则k的取值范围是[﹣，0]．故答案为：[﹣，0]点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，点到直线的距离公式，垂径定理，勾股定理，熟练掌握公式及定理是解本题的关键．12．（3分）方程a x+x2=2（a＞0且a≠1）的解的个数为2．考点：根的存在性及根的个数判断．专题：作图题；函数的性质及应用．分析：将方程解的个数化为函数交点的个数．解答：解：方程a x+x2=2（a＞0且a≠1）的解的个数为函数y=2﹣x2与函数y=a x的交点个数，作图如右图：可知，有2个交点，故答案为：2．点评：本题考查了方程与函数的关系，属于基础题．13．（3分）若a，b∈R，且4≤a2+b2≤9，则a2﹣ab+b2的最小值是2．考点：基本不等式．专题：不等式的解法及应用．分析：由题意令a=rcosθ，b=rsinθ （2≤r≤3），由三角函数的知识可得．解答：解：∵a，b∈R，且4≤a2+b2≤9∴可令a=rcosθ，b=rsinθ （2≤r≤3），∴a2﹣ab+b2=r2cos2θ﹣r2sinθcosθ+r2sin2θ=r2（1﹣sinθcosθ）=r2（1﹣sin2θ），由三角函数可知当sin2θ取最大值1且r取最小值2时，上式取到最小值2故答案为：2点评：本题考查不等式的性质，三角换元是解决问题的关键，属基础题．14．（3分）无穷数列{a n}中，a1，a2，…，a m是首项为10，公差为﹣2的等差数列；a m+1，a m+2，…，a2m是首项为，公比为的等比数列（其中m≥3，m∈N*），并且对于任意的n∈N*，都有a n+2m=a n成立．记数列{a n}的前n项和为S n，则使得S128m+5≥2013（m≥3，m∈N*）的m的取值集合为{5，6}．考点：数列与不等式的综合．专题：等差数列与等比数列．分析：由S128m+5=64S2m+a1+a2+a3+a4+a5=64[10m+（﹣2）+]+10+8+6+4+4，得S128m+5=704m﹣64m2+94﹣64•（）m≥2013，设f（m）=704m﹣64m2，g（m）=1914+64•（）m，g（m）＞1914，存在这样的m=6，使得S128m+5≥2013（m≥3，m∈N*．由此能求出m的取值集合为{6}．解答：解：等差数列通项公式：a n=10+（n﹣1）（﹣2）=﹣2n+12，等比数列通项公式：a n=•（）n﹣m﹣1=，由S128m+5=64S2m+a1+a2+a3+a4+a5=64[10m+（﹣2）+]+10+8+6+4+2，可得S128m+5=704m﹣64m2+94﹣64•（）m≥2013，设f（m）=704m﹣64m2，g（m）=1914+64•（）m，g（m）＞1919，f（m）=﹣64（m2﹣11m），存在m=5或6时取最大f（x）max=f（5）=f（6）=1920，所以存在这样的m=5或m=6，使得S128m+5≥2013（m≥3，m∈N*．因此m的取值集合为{5，6}．故答案为：{5，6}．点评：本题主要考查了数列的概念，考查了等差、等比数列的性质，考查了学生的运算求解能力，属于中档题．二、解答题：15．在锐角△ABC中，已知内角A、B、C的对边分别为a、b、c．向量，，且向量、共线．（1）求角B的大小；（2）如果b=1，求△ABC的面积S△ABC的最大值．考点：解三角形；数量积的坐标表达式；三角函数中的恒等变换应用．专题：计算题．分析：（1）由两向量共线，得到向量的坐标表示列出一个关系式，根据三角形的内角和定理得到A+C=π﹣B，利用诱导公式化简这个关系式后，再利用二倍角的正弦、余弦函数公式及同角三角函数间的基本关系化简，得到tan2B的值，又三角形为锐角三角形，由B的范围求出2B的范围，利用特殊角的三角函数值即可求出B的度数；（2）根据余弦定理表示出b2=a2+c2﹣2accosB，把（1）求出的B的度数与b的值代入得到一个关于a与c的式子，变形后，根据基本不等式即可求出ac的最大值，然后利用三角形的面积公式，由ac的最大值及sinB的值，表示出三角形ABC的面积，即为三角形面积的最大值．解答：解：（1）∵向量、共线，∴2sin（A+C）（2﹣1）﹣cos2B=0，又A+C=π﹣B，∴2sinBcosB﹣cos2B，即sin2B=cos2B，∴tan2B=，又锐角△ABC，得到B∈（0，），∴2B∈（0，π），∴2B=，故B=；（2）由（1）知：B=，且b=1，根据余弦定理b2=a2+c2﹣2accosB得：a2+c2﹣ac=1，∴1+ac=a2+c2≥2ac，即（2﹣）ac≤1，ac≤=2+，∴S△ABC=acsinB=ac≤，当且仅当a=c=时取等号，∴△ABC的面积最大值为．点评：此题考查了平面向量的数量积的坐标表示，三角函数的恒等变形，余弦定理及三角形的面积公式．学生作第二问时注意利用基本不等式求出ac的最大值是解本题的关键．16．已知四边形ABCD是等腰梯形，AB=3，DC=1，∠BAD=45°，DE⊥AB（如图1）．现将△ADE 沿DE折起，使得AE⊥EB（如图2），连接AC，AB，设M是AB的中点．（1）求证：BC⊥平面AEC；（2）判断直线EM是否平行于平面ACD，并说明理由．考点：直线与平面垂直的判定；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（1）在图1中，过C作CF⊥EB，连接CE，证明BC⊥CE，在图2中，利用AE⊥EB，AE⊥ED，可证AE⊥平面BCDE，从而可得AE⊥BC，即可证明BC⊥平面AEC（2）用反证法．假设EM∥平面ACD，从而可证面AEB∥面AC，而A∈平面AEB，A∈平面ACD，与平面AEB∥平面ACD矛盾，故可得结论．解答：（1）证明：在图1中，过C作CF⊥EB∵DE⊥EB，∴四边形CDEF是矩形，∵CD=1，∴EF=1．∵四边形ABCD是等腰梯形，AB=3，∴AE=BF=1．∵∠BAD=45°，∴DE=CF=1．连接CE，则CE=CB=，∵EB=2，∴∠BCE=90°，∴BC⊥CE．在图2中，∵AE⊥EB，AE⊥ED，EB∩ED=E，∴AE⊥平面BCDE．∵BC⊂平面BCDE，∴AE⊥BC．∵AE∩CE=E，∴BC⊥平面AEC．（2）解：用反证法．假设EM∥平面ACD．∵EB∥CD，CD平面ACD，EB平面ACD，∴EB∥平面ACD．∵EB∩EM=E，∴面AEB∥面ACD而A∈平面AEB，A∈平面ACD，与平面AEB∥平面ACD矛盾．∴假设不成立，∴EM与平面ACD不平行．点评：本题考查图形的翻折，考查线面垂直，考查三棱锥的体积，考查反证法思想的运用，解题的关键是掌握线面垂直，面面平行的判定方法，属于中档题．17．已知A（﹣2，0）、B（2，0），点C、点D依次满足．（1）求点D的轨迹方程；（2）过点A作直线l交以A、B为焦点的椭圆于M、N两点，线段MN的中点到y轴的距离为，且直线l与点D的轨迹相切，求该椭圆的方程．考点：轨迹方程；椭圆的标准方程．专题：计算题．分析：（1）设C、D点的坐标分别为C（x0，y0），D（x，y），欲求点D的轨迹方程，即寻找x，y之间的关系式，利用向量间的关系求出P点的坐标后代入距离公式即可得；（2）设椭圆方程为，根据圆的切线性质及中点条件，利用待定系数法求出待定系数a，b即可．解答：解：（1）设C、D点的坐标分别为C（x0，y0），D（x，y），则），，则，故．又代入中，整理得x2+y2=1，即为所求点D的轨迹方程．（2）易知直线l与x轴不垂直，设直线l的方程为y=k（x+2），①又设椭圆方程为，②a2﹣b2=4，因为直线l：kx﹣y+2k=0与圆x2+y2=1相切．故，解得．将①代入②整理得，（a2k2+a2﹣4）x2+4a2k2x+4a2k2﹣a4+4a2=0，③将代入上式，整理得，设M（x1，y1），N（x2，y2），则，由题意有，求得．经检验，此时③的判别式故所求的椭圆方程为．点评：求曲线的轨迹方程是解析几何的基本问题．求符合某种条件的动点的轨迹方程，其实质就是利用题设中的几何条件，用“坐标化”将其转化为寻求变量间的关系．18．围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米）．（1）将修建围墙的总费用y表示成x的函数；（2）当x为何值时，修建此矩形场地围墙的总费用最小？并求出最小总费用．考点：函数模型的选择与应用．专题：应用题．分析：（1）设矩形的另一边长为am，则根据围建的矩形场地的面积为360m2，易得，此时再根据旧墙的维修费用为45元/m，新墙的造价为180元/m，我们即可得到修建围墙的总费用y表示成x的函数的解析式；（2）根据（1）中所得函数的解析式，利用基本不等式，我们易求出修建此矩形场地围墙的总费用最小值，及相应的x值．解答：解：（Ⅰ）设矩形的另一边长为am，则y=45x+180（x﹣2）+180•2a=225x+360a﹣360．由已知ax=360，得，所以．（II）因为x＞0，所以，所以，当且仅当时，等号成立．即当x=24m时，修建围墙的总费用最小，最小总费用是10440元．点评：函数的实际应用题，我们要经过析题→建模→解模→还原四个过程，在建模时要注意实际情况对自变量x取值范围的限制，解模时也要实际问题实际考虑．将实际的最大（小）化问题，利用函数模型，转化为求函数的最大（小）是最优化问题中，最常见的思路之一．19．已知数列{a n}中，a2=1，前n项和为S n，且S n=．（1）求a1；（2）证明数列{a n}为等差数列，并写出其通项公式；（3）设lgb n=，试问是否存在正整数p，q（其中1＜p＜q），使b1，b p，b q成等比数列？若存在，求出所有满足条件的数组（p，q）；若不存在，说明理由．考点：数列的求和．专题：等差数列与等比数列．分析：（1）岭n=1，即可求a1；（2）根据等差数列的定义即可证明数列{a n}为等差数列，并写出其通项公式；（3）根据等比数列的定义和通项公式，建立方程组进行求解即可得到结论．解答：解：（1）令n=1，则a1=S1==0（2）由，即，①得．②②﹣①，得（n﹣1）a n+1=na n．③于是，na n+2=（n+1）a n+1．④③+④，得na n+2+na n=2na n+1，即a n+2+a n=2a n+1又a1=0，a2=1，a2﹣a1=1，所以，数列{a n}是以0为首项，1为公差的等差数列．所以，a n=n﹣1（3）假设存在正整数数组（p，q），使b1，b p，b q成等比数列，则lgb1，lgb p，lgb q成等差数列，于是，所以，（☆）．易知（p，q）=（2，3）为方程（☆）的一组解当p≥3，且p∈N*时，＜0，故数列{}（p≥3）为递减数列，于是≤＜0，所以此时方程（☆）无正整数解．综上，存在唯一正整数数对（p，q）=（2，3），使b1，b p，b q成等比数列点评：本题主要考查等差数列个等比数列通项公式的应用，要求熟练掌握相应的通项公式．20．已知函数f（x）=λx2+λx，g（x）=λx+lnx，h（x）=f（x）+g（x），其中λ∈R，且λ≠0．（1）当λ=﹣1时，求函数g（x）的最大值；（2）求函数h（x）的单调区间；（3）设函数若对任意给定的非零实数x，存在非零实数t（t≠x），使得φ′（x）=φ′（t）成立，求实数λ的取值范围．考点：函数的单调性与导数的关系．专题：压轴题．分析：①令g′（x）=0求出根，判断两边的符号，求出最值②导数大于零求出单增区间，导数小于零求出单调递减区间，注意单调区间一定在定义域内③不等式恒成立就是求函数的最值，注意对参数的讨论解答：解：（1）当λ=﹣1时，g（x）=lnx﹣x，（x＞0）∴令g′（x）=0，则x=1，∴g（x）=lnx﹣x在（0，1）上单调递增，在（1，+∞）上单调递减∴g（x）max=g（1）=﹣1（2）h（x）=λx2+2λx+lnx，，（x＞0）∴当λ＞0时，h'（x）＞0，∴函数h（x）的增区间为（0，+∞），当λ＜0时，，当时，h′（x）＜0，函数h（x）是减函数；当时，h′（x）＞0，函数h（x）是增函数．综上得，当λ＞0时，h（x）的增区间为（0，+∞）；当λ＜0时，h（x）的增区间为，减区间为（10分）（3）当x＞0，在（0，+∞）上是减函数，此时φ′（x）的取值集合A=（λ，+∞）；当x＜0时，φ′（x）=2λx+λ，若λ＞0时，φ′（x）在（﹣∞，0）上是增函数，此时φ′（x）的取值集合B=（﹣∞，λ）；若λ＜0时，φ′（x）在（﹣∞，0）上是减函数，此时φ′（x）的取值集合B=（λ，+∞）．对任意给定的非零实数x，①当x＞0时，∵φ′（x）在（0，+∞）上是减函数，则在（0，+∞）上不存在实数t（t≠x），使得φ′（x）=φ′（t），则t∈（﹣∞，0），要在（﹣∞，0）上存在非零实数t（t≠x），使得φ′（x）=φ′（t）成立，必定有A⊆B，∴λ＜0；②当x＜0时，φ′（x）=2λx+λ在（﹣∞，0）时是单调函数，则t∈（0，+∞），要在（0，+∞）上存在非零实数t（t≠x），使得φ′（x）=φ′（t）成立，必定有B⊆A，∴λ＜0．综上得，实数λ的取值范围为（﹣∞，0）．点评：本题考查导数研究函数的最值，单调性，值域，属于难题，在2015届高考中常出现在解答题中最后两题．。

江苏省盐城市时杨中学2014-2015学年高一上学期12月月考数学试卷

江苏省盐城市时杨中学2014-2015学年高一上学期12月月考数学试卷
一、填空题：（本大题共14小题，每小题5分，共70分．）
1．sin（﹣π）的值等于．
2．若角α在第一象限，且|cos|=﹣cos，则在第象限．
3．sin2cos3tan4的值的符号为．
4．在函数y=sin|x|、y=|sinx|、、中，最小正周期为π的函数有个．
5．已知点P（cosθ，sinθ）在第三象限，则角θ的终边落在第象限．
6．设cos80°=k，则tan100°=．
7．函数f（x）=ax+bsinx+1，若f（5）=7，则f（﹣5）=．
8．函数的值域是．
9．已知，那么tanα的值为．
10．如果sinα+cosα=，那么sinα﹣cosα的值为．
11．若f（cosx）=cos3x，则f（sin30°）的值为．
12．若集合，B={x|﹣2≤x≤2}，则A∩B=．
13．函数y=2sin（2x+）（x∈）的单调递减区间是．
14．已知sinθ=，cosθ=，若θ是第二象限角，则实数a的值是．
.﹣2，0，2﹣2，0，2﹣2，0，2﹣π，0﹣，﹣﹣，﹣﹣π，0﹣，﹣﹣，﹣kπ+，kπ+﹣，﹣1，﹣，1﹣1，1﹣1，1hslx3y3h，将问题转化为二次函数在定区间上的最值问题，而（2）的关键是根据分段函数分段处理的原则，分类讨论解方程f（a）=．。

江苏省盐城中学高二上学期12月月考试题数学(理) Word

高二年级阶段性检测数学（理科）试题命题人：盛冬山周广黎审题人：姚动蔡广军一、填空题（本大题共14小题,每小题5分,计70分） 1.已知，则的虚部是 . 2.已知)1(,11->++=x x x y ，则的最小值是 3.已知，则4.已知双曲线:的焦距是10，点P （3,4）在的渐近线上，则双曲线的标准方程是5.在直角坐标系中，不等式组⎪⎩⎪⎨⎧≤≥+-≥+a x y x y x 040表示平面区域面积是4，则常数的值_______．6.函数的图象在点处的切线方程是 .7.已知,，则的最大值是8.数列的前项和为，且，利用归纳推理，猜想的通项公式为9.已知x a x x x f ln 212)(2++-=在上是增函数，则的取值范围是 . 10.设等差数列的前项和为，则，，成等差数列；类比以上结论有：设等比数列的前项积．为，则，，成等比数列．11.函数在上有极值，则的取值范围是12.已知椭圆2222:1(0)x y C a b a b+=>>和圆,若上存在点,使得过点引圆的两条切线,切点分别为,满足,则椭圆的离心率取值范围是13.如图，已知椭圆的中心在坐标原点，焦点在轴上，为左右顶点，焦距为2，左准线与轴的交点为，∶= 6∶1．若点在直线上运动，且离心率，则的最大值为．14.已知函数2342015()12342015x x x x f x x =+-+-++，20154321)(2015432x x x x x x g --+-+-=设)3()4()(+⋅-=x g x f x F ，且函数的零点均在区间（，， Z ）内，圆的面积的最小值是_______.二、解答题（本大题共6小题，计90分.）15. （本题满分14分）已知cx bx ax x f ++=23)(在区间[0,1]上是减函数,在区间上是增函数,又 (Ⅰ)求的解析式;(Ⅱ)若在区间恒成立,求的取值范围.16. （本题满分14分）在平面直角坐标系中，已知点A(0，1)，B 点在直线上，点满足，，点的轨迹为曲线.(1)求曲线的方程；(2)斜率为1的直线过原点，求被曲线C 截得的弦长.17. (本题满分14分) 设数列的前项和为，且方程有一根为.(1)求;(2)猜想数列的通项公式，并给出证明．18. （本题满分16分）在淘宝网上，某店铺专卖盐城某种特产．由以往的经验表明，不考虑其他因素，该特产每日的销售量（单位：千克）与销售价格（单位：元/千克，）满足：当时，，；当时，．已知当销售价格为元/千克时，每日可售出该特产600千克；当销售价格为元/千克时，每日可售出150千克．（1）求的值，并确定关于的函数解析式；（2）若该特产的销售成本为1元/千克，试确定销售价格的值，使店铺每日销售该特产所获利润最大（精确到0.1元/千克）．19. （本题满分16分）如图，已知椭圆)0(12222>>=+b a bx a y 的离心率为，以椭圆的上顶点为圆心作圆)0()2(:222>=-+r r y x Q ，设圆与椭圆交于点与点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高三年级阶段性随堂练习
数学试题（2014.12）
朱启东钱俊朱丽丽
一、填空题：
1.已知集合，，则 .
2.命题 ,命题 , 是条件．
（填“充分不必要”，“必要不充分”，“充要”，“既不充分又不必要”中的一个）
3.函数的最小正周期为．
4.已知函数的单调递增区间为．
5.直线在两坐标轴上的截距之和为2，则实数的值是.
二、解答题：
15.在△ABC中，角A、B、C的对边分别为、、．已知向量，，且．
（1）求的值；
（2）若，求△ABC的面积S．
16.平面直角坐标系中，直线截以原点O为圆心的圆所得的弦长为．
（1）求圆的方程；
（2）过点的直线与圆相切，求直线的方程．
17.如图，ABCD是边长为10海里的正方形海域.现有一架飞机在该海域失事，两艘海事搜救船在处同时出发，沿直线、向前联合搜索，且（其中点、分别在边、上），搜索区域为平面四边形围成的海平面.设，搜索区域的面积为 .
5.直线在两坐标轴上的截距之和为2，则实数的值是_____.
6．若Sn为等差数列{an}的前n项和，S9=－36，S13=－104，则a5 a7的值为．32
7.若椭圆上存在一点与椭圆的两个焦点构成顶角为120的等腰三角形，则椭圆的离心率为________．
8.如图，已知正方形的边长为3，为的中点，与交于点，则 ________．
6.若Sn为等差数列{an}的前n项和，S13=－104，则a7的值为．
7.已知实数满足线性约束条件则目标函数的最大值是．
8.曲线C：在点M（1，e）处的切线方程为．
9.如图，已知正方形的边长为3，为的中点，与交于点，则．
10.已知为正实数，且则的最小值为．
11.已知函数 , ，的值域为．
（1）求圆C的方程．
（2）若直线l∥PQ，且l与圆C交于点A、B，，求直线l的方程．
解：(1)PQ为 2分
C在PQ的中垂线即y=x–1上3分
设C（n，n–1），则 4分
由题意，有 5分
∴ ∴n= 1或5，r2= 13或37（舍）7分
∴圆C为 8分
解法二：
设所求圆的方程为
由已知得解得
当时，；当时，（舍）
12.已知为正实数，且则的最小值为2．
13．已知圆C：，点P在直线l：上，若圆C上存在两点A、Bቤተ መጻሕፍቲ ባይዱ得，则点P的横坐标的取值范围是．
14.已知等比数列的首项为，公比为，其前项和记为，又设，的所有非空子集中的最小元素的和为，则的最小正整数为．
解析:45
解：由题意有，对于和，我们首先把中的元素按从小到大顺序排列，当时，，对于中的任一元素，比它大的有个，这个元素组成的集合的所有子集有个，把加进这些子集形成新的集合，每个都是以为最小元素的的子集，而最小元素为的的子集也只有这些，故在中出现次，所以
高三数学随堂练习答案（2014.10.25）
二、填空题：
1．已知集合，，则 .
解析：， .
2.函数的最小正周期为．
解析：，所以最小正周期 .
3．命题 ,命题 , 是条件．
（填“充分不必要”，“必要不充分条件”，“充要条件”，“既不充分又不必要条件”中的一个）
解析：充分不必要
4．已知函数的单调递增区间为．解析：
（1）试建立与的关系式，并指出的取值范围；
（2）求的最大值.
18.如图，在直角坐标系xOy中，椭圆的离心率为，右准线方程是 ,左、右顶点分别为A、B．
（1）求椭圆的标准方程；
（2）若动点M满足MB⊥AB，直线AM交椭圆于点P，求证：为定值；
（3）在（2）的条件下，设以线段MP为直径的圆与直线BP交于点Q，试问：直线MQ是否过定点？若过定点，求出定点的坐标；若不过定点，请说明理由．
19.设各项均为非负数的数列的前项和为，（，）．
（1）求实数的值；
（2）求数列的通项公式（用表示）；
（3）证明：当时，．
20.已知函数，，．
（1）求函数的单调区间；
（2）记函数，当时，在上有且只有一个极值点，求实数的取值范围；
（3）记函数，证明：存在，此时有一条过原点的直线与的图象有两个切点．
，时，适合上式，时，．当，不成立，当时，，，由于，，，所以，最小的为．
二、解答题：
15．在△ABC中，角A、B、C的对边分别为、、 .已知向量，，且．
（1）求的值；（2）若，求△ABC的面积S．
16.已知圆C经过P（4，–2），Q（–1，3）两点，且在y轴上截得的线段长为，半径小于5．
9.已知函数f(x)＝ ,x∈[ , ]，求f(x)的值域．
10.已知椭圆是椭圆上关于原点对称的两点，是椭圆上任意一点，且直线的斜率分别为，若椭圆的离心率为，则的最小值为．1
11.设为非零实数，偶函数在区间上存在唯一的零点，则实数的取值范围是.
解析：为偶函数，，结合图形可知 .
∴所求圆的方程为
(2)设l为 9分
由，得 10分
设A（x1，y1），B（x2，y2），则 11分
∵ ，∴ 12分
∴
∴ ∴m= 3或–4（均满足）
∴l为 14分
17.某市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4千米，BC=6千米，CD=2千米，
12.若椭圆上存在一点与椭圆的两个焦点构成顶角为120的等腰三角形，则椭圆的离心率为____．
13.设为非零实数，偶函数在区间上存在唯一的零点，则实数的取值范围是.
14.已知等比数列的首项为，公比为，其前项和记为，又设，的所有非空子集中的最小元素的和为，则的最小正整数为．
（1）请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值；
（2）因地理条件的限制，边界AD、DC不能变更，而边界AB、BC可以调整，为了提高棚户区改造建筑用地的利用率，请在圆弧ABC上设计一点P，使得棚户区改造的新建筑用地APCD的面积最大，并求最大值．
解：(1) ，由余弦定理得：