五年级奥数-图形问题练习及答案
五年级奥数专题-不规则图形面积计算含解析
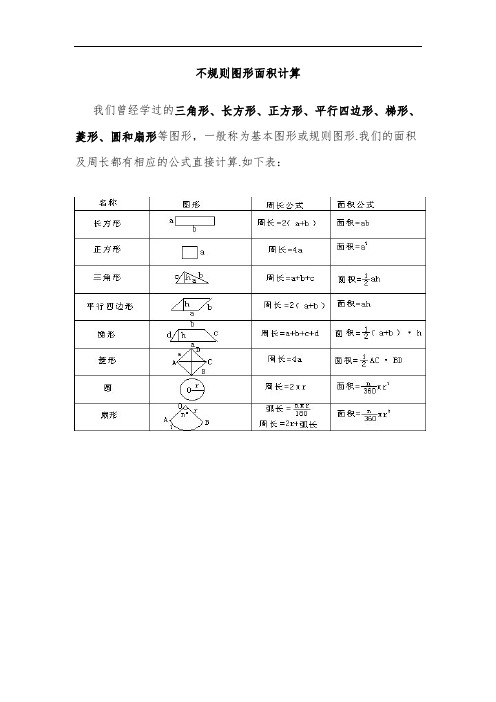
不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
一、例题与方法指导例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
思路导航:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF 与四边形AECF的面积彼此相等,求三角形AEF的面积.思路导航:∵△ABE 、△ADF 与四边形AECF 的面积彼此相等,∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。
在△ABE 中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2, ∴△ECF 的面积为2×2÷2=2。
所以S △AEF=S 四边形AECF-S △ECF=12-2=10(平方厘米)。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
思路导航:在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影部分面积=S △ABG-S △BEF=25-8=17(平方厘米)。
例4 如右图,A 为△CDE 的DE 边上中点,BC=CD ,若△ABC (阴影部分)面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航:取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,所以它们的面积相等,都等于5平方厘米.∴△ACD的面积等于15平方厘米,△ABD的面积等于10平方厘米。
五年级奥数题:图形与面积含详细答案汇总

五年级奥数题:图形与面积一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是_________厘米.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是_________.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是_________平方厘米.4.(3分)(2014•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_________平方厘米.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于_________平方厘米.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是_________厘米.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE 是_________厘米.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是_________.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是_________平方厘米.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.14.(2012•武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是_________.2010年五年级奥数题:图形与面积(B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是170厘米.考点:巧算周长.分析:要求该图形的周长,先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,然后先算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.解答:解:400÷16=25(平方厘米),因为5×5=25(平方厘米),所以每个小正方形的边长为5厘米,周长为:(5×4+5×4+5×3+5×2+5×3+5)×2,=85×2,=170(厘米);答:它的周长是170厘米.点评:此类题解答的关键是先求出每个小正方形的面积,根据正方形的面积公式,得出小正方形的边长,进而算出该图形的外周的长,因为内、外的长相等,再乘2即可得出结论.2.(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是25.考点:组合图形的面积.分析:此题需要进行图形分解:“7”分成一个长方形、一个等腰直角三角形、一个平行四边形;“2”分成一个梯形、一个平行四边形、一个长方形;“1”分成一个梯形和两个长方形.然后进行图形转换,依据题目条件即可求出结果.解答:解:“7”所占的面积和=+3+4=,“2”所占的面积和=3+4+3=10,“1”所占的面积和=+7=,那么7,2,1三个数字所占的面积之和=++10=25.故答案为:25.点评:此题关键是进行图形分解和转换.3.(3分)如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是 6.5平方厘米.考点:组合图形的面积.分析:由图可以观察出:大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积.解答:解:大正方形的面积为4×4=16(平方厘米);粗线以外的图形面积为:整格有3个,左上,右上,右中,右下,左中,右中,共有3++5×=9.5(平方厘米);所以粗线围成的图形面积为16﹣9.5=6.5(平方厘米);答:粗线围成的图形面积是6.5平方厘米.故此题答案为:6.5.点评:此题关键是对图形进行合理地割补.4.(3分)(2014•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是24平方厘米.考点:组合图形的面积.分析:两个正方形的面积减去两个空白三角形的面积.解答:解:4×4+8×8﹣×4×(4+8)﹣×8×8,=16+64﹣24﹣32,=24(cm2);答:阴影的面积是24cm2.故答案为:24.点评:求组合图形面积的化为求常用图形面积的和与差求解.5.(3分)在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于12平方厘米.考点:相似三角形的性质(份数、比例);三角形的周长和面积.分析:根据题意,连接AD,即可知道△ABD和△ADC的关系,△ADE和△BDE的关系,由此即可求出四边形AEDC的面积.解答:解:连接AD,因为BD=2DC,所以,S△ABD=2S△ADC,即,S△ABD=18×=12(平方厘米),又因为,AE=BE,所以,S△ADE=S△BDE,即,S△BDE=12×=6(平方厘米),所以AEDC的面积是:18﹣6=12(平方厘米);故答案为:12.点评:解答此题的关键是,根据题意,添加辅助线,帮助我们找到三角形之间的关系,由此即可解答.6.(3分)如图是边长为4厘米的正方形,AE=5厘米、OB是 3.2厘米.考点:组合图形的面积.分析:连接BE、AF可以看出,三角形ABE的面积是正方形面积的一半,再依据三角形面积公式就可以求出OB 的长度.解答:解:如图连接BE、AF,则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×(4×4)=8(平方厘米);OB=8×2÷5=3.2(厘米);答:OB是3.2厘米.故答案为:3.2.点评:此题主要考查三角形和正方形的面积公式,将数据代入公式即可.7.(3分)如图正方形ABCD的边长是4厘米,CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE 是 3.2厘米.考点:组合图形的面积.分析:连接AG,则可以依据题目条件求出三角形AGD的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解.解答:解:如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG,=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8(平方厘米);8×2÷5=3.2(厘米);答:长方形的宽是3.2厘米.故答案为:3.2.点评:依据题目条件做出合适的辅助线,问题得解.8.(3分)如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是243.考点:组合图形的面积.分析:从图中可以看出每上、下两个小矩形的一个边是相邻的,也就是说长是相等的,那么根据矩形的面积公式知,如果长相同,面积之比也就是宽之比,反之宽之比也就是面积之比;由中间面积20和16的矩形,可以算出空着的小矩形面积,最后把所有小矩形面积加起来就是大矩形的面积.解答:解:由图和题意知,中间上、下小矩形的面积比是:20:16=5:4,所以宽之比是5:4,那么,A:36=5:4得A=45;25:B=5:4得B=20;30:C=5:4得C=24;D:12=5:4得D=15;所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243;故答案为:243.点评:此题考查了如果长方形的长相同,宽之比等于面积之比,还考查了比例的有关知识.9.(3分)如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是60.考点:组合图形的面积.分析:根据题意:正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,可连接DP,然后再利用三角形的面积公式进行计算即可得到答案.解答:解:阴影部分的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×(AP+BP)=36+2×12=36+24=60.答:这个图形阴影部分的面积是60.点评:此题主要考查的是三角形的面积公式.10.(3分)图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是4平方厘米.考点:重叠问题;三角形的周长和面积.分析:因为S△EFC+S△GHC=四边形EFGH面积÷2=12,S△AEF+S△AGH=四边形EFGH面积÷2=12,所以S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影部分的总面积是10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣(S△ABE+S△ADH)=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.解答:解:由题意推出:S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影面积10平方厘米=2平方厘米.所以:四边形ABCD面积=S△ECH﹣(S△ABE+S△ADH)=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米.故答案为:4.点评:此题在重叠问题中考查了三角形的周长和面积公式,此题设计的非常精彩.二、解答题(共4小题,满分0分)11.图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.考点:等积变形(位移、割补).分析:如图,将正六边形ABCDEF等分为54个小正三角形,根据平行四边形对角线平分平行四边形面积,采用数小三角形的办法来计算面积.解答:解:如图,S△PEF=3,S△CDE=9,S四边形ABQP=11.上述三块面积之和为3+9+11=23.因此,阴影四边形CEPQ面积为54﹣23=31.点评:此题主要利用面积分割,用数基本小三角形面积来解决问题.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.考点:等积变形(位移、割补).分析:由图及题意知,可把涂阴影部分小正六角星形等分成12个小三角形,且都与外围的6个空白小三角形面积相等,已知涂阴影部分的小正六角星形面积是16平方厘米,可求出大正六角星形中心正六边形的面积,而这个正六边形又可等分成6个小正三角形,且它们与外围六个大角的面积相等,进而可求出大正六角星形面积解答:解:如下图所示,涂阴影部分小正六角星形可等分成12个小三角形,且都与外围的6个空白小三角形面积相等,所以正六边形ABCDEF的面积:16÷12×(12+6)=24(平方厘米);又由于正六边形ABCDEF又可等分成6个小正三角形,且它们与外围六个大角的面积相等,所以大正六角星形面积:24×2=48(平方厘米);答:大正六角星形面积是48平方厘米.点评:此题要借助求正六边形的面积来解答,它既可看作是18个小正三角形,又可看作是6个大点的正三角形组成.13.一个周长是56厘米的大长方形,按图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.考点:比的应用;图形划分.分析:要求大长方形的面积,需求出它的长和宽,由条件“在(1)中小长方形面积的比是:A:B=1:2,B:C=1:2.而在(2)中相应的比例是A':B'=1:3,B':C'=1:3.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3”可知:D的宽是大长方形宽的,D′的宽是大长方形宽的,D的长是×(28﹣大长方形的宽),D′的长是×(28﹣大长方形的宽),由此便可以列式计算.解答:解:设大长方形的宽为x,则长为28﹣x因为D的宽=x,D′的宽=x,所以,D′的宽﹣D的宽=.D长=×(28﹣x),D′长=×(28﹣x),D′长﹣D长=×(28﹣x),由题设可知:=即=,于是=,x=8.于是,大长方形的长=28﹣8=20,从而大长方形的面积为8×20=160平方厘米.答:大长方形的面积是160平方米.点评:此题比较复杂,主要考查比的关系,应利用比的意义,找清数量见的比,再利用题目条件,就可以进行计算求得结果.14.(2012•武汉模拟)如图,已知CD=5,DE=7,EF=15,FG=6,直线AB将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG的面积是40.考点:三角形的周长和面积.分析:可以把S△ADE看成是一个整体,根据各线段的关系和左右两部分面积的关系,可以列出一个方程,求出S△ADE的面积,然后再根据所求三角形与S△ADE的关系求出答案.解答:解:由题意知,S△AEG=3S△ADE,S△BFE=S△BEC,设S△ADE=X,则S△AEG=3X,S△BFE=(38﹣X),可列出方程:(38﹣X)+3X=65,解方程,得:x=10,所以S△ADG=10×(1+3)=40.故答案为:40.点评:此题考查了如何利用边的关系求三角形的面积.。
小学五年级奥数题及答案-三根铁丝

小学五年级奥数题及答案-三根铁丝
编者小语:“题海无边,题型有限”。
学习数学必须要有扎实的基本功,有了扎实的基本功再进行“奥数”的学习就显得水到渠成了。
为大家准备了小学五年级奥数题,希望小编整理奥数题阴影面积问题(中等难度),可以帮助到你们,助您快速通往高分之路!!
有三根铁丝,分别长300厘米、444厘米、516厘米。
把它们截成同样长且尽可能长的整厘米小段(不许剩余),每小段折成一个小正方形。
然后将这些小正方形混放在一起拼成一个长方形(每拼一次都必须用上所有这些小正方形),这样可能拼成的长方形有多少种?
解答:(300,444)=(300,144)=(12,144)=12 (12,516)=12 因此把它们截成长度为12厘米的小段,共可以得到(300+444+516)÷12=105段。
而105=1×105=3×35=5×21=7×15,拼成长方形有4种。
小学五年级奥数第19讲 组合图形的面积(二)(含答案分析)

第19讲组合图形的面积(二)一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题1】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1:1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
(单位:厘米)3.下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
【例题2】下图中,边长为10和15的两个正方体并放在一起,求三角形ABC (阴影部分)的面积。
练习2:1.下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
2.图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
3.图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积(ADFC不是正方形)。
【例题3】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)练习3:1.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?2.下图的梯形ABCD中,下底是上底的2倍,E是AB的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍?3.下图梯形ABCD中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的面积比三角形AOD的面积大多少平方厘米?【例题4】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
练习4:1.把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积()乙的面积。
2.如图,在三角形ABC中,D是BC的中点,E、F是AC的三等分点。
五年级下册数学试题-五升六讲义第12讲 图形周长(奥数版块)(含答案)
第十二讲 图形周长周长:封闭图形一周的长度就是图形的周长。
长方形的周长=2×(长+宽);正方形的周长=4×边长计算不是长方形和正方形周长时可以利用长方形、正方形的周长公式,来计算规则图形的周长。
除此,通过添加辅助线,运用平移、分解等方法,将不规则图形转化成规则图形来计算。
例1:如图是一个周长为50的长方形纸片,A 、B 两点分别是长和宽的中点。
将此长方形沿图中的虚线撕成甲、乙两张。
如果甲的周长是48,那么乙的周长是 。
例2: 在长方形ABCD 中,AB=120厘米,截去一个正方形EBCF 后,剩下长方形AEFD 的周长是多少?(如右图)例3:平行四边形ABCD 的一条边长为18,两条高分别为8和10,求平行四边形ABCD 的周长。
(如图)例4:10个是相同的小长方形拼成一个大长方形,长是6厘米,宽5厘米,求小长方形的周长。
(如图)例5:右图中多边形每相邻两条边都互相垂直,若要计算起其周长,那么至少要知道( )边长。
(嘉祥外国语学校2011年5升6招生数学试题) 甲 乙AB BA CD 18 10 8A.6B.5C.4D.3:例6:如图4,用四个相同的长方形拼成一个面积为100平方厘米的大正方形,每个长方形的周长是多少厘米?例7:如图.阴影部分是一个正方形.求大长方形的周长.巩固练习:1.6年级衔接班招生考试题)把一个边长为a的正方形,分成两个完全相等的长方形,这个两个长方形的周长之和是。
2.将长5厘米、宽2厘米的长方形硬纸片如图一层、二层、三层、……地排下去:(1)排到第5层,一周的长是()厘米。
(2)当周长为280厘米时,一共有()层。
3.求图2的周长图44.如图6,在长方形ABCD 中,AD=120厘米,截去一个正方形EDCF 后,问还剩下长方形AEFB 的周长是多少厘米?5. 如图12 ,10个相同的小长方形拼成一个大长方形,长是6厘米,宽是5厘米,求小长方形的周长6.下图是一个公园的平面图,A 是公园的大门.问:小明从A 门进公园,不重复地沿道路走公园一圈,他走了多少米?7.下图是某建设物的设计图,如图所示(单位:米)现根据需要在它周围绕电线一圈,试求需电线多少米?8.用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?1 11 1 123 34 4 360米 240 A 图6图129.下图是一块小麦地,已知条件如图中所示.这块地的周长是 米.10.下图“十”字的横与竖都长6厘米.问“十”间的周长是 厘米.11.求下图上“凹”形的周长.单位:厘米12.下图是由若干个相等的正方形组成的“土山”两个字,已知每个正方形的边长是3厘米,这两个字的周长分别是 、 .13.下图是由三个相同的长方形纸片组成的一个“5”字,已知长方形长4厘米,宽2厘米,“5”字周长是 厘米.14.把边长分别是5厘米、4厘米、3厘米和2厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?15.将一张边长为12厘米的正方形纸对折,再将对折后的纸沿它的竖直中线(下图虚纸)剪开,得到三个矩形纸片,5016.一个正方形被分成了5个相等的长方形.每个长方形的周长都是40厘米,求正方形的周长是多少厘米?如图所示.17.如图正方形ABCD的边长为4cm,每边被四等分.求图中所有正方形周长的和.18.如图,长方形ABCD中有一个正方形EFGH,且AF=16厘米,HC=13厘米,求长方形ABCD 的周长是多少厘米。
小学五年级奥数第3讲 长方形、正方形的周长(含答案分析)

第3讲长方形、正方形的周长一、知识要点同学们都知道,长方形的周长=(长+宽)×2.正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。
二、精讲精练【例题1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
练习1:1.下图由8个边长都是2厘米的正方形组成,求这个图形的周长。
2.下图由1个正方形和2个长方形组成,求这个图形的周长。
【例题2】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?练习2:1.有一个长方形,如果长减少4米,宽减少2米,面积就比原来减少44平方米,且剩下部分正好是一个正方形。
求这个正方形的周长。
2.有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是多少?【例题3】已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?练习3:1.有一张长40厘米,宽30厘米的硬纸板,在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒,求被剪后硬纸板的周长。
2.一个长12厘米,宽2厘米的长方形和两个正方形正好拼成下图(1)所示长方形,求所拼长方形的周长。
【例题4】下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
练习4:1.求下面图形的周长(单位:厘米)。
4cm8cm2.在()里填上“>”、“<”或“=”。
甲的周长()乙的周长【例题5】如下图,阴影部分是正方形,DF=6厘米,AB=9厘米,求最大的长方形的周长。
练习5:1.下面三个正方形的面积相等,剪去阴影部分的面积也相等,求原来正方形的周长发生了什么变化?(单位:厘米)2.下面是一个零件的平面图,图中每条短线段都是5厘米,零件长35厘米,高30厘米。
小学奥数经典图形题(适合五年级)

小学奥数经典图形题(适合五年级)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(小学奥数经典图形题(适合五年级))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为小学奥数经典图形题(适合五年级)的全部内容。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米) ②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积.的半径是3cm,求阴影部分的周长和面积. (单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积.
求阴影部分的面积.
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三
角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积.
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
小学奥数:任意四边形、梯形与相似模型(一).专项练习及答案解析

板块一 任意四边形模型任意四边形中的比例关系(“蝴蝶定理”):O DCBA s 4s 3s 2s 1①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDC BA76【考点】任意四边形模型 【难度】2星 【题型】解答 【解析】 在ABE V ,CDE V 中有AEB CED ∠=∠,所以ABE V ,CDE V 的面积比为()AE EB ⨯:()CE DE ⨯.同理有ADE V ,BCE V 的面积比为():()AE DE BE EC ⨯⨯.所以有ABE S V ×CDE S V =ADE S V ×BCE S V ,也就是说在所有凸四边形中,连接顶点得到2条对角线,有图形分成上、下、左、右4个部分,有:上、下部分的面积之积等于左右部分的面积之积. 即6ABE S ⨯V =7ADE S ⨯V ,所以有ABE V与ADE V 的面积比为7:6,ABE S V =7392167⨯=+公顷,ADE S V =6391867⨯=+公顷. 显然,最大的三角形的面积为21公顷.【答案】21【例 2】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?例题精讲任意四边形、梯形与相似模型OCDBA【考点】任意四边形模型 【难度】2星 【题型】解答 【关键词】小数报 【解析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【答案】0.58【例 3】 一个矩形分成4个不同的三角形(如右图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?【考点】任意四边形模型 【难度】3星 【题型】解答 【关键词】华杯赛,初赛,第7题 【解析】 黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的50%-15%=35%已知黄色三角形面积是21平方厘米,所以矩形面积等于21÷35%=60(平方厘米)【答案】60【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?B【考点】任意四边形模型 【难度】2星 【题型】解答 【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ; ⑵根据蝴蝶定理,()():12:361:3AG GC =++=.【答案】1:3【例 4】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.OADC BGH BCDA O【考点】任意四边形模型 【难度】3星 【题型】填空 【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S =V V ,这可以向模型一蝴蝶定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题. 解法一:∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==. 解法二:作AH BD ⊥于H ,CG BD ⊥于G .∵13ABD BCD S S ∆∆=,∴13AH CG =,∴13AOD DOC S S ∆∆=,∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【答案】2倍【例 5】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE△的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【考点】任意四边形模型 【难度】3星 【题型】解答 【解析】 ⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=, 根据蝴蝶定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+. 【答案】23【例 6】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .【考点】任意四边形模型 【难度】4星 【题型】填空 【关键词】清华附中,入学测试题 【解析】 连接AD 、CD 、BC .则可根据格点面积公式,可以得到ABC ∆的面积为:41122+-=,ACD ∆的面积为:331 3.52+-=,ABD ∆的面积为:42132+-=.所以::2:3.54:7ABC ACD BO OD S S ∆∆===,所以44123471111ABO ABD S S ∆∆=⨯=⨯=+.【答案】1211【巩固】如图,每个小方格的边长都是1,求三角形ABC 的面积.【考点】任意四边形模型 【难度】4星 【题型】解答 【解析】 因为:2:5BD CE =,且BD ∥CE ,所以:2:5DA AC =,525ABC S ∆=+510277DBC S ∆=⨯=.【答案】107【例 7】 如图,边长为1的正方形ABCD 中,2BE EC =,CF FD =,求三角形AEG 的面积.ABC DEF GABCDEF G【考点】任意四边形模型 【难度】4星 【题型】解答 【关键词】人大附中考题 【解析】 连接EF .因为2BE EC =,CF FD =,所以1111()23212DEF ABCD ABCD S S S ∆=⨯⨯=W W .因为12AED ABCD S S ∆=W ,根据蝴蝶定理,11::6:1212AG GF ==,所以6613677414AGD GDF ADF ABCD ABCD S S S S S ∆∆∆===⨯=W W .所以132221477AGE AED AGD ABCD ABCD ABCD S S S S S S ∆∆∆=-=-==W W W ,即三角形AEG 的面积是27.【答案】27【例 8】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G【考点】任意四边形模型 【难度】4星 【题型】解答 【解析】 连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEF ABCD ABCD S S S =⨯⨯=V 长方形长方形. 因为12AED ABCD S S =V 长方形,11::5:1210AG GF ==,所以510AGD GDF S S ==V V 平方厘米,所以12AFD S =V 平方厘米.因为16AFD ABCD S S =V 长方形,所以长方形ABCD 的面积是72平方厘米.【答案】72【例 9】 如图,已知正方形ABCD 的边长为10厘米,E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角形BDG 的面积.【考点】任意四边形模型 【难度】4星 【题型】解答 【解析】 设BD 与CE 的交点为O ,连接BE 、DF .由蝴蝶定理可知::BED BCD EO OC S S =V V ,而14BED ABCD S S =V W ,12BCD ABCD S S =V W ,所以::1:2BED BCD EO OC S S ==V V ,故13EO EC =.由于F 为CE 中点,所以12EF EC =,故:2:3EO EF =,:1:2FO EO =.由蝴蝶定理可知::1:2BFD BED S S FO EO ==V V ,所以1128BFD BED ABCD S S S ==V V W ,那么1111010 6.2521616BGD BFD ABCD S S S ===⨯⨯=V V W (平方厘米).【答案】6.25【例 10】 如图,在ABC ∆中,已知M 、N 分别在边AC 、BC 上,BM 与AN 相交于O ,若AOM ∆、ABO ∆和BON ∆的面积分别是3、2、1,则MNC ∆的面积是 .OM NCBA【考点】任意四边形模型 【难度】4星 【题型】填空 【解析】 这道题给出的条件较少,需要运用共边定理和蝴蝶定理来求解.根据蝴蝶定理得 31322AOM BON MON AOB S S S S ∆∆∆∆⨯⨯===设MON S x ∆=,根据共边定理我们可以得ANM ABM MNC MBC S S S S ∆∆∆∆=,33322312x x ++=++,解得22.5x =. 【答案】22.5【例 11】 正六边形123456A A A A A A 的面积是2009平方厘米,123456B B B B B B 分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.4B A 6543A A4B A 543A A【考点】任意四边形模型 【难度】4星 【题型】填空 【关键词】迎春杯,6年级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形问题练习及答案
1、如图,在三角形 ABC中, D 是 AB 的中点, E 是 DB 的中点, F 是 BC 的中点,如果三角形 ABC的面积是 96cm2,那么三角形 AEF的面积是多少平方厘米?
C
F
A D E B
解:三角形 ABF与三角形 ABC有公用的顶点 A,并且它们的底 BC 和 BF在同
一条直线上,所以它们的高相等,而三角形ABF的底BF 只有三角形ABC的底BC
的一半,所以三角形 ABF的面积等于三角形 ABC的一半,是 96÷2=48(cm2)。
同理,三角形 AFD的面积是 48÷2=24(cm2),三角形 DEF的面积是 24÷2=12(cm2),因此,三角形 AEF的面积是 24+12= 36(cm2)。
2、如图所示,大正方形的边长为 12 cm,小正方形的边长为 10 cm,求阴影部分的
面积。
解:阴影三角形的面积无法直接求出,可以用两个正方形面积的和,减去阴
影部分周围三个三角形的面积。
所以,阴影部分的面积是
122+102-12×(12+10)÷2-102÷2-12× (12-
10)÷2=144+ 100-132-50- 12
=50(cm2)。
答:阴影部分的面积是 50 cm2。
3、把三角形 ABC的边 AB 三等分, AC四等分,如图。
已知三角形ADE的面积是
1 cm2,求三角形 ABC的面积是多少平方厘米?
A
E D
B C
解:三角形 AEC的面积是三角形 AED的 4 倍,三角形 ABC的面积是三角形
AEC的 3 倍,所以三角形 ABC的面积是三角形 AED的 4× 3= 12 倍,是 12(cm2)。
答:三角形 ABC的面积是 12 cm2。
4、如图所示,在直角梯形 ABCD中, AD=8 cm,CD=10 cm, BC=12 cm,CG =GD。
阴影部分的面积是多少平方厘米?
A D
G
B C
解: (8+12)×10÷ 2- 8× (10÷ 2)÷2-12× (10÷ 2)÷2=50(平方厘米 )。
答:阴影部分的面积是50 平方厘米。
5、如图所示,将三角形 ABC的 BA边延长 1 倍到 D, CB边延长 2 倍到 E,AC
边延长 3 倍到 F。
如果三角形 ABC的面积是 1 cm2,求三角形 DEF的面积。
D
A
B C
E
F 解:连接 AE、 CD、BF,△ AEB的面积是 2,△ AED的面积是 2,△ BCF的面积是 3,△AFD的面积是 4,△ BEF的面积是 6,所以△ DEF的面积是 1+2+2+3+4+ 6= 18(cm2)。
6、如图,已知AB=3,AE=4,DC= 5, CF=6,AE⊥ED,CF⊥BF。
求阴影部分
的面积。
3 B F
A
6
4
E D5C
解:连接 AC,三角形 ADC的面积是 5× 4÷ 2= 10,三角形 ABC的面积是
3×6÷2=9,所以阴影部分的面积是10+9=19
A B E F
7、图中 ABCD是长方形 ,AD=7.2 cm, CD=5 cm,
CDEF是平行四边形。
如果 BH= 3 cm,求阴影
部分的面积。
H
D C
解:平行四边形的面积与长方形的面积相等, 都是 7.2× 5= 36(cm2)。
HC =7.2-3=4.2(cm), 三角形 HCD的面积是 5× 4.2÷ 2= 10.5(cm2 ),
阴影部分的面积是36-10.5= 25.5(cm2)。
8、平行四边形 ABCD的周长为 75cm,以 BC为底时高为 14cm,以 CD为底时高
为 16cm。
求平行四边形 ABCD的面积是多少平方厘米?
A D
1416
F
B E C
解:因为平行四边形的面积=底×高,所以BC×AE=CD×AF,即 BC×14=CD×16,而 BC+CD=75÷ 2= 37.5(cm),所以,CD= BC×14÷16=
BC×0.875。
于是 BC+ BC×0.875=37.5,BC= 37.5÷1.875= 20(cm)。
因此平行四边形 ABCD 的面积是 20×14=280(cm2)
9、如右图,正方形 ABCD的边长为 6 厘米,△ ABE、△ ADF与四边形 AECF的面积彼此相等,求三角形 AEF的面积 .
解:因为△ ABE、△ ADF 与四边形 AECF的面积彼此相等,所以四边形 AECF 的面积与△ ABE、△ ADF的面积都等于正方形 ABCD
在△ ABE中,因为 AB=6.所以 BE=4,同理 DF=4,因此 CE=CF=2,∴△ ECF的面积为 2×2÷2=2。
所以 S△ AEF=S四边形 AECF-△S ECF=12-2=10(平方厘米)。
10、如右图, A 为△ CDE的 DE 边上中点, BC= CD,若△ ABC(阴影部分)面积为 5 平方厘米 .求△ ABD 及△ ACE的面积 .
解:取 BD 中点 F,连结 AF因.为△ ADF、△ ABF 和△ ABC等底、等高,所以它们的面积相等,都等于 5 平方厘米 .
所以△ ACD的面积等于 15 平方厘米,△ ABD的面积等于 10 平方厘米。
又由于△ ACE与△ ACD等底、等高,所以△ ACE的面积是 15 平方厘米
11、左下图,四边形 ABCD被 AC 和 BD 分成甲、乙、丙、丁四个三角形。
已知
BE=80 cm,DE=40 cm,CE=60 cm,AE=30 cm。
问:丙、丁两个三角形面积
之和是甲、乙两个三角形面积之和的多少倍?
A D A D
丁丁
甲乙甲乙
E E
丙N M
丙
B C B C
解:连接BE的中点N 和CE的中点M 如右上图,三角形丁的面积与三角形ENM 的面积相等,因此,三角形丙的面积是三角形丁的4 倍。
因为BE=2ED,CE=2EA,可知三角形甲和三角形乙的面积都是三角形丁的 2 倍。
由此可以推知,丙、丁两个三角形面积之和是三角形丁的 5 倍,甲、乙两个三角形面积之和是三
角形丁的 4 倍,所以丙、丁两个三角形和是甲、乙两个三角形面积之和的5÷4=1.25 倍。
12、如图, BD、 CF将长方形ABCD分成四块,红色三角形的面积是 4 cm2,黄色三角形的面积是 6 cm2,问绿色四边形的面积是多少平方厘米?
A F D
红
绿黄
E
B C
解:连接 BF,因为三角形 BDF和三角形 CDF同底等高,所以它们的面积相等,由此得知三角形 BEF和三角形 CED的面积相等,也是 6 cm2。
而三角形 BEF 与三角形 DEF同高,所以 BE是 ED 的 6÷ 4= 1.5 倍。
同理,三角形 BEC的面积也是三角形 DEC的 1.5 倍,是 6×1.5=9(cm2)。
因为三角形 ABD 与三角形 CBD的面
积相等,都是 9+6=15(cm2),而绿色四边形的面积等于三角形 ABD的面积减去红色三角形的面积,所以绿色四边形的面积是 15-4=11(cm2)。
