五年2018-2022高考数学真题按知识点分类汇编12-数列求和(含解析)
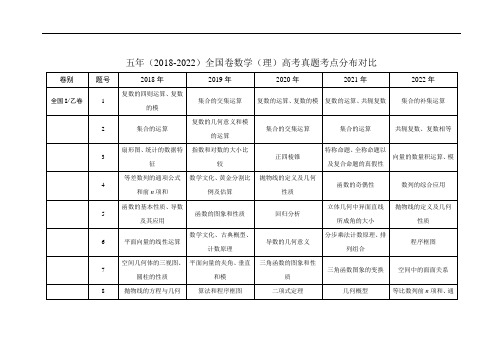
近五年高考全国卷数学真题考点分布对比(2018-2022)
23
含绝对值不等式的解法
含绝对值不等式的解法
绝对值不等式的解法、不等式成立的参数问题
绝对值不等式的解法
基本不等式、柯西不等式证明不等式的应用
全国Ⅲ卷
1
集合交集的运算
集合交集的运算
集合的运算
2
复数的运算
复数的运算
复数的运算
3
三视图
逻辑联结词的意义和统计知识
21
导数的应用、函数的零点
轨迹方程、直线与圆锥曲线的综合应用
三角函数的性质及恒等变换、导数的应用
导数在研究函数单调性以及方程根的问题中的应用
利用导数研究不等式恒成立、极值问题
22
椭圆的参数方程、直线的参数方程
极坐标方程
极坐标方程、参数方程与普通方程的互化
极坐标方程化为直角坐标方程、曲线的参数方程、判断两曲线是否存在公共点
导数的应用、函数的零点
椭圆的标准方程和几何性质、直线与椭圆的位置关系
函数的极值与导数的关系、利用导数证明不等式
椭圆的方程、定点问题
21
导数及其应用、函数的单调性、极值与最值、不等式的证明
随机变量的分布列、等比数列
函数的单调性、导数的应用、不等式
抛物线的几何性质、直线与抛物线的位置关系、圆的弦长公式
导数的几何意义、导数求函数的零点
对数函数的奇偶性和单调性
二倍角公式、同角三角函数的基本关系
圆锥的侧面积、体积
10
三角函数的单调性
二倍角公式、同角三角函数的基本关系
球的表面积、点到平面的距离
排列组合、古典概型
椭圆的方程、离心率、直线斜率
11
函数的基本性质
数列求和与数列不等式的证明--高考数学【解析版】

专题27 数列求和与数列不等式的证明等差数列、等比数列的性质、通项公式和前n 项和公式构成两类数列的重要内容,在历届高考中属于必考内容,既有独立考查的情况,也有二者与其它知识内容综合考查的情况.一般地,选择题、填空题往往独立考查等差数列或等比数列的基本运算,解答题往往综合考查等差数列、等比数列.数列求和问题是高考数列中的另一个易考类型,其中常见的是“裂项相消法”、“错位相减法”.数列求和与不等式证明相结合,又是,数列考题中的常见题型,关于数列中涉及到的不等问题,通常与数列的最值有关或证明(数列的和)不等式成立或确定参数的范围,对于数列中的最值项问题,往往要依靠数列的单调性,而对于数列的和不等式的证明问题,往往可以利用“放缩法”,要根据不等式的性质通过放缩,达到解题目的.【重点知识回眸】(一)数列的求和 1.公式法(1)等差数列的前n 项和公式: S n =n a 1+a n 2=na 1+n n -12d ; (2)等比数列的前n 项和公式: S n =⎩⎪⎨⎪⎧na 1,q =1,a 11-q n 1-q =a 1-a n q1-q ,q ≠1. 2.几种数列求和的常用方法(1)分组求和法:一个数列的通项公式是由若干个等差或等比或可求和的数列组成的,则求和时可用分组求和法,分别求和后相加减.(2)裂项相消法:把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消(注意消项规律),从而求得前n 项和.裂项时常用的三种变形: ①111(1)1n n n n =-++;②1111()(21)(21)22121n n n n =--+-+;11n n n n =+++(3)错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么求这个数列的前n 项和即可用错位相减法求解.(4)倒序相加法:如果一个数列{a n }与首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n 项和即可用倒序相加法求解.(5)并项求和法:一个数列的前n 项和中,可两两结合求解,则称之为并项求和.形如a n =(-1)n f (n )类型,可采用两项合并求解.例如,S n =1002-992+982-972+…+22-12 =(100+99)+(98+97)+…+(2+1)=5 050.(6)利用周期性求和:如果一个数列的项按某个周期循环往复,则在求和时可将一个周期内的项归为一组求和,再统计前n 项和中含多少个周期即可. (二)数列中的不等关系1.数列中的最值项,要依靠数列的单调性.如何判断数列的单调性:(1)函数角度:从通项公式入手,将其视为关于n 的函数,然后通过函数的单调性来判断数列的单调性.由于n N *∈ ,所以如果需要用到导数,首先要构造一个与通项公式形式相同,但定义域为()0,+∞ 的函数,得到函数的单调性后再结合n N *∈得到数列的单调性(2)相邻项比较:在通项公式不便于直接分析单调性时,可考虑进行相邻项的比较得出数列的单调性,通常的手段就是作差(与0比较,从而转化为判断符号问题)或作商(与1比较,但要求是正项数列) (3)对于某数列的前n 项和{}12:,,,n n S S S S ,在判断其单调性时可以考虑从解析式出发,用函数的观点解决.也可以考虑相邻项比较.在相邻项比较的过程中可发现:1n n n a S S -=-,所以{}n S 的增减由所加项n a 的符号确定.进而把问题转化成为判断n a 的符号问题. (三)利用放缩法证明不等式 1.与求和相关的不等式的放缩技巧:① 在数列中,“求和看通项”,所以在放缩的过程中通常从数列的通项公式入手② 在放缩时要看好所证不等式中不等号的方向,这将决定对通项公式是放大还是缩小(应与所证的不等号同方向)③ 在放缩时,对通项公式的变形要向可求和数列的通项公式靠拢,常见的是向等比数列与可裂项相消的数列进行靠拢.④ 若放缩后求和发现放“过”了,即与所证矛盾,通常有两条道路选择:第一个方法是微调:看能否让数列中的一些项不动,其余项放缩.从而减小放缩的程度,使之符合所证不等式;第二个方法就是推翻了原有放缩,重新进行设计,选择放缩程度更小的方式再进行尝试. 2.放缩构造裂项相消数列与等比数列的技巧:① 裂项相消:在放缩时,所构造的通项公式要具备“依项同构”的特点,即作差的两项可视为同一数列的相邻两项(或等距离间隔项)② 等比数列:所面对的问题通常为“n S <常数”的形式,所构造的等比数列的公比也要满足()0,1q ∈ ,如果题目条件无法体现出放缩的目标,则可从所证不等式的常数入手,,常数可视为11a q-的形式,然后猜想构造出等比数列的首项与公比,进而得出等比数列的通项公式,再与原通项公式进行比较,看不等号的方向是否符合条件即可.3.与数列中的项相关的不等式问题:① 此类问题往往从递推公式入手,若需要放缩也是考虑对递推公式进行变形② 在有些关于项的不等式证明中,可向求和问题进行划归,即将递推公式放缩变形成为可“累加”或“累乘”的形式,即()1n n a a f n +-<或()1n na f n a +<(累乘时要求不等式两侧均为正数),然后通过“累加”或“累乘”达到一侧为n a ,另一侧为求和的结果,进而完成证明 4.常见的放缩变形: (1)()()211111n n n n n <<+-,其中2,n n N ≥∈:可称21n为“进可攻,退可守”,可依照所证不等式不等号的方向进行选择. 注:对于21n,可联想到平方差公式,从而在分母添加一个常数,即可放缩为符合裂项相消特征的数列,例如:()()22111111111211n n n n n n ⎛⎫<==- ⎪--+-+⎝⎭,这种放缩的尺度要小于(1)中的式子.此外还可以构造放缩程度更小的,如:()()22211411111412121221214n n n n n n n ⎛⎫<==- ⎪--+-+⎝⎭- (2)n n n=+,从而有:212111n n n n n n nn n +=<<<--+++-n2,2,n n n n N n *<--≥∈ (3)分子分母同加常数:()()0,0,0,0b b m b b m b a m a b m a a m a a m++>>>>>>>>++ 此结论容易记混,通常在解题时,这种方法作为一种思考的方向,到了具体问题时不妨先构造出形式再验证不等关系.(4)()()()()()()()121222221212122212121nn n n n n n n n n n--=<=------- ()1112,2121n nn n N *-=-≥∈-- 可推广为:()()()()()()()121111111nn n n n n n n n n n k k k k k k k k k k k k --=<=------- ()1112,2,,11n nn k k n N k k *-=-≥≥∈-- 5.利用导数证明数列不等式 (四)数学归纳法证明不等式【典型考题解析】热点一 分组求和与并项求和【典例1】(2022·全国·高三专题练习)已知数列{n a }满足11a =,()*121N n n a a n +=+∈.(1)证明{1n a +}是等比数列,并求{n a }的通项公式; (2)求数列{1]n a n ++的前n 项和n S .【答案】(1)证明见解析;21nn a =-(2)()11222n n n n S ++=+-【分析】(1)根据题意结合等比数列定义可证1121n n a a ++=+,可得{}1n a +是首项为2,公比为2的等比数列,利用等比数列通项公式代入运算;(2)因为2n n b n =+,利用分组求和结合等差、等比数列求和公式整理运算.(1)由题意可得:1120a +=≠∵()11121212111n n n n n n a a a a a a +++==++=+++所以{}1n a +是首项为2,公比为2的等比数列则12nn a +=,即21n n a =-因此{n a }的通项公式为21n n a =-(2)由(1)知21nn a =-,令1n n b a n =++则2n n b n =+所以()()()121221222nn n S b b b n =+++=++++++.()12222(12)nn =++⋯++++⋯+()()2121122n n n -+=+-()11222n n n ++=+-.综上()11222n n n n S ++=+-.【典例2】.(2021·河南·高三开学考试(文))已知等比数列{}n a 的公比大于1,26a =,1320a a +=.(1)求{}n a 的通项公式;(2)若12331log log 22n n n n b a a a ++=+,求{}n b 的前n 项和n T .【答案】(1)123n n a -=⋅(2)131n n -+ 【分析】(1)设出公比q ,根据题目条件列方程求解; (2)先写出n b ,利用裂项求和,分组求和的办法表示出n T . (1)设等比数列{}n a 的公比为()1q q >,由26a =,1320a a +=得6620q q +=,解之得3q =或13q =(舍去),由26a =得,12a =,所以{}n a 的通项公式为123n n a -=⋅.(2) 由(1)知,()1112331111232311log log 22n n n n n n b a a an n n n --++=+=⋅+=⋅+-++所以{}n b 的前n 项和为()01111111233312231n n T n n -⎡⎤⎛⎫⎛⎫⎛⎫=++⋅⋅⋅++-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦13112131311n n n n -=⨯+-=--++ 【总结提升】分组转化法求和的常见类型(1)若a n =b n ±c n ,且{b n },{c n }为等差或等比数列,则可采用分组求和法求{a n }的前n 项和.(2)通项公式为a n =⎩⎪⎨⎪⎧b n ,n 为奇数,c n,n 为偶数的数列,其中数列{b n },{c n }是等比数列或等差数列,可采用分组求和法求和.热点二 裂项相消法求和【典例3】(2017·全国·高考真题(理))(2017新课标全国II 理科)等差数列{}n a 的前n 项和为n S ,33a =,410S =,则11nk kS ==∑____________. 【答案】21nn + 【解析】 【详解】设等差数列的首项为1a ,公差为d ,由题意有1123434102a d a d +=⎧⎪⎨⨯+=⎪⎩ ,解得111a d =⎧⎨=⎩ , 数列的前n 项和()()()111111222n n n n n n n S na d n --+=+=⨯+⨯=, 裂项可得12112()(1)1k S k k k k ==-++, 所以1111111122[(1)()()]2(1)223111nk knS n n n n ==-+-++-=-=+++∑. 【典例4】(2018·天津·高考真题(理))设{}n a 是等比数列,公比大于0,其前n 项和为()*n S n N ∈,{}n b 是等差数列.已知11a =,322a a =+,435a b b =+,5462a b b =+. (I )求{}n a 和{}n b 的通项公式;(II )设数列{}n S 的前n 项和为()*n T n N ∈,(i )求n T ;(ii )证明()()()()22*122122n nk k k k T b b n N k k n ++=+=-∈+++∑. 【答案】(Ⅰ)12n n a -=,n b n =;(Ⅱ)(i )122n n T n +=--.(ii )证明见解析.【解析】 【详解】分析:(I )由题意得到关于q 的方程,解方程可得2q =,则12n n a -=.结合等差数列通项公式可得.n b n =(II )(i )由(I ),有21nn S =-,则()112122nk n n k T n +==-=--∑.(ii )因为()()()212221221k k k k k T b b k k k k ++++=-++++,裂项求和可得()()()22122122n nk k k k T b b k k n ++=+=-+++∑. 详解:(I )设等比数列{}n a 的公比为q.由1321,2,a a a ==+可得220q q --=.因为0q >,可得2q =,故12n n a -=.设等差数列{}n b 的公差为d ,由435a b b =+,可得13 4.b d += 由5462a b b =+,可得131316,b d += 从而11,1,b d == 故.n b n =所以数列{}n a 的通项公式为12n n a -=,数列{}n b 的通项公式为.n b n =(II )(i )由(I ),有122112nn n S -==--,故()()1112122122212nnnk k n n k k T n n n +==⨯-=-=-=-=---∑∑.(ii )因为()()()()()()()()1121222222212121221k k k k k k k k k k T b b k k k k k k k k k +++++--+++⋅===-++++++++, 所以()()()32432122122222222123243212n n n nk k k k T b b k k n n n ++++=+⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪⎪+++++⎝⎭⎝⎭⎝⎭∑. 【典例5】(2022·湖北·襄阳五中高三阶段练习)已知数列{}n a 满足()*1232311113333n n a a a a n n ++++=∈N . (1)求数列{}n a 的通项公式;(2)设3log n n b a =,求数列121n n n b b b ++⎧⎫⎨⎬⎩⎭的前n 项和为n T .【答案】(1)()*3N n n a n =∈(2)()()1112212n T n n ⎡⎤=-⎢⎥++⎢⎥⎣⎦【分析】(1)由递推关系取1n =可求1a ,当2n ≥时,取递推关系中的1n n 可求(2)n a n ≥,由此可得数列{}n a 的通项公式;(2)由(1)可得n b n =,利用裂项相消法求数列121n n n b b b ++⎧⎫⎨⎬⎩⎭的前n 项和为n T .(1)当1n =时,13a =,当2n 时,1232311113333n na a a a n ++++=①1231231111113333n n a a a a n --++++=-② 由①-②得()1113n n a n n =--=,即()32n n a n =. 当1n =时也成立,所以数列{}n a 的通项公式为()*3N n n a n =∈(2)因为33log log 3nn n b a n ===,所以()()()()()1211111122112n n n b b b n n n n n n n ++⎡⎤==-⎢⎥+++++⎢⎥⎣⎦, 所以()()()()()11111111112122323341122212n T n n n n n n ⎡⎤⎡⎤=-+-++-=-⎢⎥⎢⎥⋅⋅⋅⋅+++++⎢⎥⎢⎥⎣⎦⎣⎦. 【规律方法】裂项相消法的步骤、原则及规律 (1)基本步骤:裂项、累加、消项; (2)裂项原则一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止. (3)消项规律消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项. 热点三 错位相减法求和【典例6】(2020·天津·高考真题)已知{}n a 为等差数列,{}n b 为等比数列,()()115435431,5,4a b a a a b b b ===-=-.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)记{}n a 的前n 项和为n S ,求证:()2*21n n n S S S n ++<∈N ;(Ⅲ)对任意的正整数n ,设()21132,,,.n nn n n n n a b n a a c a n b +-+⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数求数列{}n c 的前2n 项和.【答案】(Ⅰ)n a n =,12n n b -=;(Ⅱ)证明见解析;(Ⅲ)465421949n n n n +--+⨯. 【解析】【分析】(Ⅰ)由题意分别求得数列的公差、公比,然后利用等差、等比数列的通项公式得到结果; (Ⅱ)利用(Ⅰ)的结论首先求得数列{}n a 前n 项和,然后利用作差法证明即可;(Ⅲ)分类讨论n 为奇数和偶数时数列的通项公式,然后分别利用指数型裂项求和和错位相减求和计算211nk k c -=∑和21nk k c =∑的值,据此进一步计算数列{}n c 的前2n 项和即可.【详解】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q . 由11a =,()5435a a a =-,可得d =1. 从而{}n a 的通项公式为n a n =. 由()15431,4b b b b ==-,又q ≠0,可得2440q q -+=,解得q =2,从而{}n b 的通项公式为12n n b -=.(Ⅱ)证明:由(Ⅰ)可得(1)2n n n S +=, 故21(1)(2)(3)4n n S S n n n n +=+++,()()22211124n S n n +=++, 从而2211(1)(2)02n n n S S S n n ++-=-++<,所以221n n n S S S ++<.(Ⅲ)当n 为奇数时,()111232(32)222(2)2n n n n n n n n a b n c a a n n n n-+-+--===-++,当n 为偶数时,1112n n n n a n c b -+-==, 对任意的正整数n ,有222221112221212121k k nnnk k k c k k n --==⎛⎫=-=- ⎪+-+⎝⎭∑∑, 和223111211352321444444nnk k n n k k k n n c -==---==+++++∑∑① 由①得22314111352321444444n k n n k n n c +=--=+++++∑ ②由①②得22111211312221121441444444414n nk n n n k n n c ++=⎛⎫- ⎪--⎝⎭=+++-=---∑, 由于11211121221121156544144334444123414n n n n n n n n ++⎛⎫- ⎪--+⎝⎭--=-⨯--⨯=-⨯-, 从而得:21565994nk nk n c =+=-⨯∑. 因此,2212111465421949n nnnk k k n k k k n c c c n -===+=+=--+⨯∑∑∑. 所以,数列{}n c 的前2n 项和为465421949n n n n +--+⨯. 【典例7】(2022·云南·高三阶段练习)已知数列{}n a 的前n 项和为n S ,且243n n S a =-. (1)求数列{}n a 的通项公式; (2)令83n n nb a =⨯,求数列{}n b 的前n 项和n T . 【答案】(1)232n n a -=⋅(2)24(1)2n n T n +=+-⨯【分析】(1)根据n a 和n S 的关系式,即可求得数列{}n a 的通项公式. (2)由(1)中结论可得数列{}n b 的通项公式,再由错位相减法即可求得n T . (1)由已知得243n n S a =-. ①当1n =时,11132432S a a =-⇒=;当2n ≥时,11243243n n n n S a S a --=-⎧⎨=-⎩①②,-①②得12(2)n n a a n -=≥,所以{}n a 是以32为首项,2为公比的等比数列; 所以1232322n n n a --=⨯=⋅. (2)由(1)得1823n n n nb a n +=⨯=⋅, 所以21341222322n n T n +=⨯+⨯+⨯+⨯+⋅⋅⋅,①所以341221222(1)22n n n T n n ++=⨯+⨯+⋅⋅⋅+-⨯+⨯,②则-①②得:()234142222n n n T n ++-=-⨯+++⋅⋅⋅+,化简得24(1)2n n T n +=+-⨯.【典例8】(2020·全国卷Ⅰ)设{a n }是公比不为1的等比数列,a 1为a 2,a 3的等差中项. (1)求{a n }的公比;(2)若a 1=1,求数列{na n }的前n 项和. 【答案】【解析】(1)设{a n }的公比为q ,由题设得2a 1=a 2+a 3,即2a 1=a 1q +a 1q 2. 所以q 2+q -2=0,解得q =1(舍去)或q =-2. 故{a n }的公比为-2.(2)记S n 为{na n }的前n 项和. 由(1)及题设可得,a n =(-2)n -1. 所以S n =1+2×(-2)+…+n ×(-2)n -1,-2S n =-2+2×(-2)2+…+(n -1)×(-2)n -1+n ×(-2)n . 可得3S n =1+(-2)+(-2)2+…+(-2)n -1-n ×(-2)n =1(2)3n---n ×(-2)n .所以S n =19-(31)(2)9nn +-.【规律方法】错位相减法求和的具体步骤:热点四 其它求和方法【典例9】(2022·湖南·麻阳苗族自治县第一中学高三开学考试)德国大数学家高斯年少成名,被誉为数学界的王子.在其年幼时,对123100++++的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成;因此,此方法也称之为高斯算法.现有函数4()42xx f x =+,则1232018()()()()2019201920192019f f f f ++++等于( ) A .1008 B .1009 C .2018 D .2019【答案】B【分析】根据()(1)1f x f x +-=,利用倒序相加法求解.【详解】解:因为4()42xx f x =+,且114444()(1)1424242244--+-=+=+=+++⨯+x x x xx x x f x f x , 令1232018()()()()2019201920192019=++++S f f f f , 又 2018201720161()()()()2019201920192019=++++S f f f f , 两式相加得:212018=⨯S , 解得1009S =, 故选:B【典例10】(2022·全国·高三专题练习(文))1202年意大利数学家列昂那多-斐波那契以兔子繁殖为例,引人“兔子数列”,又称斐波那契数列.即1,1,2,3,5,8,13,21,34,55,该数列中的数字被人们称为神奇数,在现代物理,化学等领域都有着广泛的应用.若此数列各项被3除后的余数构成一新数列{}n a ,则数列{}n a 的前2022项的和为________. 【答案】2276【分析】由数列1,1,2,3,5,8,13,21,34,55,各项除以3的余数,可得{}n a 为1,1,2,0,2,2,1,0,1,1,2,0,2,2,1,知{}n a 是周期为8的数列,即可求出数列{}n a 的前2022项的和.【详解】由数列1,1,2,3,5,8,13,21,34,55,各项除以3的余数,可得{}n a 为1,1,2,0,2,2,1,0,1,1,2,0,2,2,1,{}n a ∴是周期为8的数列,一个周期中八项和为112022109+++++++=,又202225286=⨯+,∴数列{}n a 的前2022项的和2022252982276S =⨯+=. 故答案为:2276.【典例11】(2016·全国·高考真题(文))等差数列{n a }中,34574,6a a a a +=+=.(Ⅰ)求{n a }的通项公式;(Ⅱ) 设[]n n b a =,求数列{}n b 的前10项和,其中[]x 表示不超过x 的最大整数,如[0.9]=0,[2.6]=2. 【答案】(Ⅰ)235n n a +=;(Ⅱ)24. 【解析】 【详解】试题分析:(Ⅰ) 根据等差数列的通项公式及已知条件求1a ,d ,从而求得n a ;(Ⅱ)由(Ⅰ)求n b ,再求数列{}n b 的前10项和.试题解析:(Ⅰ)设数列{}n a 的公差为d ,由题意有112+54,+53a d a d ==. 解得121,5a d ==.所以{}n a 的通项公式为235n n a +=. (Ⅱ)由(Ⅰ)知235n n b +⎡⎤=⎢⎥⎣⎦. 当n=1,2,3时,2312,15n n b +≤<=; 当n=4,5时,2323,25n n b +≤<=; 当n=6,7,8时,2334,35n n b +≤<=; 当n=9,10时,2345,45n n b +≤<=. 所以数列{}n b 的前10项和为1322334224⨯+⨯+⨯+⨯=. 热点五 与裂项相消法相关的不等式证明【典例12】(2022·全国·高考真题)记n S 为数列{}n a 的前n 项和,已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列.(1)求{}n a 的通项公式; (2)证明:121112na a a +++<. 【答案】(1)()12n n n a +=(2)见解析 【解析】【分析】(1)利用等差数列的通项公式求得()121133n n S n n a +=+-=,得到()23n n n a S +=,利用和与项的关系得到当2n ≥时,()()112133n n n n n n a n a a S S --++=-=-,进而得:111n n a n a n -+=-,利用累乘法求得()12n n n a +=,检验对于1n =也成立,得到{}n a 的通项公式()12n n n a +=; (2)由(1)的结论,利用裂项求和法得到121111211n a a a n ⎛⎫+++=- ⎪+⎝⎭,进而证得.(1)∵11a =,∴111S a ==,∴111S a =, 又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列,∴()121133n n S n n a +=+-=,∴()23n n n a S +=, ∴当2n ≥时,()1113n n n a S --+=,∴()()112133n n n n n n a n a a S S --++=-=-,整理得:()()111n n n a n a --=+, 即111n n a n a n -+=-, ∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯ ()1341112212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--, 显然对于1n =也成立, ∴{}n a 的通项公式()12n n n a +=; (2)()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭ ∴12111na a a +++1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 【典例13】(2022·安徽·高三开学考试)已知数列{}n a 满足(12122n n a a a a n -+++-=-且)*N n ∈,且24a =.(1)求数列{}n a 的通项公式;(2)设数列()()1211n n n a a +⎧⎫⎪⎪⎨⎬--⎪⎪⎩⎭的前n 项和为n T ,求证:213n T <. 【答案】(1)()*2n n a n =∈N(2)证明见解析【分析】(1)将已知条件与1212n n a a a a ++++-=-两式相减,再结合等比数列的定义即可求解;(2)利用裂项相消求和法求出n T 即可证明. (1)解:因为1212n n a a a a -+++-=-,所以1212n n a a a a ++++-=-,两式相减得12(2)n n a a n +=,当2n =时,122a a -=-, 又24a =,所以1212,2a a a ==,所以()*12n n a a n +=∈N ,所以{}n a 是首项为2,公比为2的等比数列,所以()*2n n a n =∈N ;(2)证明:()()()()11122111121212121n n n n n n n n a a +++==-------, 所以2231111111111121212121212121n n n n T ++⎛⎫⎛⎫⎛⎫=-+-++-=-<⎪ ⎪ ⎪-------⎝⎭⎝⎭⎝⎭, 由1n ,得124n +,所以1121213n +--, 综上,213n T <. 【总结提升】(1)与不等式相结合考查裂项相消法求和问题应分两步:第一步,求和;第二步,利用作差法、放缩法、单调性等证明不等式.(2)放缩法常见的放缩技巧有: ①21111(1)1k k k kk <=---. ②2211111()2111k k k k <=--+-.③21111111k k k kk -<<-+-. ④2(12(1)n n n n n+<<--.热点六 与错位相减法相关的不等式证明【典例14】(2021·全国·高考真题(文))设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a 成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <. 【答案】(1)11()3n n a -=,3n nn b =;(2)证明见解析. 【解析】 【分析】(1)利用等差数列的性质及1a 得到29610q q -+=,解方程即可; (2)利用公式法、错位相减法分别求出,n n S T ,再作差比较即可. 【详解】(1)因为{}n a 是首项为1的等比数列且1a ,23a ,39a 成等差数列,所以21369a a a =+,所以211169a q a a q =+,即29610q q -+=,解得13q =,所以11()3n n a -=,所以33n n n na nb ==. (2)[方法一]:作差后利用错位相减法求和211213333n n nn nT --=++++, 012111111223333-⎛⎫=++++ ⎪⎝⎭n n S , 230121123111112333323333n n n n S n T -⎛⎫⎛⎫-=++++-++++= ⎪ ⎪⎝⎭⎝⎭012111012222333---++++111233---+n nn n .设0121111101212222Γ3333------=++++n n n , ⑧则1231111012112222Γ33333-----=++++n nn . ⑨由⑧-⑨得1121113312111113322Γ13233332313--⎛⎫--- ⎪⎛⎫⎝⎭=-++++-=-+- ⎪⎝⎭-n n n n n n n . 所以211312Γ432323----=--=-⨯⨯⨯n n n n n n . 因此10232323--=-=-<⨯⨯n n n n nS n n nT . 故2nn S T <. [方法二]【最优解】:公式法和错位相减求和法证明:由(1)可得11(1)313(1)12313n n n S ⨯-==--,211213333n n n n nT --=++++,① 231112133333n n n n nT +-=++++,② ①-②得23121111333333n n n n T +=++++-1111(1)1133(1)1323313n n n n n n ++-=-=---,所以31(1)4323n n nnT =--⋅,所以2n n S T -=3131(1)(1)043234323n n n n n n ----=-<⋅⋅, 所以2nn S T <. [方法三]:构造裂项法由(Ⅰ)知13⎛⎫= ⎪⎝⎭n n b n ,令1()3αβ⎛⎫=+ ⎪⎝⎭n n c n ,且1+=-n n n b c c ,即1111()[(1)]333αβαβ+⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭n n n n n n ,通过等式左右两边系数比对易得33,24αβ==,所以331243n n c n ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭.则12113314423nn n n n T b b b c c +⎛⎫⎛⎫=+++=-=-+ ⎪⎪⎝⎭⎝⎭,下同方法二.[方法四]:导函数法 设()231()1-=++++=-n nx x f x x x x x x,由于()()()()()()1221'111'11(1)'1(1)1n n n n nx x x x x x x x nx n x x x x +⎡⎤⎡⎤⎡⎤----⨯--+-+⎣⎦⎣⎦⎢⎥==---⎢⎥⎣⎦, 则12121(1)()123(1)+-+-+=++++='-n nn nx n x f x x x nxx .又1111333-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭n n n b n n ,所以2112311111233333n n n T b b b b n -⎡⎤⎛⎫⎛⎫=++++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦12111(1)11133333113n nn n f +⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭⋅=⨯ ⎪⎝⎭⎛⎫- ⎪⎝⎭' 13113311(1)4334423n nnn n n +⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-+=-+⎢⎥ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,下同方法二. 【整体点评】本题主要考查数列的求和,涉及到等差数列的性质,错位相减法求数列的和,考查学生的数学运算能力,是一道中档题,其中证明不等式时采用作差法,或者作商法要根据式子得结构类型灵活选择,关键是要看如何消项化简的更为简洁.(2)的方法一直接作差后利用错位相减法求其部分和,进而证得结论;方法二根据数列的不同特点,分别利用公式法和错位相减法求得,n n S T ,然后证得结论,为最优解;方法三采用构造数列裂项求和的方法,关键是构造1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,使1+=-n n n b c c ,求得n T 的表达式,这是错位相减法的一种替代方法,方法四利用导数方法求和,也是代替错位相减求和法的一种方法.【典例15】(2021·天津·高考真题)已知{}n a 是公差为2的等差数列,其前8项和为64.{}n b 是公比大于0的等比数列,1324,48b b b =-=. (I )求{}n a 和{}n b 的通项公式;(II )记2*1,n n nc b b n N =+∈,(i )证明{}22n n c c -是等比数列;(ii )证明)*12222nk k kk k a n N c a c +=∈-【答案】(I )21,n a n n N *=-∈,4,n n N b n *=∈;(II )(i )证明见解析;(ii )证明见解析.【解析】 【分析】(I )由等差数列的求和公式运算可得{}n a 的通项,由等比数列的通项公式运算可得{}n b 的通项公式;(II )(i )运算可得2224nn n c c =⋅-,结合等比数列的定义即可得证; (ii )放缩得21222422n n n n n a n c a c +<-⋅,进而可得1112222n k k n k k k k a k c c a +-==-,结合错位相减法即可得证. 【详解】(I )因为{}n a 是公差为2的等差数列,其前8项和为64. 所以12818782642a a a a ⨯++⋅⋅⋅+=+⨯=,所以11a =, 所以()12121,n n n n N a a *=+-=-∈;设等比数列{}n b 的公比为(),0q q >,所以()221321484q b b b q q b q ==-=--,解得4q =(负值舍去), 所以114,n n n b q n N b -*==∈;(II )(i )由题意,221441n n nn n b c b =++=,所以22224211442444n n nn nnn c c ⎛⎫⎛⎫=+-+=⋅ ⎪ ⎪⎝⎭⎝⎭-, 所以220nn c c ≠-,且212222124424n n n n nn c c c c +++⋅==⋅--, 所以数列{}22nn c c -是等比数列; (ii )由题意知,()()22122222121414242222n n n n n n n n n a n n c c a +-+-==<-⋅⋅⋅, 2122124222222n n n nn nna n anc c +--⋅⋅,所以1112222nk k n k k k k k a kc c a +-==-, 设10121112322222nn k n k k n T --===+++⋅⋅⋅+∑, 则123112322222n nn T =+++⋅⋅⋅+,两式相减得21111111122121222222212nn n n nn n n n T -⎛⎫⋅- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--, 所以1242n n n T -+=-, 所以11112224222222nn k k n k k k k a k n c c a +--==+⎫-<⎪-⎭ 【规律方法】等差数列的判定与证明的方法方法 解读适合题型 定义法 若a n -a n -1(n ≥2,n ∈N *)为同一常数⇔{a n }是等差数列 解答题中证明问题等差中项法 2a n =a n +1+a n -1(n ≥2,n ∈N *)成立⇔{a n }是等差数列通项公式法 a n =pn +q (p ,q 为常数)对任意的正整数n 都成立⇔{a n }是等差数列 选择、填空题中的判定问题前n 项和公式法验证S n =An 2+Bn (A ,B是常数)对任意的正整数n 都成立⇔{a n }是等差数列【精选精练】一.单选题1.(2021·全国·高三专题练习)数列{}n a 满足11a =,1(1)(1)n n na n a n n +=+++,若2cos 3=πn n n b a ,且数列{}n b 的前n 项和为n S ,则11S =( ) A .64 B .80 C .64- D .80-【答案】C【分析】由已知可得111n n a a n n +-=+,即数列n a n ⎧⎫⎨⎬⎩⎭是等差数列,由此求出22cos 3n n b n π=,分别令 1,2,3,,11n =可求出11S .【详解】数列{}n a 满足11a =,()()111n n na n a n n +=+++, 则111n na a n n+=++, 可得数列n a n ⎧⎫⎨⎬⎩⎭是首项为1、公差为1的等差数列,即有na n n=,即为2n a n =, 则222cos cos 33n n n n b a n ππ==, 则()()2222222222211112457810113692S =-++++++++++()22222222222222112334566789910112=-+--++--++--++ ()15234159642=-⨯+++=-. 故选:C.2.(2022·全国·高三专题练习(文))斐波那契数列因以兔子繁殖为例子而引入,故又称为“兔子数列”.此数列在现代物理、准晶体结构、化学等领域都有着广泛的应用.斐波那契数列{}n a 可以用如下方法定义:21n n n a a a ++=+,且121a a ==,若此数列各项除以4的余数依次构成一个新数列{}n b ,则数列{}n b 的前2022项和为( ) A .2698 B .2697 C .2696 D .2695【答案】C【分析】根据()*12123,,1n n n a a a n n a a --=+⋯∈==N , 递推得到数列{}n a ,然后再得到数列{}n b 是以6为周期的周期数列求解.【详解】因为()*12123,,1,n n n a a a n n a a --=+⋯∈==N所以数列{}n a 为 1,1,2,3,5,8,13,21,34,55,89,144,⋯此数列各项除以 4 的余数依次构成的数列{}n b 为:1,1,2,3,1,0,1,1,2,3,1,0,是以 6 为周期的周期数列, 所以20222022=(1+1+2+3+1+0)=26966S . 故选:C.3.(2018·浙江·高考真题)已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则 A .1324,a a a a << B .1324,a a a a >< C .1324,a a a a <> D .1324,a a a a >>【答案】B 【解析】 【分析】先证不等式ln 1x x ≥+,再确定公比的取值范围,进而作出判断. 【详解】令()ln 1,f x x x =--则1()1f x x'=-,令()0,f x '=得1x =,所以当1x >时,()0f x '>,当01x <<时,()0f x '<,因此()(1)0,ln 1f x f x x ≥=∴≥+,若公比0q >,则1234123123ln()a a a a a a a a a a +++>++>++,不合题意;若公比1q ≤-,则212341(1)(1)0,a a a a a q q +++=++≤但212311ln()ln[(1)]ln 0a a a a q q a ++=++>>,即12341230ln()a a a a a a a +++≤<++,不合题意; 因此210,(0,1)q q -<<∈,22113224,0a a q a a a q a ∴>=<=<,选B.【点睛】构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如ln 1,x x ≥+ 2e 1,e 1(0).x x x x x ≥+≥+≥二、填空题4.(2021·内蒙古呼和浩特·高三阶段练习(理))已知{}n a 是等比数列,公比大于1,且2420a a +=,38a =.记m b 为{}n a 在区间()*(0,]m m N ∈中的项的个数,则数列{}m b 的前60项的和60S 的值为______.【答案】243【分析】第一步求出{}n a 是等比数列的通项公式,第二步计算m b 为{}n a 在区间()*(0,]m m N ∈中的项的个数,列举求值即可。
2018年至2022年高考数学全国Ⅰ卷数列题解题分析

2018年至2022年高考数学全国Ⅰ卷数列题解题分析摘要:高考数学全国Ⅰ卷中数列题,重点考查学生对数列求通项和数列求和常见的几种通法通性的掌握情况,特别是对等差数学、等比数列的通项公式和求和公式的理解,以及对方程思想、化归和转化思想等数学思想的理解及应用情况。
此题难度并不高,但有一定的灵活性。
在数学核心素养的考查上,此题重点考查了数学运算、数学建模等数学核心素养。
关键词:高考数学;试题思维层次;数学核心素养普通高中数学课程标准中数学核心素养分别是:数学抽象、逻辑推理、数学运算、数学建模、直观想象和数据分析,并给出每个数学核心素养划分的三个水平。
“水平一”是高中毕业应达到的要求,也是高中毕业数学学业水平考试的命题依据;“水平二”是高考的要求,也是数学高考的命题依据;“水平三”可作为大学自主招生的参考。
本文选取新课标对高中数学运算、数学建模核心素养和划分的三个水平,对高考中数列题进行分析。
试题思维层次是指学生成功解答试题时所要求达到的思维水平,是基于SOLO分类理论对试题考查学生的思维水平进行划分。
在SOLO分类理论的指导下,试题思维层次由低到高可划分为四个层次:单点结构、多点结构、关联结构、抽象扩展结构。
单点结构水平层次试题的线索单一且明确,情景熟悉,成功解答只需回忆再现一个知识点,能联系单一事件进行“概括”即可。
多点结构水平层次试题的线索涉及多个孤立的素材,情景熟悉,成功解答需要回忆再现两个及两个以上知识点,能根据几个有限的、孤立的事件进行“概括”。
关联结构水平层次试题的线索丰富,涉及多个相互联系的素材,情境熟悉,成功解答需要结合问题情境,联系题干与给出的知识点相关的内容,从整体上把握解题思路,进行归纳、类比、推理。
抽象扩展结构水平层次试题的线索丰富,情境陌生新颖,成功解答需要学生在陌生的情境中,把题干给出的所有可用信息联系起来,并进一步联系新的知识点,推出合理的新的假设和猜想,进行归纳、推理、拓展。
高考数学历年(2018-2022)真题按知识点分类(数列求和)练习(附答案)

高考数学历年(2018-2022)真题按知识点分类(数列求和)练习一、单选题1.(2021ꞏ浙江ꞏ统考高考真题)已知数列{}n a满足)111,N n a a n *+==∈.记数列{}n a 的前n 项和为n S ,则( )A .100332S << B .10034S << C .100942S <<D .100952S <<二、填空题2.(2020ꞏ江苏ꞏ统考高考真题)设{an }是公差为d 的等差数列,{bn }是公比为q 的等比数列.已知数列{an +bn }的前n 项和221()n n S n n n +=-+-∈N ,则d +q 的值是_______.三、解答题3.(2022ꞏ全国ꞏ统考高考真题)记n S 为数列{}n a 的前n 项和,已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列. (1)求{}n a 的通项公式; (2)证明:121112na a a +++< . 4.(2022ꞏ全国ꞏ统考高考真题)已知函数()e e ax x f x x =-. (1)当1a =时,讨论()f x 的单调性;(2)当0x >时,()1f x <-,求a 的取值范围; (3)设n *∈Nln(1)n ++>+ .5.(2022ꞏ天津ꞏ统考高考真题)设{}n a 是等差数列,{}n b 是等比数列,且1122331a b a b a b ==-=-=.(1)求{}n a 与{}n b 的通项公式;(2)设{}n a 的前n 项和为n S ,求证:()1111n n n n n n n S a b S b S b +++++=-;(3)求211(1)nkk k k k a a b +=⎡⎤--⎣⎦∑.6.(2021ꞏ全国ꞏ统考高考真题)设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a 成等差数列. (1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <. 7.(2021ꞏ天津ꞏ统考高考真题)已知{}n a 是公差为2的等差数列,其前8项和为64.{}n b 是公比大于0的等比数列,1324,48b b b =-=. (I )求{}n a 和{}n b 的通项公式; (II )记2*1,n n nc b b n N =+∈, (i )证明{}22n n c c -是等比数列;(ii)证明)*nk n N =<∈ 8.(2020ꞏ全国ꞏ统考高考真题)设{}n a 是公比不为1的等比数列,1a 为2a ,3a 的等差中项.(1)求{}n a 的公比;(2)若11a =,求数列{}n na 的前n 项和.9.(2020ꞏ全国ꞏ统考高考真题)设数列{an }满足a 1=3,134n n a a n +=-. (1)计算a 2,a 3,猜想{an }的通项公式并加以证明; (2)求数列{2nan }的前n 项和Sn .10.(2020ꞏ天津ꞏ统考高考真题)已知{}n a 为等差数列,{}n b 为等比数列,()()115435431,5,4a b a a a b b b ===-=-.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)记{}n a 的前n 项和为n S ,求证:()2*21n n n S S S n ++<∈N ;(Ⅲ)对任意的正整数n ,设()21132,,,.n nn n n n n a b n a a c a n b +-+⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数求数列{}n c 的前2n 项和.11.(2019ꞏ天津ꞏ高考真题) 设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知113a b ==,23b a = ,3243b a =+.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足21,,,n n n c bn ⎧⎪=⎨⎪⎩为奇数为偶数求()*112222n na c a c a c n N +++∈ .12.(2019ꞏ浙江ꞏ高考真题)设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式; (2)记,n C n *∈N证明:12+.n C C C n *++<∈N 13.(2018ꞏ浙江ꞏ高考真题)已知等比数列{an }的公比q >1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{bn }满足b 1=1,数列{(bn +1−bn )an }的前n 项和为2n 2+n . (Ⅰ)求q 的值;(Ⅱ)求数列{bn }的通项公式.14.(2019ꞏ天津ꞏ高考真题)设{}n a 是等差数列,{}n b 是等比数列.已知1122334,622,24a b b a b a ===-=+,.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足111,22,1,,2,k k n kk n c c b n +⎧<<==⎨=⎩其中*k ∈N . (i )求数列(){}221n n a c -的通项公式; (ii )求()*221i ini a c n =∈∑N .15.(2018ꞏ天津ꞏ高考真题)设{an }是等差数列,其前n 项和为Sn (n ∈N*);{bn }是等比数列,公比大于0,其前n 项和为Tn (n ∈N*).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (Ⅰ)求Sn 和Tn ;(Ⅱ)若Sn +(T 1+T 2+…+Tn )=an +4bn ,求正整数n 的值.16.(2018ꞏ天津ꞏ高考真题)设{}n a 是等比数列,公比大于0,其前n 项和为()*n S n N ∈,{}n b 是等差数列.已知11a =,322a a =+,435a b b =+,5462a b b =+.(I )求{}n a 和{}n b 的通项公式; (II )设数列{}n S 的前n 项和为()*n T n N∈,(i )求n T ;(ii )证明()()()()22*122122n nk k k k T b b n N k k n ++=+=-∈+++∑.四、双空题17.(2021ꞏ全国ꞏ统考高考真题)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折,规格为20dm 12dm ⨯的长方形纸,对折1次共可以得到10dm 12dm ⨯,20dm 6dm ⨯两种规格的图形,它们的面积之和21240dm S =,对折2次共可以得到5dm 12dm ⨯,10dm 6dm ⨯,20dm 3dm ⨯三种规格的图形,它们的面积之和22180dm S =,以此类推,则对折4次共可以得到不同规格图形的种数为______;如果对折n 次,那么1nk k S ==∑______2dm .参考答案1.A【要点分析】显然可知,10032S >,利用倒数法得到21111124n n a a +⎛⎫==-⎪⎪⎭,再放12<,由累加法可得24(1)n a n ≥+,进而由1n a +=113n n a n a n ++≤+,然后利用累乘法求得6(1)(2)n a n n ≤++,最后根据裂项相消法即可得到1003S <,从而得解.【过程详解】因为)111,N n a a n *+==∈,所以0n a >,10032S >.由211111124n n n a a a ++⎛⎫=⇒==-⎪⎪⎭2111122n a +⎛⎫∴<+⇒⎪⎪⎭12<11122n n -+≤+=,当且仅当1n =时取等号,12412(1)311n n nn a n a a a n n n ++∴≥∴=≤=++++ 113n n a n a n ++∴≤+, 由累乘法可得6(1)(2)n a n n ≤++,当且仅当1n =时取等号,由裂项求和法得:所以10011111111116632334451011022102S ⎛⎫⎛⎫≤-+-+-++-=-< ⎪ ⎪⎝⎭⎝⎭,即100332S <<. 故选:A .24(1)n a n ≥+,由题目条件可知要证100S 小于某数,从而通过局部放缩得到1,n n a a +的不等关系,改变不等式的方向得到6(1)(2)n a n n ≤++,最后由裂项相消法求得1003S <.2.4【要点分析】结合等差数列和等比数列前n 项和公式的特点,分别求得{}{},n n a b 的公差和公比,由此求得d q +.【过程详解】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ≠. 等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -⎛⎫=+=+- ⎪⎝⎭, 等比数列{}n b 的前n 项和公式为()1111111n n n b q b bQ q qq q-==-+---, 依题意n n n S P Q =+,即22111212211nn b bd d n n n a n q q q ⎛⎫-+-=+--+ ⎪--⎝⎭, 通过对比系数可知111212211dd a q b q⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒112021d a q b =⎧⎪=⎪⎨=⎪⎪=⎩,故4d q +=.故答案为:4【名师点睛】本小题主要考查等差数列和等比数列的前n 项和公式,属于中档题. 3.(1)()12n n n a +=(2)见解析【要点分析】(1)利用等差数列的通项公式求得()121133n n S n n a +=+-=,得到()23n n n a S +=,利用和与项的关系得到当2n ≥时,()()112133n n n n n n a n a a S S --++=-=-,进而得:111nn a n a n -+=-,利用累乘法求得()12n n n a +=,检验对于1n =也成立,得到{}n a 的通项公式()12n n n a +=;(2)由(1)的结论,利用裂项求和法得到121111211n a a a n ⎛⎫+++=- ⎪+⎝⎭ ,进而证得. 【过程详解】(1)∵11a =,∴111S a ==∴,111S a =, 又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列,∴()121133n n S n n a +=+-=∴,()23n n n a S +=, ∴当2n ≥时,()1113n n n a S --+=,∴()()112133n n n n n n a n a a S S --++=-=-,整理得:()()111n n n a n a --=+, 即111n n a n a n -+=-, ∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯ ()1341112212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--, 显然对于1n =也成立,∴{}n a 的通项公式()12n n n a +=;(2)()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭∴12111n a a a +++ 1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦4.(1)()f x 的减区间为(),0-∞,增区间为()0,+∞.(2)12a ≤(3)见解析【要点分析】(1)求出()f x ',讨论其符号后可得()f x 的单调性.(2)设()e e 1ax x h x x =-+,求出()h x '',先讨论12a >时题设中的不等式不成立,再就102a <≤结合放缩法讨论()h x '符号,最后就0a ≤结合放缩法讨论()h x 的范围后可得参数的取值范围.(3)由(2)可得12ln t t t<-对任意的1t >恒成立,从而可得()ln 1ln n n +-<的*n ∈N 恒成立,结合裂项相消法可证题设中的不等式.【过程详解】(1)当1a =时,()()1e x f x x =-,则()e xf x x '=,当0x <时,()0f x '<,当0x >时,()0f x ¢>, 故()f x 的减区间为(),0∞-,增区间为()0,∞+.(2)设()e e 1ax xh x x =-+,则()00h =,又()()1e e ax x h x ax '=+-,设()()1e e ax xg x ax =+-, 则()()22e e ax xg x a a x '=+-,若12a >,则()0210g a '=->, 因为()g x '为连续不间断函数,故存在()00,x ∈+∞,使得()00,x x ∀∈,总有()0g x '>, 故()g x 在()00,x 为增函数,故()()00g x g >=,故()h x 在()00,x 为增函数,故()()01h x h >=-,与题设矛盾. 若102a <≤,则()()()ln 11e e ee ax ax ax xx h x ax ++'=+-=-, 下证:对任意0x >,总有()ln 1x x +<成立, 证明:设()()ln 1S x x x =+-,故()11011x S x x x-'=-=<++, 故()S x 在()0,∞+上为减函数,故()()00S x S <=即()ln 1x x +<成立. 由上述不等式有()ln 12e e e e e e 0ax ax x ax ax x ax x +++-<-=-≤, 故()0h x '≤总成立,即()h x 在()0,∞+上为减函数, 所以()()00h x h <=.当0a ≤时,有()e e e 1100ax x axh x ax '=-+<-+=,所以()h x 在()0,∞+上为减函数,所以()()00h x h <=. 综上,12a ≤. (3)取12a =,则0x ∀>,总有12e e 10x x x -+<成立, 令12e x t =,则21,e ,2ln x t t x t >==,故22ln 1t t t <-即12ln t t t<-对任意的1t >恒成立.所以对任意的*n ∈N ,有整理得到:()ln 1ln n n +-<()ln 2ln1ln 3ln 2ln 1ln n n >-+-+++- ()ln 1n =+,故不等式成立.【名师点睛】思路名师点睛:函数参数的不等式的恒成立问题,应该利用导数讨论函数的单调性,注意结合端点处导数的符号合理分类讨论,导数背景下数列不等式的证明,应根据已有的函数不等式合理构建数列不等式.5.(1)121,2n n n a n b -=-= (2)证明见解析(3)1(62)489n n +-+【要点分析】(1)利用等差等比数列的通项公式进行基本量运算即可得解; (2)由等比数列的性质及通项与前n 项和的关系结合要点分析法即可得证;(3)先求得212221212122(1)(1)k k k k k k k k a a b a a b ---+⎡⎤⎡⎤--+--⎣⎦⎣⎦,进而由并项求和可得114nk n k T k +==⋅∑,再结合错位相减法可得解.【过程详解】(1)设{}n a 公差为d ,{}n b 公比为q ,则11(1),n n n a n d b q -=+-=,由22331a b a b -=-=可得2112121d q d q d q +-=⎧⇒==⎨+-=⎩(0d q ==舍去), 所以121,2n n n a n b -=-=;(2)证明:因为120,n n b b +=≠所以要证1111()n n n n n n n S a b S b S b +++++=-, 即证111()2n n n n n n n S a b S b S b ++++=⋅-,即证1112n n n n S a S S ++++=-, 即证11n n n a S S ++=-,而11n n n a S S ++=-显然成立,所以1111()n n n n n n n S a b S b S b +++++=⋅-⋅;(3)因为212221212122(1)(1)k kk k k k k k a a b a a b ---+⎡⎤⎡⎤--+--⎣⎦⎣⎦2221(4143)2[41(41)]224k k k k k k k k --=-+-⨯++--⨯=⋅,所以211(1)nkk k k k a a b +=⎡⎤--⎣⎦∑2122212121221[((1))((1))]nk kk k k k k k k a a b a a b ---+==--+--∑ 124nk k k ==⋅∑,设124nkn k T k ==⋅∑所以2324446424nn T n =⨯+⨯+⨯+⋅⋅⋅+⨯,则2341244446424n n n T +⨯+⨯+⨯+⋅⋅⋅+⨯=,作差得()2341124(14)3244444242414n nn n n T n n ++⨯--=++++⋅⋅⋅+-⋅=-⨯-()126483n n +--=, 所以1(62)489n n n T +-+=,所以211(1)nkk k k k a a b +=⎡⎤--=⎣⎦∑1(62)489n n +-+. 6.(1)11()3n n a -=,3n n n b =;(2)证明见解析.【要点分析】(1)利用等差数列的性质及1a 得到29610q q -+=,解方程即可; (2)利用公式法、错位相减法分别求出,n n S T ,再作差比较即可.【过程详解】(1)因为{}n a 是首项为1的等比数列且1a ,23a ,39a 成等差数列,所以21369a a a =+,所以211169a q a a q =+,即29610q q -+=,解得13q =,所以11()3n n a -=,所以33n n n na nb ==. (2)[方法一]:作差后利用错位相减法求和211213333n n n n nT --=++++ ,012111111223333-⎛⎫=++++ ⎪⎝⎭ n n S , 230121123111112333323333n n nn S n T -⎛⎫⎛⎫-=++++-++++=⎪ ⎪⎝⎭⎝⎭ 012111012222333---++++111233---+n n n n .设0121111101212222Γ3333------=++++ n n n , ⑧则1231111012112222Γ33333-----=++++ n n n . ⑨由⑧-⑨得1121113312111113322Γ13233332313--⎛⎫--- ⎪⎛⎫⎝⎭=-++++-=-+- ⎪⎝⎭- n n n n n n n . 所以211312Γ432323----=--=-⨯⨯⨯n n n n n n . 因此10232323--=-=-<⨯⨯n n n n nS n n n T . 故2nn S T <. [方法二]【最优解】:公式法和错位相减求和法证明:由(1)可得11(1)313(1)12313n n n S ⨯-==--,211213333n n n n nT --=++++ ,①231112133333n n n n nT +-=++++ ,② ①-②得23121111333333n n n n T +=++++- 1111(11133(11323313n n n n n n ++-=-=---, 所以31(1)4323n n n nT =--⋅,所以2n n S T -=3131(1(1)043234323n n n n n n ----=-<⋅⋅, 所以2nn S T <. [方法三]:构造裂项法由(Ⅰ)知13⎛⎫= ⎪⎝⎭n n b n ,令1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,且1+=-n n n b c c ,即1111()[(1)]333αβαβ+⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭n n n n n n ,通过等式左右两边系数比对易得33,24αβ==,所以331243nn c n ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭.则12113314423nn n n n T b b b c c +⎛⎫⎛⎫=+++=-=-+ ⎪⎪⎝⎭⎝⎭,下同方法二.[方法四]:导函数法设()231()1-=++++=- n nx x f x x x x x x,由于()()()()()()1221'111'11(1)'1(1)1n n n n nx x x x x x x x nx n x x x x +⎡⎤⎡⎤⎡⎤----⨯--+-+⎣⎦⎣⎦⎢⎥==---⎢⎥⎣⎦, 则12121(1)()123(1)+-+-+=++++='- n nn nx n x f x x x nxx .又1111333-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭n n n b n n ,所以2112311111233333n n n T b b b b n -⎡⎤⎛⎫⎛⎫=++++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦12111(1)11133333113n nn n f +⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭⋅=⨯ ⎪⎝⎭⎛⎫- ⎪⎝⎭' 13113311(1)4334423n n nn n n +⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-+=-+⎢⎥ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,下同方法二.【整体点评】本题主要考查数列的求和,涉及到等差数列的性质,错位相减法求数列的和,考查学生的数学运算能力,是一道中档题,其中证明不等式时采用作差法,或者作商法要根据式子得结构类型灵活选择,关键是要看如何消项化简的更为简洁. (2)的方法一直接作差后利用错位相减法求其部分和,进而证得结论;方法二根据数列的不同特点,分别利用公式法和错位相减法求得,n n S T ,然后证得结论,为最优解;方法三采用构造数列裂项求和的方法,关键是构造1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,使1+=-n n n b c c ,求得n T 的表达式,这是错位相减法的一种替代方法,方法四利用导数方法求和,也是代替错位相减求和法的一种方法.7.(I )21,n a n n N *=-∈,4,n n N b n *=∈;(II )(i )证明见解析;(ii )证明见解析.【要点分析】(I )由等差数列的求和公式运算可得{}n a 的通项,由等比数列的通项公式运算可得{}n b 的通项公式;(II )(i )运算可得2224n n n c c =⋅-,结合等比数列的定义即可得证;(ii )放缩得21222422n n n n n a n c a c +<-⋅,进而可得112n n k k k-==<,结合错位相减法即可得证. 【过程详解】(I )因为{}n a 是公差为2的等差数列,其前8项和为64. 所以12818782642a a a a ⨯++⋅⋅⋅+=+⨯=,所以11a =, 所以()12121,n n n n N a a *=+-=-∈;设等比数列{}n b 的公比为(),0q q >,所以()221321484q b b b q q b q ==-=--,解得4q =(负值舍去),所以114,n n n b q n N b -*==∈;(II )(i )由题意,221441n n nn n b c b =++=,所以22224211442444n n n n n nn c c ⎛⎫⎛⎫=+-+=⋅ ⎪ ⎪⎝⎭⎝⎭-,所以220nn c c ≠-,且212222124424n n n n nn c c c c +++⋅==⋅--, 所以数列{}22n n c c -是等比数列;(ii )由题意知,()()22122222121414242222n nn n n n n n n a n n c c a +-+-==<-⋅⋅⋅,12n n -==,所以112nn k k k k -==<, 设10121112322222nn k n k k n T --===+++⋅⋅⋅+∑, 则123112322222n nn T =+++⋅⋅⋅+,两式相减得21111111122121222222212nn n n n nn n n T -⎛⎫⋅- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--, 所以1242n n n T -+=-,所以1112422nn k n k k n --==+⎫=-<⎪⎭【名师点睛】关键点名师点睛:最后一问考查数列不等式的证明,因为nk =错位相减法即可得证.8.(1)2-;(2)1(13)(2)9nn n S -+-=. 【要点分析】(1)由已知结合等差中项关系,建立公比q 的方程,求解即可得出结论; (2)由(1)结合条件得出{}n a 的通项,根据{}n na 的通项公式特征,用错位相减法,即可求出结论.【过程详解】(1)设{}n a 的公比为q ,1a 为23,a a 的等差中项,212312,0,20a a a a q q =+≠∴+-= , 1,2q q ≠∴=- ;(2)设{}n na 的前n 项和为n S ,111,(2)n n a a -==-,21112(2)3(2)(2)n n S n -=⨯+⨯-+⨯-++- ,①23121(2)2(2)3(2)(1)(2)(2)n n n S n n --=⨯-+⨯-+⨯-+--+- ,②①-②得,2131(2)(2)(2)(2)n n n S n -=+-+-++---1(2)1(13)(2)(2)1(2)3n n n n n ---+-=--=--, 1(13)(2)9nn n S -+-∴=. 【名师点睛】本题考查等比数列通项公式基本量的计算、等差中项的性质,以及错位相减法求和,考查计算求解能力,属于基础题.9.(1)25a =,37a =,21n a n =+,证明见解析;(2)1(21)22n n S n +=-⋅+.【要点分析】(1)方法一:(通性通法)利用递推公式得出23,a a ,猜想得出{}n a 的通项公式,利用数学归纳法证明即可;(2)方法一:(通性通法)根据通项公式的特征,由错位相减法求解即可. 【过程详解】(1)[方法一]【最优解】:通性通法由题意可得2134945a a =-=-=,32381587a a =-=-=,由数列{}n a 的前三项可猜想数列{}n a 是以3为首项,2为公差的等差数列,即21n a n =+.证明如下:当1n =时,13a =成立;假设()n k k *=∈N 时,21k a k =+成立.那么1n k =+时,1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立. 则对任意的*n ∈N ,都有21n a n =+成立; [方法二]:构造法由题意可得2134945a a =-=-=,32381587a a =-=-=.由123,5a a ==得212a a -=.134n n a a n +=-,则134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--.令1n n n b a a +=-,且12b =,所以134n n b b -=-,两边同时减去2,得()1232n n b b --=-,且120b -=,所以20n b -=,即12n n a a +-=,又212a a -=,因此{}n a 是首项为3,公差为2的等差数列,所以21n a n =+. [方法三]:累加法由题意可得2134945a a =-=-=,32381587a a =-=-=. 由134n n a a n +=-得1114333n n n n n a a n +++-=-,即2121214333a a -=-⨯,3232318333a a -=-⨯, (111)4(1)(2)333n n nn n a a n n ---=--⨯≥.以上各式等号两边相加得1123111412(1)33333n n n a a n ⎡⎤-=-⨯+⨯++-⨯⎢⎥⎣⎦ ,所以1(21)33n n n a n =+⋅.所以21(2)n a n n =+≥.当1n =时也符合上式.综上所述,21n a n =+. [方法四]:构造法21322345,387a a a a =-==-=,猜想21n a n =+.由于134n n a a n +=-,所以可设()1(1)3n n a n a n λμλμ++++=++,其中,λμ为常数.整理得1322n n a a n λμλ+=++-.故24,20λμλ=--=,解得2,1λμ=-=-.所以()112(1)13(21)3211n n n a n a n a +-+-=--=⋅⋅⋅=-⨯-.又130a -=,所以{}21n a n --是各项均为0的常数列,故210n a n --=,即21n a n =+.(2)由(1)可知,2(21)2n nn a n ⋅=+⋅[方法一]:错位相减法231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅ ,① 23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅ ,②由①-②得:()23162222(21)2n n n S n +-=+⨯+++-+⋅()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-,即1(21)22n n S n +=-⋅+.[方法二]【最优解】:裂项相消法112(21)2(21)2(23)2n n n n n n n a n n n b b ++=+=---=-,所以231232222n n n S a a a a =++++ ()()()()2132431n n b b b b b b b b +=-+-+-++- 11n b b +=-1(21)22n n +=-+.[方法三]:构造法当2n ≥时,1(21)2n n n S S n -=++⋅,设11()2[(1)]2n n n n S pn q S p n q --++⋅=+-+⋅,即122n n n pn q p S S ----=+⋅,则2,21,2pq p -⎧=⎪⎪⎨--⎪=⎪⎩,解得4,2p q =-=.所以11(42)2[4(1)2]2n n n n S n S n --+-+⋅=+--+⋅,即{}(42)2n n S n +-+⋅为常数列,而1(42)22S +-+⋅=,所以(42)22n n S n +-+⋅=.故12(21)2n n S n +=+-⋅.[方法四]:因为12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,令12n n b n -=⋅,则()()231()0,11n nx x f x x x x x x x-=++++=≠- ,()121211(1)()1231(1)nn n n x x nx n x f x x x nx x x +-'⎡⎤-+-+=++++==⎢⎥--⎢⎥⎣⎦' , 所以12n b b b +++L 21122322n n -=+⋅+⋅++⋅ 1(2)12(1)2n n f n n +==+-+'⋅. 故234(2)2222nn S f =++'+++ ()1212412(1)212n n nn n +-⎡⎤=+⋅-++⎣⎦-1(21)22n n +=-+.【整体点评】(1)方法一:通过递推式求出数列{}n a 的部分项从而归纳得出数列{}n a 的通项公式,再根据数学归纳法进行证明,是该类问题的通性通法,对于此题也是最优解; 方法二:根据递推式134n n a a n +=-,代换得134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--,设1n n n b a a +=-,从而简化递推式,再根据构造法即可求出n b ,从而得出数列{}n a 的通项公式; 方法三:由134n n a a n +=-化简得1114333n n n n n a a n+++-=-,根据累加法即可求出数列{}n a 的通项公式; 方法四:通过递推式求出数列{}n a 的部分项,归纳得出数列{}n a 的通项公式,再根据待定系数法将递推式变形成()1(1)3n n a n a n λμλμ++++=++,求出,λμ,从而可得构造数列为常数列,即得数列{}n a 的通项公式. (2)方法一:根据通项公式的特征可知,可利用错位相减法解出,该法也是此类题型的通性通法; 方法二:根据通项公式裂项,由裂项相消法求出,过程简单,是本题的最优解法;方法三:由2n ≥时,1(21)2nn n S S n -=++⋅,构造得到数列{}(42)2n n S n +-+⋅为常数列,从而求出;方法四:将通项公式分解成12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,利用分组求和法分别求出数列{}{}12,2n n n -⋅的前n 项和即可,其中数列{}12n n -⋅的前n 项和借助于函数()()231()0,11n nx x f x x x x x x x-=++++=≠- 的导数,通过赋值的方式求出,思路新颖独特,很好的简化了运算. 10.(Ⅰ)n a n =,12n n b -=;(Ⅱ)证明见解析;(Ⅲ)465421949n n n n +--+⨯.【要点分析】(Ⅰ)由题意分别求得数列的公差、公比,然后利用等差、等比数列的通项公式得到结果;(Ⅱ)利用(Ⅰ)的结论首先求得数列{}n a 前n 项和,然后利用作差法证明即可;(Ⅲ)分类讨论n 为奇数和偶数时数列的通项公式,然后分别利用指数型裂项求和和错位相减求和计算211n k k c -=∑和21nk k c =∑的值,据此进一步计算数列{}n c 的前2n 项和即可.【过程详解】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q . 由11a =,()5435a a a =-,可得d =1. 从而{}n a 的通项公式为n a n =. 由()15431,4b b b b ==-,又q ≠0,可得2440q q -+=,解得q =2,从而{}n b 的通项公式为12n n b -=.(Ⅱ)证明:由(Ⅰ)可得(1)2n n n S +=, 故21(1)(2)(3)4n n S S n n n n +=+++,()()22211124n S n n +=++,从而2211(1)(2)02n n n S S S n n ++-=-++<,所以221n n n S S S ++<.(Ⅲ)当n 为奇数时,()111232(32)222(2)2n n n n n nn n a b n c a a n n n n-+-+--===-++,当n 为偶数时,1112n n n n a n c b -+-==, 对任意的正整数n ,有222221112221212121k k nnnk k k c k k n --==⎛⎫=-=- ⎪+-+⎝⎭∑∑,和223111211352321444444nnk k n n k k k n n c -==---==+++++∑∑① 由①得22314111352321444444n k n n k n n c +=--=+++++∑ ②由①②得22111211312221121441444444414n n k n n n k n n c ++=⎛⎫- ⎪--⎝⎭=+++-=---∑ , 由于11211121221121156544144334444123414n n n n n n n n ++⎛⎫- ⎪--+⎝⎭--=-⨯--⨯=-⨯-, 从而得:21565994nk nk n c =+=-⨯∑. 因此,2212111465421949n nnnk k k nk k k n c c c n -===+=+=--+⨯∑∑∑. 所以,数列{}n c 的前2n 项和为465421949n n n n +--+⨯.【名师点睛】本题主要考查数列通项公式的求解,分组求和法,指数型裂项求和,错位相减求和等,属于中等题.11.(I )3n a n =,3nn b =;(II )22(21)369()2n n n n +*-++∈N【要点分析】(I )首先设出等差数列的公差,等比数列的公比,根据题意,列出方程组,求得33d q =⎧⎨=⎩,进而求得等差数列和等比数列的通项公式; (II )根据题中所给的n c 所满足的条件,将112222n n a c a c a c +++ 表示出来,之后应用分组求和法,结合等差数列的求和公式,以及错位相减法求和,最后求得结果. 【过程详解】(I )解:设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q , 依题意,得23323154q d q d =+⎧⎨=+⎩,解得33d q =⎧⎨=⎩,故33(1)3n a n n =+-=,1333n nn b -=⨯=,所以,{}n a 的通项公式为3n a n =,{}n b 的通项公式为3nn b =;(II )112222n n a c a c a c +++135212142632()()n n n a a a a a b a b a b a b -=+++++++++ 123(1)[36](6312318363)2n n n n n -=⨯+⨯+⨯+⨯+⨯++⨯ 21236(13233)n n n =+⨯⨯+⨯++⨯ ,记 1213233nn T n =⨯+⨯++⨯ ①则 231313233n n T n +=⨯+⨯++⨯ ②②-①得,231233333n n n T n +=-----+⨯ 113(13)(21)333132n n n n n ++--+=-+⨯=-, 所以122112222(21)3336332n n n n n a c a c a c n T n +-++++=+=+⨯22(21)369()2n n n n N +*-++=∈.【名师点睛】本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识,考查数列求和的基本方法和运算求解能力,属于中档题目. 12.(1)()21n a n =-,()1n b n n =+;(2)证明见解析.【要点分析】(1)首先求得数列{}n a 的首项和公差确定数列{}n a 的通项公式,然后结合三项成等比数列的充分必要条件整理计算即可确定数列{}n b 的通项公式;(2)结合(1)的结果对数列{}n c 的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中的不等式.【过程详解】(1)由题意可得:1112432332a d a d a d +=⎧⎪⎨⨯+=+⎪⎩,解得:102a d =⎧⎨=⎩, 则数列{}n a 的通项公式为22n a n =- . 其前n 项和()()02212n n n S nn +-⨯==-.则()()()()1,1,12n n n n n b n n b n n b -++++++成等比数列,即: ()()()()21112n n n n n b n n b n n b ++=-+⨯+++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦,据此有:()()()()()()()()2222121112121n n n n n n n n n b b n n n n n n b n n b b ++++=-++++++-+,故()()()()()22112121(1)(1)(1)(2)n n n n n n b n n n n n n n n n +--++==++++--+. (2)结合(1)中的通项公式可得:2n C ==<=<=,则)122022n C C C +++<+++= 【名师点睛】本题主要考查数列通项公式的求解,,裂项求和的方法,数列中用放缩法证明不等式的方法等知识,意在考查学生的转化能力和计算求解能力. 13.(Ⅰ)2q =;(Ⅱ)2115(43)()2n n b n -=-+⋅.【要点分析】要点分析:(Ⅰ)根据条件、等差数列的性质及等比数列的通项公式即可求解公比;(Ⅱ)先根据数列1{()}n n n b b a +-前n 项和求通项,解得1n n b b +-,再通过叠加法以及错位相减法求n b .【过程详解】过程详解:(Ⅰ)由42a +是35,a a 的等差中项得35424a a a +=+, 所以34543428a a a a ++=+=, 解得48a =.由3520a a +=得1820q q ⎛⎫+= ⎪⎝⎭,因为1q >,所以2q =.(Ⅱ)设()1n n n n c b b a +=-,数列{}n c 前n 项和为n S .由11,1,, 2.n nn S n c S S n -=⎧=⎨-≥⎩解得41n c n =-.由(Ⅰ)可知12n n a -=,所以()111412n n n b b n -+⎛⎫-=-⋅ ⎪⎝⎭,故()21145,22n n n b b n n --⎛⎫-=-⋅≥ ⎪⎝⎭,()()()()11123221n n n n n b b b b b b b b b b ----=-+-++-+-()()23111454973222n n n n --⎛⎫⎛⎫=-⋅+-⋅++⋅+ ⎪⎪⎝⎭⎝⎭.设()22111371145,2222n n T n n -⎛⎫⎛⎫=+⋅+⋅++-⋅≥ ⎪ ⎪⎝⎭⎝⎭ ,()()2211111137494522222n n n T n n --⎛⎫⎛⎫⎛⎫=⋅+⋅++-⋅+-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以()2211111134444522222n n n T n --⎛⎫⎛⎫⎛⎫=+⋅+⋅++⋅--⋅ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,因此()211443,22n n T n n -⎛⎫=-+⋅≥ ⎪⎝⎭,又11b =,所以()2115432n n b n -⎛⎫=-+⋅ ⎪⎝⎭.名师点睛:用错位相减法求和应注意的问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.14.(Ⅰ)31n a n =+;32nn b =⨯(Ⅱ)(i )()221941n n n a c -=⨯-(ii )()1+1*1243218n n n N +⨯+⨯-∈ 【要点分析】(Ⅰ)由题意首先求得公比和公差,然后确定数列的通项公式即可;(Ⅱ)结合(Ⅰ)中的结论可得数列(){}221n n a c -的通项公式,结合所得的通项公式对所求的数列通项公式进行等价变形,结合等比数列前n 项和公式可得()*221i ini a c n =∈∑N 的值.【过程详解】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q . 依题意得()()262426262424124q d d q d d ⎧=+-=+⎪⎨=++=+⎪⎩,解得32d q =⎧⎨=⎩,故4(1)331n a n n =+-⨯=+,16232n nn b -=⨯=⨯.所以,{}n a 的通项公式为31n a n =+,{}n b 的通项公式为32nn b =⨯.(Ⅱ)(i )()()()()22211321321941n n n n n nn a c a b -=-=⨯+⨯-=⨯-.所以,数列(){}221n n a c -的通项公式为()221941n n na c -=⨯-.(ii )()2222211=1i i i i i n n i i a c a a c ==⎡⎤-⎣⎦+∑∑()222111i i i n ni i a a c ===+-∑∑ ()212312n n ⎛⎫- ⎪=+⨯ ⎪-⎝⎭()1941ni i =+⨯-∑ ()()+1414326914n n n n -=⨯+-+⨯--()1+1*1243218n n n N +=⨯+⨯-∈.【名师点睛】本题主要考查等差数列、等比数列的通项公式及其前n 项和公式等基础知识.考查化归与转化思想和数列求和的基本方法以及运算求解能力. 15.(Ⅰ)()12n n n S +=,21nn T =-;(Ⅱ)4. 【要点分析】(I )由题意得到关于q 的方程,解方程可得2q =,则122112nn n T -==--.结合题意可得等差数列的首项和公差为11,1a d ==,则其前n 项和()12n n n S +=. (II )由(I ),知1122 2.n n T T T n ++++=-- 据此可得2340,n n --= 解得1n =-(舍),或4n =.则n 的值为4.【过程详解】(I )设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以,122112nn n T -==--.设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d +=从而11,1a d ==,故n a n =,所以,(1)2n n n S +=. (II )由(I ),有121122(12)(222)=2 2.12n nn n T T T n n n +⨯-+++=+++--=---由12()4n n n n S T T T a b ++++=+ , 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --=解得1n =-(舍),或4n =.所以n 的值为4.名师点睛:本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.16.(Ⅰ)12n n a -=,n b n =;(Ⅱ)(i )122n n T n +=--.(ii )证明见解析.【过程详解】要点分析:(I )由题意得到关于q 的方程,解方程可得2q =,则12n n a -=.结合等差数列通项公式可得.n b n =(II )(i )由(I ),有21nn S =-,则()112122nk n n k T n +==-=--∑.(ii )因为()()()212221221k k k k k T b b k k k k ++++=-++++,裂项求和可得()()()22122122n nk k k k T b b k k n ++=+=-+++∑. 过程详解:(I )设等比数列{}n a 的公比为q.由1321,2,a a a ==+可得220q q --=.因为0q >,可得2q =,故12n n a -=.设等差数列{}n b 的公差为d ,由435a b b =+,可得13 4.b d += 由5462a b b =+,可得131316,b d += 从而11,1,b d == 故.n b n =所以数列{}n a 的通项公式为12n n a -=,数列{}n b 的通项公式为.n b n =(II )(i )由(I ),有122112nn n S -==--,故()()1112122122212nnnkkn n k k T n n n +==⨯-=-=-=-=---∑∑.(ii )因为()()()()()()()()1121222222212121221k k k k k k k k k k T b b k k k k k k k k k +++++--+++⋅===-++++++++, 所以()()()32432122122222222123243212n n n nk k k k T b b k k n n n ++++=+⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪ ⎪+++++⎝⎭⎝⎭⎝⎭∑. 名师点睛:本题主要考查数列通项公式的求解,数列求和的方法,数列中的指数裂项方法等知识,意在考查学生的转化能力和计算求解能力. 17. 5 ()41537202n n -+-【要点分析】(1)按对折列举即可;(2)根据规律可得n S ,再根据错位相减法得结果.【过程详解】(1)由对折2次共可以得到5dm 12dm ⨯,10dm 6dm ⨯,20dm 3dm ⨯三种规格的图形,所以对着三次的结果有:5312561032022⨯⨯⨯⨯,,;,共4种不同规格(单位2dm ); 故对折4次可得到如下规格:5124⨯,562⨯,53⨯,3102⨯,3204⨯,共5种不同规格;(2)由于每次对着后的图形的面积都减小为原来的一半,故各次对着后的图形,不论规格如何,其面积成公比为12的等比数列,首项为120()2dm ,第n 次对折后的图形面积为111202n -⎛⎫⨯ ⎪⎝⎭,对于第n 此对折后的图形的规格形状种数,根据(1)的过程和结论,猜想为1n +种(证明从略),故得猜想1120(1)2n n n S -+=, 设()0121112011202120312042222nk n k n S S -=+⨯⨯⨯==++++∑L , 则121112021203120120(1)22222n nn n S -⨯⨯+=++++ , 两式作差得:()211201111124012022222n n n S -+⎛⎫=++++- ⎪⎝⎭ ()11601120122401212n n n -⎛⎫- ⎪+⎝⎭=+-- ()()112011203120360360222n n nn n -++=--=-, 因此,()()4240315372072022n n n n S -++=-=-. 故答案为:5;()41537202n n -+-. 【名师点睛】方法名师点睛:数列求和的常用方法: (1)对于等差等比数列,利用公式法可直接求解;(2)对于{}n n a b 结构,其中{}n a 是等差数列,{}n b 是等比数列,用错位相减法求和; (3)对于{}n n a b +结构,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭结构,其中{}n a 是等差数列,公差为()0d d ≠,则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭,利用裂项相消法求和.。
数列(解答题)(2018-2022)高考真题汇编(新高考卷与全国理科)

数列(解答题)——大数据之五年(2018-2022)高考真题汇编(新高考卷与全国理科)一、解答题(共21题;共180分)1.(10分)已知{a n}为等差数列,{b n}是公比为2的等比数列,且a2−b2=a3−b3=b4−a4.(1)(5分)证明:a1=b1;(2)(5分)求集合{k|b k=a m+a1,1≤m≤500}中元素个数.2.(10分)记S n为数列{a n}的前n项和.已知2S n n+n=2a n+1.(1)(5分)证明:{a n}是等差数列;(2)(5分)若a4,a7,a9成等比数列,求S n的最小值.3.(10分)记S n为数列{a n}的前n项和,已知a1=1,{S na n}是公差为13,的等差数列.(1)(5分)求{a n}的通项公式;(2)(5分)证明:1a1+1a2+⋯+1a n<24.(10分)记S n是公差不为0的等差数列{a n}的前n项和,若a3=S5,a2a4=S4.(1)(5分)求数列{a n}的通项公式a n;(2)(5分)求使S n>a n成立的n的最小值.5.(10分)设{a n}是首项为1的等比数列,数列{b n}满足b n=na n3,已知a1,3 a2,9 a3成等差数列.(1)(5分)求{a n}和{b n}的通项公式;(2)(5分)记S n和T n分别为{a n}和{b n}的前n项和.证明:T n< S n2.6.(5分)记S n为{a n}的前n项和,已知a n>0,a2=3a1,且数列{√S n}是等差数列.证明:{a n}是等差数列.7.(5分)已知数列{a n}的各项均为正数,记S n为{a n}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{a n}是等差数列:②数列{ √S n}是等差数列;③a2=3a1注:若选择不同的组合分别解答,则按第一个解答计分.8.(10分)记S n 为数列{a n }的前n 项和,b n 为数列{S n }的前n 项积,已知2S n +1b n=2. (1)(5分)证明:数列{b n }是等差数列; (2)(5分)求{a n }的通项公式.9.(10分)已知 {a n } 是公差为2的等差数列,其前8项和为64. {b n } 是公比大于0的等比数列, b 1=4,b 3−b 2=48 .(1)(5分)求 {a n } 和 {b n } 的通项公式;(2)(5分)记 c n =b 2n +1b n,n ∈N ∗ .(i )证明 {c n 2−c 2n } 是等比数列;(ii )证明 ∑√a k a k+1c k 2−c 2knk=1<2√2(n ∈N ∗) 10.(10分)已知数列{ a n }满足 a 1 =1, a n+1={a n +1,n 为奇数a n +2,n 为偶数(1)(5分)记 b n = a 2n ,写出 b 1 , b 2 ,并求数列 {b n } 的通项公式; (2)(5分)求 {a n } 的前20项和11.(10分)设数列{a n }满足a 1=3, a n+1=3a n −4n .(1)(5分)计算a 2,a 3,猜想{a n }的通项公式并加以证明; (2)(5分)求数列{2n a n }的前n 项和S n .12.(10分)设 {a n } 是公比不为1的等比数列, a 1 为 a 2 , a 3 的等差中项.(1)(5分)求 {a n } 的公比;(2)(5分)若 a 1=1 ,求数列 {na n } 的前n 项和.13.(10分)已知公比大于 1 的等比数列 {a n } 满足 a 2+a 4=20,a 3=8 .(1)(5分)求 {a n } 的通项公式;(2)(5分)求 a 1a 2−a 2a 3+⋯+(−1)n−1a n a n+1 .14.(10分)已知公比大于1的等比数列 {a n } 满足 a 2+a 4=20,a 3=8 .(1)(5分)求 {a n } 的通项公式;(2)(5分)记 b m 为 {a n } 在区间 (0,m](m ∈N ∗) 中的项的个数,求数列 {b m } 的前100项和 S 100 .15.(5分)已知 {a n } 为等差数列, {b n } 为等比数列, a 1=b 1=1,a 5=5(a 4−a 3),b 5=4(b 4−b 3) .(Ⅰ)求 {a n } 和 {b n } 的通项公式;(Ⅰ)记 {a n } 的前 n 项和为 S n ,求证: S n S n+2<S n+12(n ∈N ∗) ;(Ⅰ)对任意的正整数 n ,设 c n ={(3a n −2)b na n a n+2,n 为奇数,an−1b n+1,n 为偶数. 求数列 {c n } 的前2n 项和. 16.(5分)设 {a n } 是等差数列, {b n } 是等比数列,公比大于0,已知 a 1=b 1=3 , b 2=a 3 ,b 3=4a 2+3 .(Ⅰ)求 {a n } 和 {b n } 的通项公式;(Ⅰ)设数列 {c n } 满足 c n ={1,n 为奇数b n 2,n 为偶数求 a 1c 1+a 2c 2+⋯+a 2n c 2n (n ∈N ∗) . 17.(10分)已知数列{a n }和{b n }满足a 1=1,b 1=0, 4a n+1=3a n −b n +4 , 4b n+1=3b n −a n −4 .(1)(5分)证明:{a n +b n }是等比数列,{a n –b n }是等差数列; (2)(5分)求{a n }和{b n }的通项公式.18.(5分)设{a n }是等差数列,a 1=-10,且a 2+10,a 3+8,a 4+6成等比数列.(I )求{a n }的通项公式;(Ⅰ)记{a n }的前n 项和为S n ,求S n 的最小值.19.(10分)记S n 为等差数列{a n }的前n 项和,已知a 1=-7,S 3=-15.(1)(5分)求{a n }的通项公式; (2)(5分)求S n ,并求S n 的最小值。
2018高考数学理热点题型:数列 全国通用 含解析 精品

数列热点一 等差数列、等比数列的综合问题解决等差、等比数列的综合问题时,重点在于读懂题意,灵活利用等差、等比数列的定义、通项公式及前n 项和公式解决问题,求解这类问题要重视方程思想的应用. 【例1】已知首项为32的等比数列{a n }不是递减数列,其前n 项和为S n (n ∈N *),且S 3+a 3,S 5+a 5,S 4+a 4成等差数列. (1)求数列{a n }的通项公式;(2)设T n =S n -1S n(n ∈N *),求数列{T n }的最大项的值与最小项的值.解 (1)设等比数列{a n }的公比为q , 因为S 3+a 3,S 5+a 5,S 4+a 4成等差数列, 所以S 5+a 5-S 3-a 3=S 4+a 4-S 5-a 5,即4a 5=a 3, 于是q 2=a 5a 3=14.又{a n }不是递减数列且a 1=32,所以q =-12. 故等比数列{a n }的通项公式为a n =32×⎝ ⎛⎭⎪⎫-12n -1=(-1)n -1·32n .(2)由(1)得S n =1-⎝ ⎛⎭⎪⎫-12n =⎩⎪⎨⎪⎧1+12n ,n 为奇数,1-12n ,n 为偶数,当n 为奇数时,S n 随n 的增大而减小, 所以1<S n ≤S 1=32,故0<S n -1S n≤S 1-1S 1=32-23=56.当n 为偶数时,S n 随n 的增大而增大, 所以34=S 2≤S n <1,故0>S n -1S n≥S 2-1S 2=34-43=-712.综上,对于n ∈N *,总有-712≤S n -1S n≤56.所以数列{T n }最大项的值为56,最小项的值为-712.【类题通法】解决等差数列与等比数列的综合问题,既要善于综合运用等差数列与等比数列的相关知识求解,更要善于根据具体问题情境具体分析,寻找解题的突破口.【对点训练】已知数列{a n }是公差不为零的等差数列,其前n 项和为S n ,满足S 5-2a 2=25,且a 1,a 4,a 13恰为等比数列{b n }的前三项. (1)求数列{a n },{b n }的通项公式; (2)设T n 是数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n +1的前n 项和,是否存在k ∈N *,使得等式1-2T k =1b k成立?若存在,求出k 的值;若不存在,请说明理由. 解 (1)设等差数列{a n }的公差为d (d ≠0), ∴⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫5a 1+5×42d -2(a 1+d )=25,(a 1+3d )2=a 1(a 1+12d ), 解得a 1=3,d =2,∴a n =2n +1. ∵b 1=a 1=3,b 2=a 4=9,∴等比数列{b n }的公比q =3,∴b n =3n . (2)不存在.理由如下:∵1a n a n +1=1(2n +1)(2n +3)=12⎝⎛⎭⎪⎫12n +1-12n +3, ∴T n =12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13-15+⎝ ⎛⎭⎪⎫15-17+…+⎝ ⎛⎭⎪⎫12n +1-12n +3=12⎝ ⎛⎭⎪⎫13-12n +3, ∴1-2T k =23+12k +3(k ∈N *),易知数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫12k +3为单调递减数列, ∴23<1-2T k ≤1315,又1b k =13k ∈⎝ ⎛⎦⎥⎤0,13, ∴不存在k ∈N *,使得等式1-2T k =1b k成立.热点二 数列的通项与求和数列的通项与求和是高考必考的热点题型,求通项属于基本问题,常涉及与等差、等比的定义、性质、基本量运算.求和问题关键在于分析通项的结构特征,选择合适的求和方法.常考求和方法有:错位相减法、裂项相消法、分组求和法等.【例2】设等差数列{a n }的公差为d ,前n 项和为S n ,等比数列{b n }的公比为q ,已知b 1=a 1,b 2=2,q =d ,S 10=100. (1)求数列{a n },{b n }的通项公式;(2)当d >1时,记c n =a nb n,求数列{c n }的前n 项和T n .(1)解 由题意有⎩⎨⎧10a 1+45d =100,a 1d =2,即⎩⎨⎧2a 1+9d =20,a 1d =2, 解得⎩⎨⎧a 1=1,d =2或⎩⎪⎨⎪⎧a 1=9,d =29.故⎩⎨⎧a n =2n -1,b n =2n -1或⎩⎪⎨⎪⎧a n =19(2n +79),b n =9·⎝ ⎛⎭⎪⎫29n -1. (2)解 由d >1,知a n =2n -1,b n =2n -1,故c n =2n -12n -1, 于是T n =1+32+522+723+924+…+2n -12n -1,①12T n =12+322+523+724+925+…+2n -12n .② ①-②可得12T n =2+12+122+…+12n -2-2n -12n =3-2n +32n , 故T n =6-2n +32n -1.【类题通法】用错位相减法解决数列求和的模板 第一步:(判断结构)若数列{a n ·b n }是由等差数列{a n }与等比数列{b n }(公比q )的对应项之积构成的,则可用此法求和. 第二步:(乘公比)设{a n ·b n }的前n 项和为T n ,然后两边同乘以q . 第三步:(错位相减)乘以公比q 后,向后错开一位,使含有q k (k ∈N *)的项对应,然后两边同时作差. 第四步:(求和)将作差后的结果求和,从而表示出T n .【对点训练】设数列{a n }的前n 项和为S n ,已知a 1=1,a 2=2,且a n +2=3S n -S n +1+3,n ∈N *. (1)证明:a n +2=3a n ; (2)求S 2n .(1)证明 由条件,对任意n ∈N *,有a n +2=3S n -S n +1+3, 因而对任意n ∈N *,n ≥2,有a n +1=3S n -1-S n +3. 两式相减,得a n +2-a n +1=3a n -a n +1, 即a n +2=3a n ,n ≥2.又a 1=1,a 2=2, 所以a 3=3S 1-S 2+3=3a 1-(a 1+a 2)+3=3a 1, 故对一切n ∈N *,a n +2=3a n .(2)解 由(1)知,a n ≠0,所以a n +2a n =3.于是数列{a 2n -1}是首项a 1=1,公比为3的等比数列;数列{a 2n }是首项a 2=2,公比为3的等比数列. 因此a 2n -1=3n -1,a 2n =2×3n -1. 于是S 2n =a 1+a 2+…+a 2n=(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n ) =(1+3+…+3n -1)+2(1+3+…+3n -1) =3(1+3+…+3n -1)=32(3n -1). 热点三 数列的综合应用 热点3.1 数列与函数的综合问题数列是特殊的函数,以函数为背景的数列的综合问题体现了在知识交汇点上命题的特点,该类综合题的知识综合性强,能很好地考查逻辑推理能力和运算求解能力,因而一直是高考命题者的首选.【例3-1】 设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图象上(n ∈N *).(1)若a 1=-2,点(a 8,4b 7)在函数f (x )的图象上,求数列{a n }的前n 项和S n ; (2)若a 1=1,函数f (x )的图象在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln 2,求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .解 (1)由已知,b 7=2a 7,b 8=2a 8=4b 7, 有2a 8=4×2a 7=2a 7+2,解得d =a 8-a 7=2.所以,S n =na 1+n (n -1)2d =-2n +n (n -1)=n 2-3n .(2)函数f (x )=2x 在(a 2,b 2)处的切线方程为y -2a 2=(2a 2ln 2)(x -a 2), 它在x 轴上的截距为a 2-1ln 2. 由题意知,a 2-1ln 2=2-1ln 2, 解得a 2=2.所以,d =a 2-a 1=1.从而a n =n ,b n =2n , 所以T n =12+222+323+…+n -12n -1+n 2n ,2T n =11+22+322+…+n 2n -1因此,2T n -T n =1+12+122+…+12n -1-n2n=2-12n -1-n 2n =2n +1-n -22n. 所以,T n =2n +1-n -22n.热点3.2 数列与不等式的综合问题数列与不等式知识相结合的考查方式主要有三种:一是判断数列问题中的一些不等关系;二是以数列为载体,考查不等式的恒成立问题;三是考查与数列问题有关的不等式的证明.在解决这些问题时,如果是证明题要灵活选择不等式的证明方法,如比较法、综合法、分析法等.如果是解不等式问题,要使用不等式的各种不同解法,如数轴法、因式分解法.【例3-2】 在等差数列{a n }中,a 2=6,a 3+a 6=27. (1)求数列{a n }的通项公式;(2)记数列{a n }的前n 项和为S n ,且T n =S n3·2n -1,若对于一切正整数n ,总有T n ≤m成立,求实数m 的取值范围. 解 (1)设公差为d ,由题意得: ⎩⎨⎧a 1+d =6,2a 1+7d =27,解得⎩⎨⎧a 1=3,d =3,∴a n =3n . (2)∵S n =3(1+2+3+…+n )=32n (n +1), ∴T n =n (n +1)2n ,T n +1=(n +1)(n +2)2n +1,∴T n +1-T n =(n +1)(n +2)2n +1-n (n +1)2n=(n +1)(2-n )2n +1,∴当n ≥3时,T n >T n +1,且T 1=1<T 2=T 3=32, ∴T n 的最大值是32,故实数m 的取值范围是⎣⎢⎡⎭⎪⎫32,+∞.。
2018--2020年高考数学试题分类汇编数列附答案详解
2018--2020年⾼考数学试题分类汇编数列附答案详解2018---2020年⾼考数学试题分类汇编数列⼀、选择题.1、(2018年⾼考全国卷1理科4)记S n 为等差数列{a n }的前n 项和.若3S 3=S 2+S 4,a 1=2,则a 5=()A .﹣12B .﹣10C .10D .12答案:B解析:∵S n 为等差数列{a n }的前n 项和,3S 3=S 2+S 4,a 1=2,∴=a 1+a 1+d +4a 1+d ,把a 1=2,代⼊得d=﹣3 ∴a 5=2+4×(﹣3)=﹣10.故选:B .2、(2019年⾼考全国I 卷理科9)记n S 为等差数列{}n a 的前n 项和.已知4505S a ==,,则 A .25n a n =- B . 310n a n =-C .228n S n n =-D .2122n S n n =- 答案:A解析:有等差数列的性质可知54,0641514=+==+=d a a d a S ,解得2,31=-=d a所以52,42-=-=n a n n S n n ,故选A 。
3、(2019年⾼考全国III 卷理科5⽂科6)已知各项均为正数的等⽐数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=A . 16B . 8C .4D . 2答案:C解析:由题意有154=S ,即151)1(414=--=qq a S 由题意有a 5=3a 3+4a 1,即1214143a q a q a +=,故 (q 2-4)(q 2+1)=0因为各项均为正数,所以q>0,所以q=2将q=2代⼊151)1(414=--=qq a S .得a 1=1、所以43=a 故选C 4、(2019年⾼考全国III 卷⽂理科9)执⾏下边的程序框图,如果输⼊的ε为0.01,则输出s 的值等于 A.4122-B.5122-C.6122-D.7122-答案:C解析:等⽐数列前n 项和,0,1==s x 不满⾜01.0s x 不满⾜01.011,41+==s x 不满⾜01.01....41211,1281++++==s x 满⾜01.05、(2019年⾼考北京卷理科2⽂科4)执⾏如图所⽰的程序框图,输出的s 值为(A )1(B )2(C )3(D )4 答案:B解析:k=1,s=1, s=2212312?=?-,k<3,故执⾏循环体k=1+1=2,2222322s ?==?-;此时k=2<3,故继续执⾏循环体k=3,2222322s ?==?-,此时k=3,结束循环,输出s=2.故答案为:B.6、(2019年⾼考浙江卷10)设,a b R ∈,数列{}n a 中1a a =,21n n a a b +=+,21n n a a b +=+,则()A.当12b =时,1010a > B.当14b =时,1010a >C.当2b =-时,1010a >D.当2b =-时,1010a > 答案:A解答:选项B :不动点满⾜2211()042x x x -+=-=,如图,若11(0,)2a a =∈,12n a <,排除;如图若a 为不动点12,则12n a =;选项C :不动点满⾜22192()024x x x --=--=,不动点为2x =,令2a =,则210n a =<,排除;选项D :不动点满⾜221174()024x x x --=--=,不动点为1712x =,令1712a =,则171102n a =<,排除;选项A :证明:当12b =时,2211122a a =+≥,2321324a a =+≥,2431171216a a =+≥≥,处理⼀:可依次迭代到n a ;处理⼆:当4n ≥时,221112n n n a a a +=+≥≥,则117117171161616log 2log log 2n n n n a a a -++>?>,则1217()(4)16n n a n +≥≥,则641022617164(64631 1114710161616210()6a ?≥=+=++?+>++>,故选A.7、(2020?北京卷)在等差数列{}n a 中,19a =-,31a =-.记12(1,2,)n n T a a a n ==……,则数列{}n T (). A. 有最⼤项,有最⼩项 B. 有最⼤项,⽆最⼩项 C. ⽆最⼤项,有最⼩项 D. ⽆最⼤项,⽆最⼩项答案:B解:由题意可知,等差数列的公差511925151a a d --+===--,则其通项公式为:()()11912211n a a n d n n =+-=-+-?=-,注意到123456701a a a a a a a <<<<<<=<<,且由50T <可知()06,i T i i N <≥∈,由()117,ii i T a i i N T -=>≥∈可知数列{}n T 不存在最⼩项,由于1234569,7,5,3,1,1a a a a a a =-=-=-=-=-=,故数列{}n T 中的正项只有有限项:263T =,46315945T =?=.故数列{}n T 中存在最⼤项,且最⼤项为4T .故选:B.8、(2020?全国2卷)北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中⼼有⼀块圆形⽯板(称为天⼼⽯),环绕天⼼⽯砌9块扇⾯形⽯板构成第⼀环,向外每环依次增加9块,下⼀层的第⼀环⽐上⼀层的最后⼀环多9块,向外每环依次也增加9块,已知每层环数相同,且下层⽐中层多729块,则三层共有扇⾯形⽯板(不含天⼼⽯)()A. 3699块B. 3474块C. 3402块D. 3339块答案:C解:设第n 环天⽯⼼块数为n a ,第⼀层共有n 环,则{}n a 是以9为⾸项,9为公差的等差数列,9(1)99n a n n =+-?=,设n S 为{}n a 的前n 项和,则第⼀层、第⼆层、第三层的块数分别为232,,n n n n n S S S S S --,因为下层⽐中层多729块,所以322729n n n n S S S S -=-+,即3(927)2(918)2(918)(99)7292222n n n n n n n n ++++-=-+即29729n =,解得9n =,所以32727(9927)34022n S S +?===. 故选:C9、(2020?全国2卷)数列{}n a 中,12a =,m n m n a a a +=,若155121022k k k a a a ++++++=-,则k =()A. 2B. 3C. 4D. 5答案:C解:在等式m n m n a a a +=中,令1m =,可得112n n n a a a a +==,12n na a +∴=,所以,数列{}n a 是以2为⾸项,以2为公⽐的等⽐数列,则1222n nn a -=?=,()()()()1011011105101210122122212211212k k k k k k a a a a ++++++?-?-∴+++===-=---,1522k +∴=,则15k +=,解得4k =.故选:C.10、(2020?全国2卷)0-1周期序列在通信技术中有着重要应⽤.若序列12na a a 满⾜{0,1}(1,2,)i a i ∈=,且存在正整数m ,使得(1,2,)i m i a a i +==成⽴,则称其为0-1周期序列,并称满⾜(1,2,)i m i a a i +==的最⼩正整数m 为这个序列的周期.对于周期为m 的0-1序列12na a a ,11()(1,2,,1)mi i k i C k a a k m m +===-∑是描述其性质的重要指标,下列周期为5的0-1序列中,满⾜1()(1,2,3,4)5C k k ≤=的序列是()A. 11010B. 11011C. 10001D. 11001答案:C解:由i m i a a +=知,序列i a 的周期为m ,由已知,5m =,511(),1,2,3,45i i k i C k a a k +===∑,对于选项A ,511223344556111111(1)()(10000)55555i i i C a a a a a a a a a a a a +===++++=++++=≤∑52132435465711112(2)()(01010)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;对于选项B ,51122334455611113(1)()(10011)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;对于选项D ,51122334455611112(1)()(10001)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满⾜;故选:C⼆、填空题.1、(2018年⾼考全国卷1理科14)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6= ﹣63 .答案:63-解析:S n 为数列{a n }的前n 项和,S n =2a n +1,①当n=1时,a 1=2a 1+1,解得a 1=﹣1,当n ≥2时,S n ﹣1=2a n ﹣1+1,②,由①﹣②可得a n =2a n ﹣2a n ﹣1,∴a n =2a n ﹣1,∴{a n }是以﹣1为⾸项,以2为公⽐的等⽐数列,∴S 6==﹣63,故答案为:﹣632、(2018年⾼考北京卷理科9)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为 a n =6n ﹣3 .解:∵{a n }是等差数列,且a 1=3,a 2+a 5=36,∴,解得a 1=3,d=6,∴a n =a 1+(n ﹣1)d=3+(n ﹣1)×6=6n ﹣3.∴{a n }的通项公式为a n =6n ﹣3.故答案为:a n =6n ﹣3.3、(2018年⾼考浙江卷10)已知a 1,a 2,a 3,a 4成等⽐数列,且a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),若a 1>1,则()A .a 1<a 3,a 2<a 4B .a 1>a 3,a 2<a 4C .a 1<a 3,a 2>a 4D .a 1>a 3,a 2>a 4【解答】解:a 1,a 2,a 3,a 4成等⽐数列,由等⽐数列的性质可知,奇数项符号相同,偶数项符号相同, a 1>1,设公⽐为q ,当q >0时,a 1+a 2+a 3+a 4>a 1+a 2+a 3,a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),不成⽴,即:a 1>a 3,a 2>a 4,a 1<a 3,a 2<a 4,不成⽴,排除A 、D .当q=﹣1时,a 1+a 2+a 3+a 4=0,ln (a 1+a 2+a 3)>0,等式不成⽴,所以q ≠﹣1;当q <﹣1时,a 1+a 2+a 3+a 4<0,ln (a 1+a 2+a 3)>0,a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3)不成⽴,当q ∈(﹣1,0)时,a 1>a 3>0,a 2<a 4<0,并且a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3),能够成⽴,故选:B .4、(2019年⾼考全国I 卷⽂科14)记S n 为等⽐数列{a n }的前n 项和.若13314a S ==,,则S 4=___________.答案:85 解析:设数列的公⽐为q ,则有43123213=++=++=q q a a a S 解得21-=q ,所以854=S 5、(2019年⾼考全国I 卷理科14)记S n 为等⽐数列{a n }的前n 项和.若214613a a a ==,,则S 5=____________.答案:3121解析:由624a a =得51621q a q a =,解得3=q ,所以31211)1(515=--=q q a S6、(2019年⾼考全国III 卷理科14)记S n 为等差数列{a n }的前n 项和,12103a a a =≠,,则105S S =___________. 答案:4解析:因为,312a a =所以1a +,13a d =即d a =12,则()()4215211051101510=?+?+=a a a a S S 7、(2019年⾼考全国III 卷⽂科14)记S n 为等差数列{a n }的前n 项和,若375,13a a ==,则10S =___________.答案:100解析:由题意得136,521713=+==+=d a a d a a ,解得2,11==d a 所以100291010110=?+=d a S8、(2019年⾼考北京卷理科10)设等差数列{a n }的前n 项和为S n ,若a 2=-3,S 5=-10,则a 3= ________ . S n 的最⼩值为_______。
数列五年真题分类汇编(2019-2022))
专题八 数列悟知识1.通项a n 与前n 项和S n 的关系:a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2. 2.等差数列有关公式:(1)通项公式:a n =a 1+(n -1)d ;(2)前n 项和公式:S n =na 1+n (n -1)2d =n (a 1+a n )2. 3.等比数列有关公式:(1)通项公式:a n =a 1q n -1;(2)前n 项和公式:S n =⎩⎪⎨⎪⎧na 1,q =1,a 1(1-q n )1-q =a 1-a n q 1-q ,q ≠1. 悟备考数列是高考必考内容,选填题和解答题都会涉及,在备考的时候需要对数列进行如下梳理:第一,对数列与函数之间的关系要有深刻的理解,例如数列的单调性、最大(小)项等;第二,对等差数列与等比数列的定义及其性质、求和公式不仅要能运用公式解题,还要理解其意义;第三,对数列求和的方法要总结到位、计算准确.第1节 数列的概念及其表示考点1 数列的递推式和通项公式1.[全国乙(理)2022·4]嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{b n }:b 1=1+1α1,b 2=1+1α1+1α2,b 3=1+1α1+1α2+1α3,…,依此类推,其中αk ∈N *(k =1,2,…).则( )A .b 1<b 5B .b 3<b 8C .b 6<b 2D .b 4<b 72.[浙江2021·10]已知数列{a n }满足a 1=1,a n +1=a n 1+a n(n ∈N *).记数列{a n }的前n 项和为S n ,则( )A.32<S 100<3 B .3<S 100<4 C .4<S 100<92 D.92<S 100<5 3.[浙江2022·10]已知数列{a n }满足a 1=1,a n +1=a n -13a n 2(n ∈N *),则( ) A .2<100a 100<52B.52<100a 100<3 C .3<100a 100<72D.72<100a 100<4 4.[全国Ⅰ(文)2020·16]数列{a n }满足a n +2+(-1)n a n =3n -1,前16项和为540,则a 1=________.考点2 S n 与a n 的关系1.[浙江2020·7]已知等差数列{a n }的前n 项和为S n ,公差d ≠0,且错误!≤1.记b 1=S 2,b n +1=S 2n +2-S 2n ,n ∈N *,下列等式不可能...成立的是( )A .2a 4=a 2+a 6B .2b 4=b 2+b 6C .a 42=a 2a 8D .b 42=b 2b 82.[全国Ⅰ(理)2018·14]记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6=________.第2节 等差数列和等比数列考点1 等差数列及其性质1.[全国新高考Ⅱ2022·3]图1是中国古代建筑中的举架结构,AA′,BB′,CC′,DD′是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD 1,CC 1,BB 1,AA 1是举,OD 1,DC 1,CB 1,BA 1是相等的步,相邻桁的举步之比分别为DD 1OD 1=0.5,CC 1DC 1=k 1,BB 1CB 1=k 2,AA 1BA 1=k 3.已知k 1,k 2,k 3成公差为0.1的等差数列,且直线OA 的斜率为0.725,则k 3=( )图1图2A .0.75B .0.8C .0.85D .0.9 2.[北京2021·6]《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗面缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长a 1,a 2,a 3,a 4,a 5(单位:cm )成等差数列,对应的宽为b 1,b 2,b 3,b 4,b 5(单位:cm ),且长与宽之比都相等.已知a 1=288,a 5=96,b 1=192,则b 3=( )A .64B .96C .128D .1603.[北京(理)2018·9]设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为________.4.[全国甲(理)2021·18]已知数列{a n}的各项均为正数,记S n为{a n}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{a n}是等差数列;②数列{S n}是等差数列;③a2=3a1.注:若选择不同的组合分别解答,则按第一个解答计分.5.[全国甲(文)2021·18]记S n为数列{a n}的前n项和,已知a n>0,a2=3a1,且数列{S n}是等差数列,证明:{a n}是等差数列.考点2等差数列的通项与求和1.[北京2021·10]已知{a n}是各项均为整数的递增数列,且a1≥3.若a1+a2+…+a n=100,则n的最大值为()A.9 B.10 C.11 D.122.[全国Ⅱ(理)2020·4]北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )A .3 699块B .3 474块C .3 402块D .3 339块3.[全国Ⅰ(理)2019·9]记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则( )A .a n =2n -5B .a n =3n -10C .S n =2n 2-8nD .S n =12n 2-2n 4.[全国Ⅰ(理)2018·4]记S n 为等差数列{a n }的前n 项和.若3S 3=S 2+S 4,a 1=2,则a 5=( )A .-12B .-10C .10D .125.[全国Ⅰ(理)2017·4]S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为( )A .1B .2C .4D .86.[全国乙(文)2022·13]记S n 为等差数列{a n }的前n 项和.若2S 3=3S 2+6,则公差d =________.7.[全国Ⅲ(理)2019·14]记S n 为等差数列{a n }的前n 项和.若a 1≠0,a 2=3a 1,则S 10S 5=____________.8.[全国Ⅲ(文)2019·14]记S n 为等差数列{a n }的前n 项和.若a 3=5,a 7=13,则S 10=________.9.[北京(理)2019·10]设等差数列{a n }的前n 项和为S n ,若a 2=-3,S 5=-10,则a 5=________,S n 的最小值为________.10.[江苏2019·8]已知数列{a n }(n ∈N *)是等差数列,S n 是其前n 项和.若a 2a 5+a 8=0,S 9=27,则S 8的值是________.11.[全国新高考Ⅰ2022·17]记S n 为数列{a n }的前n 项和,已知a 1=1,⎩⎨⎧⎭⎬⎫S n a n 是公差为13的等差(1)求{a n }的通项公式;(2)证明:1a 1+1a 2+…+1a n<2.12.[全国新高考Ⅰ 2021·17]已知数列{a n }满足a 1=1,a n +1=⎩⎪⎨⎪⎧a n +1,n 为奇数,a n +2,n 为偶数. (1)记b n =a 2n ,写出b 1,b 2,并求数列{b n }的通项公式;(2)求{a n }的前20项和.13.[全国新高考Ⅱ 2021·17]记S n 是公差不为0的等差数列{a n }的前n 项和,若a 3=S 5,a 2a 4(1)求数列{a n}的通项公式;(2)求使S n>a n成立的n的最小值.14.[全国乙(理)2021·19]记S n为数列{a n}的前n项和,b n为数列{S n}的前n项积,已知2S n+1b n=2.(1)证明:数列{b n}是等差数列;(2)求{a n}的通项公式.15.[全国Ⅰ(文)2019·18]记S n为等差数列{a n}的前n项和.已知S9=-a5.(1)若a3=4,求{a n}的通项公式;(2)若a1>0,求使得S n≥a n的n的取值范围.16.[全国Ⅱ(理)2018·17]记S n为等差数列{a n}的前n项和,已知a1=-7,S3=-15.(1)求{a n}的通项公式;(2)求S n,并求S n的最小值.考点3等比数列及其性质1.[全国Ⅰ(文)2020·10]设{a n}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=()A.12 B.24 C.30 D.322.[北京(理)2018·4]“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于122.若第一个单音的频率为f,则第八个单音的频率为()A.32f B.322fC.1225f D.1227f3.[浙江2018·10]已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1,则()A.a1<a3,a2<a4B.a1>a3,a2<a4C.a1<a3,a2>a4D.a1>a3,a2>a44.[全国Ⅰ(文)2018·17]已知数列{a n}满足a1=1,na n+1=2(n+1)a n.设b n=a n n.(1)求b1,b2,b3;(2)判断数列{b n}是否为等比数列,并说明理由;(3)求{a n}的通项公式.考点4 等比数列的通项与求和1.[全国乙(理)2022·8]已知等比数列{a n }的前3项和为168,a 2-a 5=42,则a 6=( )A .14B .12C .6D .32.[全国甲(文)2021·9]记S n 为等比数列{a n }的前n 项和.若S 2=4,S 4=6,则S 6=( )A .7B .8C .9D .103.[全国Ⅱ(理)2020·6]数列{a n }中,a 1=2,a m +n =a m a n .若a k +1+a k +2+…+a k +10=215-25,则k =( )A .2B .3C .4D .54.[全国Ⅲ(理)2019·5]已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=( )A .16B .8C .4D .25.[全国Ⅰ(理)2019·14]记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5=________. 6.[全国Ⅰ(文)2019·14]记S n 为等比数列{a n }的前n 项和.若a 1=1,S 3=34,则S 4=________. 7.[全国Ⅲ(文)2020·17]设等比数列{a n }满足a 1+a 2=4,a 3-a 1=8.(1)求{a n }的通项公式;(2)记S n 为数列{log 3a n }的前n 项和.若S m +S m +1=S m +3,求m.8.[全国Ⅲ(理)2018·17]等比数列 {a n } 中,a 1=1,a 5=4a 3.(1)求{a n }的通项公式;(2)记S n 为 {a n } 的前n 项和.若S m =63,求m.考点5 等差、等比数列的综合1.[全国Ⅲ(理)2017·9]等差数列{a n }的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{a n }前6项的和为( )A .-24B .-3C .3D .82.[江苏2020·11]设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和S n =n 2-n +2n -1(n ∈N *),则d +q 的值是________.3.[北京(理)2017·10]若等差数列{a n }和等比数列{b n }满足a 1=b 1=-1,a 4=b 4=8,则a 2b 2=________.4.[全国甲(文)2022·18]记S n 为数列{a n }的前n 项和.已知2S n n+n =2a n +1.(1)证明:{a n}是等差数列;(2)若a4,a7,a9成等比数列,求S n的最小值.5.[全国Ⅱ(理)2019·19]已知数列{a n}和{b n}满足a1=1,b1=0,4a n+1=3a n-b n+4,4b n+1=3b n-a n-4.(1)证明:{a n+b n}是等比数列,{a n-b n}是等差数列;(2)求{a n}和{b n}的通项公式.6.[全国Ⅱ(文)2019·18]已知{a n}是各项均为正数的等比数列,a1=2,a3=2a2+16.(1)求{a n}的通项公式;(2)设b n=log2a n,求数列{b n}的前n项和.7.[浙江2019·20]设等差数列{a n}的前n项和为S n,a3=4,a4=S3.数列{b n}满足:对每个n∈N*,S n+b n,S n+1+b n,S n+2+b n成等比数列.(1)求数列{a n},{b n}的通项公式;(2)记c n=a n2b n,n∈N*,证明:c1+c2+…+c n<2n,n∈N*.8.[全国Ⅰ(文)2017·17]记S n为等比数列{a n}的前n项和.已知S2=2,S3=-6.(1)求{a n}的通项公式;(2)求S n,并判断S n+1,S n,S n+2是否成等差数列.9.[全国新高考Ⅱ2022·17]已知{a n}是等差数列,{b n}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.(1)证明:a1=b1;(2)求集合{k|b k=a m+a1,1≤m≤500}中元素的个数.第3节 数列的求和考点1 公式法与分组转化法求和1.[全国Ⅱ(文)2020·6]记S n 为等比数列{a n }的前n 项和.若a 5-a 3=12,a 6-a 4=24,则S n a n=( )A .2n -1B .2-21-nC .2-2n -1D .21-n -12.[全国新高考Ⅰ 2020·14]将数列{2n -1}与{3n -2}的公共项从小到大排列得到数列{a n },则{a n }的前n 项和为________.3.[全国Ⅱ(文)2020·14]记S n 为等差数列{a n }的前n 项和.若a 1=-2,a 2+a 6=2,则S 10=________.4.[全国新高考Ⅱ2020·18]已知公比大于 1 的等比数列{a n }满足a 2+a 4=20,a 3=8.(1)求{a n }的通项公式;(2)求a 1a 2-a 2a 3+…+(-1)n -1a n a n +1.1.[全国Ⅱ(理)2017·15]等差数列{a n }的前n 项和为S n ,a 3=3,S 4=10,则∑k =1n 1S k =________. 2.[浙江2020·20]已知数列{a n },{b n },{c n }满足a 1=b 1=c 1=1,c n =a n +1-a n ,c n +1=b n b n +2c n,n ∈N *.(1)若{b n }为等比数列,公比q >0,且b 1+b 2=6b 3,求q 的值及数列{a n }的通项公式;(2)若{b n }为等差数列,公差d >0,证明:c 1+c 2+c 3+…+c n <1+1d,n ∈N *.3.[全国Ⅲ(文)2017·17]设数列{a n }满足a 1+3a 2+…+(2n -1)a n =2n.(1)求{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n +1 的前n 项和.1.[全国新高考Ⅰ2021·16]某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20 dm ×12 dm 的长方形纸,对折1次共可以得到10 dm ×12 dm ,20 dm ×6 dm 两种规格的图形,它们的面积之和S 1=240 dm 2,对折2次共可以得到5 dm ×12 dm ,10 dm ×6 dm ,20 dm ×3 dm 三种规格的图形,它们的面积之和S 2=180 dm 2,以此类推.则对折4次共可以得到不同规格图形的种数为________;如果对折n 次,那么∑nk =1S k =________dm 2.2.[全国乙(文)2021·19]设{a n }是首项为1的等比数列,数列{b n }满足b n =na n 3.已知a 1,3a 2,9a 3成等差数列.(1)求{a n }和{b n }的通项公式;(2)记S n 和T n 分别为{a n }和{b n }的前n 项和.证明:T n <S n 2.3.[天津2021·19]已知{a n }是公差为2的等差数列,其前8项和为64.{b n }是公比大于0的等比数列,b 1=4,b 3-b 2=48.(1)求{a n }和{b n }的通项公式;(2)记c n =b 2n +1b n,n ∈N *. (ⅰ)证明{c n 2-c 2n }是等比数列;(ⅱ)证明 k =1na k a k +1c k 2-c 2k<2 2(n ∈N *).4.[浙江2021·20]已知数列{a n }的前n 项和为S n ,a 1=-94,且4S n +1=3S n -9(n ∈N *). (1)求数列{a n }的通项公式.(2)设数列{b n }满足3b n +(n -4)a n =0(n ∈N *),记{b n }的前n 项和为T n .若T n ≤λb n 对任意n ∈N *恒成立,求实数λ的取值范围.5.[全国Ⅰ(理)2020·17]设{a n}是公比不为1的等比数列,a1为a2,a3的等差中项.(1)求{a n}的公比;(2)若a1=1,求数列{na n}的前n项和.6.[全国Ⅲ(理)2020·17]设数列{a n}满足a1=3,a n+1=3a n-4n.(1)计算a2,a3,猜想{a n}的通项公式并加以证明;(2)求数列{2n a n}的前n项和S n.7.[天津2020·19]已知{a n }为等差数列,{b n }为等比数列,a 1=b 1=1,a 5=5(a 4-a 3),b 5=4(b 4-b 3).(1)求{a n }和{b n }的通项公式;(2)记{a n }的前n 项和为S n ,求证:S n S n +2<S n +12(n ∈N *);(3)对任意的正整数n ,设c n =⎩⎪⎨⎪⎧(3a n -2)b n a n a n +2,n 为奇数,a n -1b n +1,n 为偶数.求数列{c n }的前2n 项和.8.[浙江2018·20]已知等比数列{a n }的公比q>1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{b n }满足b 1=1,数列{(b n +1-b n )a n }的前n 项和为2n 2+n.(1)求q 的值;(2)求数列{b n }的通项公式.9.[山东(理)2017·19]已知{x n }是各项均为正数的等比数列,且x 1+x 2=3,x 3-x 2=2. (1)求数列{x n }的通项公式;(2)如图,在平面直角坐标系xOy 中,依次连接点P 1(x 1,1),P 2(x 2,2),…,P n +1(x n +1,n +1)得到折线P 1P 2…P n +1,求由该折线与直线y =0,x =x 1,x =x n +1所围成的区域的面积T n .10.[山东(文)2017·19]已知{a n }是各项均为正数的等比数列,且a 1+a 2=6,a 1a 2=a 3. (1)求数列{a n }的通项公式;(2){b n }为各项非零的等差数列,其前n 项和为S n .已知S 2n +1=b n b n +1,求数列⎩⎨⎧⎭⎬⎫b n a n 的前n 项和T n .考点4并项求和法1.[全国新高考Ⅰ 2020·18]已知公比大于1的等比数列{a n}满足a2+a4=20,a3=8.(1)求{a n}的通项公式;(2)记b m为{a n}在区间(0,m](m∈N*)中的项的个数,求数列{b m}的前100项和S100.第4节与数列有关的新定义问题1.[北京2020·8]在等差数列{a n}中,a1=-9,a5=-1.记T n=a1a2…a n(n=1,2,…),则数列{T n}()A.有最大项,有最小项B.有最大项,无最小项C.无最大项,有最小项D.无最大项,无最小项2.[全国Ⅰ(理)2017·12]几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,以此类推.求满足如下条件的最小整数N :N>100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A .440B .330C .220D .1103.[浙江2020·11]我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列⎩⎨⎧⎭⎬⎫n (n +1)2就是二阶等差数列.数列⎩⎨⎧⎭⎬⎫n (n +1)2(n ∈N *)的前3项和是________.4.[北京2022·21]已知Q :a 1,a 2,…,a k 为有穷整数数列.给定正整数m ,若对任意的n ∈{1,2,…,m},在Q 中存在a i ,a i +1,a i +2,…,a i +j (j ≥0),使得a i +a i +1+a i +2+…+a i +j =n ,则称Q 为m -连续可表数列.(1)判断Q :2,1,4是否为5-连续可表数列?是否为6-连续可表数列?说明理由. (2)若Q :a 1,a 2,…,a k 为8-连续可表数列,求证:k 的最小值为4.(3)若Q :a 1,a 2,…,a k 为20-连续可表数列,且a 1+a 2+…+a k <20,求证:k ≥7.5.[江苏2020·20]已知数列{a n }(n ∈N *)的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有S 1k n +1-S 1k n =λa 1k n +1成立,则称此数列为“λ~k ”数列.(1)若等差数列{a n }是“λ~1”数列,求λ的值.(2)若数列{a n}是“33~2”数列,且a n>0,求数列{a n}的通项公式.(3)对于给定的λ,是否存在三个不同的数列{a n}为“λ~3”数列,且a n≥0?若存在,求λ的取值范围;若不存在,说明理由.参考答案第1节 数列的概念及其表示考点1 数列的递推式和通项公式1.D 【解析】本题考查新定义数列的单调性在实际问题中的应用.由已知,b 1=1+1α1,b 2=1+1α1+1α2,1α1>1α1+1α2,故b 1>b 2.同理得b 2<b 3,b 1>b 3,又1α2>1α2+1α3+1α4,故b 2<b 4.则b 1>b 3>b 5>b 7>…,b 2<b 4<b 6<…,且b n <b n +1(n 为正偶数).由上可知,b 1>b 5,故A 错误;b 3>b 9>b 8,故B 错误;b 6>b 2,故C 错误;b 4<b 6<b 7,故D 正确.故选D.2.A 【解析】本题考查数列的递推关系及放缩法.由题可知,0<a n +1=a n1+a n <a n ≤1,且a n +1+a n +1a n =a n ,a 2=12,则a n +1=a n -a n +1a n<a n -a n +112(a n +a n +1)=2(a n -a n +1),则32=a 1+a 2<S 100=a 1+a 2+…+a 100<a 1+2(a 1-a 2+a 2-a 3+…+a 99-a 100)=a 1+2(a 1-a 100)<3,故选A.3.B 【解析】本题考查数列的递推关系.由a n +1=a n -13a n 2=-13⎝⎛⎭⎫a n -322+34≤34及a n ≠0,得a n +1a n =1-13a n ≥34>0(n ≥2).又a 1=1,所以a 2=a 1-13a 12=23>0,所以a n >0.由于a n +1=a n ⎝⎛⎭⎫1-13a n ,则1a n +1-1a n =13-a n >13,所以1a 2-1a 1>13,1a 3-1a 2>13,…,1a n +1-1a n >13,累加得1a n +1-1a 1>13n ,所以1a n +1>13n +1,则1a 100>993+1=34,所以a 100<134,100a 100<5017<3.由1a n +1>13n +1,可得1a n >13(n -1)+1,即a n <3n +2(n ≥2),又a 1=1,所以a n ≤3n +2,则1a n +1-1a n =13-a n≤13-3n +2=13⎝⎛⎭⎫1+1n +1,所以1a 2-1a 1≤13×⎝⎛⎭⎫1+12,1a 3-1a 2≤13×⎝⎛⎭⎫1+13,…,1a n +1-1a n ≤13⎝⎛⎭⎫1+1n +1,累加得1a n +1-1a 1≤13n +13(12+13+…+1n +1),故1a n +1≤13n +13⎝⎛⎭⎫12+13+…+1n +1+1,所以1a 100≤34+13×⎝⎛⎭⎫12+13+…+1100<34+13(12×6+18×93)<40,a 100>140,100a 100>52.综上可知52<100a 100<3,故选B.4.7【解析】本题考查数列求和及数列递推公式.当n 为偶数时,a n +2+a n =3n -1,所以(a 2+a 4)+(a 6+a 8)+(a 10+a 12)+(a 14+a 16)=5+17+29+41=92.因为前16项和为540,所以a 1+a 3+a 5+a 7+a 9+a 11+a 13+a 15=448.当n 为奇数时,a n +2-a n =3n -1,由累加法得a n +2-a 1=3(1+3+5+…+n )-1+n 2=34n 2+n +14,所以a n +2=34n 2+n +14+a 1.所以a 1+⎝⎛⎭⎫34×12+1+14+a 1+(34×32+3+14+a 1)+…+⎝⎛⎭⎫34×132+13+14+a 1=8a 1+34×(12+32+…+132)+(1+3+…+13)+14×7=448,解得a 1=7.考点2 S n 与a n 的关系1.D 【解析】本题考查等差数列的通项公式及其性质.因为b n +1=S 2n +2-S 2n =a 2n +1+a 2n+2=2a 1+(4n +1)d .对于选项A :由等差数列的性质知,2a 4=a 2+a 6成立;对于选项B :因为b 2=2a 1+5d ,b 4=2a 1+13d ,b 6=2a 1+21d ,所以2b 4-(b 2+b 6)=2(2a 1+13d )-(4a 1+26d )=0,则2b 4=b 2+b 6成立;对于选项C :若a 42=a 2a 8,则(a 1+3d )2=(a 1+d )·(a 1+7d ),即a 1=d ,所以a 1d =1,符合题意,故a 42=a 2a 8可能成立;对于选项D :由B 知,b 2=2a 1+5d ,b 4=2a 1+13d ,又b 8=2a 1+29d ,若b 42=b 2b 8,则(2a 1+13d )2=(2a 1+5d )·(2a 1+29d ),即2a 1=3d ,即a 1d =32>1,不符合题意,所以b 42=b 2b 8不可能成立.故选D.2.-63 【解析】由题知S n =2a n +1(n ≥1),① ∴S n -1=2a n -1+1(n ≥2).②当n ≥2时,①-②,得a n =2a n -2a n -1, ∴a n =2a n -1.当n =1时,S 1=a 1=2a 1+1, 解得a 1=-1.∴数列{a n }是以-1为首项,2为公比的等比数列. ∴S 6=a 1(1-q 6)1-q =-1×(1-26)1-2=-63.第2节 等差数列和等比数列考点1 等差数列及其性质1.D 【解析】本题考查等差数列的性质、斜率与倾斜角在数学文化中的应用.如图,连接OA ,延长AA 1与x 轴交于点A 2,则OA 2=4OD 1.因为k 1,k 2,k 3成公差为0.1的等差数列,所以k 1=k 3-0.2,k 2=k 3-0.1,所以CC 1=DC 1(k 3-0.2),BB 1=CB 1(k 3-0.1),AA 1=k 3BA 1,即CC 1=OD 1(k 3-0.2),BB 1=OD 1(k 3-0.1),AA 1=k 3OD 1(关键:利用等差数列的性质,将各个线段用k 3和OD 1表示出来).又DD 1OD 1=0.5,所以DD 1=0.5OD 1,所以AA 2=0.5OD 1+OD 1(k 3-0.2)+OD 1(k 3-0.1)+k 3OD 1=OD 1(3k 3+0.2).所以tan ∠AOA 2=AA 2OA 2=OD 1(3k 3+0.2)4OD 1=0.725,解得k 3=0.9,故选D.2.C 【解析】本题考查等差数列的基本运算.由于a k b k (1≤k ≤5)是常数,所以a 5b 5=a 1b 1,即96b 5=288192,所以b 5=64.因为{b n }是等差数列,所以b 3=b 1+b 52=128. 3.a n =6n -3 【解析】设等差数列{a n }的公差为d .∵a 1=3,a 2+a 5=2a 1+5d =36,解得d =6,∴a n =3+(n -1)×6=6n -3.4.【证明】本题考查等差数列的通项公式、前n 项和及等差数列的判断. 若选条件①②,则证明③: 设等差数列{a n }的公差为d ,∵数列{S n }是等差数列,∴2 S 2=S 1+S 3, ∴22a 1+d =a 1+3a 1+3d ,两边平方整理得4a 1+d =23a 1(a 1+d ),∴(4a 1+d )2=(23a 1(a 1+d ))2,∴(2a 1-d )2=0,∴d =2a 1, ∴a 2=a 1+d =3a 1.若选条件①③,则证明②:设等差数列{a n }的公差为d ,则a 2=a 1+d =3a 1,∴d =2a 1.∴S n =na 1+n (n -1)2d =n 2a 1,∴S n =n a 1,∴S n +1-S n =(n +1)a 1-n a 1=a 1(常数),当n =1时,S 1=a 1,∴数列{S n }是以a 1为首项,a 1为公差的等差数列. 若选条件②③,则证明①: ∵数列{S n }是等差数列,a 2=3a 1, ∴S 2-S 1=4a 1-a 1=a 1,∴S n =a 1+(n -1)a 1=n a 1,∴S n =n 2a 1.当n ≥2时,a n =S n -S n -1=n 2a 1-(n -1)2a 1=(2n -1)a 1,对于n =1也成立,∴a n +1-a n =(2n +1)a 1-(2n -1)a 1=2a 1(常数), ∴数列{a n }是等差数列.5.【证明】本题考查等差数列及通项与前n 项和的关系. 设数列{S n }的公差为d(d 为常数).因为{S n }是等差数列,所以当n ≥2时,S n -S n -1=d , 所以d =S 2-S 1=a 1+a 2-a 1=a 1+3a 1-a 1=a 1.于是,当n ≥2时,a n +1-a n =(S n +1-S n )-(S n -S n -1)=(S n +1+S n )(S n +1-S n )-(S n +S n -1)(S n -S n -1)=(S n +1+S n )a 1-(S n +S n -1)a 1 =[(S n +1+S n )-(S n +S n -1)]a 1 =[(S n +1-S n )+(S n -S n -1)]a 1 =2a 1,又2a 1为常数,且当n =1时,a 2-a 1=2a 1符合上式,所以数列{a n }是等差数列. 考点2 等差数列的通项与求和1.C 【解析】本题考查数列的单调性与最值.要求a 1+a 2+…+a n =100的n 的最大值,那么a 1=3,且{a k }(k =1,2,…,n -1, n ∈N *)是公差为1的等差数列,通项a k =k +2,则a 1+a 2+…+a n -1=(n -1)(n +4)2,令(n -1)(n +4)2≤100,得n ≤12,当n =12时,a n -1=13,a n =12,不满足题意.当n =11时,a n -1=12,a n =25,满足题意.综上,n 的最大值为11.2.C 【解析】本题考查等差数列的性质及其前n 项和.设由内到外每环的扇面形石板的块数构成数列{a n },由题意知a 1=9.又因为向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,所以数列{a n }为公差为9的等差数列. 方法一:设每层环数为n (n ∈N *),则上层由内向外每环的扇面形石板的块数依次为a 1,a 2,…,a n ,中层由内向外每环的扇面形石板的块数依次为a n +1,a n +2,…,a 2n ,下层由内向外每环的扇面形石板的块数依次为a 2n +1,a 2n +2,…,a 3n .由题意知(a 2n +1+a 2n +2+…+a 3n )-(a n +1+a n +2+…+a 2n )=729,由等差数列的性质知a 2n +1-a n +1=a 2n +2-a n +2=…=a 3n -a 2n =9n ,所以9n 2=729,得 n =9.则数列{a n }共有9×3=27项,故三层共有扇面形石板(不含天心石)的块数即为数列{a n }的前27项和,即27×9+27×262×9=3 402,故选C.方法二:设每层环数为n (n ∈N *),设数列{a n }的前n 项和为S n ,由等差数列的性质知,S n ,S 2n -S n ,S 3n -S 2n 成等差数列,且(S 3n -S 2n )-(S 2n -S n )=9n 2,则9n 2=729,解得n =9.则数列{a n }共有9×3=27项,故三层共有扇面形石板(不含天心石)的块数即为数列{a n }的前27项和,即27×9+27×262×9=3 402,故选C.3.A 【解析】本题考查等差数列的通项公式和前n 项和公式. 设等差数列{a n }的首项为a 1,公差为d , 则⎩⎪⎨⎪⎧S 4=4a 1+4×32d =0,a 5=a 1+4d =5,解得⎩⎪⎨⎪⎧a 1=-3,d =2.所以a n =-3+(n -1)×2=2n -5, S n =n (-3+2n -5)2=n 2-4n ,故选A.4.B 【解析】设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d =2+(n -1)d .∴S 3=3a 1+3d =6+3d ,S 2=2a 1+d =4+d ,S 4=4a 1+6d =8+6d .由题知3S 3=S 2+S 4,∴3(6+3d )=4+d +8+6d .解得d =-3,∴a 5=a 1+4d =2-12=-10.故选B.5.C 【解析】设等差数列{a n }的首项为a 1,公差为d ,则由⎩⎪⎨⎪⎧a 4+a 5=24,S 6=48,得⎩⎪⎨⎪⎧2a 1+7d =24,6a 1+15d =48,解得⎩⎪⎨⎪⎧a 1=-2,d =4,故选C.6.2 【解析】本题考查等差数列的前n 项和公式.由2S 3=3S 2+6,得2(3a 1+3d)=3(2a 1+d)+6,解得d =2.7.4 【解析】本题考查等差数列通项公式及前n 项和公式.∵{a n }为等差数列且a 2=3a 1,∴公差d =a 2-a 1=2a 1,∴a 10=a 1+9d =19a 1,a 5=a 1+4d =9a 1.∴S 10=10(a 1+a 10)2=100a 1,S 5=5(a 1+a 5)2=25a 1,∴S 10S 5=4.8.100 【解析】本题考查等差数列的通项公式和前n 项和公式.设等差数列{a n }的公差为d ,则⎩⎪⎨⎪⎧a 3=a 1+2d =5,a 7=a 1+6d =13,解得⎩⎪⎨⎪⎧a 1=1,d =2.∴S 10=10a 1+10×92d =10×1+10×92×2=100.9.0 -10 【解析】本题考查等差数列的通项公式和前n 项和的求法.设等差数列{a n }的首项为a 1,公差为d.由S 5=52(a 1+a 5)=52×2a 3=-10,得a 3=-2,∴d =a 3-a 2=-2-(-3)=1,∴a 1=-3-1=-4,∴a 5=a 1+4d =-4+4=0.方法一:∵a 1=-4,d =1,∴S n =-4n +n (n -1)2×1=12(n 2-9n)=12⎝⎛⎭⎫n -922-818.∵n ∈N *,∴当n =4或5时,S n 取最小值,为S 4=S 5=-10.方法二:∵a 1=-4,d =1,∴a n =-4+(n -1)×1=n -5.由a n ≤0得n ≤5,且n =5时,a 5=0,故当n =4或5时,S n 取最小值,为S 4=S 5=5×(-4+0)2=-10.10.16 【解析】本题考查等差数列的通项公式和前n 项和公式.设等差数列{a n }的公差为d ,则a 2a 5+a 8=(a 1+d)(a 1+4d)+a 1+7d =0,S 9=9a 1+36d =27.化简⎩⎪⎨⎪⎧(a 1+d )(a 1+4d )+a 1+7d =0,a 1+4d =3,解得⎩⎪⎨⎪⎧a 1=-5,d =2,则S 8=8a 1+28d =-40+56=16.11.本题考查等差数列的定义、数列的递推关系与通项公式、裂项相消法求和.(1)【解】由题知,数列⎩⎨⎧⎭⎬⎫S n a n 是首项为1,公差为13的等差数列,所以S n a n =1+13(n -1)=n +23,所以S n =n +23a n .当n ≥2时,S n -1=n +13a n -1, 所以a n =S n -S n -1=n +23a n -n +13a n -1, 所以a n a n -1=n +1n -1,所以a n =a n a n -1.a n -1a n -2.....a 2a 1.a 1=n +1n -1.n n -2.. (3)1·1=(n +1)n 2.当n =1时,a 1=1满足上式,所以a n =(n +1)n2.(2)【证明】由(1)知,1a n =2(n +1)n =2⎝⎛⎭⎫1n -1n +1,所以1a 1+1a 2+…+1a n =2(1-12+12-13+…+1n -1n +1)=2⎝⎛⎭⎫1-1n +1=2-2n +1<2.12.【解】本题考查数列的通项公式、数列求和. (1)b 1=a 2=a 1+1=2,b 2=a 4=a 3+1=a 2+2+1=5. ∵2n 为偶数,∴a 2n +1=a 2n +2,a 2n +2=a 2n +1+1, ∴a 2n +2=a 2n +3,即b n +1=b n +3,且b 1=2, ∴{b n }是以2为首项,3为公差的等差数列, ∴b n =3n -1.(2)当n 为奇数时,a n =a n +1-1, ∴{a n }的前20项和为 a 1+a 2+…+a 20=(a 1+a 3+…+a 19)+(a 2+a 4+…+a 20)=[(a 2-1)+(a 4-1)+…+(a 20-1)]+(a 2+a 4+…+a 20) =2(a 2+a 4+…+a 20)-10.由(1)可知,a 2+a 4+…+a 20=b 1+b 2+…+b 10=2×10+10×92×3=155,∴{a n }的前20项和为2×155-10=300.13.【解】本题考查等差数列的通项公式,与前n 项和有关的不等式的求解. (1)设等差数列{a n }的公差为d(d ≠0),则⎩⎪⎨⎪⎧a 1+2d =5a 1+10d ,(a 1+d )(a 1+3d )=4a 1+6d ,解得⎩⎪⎨⎪⎧a 1=-4,d =2, 则a n =-4+(n -1)×2=2n -6.(2)结合(1)可知,S n =-4n +n (n -1)×22=n 2-5n ,则S n >a n 等价于n 2-5n>2n -6,解得n<1或n>6,又n ∈N *,所以n ≥7, 故使S n >a n 成立的n 的最小值为7.14.本题考查等差数列的证明、数列的递推关系及通项公式.(1)【证明】当n =1时,b 1=S 1,则2b 1+1b 1=2,则b 1=32;当n ≥2时,S n =b n b n -1,代入2S n +1b n =2得2b n -1b n +1b n =2,则2b n =2b n -1+1,∴b n -b n -1=12(n ≥2).故数列{b n }是首项为32,公差为12的等差数列.(2)【解】由(1)得b n =32+12(n -1)=12n +1.当n =1时,S 1=b 1=32;当n ≥2时,S n =b nb n -1=12n +112(n -1)+1=n +2n +1, 由S 1=32满足上式,得S n =n +2n +1.当n =1时,a 1=S 1=32;当n ≥2时,a n =S n -S n -1=n +2n +1-n +1n =-1n (n +1),因为a 1=32不满足上式,故a n=⎩⎨⎧32,n =1,-1n (n +1),n ≥2.15.【解】(1)设{a n }的公差为d. 由S 9=-a 5得a 1+4d =0. 由a 3=4得a 1+2d =4. 于是a 1=8,d =-2.因此{a n }的通项公式为a n =10-2n.(2)由(1)得a 1=-4d ,故a n =(n -5)d ,S n =n (n -9)d 2.由a 1>0知d<0,故S n ≥a n 等价于n 2-11n +10≤0,解得1≤n ≤10. 所以n 的取值范围是{n|1≤n ≤10,n ∈N }.16.【解】(1)设{a n }的公差为d ,由题意得3a 1+3d =-15.由a 1=-7得d =2. 所以{a n }的通项公式为a n =2n -9. (2)由(1)得S n =n 2-8n =(n -4)2-16.所以当n =4时,S n 取得最小值,最小值为-16. 考点3 等比数列及其性质1.D 【解析】本题考查等比数列的通项公式.设等比数列{a n }的公比为q ,因为a 1+a 2+a 3=1,a 2+a 3+a 4=2,所以q (a 1+a 2+a 3)=2,解得q =2.所以a 6+a 7+a 8=q 5(a 1+a 2+a 3)=25=32,故选D.2.D 【解析】十三个单音的频率成等比数列,设为{a n },其公比为122,a 1=f ,∴a 8=f ·(122)7=1227f ,故选D.3.B 【解析】设公比为q ,∵y =ln x 在(1,0)处的切线为y =x -1,∴易知当x >0时,ln x ≤x -1<x .当q >0时,∵a 1>1,∴a 2>0,a 3>0,a 4>0,∴a 1+a 2+a 3+a 4>a 1+a 2+a 3>ln(a 1+a 2+a 3),不合题意;当q =-1时,a 1+a 2+a 3+a 4=0,a 1+a 2+a 3=a 1>1,∴ln(a 1+a 2+a 3)>a 1+a 2+a 3+a 4=0,不合题意;当q <-1时,a 1+a 2+a 3+a 4=a 1(1+q +q 2+q 3)=a 1[(1+q )+q 2(1+q )]=a 1(1+q )(1+q 2)<0,a1+a 2+a 3=a 1(1+q +q 2).∵q 2+q +1=⎝⎛⎭⎫q +122+34>1,∴a 1+a 2+a 3>a 1>1,∴ln(a 1+a 2+a 3)>ln 1=0,不合题意.综上可知,-1<q <0,此时,a 3-a 1=a 1(q 2-1)<0,∴a 3<a 1,a 4-a 2=a 1q 3-a 1q =a 1q (q 2-1)>0,∴a 4>a 2.故选B.4.【解】(1)由条件可得a n +1=2(n +1)na n . 将n =1代入得,a 2=4a 1,而a 1=1,所以a 2=4. 将n =2代入得,a 3=3a 2,所以a 3=12. 从而b 1=1,b 2=2,b 3=4. (2){b n }是等比数列.由条件可得a n +1n +1=2a nn ,即b n +1=2b n .又b 1=1,所以{b n }是首项为1,公比为2的等比数列.(3)由(2)可得a n n =2n -1,所以a n =n·2n -1.考点4 等比数列的通项与求和1.D 【解析】本题考查等比数列的基本运算.设等比数列{a n }的公比为q ,则a 1+a 2+a 3=a 2⎝⎛⎭⎫1q +1+q =a 2·1+q +q 2q =168,a 2-a 5=a 2(1-q 3)=a 2(1-q )(1+q +q 2)=42,以上两式联立整理得1q 1-q=4,解得q =12,a 2=48,所以a 6=a 2q 4=48×116=3,故选D.2.A 【解析】本题考查等比数列的前n 项和.设等比数列{a n }的公比为q ,则⎩⎪⎨⎪⎧a 1(1+q )=4,a 1(1+q +q 2+q 3)=6,可得⎩⎪⎨⎪⎧a 1(1+q )=4,q 2=12,则S 6=a 1(1-q 6)1-q=a 1(1-q 2)(1+q 2+q 4)1-q=a 1(1+q )(1+q 2+q 4)=4×74=7,故选A.3.C 【解析】本题考查等比数列的定义、前n 项和公式.因为数列{a n }中,a m +n =a m a n ,令m =1,则a n +1=a n a 1=2a n ,所以数列{a n }是首项为2,公比为2的等比数列,则a k +1=a 1·2k =2k +1.所以a k +1+a k +2+…+a k +10=a k +1(1-210)1-2=2k +1(210-1)=2k +11-2k +1,则2k +11-2k +1=215-25,所以k =4,故选C.4.C 【解析】本题考查等比数列通项公式及前n 项和公式.设S n 为等比数列{a n }的前n 项和,且公比为q (q >0).∴S 4=15.又∵{a n }各项均为正数,且a 5=3a 3+4a 1,∴a 1q 4=3a 1q 2+4a 1.∵a 1≠0,∴q 4-3q 2-4=0,解得q 2=4,∴q =2.方法一:∵S 4=a 1(1-q 4)1-q=15,∴15a 1=15,∴a 1=1.∴a 3=a 1q 2=4.故选C.方法二:∵a 1+a 2+a 3+a 4=15,∴a 3q 2+a 3q +a 3+a 3q =15,∴a 34+a 32+a 3+2a 3=15,即154a 3=15,∴a 3=4.故选C.5.1213 【解析】本题考查等比数列的前n 项和.设等比数列{a n }的公比为q(q ≠0),∵a 1=13,∴a 4=a 1q 3,a 6=a 1q 5.由a 42=a 6,得a 12q 6=a 1q 5,∴a 1q =1,∴q =3. ∴S 5=a 1(1-q 5)1-q =13×(1-35)1-3=1213.6. 58 【解析】本题考查等比数列的通项与前n 项和.设等比数列{a n }的公比为q(q ≠0),则由a 1=1,S 3=34,得1+q +q 2=34,即(2q +1)2=0,则q =-12,所以S 4=1-⎝⎛⎭⎫-1241-⎝⎛⎭⎫-12=58.7.【解】本题考查等比数列基本量的计算,等差数列的前n 项和. (1)设{a n }的公比为q ,则a n =a 1q n -1.由已知得⎩⎪⎨⎪⎧a 1+a 1q =4,a 1q 2-a 1=8.解得a 1=1,q =3.所以{a n }的通项公式为a n =3n -1. (2)由(1)知log 3a n =n -1.故S n =n (n -1)2. 由S m +S m +1=S m +3得m(m -1)+(m +1)m =(m +3)(m +2),即m 2-5m -6=0. 解得m =-1(舍去),m =6.8.【解】(1)设{a n }的公比为q ,由题设得a n =q n -1. 由已知得q 4=4q 2,解得q =0(舍去),q =-2或q =2. 故a n =(-2)n -1或a n =2n -1.(2)若a n =(-2)n -1,则S n =1-(-2)n3.由S m =63得(-2)m =-188,此方程没有正整数解. 若a n =2n -1,则S n =2n -1. 由S m =63得2m =64,解得m =6. 综上,m =6.考点5 等差、等比数列的综合1.A 【解析】令首项为a 1,公差为d (d ≠0). 由题意得a 32=a 2·a 6,∴(a 1+2d )2=(a 1+d )·(a 1+5d ),即a 12+4a 1d +4d 2=a 12+6a 1d +5d 2,∴d =-2a 1=-2×1=-2.∴S 6=6a 1+6×52d =6×1+15×(-2)=-24.故选A.2.4 【解析】本题考查等差数列与等比数列的通项公式及前n 项和. {a n +b n }的前n 项和S n =n 2-n +2n -1(n ∈N *).设数列{a n }的首项为a 1,则其通项公式a n =a 1+(n -1)d ,前n 项和为n [a 1+a 1+(n -1)d ]2=d 2n 2+(a 1-d2)n .设数列{b n }的首项为b 1,当公比q =1时,其前n 项和为nb 1,所以{a n +b n }的前n 项和S n =d 2n 2+(a 1-d2)n +nb 1,显然式子中没有出现2n ,所以q ≠1,则{b n }的前n 项和为b 1(q n -1)q -1=b 1q n q -1-b 1q -1,所以S n =d 2n 2+(a 1-d 2)n +b 1q n q -1-b 1q -1=n 2-n +2n -1(n ∈N *),可得⎩⎪⎨⎪⎧d2=1,a 1-d 2=-1,q =2,b 1q -1=1,解得⎩⎪⎨⎪⎧d =2,a 1=0,q =2,b 1=1,所以d +q =4.3.1 【解析】∵{a n }是等差数列,a 1=-1,a 4=8, ∴公差d =3,∴a 2=a 1+d =2. ∵{b n }为等比数列,b 1=-1,b 4=8, ∴公比q =-2,∴b 2=b 1q =2.故a 2b 2=1.4.本题考查等差数列的证明、前n 项和的最值问题.(1)【证明】由2S nn +n =2a n +1,得2S n =2na n -n(n -1),所以当n ≥2时,2S n -1=2(n -1)a n -1-(n -1)(n -2).两式相减,得2a n =2na n -2(n -1)a n -1-2(n -1),即2(n -1)a n -2(n -1)a n -1=2(n -1),所以a n -a n -1=1(n ≥2,n ∈N *). 所以{a n }是等差数列,公差d =1.(2)【解】若a 4,a 7,a 9成等比数列,则a 72=a 4a 9,则(a 1+6)2=(a 1+3)(a 1+8),解得a 1=-12.所以a n =n -13.当1≤n ≤12时,a n <0;当n =13时,a n =0;当n ≥14时,a n >0. 所以当n =12或n =13时,S n 取最小值,最小值为S 12=S 13=-78.5.(1)【证明】由题设得4(a n +1+b n +1)=2(a n +b n ),即a n +1+b n +1=12(a n +b n ).又因为a 1+b 1=1,所以{a n +b n }是首项为1,公比为12的等比数列.由题设得4(a n +1-b n +1)=4(a n -b n )+8, 即a n +1-b n +1=a n -b n +2.又因为a 1-b 1=1,所以{a n -b n }是首项为1,公差为2的等差数列. (2)【解】由(1)知,a n +b n =12n-1,a n -b n =2n -1.所以a n =12[(a n +b n )+(a n -b n )]=12n +n -12,b n =12[(a n +b n )-(a n -b n )]=12n -n +12.6.【解】(1)设{a n }的公比为q ,由题设得 2q 2=4q +16,即q 2-2q -8=0. 解得q =-2(舍去)或q =4.因此{a n }的通项公式为a n =2×4n -1=22n -1.(2)由(1)得b n =(2n -1)log 22=2n -1,因此数列{b n }的前n 项和为1+3+…+2n -1=n 2.7.(1)【解】设数列{a n }的公差为d ,由题意得 a 1+2d =4,a 1+3d =3a 1+3d ,解得a 1=0,d =2. 从而a n =2n -2,n ∈N *. 所以S n =n 2-n ,n ∈N *.由S n +b n ,S n +1+b n ,S n +2+b n 成等比数列得 (S n +1+b n )2=(S n +b n )(S n +2+b n ). 解得b n =1d (S n +12-S n S n +2).所以b n =n 2+n ,n ∈N *. (2)【证明】c n =a n2b n=2n -22n (n +1)=n -1n (n +1),n ∈N *.我们用数学归纳法证明.①当n =1时,c 1=0<2,不等式成立;②假设n =k (k ∈N *)时不等式成立,即c 1+c 2+…+c k <2 k . 那么,当n =k +1时,c 1+c 2+…+c k +c k +1<2 k +k(k +1)(k +2)<2 k +1k +1<2 k +2k +1+k=2 k +2(k +1-k )=2k +1,即当n =k +1时不等式也成立.根据①和②,不等式c 1+c 2+…+c n <2 n 对任意n ∈N *成立.8.【解】(1)设{a n }的公比为q ,由题设可得⎩⎪⎨⎪⎧a 1(1+q )=2,a 1(1+q +q 2)=-6.解得q =-2,a 1=-2. 故{a n }的通项公式为a n =(-2)n . (2)由(1)可得S n =a 1(1-q n )1-q=-23+(-1)n 2n +13.由于S n +2+S n +1=-43+(-1)n 2n +3-2n +23=2[-23+(-1)n2n +13]=2S n ,故S n +1,S n ,S n +2成等差数列.9.本题考查等差数列与等比数列的通项公式.(1)【证明】设等差数列{a n }的公差为d ,等比数列{b n }的公比为q ,则由a 2-b 2=a 3-b 3,得a 3-a 2=b 3-b 2,即d =b 1q 2-b 1q =2b 1①.又由a 2-b 2=b 4-a 4,得a 4+a 2=b 4+b 2,即2a 1+4d =b 1q 3+b 1q =10b 1 ②. 将①代入②,得2a 1+8b 1=10b 1,即a 1=b 1.(2)【解】由(1)可得a m =a 1+(m -1)d =b 1+(m -1)·2b 1=2mb 1-b 1. 又b k =b 1q k -1=b 1·2k -1,则由b k =a m +a 1,得b 1·2k -1=2mb 1-b 1+a 1=2mb 1-b 1+b 1=2mb 1,即2k -1=2m ,所以2k -2=m.由1≤2k -2≤500,得0≤k -2<9,即2≤k<11. 因为k ∈N *,所以k =2,3,4,5,6,7,8,9,10, 所以集合中共有9个元素.第3节 数列的求和考点1 公式法与分组转化法求和1.B 【解析】本题考查等比数列的通项公式与前n 项和公式.设等比数列{a n }的公比为q ,则由⎩⎪⎨⎪⎧a 5-a 3=a 1q 4-a 1q 2=12,a 6-a 4=a 1q 5-a 1q 3=24,解得⎩⎪⎨⎪⎧a 1=1,q =2.所以S n =a 1(1-q n )1-q =2n-1,a n =a 1q n -1=2n -1,所以S n a n =2n -12n -1=2-21-n ,故选B.2.3n 2-2n 【解析】本题考查等差数列求和.数列{2n -1}表示首项为1,公差为2的等差数列,各项均为正奇数,而数列{3n -2}表示首项为1,公差为3的等差数列,各项分别为交替出现的正奇数与正偶数,它们的公共项为数列{3n -2}中的奇数项,所以{a n }是首项为1,公差为6的等差数列,其前n 项和S n =n ×1+n (n -1)2×6=3n 2-2n .3.25 【解析】本题考查等差数列的通项公式与前n 项和公式.设等差数列{a n }的公差为d ,则a 2+a 6=a 1+d +a 1+5d =-4+6d =2,解得d =1,所以S 10=10×(-2)+10×92×1=25.4.【解】本题考查等比数列的通项公式及前n 项和公式. (1)设{a n }的公比为q.由题设得a 1q +a 1q 3=20,a 1q 2=8. 解得q =12(舍去),q =2,则a 1=2.所以{a n }的通项公式为a n =2n .(2)由(1)可知(-1)n -1a n a n +1=(-1)n -1·2n ·2n +1=(-1)n -122n +1, 则a 1a 2-a 2a 3+…+(-1)n -1a n a n +1 =23-25+27-29+…+(-1)n -1·22n +1=23[1-(-22)n ]1-(-22)=85-(-1)n ·22n +35.考点2 裂项相消法求和1.2nn +1 【解析】设等差数列{a n }的首项为a 1,公差为d ,则由题意得⎩⎪⎨⎪⎧a 3=a 1+2d =3,S 4=4a 1+6d =10,解得⎩⎪⎨⎪⎧a 1=1,d =1, ∴a n =1+(n -1)=n ,S n =(1+n )·n 2,∴1S k =2k (k +1)=2⎝⎛⎭⎫1k -1k +1,∴∑k =1n 1S k =2[(1-12)+(12-13)+…+(1n -1n +1)]=2(1-1n +1)=2nn +1.2.本题考查等比数列、等差数列的通项公式,利用累加法、累乘法求通项公式以及裂项相消法求和.(1)【解】由b 1+b 2=6b 3得1+q =6q 2,解得q =12.由c n +1=4c n 得c n =4n -1. 由a n +1-a n =4n -1得a n =a 1+1+4+…+4n -2=4n -1+23.(2)【证明】由c n +1=b n b n +2c n 得c n =b 1b 2c 1b n b n +1=1+d d ⎝⎛⎭⎫1b n -1b n +1, 所以c 1+c 2+c 3+…+c n =1+d d ⎝⎛⎭⎫1-1b n +1, 由b 1=1,d>0得b n +1>0,因此c 1+c 2+c 3+…+c n <1+1d,n ∈N *.3.【解】(1)因为a 1+3a 2+…+(2n -1)a n =2n ,。
数列(解答题)(原卷版)-五年(2018-2022)高考数学真题分项汇编(全国通用)
专题13数列(解答题)1.【2022年全国甲卷】记为数列的前n 项和.已知2+=2+1.(1)证明:是等差数列;(2)若4,7,9成等比数列,求的最小值.2.【2022年新高考1卷】记为数列的前n 项和,已知1=是公差为13的等差数列.(1)求的通项公式;(2)证明:11+12+⋯+1<2.3.【2022年新高考2卷】已知为等差数列,是公比为2的等比数列,且2−2=3−3=4−4.(1)证明:1=1;(2)求集合=+1,1≤≤500中元素个数.4.【2021年甲卷文科】记nS 为数列{}n a 的前n 项和,已知210,3n a a a >=,且数列是等差数列,证明:{}n a 是等差数列.5.【2021年甲卷理科】已知数列{}n a 的各项均为正数,记n S 为{}n a 的前n 项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{}n a 是等差数列:②数列是等差数列;③213a a =.注:若选择不同的组合分别解答,则按第一个解答计分.6.【2021年乙卷文科】设{}n a 是首项为1的等比数列,数列{}n b 满足3n n na b =.已知1a ,23a ,39a 成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2n n S T <.7.【2021年乙卷理科】记n S 为数列{}n a 的前n 项和,n b 为数列{}n S 的前n 项积,已知212n nS b +=.(1)证明:数列{}n b 是等差数列;(2)求{}n a 的通项公式.8.【2021年新高考1卷】已知数列{}n a 满足11a =,11,,2,.n n n a n a a n ++⎧=⎨+⎩为奇数为偶数(1)记2n n b a =,写出1b ,2b ,并求数列{}n b 的通项公式;(2)求{}n a 的前20项和.9.【2021年新高考2卷】记n S 是公差不为0的等差数列{}n a 的前n 项和,若35244,a S a a S ==.(1)求数列{}n a 的通项公式n a ;(2)求使n n S a >成立的n 的最小值.10.【2020年新课标1卷理科】设{}n a 是公比不为1的等比数列,1a 为2a ,3a 的等差中项.(1)求{}n a 的公比;(2)若11a =,求数列{}n na 的前n 项和.11.【2020年新课标3卷理科】设数列{an }满足a 1=3,134n n a a n +=-.(1)计算a 2,a 3,猜想{an }的通项公式并加以证明;(2)求数列{2nan }的前n 项和Sn .12.【2020年新课标3卷文科】设等比数列{an }满足124a a +=,318a a -=.(1)求{an }的通项公式;(2)记n S 为数列{log 3an }的前n 项和.若13m m m S S S +++=,求m .13.【2020年新高考1卷(山东卷)】已知公比大于1的等比数列{}n a 满足24320,8a a a +==.(1)求{}n a 的通项公式;(2)记m b 为{}n a 在区间*(0,]()m m ∈N 中的项的个数,求数列{}m b 的前100项和100S .14.【2020年新高考2卷(海南卷)】已知公比大于1的等比数列{}n a 满足24320,8a a a +==.(1)求{}n a 的通项公式;(2)求112231(1)n n n a a a a a a -+-+⋯+-.15.【2019年新课标1卷文科】记Sn 为等差数列{an }的前n 项和,已知S 9=-a 5.(1)若a 3=4,求{an }的通项公式;(2)若a 1>0,求使得Sn ≥an 的n 的取值范围.16.【2019年新课标2卷理科】已知数列{an }和{bn }满足a 1=1,b 1=0,1434n n n a a b +-=+,1434n n n b b a +-=-.(1)证明:{an +bn }是等比数列,{an –bn }是等差数列;(2)求{an }和{bn }的通项公式.17.【2019年新课标2卷文科】已知{}n a 是各项均为正数的等比数列,1322,216a a a ==+.(1)求{}n a 的通项公式;(2)设2log n n b a =,求数列{}n b 的前n 项和.18.【2018年新课标1卷文科】已知数列{}n a 满足11a =,()121n n na n a +=+,设n n a b n=.(1)求123b b b ,,;(2)判断数列{}n b 是否为等比数列,并说明理由;(3)求{}n a 的通项公式.19.【2018年新课标2卷理科】记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-.(1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.20.【2018年新课标3卷理科】等比数列{}n a 中,15314a a a ==,.(1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .。
数列(解答题)(解析版)-五年(2018-2022)高考数学真题分项汇编(全国通用)
专题13数列(解答题)1.【2022年全国甲卷】记为数列的前n项和.已知2+=2+1.(1)证明:是等差数列;(2)若4,7,9成等比数列,求的最小值.【答案】(1)证明见解析;(2)−78.【解析】【分析】(1)依题意可得2+2=2B+,根据=1,=1−K1,≥2,作差即可得到−K1=1,从而得证;(2)由(1)及等比中项的性质求出1,即可得到的通项公式与前项和,再根据二次函数的性质计算可得.(1)解:因为2+=2+1,即2+2=2B+①,当≥2时,2K1+−12=2−1K1+−1②,①−②得,2+2−2K1−−12=2B+−2−1K1−−1,即2+2−1=2B−2−1K1+1,即2−1−2−1K1=2−1,所以−K1=1,≥2且∈N*,所以是以1为公差的等差数列.(2)解:由(1)可得4=1+3,7=1+6,9=1+8,又4,7,9成等比数列,所以72=4⋅9,即1+62=1+3⋅1+8=−12,所以=−13,所以=−12+=122−252=−−6258,所以,当=12或=13时min=−78.2.【2022年新高考1卷】记为数列的前n项和,已知1=是公差为13的等差数列.(1)求的通项公式;(2)证明:11+121<2.【答案】(1)=(2)见解析【解析】【分析】(1)利用等差数列的通项公式求得=1r23,得到=的关系得到当≥2时,=−K1=−进而得:r1K1,利用累乘法求得==1也成立,得到的通项公式=(2)由(1)的结论,利用裂项求和法得到11+12+⋯+1=21−.(1)∵,∴1=1=1,∴11=1,是公差为13的等差数列,∴=1+−1=r23,∴=∴当≥2时,∴=−K1=3−整理得:−1=+1K1,即K1=r1K1,∴=1×21×32×…×K1K2=1×32×43×…×K2×r1K1=显然对于=1也成立,∴的通项公式=(2)1==2,∴11+12+⋯+1=21++⋯=21−<23.【2022年新高考2卷】已知为等差数列,是公比为2的等比数列,且2−2=3−3=4−4.(1)证明:1=1;(2)求集合=+1,1≤≤500中元素个数.【答案】(1)证明见解析;(2)9.【解析】【分析】(1)设数列的公差为,根据题意列出方程组即可证出;(2)根据题意化简可得=2K2,即可解出.(1)设数列的公差为,所以,1+−21=1+2−411+−21=81−1+3,即可解得,1=1=2,所以原命题得证.(2)由(1)知,1=1=2,所以=+1⇔1×2K1=1+−1+1,即2K1=2,亦即=2K2∈1,500,解得2≤≤10,所以满足等式的解=2,3,4,⋯,10,故集合U =+1,1≤≤500中的元素个数为10−2+1=9.4.【2021年甲卷文科】记n S 为数列{}n a 的前n 项和,已知210,3n a a a >=,且数列是等差数列,证明:{}n a 是等差数列.【答案】证明见解析.【解析】【分析】的公差d ,进一步写出的通项,从而求出{}na 的通项公式,最终得证.【详解】∵数列是等差数列,设公差为d(n +-=()n *∈N∴12n S a n =,()n *∈N ∴当2n ≥时,()221111112n n n a S S a n a n a n a -=-=--=-当1n =时,11121=a a a ⨯-,满足112n a a n a =-,∴{}n a 的通项公式为112n a a n a =-,()n *∈N ∴()()111111221=2n n a a a n a a n a a --=----⎡⎤⎣⎦∴{}n a 是等差数列.【点睛】在利用1n n n a S S -=-求通项公式时一定要讨论1n =的特殊情况.5.【2021年甲卷理科】已知数列{}n a 的各项均为正数,记n S 为{}n a 的前n 项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{}n a 是等差数列:②数列是等差数列;③213aa =.注:若选择不同的组合分别解答,则按第一个解答计分.【答案】证明过程见解析【解析】【分析】,n n a S 的关系求出n a ,利用{}n a 是等差数列可证213a a =;也可分别设出公差,写出各自的通项公式后利用两者的关系,对照系数,得到等量关系,进行证明.an b =+,结合,n n a S 的关系求出n a ,根据213a a =可求b ,然后可证{}n a 是等差数列;也可利用前两项的差求出公差,然后求出通项公式,进而证明出结论.【详解】选①②作条件证明③:[方法一]:待定系数法+n a 与n S 关系式(0)an b a =+>,则()2n S an b =+,当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b-=-=+--+()22a an a b =-+;因为{}n a 也是等差数列,所以()()222a b a a a b +=-+,解得0b =;所以()221n a a n =-,21a a =,故22133a a a ==.[方法二]:待定系数法设等差数列{}n a 的公差为d,等差数列的公差为1d ,1(1)n d =+-,将1(1)2n n n S na d -=+1(1)n d -,化简得())2222211111222d d n a n d n d n d ⎛⎫+-=+-+ ⎪⎝⎭对于n +∀∈N 恒成立.则有21211112,240,d d a d d d ⎧=⎪⎪-=-⎨-=,解得112d d a ==.所以213a a =.选①③作条件证明②:因为213a a =,{}n a 是等差数列,所以公差2112d a a a =-=,所以()21112n n n S na d n a -=+=,)1n +所以是等差数列.选②③作条件证明①:[方法一]:定义法(0)an b a =+>,则()2n S an b =+,当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b-=-=+--+()22a an a b =-+;因为213a a =,所以()()2323a a b a b +=+,解得0b =或43a b =-;当0b =时,()221,21n a a a a n ==-,当2n ≥时,2-1-2n n a a a =满足等差数列的定义,此时{}n a 为等差数列;当43a b =-4=3an b an a =+-03a=-<不合题意,舍去.综上可知{}n a 为等差数列.[方法二]【最优解】:求解通项公式因为213a a ===也为等差数列,所以公差1d ==()11n d =-=,故21n S n a =,当2n ≥时,()()221111121n n n a S S n a n a n a -=-=--=-,当1n =时,满足上式,故{}n a 的通项公式为()121n a n a =-,所以()1123n a n a -=-,112n n a a a --=,符合题意.【整体点评】这类题型在解答题中较为罕见,求解的关键是牢牢抓住已知条件,结合相关公式,逐步推演,选①②时,法一:利用等差数列的通项公式是关于n的一次函数,直接设出(0)an b a =+>,平方后得到n S 的关系式,利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩得到{}n a 的通项公式,进而得到213a a =,是选择①②证明③的通式通法;法二:分别设出{}n a 与{}n S 的公差,写出各自的通项公式后利用两者的关系,对照系数,得到等量关系1d =12d a =,进而得到213a a =;选①③时,按照正常的思维求出公差,表示出n S进行证明;选②③时,法一:利用等差数列的通项公式是关于n的一次函数,直接设出(0)an b a =+>,结合,n n a S 的关系求出n a ,根据213a a =可求b ,然后可证{}n a 是等差数1d ==的通项公式,利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩,求出{}n a 的通项公式,进而证明出结论.6.【2021年乙卷文科】设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a 成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <.【答案】(1)11(3n n a -=,3n nn b =;(2)证明见解析.【解析】【分析】(1)利用等差数列的性质及1a 得到29610q q -+=,解方程即可;(2)利用公式法、错位相减法分别求出,n n S T ,再作差比较即可.【详解】(1)因为{}n a 是首项为1的等比数列且1a ,23a ,39a 成等差数列,所以21369a a a =+,所以211169a q a a q =+,即29610q q -+=,解得13q =,所以11()3n n a -=,所以33n n n na nb ==.(2)[方法一]:作差后利用错位相减法求和211213333n n n n nT --=++++ ,012111111223333-⎛⎫=++++ ⎪⎝⎭n n S ,230121123111112333323333n n n n S n T -⎛⎫⎛⎫-=++++-++++=⎪ ⎪⎝⎭⎝⎭ 012111012222333---++++ 111233---+n n n n .设0121111101212222Γ3333------=++++ n n n ,⑧则1231111012112222Γ33333-----=++++ n n n .⑨由⑧-⑨得1121113312111113322Γ132********--⎛⎫--- ⎪⎛⎫⎝⎭=-++++-=-+- ⎪⎝⎭- n n n n nn n .所以211312Γ432323----=--=-⨯⨯⨯n n n n n n .因此10232323--=-=-<⨯⨯n n n n nS n n nT .故2nn S T <.[方法二]【最优解】:公式法和错位相减求和法证明:由(1)可得11(1313(1)12313n n n S ⨯-==--,211213333n n n n nT --=++++ ,①231112133333n n n n nT +-=++++ ,②①-②得23121111333333n n n n T +=++++- 1111(1)1133(1)1323313n n n n n n ++-=-=---,所以31(14323n n nn T =--⋅,所以2n n S T -=3131(1)(1043234323n n n n n n ----=-<⋅⋅,所以2nn S T <.[方法三]:构造裂项法由(Ⅰ)知13⎛⎫= ⎪⎝⎭n n b n ,令1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,且1+=-n n n b c c ,即1111()[(1)]333αβαβ+⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭n n n n n n ,通过等式左右两边系数比对易得33,24αβ==,所以331243nn c n ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭.则12113314423nn n n n T b b b c c +⎛⎫⎛⎫=+++=-=-+ ⎪⎪⎝⎭⎝⎭,下同方法二.[方法四]:导函数法设()231()1-=++++=- n nx x f x x x x x x,由于()()()()()()1221'111'11(1)'1(1)1n n n n nx x x x x x x x nx n x x x x +⎡⎤⎡⎤⎡⎤----⨯--+-+⎣⎦⎣⎦⎢==---⎢⎥⎣⎦,则12121(1)()123(1)+-+-+=++++='- n nn nx n x f x x x nxx .又1111333-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭n n n b n n ,所以2112311111233333n n n T b b b b n -⎡⎤⎛⎫⎛⎫=++++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎝⎭⎝⎭⎢⎥⎣⎦12111(1)11133333113n nn n f +⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭⋅=⨯ ⎪⎝⎭⎛⎫- ⎪⎝⎭'13113311(1)4334423n nnn n n +⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-+=-+⎢⎥ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,下同方法二.【整体点评】本题主要考查数列的求和,涉及到等差数列的性质,错位相减法求数列的和,考查学生的数学运算能力,是一道中档题,其中证明不等式时采用作差法,或者作商法要根据式子得结构类型灵活选择,关键是要看如何消项化简的更为简洁.(2)的方法一直接作差后利用错位相减法求其部分和,进而证得结论;方法二根据数列的不同特点,分别利用公式法和错位相减法求得,n n S T ,然后证得结论,为最优解;方法三采用构造数列裂项求和的方法,关键是构造1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,使1+=-n n n b c c ,求得n T 的表达式,这是错位相减法的一种替代方法,方法四利用导数方法求和,也是代替错位相减求和法的一种方法.7.【2021年乙卷理科】记n S 为数列{}n a 的前n 项和,n b 为数列{}n S 的前n 项积,已知212n nS b +=.(1)证明:数列{}n b 是等差数列;(2)求{}n a 的通项公式.【答案】(1)证明见解析;(2)()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【解析】【分析】(1)由已知212n n S b +=得221n n n b S b =-,且0n b ≠,取1n =,得132b =,由题意得1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---,消积得到项的递推关系111221n n n n b bb b +++=-,进而证明数列{}n b 是等差数列;(2)由(1)可得n b 的表达式,由此得到n S 的表达式,然后利用和与项的关系求得()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【详解】(1)[方法一]:由已知212n n S b +=得221n n n b S b =-,且0n b ≠,12n b ≠,取1n =,由11S b =得132b =,由于n b 为数列{}n S 的前n 项积,所以1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---,所以1121121222212121n n n b b b b b b b +++⋅⋅⋅⋅=---,所以111221n n n nb bb b +++=-,由于10n b +≠所以12121n n b b +=-,即112n n b b +-=,其中*n N ∈所以数列{}n b 是以132b =为首项,以12d =为公差等差数列;[方法二]【最优解】:由已知条件知1231-⋅=⋅⋅⋅⋅ n n n b S S S S S ①于是11231(2)--=⋅⋅⋅⋅≥ n n b S S S S n .②由①②得1nn n b S b -=.③又212n nS b +=,④由③④得112n n b b --=.令1n =,由11S b =,得132b =.所以数列{}n b 是以32为首项,12为公差的等差数列.[方法三]:由212n n S b +=,得22=-nn n S b S ,且0n S ≠,0n b ≠,1n S ≠.又因为111--=⋅⋅=⋅ n n n n n b S S S S b ,所以1122-==-n n n n b b S S ,所以()1111(2)2222212---=-==≥---n n n n n n n S S b b n S S S .在212n n S b +=中,当1n =时,1132==b S .故数列{}n b 是以32为首项,12为公差的等差数列.[方法四]:数学归纳法由已知212n n S b +=,得221n n n b S b =-,132b =,22b =,352=b ,猜想数列{}n b 是以32为首项,12为公差的等差数列,且112n b n =+.下面用数学归纳法证明.当1n =时显然成立.假设当n k =时成立,即121,21+=+=+k k k b k S k .那么当1n k =+时,11112++⎛⎫==+ ⎪⎝⎭k k k b b S k 331(1)1222k k k k ++⋅==+++.综上,猜想对任意的n ∈N 都成立.即数列{}n b 是以32为首项,12为公差的等差数列.(2)由(1)可得,数列{}n b 是以132b =为首项,以12d =为公差的等差数列,()3111222n nb n ∴=+-⨯=+,22211n n n b nS b n+==-+,当n =1时,1132a S ==,当n ≥2时,()121111n n n n n a S S n n n n -++=-=-=-++,显然对于n =1不成立,∴()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【整体点评】(1)方法一从212n n S b +=得221n n n b S b =-,然后利用n b 的定义,得到数列{}n b 的递推关系,进而替换相除消项得到相邻两项的关系,从而证得结论;方法二先从n b 的定义,替换相除得到1nn n b S b -=,再结合212n n S b +=得到112n n b b --=,从而证得结论,为最优解;方法三由212n n S b +=,得22=-n n n S b S ,由n b 的定义得1122-==-n n n n b b S S ,进而作差证得结论;方法四利用归纳猜想得到数列112n b n =+,然后利用数学归纳法证得结论.(2)由(1)的结论得到112n b n =+,求得n S 的表达式,然后利用和与项的关系求得{}n a 的通项公式;8.【2021年新高考1卷】已知数列{}n a 满足11a =,11,,2,.n n n a n a a n ++⎧=⎨+⎩为奇数为偶数(1)记2n n b a =,写出1b ,2b ,并求数列{}n b 的通项公式;(2)求{}n a 的前20项和.【答案】(1)122,5,31n b b b n ===-;(2)300.【解析】【分析】(1)方法一:由题意结合递推关系式确定数列{}n b 的特征,然后求和其通项公式即可;(2)方法二:分组求和,结合等差数列前n 项和公式即可求得数列的前20项和.【详解】解:(1)[方法一]【最优解】:显然2n 为偶数,则21222212,1n n n n a a a a +++=+=+,所以2223n n a a +=+,即13n n b b +=+,且121+12b a a ===,所以{}n b 是以2为首项,3为公差的等差数列,于是122,5,31n b b b n ===-.[方法二]:奇偶分类讨论由题意知1231,2,4a a a ===,所以122432,15b a b a a ====+=.由11n n a a +-=(n 为奇数)及12n n a a +-=(n 为偶数)可知,数列从第一项起,若n 为奇数,则其后一项减去该项的差为1,若n 为偶数,则其后一项减去该项的差为2.所以*23()n n a a n N +-=∈,则()11331n b b n n =+-⨯=-.[方法三]:累加法由题意知数列{}n a 满足*113(1)1,()22nn n a a a n +-==++∈N .所以11213(1)11222b a a -==++=+=,322433223(1)3(1)11212352222b a a a a a --==++=+=+++=++=+=,则222121222111()()()121221+n n n n n n b a a a a a a a a a ---==-+-+-+=+++++++ 12(1)131n n n =+-+=-⨯.所以122,5b b ==,数列{}n b 的通项公式31n b n =-.(2)[方法一]:奇偶分类讨论20123201351924620++++++++()()S a a a a a a a a a a a a =+=+++ 1231012310(1111)b b b b b b b b =-+-+-++-+++++ 110()102103002b b +⨯=⨯-=.[方法二]:分组求和由题意知数列{}n a 满足12212121,1,2n n n n a a a a a -+==+=+,所以2122123n n n a a a +-=+=+.所以数列{}n a 的奇数项是以1为首项,3为公差的等差数列;同理,由2221213n n n a a a ++=+=+知数列{}n a 的偶数项是以2为首项,3为公差的等差数列.从而数列{}n a 的前20项和为:201351924260()()S a a a a a a a a =+++++++++ 1091091013102330022⨯⨯=⨯+⨯+⨯+⨯=.【整体点评】(1)方法一:由题意讨论{}n b 的性质为最一般的思路和最优的解法;方法二:利用递推关系式分类讨论奇偶两种情况,然后利用递推关系式确定数列的性质;方法三:写出数列{}n a 的通项公式,然后累加求数列{}n b 的通项公式,是一种更加灵活的思路.(2)方法一:由通项公式分奇偶的情况求解前n 项和是一种常规的方法;方法二:分组求和是常见的数列求和的一种方法,结合等差数列前n 项和公式和分组的方法进行求和是一种不错的选择.9.【2021年新高考2卷】记n S 是公差不为0的等差数列{}n a 的前n 项和,若35244,a S a a S ==.(1)求数列{}n a 的通项公式n a ;(2)求使n n S a >成立的n 的最小值.【答案】(1)26n a n =-;(2)7.【解析】【分析】(1)由题意首先求得3a 的值,然后结合题意求得数列的公差即可确定数列的通项公式;(2)首先求得前n 项和的表达式,然后求解二次不等式即可确定n 的最小值.【详解】(1)由等差数列的性质可得:535S a =,则:3335,0a a a =∴=,设等差数列的公差为d ,从而有:()()22433a a a d a d d =-+=-,()()()41234333322S a a a a a d a d a a d d =+++=-+-++-=-,从而:22d d -=-,由于公差不为零,故:2d =,数列的通项公式为:()3326n a a n d n =+-=-.(2)由数列的通项公式可得:1264a =-=-,则:()()214252n n n S n n n -=⨯-+⨯=-,则不等式n n S a >即:2526n n n ->-,整理可得:()()160n n -->,解得:1n <或6n >,又n 为正整数,故n 的最小值为7.【点睛】等差数列基本量的求解是等差数列中的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用.10.【2020年新课标1卷理科】设{}n a 是公比不为1的等比数列,1a 为2a ,3a 的等差中项.(1)求{}n a 的公比;(2)若11a =,求数列{}n na 的前n 项和.【答案】(1)2-;(2)1(13)(2)9n n n S -+-=.【解析】【分析】(1)由已知结合等差中项关系,建立公比q 的方程,求解即可得出结论;(2)由(1)结合条件得出{}n a 的通项,根据{}n na 的通项公式特征,用错位相减法,即可求出结论.【详解】(1)设{}n a 的公比为q ,1a 为23,a a 的等差中项,212312,0,20a a a a q q =+≠∴+-= ,1,2q q ≠∴=- ;(2)设{}n na 的前n 项和为n S ,111,(2)n n a a -==-,21112(2)3(2)(2)n n S n -=⨯+⨯-+⨯-++- ,①23121(2)2(2)3(2)(1)(2)(2)n n n S n n --=⨯-+⨯-+⨯-+--+- ,②①-②得,2131(2)(2)(2)(2)n nn S n -=+-+-++---1(2)1(13)(2)(2)1(2)3n n n n n ---+-=--=--,1(13)(2)9nn n S -+-∴=.【点睛】本题考查等比数列通项公式基本量的计算、等差中项的性质,以及错位相减法求和,考查计算求解能力,属于基础题.11.【2020年新课标3卷理科】设数列{an }满足a 1=3,134n n a a n +=-.(1)计算a 2,a 3,猜想{an }的通项公式并加以证明;(2)求数列{2nan }的前n 项和Sn .【答案】(1)25a =,37a =,21n a n =+,证明见解析;(2)1(21)22n n S n +=-⋅+.【解析】【分析】(1)方法一:(通性通法)利用递推公式得出23,a a ,猜想得出{}n a 的通项公式,利用数学归纳法证明即可;(2)方法一:(通性通法)根据通项公式的特征,由错位相减法求解即可.【详解】(1)[方法一]【最优解】:通性通法由题意可得2134945a a =-=-=,32381587a a =-=-=,由数列{}n a 的前三项可猜想数列{}n a 是以3为首项,2为公差的等差数列,即21n a n =+.证明如下:当1n =时,13a =成立;假设()n k k *=∈N 时,21k a k =+成立.那么1n k =+时,1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立.则对任意的*n N ∈,都有21n a n =+成立;[方法二]:构造法由题意可得2134945a a =-=-=,32381587a a =-=-=.由123,5a a ==得212a a -=.134n n a a n +=-,则134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--.令1n n n b a a +=-,且12b =,所以134n n b b -=-,两边同时减去2,得()1232n n b b --=-,且120b -=,所以20n b -=,即12n n a a +-=,又212a a -=,因此{}n a 是首项为3,公差为2的等差数列,所以21n a n =+.[方法三]:累加法由题意可得2134945a a =-=-=,32381587a a =-=-=.由134n n a a n +=-得1114333n n n n n a a n +++-=-,即2121214333a a -=-⨯,3232318333a a -=-⨯, (111)4(1)(2)333n n n n n a a n n ---=--⨯≥.以上各式等号两边相加得1123111412(1)33333n nn a a n ⎡⎤-=-⨯+⨯+-⨯⎢⎥⎣⎦ ,所以1(21)33n n n a n =+⋅.所以21(2)n a n n =+≥.当1n =时也符合上式.综上所述,21n a n =+.[方法四]:构造法21322345,387a a a a =-==-=,猜想21n a n =+.由于134n n a a n +=-,所以可设()1(1)3n n a n a n λμλμ++++=++,其中,λμ为常数.整理得1322n n a a n λμλ+=++-.故24,20λμλ=--=,解得2,1λμ=-=-.所以()112(1)13(21)3211n n n a n a n a +-+-=--=⋅⋅⋅=-⨯-.又130a -=,所以{}21n a n --是各项均为0的常数列,故210n a n --=,即21n a n =+.(2)由(1)可知,2(21)2n n n a n ⋅=+⋅[方法一]:错位相减法231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅ ,①23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅ ,②由①-②得:()23162222(21)2n n n S n +-=+⨯+++-+⋅ ()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-,即1(21)22n n S n +=-⋅+.[方法二]【最优解】:裂项相消法112(21)2(21)2(23)2n n n n n n n a n n n b b ++=+=---=-,所以231232222n n n S a a a a =++++ ()()()()2132431n n b b b b b b b b +=-+-+-++- 11n b b +=-1(21)22n n +=-+.[方法三]:构造法当2n ≥时,1(21)2n n n S S n -=++⋅,设11()2[(1)]2n n n n S pn q S p n q --++⋅=+-+⋅,即122n n n pn q p S S ----=+⋅,则2,21,2pq p -⎧=⎪⎪⎨--⎪=⎪⎩,解得4,2p q =-=.所以11(42)2[4(1)2]2n n n n S n S n --+-+⋅=+--+⋅,即{}(42)2n n S n +-+⋅为常数列,而1(42)22S +-+⋅=,所以(42)22n n S n +-+⋅=.故12(21)2n n S n +=+-⋅.[方法四]:因为12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,令12n n b n -=⋅,则()()231()0,11n nx x f x x x x x x x-=++++=≠- ,()121211(1)()1231(1)nn n n x x nx n x f x x x nx x x +-'⎡⎤-+-+=++++==⎢⎥--⎢⎥⎣⎦' ,所以12n b b b +++L 21122322n n -=+⋅+⋅++⋅ 1(2)12(1)2n n f n n +==+-+'⋅.故234(2)2222nn S f =++'+++ ()1212412(1)212n n nn n +-⎡⎤=+⋅-++⎣⎦-1(21)22n n +=-+.【整体点评】(1)方法一:通过递推式求出数列{}n a 的部分项从而归纳得出数列{}n a 的通项公式,再根据数学归纳法进行证明,是该类问题的通性通法,对于此题也是最优解;方法二:根据递推式134n n a a n +=-,代换得134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--,设1n n n b a a +=-,从而简化递推式,再根据构造法即可求出n b ,从而得出数列{}n a 的通项公式;方法三:由134n n a a n +=-化简得1114333n n n n n a a n+++-=-,根据累加法即可求出数列{}n a 的通项公式;方法四:通过递推式求出数列{}n a 的部分项,归纳得出数列{}n a 的通项公式,再根据待定系数法将递推式变形成()1(1)3n n a n a n λμλμ++++=++,求出,λμ,从而可得构造数列为常数列,即得数列{}n a 的通项公式.(2)方法一:根据通项公式的特征可知,可利用错位相减法解出,该法也是此类题型的通性通法;方法二:根据通项公式裂项,由裂项相消法求出,过程简单,是本题的最优解法;方法三:由2n ≥时,1(21)2nn n S S n -=++⋅,构造得到数列{}(42)2n n S n +-+⋅为常数列,从而求出;方法四:将通项公式分解成12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,利用分组求和法分别求出数列{}{}12,2n n n -⋅的前n 项和即可,其中数列{}12n n -⋅的前n 项和借助于函数()()231()0,11n nx x f x x x x x x x-=++++=≠- 的导数,通过赋值的方式求出,思路新颖独特,很好的简化了运算.12.【2020年新课标3卷文科】设等比数列{an }满足124a a +=,318a a -=.(1)求{an }的通项公式;(2)记n S 为数列{log 3an }的前n 项和.若13m m m S S S +++=,求m .【答案】(1)13-=n n a ;(2)6m =.【解析】【分析】(1)设等比数列{}n a 的公比为q ,根据题意,列出方程组,求得首项和公比,进而求得通项公式;(2)由(1)求出3{log }n a 的通项公式,利用等差数列求和公式求得n S ,根据已知列出关于m 的等量关系式,求得结果.【详解】(1)设等比数列{}n a 的公比为q ,根据题意,有1121148a a q a q a +=⎧⎨-=⎩,解得113a q =⎧⎨=⎩,所以13-=n n a ;(2)令313log log 31n n n b a n -===-,所以(01)(1)22n n n n n S +--==,根据13m m m S S S +++=,可得(1)(1)(2)(3)222m m m m m m -++++=,整理得2560m m --=,因为0m >,所以6m =,【点睛】本题考查等比数列通项公式基本量的计算,以及等差数列求和公式的应用,考查计算求解能力,属于基础题目.13.【2020年新高考1卷(山东卷)】已知公比大于1的等比数列{}n a 满足24320,8a a a +==.(1)求{}n a 的通项公式;(2)记m b 为{}n a 在区间*(0,]()m m ∈N 中的项的个数,求数列{}m b 的前100项和100S .【答案】(1)2n n a =;(2)100480S =.【解析】【分析】(1)利用基本元的思想,将已知条件转化为1,a q 的形式,求解出1,a q ,由此求得数列{}n a 的通项公式.(2)方法一:通过分析数列{}m b 的规律,由此求得数列{}m b 的前100项和100S .【详解】(1)由于数列{}n a 是公比大于1的等比数列,设首项为1a ,公比为q ,依题意有31121208a q a q a q ⎧+=⎨=⎩,解得解得12,2a q ==,或1132,2a q ==(舍),所以2n n a =,所以数列{}n a 的通项公式为2n n a =.(2)[方法一]:规律探索由于123456722,24,28,216,232,264,2128=======,所以1b 对应的区间为(0,1],则10b =;23,b b 对应的区间分别为(0,2],(0,3],则231b b ==,即有2个1;4567,,,b b b b 对应的区间分别为(0,4],(0,5],(0,6],(0,7],则45672b b b b ====,即有22个2;8915,,,b b b 对应的区间分别为(0,8],(0,9],,(0,15] ,则89153b b b ==== ,即有32个3;161731,,,b b b 对应的区间分别为(0,16],(0,17],,(0,31] ,则1617314b b b ==== ,即有42个4;323363,,,b b b 对应的区间分别为(0,32],(0,33],,(0,63] ,则3233635b b b ====L ,即有52个5;6465100,,,b b b L 对应的区间分别为(0,64],(0,65],,(0,100] ,则64651006b b b ====L ,即有37个6.所以23451001222324252637480S =⨯+⨯+⨯+⨯+⨯+⨯=.[方法二]【最优解】:由题意,2n m ≤,即2log n m ≤,当1m =时,10b =.当)12,21k k m +⎡∈-⎣时,,m b k k *=∈N ,则()()()()1001234573233636465100S b b b b b b b b b b b b =++++++++++++++ 0122438416532637480=+⨯+⨯+⨯+⨯+⨯+⨯=.[方法三]:由题意知)1,2,2k k m b k m +⎡=∈⎣,因此,当1m =时,10b =;[2,4)m ∈时,1m b =;[4,8)m ∈时,2m b =;[8,16)m ∈时,3m b =;[16,32)m ∈时,4m b =;[32,64)m ∈时,5m b =;[64,128)m ∈时,6m b =.所以1001234100S b b b b b =+++++ 0(11)(222)(666)=++++++++++ 0122438416532637480=+⨯+⨯+⨯+⨯+⨯+⨯=.所以数列{}n b 的前100项和100480S =.【整体点评】(2)方法一:通过数列{}n a 的前几项以及数列{}m b 的规律可以得到12100,,,b b b 的值,从而求出数列{}m b 的前100项和,这是本题的通性通法;方法二:通过解指数不等式可得数列{}m b 的通项公式,从而求出数列{}m b 的前100项和,是本题的最优解;方法三,是方法一的简化版.14.【2020年新高考2卷(海南卷)】已知公比大于1的等比数列{}n a 满足24320,8a a a +==.(1)求{}n a 的通项公式;(2)求112231(1)n n n a a a a a a -+-+⋯+-.【答案】(1)2nn a =;(2)2382(1)55n n +--【解析】【分析】(1)由题意得到关于首项、公比的方程组,求解方程组得到首项、公比的值即可确定数列的通项公式;(2)首先求得数列(){}111n n n a a -+-的通项公式,然后结合等比数列前n 项和公式求解其前n 项和即可.【详解】(1)设等比数列{}n a 的公比为q (q >1),则32411231208a a a q a q a a q ⎧+=+=⎨==⎩,整理可得:22520q q -+=,11,2,2q q a >== ,数列的通项公式为:1222n nn a -=⋅=.(2)由于:()()()1121111122112n n n n n n n n a a --++-+=-⨯⨯=--,故:112231(1)n n n a a a a a a -+-+⋯+-35791212222(1)2n n -+=-+-+⋯+-⋅()()3223221282(1)5512n n n +⎡⎤--⎢⎥⎣⎦==----.【点睛】等比数列基本量的求解是等比数列中的一类基本问题,解决这类问题的关键在于熟练掌握等比数列的有关公式并能灵活运用,等差数列与等比数列求和公式是数列求和的基础.15.【2019年新课标1卷文科】记Sn 为等差数列{an }的前n 项和,已知S 9=-a 5.(1)若a 3=4,求{an }的通项公式;(2)若a 1>0,求使得Sn ≥an 的n 的取值范围.【答案】(1)210n a n =-+;(2)110()n n *≤≤∈N .【解析】【分析】(1)首项设出等差数列的首项和公差,根据题的条件,建立关于1a 和d 的方程组,求得1a 和d 的值,利用等差数列的通项公式求得结果;(2)根据题意有50a =,根据10a >,可知0d <,根据n n S a >,得到关于n 的不等式,从而求得结果.【详解】(1)设等差数列{}n a 的首项为1a ,公差为d ,根据题意有111989(4)224a d a d a d ⨯⎧+=-+⎪⎨⎪+=⎩,解答182a d =⎧⎨=-⎩,所以8(1)(2)210n a n n =+-⨯-=-+,所以等差数列{}n a 的通项公式为210n a n =-+;(2)由条件95S a =-,得559a a =-,即50a =,因为10a >,所以0d <,并且有5140a a d =+=,所以有14a d =-,由n n S a ≥得11(1)(1)2n n na d a n d -+≥+-,整理得2(9)(210)n n d n d -≥-,因为0d <,所以有29210n n n -≤-,即211100n n -+≤,解得110n ≤≤,所以n 的取值范围是:110()n n *≤≤∈N【点睛】该题考查的是有关数列的问题,涉及到的知识点有等差数列的通项公式,等差数列的求和公式,在解题的过程中,需要认真分析题意,熟练掌握基础知识是正确解题的关键.16.【2019年新课标2卷理科】已知数列{an }和{bn }满足a 1=1,b 1=0,1434n n n a a b +-=+,1434n n n b b a +-=-.(1)证明:{an +bn }是等比数列,{an –bn }是等差数列;(2)求{an }和{bn }的通项公式.【答案】(1)见解析;(2)1122nn a n =+-,1122nnb n =-+.【解析】【分析】(1)可通过题意中的1434n n n a a b +-=+以及1434n n n b b a +-=-对两式进行相加和相减即可推导出数列{}n n a b +是等比数列以及数列{}n n a b -是等差数列;(2)可通过(1)中的结果推导出数列{}n n a b +以及数列{}n n a b -的通项公式,然后利用数列{}n n a b +以及数列{}n n a b -的通项公式即可得出结果.【详解】(1)由题意可知1434n n n a a b +-=+,1434n n n b b a +-=-,111a b +=,111a b -=,所以1144323442n n n n n n n n a b a b b a a b ++=+=--+++-,即()1112n n nn a b ab ++++=,所以数列{}n n a b +是首项为1、公比为12的等比数列,()112n n n a b -+=,因为()11443434448n n n n n n n n a b a b b a a b ++---=+-=-+-,所以112n n n n a b a b ++=-+-,数列{}n n a b -是首项1、公差为2的等差数列,21n n a b n -=-.(2)由(1)可知,()112n n n a b -+=,21n n a b n -=-,所以()111222nn nn n n a ab a b n =++-=+-,()111222n n n n n n b a b a b n 轾=+--=-+臌.【点睛】本题考查了数列的相关性质,主要考查了等差数列以及等比数列的相关证明,证明数列是等差数列或者等比数列一定要结合等差数列或者等比数列的定义,考查推理能力,考查化归与转化思想,是中档题.17.【2019年新课标2卷文科】已知{}n a 是各项均为正数的等比数列,1322,216a a a ==+.(1)求{}n a 的通项公式;(2)设2log n n b a =,求数列{}n b 的前n 项和.【答案】(1)212n n a -=;(2)2n S n =.【解析】【分析】(1)本题首先可以根据数列{}n a 是等比数列将3a 转化为21a q ,2a 转化为1a q ,再然后将其带入32216a a =+中,并根据数列{}n a 是各项均为正数以及12a =即可通过运算得出结果;(2)本题可以通过数列{}n a 的通项公式以及对数的相关性质计算出数列{}n b 的通项公式,再通过数列{}n b 的通项公式得知数列{}n b 是等差数列,最后通过等差数列求和公式即可得出结果.【详解】(1)因为数列{}n a 是各项均为正数的等比数列,32216a a =+,12a =,所以令数列{}n a 的公比为q ,2231=2a a q q =,212a a q q ==,所以22416q q =+,解得2q =-(舍去)或4,所以数列{}n a 是首项为2、公比为4的等比数列,121242n n n a --=⨯=.(2)因为2log n n b a =,所以21n b n =-,+121n b n =+,12n n b b +-=,所以数列{}n b 是首项为1、公差为2的等差数列,21212n n S n n +-=´=.【点睛】本题考查数列的相关性质,主要考查等差数列以及等比数列的通项公式的求法,考查等差数列求和公式的使用,考查化归与转化思想,考查计算能力,是简单题.18.【2018年新课标1卷文科】已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=.(1)求123b b b ,,;(2)判断数列{}n b 是否为等比数列,并说明理由;(3)求{}n a 的通项公式.【答案】(1)11b =,22b =,34b =;(2){}n b 是首项为1,公比为2的等比数列.理由见解析;(3)12n n a n -=⋅.【解析】【分析】(1)根据题中条件所给的数列{}n a 的递推公式()121n n na n a +=+,将其化为()121n n n a a n++=,分别令1n =和2n =,代入上式求得24a =和312a =,再利用nn a b n=,从而求得11b =,22b =,34b =;(2)利用条件可以得到121n na a n n+=+,从而可以得出12n n b b +=,这样就可以得到数列{}n b 是首项为1,公比为2的等比数列;(3)借助等比数列的通项公式求得12n na n-=,从而求得12n n a n -=⋅.【详解】(1)由条件可得()121n n n a a n++=.将1n =代入得,214a a =,而11a =,所以,24a =.将2n =代入得,323a a =,所以,312a =.从而11b =,22b =,34b =;(2){}n b 是首项为1,公比为2的等比数列.由条件可得121n na a n n+=+,即12n n b b +=,又11b =,所以{}n b 是首项为1,公比为2的等比数列;(3)由(2)可得11122n n nn a b n--==⨯=,所以12n n a n -=⋅.【点睛】该题考查的是有关数列的问题,涉及到的知识点有根据数列的递推公式确定数列的项,根据不同数列的项之间的关系,确定新数列的项,利用递推关系整理得到相邻两项之间的关系确定数列是等比数列,根据等比数列通项公式求得数列{}n b 的通项公式,借助于{}n b 的通项公式求得数列{}n a 的通项公式,从而求得最后的结果.19.【2018年新课标2卷理科】记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-.(1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.【答案】(1)an =2n –9,(2)Sn =n 2–8n ,最小值为–16.【解析】【详解】分析:(1)根据等差数列前n 项和公式,求出公差,再代入等差数列通项公式得结果,(2)根据等差数列前n 项和公式得n S 的二次函数关系式,根据二次函数对称轴以及自变量为正整数求函数最值.详解:(1)设{an }的公差为d ,由题意得3a 1+3d =–15.由a 1=–7得d =2.所以{an }的通项公式为an =2n –9.(2)由(1)得Sn =n 2–8n =(n –4)2–16.所以当n =4时,Sn 取得最小值,最小值为–16.点睛:数列是特殊的函数,研究数列最值问题,可利用函数性质,但要注意其定义域为正整数集这一限制条件.20.【2018年新课标3卷理科】等比数列{}n a 中,15314a a a ==,.(1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .【答案】(1)()12n n a -=-或12n n a -=.(2)6m =.【解析】【详解】分析:(1)列出方程,解出q 可得;(2)求出前n 项和,解方程可得m .详解:(1)设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去),2q =-或2q =.故()12n n a -=-或12n n a -=.(2)若()12n n a -=-,则()123nn S --=.由63m S =得()2188m -=-,此方程没有正整数解.若12n n a -=,则21nn S =-.由63m S =得264m =,解得6m =.综上,6m =.点睛:本题主要考查等比数列的通项公式和前n 项和公式,属于基础题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年2018-2022高考数学真题按知识点分类汇编12-数列求和(含解析)一、单选题1.(2021·浙江·统考高考真题)已知数列{}n a满足)111,N n a a n *+==∈.记数列{}n a 的前n 项和为n S ,则( )A .100332S << B .10034S << C .100942S <<D .100952S <<二、填空题2.(2020·江苏·统考高考真题)设{an }是公差为d 的等差数列,{bn }是公比为q 的等比数列.已知数列{an +bn }的前n 项和221()n n S n n n +=-+-∈N ,则d +q 的值是_______.三、解答题3.(2022·全国·统考高考真题)记n S 为数列{}n a 的前n 项和,已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列. (1)求{}n a 的通项公式; (2)证明:121112na a a +++<. 4.(2022·全国·统考高考真题)已知函数()e e ax x f x x =-. (1)当1a =时,讨论()f x 的单调性;(2)当0x >时,()1f x <-,求a 的取值范围; (3)设n *∈N21ln(1)n n ++>++.5.(2022·天津·统考高考真题)设{}n a 是等差数列,{}n b 是等比数列,且1122331a b a b a b ==-=-=.(1)求{}n a 与{}n b 的通项公式;(2)设{}n a 的前n 项和为n S ,求证:()1111n n n n n n n S a b S b S b +++++=-;(3)求211(1)nkk k k k a a b +=⎡⎤--⎣⎦∑.6.(2021·全国·统考高考真题)设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a 成等差数列. (1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <. 7.(2021·天津·统考高考真题)已知{}n a 是公差为2的等差数列,其前8项和为64.{}n b 是公比大于0的等比数列,1324,48b b b =-=. (I )求{}n a 和{}n b 的通项公式;(II )记2*1,n n nc b b n N =+∈,(i )证明{}22nn c c -是等比数列; (ii)证明)*nk n N =∈ 8.(2020·全国·统考高考真题)设{}n a 是公比不为1的等比数列,1a 为2a ,3a 的等差中项.(1)求{}n a 的公比;(2)若11a =,求数列{}n na 的前n 项和.9.(2020·全国·统考高考真题)设数列{an }满足a 1=3,134n n a a n +=-. (1)计算a 2,a 3,猜想{an }的通项公式并加以证明; (2)求数列{2nan }的前n 项和Sn .10.(2020·天津·统考高考真题)已知{}n a 为等差数列,{}n b 为等比数列,()()115435431,5,4a b a a a b b b ===-=-.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)记{}n a 的前n 项和为n S ,求证:()2*21n n n S S S n ++<∈N ;(Ⅲ)对任意的正整数n ,设()21132,,,.n nn n n n n a b n a a c a n b +-+⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数求数列{}n c 的前2n 项和.11.(2019·天津·高考真题) 设{}n a 是等差数列,{}n b 是等比数列,公比大于0,已知113a b ==,23b a = ,3243b a =+.(Ⅰ)求{}n a 和{}n b 的通项公式; (Ⅱ)设数列{}n c 满足21,,,n n n c bn ⎧⎪=⎨⎪⎩为奇数为偶数求()*112222n na c a c a c n N +++∈.12.(2019·浙江·高考真题)设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式; (2)记,n C n *=∈N证明:12+.n C C C n *++<∈N13.(2018·浙江·高考真题)已知等比数列{an }的公比q >1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{bn }满足b 1=1,数列{(bn +1−bn )an }的前n 项和为2n 2+n . (Ⅰ)求q 的值;(Ⅱ)求数列{bn }的通项公式.14.(2019·天津·高考真题)设{}n a 是等差数列,{}n b 是等比数列.已知1122334,622,24a b b a b a ===-=+,.(Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足111,22,1,,2,k k n kk n c c b n +⎧<<==⎨=⎩其中*k ∈N . (i )求数列(){}221n n a c -的通项公式; (ii )求()*221i ini a c n =∈∑N .15.(2018·天津·高考真题)设{an }是等差数列,其前n 项和为Sn (n ∈N*);{bn }是等比数列,公比大于0,其前n 项和为Tn (n ∈N*).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (Ⅰ)求Sn 和Tn ;(Ⅱ)若Sn +(T 1+T 2+…+Tn )=an +4bn ,求正整数n 的值.16.(2018·天津·高考真题)设{}n a 是等比数列,公比大于0,其前n 项和为()*n S n N∈,{}n b 是等差数列.已知11a =,322a a =+,435a b b =+,5462a b b =+.(I )求{}n a 和{}n b 的通项公式;(II )设数列{}n S 的前n 项和为()*n T n N ∈,(i )求n T ;(ii )证明()()()()22*122122n nk k k k T b b n N k k n ++=+=-∈+++∑.四、双空题17.(2021·全国·统考高考真题)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折,规格为20dm 12dm ⨯的长方形纸,对折1次共可以得到10dm 12dm ⨯,20dm 6dm ⨯两种规格的图形,它们的面积之和21240dm S =,对折2次共可以得到5dm 12dm ⨯,10dm 6dm ⨯,20dm 3dm ⨯三种规格的图形,它们的面积之和22180dm S =,以此类推,则对折4次共可以得到不同规格图形的种数为______;如果对折n 次,那么1nk k S ==∑______2dm .参考答案:1.A【分析】显然可知,10032S >,利用倒数法得到21111124n n a a +⎛⎫==-⎪⎪⎭,再放缩可12<,由累加法可得24(1)n a n ≥+,进而由1n a +=113n n a n a n ++≤+,然后利用累乘法求得6(1)(2)n a n n ≤++,最后根据裂项相消法即可得到1003S <,从而得解.【详解】因为)111,N n a a n *+==∈,所以0n a >,10032S >.由211111124n n n a a a ++⎛⎫==-⎪⎪⎭2111122n a +⎛⎫∴<⎪⎪⎭1211122n n -+≤+=,当且仅当1n =时取等号,12412(1)311n n n n a n a a a n n n ++∴≥∴=≤=++++ 113n n a n a n ++∴≤+, 由累乘法可得6(1)(2)n a n n ≤++,当且仅当1n =时取等号,由裂项求和法得:所以10011111111116632334451011022102S ⎛⎫⎛⎫≤-+-+-++-=-< ⎪ ⎪⎝⎭⎝⎭,即100332S <<. 故选:A .24(1)n a n ≥+,由题目条件可知要证100S 小于某数,从而通过局部放缩得到1,n n a a +的不等关系,改变不等式的方向得到6(1)(2)n a n n ≤++,最后由裂项相消法求得1003S <.2.4【分析】结合等差数列和等比数列前n 项和公式的特点,分别求得{}{},n n a b 的公差和公比,由此求得d q +.【详解】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ≠. 等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -⎛⎫=+=+- ⎪⎝⎭, 等比数列{}n b 的前n 项和公式为()1111111n n n b q b bQ q qq q-==-+---, 依题意n n n S P Q =+,即22111212211nn b b d d n n n a n q q q ⎛⎫-+-=+--+ ⎪--⎝⎭, 通过对比系数可知111212211dd a q b q⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒112021d a q b =⎧⎪=⎪⎨=⎪⎪=⎩,故4d q +=.故答案为:4【点睛】本小题主要考查等差数列和等比数列的前n 项和公式,属于中档题. 3.(1)()12n n n a +=(2)见解析【分析】(1)利用等差数列的通项公式求得()121133n n S n n a +=+-=,得到()23nn n a S +=,利用和与项的关系得到当2n ≥时,()()112133n n n n n n a n a a S S --++=-=-,进而得:111n n a n a n -+=-,利用累乘法求得()12n n n a +=,检验对于1n =也成立,得到{}n a 的通项公式()12n n n a +=;(2)由(1)的结论,利用裂项求和法得到121111211n a a a n ⎛⎫+++=- ⎪+⎝⎭,进而证得. 【详解】(1)∵11a =,∴111S a ==,∴111S a =,又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列,∴()121133n n S n n a +=+-=,∴()23n n n a S +=,∴当2n ≥时,()1113n n n a S --+=,∴()()112133n n n n n n a n a a S S --++=-=-,整理得:()()111n n n a n a --=+, 即111n n a n a n -+=-, ∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯ ()1341112212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--, 显然对于1n =也成立, ∴{}n a 的通项公式()12n n n a +=; (2)()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭∴12111na a a +++1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦4.(1)()f x 的减区间为(),0-∞,增区间为()0,+∞. (2)12a ≤(3)见解析【分析】(1)求出()f x ',讨论其符号后可得()f x 的单调性.(2)设()e e 1ax x h x x =-+,求出()h x '',先讨论12a >时题设中的不等式不成立,再就102a <≤结合放缩法讨论()h x '符号,最后就0a ≤结合放缩法讨论()h x 的范围后可得参数的取值范围. (3)由(2)可得12ln t t t<-对任意的1t >恒成立,从而可得()ln 1ln n n +-<的*n ∈N 恒成立,结合裂项相消法可证题设中的不等式.【详解】(1)当1a =时,()()1e x f x x =-,则()e xf x x '=,当0x <时,()0f x '<,当0x >时,0fx ,故()f x 的减区间为(),0∞-,增区间为()0,∞+.(2)设()e e 1ax xh x x =-+,则()00h =,又()()1e e ax x h x ax '=+-,设()()1e e ax xg x ax =+-, 则()()22e e ax xg x a a x '=+-,若12a >,则()0210g a '=->, 因为()g x '为连续不间断函数,故存在()00,x ∈+∞,使得()00,x x ∀∈,总有()0g x '>, 故()g x 在()00,x 为增函数,故()()00g x g >=,故()h x 在()00,x 为增函数,故()()01h x h >=-,与题设矛盾. 若102a <≤,则()()()ln 11e e ee ax ax ax xx h x ax ++'=+-=-, 下证:对任意0x >,总有()ln 1x x +<成立, 证明:设()()ln 1S x x x =+-,故()11011x S x x x-'=-=<++, 故()S x 在()0,∞+上为减函数,故()()00S x S <=即()ln 1x x +<成立. 由上述不等式有()ln 12e e e e e e 0ax ax x ax ax x ax x +++-<-=-≤, 故()0h x '≤总成立,即()h x 在()0,∞+上为减函数, 所以()()00h x h <=.当0a ≤时,有()e e e 1100ax x axh x ax '=-+<-+=,所以()h x 在()0,∞+上为减函数,所以()()00h x h <=. 综上,12a ≤. (3)取12a =,则0x ∀>,总有12e e 10x x x -+<成立, 令12e x t =,则21,e ,2ln xt t x t >==,故22ln 1t t t <-即12ln t t t<-对任意的1t >恒成立.所以对任意的*n ∈N ,有 整理得到:()ln 1ln n n +-<()21ln 2ln1ln 3ln 2ln 1ln n n n n+>-+-+++-+()ln 1n =+, 故不等式成立.【点睛】思路点睛:函数参数的不等式的恒成立问题,应该利用导数讨论函数的单调性,注意结合端点处导数的符号合理分类讨论,导数背景下数列不等式的证明,应根据已有的函数不等式合理构建数列不等式.5.(1)121,2n n n a n b -=-= (2)证明见解析 (3)1(62)489n n +-+【分析】(1)利用等差等比数列的通项公式进行基本量运算即可得解; (2)由等比数列的性质及通项与前n 项和的关系结合分析法即可得证;(3)先求得212221212122(1)(1)k k k k k k k k a a b a a b ---+⎡⎤⎡⎤--+--⎣⎦⎣⎦,进而由并项求和可得114nk n k T k +==⋅∑,再结合错位相减法可得解.【详解】(1)设{}n a 公差为d ,{}n b 公比为q ,则11(1),n n n a n d b q -=+-=,由22331a b a b -=-=可得2112121d q d q d q +-=⎧⇒==⎨+-=⎩(0d q ==舍去), 所以121,2n n n a n b -=-=;(2)证明:因为120,n n b b +=≠所以要证1111()n n n n n n n S a b S b S b +++++=-, 即证111()2n n n n n n n S a b S b S b ++++=⋅-,即证1112n n n n S a S S ++++=-, 即证11n n n a S S ++=-,而11n n n a S S ++=-显然成立,所以1111()n n n n n n n S a b S b S b +++++=⋅-⋅;(3)因为212221212122(1)(1)k kk k k k k k a a b a a b ---+⎡⎤⎡⎤--+--⎣⎦⎣⎦2221(4143)2[41(41)]224k k k k k k k k --=-+-⨯++--⨯=⋅,所以211(1)nkk k k k a a b +=⎡⎤--⎣⎦∑2122212121221[((1))((1))]nk kk k k k k k k a a b a a b ---+==--+--∑124nk k k ==⋅∑,设124nk n k T k ==⋅∑所以2324446424nn T n =⨯+⨯+⨯+⋅⋅⋅+⨯,则2341244446424n n n T +⨯+⨯+⨯+⋅⋅⋅+⨯=,作差得()2341124(14)3244444242414n nn n n T n n ++⨯--=++++⋅⋅⋅+-⋅=-⨯-()126483n n +--=, 所以1(62)489n n n T +-+=,所以211(1)nkk k k k a a b +=⎡⎤--=⎣⎦∑1(62)489n n +-+. 6.(1)11()3n n a -=,3n n n b =;(2)证明见解析.【分析】(1)利用等差数列的性质及1a 得到29610q q -+=,解方程即可; (2)利用公式法、错位相减法分别求出,n n S T ,再作差比较即可.【详解】(1)因为{}n a 是首项为1的等比数列且1a ,23a ,39a 成等差数列,所以21369a a a =+,所以211169a q a a q =+,即29610q q -+=,解得13q =,所以11()3n n a -=,所以33n n n na nb ==. (2)[方法一]:作差后利用错位相减法求和211213333n n n n nT --=++++,012111111223333-⎛⎫=++++ ⎪⎝⎭n n S ,230121123111112333323333n n n n S n T -⎛⎫⎛⎫-=++++-++++= ⎪ ⎪⎝⎭⎝⎭012111012222333---++++111233---+n nn n .设0121111101212222Γ3333------=++++n n n , ⑧ 则1231111012112222Γ33333-----=++++n nn . ⑨由⑧-⑨得1121113312111113322Γ13233332313--⎛⎫--- ⎪⎛⎫⎝⎭=-++++-=-+- ⎪⎝⎭-n n n n n n n . 所以211312Γ432323----=--=-⨯⨯⨯n n n n n n . 因此10232323--=-=-<⨯⨯n n n n nS n n nT . 故2nn S T <. [方法二]【最优解】:公式法和错位相减求和法证明:由(1)可得11(1)313(1)12313n n n S ⨯-==--,211213333n n n n nT --=++++,① 231112133333n n n n nT +-=++++,② ①-②得23121111333333n n n n T +=++++- 1111(1)1133(1)1323313n n n n n n ++-=-=---, 所以31(1)4323n n nnT =--⋅,所以2n n S T -=3131(1)(1)043234323n n n n n n ----=-<⋅⋅, 所以2nn S T <. [方法三]:构造裂项法由(Ⅰ)知13⎛⎫= ⎪⎝⎭n n b n ,令1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,且1+=-n n n b c c ,即1111()[(1)]333αβαβ+⎛⎫⎛⎫⎛⎫=+-++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭nnn n n n ,通过等式左右两边系数比对易得33,24αβ==,所以331243nn c n ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭.则12113314423nn n n n T b b b c c +⎛⎫⎛⎫=+++=-=-+ ⎪⎪⎝⎭⎝⎭,下同方法二.[方法四]:导函数法 设()231()1-=++++=-n n x x f x x x x x x,由于()()()()()()1221'111'11(1)'1(1)1n n n n nx x x x x x x x nx n x x x x +⎡⎤⎡⎤⎡⎤----⨯--+-+⎣⎦⎣⎦⎢⎥==---⎢⎥⎣⎦, 则12121(1)()123(1)+-+-+=++++='-n nn nx n x f x x x nxx .又1111333-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭n n n b n n ,所以2112311111233333n n n T b b b b n -⎡⎤⎛⎫⎛⎫=++++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦12111(1)11133333113n nn n f +⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭⋅=⨯ ⎪⎝⎭⎛⎫- ⎪⎝⎭' 13113311(1)4334423n nnn n n +⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-+=-+⎢⎥ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,下同方法二. 【整体点评】本题主要考查数列的求和,涉及到等差数列的性质,错位相减法求数列的和,考查学生的数学运算能力,是一道中档题,其中证明不等式时采用作差法,或者作商法要根据式子得结构类型灵活选择,关键是要看如何消项化简的更为简洁. (2)的方法一直接作差后利用错位相减法求其部分和,进而证得结论;方法二根据数列的不同特点,分别利用公式法和错位相减法求得,n n S T ,然后证得结论,为最优解;方法三采用构造数列裂项求和的方法,关键是构造1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ,使1+=-n n n b c c ,求得n T 的表达式,这是错位相减法的一种替代方法,方法四利用导数方法求和,也是代替错位相减求和法的一种方法.7.(I )21,n a n n N *=-∈,4,n n N b n *=∈;(II )(i )证明见解析;(ii )证明见解析.【分析】(I )由等差数列的求和公式运算可得{}n a 的通项,由等比数列的通项公式运算可得{}n b 的通项公式;(II )(i )运算可得2224nn n c c =⋅-,结合等比数列的定义即可得证;(ii )放缩得21222422n n n n na n c a c +<-⋅,进而可得112n n k k k k -==,结合错位相减法即可得证. 【详解】(I )因为{}n a 是公差为2的等差数列,其前8项和为64. 所以12818782642a a a a ⨯++⋅⋅⋅+=+⨯=,所以11a =, 所以()12121,n n n n N a a *=+-=-∈;设等比数列{}n b 的公比为(),0q q >,所以()221321484q b b b q q b q ==-=--,解得4q =(负值舍去), 所以114,n n n b q n N b -*==∈;(II )(i )由题意,221441n n nn n b c b =++=,所以22224211442444n n nn nn n c c ⎛⎫⎛⎫=+-+=⋅ ⎪ ⎪⎝⎭⎝⎭-, 所以220nn c c ≠-,且212222124424n n n n nn c c c c +++⋅==⋅--, 所以数列{}22nn c c -是等比数列; (ii )由题意知,()()22122222121414242222n n n n n n n n n a n n c c a +-+-==<-⋅⋅⋅,12n n-,所以112nn k k k-==, 设10121112322222nn k n k k nT --===+++⋅⋅⋅+∑,则123112322222n nn T =+++⋅⋅⋅+, 两式相减得21111111122121222222212nn n n nn n n n T -⎛⎫⋅- ⎪+⎝⎭=+++⋅⋅⋅+-=-=--, 所以1242n n n T -+=-,所以1112422nn k n k k n --==+⎫=-<⎪⎭【点睛】关键点点睛:最后一问考查数列不等式的证明,因为nk =错位相减法即可得证.8.(1)2-;(2)1(13)(2)9nn n S -+-=. 【分析】(1)由已知结合等差中项关系,建立公比q 的方程,求解即可得出结论; (2)由(1)结合条件得出{}n a 的通项,根据{}n na 的通项公式特征,用错位相减法,即可求出结论.【详解】(1)设{}n a 的公比为q ,1a 为23,a a 的等差中项,212312,0,20a a a a q q =+≠∴+-=,1,2q q ≠∴=-;(2)设{}n na 的前n 项和为n S ,111,(2)n n a a -==-,21112(2)3(2)(2)n n S n -=⨯+⨯-+⨯-++-,①23121(2)2(2)3(2)(1)(2)(2)n n n S n n --=⨯-+⨯-+⨯-+--+-,②①-②得,2131(2)(2)(2)(2)n n n S n -=+-+-++---1(2)1(13)(2)(2)1(2)3n n n n n ---+-=--=--, 1(13)(2)9nn n S -+-∴=. 【点睛】本题考查等比数列通项公式基本量的计算、等差中项的性质,以及错位相减法求和,考查计算求解能力,属于基础题.9.(1)25a =,37a =,21n a n =+,证明见解析;(2)1(21)22n n S n +=-⋅+.【分析】(1)方法一:(通性通法)利用递推公式得出23,a a ,猜想得出{}n a 的通项公式,利用数学归纳法证明即可;(2)方法一:(通性通法)根据通项公式的特征,由错位相减法求解即可. 【详解】(1)[方法一]【最优解】:通性通法由题意可得2134945a a =-=-=,32381587a a =-=-=,由数列{}n a 的前三项可猜想数列{}n a 是以3为首项,2为公差的等差数列,即21n a n =+.证明如下:当1n =时,13a =成立;假设()n k k *=∈N 时,21k a k =+成立.那么1n k =+时,1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立. 则对任意的*n ∈N ,都有21n a n =+成立; [方法二]:构造法由题意可得2134945a a =-=-=,32381587a a =-=-=.由123,5a a ==得212a a -=.134n n a a n +=-,则134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--.令1n n n b a a +=-,且12b =,所以134n n b b -=-,两边同时减去2,得()1232n n b b --=-,且120b -=,所以20n b -=,即12n n a a +-=,又212a a -=,因此{}n a 是首项为3,公差为2的等差数列,所以21n a n =+. [方法三]:累加法由题意可得2134945a a =-=-=,32381587a a =-=-=. 由134n n a a n +=-得1114333n n n n n a a n+++-=-,即2121214333a a -=-⨯,3232318333a a -=-⨯, (111)4(1)(2)333n n n n n a a n n ---=--⨯≥.以上各式等号两边相加得1123111412(1)33333n nn a a n ⎡⎤-=-⨯+⨯++-⨯⎢⎥⎣⎦,所以1(21)33n n n a n =+⋅.所以21(2)n a n n =+≥.当1n =时也符合上式.综上所述,21n a n =+.[方法四]:构造法21322345,387a a a a =-==-=,猜想21n a n =+.由于134n n a a n +=-,所以可设()1(1)3n n a n a n λμλμ++++=++,其中,λμ为常数.整理得1322n n a a n λμλ+=++-.故24,20λμλ=--=,解得2,1λμ=-=-.所以()112(1)13(21)3211n n n a n a n a +-+-=--=⋅⋅⋅=-⨯-.又130a -=,所以{}21n a n --是各项均为0的常数列,故210n a n --=,即21n a n =+.(2)由(1)可知,2(21)2n n n a n ⋅=+⋅[方法一]:错位相减法231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅,①23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅,②由①-②得:()23162222(21)2n n n S n +-=+⨯+++-+⋅()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-,即1(21)22n n S n +=-⋅+.[方法二]【最优解】:裂项相消法112(21)2(21)2(23)2n n n n n n n a n n n b b ++=+=---=-,所以231232222n n n S a a a a =++++()()()()2132431n n b b b b b b b b +=-+-+-++-11n b b +=-1(21)22n n +=-+. [方法三]:构造法当2n ≥时,1(21)2n n n S S n -=++⋅,设11()2[(1)]2n n n n S pn q S p n q --++⋅=+-+⋅,即122nn n pn q p S S ----=+⋅,则2,21,2pq p -⎧=⎪⎪⎨--⎪=⎪⎩,解得4,2p q =-=.所以11(42)2[4(1)2]2n n n n S n S n --+-+⋅=+--+⋅,即{}(42)2n n S n +-+⋅为常数列,而1(42)22S +-+⋅=,所以(42)22n n S n +-+⋅=.故12(21)2n n S n +=+-⋅.[方法四]:因为12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,令12n n b n -=⋅,则()()231()0,11n n x x f x x x x x x x-=++++=≠-,()121211(1)()1231(1)nn n n x x nx n x f x x x nx x x +-'⎡⎤-+-+=++++==⎢⎥--⎢⎥⎣⎦', 所以12n b b b +++21122322n n -=+⋅+⋅++⋅1(2)12(1)2n nf n n +==+-+'⋅.故234(2)2222nn S f =++'+++()1212412(1)212n n n n n +-⎡⎤=+⋅-++⎣⎦-1(21)22n n +=-+.【整体点评】(1)方法一:通过递推式求出数列{}n a 的部分项从而归纳得出数列{}n a 的通项公式,再根据数学归纳法进行证明,是该类问题的通性通法,对于此题也是最优解; 方法二:根据递推式134n n a a n +=-,代换得134(1)(2)n n a a n n -=--≥,两式相减得()1134n n n n a a a a +--=--,设1n n n b a a +=-,从而简化递推式,再根据构造法即可求出n b ,从而得出数列{}n a 的通项公式; 方法三:由134n n a a n +=-化简得1114333n n n n n a a n +++-=-,根据累加法即可求出数列{}n a 的通项公式; 方法四:通过递推式求出数列{}n a 的部分项,归纳得出数列{}n a 的通项公式,再根据待定系数法将递推式变形成()1(1)3n n a n a n λμλμ++++=++,求出,λμ,从而可得构造数列为常数列,即得数列{}n a 的通项公式. (2)方法一:根据通项公式的特征可知,可利用错位相减法解出,该法也是此类题型的通性通法; 方法二:根据通项公式裂项,由裂项相消法求出,过程简单,是本题的最优解法;方法三:由2n ≥时,1(21)2nn n S S n -=++⋅,构造得到数列{}(42)2n n S n +-+⋅为常数列,从而求出;方法四:将通项公式分解成12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+,利用分组求和法分别求出数列{}{}12,2n n n -⋅的前n 项和即可,其中数列{}12n n -⋅的前n 项和借助于函数()()231()0,11n nx x f x x x x x x x-=++++=≠-的导数,通过赋值的方式求出,思路新颖独特,很好的简化了运算.10.(Ⅰ)n a n =,12n n b -=;(Ⅱ)证明见解析;(Ⅲ)465421949n n n n +--+⨯. 【分析】(Ⅰ)由题意分别求得数列的公差、公比,然后利用等差、等比数列的通项公式得到结果;(Ⅱ)利用(Ⅰ)的结论首先求得数列{}n a 前n 项和,然后利用作差法证明即可;(Ⅲ)分类讨论n 为奇数和偶数时数列的通项公式,然后分别利用指数型裂项求和和错位相减求和计算211n k k c -=∑和21nk k c =∑的值,据此进一步计算数列{}n c 的前2n 项和即可.【详解】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q . 由11a =,()5435a a a =-,可得d =1. 从而{}n a 的通项公式为n a n =. 由()15431,4b b b b ==-,又q ≠0,可得2440q q -+=,解得q =2,从而{}n b 的通项公式为12n n b -=.(Ⅱ)证明:由(Ⅰ)可得(1)2n n n S +=, 故21(1)(2)(3)4n n S S n n n n +=+++,()()22211124n S n n +=++, 从而2211(1)(2)02n n n S S S n n ++-=-++<,所以221n n n S S S ++<.(Ⅲ)当n 为奇数时,()111232(32)222(2)2n n n n n n n n a b n c a a n n n n-+-+--===-++,当n 为偶数时,1112n n n n a n c b -+-==, 对任意的正整数n ,有222221112221212121k k nnnk k k c k k n --==⎛⎫=-=- ⎪+-+⎝⎭∑∑,和223111211352321444444nnk kn n k k k n n c -==---==+++++∑∑① 由①得22314111352321444444n k n n k n n c +=--=+++++∑ ② 由①②得22111211312221121441444444414n nk n n n k n n c ++=⎛⎫-⎪--⎝⎭=+++-=---∑, 由于11211121221121156544144334444123414n n n n n n n n ++⎛⎫- ⎪--+⎝⎭--=-⨯--⨯=-⨯-, 从而得:21565994nk nk n c =+=-⨯∑. 因此,2212111465421949n nnnk k k nk k k n c c c n -===+=+=--+⨯∑∑∑. 所以,数列{}n c 的前2n 项和为465421949n n n n +--+⨯. 【点睛】本题主要考查数列通项公式的求解,分组求和法,指数型裂项求和,错位相减求和等,属于中等题.11.(I )3n a n =,3nn b =;(II )22(21)369()2n n n n +*-++∈N 【分析】(I )首先设出等差数列的公差,等比数列的公比,根据题意,列出方程组,求得33d q =⎧⎨=⎩,进而求得等差数列和等比数列的通项公式;(II )根据题中所给的n c 所满足的条件,将112222n n a c a c a c +++表示出来,之后应用分组求和法,结合等差数列的求和公式,以及错位相减法求和,最后求得结果. 【详解】(I )解:设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,依题意,得23323154q d q d =+⎧⎨=+⎩,解得33d q =⎧⎨=⎩,故33(1)3n a n n =+-=,1333n nn b -=⨯=,所以,{}n a 的通项公式为3n a n =,{}n b 的通项公式为3nn b =;(II )112222n n a c a c a c +++135212142632()()n n n a a a a a b a b a b a b -=+++++++++123(1)[36](6312318363)2n n n n n -=⨯+⨯+⨯+⨯+⨯++⨯21236(13233)n n n =+⨯⨯+⨯++⨯, 记 1213233n n T n =⨯+⨯++⨯ ① 则 231313233n n T n +=⨯+⨯++⨯ ②②-①得,231233333n n n T n +=-----+⨯113(13)(21)333132n n n n n ++--+=-+⨯=-,所以122112222(21)3336332n n n n n a c a c a c n T n +-++++=+=+⨯22(21)369()2n n n n N +*-++=∈.【点睛】本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识,考查数列求和的基本方法和运算求解能力,属于中档题目. 12.(1)()21n a n =-,()1n b n n =+;(2)证明见解析.【分析】(1)首先求得数列{}n a 的首项和公差确定数列{}n a 的通项公式,然后结合三项成等比数列的充分必要条件整理计算即可确定数列{}n b 的通项公式;(2)结合(1)的结果对数列{}n c 的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中的不等式.【详解】(1)由题意可得:1112432332a d a d a d +=⎧⎪⎨⨯+=+⎪⎩,解得:102a d =⎧⎨=⎩, 则数列{}n a 的通项公式为22n a n =- . 其前n 项和()()02212n n n S nn +-⨯==-.则()()()()1,1,12n n n n n b n n b n n b -++++++成等比数列,即: ()()()()21112n n n n n b n n b n n b ++=-+⨯+++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦,据此有:()()()()()()()()2222121112121n n n n n n n n n b b n n n n n n b n n b b ++++=-++++++-+,故()()()()()22112121(1)(1)(1)(2)n n n n n n b n n n n n n n n n +--++==++++--+. (2)结合(1)中的通项公式可得:2n C =<=,则()()()12210221212n C C C n n n +++<-+-++--=【点睛】本题主要考查数列通项公式的求解,,裂项求和的方法,数列中用放缩法证明不等式的方法等知识,意在考查学生的转化能力和计算求解能力. 13.(Ⅰ)2q;(Ⅱ)2115(43)()2n n b n -=-+⋅.【分析】分析:(Ⅰ)根据条件、等差数列的性质及等比数列的通项公式即可求解公比;(Ⅱ)先根据数列1{()}n n n b b a +-前n 项和求通项,解得1n n b b +-,再通过叠加法以及错位相减法求n b . 【详解】详解:(Ⅰ)由42a +是35,a a 的等差中项得35424a a a +=+, 所以34543428a a a a ++=+=, 解得48a =.由3520a a +=得1820q q ⎛⎫+= ⎪⎝⎭,因为1q >,所以2q.(Ⅱ)设()1n n n n c b b a +=-,数列{}n c 前n 项和为n S .由11,1,, 2.n nn S n c S S n -=⎧=⎨-≥⎩解得41n c n =-.由(Ⅰ)可知12n n a -=,所以()111412n n n b b n -+⎛⎫-=-⋅ ⎪⎝⎭,故()21145,22n n n b b n n --⎛⎫-=-⋅≥ ⎪⎝⎭,()()()()11123221n n n n n b b b b b b b b b b ----=-+-++-+-()()23111454973222n n n n --⎛⎫⎛⎫=-⋅+-⋅++⋅+ ⎪⎪⎝⎭⎝⎭.设()22111371145,2222n n T n n -⎛⎫⎛⎫=+⋅+⋅++-⋅≥ ⎪ ⎪⎝⎭⎝⎭,()()2211111137494522222n n n T n n --⎛⎫⎛⎫⎛⎫=⋅+⋅++-⋅+-⋅ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭所以()2211111134444522222n n n T n --⎛⎫⎛⎫⎛⎫=+⋅+⋅++⋅--⋅ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,因此()211443,22n n T n n -⎛⎫=-+⋅≥ ⎪⎝⎭,又11b =,所以()2115432n n b n -⎛⎫=-+⋅ ⎪⎝⎭.点睛:用错位相减法求和应注意的问题:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.14.(Ⅰ)31n a n =+;32n n b =⨯(Ⅱ)(i )()221941n n n a c -=⨯-(ii )()1+1*1243218n n n N +⨯+⨯-∈ 【分析】(Ⅰ)由题意首先求得公比和公差,然后确定数列的通项公式即可;(Ⅱ)结合(Ⅰ)中的结论可得数列(){}221n n a c -的通项公式,结合所得的通项公式对所求的数列通项公式进行等价变形,结合等比数列前n 项和公式可得()*221i ini a c n =∈∑N 的值.【详解】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q . 依题意得()()262426262424124q d dq d d ⎧=+-=+⎪⎨=++=+⎪⎩,解得32d q =⎧⎨=⎩,故4(1)331n a n n =+-⨯=+,16232n nn b -=⨯=⨯.所以,{}n a 的通项公式为31n a n =+,{}n b 的通项公式为32nn b =⨯.(Ⅱ)(i )()()()()22211321321941n n n n n nn a c a b -=-=⨯+⨯-=⨯-.所以,数列(){}221n n a c -的通项公式为()221941n n na c -=⨯-.(ii )()2222211=1i i i i i n n i i a c a a c ==⎡⎤-⎣⎦+∑∑()222111i i i n ni i a a c ===+-∑∑ ()212312n n ⎛⎫- ⎪=+⨯ ⎪-⎝⎭()1941ni i =+⨯-∑ ()()+1414326914n n n n -=⨯+-+⨯--()1+1*1243218n n n N +=⨯+⨯-∈.【点睛】本题主要考查等差数列、等比数列的通项公式及其前n 项和公式等基础知识.考查化归与转化思想和数列求和的基本方法以及运算求解能力. 15.(Ⅰ)()12n n n S +=,21nn T =-;(Ⅱ)4. 【分析】(I )由题意得到关于q 的方程,解方程可得2q ,则122112nn n T -==--.结合题意可得等差数列的首项和公差为11,1a d ==,则其前n 项和()12n n n S +=. (II )由(I ),知1122 2.n n T T T n ++++=-- 据此可得2340,n n --= 解得1n =-(舍),或4n =.则n 的值为4.【详解】(I )设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q,故12n n b -=.所以,122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d +=从而11,1a d ==,故n a n =,所以,(1)2n n n S +=. (II )由(I ),有121122(12)(222)=2 2.12n nn n T T T n n n +⨯-+++=+++--=---由12()4n n n n S T T T a b ++++=+,可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --=解得1n =-(舍),或4n =.所以n 的值为4.点睛:本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.16.(Ⅰ)12n n a -=,n b n =;(Ⅱ)(i )122n n T n +=--.(ii )证明见解析.【详解】分析:(I )由题意得到关于q 的方程,解方程可得2q =,则12n n a -=.结合等差数列通项公式可得.n b n =(II )(i )由(I ),有21nn S =-,则()112122nk n n k T n +==-=--∑.(ii )因为()()()212221221k k k k k T b b k k k k ++++=-++++,裂项求和可得()()()22122122n nk k k k T b b k k n ++=+=-+++∑. 详解:(I )设等比数列{}n a 的公比为q.由1321,2,a a a ==+可得220q q --=.因为0q >,可得2q =,故12n n a -=.设等差数列{}n b 的公差为d ,由435a b b =+,可得13 4.b d += 由5462a b b =+,可得131316,b d += 从而11,1,b d == 故.n b n =所以数列{}n a 的通项公式为12n n a -=,数列{}n b 的通项公式为.n b n =(II )(i )由(I ),有122112nn n S -==--, 故()()1112122122212nn nkkn n k k T n n n +==⨯-=-=-=-=---∑∑.(ii )因为()()()()()()()()1121222222212121221k k k k k k k k k k T b b k k k k k k k k k +++++--+++⋅===-++++++++,所以()()()32432122122222222123243212n n n nk k k k T b b k k n n n ++++=+⎛⎫⎛⎫⎛⎫=-+-++-=- ⎪ ⎪⎪+++++⎝⎭⎝⎭⎝⎭∑. 点睛:本题主要考查数列通项公式的求解,数列求和的方法,数列中的指数裂项方法等知识,意在考查学生的转化能力和计算求解能力. 17. 5 ()41537202n n -+-【分析】(1)按对折列举即可;(2)根据规律可得n S ,再根据错位相减法得结果. 【详解】(1)由对折2次共可以得到5dm 12dm ⨯,10dm 6dm ⨯,20dm 3dm ⨯三种规格的图形,所以对着三次的结果有:5312561032022⨯⨯⨯⨯,,;,共4种不同规格(单位2dm ); 故对折4次可得到如下规格:5124⨯,562⨯,53⨯,3102⨯,3204⨯,共5种不同规格;(2)由于每次对着后的图形的面积都减小为原来的一半,故各次对着后的图形,不论规格如何,其面积成公比为12的等比数列,首项为120()2dm ,第n 次对折后的图形面积为111202n -⎛⎫⨯ ⎪⎝⎭,对于第n 此对折后的图形的规格形状种数,根据(1)的过程和结论,猜想为1n +种(证明从略),故得猜想1120(1)2n n n S -+=, 设()0121112011202120312042222nk n k n S S -=+⨯⨯⨯==++++∑, 则121112021203120120(1)22222n nn n S -⨯⨯+=++++, 两式作差得:()211201111124012022222n nn S -+⎛⎫=++++-⎪⎝⎭ ()11601120122401212n n n -⎛⎫- ⎪+⎝⎭=+-- ()()112011203120360360222n n nn n -++=--=-,因此,()()4240315372072022n n n n S -++=-=-. 故答案为:5;()41537202n n -+-. 【点睛】方法点睛:数列求和的常用方法: (1)对于等差等比数列,利用公式法可直接求解;(2)对于{}n n a b 结构,其中{}n a 是等差数列,{}n b 是等比数列,用错位相减法求和; (3)对于{}n n a b +结构,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭结构,其中{}n a 是等差数列,公差为()0d d ≠,则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭,利用裂项相消法求和.。
