对偶问题的解
管理运筹学03对偶问题

收购方的意愿: min w 15 y1 24 y2 5 y3
Ⅰ 设备A 设备B 调试工序 利润(元) 0 6 1 2 Ⅱ 5 2 1 1 D 15时 24时 5时
原 问 题
max z 2 x1 x 2 s.t. 5 x 2 15 6 x1 2 x 2 24 x1 x 2 5 x1, x 2 0
其它形式 的对偶
?
2.限定向量b
(资源向量)
3.一个约束 一个变量。
4. max z 的LP约束“
”
min z
的
LP是“ ”的约束。
5.变量都是非负限制。
原问题(或对偶问题) 对偶问题(或原问题) 约束条件右端项 目标函数变量的系数 目标函数变量的系数 约束条件右端项 目标函数 max 目标函数 min 约 m个 m个 束 变 ≤ ≥0 条 量 ≥ ≤0 件 = 无约束 n个 n个 约 变 束 ≥0 ≥ 量 条 ≤0 ≤ 件 = 无约束
w Yb YA C Y 0
一 般 规 律
3个约束 2个变量
2个约束 3个变量
C (c1 , c2 )
x1 X x2
Y (y1,y2 ,y3 )
A (aij )
b1 b b2 b3
特点:
1. max
min
价值向量C
min w 15 y1 24 y2 5 y3 s.t 6y y 2 对
2 3
收 购
5y 2y y 1
1 2 3
y ,y ,y 0
1 2 3
厂 家
偶 问 题
原问题
对偶问题
max s.t.
线性规划问题的对偶问题

1 2
2 2
12
4
0
0 5
x x
1 2
16 15
x1
x
2
0
y1
min 12
16
15y2
y3
2
2
4 0
0 5
y y y
1 2 3
2
3
y1
y
2
0
y 3
2021/8/17
13
线性规划的对偶关系:
(I) Max z = C x
s.t. Ax b
16h
5h
15h
3
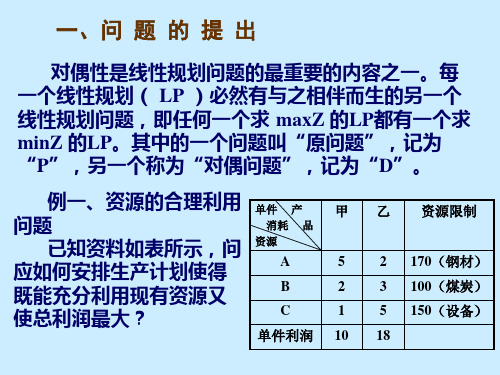
问该企业因安排生产两种产品各多少件,使总的 利润收入为最大?
2021/8/17
10
数学模型
max Z=2x1+3x2
s.t. 2x1+2x2 12
4x1
16
5x2 15
x1,x2 0
现某机械厂为扩大生产租借常山机器厂 拥有的设备资源,问常山厂分别以每小时 什么样的价格才愿意出租自己的设备?
-3x1-6x2-4x3≥15 5x2+3x3=30
x1≤0,x2取值无约束,x3≥0
2021/8/17
27
Max w=24y1+15y2+30y3 s.t. -4y1-3y2 ≥7
2y1-6y2+5y3=4 -6y1-4y2+3y3≤-3 y1≤0,y2≥0,y3无约束
2021/8/17
28
例2-8:写出下列线性规划问题的对 偶问题
50小时。问该厂如何组织生产才能使每
月的销售收入最大?
2021/8/17
2
数学模型
max g= 50x1 + 30x2
运筹学课件 第2章:线性规划的对偶理论

min w 16y1 36y2 65y3
90 y1 3 y 2 y1 2 y 2 5 y 3 70 y , y , y 0 1 2 3
原问题 A b C 约束系数矩阵
对偶问题 约束系数矩阵的转臵
约束条件的右端项向量 目标函数中的价格系数向量 目标函数中的价格系数向量 约束条件的右端项向量 Max z=CX Min w=Y’b 目标函数 AX≤b A’Y≥C’ 约束条件 X≥0 Y≥0 决策变量
若原问题为求极小形式的对称形式线性规划问题, 对偶问题应该具有什么形式?
Min w Y 'b A'Y C Y 0
max w Y 'b A'Y C Y 0
min z CX
Max z CX
AX b X 0
AX b X 0
min w 5 y1 4 y2 6 y3 4 y1 3 y2 2 y3 2 y1 2 y2 3 y3 3 3 y1 4 y3 5 2 y 7 y y 1 2 3 1 y1 0, y2 0, y3无约束
对偶问题 约束系数矩阵的转臵
目标函数中的价格系数向量
目标函数 约束条件
变量
Max z=CX m个 ≤ ≥ = n个 ≥0 ≤0 无约束
约束条件的右端项向量 目标函数 Min w=Y’b m个 ≥0 变量 ≤0 无约束 n个 ≥ 约束条件 ≤ =
【例2-3】写出下列线性规划问题的对偶问题
min 2x1 3x2 5x3 x4
1.初始表中单位阵在迭代后单纯形表中对应的位臵就是B-1 2.对于原问题的最优解,各松弛变量检验数的相反数恰好 是其对偶问题的一个可行解,且两者具有相同的目标函数 值。根据下面介绍的对偶问题的基本性质还将看到,若原 问题取得最优解,则对偶问题的解也为最优解。
原问题和对偶问题最优解的关系

目录1. 原问题和对偶问题的定义2. 最优解的概念和求解方法3. 原问题和对偶问题最优解的关系4. 应用举例5. 结论1. 原问题和对偶问题的定义在数学和优化领域,原问题和对偶问题是一对相关的问题,它们通常是相互关联的,并且在求解过程中起到互补的作用。
原问题是指在优化理论中所要解决的实际问题,通常以最大化或最小化某个目标函数为目标,同时满足一系列约束条件。
上线性规划中,原问题可以表示为:Maximize(或Minimize):C^T*xSubject to:Ax ≤ b其中C和x分别为目标函数系数和决策变量,A和b则表示约束条件。
而对偶问题则是通过原问题的构造,利用拉格朗日对偶性得到的一个与原问题等价的问题。
对偶问题通常与原问题具有相同的最优解,在某些情况下,对偶问题甚至比原问题更容易求解。
对偶问题的一般形式可以表示为:Minimize:b^T * ySubject to:A^T * y ≥ C其中y为对偶变量,A^T为A的转置。
2. 最优解的概念和求解方法我们需要定义最优解的概念。
在数学和优化领域中,最优解通常指的是在给定条件下能够最大化或最小化一个特定目标函数的解。
上线性规划中,最优解即为能够最大化或最小化目标函数的决策变量取值。
为了求解原问题和对偶问题的最优解,通常可以采用不同的优化算法,如线性规划中的单纯形法、内点法等。
这些算法能够根据问题的特点和约束条件,有效地寻找到最优解。
3. 原问题和对偶问题最优解的关系在优化理论中,原问题和对偶问题之间存在着一种重要的对偶关系。
具体来说,对偶问题的最优解可以与原问题的最优解相互通联,满足一定的关系。
对于原问题的最优解x*和对偶问题的最优解y*,它们之间存在着强对偶性(strong duality)的关系。
强对偶性是指下面的不等式成立:C^T * x* ≤ b^T * y*A^T * y* ≥ C这个关系意味着原问题和对偶问题的最优解是互相约束的,当原问题的最优解达到最大值时,对偶问题的最优解也能达到最小值,反之亦然。
线性规划的对偶问题及其经济含义

线性规划的对偶问题及其经济含义线性规划的对偶问题及其经济含义信息工程学院数学12112421001崔旭在线性规划早期发展中最重要的发现就是对偶问题,即每一个线性规划问题(称为原始问题)都有一个与它对应的对偶线性规划问题(称为对偶问题)。
对偶理论主要研究经济学中的相互确定关系,涉及到经济学的诸多方面。
产出与成本的对偶、效用与支出的对偶,是经济学中典型的对偶关系。
当然,经济系统中还有许多其他这样的对偶关系。
对偶理论有许多重要应用:在原始的和对偶的两个线性规划中求解任何一个规划时,会自动地给出另一个规划的最优解;当对偶问题比原始问题有较少约束时,求解对偶规划比求解原始规划要方便得多;对偶规划中的变量就是影子价格。
对偶定理:有一对对偶的线性规划问题,若其一有一个有限的最优解,则另一个也有最优解,且相应的目标函数值相等。
若任一个问题具有无界解,则另一个问题无可行解。
对称形式的对偶:原问题和对偶问题只含有不等式约束时,一对对偶问题的模型是对称的,称为对称形式的对偶。
例如:原问题:minz=CX AX>=b X>=0对偶问题:max=Yb YA<=C X>=0对称性定理:对偶问题的对偶是原问题。
弱对偶性定理:若()0Y分别是原问题和对偶问题的可行解,则有X和()0C()()00b≥X Y最优性定理:若()0Y分别是原问题和对偶问题的可行解,且有X和()0()0CX=()0bY,则()0Y分别是原问题和对偶问题的最优解。
X和()0最优对偶变量(影子价格)的经济解释:由对偶定理可知,当达到最优解时,原问题和对偶问题的目标函数值相等。
如果在得到最优解时,某种资源并未完全利用,其剩余量就是该约束中剩余变量的取值,那么该约束相对应的影子价格一定为零。
因为在得到最优解时,这种资源并不紧缺,故此时再增加这种资源不会带来任何效益。
反之,如果某种资源的影子价格大于零,就说明再增加这种资源的可获量,还回带来一定的经济效益,即在原问题的最优解中,这种资源必定已被全部利用,相应的约束条件必然保持等式。
第二章对偶理论
3 5
x1 , x2 , x3 0
解:首先将原式变形
max Z 2 x1 3 x2 4 x3
2 x 3 x2 5 x3 2
3 x1 x2 7 x3 3
x1 4 x2 6 x3
5
x1 , x2 , x3 0
注意:以后不强调等式右段项 b≥0,原因在对偶单
纯型表中只保证 而j 不0 保证
=(1.1),分别是
(P_)_ 和__(D)的可行解。Z=10 ,W=40,故有
C X < Y b ,弱对偶定理成立。由推论⑴可知,W 的最
小值不能小于10,Z 的最大值不能超过40。
例二、已知
p : max Z x1 2x2
D : minW 2 y1 y2
x1 x2 x3 2
2x1 x2 x3 1
n
j 1
aij
yi
cj
(对偶问题)
yi 0
目标函数 约束条件
原问题
对偶问题
max
min
≤
≥
变量数量 约束条件个数
约束条件个数 变量数量
例三、
23
x1
x2
原问题
12 y1 2
2
≤ 12
8
y2
1
2
≤
8
16 y3 4 0 ≤ 16 12 y4 0 4 ≤ 12
对偶问题 2 3
二、线性规划的对偶理论
原问题 问题无界
无可 行解
对偶问题 无可 行解
问题无界
(对)
y1 y1
y1
y2 y2 0, y2
2 1 0
无可 行解
推论⑶.在一对对偶问题(P)和(D)中,若一个可 行(如P),而另一个不可行,(如D),则该可行的 问题无界。
对偶问题

123123123123123max ()53621816.16,0,f x x x x x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎪⎨++=⎪⎪≥⎩不限写出对偶问题,用单纯形法求原问题以及对偶问题的解。
解:对应于1,2,3对偶变量分别为1y ,2y ,3y ;根据课本可以直接写出原问题的对偶问题。
123123123123123minz=18y +16y +10y 2523..36,0,y y y y y y s t y y y y y y ++≥⎧⎪++≥⎪⎨++=⎪⎪≥⎩无限(1) 对原问题用单纯形法求解:将原问题化为标准型 (M 任意大的数)()124567812456124571245818Max f x 5x 3x 6x 6x 0x 0x Mx 2x 1823x 316.x 10 0x x x x x x x x s t x x x x x x =++-++-++-+=⎧⎪++-+=⎪⎨++-+=⎪⎪≥⎩列单纯型表如下、最终表中得到最优解为1x =14,5x =4 ,2x =4x =6x =7x =8x =0f(x)=5*14-4*6=46(2)对偶问题求解。
令y 3=y 4-y 5,并加入剩余变量y 6、y 8,人工变量y 7、y 9、y 10则有: Min f(y) =18y 1+16y 2+10y 4-10y 5+0y 6+My 7+0y 8+My 9+My 10124567124589124510110252336 0y y y y y y y y y y y y y y y y y y y ++--+=⎧⎪++--+=⎪⎨++-+=⎪⎪≥⎩y=因为非基变量都大于等于零。
则最优解为(0,1,3,0,0,0,1,0,0)T同时Z=46.总结:从此题目中可以看出来。
若原问题有最优解,则对偶问题也有最优解,而且目标函数的得数想同。
Q;Max f(x) =5x1+3x2+6x3求其对偶问题并分别用单纯形法求解解:设对应于约束条件①、②、③的对偶变量分别为y1、y2、y3,则根据原问题和对偶问题的对应关系,可以直接写出上述问题的对偶问题,即:Min f(y) =18y1+16y2+10y3对原问题用单纯形法求解:将原问题化为标准型Max f(x) =5x1+3x2+6x4-6x5+0x6+0x7-Mx8这里M是一个任意大的正数,列出单纯形表一.-3/2最终,非基变量的检验数都小于或等于0,最优解为对其对偶问题。
运筹学:第1章 线性规划 第3节 对偶问题与灵敏度分析

s.t.
4x1 3x1
5x2 200 10x2 300
x1, x2 0
9x1 4x2 360
s.t.
34xx11
5x2 10 x
200 2 300
3x1 10x2 300
x1, x2 0
则D为
min z 360y1 200y2 300y3 300y4
9 y1 4 y2 3y3 3y4 7 s.t.4 y1 5y2 10 y3 10 y4 12
amn xn bm ym xn 0
机会成本 a1 j y1 a2 j y2 aij yi amj ym
表示减少一件产品所节省的可以增加的利润
(3)对偶松弛变量的经济解释——产品的差额成本
机会成本
利润
min w b1 y1 b2 y2 bm ym
a11 y1
st
a12
y1
a1n y1
max z CX
(P)
AX b
s
.t
.
X
0
(D)
min w Yb
s.t.
YA C Y 0
• (2)然后按照(D)、(P)式写出其对偶
例:写出下面线性规划的对偶规划模型:
max z 2x1 3x2
min w 3 y1 5y2 1y3
x1 2x2 3 y1 0
s.t.
2xx11
例如,在前面的练习中已知
max z 2.5x1 x2 的终表为
3x1 5x2 15 s.t.5x1 2x2 10
x1, x2 0
0 x3 9 2.5 x1 2
0 19 1 - 3
5
5
1
2
0
1
5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对偶问题的解
对偶问题是原始优化问题的一种等价形式,通过转换变量和约束条件来得到。
对偶问题可以提供原始问题的下界,并且在某些情况下,其解与原始问题的解是相等的。
通常,求解对偶问题的步骤如下:
1. 确定原始问题的拉格朗日函数:根据原始问题的约束条件,构建拉格朗日函数。
该函数包括原始问题的目标函数和约束条件的乘子项。
2. 构建对偶问题:将拉格朗日函数进行最大化或最小化,并移除原始问题的变量和约束条件。
这样就得到了对偶问题。
3. 求解对偶问题:使用合适的优化方法(如KKT条件、凸优化理论等)来求解对偶问题。
可以使用梯度法、内点法、对偶分解等算法来求解对偶问题。
4. 根据对偶问题的解,获得原始问题的下界:通过对偶问题的解,计算原始问题的下界值。
如果对偶问题达到最优解,则其下界是原始问题的最优解。
5. 分析对偶问题的解与原始问题的关系:根据所使用的对偶性质和定理,分析对偶问题的解与原始问题的解之间的关系。
在某些情况下,二者是相等的,即对偶问题的解也是原始问题的解。
需要注意的是,对偶问题并不总是存在或者有意义。
它们的存在和有效性取决于原始问题的结构和特性。
因此,在求解对偶问题之前,需要对原始问题进行分析,并确保对偶问题的适用性。
同时,对偶问题的解也可以提供一些关于原始问题的额外信息,如灵敏度分析、约束条件的松弛程度等。
这些信息对于理解和优化原始问题都是有益的。
综上所述,通过对偶问题的解,我们可以获得原始问题的下界,并在一些情况下得到原始问题的最优解。
