初中物理竞赛及自主招生专题讲义第六讲热学第三节热平衡方程与热平衡问题含解析
初中物理竞赛专题——热学
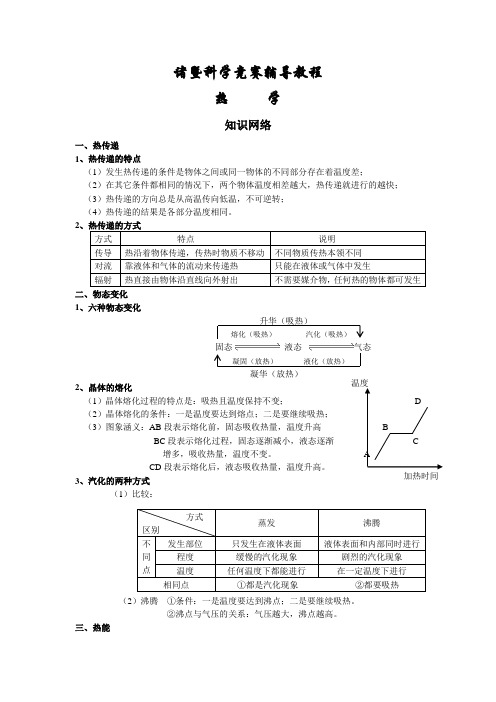
诸暨科学竞赛辅导教程热 学知识网络一、热传递1、热传递的特点(1)发生热传递的条件是物体之间或同一物体的不同部分存在着温度差;(2)在其它条件都相同的情况下,两个物体温度相差越大,热传递就进行的越快;(3)热传递的方向总是从高温传向低温,不可逆转;(4)热传递的结果是各部分温度相同。
2二、物态变化1、六种物态变化凝华(放热) 2、晶体的熔化 (1)晶体熔化过程的特点是:吸热且温度保持不变; (2)晶体熔化的条件:一是温度要达到熔点;二是要继续吸热; (3)图象涵义:AB 段表示熔化前,固态吸收热量,温度升高 BC 段表示熔化过程,固态逐渐减小,液态逐渐 增多,吸收热量,温度不变。
CD 段表示熔化后,液态吸收热量,温度升高。
3、汽化的两种方式(1)比较:(2)沸腾 ①条件:一是温度要达到沸点;二是要继续吸热。
②沸点与气压的关系:气压越大,沸点越高。
三、热能加热时间1、分子运动论的内容物质是由分子构成的;分子永不停息地做无规则的运动;分子之间有相互作用的引力和斥力。
2、热能、热量和温度(1)物体中大量分子做无规则运动所具有的能,叫做热能;(2)热量是物体在热传递过程中,吸收或放出热的多少,是物体改变热能的多少;(3)温度表示物体的冷热程度;(4)物体温度升高,热能增加;温度降低,热能减小。
3、改变热能的两种方法做功 外界对物体做功,物体的热能增加(机械能 热 能)方法 物体对外界做功,物体的热能减小(热 能 机械能)热传递 物体吸收热量,热能增加(别的物体 物体)物体放出热量,热能减小(物体 别的物体)4、物质的比热(1)比热是物质的一种特性。
比热的定义式:C= Q 吸/(m △t ),物质的比热与物体的质量、体积、温度变化的大小等无关。
水的比热是4.2×103焦/(千克·℃),水的比热比一般物质的比热要大。
(2)热平衡方程:①物体温度改变时,吸热和放热的计算公式:Q 吸 = c m ( t -t 0 ) Q 放 = c m ( t 0-t )②在热传递过程中,如果没有热量损失,高温物体放出的热量等于低温物体吸收的热量Q 吸 = Q 放四、热能的利用——热机热机是把热能转化为机械能的机器。
热平衡方程题

热平衡方程题摘要:1.热平衡方程题的概述2.热平衡方程题的解题思路3.热平衡方程题的实例解析正文:一、热平衡方程题的概述热平衡方程题是物理学中关于热力学平衡的一个基本问题,主要涉及到热力学第一定律和热力学第二定律的应用。
在热平衡方程题中,通常会给定一个或多个物体,以及它们之间的热交换过程,要求求解物体间的热力学状态参量,如温度、内能等。
二、热平衡方程题的解题思路解决热平衡方程题,通常需要以下几个步骤:1.确定研究对象:根据题目描述,确定涉及到的物体,并明确它们之间的热交换关系。
2.建立热平衡方程:根据热力学第一定律,物体的内能变化等于物体所吸收的热量和对外做的功的和,即ΔU = Q - W。
在热平衡状态下,物体的内能变化为零,因此有ΔU = 0。
同时,根据热力学第二定律,热量不可能自发地从低温物体传递到高温物体,即Q = W。
3.解方程求解:将已知条件代入热平衡方程,解出物体间的热力学状态参量。
三、热平衡方程题的实例解析假设有两个物体A 和B,A 的温度为TA,B 的温度为TB,A 和B 之间存在热交换。
已知TA > TB,求交换后的温度。
根据热平衡方程,有:ΔUA = QA - WA = 0ΔUB = QB - WB = 0由于QA = QB,且WA = WB(在热平衡状态下,物体对外做的功为零),因此:QA = QBTA * cA * mA = TB * cB * mB其中,c 为比热容,m 为质量。
解上式,可得:TA / TB = cB / cA * mB / mA由此可见,在热平衡状态下,物体A 和B 的温度与它们的比热容和质量成正比。
总结:热平衡方程题是热力学中的一个基本问题,解决此类问题需要掌握热力学基本定律和解题方法。
热学解题技巧热平衡和热容的关系计算

热学解题技巧热平衡和热容的关系计算热学解题技巧——热平衡和热容的关系计算热学是研究热现象及其规律的学科,它在物理学和工程学中具有重要的地位。
在热学中,热平衡和热容是两个基本概念,它们之间有着紧密的关系。
本文将介绍热平衡和热容的基本概念,并探讨它们之间的关系,同时还将给出一些解题的技巧和方法。
一、热平衡的概念热平衡是指在没有外界热交换的条件下,系统内部各部分之间达到的一种稳定状态。
在热平衡状态下,系统内外部的温度是相等的,不存在温度差,也就是热平衡状态下的热交换为零。
热平衡是热学研究的重要前提,只有在热平衡条件下,热力学定律和热学公式才能成立。
二、热容的概念热容是指物体在单位温度变化时吸收或释放的热量。
热容是物质对热量变化的响应性指标,它表示物体对热量变化的敏感程度。
热容的单位通常用焦耳/摄氏度(J/℃)表示。
热容与物体的质量、物质种类和温度相关,不同物质的热容也不同。
三、热容与热平衡的关系在热平衡状态下,系统内外温度相等,因此热平衡时系统吸收或释放的热量为零。
根据热容的定义,我们可以得出在热平衡条件下物体的热容为零。
这是因为物体不吸收或释放热量,热容为零意味着物体对温度变化不敏感。
四、热容的计算方法1. 对于固体物体,其热容可以通过下面的公式计算:C = mc其中,C表示热容,m表示物体的质量,c表示物体的比热容。
2. 对于液体物体,其热容可以通过下面的公式计算:C = mc其中,C表示热容,m表示液体的质量,c表示液体的比热容。
3. 对于气体物体,其热容可以通过下面的公式计算:C = mc其中,C表示热容,m表示气体的质量,c表示气体的比热容。
需要注意的是,在计算热容时,物体的质量、温度和比热容都需要使用相应的单位,以确保计算结果的准确性。
五、热容的应用热容在热学中有着广泛的应用,特别是在热传导、热量计算和能量转化等方面。
热容是计算物体热力学性质的重要指标,可以用于设计和优化热能设备,提高能源利用效率。
热平衡方程题

热平衡方程题引言热平衡方程是热力学中一个重要的概念,用于描述系统在热平衡状态下的能量交换。
它是基于能量守恒定律和熵增加原理推导出来的,并在工程学、物理学、化学等领域有广泛应用。
本文将介绍热平衡方程的基本概念、推导过程以及一些典型的应用实例。
1. 热平衡方程的基本概念热平衡方程描述了一个系统在热平衡状态下的能量交换情况。
在一个封闭系统中,如果系统与外界没有任何物质和能量交换,那么系统内部各个部分之间的温度将会趋于一致,达到热平衡状态。
根据能量守恒定律,系统内部各个部分之间的能量转移可以通过传导、对流和辐射三种方式进行。
传导是指由于温度差引起的分子或电子运动传递能量;对流是指由于流体或气体的运动带走或带来能量;辐射是指通过电磁波辐射来传递能量。
根据熵增加原理,系统内部的能量转移会使系统的熵增加。
熵是描述系统无序程度的物理量,它与能量转移过程中产生的不可逆性有关。
在热平衡状态下,系统内部各个部分之间的能量转移是无序的,因此系统的熵不会发生变化。
综上所述,可以得到热平衡方程的基本表达式:∑Q=0其中,∑Q表示系统内部各个部分之间的能量转移总和。
在热平衡状态下,这个总和必须等于零。
2. 热平衡方程的推导过程为了推导出热平衡方程,我们需要借助一些基本的热力学定律和关系。
首先,根据能量守恒定律,在一个封闭系统中,能量不能被创造或消灭,只能从一种形式转化为另一种形式。
因此,在任意一个小区域内,能量转移可以通过传导、对流和辐射三种方式进行。
其次,在一个封闭系统中,在没有外界物体交换物质和能量的情况下,可以假设该封闭系统是一个孤立系统。
在孤立系统中,由于没有外界物体与之交换,系统内部的能量转移只能在系统内部进行。
最后,根据熵增加原理,在一个封闭系统中,系统的熵不会减少,只能增加或保持不变。
在热平衡状态下,系统内部各个部分之间的能量转移是无序的,因此系统的熵不会发生变化。
综合以上几点,可以得到热平衡方程的推导过程如下:1.假设封闭系统中有n个小区域,每个小区域之间存在能量转移。
物理竞赛讲座《热学》

2
1熔解和凝固 物质从固态变为液态叫熔解,从液态变为固态叫凝固。 晶体在物质熔解时,固态和液态可以共存的温度叫熔点。同种晶 体在某一压强下的熔点也是其凝固点。
物态变化
晶体在熔解(或凝固)过程中温度保持在熔点(或凝固点)不变。 非晶体无一定的熔点。非晶体在熔解(或凝固)过程中,温度不 停地上升或下降。 晶体的熔点与压强有关。熔解时体积膨胀的晶体,随所受压强增 大,溶点升高;熔解时体积缩小的晶体(如冰、锑),随所受压 强增大,溶点降低。 晶体中渗杂质后,溶点一般降低。
沸腾是在液体表面和内部同时发生的汽化 过程,沸腾发生时,它的饱和汽压必须等于外 界压强,沸腾时液体的温度不变,这个温度称 为该液体的沸点;外部压强增大,液体的沸点 升高;外部压强降低,沸点降低;不同的液体 在相同的压强下沸点不同。 从宏观角度,沸腾不同于蒸发,但从分子 运动论观点,两者并无本质差别。沸腾时,在 气、液分界面上汽化仍以蒸发的方式在进行, 只是在液体内部同时出现大量小气泡上浮起至 液面破裂,大大增加了汽化的速度。
有同学采用这样的解法
(76 20) 60 76 96 300 T2
T2 380K
P PV 1V1 2 2 T1 T2
水银溢出经历了哪几个阶段?
第1阶段为等压膨胀过程,水银上升了16cm
V1 V2 T1 T2
T2 380K
第2阶段,继续加热,水银将外溢,气体 压强将减小,体积V将增大,PV乘积的变 化规律就只能借助于数学工具进行讨论, PV/T=C,当PV最大时,T就是题中要求的 最高温度。
由此得到 b1 b H 时,
注入细管内水银柱的长度有最大值xmax
xmax b H
物理热平衡方程计算方法

物理热平衡方程计算方法热平衡是物理学中的重要概念,它描述了物体之间热量的交换达到平衡的状态。
在研究热平衡问题时,我们常常使用热平衡方程来计算物体之间的热量交换。
本文将介绍热平衡方程的计算方法。
热平衡方程是基于热力学第一定律的能量守恒原理而推导出来的。
根据这一定律,能量在物体之间的传递是通过热量的形式进行的。
热平衡方程的一般形式如下:Q = mcΔT其中,Q表示热量的大小,单位为焦耳(J);m表示物体的质量,单位为千克(kg);c表示物体的比热容,单位为焦耳/千克·摄氏度(J/(kg·℃));ΔT表示温度的变化,单位为摄氏度(℃)。
通过热平衡方程,我们可以计算物体之间的热量交换。
首先,我们需要确定物体的质量、比热容以及温度的变化。
然后,代入热平衡方程中进行计算,即可得到热量的大小。
例如,假设有两个物体A和B,它们之间存在热量交换。
物体A的质量为1kg,比热容为500J/(kg·℃),温度从20℃升高到50℃;物体B的质量为2kg,比热容为800J/(kg·℃),温度从50℃降低到30℃。
我们可以使用热平衡方程来计算它们之间的热量交换。
我们计算物体A的温度变化ΔT1 = 50℃ - 20℃ = 30℃。
代入热平衡方程,可以得到物体A的热量变化Q1 = 1kg × 500J/(kg·℃) × 30℃ = 15000J。
接下来,我们计算物体B的温度变化ΔT2 = 30℃ - 50℃ = -20℃。
注意到温度变化为负值,表示温度降低。
代入热平衡方程,可以得到物体B的热量变化Q2 = 2kg × 800J/(kg·℃) × (-20℃) = -32000J。
根据热平衡方程,物体A释放了15000J的热量,而物体B吸收了32000J的热量。
由于热量的守恒,物体A释放的热量等于物体B 吸收的热量,即15000J = -32000J。
热平衡问题的综合计算、物态变化图象与比热容综合+课件---+2024-2025学年人教版物理九年级全

公式列出一个平衡方程,以此解决相应问题。
1.(2024·开州区期中)质量和初温都相等的铁块和水,已知铁的比热容
小于水的比热容,如果它们放出相同的热量后,将铁块放入水中,则
( C )
A.它们之间没有热传递
B.热量从铁块传向水
C.热量从水传向铁块
D.条件不足,无法判断
2.(2023·江津中学月考)冷水与热水混合时,水
小于
容______(选填“大于”“等于”或“小于”)段的比热容。
1
2
3
4
5
2.为探究固体熔化时的温度变化规律,小欢
在绝热容器内装入 某固体物质,其温度
为− ℃。把一个每分钟放出相同热量的电
加热器放入容器内的固体物质中,外接电源,
闭合开关,开始加热并计时。加热器在 内放出的热量为
C.甲、乙两金属球升高的温度相等
D.甲、乙两金属球的比热容相等
6.(2023·凤鸣山中学期末改编)甲、乙两容器中装有质量相等的水,水
温分别为 ℃和 ℃,现将一温度为 ℃的金属球放入甲容器中,热
平衡后水温升高到 ℃,然后迅速取出金属球并放入乙容器中,热平衡
后乙容器中的水温为(不计热量损失和水的质量的变化)( A )
对应物质的比热容较小。
1.某同学用一种加热器将质量为 的
冰持续加热,使其熔化直至沸腾,记录
并绘制出温度随时间变化的图象如图所
示。根据图象可以看出该物质在点的
大于
内能______(选填“大于”“等于”或“小于”)在点的内能,原因是
晶体在熔化过程中吸热,内能增大
________________________________。根据图象还可以看出段的比热
. × ,由实验数据得到的图象如图所示。该物质在 ∼
(完整版)初中物理提高与自招---比热容与热平衡方程

初中物理自招与提高------- 比热容与热平衡方程一.基本看法1、热传达(1)热传达是能量从 的物体传到 的物体,也许从物体的 部分传到部分的一种现象。
(2)热传达的条件:。
( 3)热传达的本质:。
(4)热传达的三种方式:①热传导②热对流 ③热辐射2、热量(1)热量是为了衡量在热传达过程中 的多少而引入的。
通常用 Q 来表示,它的国际单位是。
一根火柴棒完满燃烧大体能够放出 的热量。
注意:热量对应于热传达过程,我们只能说物体吸取也许放出多少热量,不能够说“物体拥有多少热量” !(2)热传达过程中,高温物体 热量,温度,低温物体热量,温度。
3. 比热容物体温度高升时,吸取的热量与那些因素有关呢?阅读以下内容,请回答以下问题。
质量 m ( Kg )物质种类高升温度t ( 1 水 1 C 1 水 2 C 2 水 2 C 1 酒精 1 C 1酒精 2 C 2酒精2 CC ) 吸取热量 Q ( 103J )(1) 1Kg 的水,温度高升 1 C ,要吸取的热量,温度高升 2 C ,要吸取的热量。
1Kg 的酒精,温度高升 1C ,要吸取的热量,温度高升 2C ,要吸取的热量。
结论 1: :质量同样的同种物质,吸取热量与高升温度成 比。
(2) 1Kg 的水,温度高升 2 C ,吸取的热量是; 2Kg 的水,温度高升 2 C ,吸收的热量是1Kg 的酒精, 温度高升 2 C ,吸取的热量是 ; 2Kg 的酒精, 温度高升 2 C ,吸取的热量是结论 2:质量不同样的同种物质,高升同样的温度时,吸取的热量与 成正比。
(3)1Kg 的水, 温度高升 1 C ,要吸取的热量, 1Kg 的酒精, 温度高升 1 C ,要吸取的热量,可见,它们质量同样、高升温度同样,但由于 不同样,吸取热量也不同样结论 3:不同样种物质,即使质量同样、高升温度同样,吸取热量也经常不同样。
因此可知,物体吸取热量的多少,与 、 、 都有关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 热平衡方程与热平衡问题两个温度不同的物体靠近时,会发生热传递。
高温物体放出热量,温度降低,低温物体吸收热量,温度升高。
当两者温度相同时,热传递停止,此时物体即处于热平衡状态。
1.热平衡方程设高温物体的比热容为1c ,质量为1m ,初始温度为1t ,低温物体的比热容为2c ,质量为2m ,初始温度为()221t t t <,当两者达到热平衡时,共同温度为0t ,则可知201t t t <<。
若不计能量损失,则高温物体放出的热量Q 放等于低温物体吸收的热量Q 吸,即Q Q =吸放,或()()11102202c m t t c m t t -=-,这即是两个物体热交换时的平衡方程,可解得t 11122212012c m t c m t m m t c c ++=,若已测得0t 的值,则可求得()()11102202c m t t c m t t -=-,因此可以用这种方法测物体的比热容。
例1 (上海第5届初中物理竞赛复赛)温度不同的两个物体相互接触后将会发生热传递现象。
若不计热量的损失,则当两物体达到热平衡状态时,它们的温度相同,且高温物体放出的热量等于低温物体所吸收的热量。
现有三种不同的液体A ,B ,C ,它们的初温度分别为15℃,25℃,35℃。
当A 和B 液体混合并到达平衡状态时,其平衡温度为21℃;当B 和C 液体混合并到达平衡状态时,其平衡温度为32℃。
求A 和C 液体混合并到达平衡状态时的平衡温度。
分析与解 设A ,B ,C 三种液体的比热容分别为1c ,2c ,3c ;质量分别为1m ,2m ,3m 。
则A 与B 混合时,有()()112221152521c m c m -=-℃℃℃℃,即112223c m c m =;B 与C 混合时,有()()223332253532c m c mc -=-℃℃℃℃,即332273c m c m =;当A 与C 混合时,设热平衡后的温度为t ,则有()()11331535c m t c m t -=-℃℃,将以上各式代入,可解得30.56t =℃。
例2 (上海第27届大同杯初赛改编)将一杯热水倒入盛有冷水的容器中,冷水的温度升高了10℃,再向容器内倒入一杯相同质量和温度的热水,容器中的水温又升高了6℃.则:(1)一杯热水与容器中原有的冷水质量之比为________。
(2)热水与容器中原有的冷水的温差为________℃。
(3)如果继续向容器中倒入一杯同样的热水,则容器中的冷水水温会继续升高________℃.分析与解 不妨设容器中原有冷水的质量为M ,温度为1t ,一杯热水质量为m ,温度为2t ,第一次倒入热水平衡后,水温均变为110t +℃,冷水温度升高了10℃,热水温度降低了()2110t t -+℃,由吸热等于放热,有()211016cM cm t t ⋅=-+⎡⎤⎣⎦① 第二次倒入热水平衡后,水温均变为116t +℃,冷水温度再次升高了6℃,热水温度降低了()2116t t -+℃,有()()21616c M m cm t t +⋅=-+⎡⎤⎣⎦ ②由①式可得()2111010M t t m =--⎡⎤⎣⎦ ③ 由②式可得()2111166M t t m +=--⎡⎤⎣⎦ ④ 联立③④式,可解得3Mm =,2140t t -=℃。
第三次倒入热水平衡后,设冷水温度又升高了t ∆,则冷水与热水水温均为116t t ++∆℃,热水温度降低了()2116t t t -++∆℃,则有()()21216c M m t cm t t t +⋅∆=-++∆⎡⎤⎣⎦℃ ⑤变形后,得()211216M t t t m t +=---∆⎡⎤⎣⎦∆ ⑥ 将3Mm =,2140t t -=℃代入⑥式,可解得4t ∆=℃.上文提供的方法可以解决两种物质彼此进行热交换时的一些问题,如果有三种或者三种以上的物质彼此进行热交换,则情况要复杂些.2.多个物体的热平衡问题例3 设有N 个物体,它们的比热容、质量、初温分别为()111,,c m t ,()222,,c m t ,()333,,c m t ,…,(),,N N N c m t ,现将这N 个物体置于封闭绝热的容器中充分进行热交换,假设容器不吸热且各物体之间不发生化学反应,也无物态变化,问热平衡后,物体的温度是多少?分析与解 本题的困难在于,无法确定热平衡后系统的温度0t 与各物体初温1t ,2t ,3t 等的大小关系,也就无法确定是哪些物体吸热,哪些物体放热。
不妨规定如下:令()0Q cm t t =-,若0t t >,则0Q >,Q 为物体放出的热量;若0t t <,则0Q <,Q 为物体吸收的热量。
则根据放出的总热量与吸收的总热量相等,有1230N Q Q Q Q +++⋅⋅⋅+=即()()()()11102220333000N N N c m t t c m t t c m t t c m t t -+-+-+⋅⋅⋅+-=解得1112223330112233N N N N Nc m t c m t c m t c m t t c m c m c m c m +++⋅⋅⋅+=+++⋅⋅⋅+ 3.有物态发生变化的热平衡问题物体在吸热或者放热时,有时要发生物态变化,比如0℃的冰吸热融化成0℃的水,或0℃的水放热凝固成0℃冰等。
由于即使是同种物质,状态不同时,比热容也会发生变化,再者物质虽然温度不变,但由一种状态变为另一种状态时,也要吸热或者放热,因此这类热平衡问题必须要考虑物质的熔化热。
例4 (上海第8届普陀杯复赛)已知冰的比热容为()32.110J/kg ⨯⋅℃,冰的熔化热为33.3610J/kg ⨯,水的比热容为()34.210J/kg ⨯⋅℃。
把质量为10g 、温度为0℃的冰和质量为200g 、温度为100℃的金属块同时投入质量为100g 、温度为20℃的水中,当它们达到热平衡时,它们的共同温度为30℃。
若不计热量损失,求金属块的比热容。
分析与解 先将本题中各物质吸热、放热情况计算如下: 0℃的冰融化成0℃的水,需吸热为()31 3.3610J/kg 0.01kg 33.6J Q =⨯⋅⨯=℃冰融化成0℃的水后,质量仍为0.01kg ,这些0℃的水温度升高30℃需吸收的热量为()32 4.210J/kg 0.01kg 301260J Q -=⨯⋅⨯⨯=℃℃质量为100g 、初温为20℃的水温度升高到30℃需吸收的热量为()33 4.210J/kg 0.1kg 104200J Q =⨯⋅⨯⨯=℃℃金属块放出的热量为()40.2kg 10030Q c =⨯⨯-金℃℃又41235493.6J Q Q Q Q =++=因此,可解得()392.4J/kg c =⋅金℃。
4.物体的散热问题高温物体散热的快慢,除了和物体的表面积、物体周围的介质以及物体表面介质的流动性等有关以外,还和物体与环境的温差有关.例5 (上海第29届大同杯复赛)把一个装满80℃热水的热水袋悬挂在空中,并用一支温度计插入热水中来测量水温,假设室温维持在20℃不变,测得温度与时间的数据如表6.1所示.表6.1T t - (2)试问水的温度由80℃降为30℃,经过的时间为多少? 分析与解 水的最终温度为室温(20℃),水降温的快慢与温差有关,故将表改列表6。
2。
表6.2由表可以看出,每隔10min 得到的温度与室温之差是以等比级数下降的:60.0 1.6536.4=,36.4 1.6522.1=,22.1 1.6513.4=……以此类推,则可得11060 1.6520T =-。
因此解得当30T =℃时,35.8min t =.练习题1.(上海第5届大同杯初赛)质量相同的三杯水,初温分别是1t ,2t ,3t ,而且123t t t <<,把它们混合后,不计热损失,则混合温度是( )。
A .1232t tt ++B .1233t t t ++C .3122t t t -+D .2312t t t -+ 2.(上海第8届大同杯初赛)两种不同的液体,它们的质量、比热、初温度分别为1m 和2m ,1c 和2c ,1t 和2t ,且21t t >.若不计热量损失,则把它们混合后的共同温度为( )。
A .2221112211cm t c m t c m c m --B .2221112211c m t c m t c m c m ++ C .2221112211c m t c m t c m c m -+ D .1112221122c m t c m t c m c m -+3.(上海第2届大同杯初赛)将放在100℃的水中的铜块取出,放进10℃的煤油中,当达到热平衡时,若不计过程中的热损失,则下列说法中正确的是( )。
A .煤油吸收的热量一定等于铜块放出的热量B .煤油升高的温度一定等于铜块降低的温度C .热平衡时的温度一定大于10℃而小于100℃D .煤油升高的温度一定小于铜块降低的温度4.(上海第29届大同杯初赛)甲、乙两液体的密度比为5:4ρρ=甲乙:,体积比为:2:3V V =甲乙,比热容比为:1:2c c =甲乙,且它们的初温不等。
现将它们混合(不发生化学反应),不计混合过程中的热损失,达到热平衡后液体温度相对各自初温变化量的绝对值分别为t∆甲和t∆乙,则:t t∆∆甲乙为().A.16:15 B.15:16 C.12:5 D.5:125.(上海第31届大同杯初赛)在两个相同的杯子内盛有质量相等的热水和冷水,将一半热水倒入冷水杯内,冷水杯内的温度升高21℃,若再将热水杯内剩余热水的一半再次倒入冷水杯内,冷水杯内的水温会升高()。
A.9℃B.8℃C.6℃D.5℃6.(上海第28届大同杯初赛)A,B两物体质量相等,温度均为10℃;甲乙两杯水质量相等,温度均为50℃。
现将A放入甲杯,B放入乙杯,热平衡后甲杯水温降低了4℃,乙杯水温降低了8℃,不考虑热量的损耗,则A,B两物体的比热容之比为()。
A.4:9 B.3:5 C.2:3 D.1:27.(上海第26届大同杯初赛)甲、乙两容器中装有质量相等的水,水温分别为25℃和75℃,现将一个温度为65℃的金属球放入甲容器中,热平衡后水温升高到45℃;然后迅速取出金属球并放入到乙容器中,热平衡后乙容器中的水温为(不计热量损失和水的质量变化)()。
A.65℃B.60℃C.55℃D.50℃8.(上海第24届大同杯初赛)将质量为m、温度为0℃的雪(可看成是冰水混合物)投入装有热水的容器中,热水的质量为M ,平衡后水温下降了t ;向容器中再投入质量为2m 的上述同样性质的雪,平衡后容器中的水温恰好又下降了t 。
