金字塔模型证明过程
小学奥数平面几何五种面积模型

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型),掌握五大面积模型的各种变形知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如右图S :S2 a:b③夹在一组平行线之间的等积变形,如右图S^ACD S^BCD;反之,如果S A ACD S A BCD,则可知直线AB平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在△ABC中,D,E分别是AB, AC上的点如图⑴(或D在BA的延长线上,E在AC上),蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径•通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝶形定理”):2 2①S i: S3 a : b②S1: S3: S?: S4 a2: b2 : ab : ab ;③S的对应份数为 a b 2.四、相似模型(一)金字塔模型(AB AC) :(AD AE)则S AABCS A ADE图⑴三、蝶形定理任意四边形中的比例关系图⑵(“蝶形定理”):① S i :S2S4 : S3 或者S i S3 S2 S4 ② AO : OC S| S2 : S4 S 3)沙漏模型bAEB C CG GB A EFOBDGGBB【解析】 EEBF【巩固】 几厘米?A EA E长方形EBGF 的长BG 为10厘米,那么长方形的宽为2 4.5 4 2 16.5 ,所以长方形EFGH 面积为33.如图所示,正方形ABCD 的边长为8厘米 如图,正方形 ABCD 勺边长为6,AE 的面积为F CF C连接DE DF 则长方形EFGH 勺面积是三角形 DEF 面积的二倍 三角形DEF 的面积等于正方形的面积减去三个三角形的面积,1. 5, CF2.长方形 EFGH (只要其形状不改变,不论大小怎样改变它们 S A DEF6 6 1.5 6 2 2 6 ① J AD A E AB AC ② S A ADE : ABC所谓的相似三角形,就是形状相同,大小不同的三角形 都相似),与相似三角形相关的常用的性质及定理如下⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型) 在三角形 ABC 中,AD , BE , CF 相交于同一点 0,那么 S ABO : S ACO BD : DC . 上述定理给出了一个新的转化面积比与线段比的手段,因为 ABO 和 ACO 的形状很象燕子的尾巴,所以这个定理被称为燕尾定理•该定理在许多几何 题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形 之中,为三角形中的三角形面积对应底边之间提供互相联系的途径 典型例题 【例1】DE BC AF AG ;AF 2:AG 2 CD GD GB A---- 7/ /1 /F J|\ /C【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)•三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG •(我们通过△ ABG 把这两个长方形和正方形联系在一起)•1•••在正方形 ABCD 中,S A ABG — AB AB 边上的高,21二S A ABGS AABCD (三角形面积等于与它等底等高的平行四边形面积的一半)21冋理,S A ABG — S EFGB ••••正方形ABCD 与长方形EFGB 面积相等. 长方形的宽 8 8 10 6.4(厘米)•【例2】 长方形ABCD 的面积为36cm 2, E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影 部分面积是多少?【解析】 解法一:寻找可利用的条件,连接 BH 、HC ,如下图:可得:SEHB-S 2AHB 、SFHB—S CHB 2、 SDHG— S DHC2,S A BCDS AHB S CHBS CHD36即 S EHB SBHFSDHG —(S AHBS CHBS C HD )-36218 ;而SEHBSBHFS DHGs阴影SEBFSEBF1-BE BF 1AB) 1(二 BC) 1 36 4.5222 2 8所以阴影部分的面积是: 解法二:特殊点法•找 那么图形就可变成右图:S 阴影 18 S EBF 18 4・5 13・5AD (H)E 、—GB F C这样阴影部分的面积就是DEF的面积,根据鸟头定理,则有s 阴影 S ABCD S AED S BEF S CFD 36- - 36 - - - 36 -- 2 2 2 2 2 2 2【巩固】在边长为6厘米的正方形 ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与 P 点连接,求阴影部分面积.【解析】(法1)特殊点法.由于P 是正方形内部任意一点, 可采用特殊点法,假设P 点与A 点重合,贝U 阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的 丄和-, 4 6所以阴影部分的面积为 62 (- -) 15平方厘米. 4 6(法2)连接PA 、PC .由于 PAD 与 PBC 的面积之和等于正方形 ABCD 面积的一半,所以上、下两个阴影三角形 的面积之和等于正方形 ABCD 面积的-,同理可知左、右两个阴影三角形的面积之和等于正4 方形ABCD 面积的1 ,所以阴影部分的面积为 62 (-丄)15平方厘米.6 4 6【例3】 如图所示,长方形ABCD 内的阴影部分的面积之和为70, AB 8 , AD 15,四边形EFGO的面积为 _________ .【解析】利用图形中的包含关系可以先求出三角形 AOE 、DOG 和四边形EFGO 的面积之和,以及三 角形AOE 和DOG 的面积之和,进而求出四边形 EFGO 的面积.由于长方形 ABCD 的面积为15 8 120,所以三角形BOC 的面积为120 130 ,所以三角4形AOE 和DOG 的面积之和为120 370 20 ; 4又三角形AOE 、DOG 和四边形EFGO 的面积之和为120 1- 30,所以四边形EFGO2 4的面积为30 20 10.另解:从整体上来看,四边形 EFGO 的面积 三角形AFC 面积 三角形BFD 面积 白色部 分的面积,而三角形 AFC 面积 三角形BFD 面积为长方形面积的一半,即 60,白色部分的 面积等于长方形面积减去阴影部分的面积,即120 70 50 ,所以四边形的面积为60 50 10 .36 13.5.如图,长方形 ABCD 的面积是36, E 是AD 的三等分点,AE 2ED ,则阴影部分的面积 为 ________ .1 1 3 — 6 -2.7 .25已知ABC 为等边三角形,面积为 400, D 、E 、F 分别为三边的中点,已知甲、乙、丙面 积和为143,求阴影五边形的面积.(丙是三角形HBC )所以 DE 、DF 、EF 是三角形ABC 的中位线,也就与 三角形ABN 和三角形AMC 的面积都等于三角形 ABC 的半,即为200.即400 S 丙 200 200SAMHN,所以 S ^S AMHN.又?阴影S ADF S 甲 S 乙S AMHN,所以S阴影S 甲s 丙SADF1 143400 43 .4如图, 已知 CD 5 , DE 7 ,EF 15, FG 6,线段AB 将图形分成两部分,左边部分 【例5】根据图形的容斥关系,有 S ABCS 丙S ABN S AMC S AMHN,面积是38,右边部分面积是 65,那么三角形 ADG 的面积是 ______________【巩固】 【解析】 如图,连接0E .根据蝶形定理,ON : NDS COE: SCDEOM : MABOE: SBAE1SS BDE2:S BAEOED~ S 矩形ABCD4S OEA 1 1 2S CAE :S CDE 1:1,所以S OEN2S OED ;1:4,所以 S OEM 1 S OEA .52S OED 6 ,所以阴影部分面积为:【例4】 【解析】 因为D 、E 、F 分别为三边的中点, 对应的边平行,根据面积比例模型,【例6】 如图在 △ ABC 中,D,E 分别是 AB,AC 上的点,且AD: AB 2:5 , AE : AC 4:7 , S A ADE 平方厘米,求 △ ABC 的面积.【解析】连接 BE , S A ADE : S A ABE AD : AB 2:5 (2 4) : (5 4),S\ ABE : S A ABC AE : AC4: 7 (45) : (7 5),所以 S A ADE: S A ABC(2 4): (75),设S A ADE 8份,则S A ABC 35份,Sx ADE 16平方厘米,所以1份是2平方厘米,35份就是70 平方厘米,△ABC 的面积是70平方厘米•由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角 (相等角或互补角)两夹边的乘积之比根据题意可知,CF 5 7 15 27;DG 715 6 28;151221所以, S BEFSCBF ,S BECS CBF , S AEGS SADG , S AED2/27282115712于是: S ADG S CBF 65 ; SADGSCBF38 ;2827282/可得S ADG 40 . 故三角形 ADG 的面积是 40—S 28ADG16【巩固】如图,三角形 ABC 中,AB 是AD 的5倍1,那么三角形 ABC 的面积是多少?AC 是AE 的3倍,如果三角形 ADE 的面积等于【解析】连接BE .••• EC 3AE…S VABC 3S VA BE 又 T AB 5AD --S V ADES VABE 5 S VABC 15,…S VABC【巩固】如图,三角形 ABC 被分成了甲(阴影部分)、乙两部分,BD DC 4 , BE 3 , AE 6,乙 部分面积是甲部分面积的几倍?ACAG【解析】连接AF , BD .所以S EFGHSA AEHSA CFGSA DHGSA BEFSABCD8 8 15+3+236 .平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC 的面积是50平方厘米.由 此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角 (相等角或互补角)两夹边的乘积之比的面积是2,求平行四边形 ABCD 与四边形EFGH 的面积比.【解析】 连接AD .••• BE 3, AE 6二 AB 3BE , S VABD3S VBDE又••• DC 4,…S V ABC2S VABD ,… S VABC6S VBD E , S 乙5S 甲 .如图在 △ ABC中,D 在BA 的延长线上,E 在AC 上, AE: EC 3: 2 , S A ADE 12平方厘米,求 △ ABC 的面积连接 BE , ADE : S ^ ABEAD: ABS A ABE : S A ABC AE : AC 3: (3 2) 所以 S A ADE: S A ABC (3 2) : 5(3 2:5 AB: AD 5:2 , (2 3):(5 3)(3 5): (3 2) 5 ,2) 6:25,设 S A ADE 6 份,则 S ^ ABC 25 份,S ^ADE 12【例8】 如图,平行四边形 ABCD , BE AB ,CF2CB ,GD 3DC ,HA4AD ,平行四边形 ABCDA AC【解析】【例7】且所以S EFGHSA AEHSA CFGSA DHGSA BEFSABCD8 8 15+3+236 .【解析】连接AC 、BD •根据共角定理.S A ABCAB BC 1 1 1 SA FBEBE BF 1 3 3 又 S A ABC1,所以 S A FBE 3 .冋理可得 S A GCF 8 , S A DHG 15 , S A AEH8.•••在△ ABC 和厶BFE 中, ABC 与 FBE 互补,【例9】 如图所示的四边形的面积等于多少?【解析】题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点0逆时针旋转,使长为13的两条边重合,此时三角形 OAB 将旋转到三 角形OCD 的位置•这样,通过旋转后所得到的新图形是一个边长为 12的正方形,且这个正 方形的面积就是原来四边形的面积 •因此,原来四边形的面积为 12 12 144.(也可以用勾股定理) ACDE ,中心为 0,求 OBC 的面积.【解析】如图,将 OAB 沿着O 点顺时针旋转90,到达 OCF 的位置.由于 ABC 90 , AOC 90,所以 OAB OCB 180 •而 OCF OAB , 所以 OCF OCB 180,那么B 、C 、F 三点在一条直线上.由于OB OF , BOF AOC 90,所以 BOF 是等腰直角三角形,且斜边BF 为5 3 8, 所以它的面积为82 116 .4根据面积比例模型,OBC 的面积为16 - 10 .8【例11】如图,以正方形的边 AB 为斜边在正方形内作直角三角形 ABE , AEB 90 , AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形 OBE 的面积.所以SABCDS EFGH2 36 118【例10】如图所示,ABC 中, ABC 90,AB3 , BC 5,以AC 为一边向 ABC 外作正方形【解析】【例12】【解析】如图,连接DE,以A点为中心,将那么EAF EAB BAF EAB 直角梯形,且AF AE3 , 所以梯形AFBE的面积为:1 23 — 12( cm ).2ABE是直角三角形,根据勾股定理,^AB22又因为S ABD那么S BDE所以S OBE17( cm2).ADE顺时针旋转90至U ABF的位置.DAE 90SABDSABESADESABD12 S BDE2・5 ( cm?).,而AEB也是90,所以四边形AFBE是AB2SAFBE2 2AE BE17 12 5(325234,所以2cm ),如下图,六边形ABCDEF中,AB ED,平行于CD,BC平行于EF,对角线FD垂直于BD,已知请问六边形ABCDEF的面积是多少平方厘米?AF CD , BC EF ,且有AB平行于ED, AFFD 24厘米,BD 18厘米,CD与AF重合,将DEF平移使得ED与AB重合,这样EF、BGFD,它的面积与原六边形的面积ABCDEF的面积为如图,我们将BCD平移使得BC都重合到图中的AG 了 .这样就组成了一个长方形相等,显然长方形BGFD的面积为24 18 432平方厘米,所以六边形432平方厘米.【例13】如图,三角形ABC的面积是1 , E是AC的中点,点D在BC上,且BD :DC 1:2 , AD与BE交于点F .则四边形DFEC的面积等于__________ .【解析】在本题中,四边形 ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形•看 到题目中给出条件 S VABD : S/BCD 1: 3,这可以向模型一蝶形定理靠拢,于是得出一种解 法•又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法, 但是第二种解法需要一个中介来改造这个” 不良四边形”,于是可以作 AH 垂直BD 于H ,CG垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之 比,得出结果•请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意 掌握并使用蝶形定理解决问题.解法一:••• 解法二:作••• SABDAO : OC S ABD AH BD 于 H , -S3BCD , • AH:S BDC CG1: 3 OC 2 3 6 ,••• OC:OD 6:3 2:1 .BD 于 G •-CG,-■. S AODDOC ,【解析】方法一:连接CF ,根据燕尾定理, 仏 ED 丄,占 善1, S A ACF DC 2 S A CBF EC方法二:连接DE ,由题目条件可得到 S A ABD -S A ABC-3 3【例14】四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形 ABD 的面积等于三角 形BCD 的面积的1,且AO3& ADE-S A 21ADC—22S 3 S A ABC1 BF,所以-3FESA ABD1SA ADE111 1 1 1 1 S1 S A DEFS A DEBSA BEC― S ABC22 32 3212 '而 S A CD E2 1 S A ABC 1• 所以则四边形DFEC 的面积等于 53 2312 【巩固】如图,长方形 ABCD 的面积是2 平方厘米,EC2DE , F 是DG 的中点.阴影部分的面积是多少平方厘米?A 设 & BDF 1份,则S A DCF 2 份,S A ABF5 S5 所以S DCEFSA ABC12123 份,S A AEF S A EFC 3份,如图所标【解析】 设S A DEF 1份,则根据燕尾定理其他面积如图所示S阴影 12 S A pc 。
金字塔原理思维导图:第五章演绎推理与归纳推理

金字塔原理思维导图:第五章演绎推理与归纳推理演绎推理与归纳推理演绎推理与归纳推理 (1)1.演绎推理(三段法) (2)1.1.第一种模式 (2)1.1.1.阐述世界上已存在的某种情况 (2)1.1.2.阐述世界上同时存在的相关情况 (2)1.1.3.说明两种情况同时存在的隐含意义 (2)1.2.第二种模式 (2)1.2.1.出现的问题或存在的现象 (2)1.2.2.产生问题的根源,原因 (2)1.2.3.解决问题的方案 (2)2.归纳推理 (3)2.1.正确定义该组思想,找到一个能表达该组思想所有共同点的名词 (3)2.2.识别并剔除该组思想中与其它思想不相称的思想(不属同类,不具有共同点)31.演绎推理(三段法)1: 由一个大前提和一个小前提推导出一个结论的形式2: 推导过程不要超过四个步骤3:尽量放在较低层次,减少推理过程中插入其它干扰信息。
1.1.第一种模式1.1.1.阐述世界上已存在的某种情况1.1.2.阐述世界上同时存在的相关情况第二个思想必须是对第一个思想的主语或谓语的评述1.1.3.说明两种情况同时存在的隐含意义1.2.第二种模式1.2.1.出现的问题或存在的现象1.2.2.产生问题的根源,原因1.2.3.解决问题的方案2.归纳推理1:比演绎推理更难,更需要创造性思维。
2:大脑首先要找到若干不同的事物(思想,事件,事实)具有共性,共同点,然后将其归纳到同一个目标组中,说明其共性。
2.1.正确定义该组思想,找到一个能表达该组思想所有共同点的名词2.2.识别并剔除该组思想中与其它思想不相称的思想(不属同类,不具有共同点)。
金字塔原理演绎法

金字塔原理演绎法
【原创实用版】
目录
1.金字塔原理的概念与特点
2.金字塔原理的演绎法
3.金字塔原理演绎法的应用实例
4.金字塔原理演绎法对知识类写作的启示
正文
金字塔原理是一种常见的思维方式和表达方法,它的核心思想是将复杂的问题分解成相对简单的子问题,然后通过逻辑演绎的方式逐步推导出最终的结论。
这种原理由于其形状像金字塔而得名,底层是基础概念,中间是概念的分支,顶部是结论。
金字塔原理的演绎法,就是通过逻辑演绎的方式,从基础概念开始,逐步推导出结论。
这种方法不仅可以帮助我们更好地理解问题,还可以帮助我们更清晰地表达观点,使读者或听众更容易理解和接受。
举个例子,如果我们要论证“提高教育投入可以促进经济增长”,我们可以先确立基础概念:提高教育投入、经济增长。
然后通过推导,得出提高教育投入可以提高人民的知识水平,进而提高劳动力的素质,最后促进经济增长。
这就是金字塔原理演绎法的应用。
对于知识类写作来说,金字塔原理演绎法有着重要的启示。
首先,我们可以通过这种方法,更清晰、更有逻辑地表达我们的观点和论证过程。
其次,我们可以通过这种方法,更好地组织文章的结构和内容,使文章更有层次感。
最后,我们可以通过这种方法,提高文章的可读性和说服力,使读者更容易理解和接受我们的观点。
第1页共1页。
金字塔原理举例说明

金字塔原理举例说明
【原创版】
目录
一、金字塔原理的概念和好处
二、金字塔原理的应用场景
三、金字塔原理的结构和要素
四、如何运用金字塔原理进行思考和表达
正文
一、金字塔原理的概念和好处
金字塔原理是一种自上而下的表达方式,主张结论先行,以上统下,归类分组,逻辑推进。
金字塔原理能有效提升沟通效率和说服力,尤其在报告编写、演讲或商务谈判等场合,效果显著。
二、金字塔原理的应用场景
金字塔原理广泛应用于各种场景,如商业报告、项目计划、演讲、写作等。
在这些场景中,金字塔原理可以帮助人们更好地组织和表达自己的思想,使受众更容易理解和接受。
三、金字塔原理的结构和要素
金字塔原理的结构包括核心结论、支撑结论的论据和细节。
在金字塔原理中,核心结论位于塔尖,支撑结论的论据位于塔身,而细节则位于塔底。
金字塔原理的要素包括:结论先行、以上统下、归类分组和逻辑推进。
四、如何运用金字塔原理进行思考和表达
要运用金字塔原理进行思考和表达,首先需要明确核心结论,然后将相关论据和细节按照逻辑关系进行归类分组。
在表达时,应先提出核心结论,然后逐层呈现支撑结论的论据和细节,确保受众能够容易理解和接受。
总之,金字塔原理是一种有效的思考和表达方法,可以帮助人们提高沟通效率和说服力。
小学奥数几何五大模型.pdf
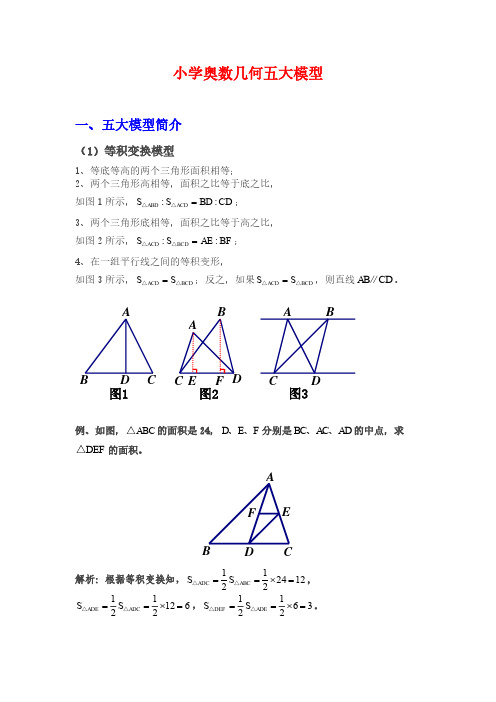
(4)相似模型
1、相似三角形:形状相同、大小不相等的两个三角形相似;
2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:
①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;
②相似三角形周长的比等于相似比;
③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型
结论:因为DE BC ∥,所以ADE ABC △∽△,则
①AD AE DE
==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;
E
D C B
A E D
C
B A
③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型
例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?
G
F
E D C
B
A。
金字塔数学原理

金字塔数学原理嘿,大伙儿,今儿咱们聊聊那金字塔数学原理,听起来高大上不?别怕,咱用大白话,让这学问也接地气儿。
想象一下,你站在一片广袤无垠的沙漠里,烈日当头,眼前忽地冒出一座金光闪闪的大金字塔,那可不是古埃及的奇观,而是咱们数学里头的宝贝疙瘩。
这金字塔啊,藏着不少奥秘,特别是它那层层叠加、稳如泰山的结构,简直就是数学里的“稳如老狗”,让人不得不服。
咱们先从最底下那层开始聊。
这层啊,就像是数学里的基础,打好了,上面才能一层层往上摞。
就像你学算术,先得会加减法,才能玩转乘除,对吧?金字塔的底层,就是那些看似简单,实则无比重要的基础知识。
没有它们,上面的高楼大厦就是空中楼阁,一吹就倒。
再往上看,金字塔的每一层都比下面一层小那么一丢丢,但它们之间的关系可紧密了。
这就像是你解数学题,一步步推导,每个步骤都环环相扣,缺了哪个都不行。
这种层层递进的感觉,就像是爬山,虽然累,但每当你爬上一层,看到的风景就更美一分,成就感也油然而生。
而且啊,这金字塔还有个神奇的地方,就是它的稳定性。
不管风怎么吹,雨怎么打,它都屹立不倒。
这就像咱们的数学体系,虽然里面包含了无数复杂的公式和定理,但只要基础扎实,逻辑清晰,就能像金字塔一样稳固。
这种稳,让人心里踏实,也让人对数学充满了敬畏。
说到这,我得提提金字塔里的那些小石头。
每一块都不起眼,但组合起来就成了伟大的建筑。
这就像咱们解题时用的每一个小技巧、每一个小公式,单独看可能没什么大不了,但放在一起,就能解决大问题。
所以啊,别小看了那些看似微不足道的知识点,它们可是构建数学大厦的基石呢!再来说说这金字塔的顶端吧。
那可是无数人梦寐以求的地方,就像咱们学习数学时追求的那种高境界。
但你知道吗?想要到达那里,可不是一蹴而就的。
你得一步步走,一层层爬,还得不断思考、不断总结。
只有这样,你才能在数学的海洋里畅游无阻,最终登上那令人向往的顶峰。
总而言之呢,这金字塔数学原理啊,就像咱们的人生一样。
小学奥数几何五大模型
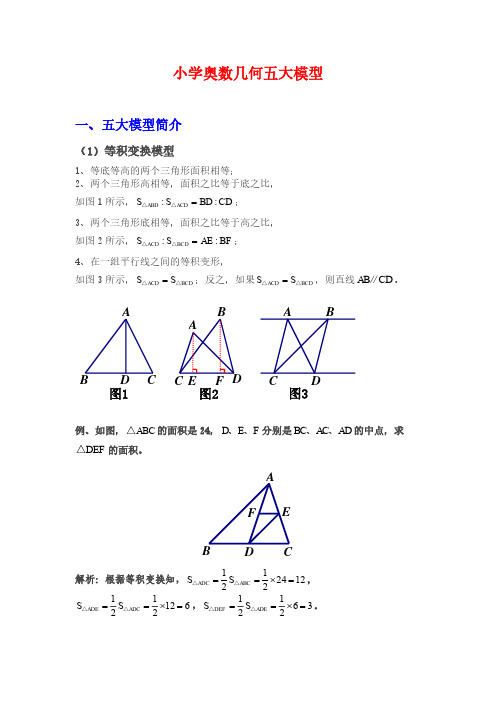
(4)相似模型1、相似三角形:形状相同、大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论:因为DE BC ∥,所以ADE ABC △∽△,则①AD AE DE==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?GFE D CBA解析:把另外三个三等分点标出之后,正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接,这样就把整个正方形分割成了9个形状各不相同的三角形,同时我们把空白部分的6个三角形按顺时针标记1~6。
这9个三角形的底边都是正方形边长的三分之一;阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知,CD 边上的阴影三角形的面积与第1、2个三角形相等;BC 边上的阴影三角形与第3、4个三角形相等;AB 边上的阴影三角形与第5、6个三角形相等。
因此,阴影面积是空白面积的二分之一,是正方形面积的三分之一,即:12×12÷3=48。
例2、如图所示,Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点,且DQ CP ME 、、彼此平行,已知5753AD BC AE EB ====、、、,求阴影部分三角形PQM 的面积。
金字塔原理应用的例子

金字塔原理应用的例子什么是金字塔原理?金字塔原理是一种有效的思考和表达工具,通过将信息进行层次化,使得读者可以更容易地理解和接受所传达的信息。
金字塔原理包含以下几个要点: 1. 结论优先:在表达信息时,先提出结论,再进行论证和解释。
2. 构建层次结构:将信息按照逻辑结构进行组织,形成层次化的架构。
3. 使用顶层方法:用简洁的语言和少量的关键字来概括每个层次的内容。
4. 限制每个层次的信息量:每个层次应该只包含一个主要观点或概念。
金字塔原理的应用可以帮助我们更好地组织和呈现信息,使得读者能够更容易地理解和接受所传达的内容。
金字塔原理应用的例子以下是几个金字塔原理应用的例子,通过这些例子我们可以更好地理解金字塔原理的具体应用方式。
例子1:销售提案假设你需要向某个公司提交一个销售提案,你可以使用金字塔原理来组织你的提案。
以下是一个简单的金字塔结构示例:•结论:我们建议采用我们的产品来提高您公司的销售额。
–理由1:我们的产品具有先进的功能和性能。
•优势1:能够更好地满足客户需求。
•优势2:提供更好的用户体验。
–理由2:我们的产品价格合理。
•优势1:相比竞争对手,我们的产品价格更低。
•优势2:产品性价比更高。
–理由3:我们有丰富的经验和成功案例。
•优势1:已经为多家类似公司提供服务。
•优势2:客户对我们的产品和服务评价很高。
通过使用金字塔原理,你能够直截了当地表达你的结论,并逐层论证支持你的结论的每个理由和优势。
这样,读者能够很快地了解你的提案,并认可你的观点。
例子2:演讲陈述假设你需要进行一个与金字塔原理相关的演讲,你可以使用金字塔原理来组织你的陈述。
以下是一个简单的金字塔结构示例:•结论:学习和应用金字塔原理可以提高我们的思考和表达效果。
–学习金字塔原理的好处:•帮助我们组织思维。
•提高沟通的清晰度。
•增强文档和演讲的说服力。
–学习金字塔原理的方法:•阅读相关的书籍和资料。
•参加培训课程或研讨会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金字塔模型证明过程
金字塔模型是一种常见的可视化形式,常用于展示层次结构等结构化
数据。
它由三角形组成,每个三角形可以代表一个概念。
下面就来看
看金字塔模型证明过程:
1.构建金字塔模型:金字塔模型的构建很容易,首先需要准备一个三角形的模板,从而方便以后每个层次内容的填写。
接着,根据需要填充
每个层次,填充的内容可以是以文本的形式或者形象的形式展示。
2.详细介绍层次内容:在填充完结构之后,要对金字塔模型中各层次的内容进行大量的介绍,使得它在读者看来更加清晰明了。
比如,第一
层是最重要的层次,那么就要介绍它是什么内容,为什么特别重要,
及它里面包含的主要概念。
3.进行相关证明:金字塔模型是一种可视化的表现,所以要做到让它更具说服力,就需要提供一定量的证明,使得每层内容都有实际的说明,而不是只是空洞的展示,“言之有物”非常重要。
4.进行分类梳理:进行证明的同时,也要进行分类的梳理,从而使金字塔模型呈现出更专业的结构,方便读者更清晰的了解它之间的相互联系。
5.对金字塔模型进行概括总结:最后,对金字塔模型进行概括总结,通过几句简单的话,使得读者对整个金字塔模型有一个整体的认识,充分的了解它的重要性和意义。
金字塔模型是一种极为有效的可视化方式,可以帮助用户清晰的了解某个概念或者知识结构,因此它完美的证明过程也是至关重要的。
实践出真知,只有通过亲身实践,才能够更好的掌握这种模式,从而实现它在实际中的更好应用。
