大学数学(高数微积分)专题七第1讲(课堂讲义)
合集下载
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
12
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
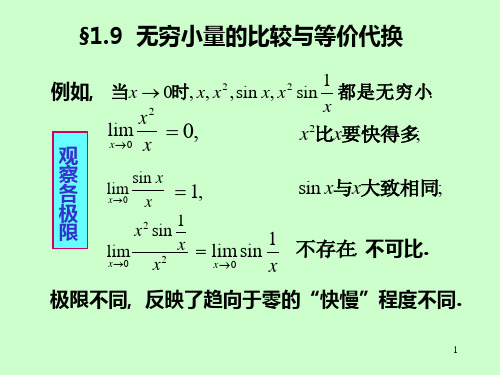
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x ),
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2,
0
x0
x
lim f ( x) lim x2 4 f (2),
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义;
(2) lim f (x)存在; xx0
(3)lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
高等数学第七章资料

两边积分得
ln y ln( x 2) lnC 所以方程的通解为
y C( x 2)
例1 求方程 ( x 2) dy y dx
解2 方程改写为
的通解
y C e P( x)dx
dy 1 y 0 dx x 2
所以
p( x) 1 x2
由公式得通解
y
y2 C(1 x2 ) 1
三、小结
分离变量法步骤: 1.分离变量; 2.两端积分-------隐(显)式通解.
作业 P304习题7-2 1(1)(3)(7)(8), 2(1)(2)
第三节 齐次方程
一、齐次方程
定义1 可化为形如 dy f ( y ) 的一阶微分方程称为 dx x 齐次方程.
解: 设所求曲线方程为 y = y(x) , 则有如下关系式:
y' 2x
①
由①得
y x1 2
② (C为任意常数)
由 ② 得 C = 1, 因此所求曲线方程为 y x2 1 .
例2 列车在平直的线路上以20米/秒的速度行驶,
当制动时列车获得加速度 0.4 米/秒2, 问
(1)开始制动后多少时间列车才能停住? (2)在这段时间内列车行驶了多少路程?
解 分离变量
两边积分
ey ex C
即 (ex C )ey 1 0 ( C < 0 )
2、 求微分方程 dy 1 x y2 xy2 的通解 dx
解 方程可化为 分离变量,得 两边积分,得 得通解
dy (1 x)(1 y2 ) dx
dy 1 y2
y C1C2e x e2x是否 y 3 y 2 y 0的通解?
ln y ln( x 2) lnC 所以方程的通解为
y C( x 2)
例1 求方程 ( x 2) dy y dx
解2 方程改写为
的通解
y C e P( x)dx
dy 1 y 0 dx x 2
所以
p( x) 1 x2
由公式得通解
y
y2 C(1 x2 ) 1
三、小结
分离变量法步骤: 1.分离变量; 2.两端积分-------隐(显)式通解.
作业 P304习题7-2 1(1)(3)(7)(8), 2(1)(2)
第三节 齐次方程
一、齐次方程
定义1 可化为形如 dy f ( y ) 的一阶微分方程称为 dx x 齐次方程.
解: 设所求曲线方程为 y = y(x) , 则有如下关系式:
y' 2x
①
由①得
y x1 2
② (C为任意常数)
由 ② 得 C = 1, 因此所求曲线方程为 y x2 1 .
例2 列车在平直的线路上以20米/秒的速度行驶,
当制动时列车获得加速度 0.4 米/秒2, 问
(1)开始制动后多少时间列车才能停住? (2)在这段时间内列车行驶了多少路程?
解 分离变量
两边积分
ey ex C
即 (ex C )ey 1 0 ( C < 0 )
2、 求微分方程 dy 1 x y2 xy2 的通解 dx
解 方程可化为 分离变量,得 两边积分,得 得通解
dy (1 x)(1 y2 ) dx
dy 1 y2
y C1C2e x e2x是否 y 3 y 2 y 0的通解?
大一高数课件第七章7-3-1

对角线的长为 |m n || ,m n |, n m n { 1 , 1 ,1 }m , n { 1 ,3 , 1 } m
|m n |3 , |m n |1,1
平 行 四 边 形 的 对 角 线 的 长 度 各 为3, 1.1
;
b0
=__________;
c0=____________;
5、一向量与xoy, yoz,zox三个坐标平面的夹角,,
满足cos2+cos2 +cos2 =____________ .
二、一向量的终点在点B(2,1,7),它在 X轴, Y轴 和Z轴上的投影依次为4,4和7,求这向量的 起点A的坐.标
zz1
(z2z)
zz1z2 1
,
M 为有向线段 AB的定比分点. M 为中点时,
x x1 x2 , 2
y y1 y2 , 2
z z1 z2 . 2
三、向量的模与方向余弦的坐标表示式
非零向量 a的方向角:
z
、、
非零向量与三条坐标轴的 正向的夹角称为方向角.
向向量量的的坐坐标 标: 表达ax式, :ay,a az ,{a x,a y,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
向量的加减法、向量与数的乘法运算的坐标表达式
a a b {{ a a x x , a b yx ,, a a zy } ,b y b , a { z b x b ,z b } y,b z},
空间两向量的夹角的概念:
a0,
b0,
向量a 与向量b 的夹角
|m n |3 , |m n |1,1
平 行 四 边 形 的 对 角 线 的 长 度 各 为3, 1.1
;
b0
=__________;
c0=____________;
5、一向量与xoy, yoz,zox三个坐标平面的夹角,,
满足cos2+cos2 +cos2 =____________ .
二、一向量的终点在点B(2,1,7),它在 X轴, Y轴 和Z轴上的投影依次为4,4和7,求这向量的 起点A的坐.标
zz1
(z2z)
zz1z2 1
,
M 为有向线段 AB的定比分点. M 为中点时,
x x1 x2 , 2
y y1 y2 , 2
z z1 z2 . 2
三、向量的模与方向余弦的坐标表示式
非零向量 a的方向角:
z
、、
非零向量与三条坐标轴的 正向的夹角称为方向角.
向向量量的的坐坐标 标: 表达ax式, :ay,a az ,{a x,a y,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
向量的加减法、向量与数的乘法运算的坐标表达式
a a b {{ a a x x , a b yx ,, a a zy } ,b y b , a { z b x b ,z b } y,b z},
空间两向量的夹角的概念:
a0,
b0,
向量a 与向量b 的夹角
大学数学(高数微积分)第九章欧几里得空间第七节(课堂讲义)PPT课件

一条直线)上所有点的距离以垂线最短.
下面可以证
明一个固定向量和一个子空间中各向量的距离也是
以“垂线最短” .
先设一个子空间 W,它是由向量 1, 2, …, k
所生成,即 W = L(1, 2, …, k) .
说一个向量 垂
直于子空间 W,就是指向量 垂直于 W 中任何一
个向量. 容易验证 垂直于 W 的充分必要条件是
我们想找出 y 对 x 的一个近似公式.
解 把表中数值画出图来看,发现它的变化
趋势近于一条直线.
因此我们决定选取 x 的一次式
ax + b 来表达 .
当然最好能选到适当的 a , b 使得
下面的等式
3.6a + b - 1.00 = 0 , 3.7a + b - 0.9 = 0 ,
9
3.8a + b - 0.9 = 0 , 3.9a + b - 0.81 = 0 , 4.0a + b - 0.60 = 0 , 4.1a + b - 0.56 = 0 , 4.2a + b - 0.35 = 0
都成立. 实际上是不可能的.
任何 a , b 代入上面
各式都会发生些误差.
于是想找 a , b 使得上面各
式的误差的平方和最小,即找 a , b 使
10
(3.6a + b - 1.00 )2 + (3.7a + b - 0.9 )2 + (3.8a + b - 0.9 )2 + (3.9a + b - 0.81 )2 + (4.0a + b - 0.60 )2 + (4.1a + b - 0.56 )2 + (4.2a + b - 0.35 )2 最小. 这里讨论的是误差的平方即二乘方,故称为 最小二乘法. 现在转向一般的最小二乘法问题.
大学数学(高数微积分)第七章线性变换第五节课件(课堂讲义)

等于空间的维数.
V1 , ,Vr 的维数之和
当线性变换 A 在一组基下的矩阵 A 是对角形
时:
1
A
2
.
n
整理课件
12
A 的特征多项式就是
| E - A | = ( - 1) ( - 2) … ( - n) .
因此,如果线性变换 A 在一组基下的矩阵是对角
形,那么主对角线上的元素除排列次序外是确定的. 它们正是 A 的特征多项式全部的根 (重根按重数计 算) .
第五节 对角矩阵
主要内容
充分必要条件 特征值与特征向量的性质 举例
整理课件
1
பைடு நூலகம்
一、充分必要条件
对角矩阵可以认为是矩阵中最简单的一种.
现
在我们来考察,究竟哪些线性变换的矩阵在一组适
当的基下可以是对角矩阵.
定理 8 设 A 是 n 维线性空间 V 的一个线性 变换, A 的矩阵可以在某一组基下为对角矩阵的 充分必要条件是, A 有 n 个线性无关的特征向量.
整理课件
13
三、举例
例 1 设线性变换 A 在基 1 , 2 , 3 下的矩阵
为
2 1 2 A 5 3 3
1 0 2 问是否存在一组基,使 A 在这组基下的矩阵为对
形?若存在,求出这组基.
整理课件
14
例 2 设线性变换 A 在基 1 , 2 , 3 下的矩阵
为
2 2 2 A 2 5 4.
a111 + a222 +…+ akkk + ak+1k+1k+1 = 0
第三式减去第二式得
a1(1 - k+1)1 + … + ak (k - k+1) k = 0 .
V1 , ,Vr 的维数之和
当线性变换 A 在一组基下的矩阵 A 是对角形
时:
1
A
2
.
n
整理课件
12
A 的特征多项式就是
| E - A | = ( - 1) ( - 2) … ( - n) .
因此,如果线性变换 A 在一组基下的矩阵是对角
形,那么主对角线上的元素除排列次序外是确定的. 它们正是 A 的特征多项式全部的根 (重根按重数计 算) .
第五节 对角矩阵
主要内容
充分必要条件 特征值与特征向量的性质 举例
整理课件
1
பைடு நூலகம்
一、充分必要条件
对角矩阵可以认为是矩阵中最简单的一种.
现
在我们来考察,究竟哪些线性变换的矩阵在一组适
当的基下可以是对角矩阵.
定理 8 设 A 是 n 维线性空间 V 的一个线性 变换, A 的矩阵可以在某一组基下为对角矩阵的 充分必要条件是, A 有 n 个线性无关的特征向量.
整理课件
13
三、举例
例 1 设线性变换 A 在基 1 , 2 , 3 下的矩阵
为
2 1 2 A 5 3 3
1 0 2 问是否存在一组基,使 A 在这组基下的矩阵为对
形?若存在,求出这组基.
整理课件
14
例 2 设线性变换 A 在基 1 , 2 , 3 下的矩阵
为
2 2 2 A 2 5 4.
a111 + a222 +…+ akkk + ak+1k+1k+1 = 0
第三式减去第二式得
a1(1 - k+1)1 + … + ak (k - k+1) k = 0 .
《大学数学课件一元函数微积分学》

曲线长度与曲率
曲线长度公式
曲线长度的计算需要对曲线进行参数化,然 后对其微分求和。实数的曲线长度困难,函 数的曲线长度一般参数化之后再求积分。
计算曲率
曲率定义为在曲线某一点处曲线凝聚程度的 量,凡是具有确定的曲率的曲线上的点组成 的集合,成为曲线的曲率线。
微积分的实际应用举例
金融领域应用
微积分在金融等经济学领域中有广泛的应用,能 够帮助我们更好地理解时间价值、股市价格、股 息、衍生证券等。
龙虾曲线
一种分段光滑的曲线,通过迭代形成,是高阶 导数比较经典的应用之一。
复分析
复函数又叫做复变量函数,它是一个变量为一 个复数的函数。复分析是以复函数为研究对象 的数学分支。
不定积分的概念与求法
基本积分法
通过多种方法计算不定积 分:代换法、分部积分法、 三角函数积分法、有理函 数积分法、分式分解。
应用于牛顿第二定律
在物理领域中,微积分的应用非常广泛,牛顿第 二定律是牛顿—莱布尼茨公式的一个重要应用例 子。
定积分的概念与性质
定积分概念
在一定区间内,用先进(上)的近似值与落后(下)的近似值的平均数来逐 渐缩小误差范围的整个过程,那么最后这个误差的范围越来越小。
牛顿—莱布尼茨公式
定积分的本质意义就是计算曲线下对应的面积,和物理中的质量、体积密度、 功力密度有关,是牛顿—莱布尼茨公式的重要应用场景。
极限概念
当自变量趋近于某个值时,函数值趋近于一个限的极限。
高阶导数及其应用
高阶导数的定义
高阶导数指的是对导数的导数(即二阶导数、三阶导数……)
泰勒展开式
泰勒公式是一个非常重要的工具.利用泰勒公式,可以把函数转化成为一些比较简单的多项式的和的 形式,从而来研究一些不易计算的函数。
高等数学-第7章 微分方程
将上式两端积分,并由
中的函数可写成的函数,即
(引进新的未知函数(
代入方程(),便得方程
分离变量,得两端积分,得
代替
解方程
因此是齐次方程。
令,则
两端积分,得
以代入上式中的
方程
离变量后得,两端积分,得
,这是对应的齐次线性方程(
把上式代入(
.
以除)的两端,再通过上述代换得线性方程
型的微分方程
(
..
,那末而方程就成为
但是,因此又得到一个一阶微分方程
)的通解为
(3)
合函数的求导法则把化为对
)就成为
通解为
)的通解为
如果函数均是方程的解,那末
我们所求得的解是不是方程的通解呢?
,那末称此两函数在区间,否则,即
如果
就是该方程的通解,其中
的任一特解,
就是方程的通解。
.如果
的解,那末
(
的系数(
和它的各阶导数都只相差一个常数因子。
将
把代入方程(
(
)的两个根。
特征方程微分方程
(
型,
(是与
不是特征方程的根,
若
型
,
,)其中、
)的重复次数。
高等数学上册第七章课件.ppt
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
《高等数学(一)微积分》讲义
1.概念回顾
2、极限的求法, )
1)数列极限 lim an = A , 函数极限 lim f ( x ) = A .
n→∞ x
2)函数极限与单侧极限之间的关系
⎧ f ( x0 + ) = lim+ f ( x ) = A x → x0 ⎪ lim f ( x ) = A. ⇔ ⎨ x → x0 f ( x0 − ) = lim− f ( x ) = A ⎪ x → x0 ⎩
知识点:设 a0 ≠ 0, b0 ≠ 0, m , n ∈ N ,
⎧ am b m ⎪ n a x + L + a1 x + a0 ⎪ 则 lim m n =⎨0 x →∞ b x + L + b x + b n 1 0 ⎪∞ ⎪ ⎩ m=n m<n m>n
6/69
5n − 4 n − 1 例 6.(1) lim n+1 n→∞ 5 + 3n+ 2
5
2、 极限的求法
利用极限四则运算、 连续函数、重要极限、无穷小代换、洛比达法则等 例 5:
x+5 . 求 lim 2 x →∞ x − 9
解:
1 5 1 5 lim( + 2 ) + 2 x+5 x →∞ x x = 0 = 0. lim 2 = lim x x = x →∞ x − 9 x →∞ 9 9 1 1− 2 lim(1 − 2 ) x →∞ x x
2
x 2 ⋅ (3 x ) 3 所以 lim = lim = x → 0 (1 − cos 2 x )ln(1 + x ) x → 0 (2 x 2 ) ⋅ x 2
(3) lim x[ln( x + 2) − ln x ] = lim x ln(1 +
2、极限的求法, )
1)数列极限 lim an = A , 函数极限 lim f ( x ) = A .
n→∞ x
2)函数极限与单侧极限之间的关系
⎧ f ( x0 + ) = lim+ f ( x ) = A x → x0 ⎪ lim f ( x ) = A. ⇔ ⎨ x → x0 f ( x0 − ) = lim− f ( x ) = A ⎪ x → x0 ⎩
知识点:设 a0 ≠ 0, b0 ≠ 0, m , n ∈ N ,
⎧ am b m ⎪ n a x + L + a1 x + a0 ⎪ 则 lim m n =⎨0 x →∞ b x + L + b x + b n 1 0 ⎪∞ ⎪ ⎩ m=n m<n m>n
6/69
5n − 4 n − 1 例 6.(1) lim n+1 n→∞ 5 + 3n+ 2
5
2、 极限的求法
利用极限四则运算、 连续函数、重要极限、无穷小代换、洛比达法则等 例 5:
x+5 . 求 lim 2 x →∞ x − 9
解:
1 5 1 5 lim( + 2 ) + 2 x+5 x →∞ x x = 0 = 0. lim 2 = lim x x = x →∞ x − 9 x →∞ 9 9 1 1− 2 lim(1 − 2 ) x →∞ x x
2
x 2 ⋅ (3 x ) 3 所以 lim = lim = x → 0 (1 − cos 2 x )ln(1 + x ) x → 0 (2 x 2 ) ⋅ x 2
(3) lim x[ln( x + 2) − ln x ] = lim x ln(1 +
大学数学(高数微积分)专题七第2讲(课堂讲义)
力和速度.具体操作时,应注意以下几点:
(1)准确画出函数图象,注意函数的定义域.
5
思想方法概述
(2)用图象法讨论方程(特别是含参数的方程)的解的个数是一
本 种行之有效的方法,值得注意的是首先要把方程两边的代数
讲 栏
式看作是两个函数的表达式(有时可能先作适当调整,以便于
目 开
作图),然后作出两个函数的图象,由图求解.
栏
目 开
由图可知x·f(x)<0的x的取值范围是
关 (-1,0)∪(0,1).
13
热点分类突破
求参数范围或解不等式问题经常联系函数的图象,
本 讲
根据不等式中量的特点,选择适当的两个(或多个)函数,利
栏 用两个函数图象的上、下位置关系转化数量关系来解决问
目
开 题,往往可以避免繁琐的运算,获得简捷的解答.
由图知10<c<12,∴abc∈(10,12).
答案 (1)(-1,0)
(2)C
16
热点分类突破
类型三 利用数形结合思想求最值
例3 若a,b,c均为单位向量,且a·b=0,(a-c)·(b-c)≤0,
则|a+b-c|的最大值为
()
A. 2-1 B.1
C. 2
D.2
本
讲 解析 设a=(1,0),b=(0,1),c=(x,y),
目 开
速度.
关 5.数形结合思想常用模型:一次、二次函数图象;斜率公
式;两点间的距离公式(或向量的模、复数的模);点到直
线的距离公式等.
22
名师押题我来做
1.已知0<a<1,则方程a|x|=|logax|的实根个数为
A.1
B.2
