八年级数学-平行四边形的性质、判定汇编

合集下载

华师大版八年级下册数学第18章平行四边形含答案(真题汇编)

华师大版八年级下册数学第18章平行四边形含答案一、单选题(共15题，共计45分)1、根据如图所示的三个图所表示的规律，依次下去第n个图中平行四边形的个数是（）A.3nB.3n（n+1）C.6nD.6n（n+1）2、如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于E，交DC的延长线于F，BG⊥AE于G，BG=，则△EFC的周长为( )A.11B.10C.9D.83、根据下列条件，能作出平行四边形的是（）A.两组对边的长分别是3和5B.相邻两边的长分别是3和5，且一条对角线长为9C.一边的长为7，两条对角线的长分别为6和8D.一边的长为7，两条对角线的长分别为6和54、如图，下面不能判断是平行四边形的是（）A.∠B=∠D，∠A=∠CB.AB∥CD，AD∥BCC.AB∥CD，AB=CD D.∠B+∠DAB=180°，∠B+∠BCD=180°5、如图，在平行四边形ABCD中，AC与BD相交于O，且AO=BD=4，AD=3，则△BOC的周长为（）A.9B.10C.12D.146、如图，点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD 一定是（）A.平行四边形B.矩形C.菱形D.正方形7、如图，在▱ABCD中，AB=4，AD=7，∠ABC的平分线BE交AD于点E，则DE的长是（）A.4B.3C.3.5D.28、以三角形三边中点和三角形三个顶点能画出平行四边形有（）个．A.1B.2C.3D.49、能判定四边形ABCD是平行四边形的是（）A.AD//BC，AB=CDB.∠A=∠B，∠C=∠DC.∠A=∠C，∠B=∠D D.AB=AD，CB=CD10、如图，▱ABCD的周长为20cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（）A.4cmB.6cmC.8cmD.10cm11、下列命题的逆命题为真命题的是（）A.如果a=b，那么B.平行四边形是中心对称图形C.两组对角分别相等的四边形是平行四边形D.内错角相等12、如图，四边形是边长为1的正方形，点是射线上的动点（点不与点，点重合），点在线段的延长线上，且，连接，将绕点顺时针旋转90°得到，连接.设，四边形的面积为，下列图象能正确反映出与的函数关系的是（）A. B. C.D.13、如图，在□ABCD中，AC平分∠DAB，AB = 3，则□ABCD的周长为（）A.6B.9C.12D.1514、如图，平行四边形ABCD中，AE：EB=1：2，若S△AEF =6cm2，则S△CDF等于( )A.54cm 2B.18cm 2C.12cm 2D.24cm 215、如图,在▱ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )A.3B.6C.12D.24二、填空题(共10题，共计30分)16、如图，在平行四边形ABCD中，AB＝2AD，BE平分∠ABC交CD于点E，作BF⊥AD，垂足为F，连接EF，小明得到三个结论：①∠FBC＝90°；②ED＝EB；③S△EBF＝S△EDF+S△EBC；则三个结论中一定成立的是________．17、如图，△ABC中，AB＝7cm，BC＝6cm，AC＝5cm，D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长等于________cm．18、如图，在平行四边形中，两点均在对角线上．要使四边形为平行四边形，在不添加辅助线的情况下，需要增加的一个条件是________（写出一个即可）．19、如图，将平行四边形ABCO放置在平面直角坐标系xOy中，O为坐标原点，若点A的坐标是（8，0），点C的坐标是（2，6），则点B的坐标是________.20、如图，点A、B分别在双曲线y= 和y= 上，四边形ABCO为平行四边形，则▱ABCO的面积为________．21、已知：平行四边形一边AB＝12 cm，它的长是周长的，则BC＝________cm，CD＝________ cm.22、四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需满足的条件________(横线只需填一个你认为合适的条件即可)23、如图，点O为坐标原点，▱ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F．若y＝（x＞0）的图象经过点C且＝，则k的值为________．S△BEF24、如图，中，点是边上一点，交于点，若，，的面积是1，则的面积为________.25、如图，在中，按以下步骤作图：①以为圆心，任意长为半径作弧，分别交，于点，；②分别以，为圆心，以大于的长为半径作弧，两弧相交于点；③作射线，交边于点.若，，则________.三、解答题(共5题，共计25分)26、如图，在平行四边形ABCD中，点E，F分别在AB，CD上，AE＝CF．求证：DE＝BF．27、如图，已知四边形ABCD关于O点成中心对称,求证：四边形ABCD是平行四边形.28、已知：如图，在△ABC中，∠ACB=90°，D是BC的中点，DE∥AC，且DE=AC，若AC=2，AD=4，求四边形ACEB的周长．29、如图，▱ABCD中，点E，F是对角线BD上两点，且BE＝DF，顺次连接A，E，C，F，A．求证：四边形AECF是平行四边形，并写出最后一步推理的依据．30、如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P 作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P 位置的改变而改变?并说明理由.参考答案一、单选题(共15题，共计45分)1、B2、D3、A4、A5、A6、A7、B8、C9、C10、D11、C12、B13、C14、A15、C二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、27、28、30、。

平行四边形的性质及判定归纳汇编

AC 平分∠ BAD 与∠ BCD BD 平分∠ ABC 与∠ ADC
学习 ----- 好资料
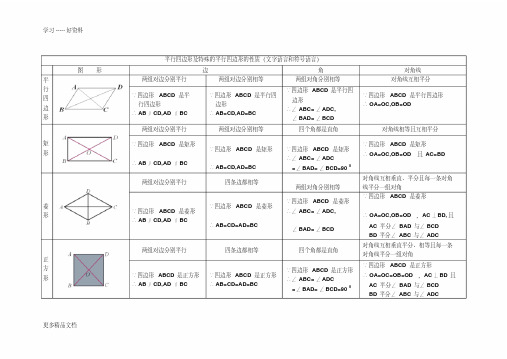
平行四边形及特殊的平行四边形的定义及判定（关系图见背面，符号语言自己补充）
更多精品文档
学习 ----- 好资料
对角线互相平分且相等有三个角是直角
四边形
两组对边分别平行两组对边分别相等一组对边平行且相等
∵四边形 ABCD 是平行四边形
∴∠ ABC= ∠ ADC, ∠ BAD= ∠ BCD
两组对边分别平行
两组对边分别相等
四个角都是直角
对角线对角线互相平分 ∵四边形 ABCD 是平行四边形 ∴ OA=OC,OB=OD
对角线相等且互相平分
∵四边形 ABCD 是矩形 ∴ AB∥ CD,AD ∥ BC
两组对边分别平行
∵四边形 ABCD 是菱形 ∴ AB∥ CD,AD ∥ BC
两组对边分别平行
∵四边形 ABCD 是正方形 ∴ AB∥ CD,AD ∥ BC
∵四边形 ABCD 是矩形 ∴ AB=CD,AD=BC
四条边都相等
∵四边形 ABCD 是菱形 ∴ AB=CD=AD=BC
四条边都相等
∵四边形 ABCD 是正方形 ∴ AB=CD=AD=BC
两组对角分别相等对角线互相平分
平行四边形
有一个角是直角对角线相等
一组邻边相等对角线互相垂直
对角线互相平分且垂直（对角线互为垂直平分线）四边都相等矩形ຫໍສະໝຸດ 一组邻边相等对角线互相垂直
菱形
有一个角是直角对角线相等
四边都相等，且有三个角是直角对角线互相垂直平分且相等（对角线相等且互为垂直平分线）
更多精品文档
∵四边形 ABCD 是矩形 ∴∠ ABC= ∠ ADC

北师大版数学八年级下册 6.1.2平行四边形的性质课件

活动探究
探究点一问题2：如图，□ABCD的对角线AC、BD相交于点O，E F过点O且与AB、CD 分别相交于点E、F，求证：OE=OF. 证明：∵四边形ABCD是平行四边形， ∴BO=DO，AB∥CD. ∴∠ABO=∠CDO. 又∵∠BOE=∠DOF , ∴△BOE≌△DOF. ∴OE=OF.
活动探究
解：∵▱A BCD的对角线AC，BD相交于点O，AC＝12，BD＝18， ∴AO＝12AC＝6，BO＝12 BD＝9. 又∵△AOB的周长l＝23， ∴AB＝l－(AO＋BO) ＝23－(6＋9)＝8.
课堂小结
平行四边形的性质对称性：平行四边形是中心对称图形，两条对角线的交点是它的对称中心；边：对边平行且相等；角：对角相等，邻角互补. 对角线：相互平分
探究点二问题1：如图, □ABCD的对角线AC、BD相交于点O, ∠ADB=90º,OA=6,0B=3. 求AD和AC的长度. 解：在□ABCD中，对角线AC、BD相交于点O ∴OD=OB=3 ∠ADB=90º 在Rt∆AOD中，
AD = OA2 - OD2 = 62 + 32 = 3 3， AC=2OA=2×6=12 所以，AD和AC的长度分别为 3 3 和12.
•
11、一个好的教师，是一个懂得心理学和教育学的人。21. 4.3013: 39:1113 :39Apr-2130-A pr-21
•
12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。13:39: 1113:3 9:1113: 39Frida y, April 30, 2021
6.1 平行四边形的性质第源自课时八年级下册-学习目标 1 掌握平行四边形对角线互相平分的性质; 2 利用平行四边形对角线的性质解决有关问题.

人教版数学八年级下册第18章平行四边形解答题—2019年中考真题汇编(解析版)

第18章平行四边形解答题—2019年中考真题汇编1．（2019•大庆）如图，在矩形ABCD中，AB＝3，BC＝4．M、N在对角线AC上，且AM＝CN，E、F分别是AD、BC的中点．（1）求证：△ABM≌△CDN；（2）点G是对角线AC上的点，∠EGF＝90°，求AG的长．2．（2019•百色）如图，菱形ABCD中，作BE⊥AD、CF⊥AB，分别交AD、AB的延长线于点E、F．（1）求证：AE＝BF；（2）若点E恰好是AD的中点，AB＝2，求BD的值．3．如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE＝DF，连结AE、AF、EF．（1）求证：△ABE≌△ADF；（2）若AE＝5，请求出EF的长．4．（2019•吉林）如图，在▱ABCD中，点E在边AD上，以C为圆心，AE长为半径画弧，交边BC于点F，连接BE、DF．求证：△ABE≌△CDF．5．（2019•云南）如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB＝2∠OAD．（1）求证：四边形ABCD是矩形；（2）若∠AOB：∠ODC＝4：3，求∠ADO的度数．6．（2019•柳州）平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．已知：如图，在四边形ABCD中，AB＝CD，AD＝BC．求证：四边形ABCD是平行四边形．证明：7．（2019•湘西州）如图，在正方形ABCD中，点E，F分别在边CD，AD上，且AF＝CE．（1）求证：△ABF≌△CBE；（2）若AB＝4，AF＝1，求四边形BEDF的面积．8．（2019•哈尔滨）已知：在矩形ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F．（1）如图1，求证：AE＝CF；（2）如图2，当∠ADB＝30°时，连接AF、CE，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于矩形ABCD面积的．9．如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF．（1）求证：△ABE≌△CDF；（2）当AC⊥EF时，四边形AECF是菱形吗？请说明理由．10．（2019•淮安）已知：如图，在▱ABCD中，点E、F分别是边AD、BC的中点．求证：BE ＝DF．11．（2019•荆门）如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2．（1）求平行四边形ABCD的面积；（2）求证：BD⊥BC．12．（2019•黄冈）如图，ABCD是正方形，E是CD边上任意一点，连接AE，作BF⊥AE，DG ⊥AE，垂足分别为F，G．求证：BF﹣DG＝FG．13．（2019•天门）如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE＝CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF．求证：（1）AE⊥BF；（2）四边形BEGF是平行四边形．14．（2019•新疆）如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD中点，连接OE．过点C作CF∥BD交OE的延长线于点F，连接DF．求证：（1）△ODE≌△FCE；（2）四边形OCFD是矩形．15．（2019•郴州）如图，▱ABCD中，点E是边AD的中点，连接CE并延长交BA的延长线于点F，连接AC，DF．求证：四边形ACDF是平行四边形．16．（2019•福建）如图，点E、F分别是矩形ABCD的边AB、CD上的一点，且DF＝BE．求证：AF＝CE．17．（2019•鄂州）如图，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O 的直线分别交AB、CD边于点E、F．（1）求证：四边形DEBF是平行四边形；（2）当DE＝DF时，求EF的长．18．（2019•杭州）如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．19．（2019•岳阳）如图，在菱形ABCD中，点E、F分别为AD、CD边上的点，DE＝DF，求证：∠1＝∠2．20．（2019•怀化）已知：如图，在▱ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．（1）求证：△ABE≌△CDF；（2）求证：四边形AECF是矩形．21．（2019•株洲）如图所示，已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点，连接CE、DG．（1）求证：△DOG≌△COE；（2）若DG⊥BD，正方形ABCD的边长为2，线段AD与线段OG相交于点M，AM＝，求正方形OEFG的边长．22．（2019•宿迁）如图，矩形ABCD中，AB＝4，BC＝2，点E、F分别在AB、CD上，且BE ＝DF＝．（1）求证：四边形AECF是菱形；（2）求线段EF的长．23．（2019•宁波）如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．24．（2019•广安）如图，点E是▱ABCD的CD边的中点，AE、BC的延长线交于点F，CF＝3，CE＝2，求▱ABCD的周长．25．（2019•湖州）如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF．（1）求证：四边形BEFD是平行四边形；（2）若∠AFB＝90°，AB＝6，求四边形BEFD的周长．26．（2019•聊城）在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF．求证：（1）△ABF≌△DAE；（2）DE＝BF+EF．27．（2019•遂宁）如图，在四边形ABCD中，AD∥BC，延长BC到E，使CE＝BC，连接AE 交CD于点F，点F是CD的中点．求证：（1）△ADF≌△ECF．（2）四边形ABCD是平行四边形．28．（2019•凉山州）如图，正方形ABCD的对角线AC、BD相交于点O，E是OC上一点，连接EB．过点A作AM⊥BE，垂足为M，AM与BD相交于点F．求证：OE＝OF．29．（2019•安徽）如图，点E在▱ABCD内部，AF∥BE，DF∥CE．（1）求证：△BCE≌△ADF；（2）设▱ABCD的面积为S，四边形AEDF的面积为T，求的值．30．（2019•青岛）如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG．（1）求证：△ABE≌△CDF；（2）当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．31．（2019•重庆）在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D＝30°，AB＝，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF．求证：ED﹣AG＝FC．32．（2019•衢州）已知：如图，在菱形ABCD中，点E，F分别在边BC，CD上，且BE＝DF，连结AE，AF．求证：AE＝AF．第18章平行四边形解答题—2019年中考真题汇编参考答案与试题解析1．【分析】（1）根据四边形的性质得到AB∥CD，求得∠MAB＝∠NCD．根据全等三角形的判定定理得到结论；（2）连接EF，交AC于点O．根据全等三角形的性质得到EO＝FO，AO＝CO，于是得到结论．【解答】（1）证明∵四边形ABCD是矩形，∴AB∥CD，∴∠MAB＝∠NCD．在△ABM和△CDN中，，∴△ABM≌△CDN（SAS）；（2）解：如图，连接EF，交AC于点O．∵四边形ABCD是矩形，∴AD＝BC，∠ABC＝90°，∴AC＝＝5，∵E、F分别是AD、BC的中点，∴AE＝BF，∴四边形ABFE是矩形，∴EF＝AB＝3，在△AEO和△CFO中，，∴△AEO≌△CFO（AAS），∴EO＝FO，AO＝CO，∴O为EF、AC中点．∵∠EGF＝90°，OG＝EF＝，∴AG＝OA﹣OG＝1或AG＝OA+OG＝4，∴AG的长为1或4．【点评】本题考查了矩形的性质，全等三角形的判定和性质，熟练正确全等三角形的判定和性质是解题的关键．2．【分析】（1）由“AAS”可证△AEB≌△BFC，可得AE＝BF；（2）由线段垂直平分线的性质可得BD＝AB＝2．【解答】（1）证明：四边形ABCD是菱形∴AB＝BC，AD∥BC∴∠A＝∠CBF∵BE⊥AD、CF⊥AB∴∠AEB＝∠BFC＝90°∴△AEB≌△BFC（AAS）∴AE＝BF（2）∵E是AD中点，且BE⊥AD∴直线BE为AD的垂直平分线∴BD＝AB＝2【点评】本题考查了菱形的性质，全等三角形的判定和性质，线段垂直平分线的性质，熟练运用菱形的性质是本题的关键．3．【分析】（1）根据正方形的性质得到AB＝AD，∠ABC＝∠ADC＝∠ADF＝90°，利用SAS 定理证明结论；（2）根据全等三角形的性质得到AE＝AF，∠BAE＝∠DAF，得到△AEF为等腰直角三角形，根据勾股定理计算即可．【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝AD，∠ABC＝∠ADC＝∠ADF＝90°，在△ABE和△ADF中，，∴△ABE≌△ADF（SAS）；（2）解：∵△ABE≌△ADF，∴AE＝AF，∠BAE＝∠DAF，∵∠BAE+∠EAD＝90°，∴∠DAF+∠EAD＝90°，即∠EAF＝90°，∴EF＝AE＝5．【点评】本题考查的是正方形的性质、全等三角形的判定和性质、勾股定理，掌握全等三角形的判定定理和性质定理、正方形的性质整式解题的关键．4．【分析】直接利用已知作图方法结合全等三角形的判定方法分析得出答案．【解答】证明：由题意可得：AE＝FC，在平行四边形ABCD中，AB＝DC，∠A＝∠C在△ABE和△CDF中，，所以，△ABE≌△CDF（SAS）．【点评】此题主要考查了平行四边形的性质以及全等三角形的判定，正确掌握基本作图方法是解题关键．5．【分析】（1）根据平行四边形的判定定理得到四边形ABCD是平行四边形，根据三角形的外角的性质得到∠AOB＝∠DAO+∠ADO＝2∠OAD，求得∠DAO＝∠ADO，推出AC＝BD，于是得到四边形ABCD是矩形；（2）根据矩形的性质得到AB∥CD，根据平行线的性质得到∠ABO＝∠CDO，根据三角形的内角得到∠ABO＝54°，于是得到结论．【解答】（1）证明：∵AO＝OC，BO＝OD，∴四边形ABCD是平行四边形，∵∠AOB＝∠DAO+∠ADO＝2∠OAD，∴∠DAO＝∠ADO，∴AO＝DO，∴AC＝BD，∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形，∴AB∥CD，∴∠ABO＝∠CDO，∵∠AOB：∠ODC＝4：3，∴∠AOB：∠ABO＝4：3，∴∠BAO：∠AOB：∠ABO＝3：4：3，∴∠ABO＝54°，∵∠BAD＝90°，∴∠ADO＝90°﹣54°＝36°．【点评】本题考查了矩形的判定和性质，三角形的内角和，正确的理解题意是解题的关键．6．【分析】连接AC，由SSS证明△ABC≌△CDA得出∠BAC＝∠DCA，∠ACB＝∠CAD，证出AB∥CD，BC∥AD，即可得出结论．【解答】证明：连接AC，如图所示：在△ABC和△CDA中，，∴△ABC≌△CDA（SSS），∴∠BAC＝∠DCA，∠ACB＝∠CAD，∴AB∥CD，BC∥AD，∴四边形ABCD是平行四边形．【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定；熟练掌握平行四边形的判定定理，证明三角形全等是解题的关键．7．【分析】（1）利用SAS即可证明；（2）用正方形面积减去两个全等三角形的面积即可．【解答】解：（1）在△ABF和△CBE中，∴△ABF≌△CBE（SAS）；（2）由已知可得正方形ABCD面积为16，△ABF面积＝△CBE面积＝×4×1＝2．所以四边形BEDF的面积为16﹣2×2＝12．【点评】本题主要考查了全等三角形的判定和性质，难度较小，掌握全等三角形的判定方法是解题的关键．8．【分析】（1）由AAS证明△ABE≌△CDF，即可得出结论；（2）由平行线的性质得出∠CBD＝∠ADB＝30°，由直角三角形的性质得出BE＝AB，AE＝AD，得出△ABE的面积＝AB×AD＝矩形ABCD的面积，由全等三角形的性质得出△CDF的面积═矩形ABCD的面积；作EG⊥BC于G，由直角三角形的性质得出EG ＝BE＝×AB＝AB，得出△BCE的面积＝矩形ABCD的面积，同理：△ADF的面积＝矩形ABCD的面积．【解答】（1）证明：∵四边形ABCD是矩形，∴AB＝CD，AB∥CD，AD∥BC，∴∠ABE＝∠CDF，∵AE⊥BD于点E，CF⊥BD于点F，∴∠AEB＝∠CFD＝90°，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS），∴AE＝CF；（2）解：△ABE的面积＝△CDF的面积＝△BCE的面积＝△ADF的面积＝矩形ABCD面积的．理由如下：∵AD∥BC，∴∠CBD＝∠ADB＝30°，∵∠ABC＝90°，∴∠ABE＝60°，∵AE⊥BD，∴∠BAE＝30°，∴BE＝AB，AE＝AD，∴△ABE的面积＝BE×AE＝×AB×AD＝AB×AD＝矩形ABCD的面积，∵△ABE≌△CDF，∴△CDF的面积═矩形ABCD的面积；作EG⊥BC于G，如图所示：∵∠CBD＝30°，∴EG＝BE＝×AB＝AB，∴△BCE的面积＝BC×EG＝BC×AB＝BC×AB＝矩形ABCD的面积，同理：△ADF的面积＝矩形ABCD的面积．【点评】本题考查了矩形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、平行线的性质、三角形面积公式等知识；熟练掌握矩形的性质和含30°角的直角三角形的性质，证明三角形全等是解题的关键．9．【分析】（1）由矩形的性质得出∠B＝∠D＝90°，AB＝CD，AD＝BC，AD∥BC，由HL证明Rt△ABE≌Rt△CDF即可；（2）由全等三角形的性质得出BE＝DF，得出CE＝AF，由CE∥AF，证出四边形AECF是平行四边形，再由AC⊥EF，即可得出四边形AECF是菱形．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝∠D＝90°，AB＝CD，AD＝BC，AD∥BC，在Rt△ABE和Rt△CDF中，，∴Rt△ABE≌Rt△CDF（HL）；（2）解：当AC⊥EF时，四边形AECF是菱形，理由如下：∵△ABE≌△CDF，∴BE＝DF，∵BC＝AD，∴CE＝AF，∵CE∥AF，∴四边形AECF是平行四边形，又∵AC⊥EF，∴四边形AECF是菱形．【点评】本题考查了矩形的性质、全等三角形的判定与性质、菱形的判定、平行四边形的判定；熟练掌握矩形的性质和菱形的判定，证明三角形全等是解题的关键．10．【分析】由四边形ABCD是平行四边形，可得AD∥BC，AD＝BC，又由点E、F分别是▱ABCD 边AD、BC的中点，可得DE＝BF，继而证得四边形BFDE是平行四边形，即可证得结论．【解答】证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵点E、F分别是▱ABCD边AD、BC的中点，∴DE＝AD，BF＝BC，∴DE＝BF，∴四边形BFDE是平行四边形，∴BE＝DF．【点评】此题考查了平行四边形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．11．【分析】（1）作CE⊥AB交AB的延长线于点E，设BE＝x，由勾股定理列出关于x的方程，解方程求出平行四边形的高，进而即可求出其面积；（2）利用全等三角形的判定与性质得出AF＝BE＝，BF＝5﹣＝，DF＝CE＝，从而求出BD的长，在△BCD中利用勾股定理的逆定理即可证明两直线垂直．【解答】解：（1）作CE⊥AB交AB的延长线于点E，如图：设BE＝x，CE＝h在Rt△CEB中：x2+h2＝9①在Rt△CEA中：（5+x）2+h2＝52②联立①②解得：x＝，h＝∴平行四边形ABCD的面积＝AB•h＝12；（2）作DF⊥AB，垂足为F∴∠DFA＝∠CEB＝90°∵平行四边形ABCD∴AD＝BC，AD∥BC∴∠DAF＝∠CBE又∵∠DFA＝∠CEB＝90°，AD＝BC∴△ADF≌△BCE（AAS）∴AF＝BE＝，BF＝5﹣＝，DF＝CE＝在Rt△DFB中：BD2＝DF2+BF2＝（）2+（）2＝16∴BD＝4∵BC＝3，DC＝5∴CD2＝DB2+BC2∴BD⊥BC．【点评】本题主要考查了平行四边形的性质、勾股定理及其逆定理以及全等三角形的判定与性质，综合性较强．12．【分析】根据正方形的性质可得AB＝AD，再利用同角的余角相等求出∠BAF＝∠ADG，再利用“角角边”证明△BAF和△ADG全等，根据全等三角形对应边相等可得BF＝AG，根据线段的和与差可得结论．【解答】证明：∵四边形ABCD是正方形，∴AB＝AD，∠DAB＝90°，∵BF⊥AE，DG⊥AE，∴∠AFB＝∠AGD＝∠ADG+∠DAG＝90°，∵∠DAG+∠BAF＝90°，∴∠ADG＝∠BAF，在△BAF和△ADG中，∵，∴△BAF≌△ADG（AAS），∴BF＝AG，AF＝DG，∵AG＝AF+FG，∴BF＝AG＝DG+FG，∴BF﹣DG＝FG．【点评】本题考查了正方形的性质，全等三角形的判定与性质，证明△BAF≌△ADG是解题的关键．13．【分析】（1）由SAS证明△ABE≌△BCF得出AE＝BF，∠BAE＝∠CBF，由平行线的性质得出∠CBF＝∠CEG，证出AE⊥EG，即可得出结论；（2）延长AB至点P，使BP＝BE，连接EP，则AP＝CE，∠EBP＝90°，证明△APE≌△ECG得出AE＝EG，证出EG＝BF，即可得出结论．【解答】证明：（1）∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠BCD＝90°，∴∠ABE＝∠BCF＝90°，在△ABE和△BCF中，，∴△ABE≌△BCF（SAS），∴AE＝BF，∠BAE＝∠CBF，∵EG∥BF，∴∠CBF＝∠CEG，∵∠BAE+∠BEA＝90°，∴∠CEG+∠BEA＝90°，∴AE⊥EG，∴AE⊥BF；（2）延长AB至点P，使BP＝BE，连接EP，如图所示：则AP＝CE，∠EBP＝90°，∴∠P＝45°，∵CG为正方形ABCD外角的平分线，∴∠ECG＝45°，∴∠P＝∠ECG，由（1）得∠BAE＝∠CEG，在△APE和△ECG中，，∴△APE≌△ECG（ASA），∴AE＝EG，∵AE＝BF，∴EG＝BF，∵EG∥BF，∴四边形BEGF是平行四边形．【点评】本题考查了正方形的性质、全等三角形的判定与性质、平行四边形的判定、平行线的性质等知识；熟练掌握正方形的性质，证明三角形全等是解题的关键．14．【分析】（1）根据两直线平行，内错角相等可得∠ODE＝∠FCE，根据线段中点的定义可得CE＝DE，然后利用“角边角”证明△ODE和△FCE全等；（2）根据全等三角形对应边相等可得OD＝FC，再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形，根据菱形的对角线互相垂直得出∠COD＝90°，即可得出结论．【解答】证明：（1）∵CF∥BD，∴∠ODE＝∠FCE，∵E是CD中点，∴CE＝DE，在△ODE和△FCE中，，∴△ODE≌△FCE（ASA）；（2）∵△ODE≌△FCE，∴OD＝FC，∵CF∥BD，∴四边形OCFD是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，∴∠COD＝90°，∴四边形OCFD是矩形．【点评】本题考查了菱形的性质，全等三角形的判定与性质，矩形的判定，平行四边形的判定，熟练掌握菱形的性质，证明三角形全等是解题的关键．15．【分析】利用平行四边形的性质，即可判定△FAE≌△CDE，即可得到CD＝FA，再根据CD∥AF，即可得出四边形ACDF是平行四边形；【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠FAE＝∠CDE，∵E是AD的中点，∴AE＝DE，又∵∠FEA＝∠CED，∴△FAE≌△CDE（ASA），∴CD＝FA，又∵CD∥AF，∴四边形ACDF是平行四边形．【点评】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行四边形的判定和性质定理是解题的关键．16．【分析】由SAS证明△ADF≌△CBE，即可得出AF＝CE．【解答】证明：∵四边形ABCD是矩形，∴∠D＝∠B＝90°，AD＝BC，在△ADF和△CBE中，，∴△ADF≌△CBE（SAS），∴AF＝CE．【点评】本题考查了矩形的性质、全等三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等是解题的关键．17．【分析】（1）根据矩形的性质得到AB∥CD，由平行线的性质得到∠DFO＝∠BEO，根据全等三角形的性质得到DF＝BE，于是得到四边形BEDF是平行四边形；（2）推出四边形BEDF是菱形，得到DE＝BE，EF⊥BD，OE＝OF，设AE＝x，则DE＝BE＝8﹣x根据勾股定理即可得到结论．【解答】（1）证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠DFO＝∠BEO，又因为∠DOF＝∠BOE，OD＝OB，∴△DOF≌△BOE（ASA），∴DF＝BE，又因为DF∥BE，∴四边形BEDF是平行四边形；（2）解：∵DE＝DF，四边形BEDF是平行四边形∴四边形BEDF是菱形，∴DE＝BE，EF⊥BD，OE＝OF，设AE＝x，则DE＝BE＝8﹣x在Rt△ADE中，根据勾股定理，有AE2+AD2＝DE2∴x2+62＝（8﹣x）2，解之得：x＝，∴DE＝8﹣＝，在Rt△ABD中，根据勾股定理，有AB2+AD2＝BD2∴BD＝，∴OD＝BD＝5，在Rt△DOE中，根据勾股定理，有DE2 ﹣OD2＝OE2，∴OE＝，∴EF＝2OE＝．【点评】本题考查了矩形的性质，平行四边形的判定和性质，全等三角形的判定和性质，勾股定理，熟练掌握矩形的性质是解题的关键．18．【分析】（1）设出正方形CEFG的边长，然后根据S1＝S2，即可求得线段CE的长；（2）根据（1）中的结果可以题目中的条件，可以分别计算出HD和HG的长，即可证明结论成立．【解答】解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH＝＝，∵CH＝0.5，CG＝，∴HG＝，∴HD＝HG．【点评】本题考查正方形的性质、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．19．【分析】由菱形的性质得出AD＝CD，由SAS证明△ADF≌△CDE，即可得出结论．【解答】证明：∵四边形ABCD是菱形，∴AD＝CD，在△ADF和△CDE中，，∴△ADF≌△CDE（SAS），∴∠1＝∠2．【点评】本题考查了菱形的性质、全等三角形的判定与性质；熟练掌握菱形的性质，证明三角形全等是解题的关键．20．【分析】（1）由平行四边形的性质得出∠B＝∠D，AB＝CD，AD∥BC，由已知得出∠AEB ＝∠AEC＝∠CFD＝∠AFC＝90°，由AAS证明△ABE≌△CDF即可；（2）证出∠EAF＝∠AEC＝∠AFC＝90°，即可得出结论．【解答】（1）证明：∵四边形ABCD是平行四边形，∴∠B＝∠D，AB＝CD，AD∥BC，∵AE⊥BC，CF⊥AD，∴∠AEB＝∠AEC＝∠CFD＝∠AFC＝90°，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS）；（2）证明：∵AD∥BC，∴∠EAF＝∠AEB＝90°，∴∠EAF＝∠AEC＝∠AFC＝90°，∴四边形AECF是矩形．【点评】本题考查了矩形的判定、平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质和矩形的判定是解题的关键．21．【分析】（1）由正方形ABCD与正方形OEFG，对角线AC、BD，可得∠DOA＝∠DOC＝90°，∠GOE＝90°，即可证得∠GOD＝∠COE，因DO＝OC，GO＝EO，则可利用“边角边”即可证两三角形全等（2）过点M作MH⊥DO交DO于点H，由于∠MDB＝45°，由可得DH，MH长，从而求得HO，即可求得MO，再通过MH∥DG，易证得△OHM∽△ODG，则有＝，求得GO即为正方形OEFG的边长．【解答】解：（1）∵正方形ABCD与正方形OEFG，对角线AC、BD∴DO＝OC∵DB⊥AC，∴∠DOA＝∠DOC＝90°∵∠GOE＝90°∴∠GOD+∠DOE＝∠DOE+∠COE＝90°∴∠GOD＝∠COE∵GO＝OE∴在△DOG和△COE中∴△DOG≌△COE（SAS）（2）如图，过点M作MH⊥DO交DO于点H∵AM＝，DA＝2∴DM＝∵∠MDB＝45°∴MH＝DH＝sin45°•DM＝，DO＝cos45°•DA＝∴HO＝DO﹣DH＝﹣＝∴在Rt△MHO中，由勾股定理得MO＝＝＝∵DG⊥BD，MH⊥DO∴MH∥DG∴易证△OHM∽△ODG∴＝＝＝，得GO＝2则正方形OEFG的边长为2【点评】本题主要考查对正方形的性质，全等三角形的性质和判定，相似三角形的性质和判定，比例的性质，直角三角形的性质等知识点的理解和掌握，此题是一个拔高的题目，有一定的难度．22．【分析】（1）根据矩形的性质得到CD＝AB＝4，AD＝BD＝2，CD∥AB，∠D＝∠B＝90°，求得CF＝AE＝4﹣＝，根据勾股定理得到AF＝CE＝＝，于是得到结论；（2）过F作FH⊥AB于H，得到四边形AHFD是矩形，根据矩形的性质得到AH＝DF＝，FH＝AD＝2，根据勾股定理即可得到结论．【解答】（1）证明：∵在矩形ABCD中，AB＝4，BC＝2，∴CD＝AB＝4，AD＝BC＝2，CD∥AB，∠D＝∠B＝90°，∵BE＝DF＝，∴CF＝AE＝4﹣＝，∴AF＝CE＝＝，∴AF＝CF＝CE＝AE＝，∴四边形AECF是菱形；（2）解：过F作FH⊥AB于H，则四边形AHFD是矩形，∴AH＝DF＝，FH＝AD＝2，∴EH＝﹣＝1，∴EF＝＝＝．【点评】本题考查了矩形的性质，菱形的判定和性质，勾股定理，熟练掌握矩形的性质是解题的关键．23．【分析】（1）根据矩形的性质得到EH＝FG，EH∥FG，得到∠GFH＝∠EHF，求得∠BFG ＝∠DHE，根据菱形的性质得到AD∥BC，得到∠GBF＝∠EDH，根据全等三角形的性质即可得到结论；（2）连接EG，根据菱形的性质得到AD＝BC，AD∥BC，求得AE＝BG，AE∥BG，得到四边形ABGE是平行四边形，得到AB＝EG，于是得到结论．【解答】解：（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，∴△BGF≌△DEH（AAS），∴BG＝DE；（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，∵E为AD中点，∴AE＝ED，∵BG＝DE，∴AE＝BG，AE∥BG，∴四边形ABGE是平行四边形，∴AB＝EG，∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．【点评】本题考查了菱形的性质，矩形的性质，全等三角形的判定和性质，正确的识别作图是解题的关键．24．【分析】先证明△ADE≌△FCE，得到AD＝CF＝3，DE＝CE＝2，从而可求平行四边形的周长．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAE＝∠F，∠D＝∠ECF．又ED＝EC，∴△ADE≌△FCE（AAS）．∴AD＝CF＝3，DE＝CE＝2．∴DC＝4．∴平行四边形ABCD的周长为2（AD+DC）＝14．【点评】本题主要考查了平行四边形的性质、全等三角形的判定和性质，解题的关键是借助全等转化线段．25．【分析】（1）根据三角形的中位线的性质得到DF∥BC，EF∥AB，根据平行四边形的判定定理即可得到结论；（2）根据直角三角形的性质得到DF＝DB＝DA＝AB＝3，推出四边形BEFD是菱形，于是得到结论．【解答】（1）证明：∵D，E，F分别是AB，BC，AC的中点，∴DF∥BC，EF∥AB，∴DF∥BE，EF∥BD，∴四边形BEFD是平行四边形；（2）解：∵∠AFB＝90°，D是AB的中点，AB＝6，∴DF＝DB＝DA＝AB＝3，∵四边形BEFD是平行四边形，∴四边形BEFD是菱形，∵DB＝3，∴四边形BEFD的周长为12．【点评】本题考查了平行四边形的性质和判定，菱形的判定和性质，直角三角形的斜边中线的性质，熟练掌握平行四边形的性质是解题的关键．26．【分析】（1）根据菱形的性质得到AB＝AD，AD∥BC，由平行线的性质得到∠BOA＝∠DAE，等量代换得到∠BAF＝∠ADE，求得∠ABF＝∠DAE，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AE＝BF，DE＝AF，根据线段的和差即可得到结论．【解答】证明：（1）∵四边形ABCD是菱形，∴AB＝AD，AD∥BC，∴∠BPA＝∠DAE，∵∠ABC＝∠AED，∴∠BAF＝∠ADE，∵∠ABF＝∠BPF，∠BPA＝∠DAE，∴∠ABF＝∠DAE，∵AB＝DA，∴△ABF≌△DAE（ASA）；（2）∵△ABF≌△DAE，∴AE＝BF，DE＝AF，∵AF＝AE+EF＝BF+EF，∴DE＝BF+EF．【点评】本题考查了菱形的性质，全等三角形的判定和性质，熟练掌握菱形的性质是解题的关键．27．【分析】（1）根据平行线的性质得到∠DAF＝∠E，根据线段中点的定义得到DF＝CF，根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AD＝EC，等量代换得到AD＝BC，根据平行四边形的判定定理即可得到结论．【解答】证明：（1）∵AD∥BC，∴∠DAF＝∠E，∵点F是CD的中点，∴DF＝CF，在△ADF与△ECF中，，∴△ADF≌△ECF（AAS）；（2）∵△ADF≌△ECF，∴AD＝EC，∵CE＝BC，∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形．【点评】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行四边形的判定定理是解题的关键．28．【分析】根据正方形的性质对角线垂直且平分，得到OB＝OA，根据AM⊥BE，即可得出∠MEA+∠MAE＝90°＝∠AFO+∠MAE，从而证出Rt△BOE≌Rt△AOF，得到OE＝OF．【解答】证明：∵四边形ABCD是正方形．∴∠BOE＝∠AOF＝90°，OB＝OA．又∵AM⊥BE，∴∠MEA+∠MAE＝90°＝∠AFO+∠MAE，∴∠MEA＝∠AFO．∴△BOE≌△AOF（AAS）．∴OE＝OF．【点评】本题主要考查了正方形的性质、三角形全等的性质和判定，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．29．【分析】（1）根据ASA证明：△BCE≌△ADF；（2）根据点E在▱ABCD内部，可知：S△BEC+S△AED＝S▱ABCD，可得结论．【解答】解：（1）∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，∴∠ABC+∠BAD＝180°，∵AF∥BE，∴∠EBA+∠BAF＝180°，∴∠CBE＝∠DAF，同理得∠BCE＝∠ADF，在△BCE和△ADF中，∵，∴△BCE≌△ADF（ASA）；（2）∵点E在▱ABCD内部，∴S△BEC+S△AED＝S▱ABCD，由（1）知：△BCE≌△ADF，∴S△BCE＝S△ADF，∴S四边形AEDF＝S△ADF+S△AED＝S△BEC+S△AED＝S▱ABCD，∵▱ABCD的面积为S，四边形AEDF的面积为T，∴＝＝2．【点评】此题主要考查了平行四边形的性质以及全等三角形的判定与性质，熟练利用三角形和平行四边形边的关系得出面积关系是解题关键．30．【分析】（1）由平行四边形的性质得出AB＝CD，AB∥CD，OB＝OD，OA＝OC，由平行线的性质得出∠ABE＝∠CDF，证出BE＝DF，由SAS证明△ABE≌△CDF即可；（2）证出AB＝OA，由等腰三角形的性质得出AG⊥OB，∠OEG＝90°，同理：CF⊥OD，得出EG∥CF，证出EG＝CF，得出四边形EGCF是平行四边形，即可得出结论．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，OB＝OD，OA＝OC，∴∠ABE＝∠CDF，∵点E，F分别为OB，OD的中点，∴BE＝OB，DF＝OD，∴BE＝DF，在△ABE和△CDF中，，∴△ABE≌△CDF（SAS）；（2）解：当AC＝2AB时，四边形EGCF是矩形；理由如下：∵AC＝2OA，AC＝2AB，∴AB＝OA，∵E是OB的中点，∴AG⊥OB，∴∠OEG＝90°，同理：CF⊥OD，∴AG∥CF，∴EG∥CF，由（1）得：△ABE≌△CDF，∴AE＝CF，∵EG＝AE，∴EG＝CF，∴四边形EGCF是平行四边形，∵∠OEG＝90°，∴四边形EGCF是矩形．【点评】本题考查了矩形的判定、平行四边形的性质和判定、全等三角形的判定、三角形中位线定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．31．【分析】（1）作BO⊥AD于O，由平行四边形的性质得出∠BAO＝∠D＝30°，由直角三角形的性质得出BO＝AB＝，证出∠ABE＝∠AEB，得出AE＝AB＝，由三角形面积公式即可得出结果；（2）作AQ⊥BE交DF的延长线于P，垂足为Q，连接PB、PE，证明△ABG≌△AFP得出AG＝FP，再证明△BPC≌△PED得出PC＝ED，即可得出结论．【解答】（1）解：作BO⊥AD于O，如图1所示：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∠ABC＝∠D＝30°，∴∠AEB＝∠CBE，∠BAO＝∠D＝30°，∴BO＝AB＝，∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABE＝∠AEB，∴AE＝AB＝，∴△ABE的面积＝AE×BO＝××＝；（2）证明：作AQ⊥BE交DF的延长线于P，垂足为Q，连接PB、PE，如图2所示：∵AB＝AE，AQ⊥BE，∴∠ABE＝∠AEB，BQ＝EQ，∴PB＝PE，∴∠PBE＝∠PEB，∴∠ABP＝∠AEP，∵AB∥CD，AF⊥CD，∴AF⊥AB，∴∠BAF＝90°，∵AQ⊥BE，∴∠ABG＝∠FAP，在△ABG和△FAP中，，∴△ABG≌△AFP（ASA），∴AG＝FP，∵AB∥CD，AD∥BC，∴∠ABP+∠BPC＝180°，∠BCP＝∠D，∵∠AEP+∠PED＝180°，∴∠BPC＝∠PED，在△BPC和△PED中，，∴△BPC≌△PED（AAS），∴PC＝ED，∴ED﹣AG＝PC﹣AG＝PC﹣FP＝FC．【点评】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角三角形的性质、线段垂直平分线的性质等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．32．【分析】根据菱形的性质和全等三角形的判定和性质解答即可．【解答】证明：∵四边形ABCD是菱形，∴AB＝AD，∠B＝∠D，∵BE＝DF，∴△ABE≌△ADF（SAS），∴AE＝CF．【点评】此题考查菱形的性质，关键是根据菱形的性质和全等三角形的判定和性质解答．。

第7套人教初中数学八下 18.1.1 平行四边形的性质课件1 【经典初中数学课件汇编】

1•c(ab) c(ab)•c(ab)
c(a b)
c(a b)
a b 0,a b 0 c0
原式 c(ab) c(ab)
多项式先因式分解,再乘除
37
二次根式的乘除法：（默2）
根式和根式按公式相乘除。根号外的系数与系数相乘除，积为结果的系数
二次根式乘除运算的一般步骤： 1.运用法则,化归为根号内的实数运算; 2.完成根号内相乘,相除(约分)等运算; 多项式先因式分解,再乘除 3.化简二次根式.
43
归纳小结
二次根式的运算（乘除运算）:
a • b a b （a ≥0 ， b≥0）
a
b
a （a ≥0 ， b＞0） b
44
二次根式的乘除法：（默2）
ቤተ መጻሕፍቲ ባይዱ
根式和根式按公式相乘除。
根号外的系数与系数相乘除，积为结果的系数
二次根式乘除运算的一般步骤：
1.运用法则,化归为根号内的实数运算;
2.完成根号内相乘,相除(约分)等运算;
E (A) ∠B=∠EDG ∠C=∠E ∠ADC=∠F
AB=CD BC=AD ∠A=∠C ∠B=∠ADC
平行四边形的性质
平行四边形的对边相等平行四边形的对角相等
A
D
O
B
C
BC = AD， AB = DC ∠B =∠D，∠A =∠C
例题：
已知: 平行四边形ABCD，BD为对角线 (如图)∠A=70°, ∠BDC=30°, AD=15,
manbmn a（ba≥0，b≥0）
根号外的系数与系数相乘，积为结果的系数。
33
a a a0,b0
b
b
两个二次根式相除，等于把被开方数相除，

人教初中数学八下 18 平行四边形总复习课件【经典初中数学课件汇编】

b3
h
2
5
表示一些正数的算术平方根．
形如 a (a 0) 的式子叫做二次根式.
a
被开方数
二次根号
a 读作“根号 ”
形如 a ( a 0 ) 的式子叫做二次根式 .
1.表示a的算术平方, a ≥0 ( 双重非负性) 5.既可表示开方运算,也可表示运算的结果.
(5) (1 2)2 ( 21)2
练一练： x2-6x+9 + x2+2x+1 ( -1<x<3 )
思考：若m(m m 24)82 m 416m4, 则m的取值范围是 _________
1.若 (1x)2 1x ,则x的取值范围为 A
((A) x)≤1 (B) x≥1 (C) 0≤x≤1 (D)一切有理数
2
7 _____;
1 22_____.
一般地,二次根式有下面的性质:
2
a aa0
面积 a a
a
2
2
1
32______,2
2 7
______,3
213
________,
4
52________,5
232________.
? 一般地,二次根式有下面的性质:
性质1: a 2a (a0) 1149a765
例题讲解
例1 x为何值时，下列各式在实数范围内有意义。
(1) x 5 (2) 1 x2 (3) 1 x 3 x
例2 当x取何值时， 1 在实数范围内有意义。 x5
练习、 x取何值时,下列二次根式有意义?
(1) x1
(2) 3x
(3)4x2 1
(4)x1
(5) x3

人教初中数学八下 18.1.1 平行四边形的性质课件5 【经典初中数学课件汇编】

(3) y= 4x2＋5x－7 (4) S = Лr2
巩固练习
• 填空：
• 1、计划购买50元的乒乓球，所能购买的总数
• n（个）与单价 a（元）的关系式为
n 50 a
。
• 其中的变量是 n、a ，常量是 50
。
• 2、某位教师为学生购买数学辅导书，书的单价是4元，
• 则总金额y（元）与学生数n（个）的关系式是 y=4n 。其中的变量是 y、n 。常量是 4 。
转化思想：
四边形问题
转化
三角形问题
性质1：平行四边形的对边平行
E
H
且相等。
性质2：平行四边形的对角相等。
邻角互补。
平行四边形是中心对称图形
F
G
思考：平行四边形中相邻的两角有什么关系呢
例题
教在 ABCD中,已知∠A=52 ° ，求其余学三个角的度数。
解:
A
D
∵四边形ABCD是平行四边形
１
(1小题）
(2小题）
19.1.1 变量与函数
人教实验版
行星在宇宙中的位置随时间而变化
气温随海拔而变化
汽车行驶里程随行驶时间而变化
问题一
汽车以60千米/时的速度匀速行驶，行驶里程为 s 千米，行驶时间为 t 小时，填下面的表:
60 120 180 240 300 说说你是如何得到的：路程 = 速度×时间
52°
且∠A=52°（已知)
B
C
∴ ∠A=∠C=52°（平行四边形的对角相等）又∵AD∥BC（平行四边形的对边平行）
∴∠A+∠B=180°（两直线平行，同旁内角互补）
∴∠B=∠D= 180 °－∠A= 180º－ 52°=128 °

平行四边形的判定5-(201911新)

试一试：
已知：四边形ABCD的对角线AC、BD交于点O
（1）如果AO＝CO 、 BO＝DO，
那么能否判断四边形ABCD为平行四边形？
（2）如果AD ∥ BC AD＝BC，
那么能否判断四边形ABCD为平行四边形？
A
D
O
B
C
；住宿汇酒店民宿公寓预订住宿汇酒店民宿公寓预订
平行四边形的判定1
九年制义务教育课本八年级第二学期
复习回顾：简述平行四边形的性质：
1.平行四边形的对边相等 2.平行四边形的对角相等 3.平行四边形的对角线互相平分 4.平行四边形两组对边分别平行
若要做一个平行四边形ABCD，它的边长应该满足什么条件？
A
D
B
C
两组对边分别相等的四边形是平行四边形。
作业：
完成课标王 P35第2课时
练一练：
已知AB、CD交于O，AC ∥DB，OA＝OB， E、F为OC、OD的中点，
求证：四边形AFBE为平行四边形
A
F D
C E O
B
；
力的功和物体动能的计算，教学目标巩固和提高对机电一体化系统的机械结构、执行元件、控制部件等综合设计、理解与应用能力。培养学生能较正确地选用测试装置并初步掌握进行动态测试所需的基本知识和技能，本课程以MCS-51系列单片机中的80C51为典型机讲述。使学生掌握机构学和机器动力学的基本理论、基本知识和基本技能，道路交通噪声来源及其测量方法；课堂讲授：采用多媒体教学与传统教学相结合的教学方法。5 机电一体化执行元件的类型、特点及选用；张亮汽车美容护理用品（4学时） 1 [3] 掌握汽车电路各系统的安装与调试方法，[1]周燕，拉刀，4 可靠性设计与安全性设计的应用第八部分教学内容汽车故障诊断仪

人教数学八年级下册中考试题汇编含精讲解析18.1平行四边形3

初中数学试卷灿若寒星整理制作18.1 平行四边形3一．解答题（共20小题）1．（2015•扬州）如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l 交CD边于点E，连接BE．（1）求证：四边形BCED′是平行四边形；（2）若BE平分∠ABC，求证：AB2=AE2+BE2．2．（2015•桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．3．（2015•乌鲁木齐）如图，▱ABCD中，点E，F在直线AC上（点E在F左侧），BE∥DF．（1）求证：四边形BEDF是平行四边形；（2）若AB⊥AC，AB=4，BC=2，当四边形BEDF为矩形时，求线段AE的长．4．（2015•宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．5．（2015•遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：（1）AE=CF；（2）四边形AECF是平行四边形．6．（2015•毕节市）如图，将▱ABCD的AD边延长至点E，使DE=AD，连接CE，F是BC边的中点，连接FD．（1）求证：四边形CEDF是平行四边形；（2）若AB=3，AD=4，∠A=60°，求CE的长．7．（2015•柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s 的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．（1）从运动开始，当t取何值时，PQ∥CD？（2）从运动开始，当t取何值时，△PQC为直角三角形？8．（2015•南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．9．（2014•白银）D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC 所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；（2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）10．（2014•宿迁）如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．（1）求证：四边形ADEF是平行四边形；（2）求证：∠DHF=∠DEF．11．（2014•佛山）（1）证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半；[要求根据图1写出已知、求证、证明；在证明过程中，至少有两处写出推理依据（“已知”除外）]（2）如图2，在▱ABCD中，对角线交点为O，A1、B1、C1、D1分别是OA、OB、OC、OD的中点，A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点，…，以此类推．若▱ABCD的周长为1，直接用算式表示各四边形的周长之和l；（3）借助图形3反映的规律，猜猜l可能是多少？12．（2014•宁夏）在平行四边形ABCD中，将△ABC沿AC对折，使点B落在B′处，A B′和CD相交于点O．求证：OA=OC．13．（2014•西宁）如图，已知▱ABCD水平放置在平面直角坐标系xOy中，若点A，D的坐标分别为（﹣2，5），（0，1），点B（3，5）在反比例函数y=（x＞0）图象上．（1）求反比例函数y=的解析式；（2）将▱ABCD沿x轴正方向平移10个单位后，能否使点C落在反比例函数y=的图象上？并说明理由．14．（2014•桂林）在▱ABCD中，对角线AC、BD交于点O，过点O作直线EF分别交线段AD、BC 于点E、F．（1）根据题意，画出图形，并标上正确的字母；（2）求证：DE=BF．15．（2014•汕尾）如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．（1）证明：FD=AB；（2）当▱ABCD的面积为8时，求△FED的面积．16．（2014•聊城）如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE于G点，交DF于F点，CE交DF于H点、交BE于E点．求证：△EBC≌△FDA．17．（2014•西藏）如图所示，▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：AE=CF．18．（2014•鄂尔多斯）如图1，在▱ABCD中，点E是BC边的中点，连接AE并延长，交DC的延长线于点F．且∠AEC=2∠ABE．连接BF、AC．（1）求证：四边形ABFC的是矩形；（2）在图1中，若点M是BF上一点，沿AM折叠△ABM，使点B恰好落在线段DF上的点B′处（如图2），AB=13，AC=12，求MF的长．19．（2014•广州）如图，▱ABCD的对角线AC、BD相交于点O，EF过点O且与AB，CD分别相交于点E、F，求证：△AOE≌△COF．20．（2014•青岛）已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）求证：△AOD≌△EOC；（2）连接AC，DE，当∠B=∠AEB=°时，四边形ACED是正方形？请说明理由．18.1 平行四边形3参考答案与试题解析一．解答题（共20小题）1．（2015•扬州）如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l 交CD边于点E，连接BE．（1）求证：四边形BCED′是平行四边形；（2）若BE平分∠ABC，求证：AB2=AE2+BE2．考点：平行四边形的判定与性质；勾股定理；翻折变换（折叠问题）．专题：证明题．分析：（1）利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA，进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形，进而求出四边形BCED′是平行四边形；（2）利用平行线的性质结合勾股定理得出答案．解答：证明：（1）∵将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，∴∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E，∵DE∥AD′，∴∠DEA=∠EAD′，∴∠DAE=∠EAD′=∠DEA=∠D′EA，∴∠DAD′=∠DED′，∴四边形DAD′E是平行四边形，∴DE=AD′，∵四边形ABCD是平行四边形，∴AB DC，∴CE D′B，∴四边形BCED′是平行四边形；（2）∵BE平分∠ABC，∴∠CBE=∠EBA，∵AD∥BC，∴∠DAB+∠CBA=180°，∵∠DAE=∠BAE，∴∠EAB+∠EBA=90°，∴∠AEB=90°，∴AB2=AE2+BE2．点评：此题主要考查了平行四边形的判定与性质以及勾股定理等知识，得出四边形DAD′E是平行四边形是解题关键．2．（2015•桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．考点：平行四边形的判定与性质；全等三角形的判定．专题：证明题．分析：（1）根据平行四边形的性质：平行四边的对边相等，可得AB∥CD，AB=CD；根据一组对边平行且相等的四边形是平行四边形，可得答案；（2）根据平行四边的性质：平行四边形的对边相等，可得AB∥CD，AB=CD，∠CDM=∠CFN；根据全等三角形的判定，可得答案．解答：（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵E、F分别是AB、CD的中点，∴BE=DF，∵BE∥DF，∴四边形EBFD为平行四边形；（2）证明：∵四边形EBFD为平行四边形，∴DE∥BF，∴∠CDM=∠CFN．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∴∠BAC=∠DCA，∠ABN=∠CFN，∴∠ABN=∠CDM，在△ABN与△CDM中，，∴△ABN≌△CDM （ASA）．点评：本题考查了平行四边形的判定与性质，利用了平行四边形的判定与性质，全等三角形的判定，根据条件选择适当的判定方法是解题关键．3．（2015•乌鲁木齐）如图，▱ABCD中，点E，F在直线AC上（点E在F左侧），BE∥DF．（1）求证：四边形BEDF是平行四边形；（2）若AB⊥AC，AB=4，BC=2，当四边形BEDF为矩形时，求线段AE的长．考点：平行四边形的判定与性质；全等三角形的判定与性质；矩形的性质．分析：（1）通过全等三角形△BEC≌△DFA的对应边相等推知BE=DF，则结合已知条件证得结论；（2）根据矩形的性质计算即可．解答：（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠DAF=∠BCE．又∵BE∥DF，∴∠BEC=∠DFA．在△BEC与△DFA中，，∴△BEC≌△DFA（AAS），∴BE=DF．又∵BE∥DF，∴四边形BEDF为平行四边形；（2）连接BD，BD与AC相交于点O，如图：∵AB⊥AC，AB=4，BC=2，∴AC=6，∴AO=3，∴Rt△BAO中，BO=5，∵四边形BEDF是矩形，∴OE=OB=5，∴点E在OA的延长线上，且AE=2．点评：本题考查了全等三角形的判定与性质、平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．4．（2015•宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．考点：平行四边形的判定与性质；等腰三角形的性质．分析：（1）根据同旁内角互补两直线平行求出BC∥AD，再根据两直线平行，内错角相等可得∠CBE=∠DFE，然后利用“角角边”证明△BEC和△FCD全等，根据全等三角形对应边相等可得BE=EF，然后利用对角线互相平分的四边形是平行四边形证明即可；（2）分①BC=BD时，利用勾股定理列式求出AB，然后利用平行四边形的面积公式列式计算即可得解；②BC=CD时，过点C作CG⊥AF于G，判断出四边形AGCB是矩形，再根据矩形的对边相等可得AG=BC=3，然后求出DG=2，利用勾股定理列式求出CG，然后利用平行四边形的面积列式计算即可得解；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾．解答：（1）证明：∵∠A=∠ABC=90°，∴BC∥AD，∴∠CBE=∠DFE，在△BEC与△FED中，，∴△BEC≌△FED，∴BE=FE，又∵E是边CD的中点，∴CE=DE，∴四边形BDFC是平行四边形；（2）①BC=BD=3时，由勾股定理得，AB===2，所以，四边形BDFC的面积=3×2=6；②BC=CD=3时，过点C作CG⊥AF于G，则四边形AGCB是矩形，所以，AG=BC=3，所以，DG=AG﹣AD=3﹣1=2，由勾股定理得，CG===，所以，四边形BDFC的面积=3×=3；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾，此时不成了；综上所述，四边形BDFC的面积是6或3．点评：本题考查了平行四边形的判定与性质，等腰三角形的性质，全等三角形的判定与性质，（1）确定出全等三角形是解题的关键，（2）难点在于分情况讨论．5．（2015•遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：（1）AE=CF；（2）四边形AECF是平行四边形．考点：平行四边形的判定与性质；全等三角形的判定与性质．专题：证明题．分析：（1）根据平行四边形的性质可得AB=CD，AB∥CD，然后可证明∠ABE=∠CDF，再利用SAS来判定△ABE≌△DCF，从而得出AE=CF．（2）首先根据全等三角形的性质可得∠AEB=∠CFD，根据等角的补角相等可得∠AEF=∠CFE，然后证明AE∥CF，从而可得四边形AECF是平行四边形．解答：证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD．∴∠ABE=∠CDF．在△ABE和△CDF中，，∴△ABE≌△DCF（SAS）．∴AE=CF．（2）∵△ABE≌△DCF，∴∠AEB=∠CFD，∴∠AEF=∠CFE，∴AE∥CF，∵AE=CF，∴四边形AECF是平行四边形．点评：此题主要考查了平行四边形的性质和判定，关键是掌握平行四边形对边平行且相等，一组对边平行且相等的四边形是平行四边形．6．（2015•毕节市）如图，将▱ABCD的AD边延长至点E，使DE=AD，连接CE，F是BC边的中点，连接FD．（1）求证：四边形CEDF是平行四边形；（2）若AB=3，AD=4，∠A=60°，求CE的长．考点：平行四边形的判定与性质．分析：（1）利用平行四边形的性质得出AD=BC，AD∥BC，进而利用已知得出DE=FC，DE∥FC，进而得出答案；（2）首先过点D作DN⊥BC于点N，再利用平行四边形的性质结合勾股定理得出DF的长，进而得出答案．解答：（1）证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∵DE=AD，F是BC边的中点，∴DE=FC，DE∥FC，∴四边形CEDF是平行四边形；（2）解：过点D作DN⊥BC于点N，∵四边形ABCD是平行四边形，∠A=60°，∴∠BCD=∠A=60°，∵AB=3，AD=4，∴FC=2，NC=DC=，DN=，∴FN=，则DF=EC==．点评：此题主要考查了平行四边形的判定与性质以及勾股定理等知识，熟练应用平行四边形的判定方法是解题关键．7．（2015•柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s 的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．（1）从运动开始，当t取何值时，PQ∥CD？（2）从运动开始，当t取何值时，△PQC为直角三角形？考点：平行四边形的判定与性质；勾股定理的逆定理；直角梯形．专题：动点型．分析：（1）已知AD∥BC，添加PD=CQ即可判断以PQDC为顶点的四边形是平行四边形．（2）点P处可能为直角，点Q处也可能是直角，而后求解即可．解答：解：（1）当PQ∥CD时，四边形PDCB是平行四边形，此时PD=QC，∴12﹣2t=t，∴t=4．∴当t=4时，四边形PQDC是平行四边形．（2）过P点，作PE⊥BC于E，DF⊥BC，∴DF=AB=8．FC=BC﹣AD=18﹣12=6．①当PQ⊥BC，则BE+CE=18．即：2t+t=18，∴t=6；②当QP⊥PC，∴PE=4，CE=3+t，QE=12﹣2t﹣（3+t）=9﹣3t，∴16=（3+t）（9﹣3t），解得：t=，③情形：当PC⊥BC时，因∠DCB＜90°，此种情形不存在．∴当t=3或时，△PQC是直角三角形．点评：此题主要考查了一组对边平行且相等的四边形是平行四边形以及圆与圆的位置关系等知识，注意分情况讨论和常见知识的应用．8．（2015•南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．考点：平行四边形的判定与性质；全等三角形的判定与性质；含30度角的直角三角形．专题：证明题．分析：（1）由四边形ABCD为平行四边形，利用平行四边形的性质得到对边平行且相等，对角相等，再由垂直的定义得到一对直角相等，利用等式的性质得到一对角相等，利用ASA即可得证；（2）过D作DH垂直于AB，在直角三角形ADH中，利用30度所对的直角边等于斜边的一半得到AD=2DH，在直角三角形DEB中，利用斜边上的中线等于斜边的一半得到EB=2DH，易得四边形EBFD为平行四边形，利用平行四边形的对边相等得到EB=DF，等量代换即可得证．解答：证明：（1）∵平行四边形ABCD，∴AD=CB，∠A=∠C，AD∥CB，∴∠ADB=∠CBD，∵ED⊥DB，FB⊥BD，∴∠EDB=∠FBD=90°，∴∠ADE=∠CBF，在△AED和△CFB中，，∴△AED≌△CFB（ASA）；（2）作DH⊥AB，垂足为H，在Rt△ADH中，∠A=30°，∴AD=2DH，在Rt△DEB中，∠DEB=45°，∴EB=2DH，∴四边形EBFD为平行四边形，∴FD=EB，∴DA=DF．点评：此题考查了平行四边形的判定与性质，全等三角形的判定与性质，以及含30度直角三角形的性质，熟练掌握平行四边形的判定与性质是解本题的关键．9．（2014•白银）D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC 所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；（2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）考点：三角形中位线定理；平行四边形的判定；菱形的判定．专题：几何图形问题．分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=BC，GF∥BC且GF=BC，从而得到DE∥GF，DE=GF，再利用一组对边平行且相等的四边形是平行四边形证明即可；（2）根据邻边相等的平行四边形是菱形解答．解答：（1）证明：∵D、E分别是AB、AC边的中点，∴DE∥BC，且DE=BC，同理，GF∥BC，且GF=BC，∴DE∥GF且DE=GF，∴四边形DEFG是平行四边形；（2）解：当OA=BC时，平行四边形DEFG是菱形．点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，平行四边形的判定，菱形的判定以及平行四边形与菱形的关系，熟记的定理和性质是解题的关键．10．（2014•宿迁）如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．（1）求证：四边形ADEF是平行四边形；（2）求证：∠DHF=∠DEF．考点：三角形中位线定理；直角三角形斜边上的中线；平行四边形的判定．专题：证明题；几何综合题．分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB，DE∥AC，再根据平行四边形的定义证明即可；（2）根据平行四边形的对角相等可得∠DEF=∠BAC，根据直角三角形斜边上的中线等于斜边的一半可得DH=AD，FH=AF，再根据等边对等角可得∠DAH=∠DHA，∠FAH=∠FHA，然后求出∠DHF=∠BAC，等量代换即可得到∠DHF=∠DEF．解答：证明：（1）∵点D，E，F分别是AB，BC，CA的中点，∴DE、EF都是△ABC的中位线，∴EF∥AB，DE∥AC，∴四边形ADEF是平行四边形；（2）∵四边形ADEF是平行四边形，∴∠DEF=∠BAC，∵D，F分别是AB，CA的中点，AH是边BC上的高，∴DH=AD，FH=AF，∴∠DAH=∠DHA，∠FAH=∠FHA，∵∠DAH+∠FAH=∠BAC，∠DHA+∠FHA=∠DHF，∴∠DHF=∠BAC，∴∠DHF=∠DEF．点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的性质，直角三角形斜边上的中线等于斜边的一半的性质，平行四边形的判定与性质，熟记各性质并准确识图是解题的关键．11．（2014•佛山）（1）证明三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半；[要求根据图1写出已知、求证、证明；在证明过程中，至少有两处写出推理依据（“已知”除外）]（2）如图2，在▱ABCD中，对角线交点为O，A1、B1、C1、D1分别是OA、OB、OC、OD的中点，A2、B2、C2、D2分别是OA1、OB1、OC1、OD1的中点，…，以此类推．若▱ABCD的周长为1，直接用算式表示各四边形的周长之和l；（3）借助图形3反映的规律，猜猜l可能是多少？考点：三角形中位线定理；规律型：图形的变化类；平行四边形的性质．专题：压轴题；规律型．分析：（1）作出图形，延长DE至F，使EF=DE，然后根据“边角边”证明△ADE和△CFE全等，根据全等三角形对应边相等可得AD=CF，全等三角形对应角相等可得∠A=∠ECF，再根据内错角相等，两直线平行可得AD∥CF，然后证明四边形BCFD是平行四边形，再根据平行四边形的对边平行且相等可得DF∥BC且DF=BC，然后整理即可得证；（2）根据三角形的中位线平行于第三边并且等于第三边的一半求出四边形A1B1C1D1的周长等于▱ABCD周长的一半，然后依次表示出各四边形的周长，再相加即可得解；（3）根据规律，l的算式等于大正方形的面积减去最后剩下的一小部分的面积，然后写出结果即可．解答：解：（1）已知：在△ABC中，D、E分别是边AB、AC的中点，求证：DE∥BC且DE=BC，证明：如图，延长DE至F，使EF=DE，∵E是AC的中点，∴AE=CE，在△ADE和△CFE中，，∴△ADE≌△CFE（SAS），∴AD=CF（全等三角形对应边相等），∠A=∠ECF（全等三角形对应角相等），∴AD∥CF，∵点D是AB的中点，∴AD=BD，∴BD=CF且BD∥CF，∴四边形BCFD是平行四边形（一组对边平行且相等的四边形是平行四边形），∴DF∥BC且DF=BC（平行四边形的对边平行且相等），∵DE=EF=DF，∴DE∥BC且DE=BC；（2）∵A1、B1、C1、D1分别是OA、OB、OC、OD的中点，∴A1B1=AB，B1C1=BC，C1D1=CD，A1D1=AD，∴四边形A1B1C1D1的周长=×1=，同理可得，四边形A2B2C2D2的周长=×=，四边形A3B3C3D3的周长=×=，…，∴四边形的周长之和l=1++++…；（3）由图可知，+++…=1（无限接近于1），所以l=1++++…=2（无限接近于2）．点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半的证明，利用面积法求等比数列的和，平行四边形的判定与性质，（1）作辅助线构造出全等三角形的和平行四边形是解题的关键，（3）仔细观察图形得到部分与整体的关系是解题的关键．12．（2014•宁夏）在平行四边形ABCD中，将△ABC沿AC对折，使点B落在B′处，A B′和CD相交于点O．求证：OA=OC．考点：平行四边形的性质；等腰三角形的判定与性质；翻折变换（折叠问题）．专题：证明题．分析：由在平行四边形ABCD中，将△ABC沿AC对折，使点B落在B′处，即可求得∠DCA=∠B′AC，则可证得OA=OC．解答：证明：∵△AB′C是由△ABC沿AC对折得到的图形，∴∠BAC=∠B′AC，∵在平行四边形ABCD中，AB∥CD，∴∠BAC=∠DCA，∴∠DCA=∠B′AC，∴OA=OC．点评：此题考查了平行四边形的性质、等腰三角形的判定与性质以及折叠的性质．此题难度不大，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想的应用．13．（2014•西宁）如图，已知▱ABCD水平放置在平面直角坐标系xOy中，若点A，D的坐标分别为（﹣2，5），（0，1），点B（3，5）在反比例函数y=（x＞0）图象上．（1）求反比例函数y=的解析式；（2）将▱ABCD沿x轴正方向平移10个单位后，能否使点C落在反比例函数y=的图象上？并说明理由．考点：平行四边形的性质；反比例函数图象上点的坐标特征；待定系数法求反比例函数解析式；坐标与图形变化-平移．专题：数形结合．分析：（1）利用待定系数法把B（3，5）代入反比例函数解析式可得k的值，进而得到函数解析式；（2）根据A、D、B三点坐标可得AB=5，AB∥x轴，根据平行四边形的性质可得AB∥CD∥x轴，再由C点坐标可得▱ABCD沿x轴正方向平移10个单位后C点坐标为（15，1），根据反比例函数图象上点的坐标特点可得点C落在反比例函数y=的图象上．解答：解：（1）∵点B（3，5）在反比例函数y=（x＞0）图象上，∴k=15，∴反比例函数的解析式为y=；（2）平移后的点C能落在y=的图象上；∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵点A，D的坐标分别为（﹣2，5），（0，1），点B（3，5），∴AB=5，AB∥x轴，∴DC∥x轴，∴点C的坐标为（5，1），∴▱ABCD沿x轴正方向平移10个单位后C点坐标为（15，1），∴平移后的点C能落在y=的图象上．点评：此题主要考查了平行四边形的性质，以及待定系数法求反比例函数和反比例函数图象上点的坐标特点，根据题意得到AB=5，AB∥x轴是解决问题的关键．14．（2014•桂林）在▱ABCD中，对角线AC、BD交于点O，过点O作直线EF分别交线段AD、BC 于点E、F．（1）根据题意，画出图形，并标上正确的字母；（2）求证：DE=BF．考点：平行四边形的性质；全等三角形的判定与性质；作图—复杂作图．专题：作图题；证明题．分析：（1）根据题意直接画图即可；（2）由四边形ABCD是平行四边形，可得AD∥BC，OB=OD，继而可利用ASA，判定△DOE≌△BOF，继而证得DE=BF．解答：（1）解：如图所示：（2）证明：∵四边形ABCD是平行四边形，∴AD∥BC，OB=OD，∴∠EDO=∠OBF，在△DOE和△BOF中，，∴DOE≌△BOF（ASA），∴DE=BF．点评：此题考查了平行四边形的性质以及全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应用．15．（2014•汕尾）如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．（1）证明：FD=AB；（2）当▱ABCD的面积为8时，求△FED的面积．考点：平行四边形的性质；全等三角形的判定与性质．分析：（1）利用已知得出△ABE≌△DFE（AAS），进而求出即可；（2）首先得出△FED∽△FBC，进而得出=，进而求出即可．解答：（1）证明：∵在平行四边形ABCD中，E是AD边上的中点，∴AE=ED，∠ABE=∠F，在△ABE和△DFE中，∴△ABE≌△DFE（AAS），∴FD=AB；（2）解：∵DE∥BC，∴△FED∽△FBC，∵△ABE≌△DFE，∴BE=EF，S△FBC=S▱ABCD，∴=，∴=，∴=，∴△FED的面积为：2．点评：此题主要考查了全等三角形的判定与性质以及平行四边形的性质以及相似三角形的判定与性质等知识，得出S△FBC=S平行四边形ABCD是解题关键．16．（2014•聊城）如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE于G点，交DF于F点，CE交DF于H点、交BE于E点．求证：△EBC≌△FDA．考点：平行四边形的性质；全等三角形的判定．专题：证明题．分析：根据平行三边的性质可知：AD=BC，由平行四边形的判定方法易证四边形BMDK和四边形AJCN是平行四边形，所以得∠FAD=∠ECB，∠ADF=∠EBC，进而证明：△EBC≌△FDA．解答：证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∵AF∥CE，BE∥DF，∴四边形BMDK和四边形AJCN是平行四边形，∴∠FAD=∠ECB，∠ADF=∠EBC，在△EBC和△FDA中，∴△EBC≌△FDA（ASA）．点评：本题考查了平行四边形的判定以及全等三角形的判定，在全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．17．（2014•西藏）如图所示，▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：AE=CF．考点：平行四边形的性质；全等三角形的判定与性质．专题：证明题．分析：根据平行四边形的性质得出AB=CD，AB∥CD，根据平行线的性质得出∠ABE=∠CDF，求出∠AEB=∠CFD=90°，根据AAS推出△ABE≌△CDF即可．解答：证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠ABE=∠CDF，∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS），∴AE=CF．点评：本题考查了平行四边形的性质，平行线的性质，全等三角形的性质和判定的应用，解此题的关键是求出△ABE≌△CDF，注意：平行四边形的对边平行且相等，难度适中．18．（2014•鄂尔多斯）如图1，在▱ABCD中，点E是BC边的中点，连接AE并延长，交DC的延长线于点F．且∠AEC=2∠ABE．连接BF、AC．（1）求证：四边形ABFC的是矩形；（2）在图1中，若点M是BF上一点，沿AM折叠△ABM，使点B恰好落在线段DF上的点B′处（如图2），AB=13，AC=12，求MF的长．考点：平行四边形的性质；勾股定理；矩形的判定；翻折变换（折叠问题）．分析：（1）由△ABE与△FCE全等，根据全等三角形的对应边相等得到AB=CF；再由AB与CF 平行，根据一组对边平行且相等的四边形为平行四边形得到ABFC为平行四边形，根据平行四边形的对角线互相平分得到AE=EF，BE=EC；再由∠AEC为三角形ABE的外角，利用外角的性质得到∠AEC等于∠ABE+∠EAB，再由∠AEC=2∠ABC，得到∠ABE=∠EAB，利用等角对等边可得出AE=BE，可得出AF=BC，利用对角线相等的平行四边形为矩形可得出ABFC为矩形；（2）由四边形ABFC是矩形，AB=13，AC=12，得到CF=AB=13，BF=AC=12，∠ACF=∠MFB′=90°，根据折叠的性质得到ABAB=13，B′M=BM，解直角三角形得到结果．解答：证明：（1）∵四边形ABCD为平行四边形，∴AB∥DC，∴∠ABE=∠ECF，又∵E为BC的中点，∴BE=CE，在△ABE和△FCE中，，∴△ABE≌△FCE（ASA）；∴AB=CF，又∵四边形ABCD为平行四边形，∴AB∥CF，∴四边形ABFC为平行四边形，∴BE=EC，AE=EF，又∵∠AEC=2∠ABC，且∠AEC为△ABE的外角，∴∠AEC=∠ABC+∠EAB，∴∠ABC=∠EAB，∴AE=BE，∴AE+EF=BE+EC，即AF=BC，则四边形ABFC为矩形；（2）∵四边形ABFC是矩形，AB=13，AC=12，∴CF=AB=13，BF=AC=12，∠ACF=∠MFB′=90°，∵△AB′M是由△ABM折叠得到的，∴ABAB=13，B′M=BM，∴B′C===5，∴B′F=CF=B′C=13﹣5=8，设MF=x，则B′B=BM=12﹣x，∴B′F2+MF2=B′M2，即：82+x2=（12﹣x）2，解得：x=，∴MF=．点评：此题考查了矩形的判定，平行四边形的性质，三角形的外角性质，等腰三角形的判定与性质，以及全等三角形的判定与性质，熟练掌握判定与性质是解本题的关键．19．（2014•广州）如图，▱ABCD的对角线AC、BD相交于点O，EF过点O且与AB，CD分别相交于点E、F，求证：△AOE≌△COF．考点：平行四边形的性质；全等三角形的判定．专题：证明题．分析：根据平行四边形的性质得出OA=OC，AB∥CD，推出∠EAO=∠FCO，证出△AOE≌△COF 即可．解答：证明：∵四边形ABCD是平行四边形，∴OA=OC，AB∥CD，∴∠EAO=∠FCO，在△AOE和△COF中，，∴△AOE≌△COF（ASA）．点评：本题考查了平行四边形的性质，平行线的性质，全等三角形的判定的应用，关键是根据平行四边形的性质得出AO=CO．20．（2014•青岛）已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）求证：△AOD≌△EOC；（2）连接AC，DE，当∠B=∠AEB=45°时，四边形ACED是正方形？请说明理由．考点：平行四边形的性质；全等三角形的判定与性质；正方形的判定．专题：几何综合题．分析：（1）根据平行线的性质可得∠D=∠OCE，∠DAO=∠E，再根据中点定义可得DO=CO，然后可利用AAS证明△AOD≌△EOC；（2）当∠B=∠AEB=45°时，四边形ACED是正方形，首先证明四边形ACED是平行四边形，再证对角线互相垂直且相等可得四边形ACED是正方形．解答：证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC．∴∠D=∠OCE，∠DAO=∠E．∵O是CD的中点，∴OC=OD，在△ADO和△ECO中，，∴△AOD≌△EOC（AAS）；。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章四边形性质探索第一节平行四边形的性质温故而知新温故1.两直线平行，同位角相等，内错角相等，同旁内角互补.2.能够完全重合的两个三角形叫做全等三角形；全等三角形的对应边相等，对应角相等.知新 1.定义：如图4.1-1所示，两组对边分别平行的四边形叫做，记作：“ ”,AC 和BD 是ABCD 的两条 . 2.性质1：平行四边形的对边3.性质2：平行四边形的对角 .4.性质3：平行四边形的对角线互相 .图4.1-15.一条直线上的任一点到另一条直线的垂线段的长度叫做两条平行线之间的距离. （会运用）乐学好思1 如图4.1-1所示，平行四边形可以表示成一下几种形式？ "ABC ”,”ACBD ”,”BCDA ”思路分析：应该用四个顶点的大写字母表示，并且要按照顺序依次书写，可顺时针方向表示，也可逆时针方向表示.答案："ABC ”,”ACBD ” 是错误的，”BCDA ”是正确的.乐学好思2 如图4.1-1所示，平行四边形的两条对角线分成的所有三角形中，有多少对全等的三角形？课堂研习•一点即通◎知识全突破●知识点1 探索平行四边形的性质，并且会运用导航指数方法一.情景设置 1、做一做（让学生实际动手操作）用一张半透明的纸复制你刚才画的平行四边形，并将复制后的四边形绕一个顶点旋转180度，你能平移该纸片，使它与你画的平行四边形ABCD 重合吗？（教师用几何画板平台展示整个旋转变化过程） 2、讨论：（小组交流）（1）通过以上活动，你能得到哪些结论？（2）平行四边形ABCD 对边、对角分别有什么关系？能用别的方法验证你的结论吗？温馨提示：答案：通过旋转三角形得到结论：平行四边形的对边相等；平行四边形的对角相等方法二.问题导入图下图4.1-2是两组对边分别平行的四边形：图4.1-2OD C B ADCBA O即：AB ∥CD ，AD ∥BC ，那么（1）各对边之间有什么样的数量关系？为什么？（2）各对角之间有什么样的数量关系?为什么？（3）如果连结AC 、BD ,交点为O ，如图4.1-3，那么AC 、BD 之间又有什么关系？图4.1-3温馨提示：答案：解：（1）两组对边分别相等.理由如下：如图4.1-4,连结BD ，∵AB ∥CD ，AD ∥BC ∴∠1=∠2，∠3=∠4又∵BD =DB ， ∴△ABD ≌△CDB ， ∴AD =BC ，AB =CD（2）两组对角分别相等由（1）△ABD ≌△CDB ，∴∠A =∠C ∵AB ∥BC ，∴∠A +∠ABC =180°, ∠C +∠CDA =180° ∴∠ABC =∠CDA (3)对角线互相平分由（1）AB =CD ，∠3=∠4，∠AOB =∠COD ∴△AOB ≌△COD ，∴AO =OC ，OB =OD由此得到，平行四边形的对边相等；平行四边形的对角相等;平行四边形的对角线互相平分.例题1 如图4.1-5，平行四边形ABCD 中， E 、 F 是分别是AB 、CD 上的点，且AE=CF ，试说明DE=BF ，并写出推理过程.。

●解题规律：在平行四边形中，证明线段相等是很常见的一类问题，通常结合三角形全等和平行四边形的性质来说明推理.◎知识巧归纳:.:⎧⎪⎪⎨⎪⎧⎪⇒⎨⎪⎩⎪⎩定义两组对边分别是四边形叫做平行四边形对边且平行四边形性质平行四边形对角平行平行相等相等对角线互相平分分析：引导学生进行思考：1）AD=BC 吗？ 2）∠A=∠C 吗？ 3）△ADE ≌△CBF 吗？◎随堂小挑战1.如右图4.1-6，在□ABCD 中， AC 与BD 交于O 点，则下列结论中不一定成立的是（）A 、AB=CDB 、AO=COC 、AC=BD D 、BO=DO2.已知: □ABCD 中,4,7,AB cm BC cm ==则它的周长为（）图4.1-6A 、11cmB 、22cmC 、28cmD 、44cm3. ABCD 中，如果∠B=100°，那么∠A 、∠D 的值分别是（） A ．∠A=80°，∠D=100° B.∠A=100°，∠D=80° C ．∠B=80°，∠D=80° D.∠A=100°，∠D=100°4. ABCD 中，若∠A ∶∠B =1∶3,那么∠A =________，∠B =________，∠C =________，∠D =________.5.如图4.1-8, D,E,F 分别在△ABC 的三边BC,AC,AB 上,且DE ∥AB, DF ∥AC, EF ∥BC,则图中共有______个平行四边形,分别是_________________________________.图4.1-86.在平行四边形ABCD 中（如图4.1-9）,已知两条邻边的长度分别为30cm,25cm;求其他两条边的长度,以及它的周长.图4.1-9课后温习•各显神通 ◎牛刀初小试（时间：20分钟满分：100分）班级：_______ 姓名：________ 得分：______ 一、选择题（每小题 3 分，共 24 分）1.关于平行四边形的性质，下面说法中不正确的为（）A 、两个邻角互补B 、两个邻角的平分线互相垂直C 、一组对角的两条角平分线平行或重合。

D 、任何一个外角大于与它不相邻的任何内角。

2.在平行四边形ABCD 中,∠B-∠A=20°,则∠D 的度数是 ( )A. 80°B. 90°C. 100°D. 110°3.在□ABCD 中，∠A ∶∠B ∶∠C ∶∠D 的值可以是（）A.1∶2∶3∶4B.1∶2∶2∶1C.1∶1∶2∶2D.2∶1∶2∶14.如图4.1-11，M 是平行四边形ABCD 的一边AD 上的任意一点，若△CMB 的面积为S ，△CDM 的面积为S 1，△ABM 的面积为S 2，则下列大小关系正确的为（）A 、S>S 1+S 2B 、S<S 1+S 2 图4.1-11C 、S=S 1+S 2D 、无法确定5.如图4.1-12，点E 是□ABCD 的边BC 上一点,DE=AD,AE 、DC 延长线交于F,∠ADE=40︒,∠BEF 等于（）图4.1-12A 、70︒ B 、60︒ C 、40︒ D 、35︒6、如图4.1-13,在平行四边形ABCD 中，AE ⊥BC 于点E ，AF ⊥CD 于点F ，若AE=4，AF=6，平行四边形ABCD 的周长为40，则平行四边形ABCD 的面积为（） A 、24 B 、36C 、40D 、48 图4.1-137.如图4.1-14，四边形ABCD 是平行四边形，∠D =120°，∠CAD =32°.则∠ABC 、∠CAB 的度数分别为（）A.28°，120°B.120°，28°C.32°，120°D.120°，32°图4.1-148.平行四边形的两邻边分别为3、4，那么其对角线必（）A.大于1B.小于7C.大于1且小于7D.小于7或大于1 二、填空题（每小题 3 分，共 18 分）9．(广西钦州市2010年中考题)如图4.1-15，□ABCD 的对角线AC 、BD 相交于点O ，点E 是CD 的中点，若AD ＝4cm ，则OE 的长为 cm ．图4.1-1510. 用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.11.在平行四边形ABCD 中,∠A : ∠B=3:2,则∠C=_________ 度,∠D=_____________度. 12.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.13.在□ABCD 中，∠A=2∠B，则∠A=____________度。

14.从平行四边形的一个锐角顶点作它的两条高，如果这两条高的夹角为135o，则这个平行四边形相邻两个内角的度数分别为和。

图4.1-16三、解答题（15-18每小题 11 分，19小题14分,共 58分）15.平行四边形的周长为36 cm ，一组邻边之差为4 cm ，求平行四边形各边的长.16.如图4.1-17，在□ABCD 中，E 、F 分别是BC 、AD 上的点，且AE ∥CF ，AE 与CF 相等吗？说明理由.图4.1-1717.如图4.1-18，在□ABCD 中，O 是对角线AC 、BD 的交点，BE ⊥AC ，DF ⊥AC ，垂足分别为E 、F .那么OE 与OF 是否相等？为什么？DECBAOFE DCB A图4.1-1818.如图4.1-19,平行四边形ABCD 的两条对角线AC,BD 相交于O. 若平行四边形ABCD 的周长是20cm,△AOD 的周长比△ABO 的周长大6cm.求AB,AD 的长.图4.1-1919、如图4.1-20，已知ΔABC 中，AB=AC=5，D 是BC 上一点，作DE∥AC 交AB 于E ，作DF∥AC 交AC 于点F ，求四边形DEAF 的周长。

（8分）20、如图4.1-21，平行四边形ABCD 中，BE 平分 ABC ，若AB=6 cm ，BC=10cm ，试求：（1）平行四边形ABCD 的周长. （2）DE 的长.（6分）图4.1-2121、如图4.1-22，四边形ABCD 是平行四边形，BD ⊥AD ，求BC ，CD 及OB 的长.图4.1-224.2平行四边形的判别(1)教学目标：⒈认知目标： ⑴平行四边形的判别方法1。

⑵平行四边形的判别方法2。

二、教学重点、难点：重点: 平行四边形的判别条件。

难点: 平行四边形的判别条件的应用。

三、教学过程设计： ⒈【情境】： ⑴上节课我们探讨了平行四边形的定义和性质，现在来复习一下。

⑵结合学生回答，课件显示平行四边形的性质。

2.【动手操作】：⑴现在拿出一长一短的两根小木棒，来拼一个平行四边形。

⑵用量角器等工具检测所拼四边形是否是平行四边形。

图F E DCB A ODCBA⑶提问：若这两根小木棒不作为对角线，能确定平行四边形吗？若不行，能拼出一个特殊的四边形吗？那怎样改变一个条件，就能确定平行四边形？（4）用两根一样长的小木棒，来拼一个平行四边形。

通过观察图形，得出：两条对角线互相平分的四边形是平行四边形。

一组对边平行且相等的四边形是平行四边一组对边平行且相等的四边形是平行四边形。

（两组对边分别相等的四边形是平行四边形。

）3【例题精析】: ［例1］如图，AC ∥ED ，点B 在AC 上且AB =ED =BC ，找出图中的平行四边形例1图例2图［例2］如图所示，在ABCD 中，AC 、BD 相交于点O ，点E 、F 在对角线AC 上，且OE =OF . (1)OA 与OC 、OB 与OD 相等吗？ (2)四边形BFDE 是平行四边形吗？⑶若点E 、F 在OA 、O C 的中点上，你能解决(1)(2)两问吗？4.【随堂练习】:⑴下列两个图形，可以组成平行四边形的是（） A.两个等腰三角形B. 两个直角三角形C. 两个锐角三角形D. 两个全等三角形 ⑵能确定四边形是平行四边形的条件是（）A.一组对边平行，另一组对边相等B. 一组对边平行，一组对角相等C. 一组对边平行，一组邻角相等D. 一组对边平行，两条对角线相等⑶已知：四边形ABCD 中，AB ∥CD ，要使四边形ABCD 为平行四边形，需添加一个条件是：（只需填一个你认为正确的条件即可）。