第22届华杯赛小学高年级组初赛试题及答案解析
华杯赛初赛小高组试题卷(含答案)

华杯赛初赛模拟题(小高组)1.计算:22222221234201520162017-+-++-+ 【解析】 原式22222222017201654321=-++-+-+ (20172016)(20172016)(32)(32)1=-⨯+++-⨯++2017201620152014321=+++++++()120171201720351532=⨯+⨯= 2.幼儿园的老师把一些画片分别给A 、B 、C 三个班,每人都分到6张,如果只分给B 班,每人能得15张,如果只分给C 班,每人能得14张,如果只分给A 班,每人能得 张.【解析】 设三个班的总人数为x 人,A 班、B 班、C 班的人数分别为a ,b ,c , 则61514x b c ==,从而62155b x x ==,63147c x x ==,所以2365735a x x x x =--=,因此将这些画片分给A 班,每人能得663535x x ÷=(张). 3.A 、B 两杯食盐水各有40克,浓度比是3:2.在B 中加入60克水,然后倒入A 中________克,再在A 、B 中加入水,使它们均为100克,这时浓度比为7:3.【解析】 在B 中加入60克水后,B 盐水浓度减少为原来的25,但溶质质量不变,此时两杯盐水中的盐的质量比仍然为3:2,B 中的盐占所有盐的质量的22325=+,但最终状态下B 中的盐占所有盐的质量的337310=+,也就是说B 中的盐减少了32111054-÷=,所以从B 中倒出了14的盐水到A ,即25克. 4.如图,点E 是长方形ABCD 的对角线AC 上任一点,过E 作AB 与BC 的垂线分别交AB 、BC 于F 、G ,连接DF 、FG 和GD 。
已知8AB =、10AD =、三角形DFG 的面积为30,则长方形BGEF 的面积为 。
G F EC DB A解析:205.四边形ABCD 中,,,E F I 是AB 上的四等分点,,,H G J 是DC 上的三等分的点,如果30,25,AEHD EFGH S S ==,求IBCJ S 。
2017年第22届华杯赛(小高组)决赛模拟试题(1)-T版

2017年第22届华杯赛决赛模拟试题(1)(小学高年级组)(时间:90分钟,满分:150分)一、填空题。
(每小题10分,共80分)1.2016年1月24日,“华罗庚金杯中外少年数学精英趣味对抗赛”在美国开赛,2016年7月18日,“华罗庚金杯少年数学邀请赛30周年纪念大会”召开,已知2016年1月24日是星期日,2016年7月18日是星期 。
【难度】★★【考点】周期问题【答案】一【解析】注意2016年是闰年。
1月25日至1月31日共31-25+1=7(天);2月至6月共29+31+30+31+30=151(天);7月1日至7月18日共18天。
故20166年1月25至7月18日共7+151+18=176(天)。
176÷7=25……1,故2016年1月24日之后第176天为星期一。
2.计算:=⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛+⨯⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛--1541212322211%2532394475.0 。
【难度】★★【考点】计算 【答案】92 【解析】原式 = ⎥⎦⎤⎢⎣⎡--÷⎪⎭⎫ ⎝⎛+⨯⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛--+-15412123212124196394443 = ⎪⎭⎫ ⎝⎛--÷+⨯⎪⎭⎫ ⎝⎛⨯-154125351419743 = ⎪⎭⎫ ⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛-1543241973 =15641920⨯⨯ = 923.如图,将侧面积是314平方厘米的圆柱体,切拼成一个近似长方体,表面积比原来增加厘米。
(π取3.14)【难度】★★【考点】几何【答案】100【解析】设圆柱体高为h,底面积的半径为r.则2πrh=314,rh=50.增加面积为2rh=100(平方厘米)。
4.仅使用加、减、乘、除、括弧,可由4个4运算得到3。
例如(4 + 4 + 4)÷4 = 3。
请你另给一种运算算式。
【难度】★★【考点】巧填运算符号【答案】(4×4 - 4)÷4 = 3【解析】三个4很容易得到3,即4-4÷4=3.将除以4看成乘以1/4,利用乘法分配率可将3个4变成4个4,即4-4÷4=(4×4-4)除以4.5.将自然数从1开始,按图所表示的规律排列。
22届华杯赛试题及答案

22届华杯赛试题及答案一、选择题(每题5分,共20分)1. 已知函数f(x) = 3x^2 - 5x + 2,求f(2)的值。
A. 4B. 6C. 8D. 10答案:B2. 一个圆的直径为10cm,求其面积。
A. 25π cm²B. 50π cm²C. 100π cm²D. 200π cm²答案:B3. 已知一个等差数列的前三项分别为2, 5, 8,求第四项的值。
A. 11B. 12C. 15D. 18答案:A4. 已知一个三角形的两边长分别为3cm和4cm,夹角为60°,求第三边的长度。
A. 5cmB. 7cmC. √13 cmD. √21 cm答案:C二、填空题(每题5分,共20分)5. 已知等比数列的前三项为2, 6, 18,求第四项的值。
答案:546. 已知一个直角三角形的两条直角边长分别为3cm和4cm,求斜边的长度。
答案:5cm7. 已知一个二次方程x^2 - 5x + 6 = 0,求该方程的根。
答案:2, 38. 已知一个正方体的体积为64cm³,求其边长。
答案:4cm三、解答题(每题10分,共60分)9. 已知函数f(x) = x^3 - 3x^2 + 2,求其在x=1处的导数值。
解答:首先求导数f'(x) = 3x^2 - 6x。
将x=1代入,得到f'(1) = 3(1)^2 - 6(1) = -3。
答案:-310. 已知一个等差数列的前三项为1, 4, 7,求其第n项的通项公式。
解答:设数列的公差为d,则d = 4 - 1 = 3。
根据等差数列的通项公式,第n项an = a1 + (n - 1)d,代入已知值,得到an = 1 +(n - 1) * 3 = 3n - 2。
答案:an = 3n - 211. 已知一个圆的半径为5cm,求其内接正六边形的边长。
解答:设正六边形的边长为a,由于正六边形可以分成六个等边三角形,每个等边三角形的边长等于圆的半径,所以正六边形的边长a等于圆的半径5cm。
第二十二届“华杯赛”小学中年级组初赛试题

第二十二届“华杯赛”小学中年级组初赛试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(第二十二届“华杯赛”小学中年级组初赛试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为第二十二届“华杯赛”小学中年级组初赛试题的全部内容。
第二十二届华罗庚金杯少年邀请赛初赛试题(小学中年级组)一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1、两个小三角形不重叠放置可以拼成一个大三角形, 那么这个大三角形不可能由()拼成。
(A)两个锐角三角形(B)两个直角三角形(C)两个钝角三角形(D)一个锐角三角形和一个钝角三角形2、从1至10这10个整数中,至少取()个数,才能保证其中有两个数的和等于10。
(A)4 (B)5 (C)6 (D)73、小明行李箱锁的密码是由两个数字8与5构成的三位数。
某次旅行,小明忘记了密码,他最少要试()次, 才能确保打开箱子。
(A)9 (B)8 (C)7 (D)64、猎豹跑一步长为2米, 狐狸跑一步长为1米.猎豹跑2 步的时间狐狸跑3步,猎豹距离狐狸30米, 则猎豹跑动()米可追上狐狸。
(A)90 (B)105 (C)120 (D)1355、图1 中的八边形是将大长方形纸片剪去一个小长方形得到。
则至少需要知道()条线段的长度,才可以计算出这个八边形的周长.(A)4 (B)3 (C)5 (D)106、一个数串219…,从第4个数字开始, 每个数字都是前面3个数字和的个位数。
下面有4个四位数:1113, 2226, 2125,2215 ,其中共有()个不出现在该数串中。
2017年第二十二届华杯赛初赛模考考后分析(小学高年级组)
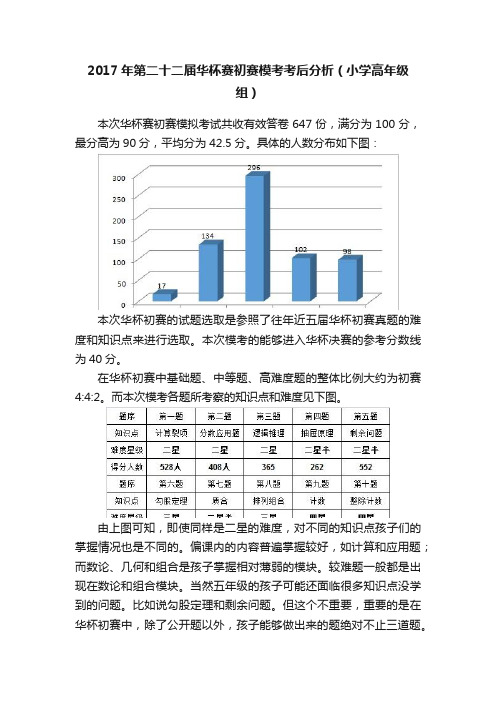
2017年第二十二届华杯赛初赛模考考后分析(小学高年级组)本次华杯赛初赛模拟考试共收有效答卷647份,满分为100分,最分高为90分,平均分为42.5分。
具体的人数分布如下图:本次华杯初赛的试题选取是参照了往年近五届华杯初赛真题的难度和知识点来进行选取。
本次模考的能够进入华杯决赛的参考分数线为40分。
在华杯初赛中基础题、中等题、高难度题的整体比例大约为初赛4:4:2。
而本次模考各题所考察的知识点和难度见下图。
由上图可知,即使同样是二星的难度,对不同的知识点孩子们的掌握情况也是不同的。
偏课内的内容普遍掌握较好,如计算和应用题;而数论、几何和组合是孩子掌握相对薄弱的模块。
较难题一般都是出现在数论和组合模块。
当然五年级的孩子可能还面临很多知识点没学到的问题。
比如说勾股定理和剩余问题。
但这个不重要,重要的是在华杯初赛中,除了公开题以外,孩子能够做出来的题绝对不止三道题。
因为,每年进入华杯决赛的分数线一般都是30~40分。
好啦,让我们来看看每一道题的情况。
第一题是计算,考查的是分数裂项。
但是用普通的乘法分配率算也是可以的。
这也是华杯赛近几年考察的一个趋势:难度不断在降低,对基础的重视程度越来越高。
六年级的孩子可能会完全没压力,但是对于五年级的孩子,一定要加强对分数计算训练,尤其是分数小数的四则混合运算。
计算中还常考的有整体约分和繁分数计算。
在后期的备考中,可以着重去练习。
第二题分数应用题。
华杯赛对应用题的考察主要有分数比例应用题,包括经济浓度和工程问题。
这里可能很多五年级孩子还没有具体学习过,务必利用寒假的时间去学习。
因为决赛也是会考查这些内容。
第三题逻辑推理。
华杯赛中出现不多,常见的处理方法有假设法和列表法综合运用。
第四题抽屉原理,华杯赛绝对重难点。
出现频率特别高,而孩子的掌握又不是很好。
但是一般而言,在华杯赛中难度不是很大,赛前可以好好找找高斯数学思维训练导引上的练习题进行训练。
第五题余数问题中的剩余。
小学华杯赛试题及答案

小学华杯赛试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项是华杯赛的全称?A. 华罗庚数学竞赛B. 华罗庚杯数学竞赛C. 华杯数学竞赛D. 华罗庚数学邀请赛答案:B2. 华杯赛的举办周期是多久?A. 每年一次B. 每两年一次C. 每三年一次D. 每四年一次答案:A3. 华杯赛的参赛对象通常是:A. 小学生B. 初中生C. 高中生D. 大学生答案:A4. 华杯赛的试题类型包括:A. 选择题B. 填空题C. 计算题D. 所有以上答案:D二、填空题(每题5分,共20分)1. 华杯赛的试题通常由_________组成。
答案:选择题、填空题、解答题2. 华杯赛的举办地点通常在_________。
答案:学校或指定的考试中心3. 华杯赛的参赛者需要具备_________。
答案:数学竞赛的基本知识和解题技巧4. 华杯赛的获奖者通常会获得_________。
答案:证书和奖品三、解答题(每题10分,共60分)1. 已知一个数列的前三项为1,2,4,求第四项的值。
答案:82. 一个长方形的长是宽的两倍,如果宽增加3厘米,长减少2厘米,面积不变,求原来长方形的长和宽。
答案:设原来长方形的宽为x厘米,则长为2x厘米。
根据题意得方程:x(2x-2) = (x+3)(2x-2-3),解得x=6,所以原来长方形的长为12厘米,宽为6厘米。
3. 甲乙两人同时从A地出发,甲的速度是乙的1.5倍,如果甲到达B地后立即返回,与乙在C地相遇,求甲乙两人的速度比。
答案:设乙的速度为v,则甲的速度为1.5v。
设A、B两地之间的距离为d,则甲从A到B再返回C的总距离为2d,乙从A到C的距离为d。
由于甲乙两人相遇,所以他们所用的时间相同,即2d/1.5v = d/v,解得v = 2d/3,所以甲乙两人的速度比为1.5:1。
4. 一个水池有甲乙两个进水管,甲管单独注满水池需要4小时,乙管单独注满水池需要6小时。
如果两管同时开启,需要多少时间才能注满水池?答案:设水池的容量为1,甲管的注水速度为1/4,乙管的注水速度为1/6。
17至22届华杯赛小中组解析
第17届华杯赛小中组解析1.答案:D算式中9个汉字,分别代表1~9,由于1+2+3+4+5+6+7+8+9=45,45是9的倍数,所以和也是9的倍数,选项只有D选项18是9的倍数。
例如324+657=981。
2.答案:D从镜子里看到的指针与实际是相反的,可将题中的指针以秒针为对称轴作对称,可知D选项15:55是最接近16时的。
3.答案:B最少4个三角形,如图4.答案:B最大值为109,10×10+10-10÷10=109。
5.答案:C设长方形长为a,宽为b,a+2b=30,2ab最大值为15×15,但a、b均为偶数,2ab最大值为14×16,长宽分别为14和8,面积最大112。
6.答案:A45=3×3×5,约数15小于19,所以不变的边长应为15,另一边最长为19,所以小虎最多用了15×19=285枚棋子。
7.答案:665将第二堆剩下的17颗小球除去,剩下的恰好是第三堆球数的3倍,如图第一堆第二堆第三堆所以第三堆原有小球(2012-17)÷3=665颗。
8.答案:925三个档上的算珠合起来是1110,1110=2×3×5×37,要求上面的三位数字不同,而,37×3=111,所以1110=37×5×6=37×5×(5+1)。
那么满足题意的上面的三位数是:37×5×5=9259.答案:105,2520小正方形的边长应为90和42的最大公因数,(90,42)=6,所以最少能剪出90/6×42/6=105块;所有正方形纸片的周长之和为6×4×105=2520厘米。
10.答案:20两桌单打的人数和一桌双打的人数相同,要想双打的人数和单打的多4人,则双打的桌数应为单打的一半多一桌。
已知乒乓球台共13张,所以双打的乒乓球台应有(13-1)÷3+1=5张,人数为5×4=20人。
小学华杯赛试题及答案
小学华杯赛试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项是华杯赛的全称?A. 中国数学奥林匹克竞赛B. 中国数学奥林匹克竞赛华罗庚杯C. 中国数学竞赛华罗庚杯D. 华罗庚数学竞赛答案:B2. 小学华杯赛通常在每年的哪个月份举行?A. 3月B. 6月C. 9月D. 12月答案:A3. 华杯赛的参赛对象是哪些年级的学生?A. 一年级至三年级B. 四年级至六年级C. 一年级至六年级D. 四年级至九年级答案:B4. 华杯赛的题目类型通常包括哪些?A. 选择题和填空题B. 选择题和解答题C. 选择题、填空题和解答题D. 只有解答题答案:C二、填空题(每题5分,共20分)1. 华杯赛的创立者是______。
答案:华罗庚2. 小学华杯赛的题目难度通常分为______个等级。
答案:三个3. 华杯赛的奖项设置通常包括______、______和______。
答案:一等奖、二等奖、三等奖4. 参加华杯赛的学生需要通过______选拔才能进入决赛。
答案:初赛三、解答题(每题10分,共60分)1. 已知一个长方形的长是宽的两倍,且周长为24厘米,求长方形的长和宽。
答案:设长方形的宽为x厘米,则长为2x厘米。
根据周长公式,2(x + 2x) = 24,解得x = 4,所以宽为4厘米,长为8厘米。
2. 一个数加上它的一半等于30,求这个数。
答案:设这个数为x,则x + 0.5x = 30,解得x = 20。
3. 一个班级有男生和女生,男生人数是女生人数的两倍,全班共有40人,求男生和女生各有多少人。
答案:设女生人数为x,则男生人数为2x。
根据题意,x + 2x = 40,解得x = 13.33,但人数应为整数,题目可能有误。
4. 一个数的3倍减去它的一半等于40,求这个数。
答案:设这个数为x,则3x - 0.5x = 40,解得x = 20。
5. 一个长方体的长、宽、高分别是8厘米、6厘米和4厘米,求这个长方体的体积。
第17至22届小高组华杯赛试卷
第十九届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组)(时间:2014年3月15日10:00~11:00)一、选择题(每小题10分,满分60分.以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.)1.平面上的四条直线将平面分割成八个部分,则这四条直线中至多有()条直线互相平行.(A )0(B )2(C )3(D )42.某次考试有50道试题,答对一道题得3分,答错一道题扣1分,不答题不得分.小龙得分120分,那么小龙最多答对了()道试题.(A )40(B )42(C )48(D )503.用左下图的四张含有4个方格的纸板拼成了右下图所示的图形.若在右下图的16个方格分别填入1,3,5,7(每个方格填一个数),使得每行、每列的四个数都不重复,且每个纸板内四个格子里的数也不重复,那么A ,B ,C ,D 四个方格中数的平均数是()..(A )4(B )5(C )6(D )74.小明所在班级的人数不足40人,但比30人多,那么这个班男、女生人数的比不可能是().(A )2:3(B )3:4(C )4:5(D )3:7装订线总分5.某学校组织一次远足活动,计划10点10分从甲地出发,13点10分到达乙地,但出发晚了5分钟,却早到达了4分钟.甲乙两地之间的丙地恰好是按照计划时间到达的,那么到达丙地的时间是().(A )11点40分(B )11点50分(C )12点(D )12点10分6.如右图所示,7=AF cm,4=DH cm,5=BG cm,1=AE cm.若正方形ABCD 内的四边形EFGH 的面积为78cm 2,则正方形的边长为()cm.(A )10(B )11(C )12(D )13二、填空题(每小题10分,满分40分)7.五名选手A,B,C,D,E 参加“好声音”比赛,五个人站成一排集体亮相.他们胸前有每人的选手编号牌,5个编号之和等于35.已知站在E 右边的选手的编号和为13;站在D 右边的选手的编号和为31;站在A 右边的选手的编号和为21;站在C 右边的选手的编号和为7.那么最左侧与最右侧的选手编号之和是________.8.甲乙同时出发,他们的速度如下图所示,30分钟后,乙比甲一共多行走了________米.9.四个黑色1×1×1的正方体和四个白色1×1×1的正方体可以组成________种不同的2×2×2的正方体(经过旋转得到相同的正方体视为同一种情况).10.在一个圆周上有70个点,任选其中一个点标上1,按顺时针方向隔一个点的点上标2,隔两个点的点上标3,再隔三个点的点上标4,继续这个操作,直到1,2,3,…,2014都被标记在点上.每个点可能不只标有一个数,那么标记了2014的点上标记的最小整数是________.。
小学组华杯赛试题及答案
小学组华杯赛试题及答案华杯赛是一个知名的小学生数学竞赛,每年都吸引着众多小学生的参与。
为了让小学生更好地备战华杯赛,组委会发布了一套试题及答案供参赛选手进行练习。
以下是小学组华杯赛试题及答案的详细内容。
第一部分:选择题(共20题,每题2分,共40分)1. 下面哪个数是42的因数?A) 7 B) 12 C) 5 D) 32. 请计算下列各数的和:25 + 17 + 9 = ?A) 31 B) 51 C) 61 D) 413. 小明有12个苹果,他想分给3个朋友,每个朋友可以得几个苹果?A) 3 B) 4 C) 1 D) 24. 下面哪个是一个乘法算式的结果?A) 10 - 3 B) 5 + 8 C) 6 × 4 D) 7 ÷ 25. 如果一个矩形的长是8厘米,宽是4厘米,那么它的周长是多少?A) 8厘米 B) 12厘米 C) 32厘米 D) 16厘米6. 请找出下列各数中最大的数:A) 25 B) 13 C) 9 D) 167. 用两个相同的正方形可以拼成一个什么形状?A) 长方形 B) 圆形 C) 三角形 D) 正方形8. 下面哪个数是一个奇数?A) 10 B) 12 C) 9 D) 89. 请填写下面数列中的空格:1, 3, 5, __, 9A) 6 B) 7 C) 8 D) 410. 请计算下列各数的差:17 - 9 = ?A) 7 B) 10 C) 8 D) 611. 如果一个正方形的面积是36平方厘米,那么它的边长是多少?A) 9厘米 B) 6厘米 C) 12厘米 D) 18厘米12. 小明的年龄是7岁,小红的年龄是小明的2倍,小红的年龄是多少?A) 9岁 B) 5岁 C) 14岁 D) 12岁13. 下面哪个数是一个负数?A) 5 B) -2 C) 10 D) 314. 小明在常温下用一个透明的玻璃杯装满了热水,过了一段时间后,杯子外面出现了水珠。
这是因为什么原因?A) 杯子漏水了 B) 杯子外面很湿 C) 热水变成了水珠 D) 杯子里的水蒸发了15. 下面哪个图形是一个正方形?A) B) C) D)16. 小明在一个商店里买了一本书,价格是28元,他给了收银员50元,需要找回多少钱给小明?A) 22元 B) 28元 C) 32元 D) 50元17. 请计算下列各数的积:5 × 3 = ?A) 15 B) 8 C) 12 D) 2418. 一个三角形有几个顶点?A) 1 B) 2 C) 3 D) 419. 请找出下列各数中最小的数:A) 15 B) 27 C) 9 D) 1820. 在数字7的左边填入一个数,使得这个数比7大,并且和7的差是9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 22 届华罗庚金杯少年数学邀请赛初赛试卷(小学高年级组) 一、选择题(每小题 10 分,共 60 分。以下每题的四个选项中,仅有一个是正确 的,请将表示正确答案的英文字母写在每题的圆括号内。 ) 1、两个有限小数的整数部分分别是 7和 10,那么这两个有限小数的积的整数部 分有( )种可能的取值。 A、16 B 、 17 C 、18 D 、19 2、小明家距学校,乘地铁需要 30分钟,乘公交车需要 50 分钟。某天小明因故 先乘地铁,再乘公交车,用了 40分钟到达学校,其中换乘过程用了 6 分钟,那 么这天小明乘坐公交车用了( )分钟。 A、6 B 、8 C 、10 D 、 12
3、将长方形 ABCD对角线平均分成 12段,连接成下图,长方形 ABCD内部空白部 分的面积总和是 10 平方厘米,那么阴影部分面积总和是( )平方厘米。 A、14 B 、 16 C 、18 D 、20
4、请在上图中每个方框中填入适当的数字,使得乘法竖式成立,那么乘积是 ( )。 A、2986 B 、2858 C 、2672 D 、2754 5、在序列 20170⋯⋯中,从第 5 个数字开始,每个数字都是前面 4 个数字和的 个位数, 这样的序列可以一直写下去, 那么从第 5 个数字开始, 该序列中一定不 会出现的数组是( )。 A、8615 B 、2016 C 、4023 D 、2017 6、从 0至 9中选择四个不同的数字分别填入方框中的四个括号中,共有( ) 种填法使得方框中话是正确的。 这句话里有( )个数大于 1,有( )个数大于 2,有( )个数大于 3,有( )个数大 A、1 B 、2 C 、3 D 、4
、填空题(每小题 10 分,满分 40 分)
续自然数。 9、上图中, ABCD是平行四边形, E为 CD的中点, AE和 BD的交点为 F,AC和BE 的交点为 H,四边形 EFGH的面积是 15 平方厘米,则 ABCD的面积是 平 方厘米。 10、若2017,1029和725除以d的余数均为 r ,那么d—r 的最大值是 。 第 22 届华罗庚金杯少年数学邀请赛初赛答案解析(小学高年级组) 一、选择题 1、答案: C 解析:【考查目标】最值问题。 因为两个有限小数的整数部分分别是 7 和 10,所以这两个有限小数分别在 7—— 8 之间和 10—— 11 之间,所以这两个有限小数的乘积在 70—— 88 之间,其中整 数部分有 70、71、72、73、74⋯⋯87,共 18 种。故正确答案是 C。 2、答案: C 解析:【考查目标】行程问题中的工程问题及假设法解应用题。 设全程的路程是单位“ 1”,则乘地铁的速度是 1 ,乘公交车的速度是 1 , 30 50 40—6=34(分钟)
1 5 1+24 A 8、下图中, “华罗庚金杯”五个汉字分别代表 7、若 32 35 ÷ 23 +2.25=4,那么
25 33 74
A的值是
1—5 这五个不同的数字, 将各线 段两端点的数字相加得到五个和,共有 种情况使得这五个和恰为五个连 假设 34 分钟都是乘地铁,则可以走的路程是: 1 × 34= 17 ,而全程的路程只 30 15 有“1”,多算了 17 —1= 2 ,为什么会多算呢?是因为把乘公交车的速度看成 15 15
了乘地铁的速度,所以乘公交车的时间是: 2 ÷ 1 — 1 =10 分钟
。故正确
15 30 50
答案是 C。 3、答案: A 解析:【考查目标】鸟头模型问题。 长方形的对角线把长方形分成了 4 个相同的三角形,我们对其中的 1 个三角形进 行分析,设最里面空白小三角形的面积是 1 份,根据鸟头模型, 则空白部分的面 积和是 1+ 5+9=15(份),阴影部分的面积是: 3+7+11= 21(份),则阴影部 分的面积是空白部分面积的 21÷15=1.4 ,又知空白部分的面积是 10 平方厘米, 所以 S 阴影=10× 1.4 = 14(平方厘米)。故正确答案是 A。 4、答案: D 解析:【考查目标】数字谜。 如下图,首先三位数 abc ×7=三位数 e1g ,可知 a=1;
再看 f,f=1或 2,若 f=1,则 e=9,h=9,则abc=109,d=1,但 109×7= 763,个位不是 1,不符合题意。所以 f =2,d=2,b=0;我们再来看 c,c×7 =两位数 1g ,所以 c=2,那这样这个乘法算式就是:
所以正确答案是 D。 5、答案: B 解析:【考查目标】找规律。 按照题目规则,写出数列:2017086150285508⋯⋯发现这个数列的奇偶性是: “偶 偶奇奇偶偶偶奇奇偶偶偶奇奇”,所以不可能出现 2016 这样“偶偶奇偶”的情 况,所以正确答案是 B。 6、答案: B 解析:【考查目标】逻辑推理。 设四个空填的依次是 a、b、c、d,即这句话里有 a 个数大于 1,b 个数大于 2,c 个数大于 3, d 个数大于 4,根据包含关系 a>b>c>d≥0,所以 2、 3、4、a、b 这 5 个数都大于 1,即 a≥5, d≥1。 若 d=1,则 a、 b、c 都大于 1,这时有 2、3、4、a、b、 c 这 6 个数都大于 1, 则 a=6,这时满足条件的 b=4,c=3,但这是有 6、4、3、3、4 这 5 个数都大 于 2 ,和这句话中“有 4 个数大于 2 ”相矛盾,所以这种情况不符合题意。 若 d=2,则有 2 个数大于 4,这 2 个数只能是 a 和 b,则 a= 6,b=5,这时满足 条件的和分别是 c= 3, d= 2 或 c=4,d=2。 若 d=3,则有 3 个数大于 4,这 3 个数只能是 a、 b、 c,则 a=6,b=5,c
=4, 但和 c>4 相矛盾,所 d=3 也不符合题意。 若 d=4,则有 4 个数大于 4,这 4 个数为 a、b、c、d,而 d=4 相矛盾,所以 d =4,也不符合题意。 显然 d=5 不存在,所以只有 2 组解。故正确答案是 B。 、填空题。 7、答案: 4 解析:【考查目标】繁分数方程。 8、答案: 10 解析:【考查目标】方阵问题。 计算五角星上 5 条线段上 10 个端点的总和,相当于五角星上每个顶点都被算了 2 次,所以和为( 1+ 2+3+4+5)×2=30,又知这 5 条线的和是 5 个连续的自 然数,那么中间数是: 30÷5=6,即这 5 条线的和分别是 4、5、6、7、8,其中 4必须是 1+3;8必须是 3+5,则 5 只能是 1+4,6是 2+4,7是 2+5,如果 杯”是 1,则有 2 种可能的情况,如下图所示:
同“杯”还可以是 2、是 3、是 4、是 5,所以有 2× 5= 10
9、答案: 180
解析:【考查目标】沙漏模型及同高不同底的三角形面积之间的关系。 在△AHB
和△EHC中,因为 E为 CD的中点,再根据沙漏模型 HC:AH=EC:AB=1: 2,则 AH=2HC,HC= 1AC 3 1 1 1 1 连接 GE,G为 AC的中点,所以 GC=12 AC,则 GH= 12 AC—31 AC=16AC
,所
以
1 —5 3 ÷2
+2.25=5 —9 25 33
24 7 4 1+ A
1 5 7 19 15 38 — = = 5 9 4 21 8 45
24 1+ A
1 5
1+24
A
1+ 24 A
1+ 24 A
解得 A=4
21 15 7 = 19 8 4
55 7 1+ 24=7
A 1 1 1 S△GHE= S△AEC= S 平行四边形 ABCD,同理: S△EFG= S 平行四边形 ABCD
6 24 24
1 所以 S 四边形 EFGH= S 平行四边形 ABCD, 又因为四边形 EFGH的面积是 15平方厘米,所
以 S 12
1 平行四边形 ABCD
= 15÷
=180(平方厘米)。 12
10、答案: 35
解析:【考查目标】同余的性质。 2017,1029 和 725 除以 d 的余数均为 r ,根据同余的性质,则 2017—1029=988 和 1029—725=304都能被 d整除,则 d 是 988和 304的公因数;通过短除法易 知:(988,304)=76;若 d=76,725÷76=9⋯⋯41,则 r=41,d—r=76—41 =35;若 d=38,725 ÷38= 19⋯⋯ 3,则 r =3,d—r =38—3=35。如果 d<35, 则 r 。
