串行乘法器原理
脉动映射的位串行乘法器

脉动映射的位串行乘法器
脉动映射的位串行乘法器(Bit-Serial Multiplier with
Pulsed Mapping)是一种数字电路设计,用于实现乘法操作。
它采用
了脉动映射技术,将乘法操作拆分为多个位乘操作,并通过串行的方
式逐位计算,最终得到乘法的结果。
脉动映射的位串行乘法器的实现包括以下步骤:
1. 输入端提供两个乘法运算的操作数A和B,可以是二进制位串。
2. 对于A的每一位ai和B的每一位bi,执行位乘操作,得到结果ci = ai * bi。
3. 利用脉冲信号(Pulsed Mapping)将位乘操作的结果ci映射到不
同的时钟周期中。
4. 在每个时钟周期中,将位乘操作的结果ci与当前的积累结果相加,并保存为新的积累结果。
5. 重复上述步骤,直到所有位都计算完毕,得到最终的乘法结果。
脉动映射的位串行乘法器具有以下特点:
1. 采用串行计算的方式,在每个时钟周期中只计算一位乘法操作,因此可以减少电路的复杂性和面积。
2. 采用脉动映射技术,将位乘操作的结果分散到不同的时钟周期中,
可以提高计算的并行度。
3. 由于使用了位乘操作,可以通过逻辑门电路实现,避免了乘法运算
中的乘法器的复杂性和延迟。
4. 由于采用了串行计算,计算速度较慢,适用于对计算速度要求不高
的场景。
脉动映射的位串行乘法器可以应用于各种数字电路设计中,尤其
是在低功耗和面积有限的嵌入式系统中,可以提供高效的乘法运算功能。
乘法器电路原理

乘法器电路原理你看啊,乘法器电路呢,简单来说就是一个能把两个输入信号变成它们乘积的电路。
想象一下,就好像有两个小数字精灵,它们钻进了这个电路小盒子里,然后这个小盒子就像个超级魔法师,“噗”的一下就把这两个数字精灵变成了它们相乘之后的结果精灵。
咱们先从最基础的模拟乘法器说起。
模拟乘法器就像是一个很细腻的画家。
它有两个输入端,就像画家有两支画笔。
一支画笔蘸着一种颜色(一个输入信号),另一支蘸着另一种颜色(另一个输入信号)。
然后呢,它在画布(输出端)上画出的颜色就像是这两种颜色混合起来的效果,但这个混合可不是简单的加法哦,而是按照乘法的规则来的。
在模拟乘法器电路里,有很多神奇的元件在起作用呢。
比如说,有一些晶体管就像是一群勤劳的小工人。
它们按照一定的规律排列组合,就像小工人按照特定的工序工作一样。
当输入信号进来的时候,这些晶体管就开始忙乎起来啦。
它们会根据输入信号的大小来调整自己的工作状态,就像小工人根据工作量来调整自己的干活速度。
如果输入信号大,它们就干得更起劲,然后通过它们的通力合作,在输出端就产生了一个和两个输入信号乘积相关的信号。
再来说说数字乘法器。
这就像是一个非常严谨的数学家。
数字乘法器处理的是数字信号,就像数学家处理的是一个个精确的数字。
数字信号只有0和1这两个小伙伴,看起来很简单对吧?但是这个乘法器电路可一点都不简单呢。
它里面有很多逻辑门,就像一个个小小的逻辑精灵。
这些逻辑门有与门、或门、非门等等。
它们按照特定的逻辑规则来工作。
比如说,要计算两个二进制数的乘法。
就像把两个由0和1组成的小队伍拉到这个乘法器的战场上。
这些逻辑门就开始对这些0和1进行各种操作。
与门就像一个很挑剔的裁判,如果两个输入都是1,它才会让1通过,就像只有两个条件都满足才会判定成功一样。
通过这些逻辑门的层层把关和计算,最后就得出了这两个数字相乘的结果。
乘法器电路在我们的生活中可有着大用处呢!就像在音频处理中,它可以用来调节音量。
乘法器电路的设计与实现

乘法器电路的设计与实现乘法器电路是一种用于实现数字信号的乘法运算的电路。
在数字电子系统中,乘法运算是十分常见的操作之一。
乘法器电路的设计与实现对于数字电子系统的性能和效率具有重要影响。
乘法器电路的设计是基于数字逻辑门电路的原理。
在数字电子系统中,逻辑门电路是基本的构建模块。
常用的逻辑门包括与门、或门、非门等。
乘法器电路的设计可以通过组合逻辑电路和时序逻辑电路来实现。
组合逻辑电路是指输出只与当前的输入有关,不依赖于之前的输入。
而时序逻辑电路是指输出不仅与当前的输入有关,还与之前的输入有关。
乘法器电路的设计过程可以分为几个关键步骤。
首先是确定乘法器的位数。
乘法器电路的位数决定了它可以处理的数字的范围。
位数越多,乘法器可以处理的数字范围越大。
然后是确定乘法器的输入和输出的编码方式。
在数字电子系统中,常用的编码方式包括二进制和十进制。
接下来是确定乘法器的运算规则。
乘法器可以实现有符号数和无符号数的乘法运算。
最后是选择适当的逻辑门电路来实现乘法器。
乘法器电路的实现需要考虑一些关键因素。
首先是电路的布局和连接。
乘法器电路中的逻辑门电路需要正确地布局和连接,以确保信号能够正确地传输和处理。
其次是电源和地的连接。
电源和地的连接是电路正常工作的基础,必须保证良好的接触和稳定的电源供应。
此外,还需要考虑电路的稳定性和抗干扰能力。
乘法器电路需要能够稳定地工作,并且能够抵抗来自外部的干扰。
乘法器电路的设计和实现也可以通过计算机辅助设计软件来完成。
计算机辅助设计软件可以提供方便快捷的设计工具和仿真环境,大大提高了设计的效率和准确性。
通过计算机辅助设计软件,设计人员可以轻松地进行逻辑门电路的布局和连接,并进行电路的仿真和验证。
乘法器电路的设计与实现是数字电子系统设计的重要组成部分。
乘法器电路的性能和效率对于数字电子系统的整体性能具有重要影响。
设计人员需要仔细考虑乘法器电路的位数、编码方式、运算规则等因素,并选择适当的逻辑门电路来实现乘法器。
乘法器工作原理

乘法器工作原理
乘法器是一种电子设备,用于实现两个数字(或模拟)信号的乘法运算。
其工作原理可以简单地描述如下:
1. 输入信号:乘法器通常有两个输入端,分别用于接收待相乘的数字信号A和B。
2. 位展开:乘法器将输入信号A和B进行位展开操作,即将
每一个输入位(或字节)进行分离和独立处理。
这可以通过触发器、逻辑门电路等实现。
3. 部分乘积计算:对每一对输入位进行乘法运算,并将结果存储在部分乘积寄存器中。
这可以通过加法器电路来实现,其中每一个乘积被加到累加器中。
4. 乘积累加:将所有的部分乘积相加得到最终的乘积结果。
这可以通过多级加法器电路来实现。
一般来说,乘法器采用树形结构或布斯-舍乘法算法(Booth's algorithm)来提高计算效率。
5. 结果输出:输出端给出乘法运算的结果。
根据需求,这个结果可以是数字信号,模拟电压或电流等形式。
乘法器的工作原理可以根据底层电路和算法的不同而有所变化。
现代的乘法器采用复杂的电路设计和优化算法,以实现更高的运算速度和精度。
串行乘法器与并行乘法器的设计

state <= s1;
end
end
s2: begin
result <= P;
input [7:0] x, y;
output [15:0] result;
reg [15:0] result;
parameter s0 = 0, s1 = 1, s2 = 2;
reg [2:0] count = 0;
state <= s0;
end
default: ;
endcase
end
endmodule
module multi_CX(clk, x, y, result);
reg [1:0] state = 0;
reg [15:0] P, T;
reg [7:0] y_reg;
always @(posedge clk) begin
case (state)
s0: begin
input clk;
input rst_n;
output [7:0] mul_out;
reg [7:0] mul_out;
reg [7:0] stored0;
reg [7:0] stored1;
下面是用Verilog HDL实现一个4位的流水线乘法器:
Java代码
module multi_4bits_pipelining(mul_a, mul_b, clk, rst_n, mul_out);
input [3:0] mul_a, mul_b;
法器的Verilog HDL实现
博客分类: FPGA
阵列乘法器

和最下面的一行。因而
得n位×n位不带符
号的阵列乘法器总的乘法时间为:
tm=Ta+ (n-2)6T+5T+(n-1)]×Tf =2T+6nT-12T+5T+(n-1)×2T
=(4n-2)×2T
(2.27)
2.带符号的阵列乘法器
(1) 对2求补器电路
我们先来看看算术运算部件设计中经常用到的求补电路。一个具
的补码阵列乘法所需要增加的硬件较多。为了完成所必需的求 补与乘法操作,时间大约比原码阵列乘法增加1倍。
例17:设x=+15,y=-13,用带求补器的原码阵列乘法器求出 乘积x·y=?
[解:] 设最高位为符号位,则输入数据为[x]原 =01111 [y]原 = 11101
符号位单独考虑,算前求补级后 |x|=1111,|y|=1101
A=am-1…a1a0 B=bn-1…b1b0 它们的数值分别为a和b,即
m-1
a ∑ = i=a0 i2i
n-1
b ∑ = j=b0j2j
在二进制乘法中,被乘数A与乘数B相乘,产生m+n位乘积P: P=pm+n-1…p1p0 乘积P 的数值为
实现这个乘法过程所需要的操作和人们的习惯方法非常类 似:(如下页图所示):
有使能控制的二进制对2求补器电路图演示,其逻辑表达式如下:
C-1=0, Ci=ai+Ci-1
ai*=ai⊕ECi-1,
0≤i≤n
在对2求补时,要采用按位扫描技术来执行所需要的求补操作。令
A=an…a1a0是给定的(n+1)为带符号的数,要求确定它的补码形式 。进行求补的方法就是从数的最右端a0开始,,由右向左,直到找出第 一个“1”,例如ai=1, 0≤i≤n。这样,ai以左的每一个输入位都求反, 即1变0,0变1。最右端的起始链式输入C-1必须永远置成“0”。当控 制信号线E为“1”时,启动对2求补的操作。当控制信号线E为“0”时
4位乘法器
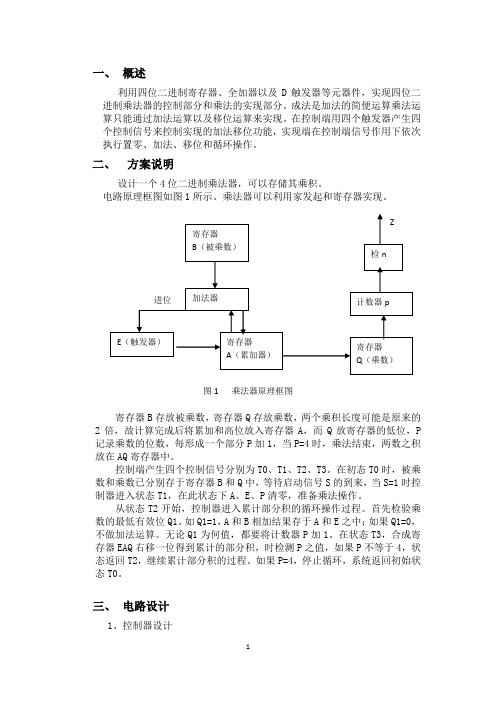
一、概述利用四位二进制寄存器、全加器以及D触发器等元器件,实现四位二进制乘法器的控制部分和乘法的实现部分。
成法是加法的简便运算乘法运算只能通过加法运算以及移位运算来实现。
在控制端用四个触发器产生四个控制信号来控制实现的加法移位功能,实现端在控制端信号作用下依次执行置零、加法、移位和循环操作。
二、方案说明设计一个4位二进制乘法器,可以存储其乘积。
电路原理框图如图1所示。
乘法器可以利用家发起和寄存器实现。
图1 乘法器原理框图寄存器B存放被乘数,寄存器Q存放乘数,两个乘积长度可能是原来的2倍,故计算完成后将累加和高位放入寄存器A,而Q放寄存器的低位,P 记录乘数的位数,每形成一个部分P加1,当P=4时,乘法结束,两数之积放在AQ寄存器中。
控制端产生四个控制信号分别为T0、T1、T2、T3。
在初态T0时,被乘数和乘数已分别存于寄存器B和Q中,等待启动信号S的到来,当S=1时控制器进入状态T1,在此状态下A、E、P清零,准备乘法操作。
从状态T2开始,控制器进入累计部分积的循环操作过程。
首先检验乘数的最低有效位Q1。
如Q1=1,A和B相加结果存于A和E之中;如果Q1=0,不做加法运算。
无论Q1为何值,都要将计数器P加1。
在状态T3,合成寄存器EAQ右移一位得到累计的部分积,时检测P之值,如果P不等于4,状态返回T2,继续累计部分积的过程。
如果P=4,停止循环,系统返回初始状态T0。
三、电路设计1、控制器设计根据图2所示的ASM图表,可以设计二进制乘法器的控制器。
图2 二进制乘法器ASM图表四个D触发器的驱动方程为:D0=T0S’+T3Z=((T0S’)’·(T3Z)’)’D1=T0S=((T0S)’)’D2=T1+T3Z’=(T1’·(T3Z’)’)’D3=T2控制器仿真电路如图2所示。
控制器中S为启动信号,高电平有效,系统开始工作时应使T0=1,T1=T2=T3=0,故图中设置了Reset信号(负脉冲)图2 二进制乘法器的控制逻辑图2. 二进制乘法器数据处理器(1) A寄存器A寄存器具有并入、移位、同步清0和保持功能。
乘法器

0
1 0 1 1
1
1
1
1
1
Company Logo
一位全加器的实现(表达式) 由真值表,可得: S=Add_1 xor Add_2 xor cin; cout=(Add_1 and Add_2) or (Add_1 and cin )or (Add_2 and cin);
所以,一位全加器的实现需要的器件有: 3输入的异或门(1个) 3输入的或门(1个);2输入的与门(3个)
Company Logo
Company Logo
串并乘法原理与步骤
假设被乘数X=1101,乘数Y=1011,步骤如下: ①1101*1=1101 ,result=1 1 0 1(放在锁存器中) ②1101*1=1101 sum=1101,把result的值左移 一位,即0 1 1 0,结果与sum相加(一位相加)
Company Logo
一位全加器的实现(电路)
Company Logo
串-并乘法器的实现
LOGO
Company Logo
加法树乘法器 加法树乘法器的基本 思想也是移位相加,不 过,它是先移位(*2), 后相乘.而且它是同时移 位。 优点:速度快 缺点:耗资源
Company Logo
混合加法器
混合加法器就是把移位相加与查找表结合起来。假设 现在把1101与1011相乘。用两位相乘实现。步骤如下: 1. 1101与11相乘,把1101看成1100+01。这样, 1101*11=(11*11)>>2+01*11; 两位乘法直接在查找表中找到,不用进行运算。所以,只 需 进行加法运算; 2.1101与10(高位)相乘,方法与1相同; 3.把2的结果移2位,再与1的结果相加。 这样,在查找表中只需保存22 *22,同样是4位的乘法 器,比单纯用查找表法( 24 * 24 ),资源少了不少。当 然在速度也要慢一下。所以混合加法器的速度与资源的利 用都是介于查找表与移位加法这两种方法之间
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
串行乘法器原理
串行乘法器是一种数字电路,可以用来实现两个数的乘法运算。
它的原理是将乘法拆分成若干个基本的位运算操作,并通过按位移位、加法和累加操作实现乘法运算。
具体来说,串行乘法器将两个数乘以每一位时得到的结果分别存储在一个寄存器中。
首先,将被乘数的最低位和乘数的各个二进制位相乘,然后将得到的乘积存储在寄存器中。
紧接着,将被乘数向右移一位,将乘数向左移一位,然后再次乘法运算得到一个新的乘积,并累加到寄存器中之前的乘积上(类似于竖式计算中的进位操作),依次进行上述操作直到所有的位都计算完毕。
最终,寄存器中存储的就是两个数的乘积。
串行乘法器原理相比于其他乘法器来说比较简单,其设计简单且可靠,运算速度较慢,但是适合实现在基于FPGA和ASIC的数字电路中,被广泛应用于各种嵌入式系统、数字信号处理器和通信设备中。
