中学课件_对数与对数函数
合集下载
对数函数概念课件

ln(e)
由于e的底数等于e,所以ln(e) = 1。
logₐ(b)
当a > 1且b > 0时,logₐ(b)是 正数。具体数值取决于a和b的值
。
答案及解析
2. 下列各式中正确的是
log₂(4) = 2 和 log₂(8) = 3 是正确的。其他两 个是错误的。因为2的平方是4,而3次方是8。 但2的四次方是16,不是16。同样,32也不是2 的5次方。
对于每个函数,定义域是使函数内部大于0的x值范围。例如,对于y = log₂(x - 2),需 要x - 2 > 0,即x > 2。对于其他函数也有类似的要求。
6. 下列各式中,对数式正确的是
根据对数的定义和性质来判断。例如,2^(log₂(x))确实等于x,因为如果log₂(x)是y, 那么2的y次方就是x。其他选项可以通过类似的逻辑来判断是否正确。
logₐ(a^b) = b (a > 1) 若 ln x = n,则 x = _______.
答案及解析
01Байду номын сангаас
基础练习题答案及解析
02
1. 计算下列函数值
03
log₂(4): 由于2的平方等于4,所以log₂(4) = 2。
答案及解析
log₁₀(0.001)
由于10的负三次方等于0.001, 所以log₁₀(0.001) = -3。
有应用。
05
对数函数的图像和 性质
对数函数的图像
总结词
对数函数的图像是单调递增或递减的,取决于底数的大小。
详细描述
对数函数的图像通常在第一象限和第四象限内。当底数大于1时,函数图像是单调递增的;当底数在0 到1之间时,函数图像是单调递减的。对数函数的图像还可以通过绘制对数函数图来观察其变化趋势 和特点。
高中数学 对数与对数运算课件(精品课件)

3
log9 92
3 2
(2) log 4 3 81
解法一:设 x
log4 3 81
则
x
43
x
81, 34
34 ,
解法二: log4 3 81 log4 3 ( 4 3)16 16
x3 2
x 16
对数运算性质
理论证明:
1 loga(MN)= logaM +logaN
理论证明:
1 loga(MN)= logaM +logaN
例如: log e 3 简记作ln3 ; log e 10 简记作ln10
(6)底数a的取值范围: (0,1) (1, )
真数N的取值范围: (0, )
讲解范例
例2 将下列对数式写成指数式:
(1) log1 27 3
(2)
3
log5
1 125
3
13 27
3 53 1
125
(3) ln10 2.303
对数的概念及运算性质
定义: 一般地,如果 a a 0, a 1
的b次幂等于N, 就是 ab N ,那么数 b叫做
以a为底 N为真数的对数,记作 loga N b a叫做对数的底数,N叫做真数。
例如:
42 16
102 100
1
42 2
10 2 0.01
log4 16 2
log10 100 2
log4 2
3 31 log3 2
1 lg9
1002
解: 2 log2 3 log3 7 log7 8
lg 3 lg 7 lg 8 lg 23 3
lg 2 lg 3 lg 7 lg 2
例1:计算:
高三数学课件:第八讲 对数与对数函数

作业手册:2.5
第十七页,编辑于星期日:二十二点 四十八分。
B、 43 ,1
C、 94
பைடு நூலகம்
,
D、1,94
第十四页,编辑于星期日:二十二点 四十八分。
已知函数f(x)=lg(ax-bx) (a>1>b
>0).
(1)求f(x)的定义域; (2)在函数y=f(x)的图象上是否存在不同 两点,使过这两点的直线平行于x轴? (3)当a,b满足什么条件时,f(x)在(1,+∞)
已知函数f (x) ln(x x2 1) (1)证明f (x)为奇函数 (2)若f (x) ln(2 5),求x的值.
第十三页,编辑于星期日:二十二点 四十八分。
若函数f (x) loga (x3 ax)(a 0, a 1)在区间
1 2
,0 内单调递增,则a的取值范围是(
)
A、 14 ,1
第六页,编辑于星期日:二十二点 四十八分。
基础自测
1、D
2、D 3、D
4、C 5、 2
第七页,编辑于星期日:二十二点 四十八分。
题型一、对数的运算
例1、求值 P29例1
第八页,编辑于星期日:二十二点 四十八分。
变式练习
(1)若2a 5b 10,求 1 1 的值. ab
(2)若x loga 4 1, 求4x 4x的值.
第九页,编辑于星期日:二十二点 四十八分。
题型二、对数函数的图像与性质
例2、设函数f (x) lg x ,若0 a b, 且f (a) f (b)证明:ab 1
第十页,编辑于星期日:二十二点 四十八分。
若函数f (x)满足对于(0, )上的任意实数 x, y都有f (xy) f (x) f ( y),且x 1时 f (x) 0求证: (1) f ( x ) f (x) f ( y)
第十七页,编辑于星期日:二十二点 四十八分。
B、 43 ,1
C、 94
பைடு நூலகம்
,
D、1,94
第十四页,编辑于星期日:二十二点 四十八分。
已知函数f(x)=lg(ax-bx) (a>1>b
>0).
(1)求f(x)的定义域; (2)在函数y=f(x)的图象上是否存在不同 两点,使过这两点的直线平行于x轴? (3)当a,b满足什么条件时,f(x)在(1,+∞)
已知函数f (x) ln(x x2 1) (1)证明f (x)为奇函数 (2)若f (x) ln(2 5),求x的值.
第十三页,编辑于星期日:二十二点 四十八分。
若函数f (x) loga (x3 ax)(a 0, a 1)在区间
1 2
,0 内单调递增,则a的取值范围是(
)
A、 14 ,1
第六页,编辑于星期日:二十二点 四十八分。
基础自测
1、D
2、D 3、D
4、C 5、 2
第七页,编辑于星期日:二十二点 四十八分。
题型一、对数的运算
例1、求值 P29例1
第八页,编辑于星期日:二十二点 四十八分。
变式练习
(1)若2a 5b 10,求 1 1 的值. ab
(2)若x loga 4 1, 求4x 4x的值.
第九页,编辑于星期日:二十二点 四十八分。
题型二、对数函数的图像与性质
例2、设函数f (x) lg x ,若0 a b, 且f (a) f (b)证明:ab 1
第十页,编辑于星期日:二十二点 四十八分。
若函数f (x)满足对于(0, )上的任意实数 x, y都有f (xy) f (x) f ( y),且x 1时 f (x) 0求证: (1) f ( x ) f (x) f ( y)
人教A版高中数学必修一2.2.1《对数与对数运算》精品课件(共15张PPT)
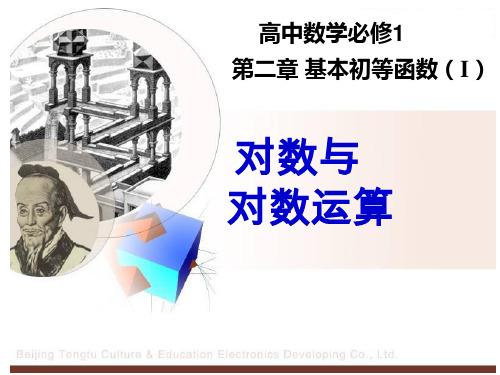
⑵ loga 1 0, loga a 1
对任意 a0 且 a 1 都有 a0 1 loga10
a1 a loga a1
⑶对数恒等式 loga ab b
aloga N N
两种特殊的对数
1.常用对数:以10作底 log10 N 写成 l g N
2.自然对数:以无理数e = 2.71828…… 作底 的对数 ,
loge N 写成 ln N
例题讲解
例1 将下列指数式写成对数式:
(1) 54 625lo5g6254
(2)
26 1 64
1 log2 64 6
(3) 3a 27 log327a
(4)
1
m
5.13
3
log1 5.13m
3
例题讲解
例2 将下列对数式写成指数式:
(1)log1 164
2
1 2
(4) lg 0.0013
练习 4.求下列各式的值
(1) lo g15 1 5 1
(2) lo g 0 .4 1 0
(3) lo g 9 8 1 2 (4) log2.5 6.25 2
(5) lg 7 3 4 3 3
(6) log 3 243 5
引申练习
1 .已 知 l o g a 2 m ,l o g a 3 n ,求 a 2 m n 的 值 。
把下列指数式写成对数式
2 的b次幂等于N, 就是 解: (1)因 为 log x , 所 以 的b次幂等于N, 就是
(2)由16,4求底数2的运算是
3 以a为底 N的对数,记作 x64 (4) 4 1 例1 将下列指数式写成对数式:
64 2 3
3
2 3
2
16
4.4.1对数函数的概念课件(人教版)

学习目标
新课讲授
课堂总结
例3 假设某地初始物价为1,每年以5%的增长率递增,经过y年后的物价为x.
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x 1
2
3
4
5
6
7
8
9
10
年数y 0
(2)根据函数y=log1.05x,x∈[1,+∞),利用计算工具,可得下表
物价x 1 年数y 0
2
3
学习目标
新课讲授
课堂总结
例1 下列函数中,哪些是对数函数?
(1)y=logax2(a>0,且a≠1);(2)y=log2x-1;
(数
学习目标
新课讲授
课堂总结
总结归纳 判断一个函数是对数函数的方法 (1)底数a>0,且为不等于1的常数,也不含有自变量x; (2)真数位置是自变量x,且x的系数是1; (3)logax的系数是1.
4
5
6
7
8
9
10
14 23 28 33 37 40 43 45 47
由表中的数据可以发现,该地区的物价随时间的增长而增长, 但大约每增加1倍所需要的时间在逐渐缩小.
学习目标
新课讲授
课堂总结
练一练 已知f(x)=log3x. (1)作出这个函数的图象; (2)若f(a)<f(2),利用图象求a的取值范围.
4.4.1 对数函数的概念
学习目标
新课讲授
课堂总结
1.理解对数函数的概念 2.会求对数函数的定义域
学习目标
新课讲授
课堂总结
知识点:对数函数的概念
思考:已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢? 死亡时间x是碳14的含量y的函数吗?
高一数学对数函数的概念与图象(中学课件201909)

0<a<1
1 1
01
x
01
x
思考5:函数 y | log2 x | 与 y log2 | x |
的图象分别如何?
理论迁移
例1 求下列函数的定义域:
(1) y=log0.5|x+1| ; (2) y=log2(4-x) 知函数
f
(
x)
log 2
有 m an.由此可知点Q(n,m)在哪个
函数的图象上?
思考3:点P(m,n)与点Q(n,m)有怎样的 位置关系?由此说明对数函数 y loga x
的图象与指数函数 y ax 的图象有怎样
的位置关系?
yQ
P
o
x
思考4:一般地,对数函数的图象可分为
几类?其大致形状如何? y a>1 y
思考5:对数函数的定义域、值域分别是 什么?
思考6:函数 y log3 x2 与 y 2log3 x 相同吗? 为什么?
知识探究(二):对数函数的图象
思考1:研究对数函数的基本特性应先研 究其图象.你有什么方法作对数函数的图 象?
思考2:设点P(m,n)为对数函数 y loga x 图象上任意一点,则 n loga m ,从而
知识探究(一):对数函数的概念
思考1:在上面的问题中,若要使残留的 污垢为原来的 1 ,则要漂洗几次?
64
思考2:在关系式y log 1 x中,取 x a(a 0)
4
对应的y的值存在吗?怎样计算?
思考3:函数 y log 1 x 称为对数函数,
4
一般地,什么叫对数函数?
思考4:为什么在对数函数中要求a>0, 且a≠l?
对数函数的图像和性质课件人教A版高中数学必修第一册(共32张PPT)
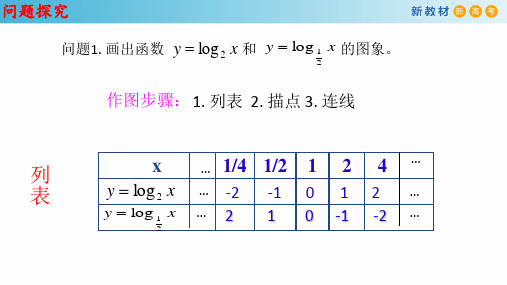
对数函数y=log a x (a>0, a≠1)
y o1
y=logax (a>1)
x
y=logax (0<a<1) (1)定义域: (0,+∞) (2)值域:R
(3)过点(1,0), 即x=1 时, y=0
(4) a>1时, x<0,0<y<1; x>0,y>1 (4) a>1时,0<x<1,y<0; x>1,y>0
⑴定义域:
性 ⑵值域:
(0,+∞) R
质 ⑶过特殊点: 过点(1,0),即x=1时y=0 ⑷单调性 : 在(0,+∞)上是增函数 ⑷单调性:在(0,+∞)上是减函数
记忆口诀
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数; 底数只能大于0, 等于1来也不行; 底数若是大于1, 图象从下往上增; 底数0到1之间, 图象从上往下减; 无论函数增和减, 图象都过(1,0)点.
解(2):考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间(0,+∞)上是减函数; ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
例题解析
例1:比较下列各组中,两个值的大小:
(3) log a 5.1与 log a 5.9 (a>0,且a≠1)
解(3):考察函数log a 5.1与 log a 5.9 可看作函数y=log a x的 两个函值 , 对数函数的单调性取决于底数a是大于1还是小于1, 因此需要对底数a进行讨论
线
-2
y=log1/2x
关于x轴对称
问题探究
