第9章SPSS的线性回归分析
线性回归spss

线性回归spss线性回归是一种集总结统计、回归分析和假设检验于一体的一种统计学方法,以回归方程的形式表示它表示两个或多个被观测变量之间的关系。
线性回归分析是建立变量间的因果关系的有效方法,且可分析出不同变量之间的先后关系。
在线性回归思想的引入下,研究者可以发现单一变量的变化对另一变量的影响,观察不同变量的相关性,从而较为精确地预测出因变量、解决现实中的实际问题。
SPSS是一款统计分析软件,全称为Statistical Package for Social Sciences,也就是社会科学统计分析软件。
它包括数据预处理、数据探索,描述性统计和假设检验,以及多重回归分析等功能。
在SPSS中,线性回归分析可以根据因变量的取值判断单因素、双因素及多因素的线性回归模型,根据实际情况考虑因变量的取值范围,为研究者提供多种类型的线性回归分析模型。
二、SPSS线性回归分析SPSS线性回归分析主要分为单变量回归、双变量回归和多变量回归三类。
1、单变量回归单变量回归指的是一个自变量与一个因变量之间的线性关系,即在给定的一组自变量值情况下,比较其对应的因变量值,从而推断出自变量与因变量之间的关系。
SPSS中的单变量回归可以实现以下功能:(1)获取变量本身的描述统计量,如平均数、极差、四分位数等;(2)计算变量的相关系数和线性回归方程;(3)建立变量的拟合曲线;(4)计算变量的估计值.2、双变量回归双变量回归是讨论两个自变量之间的关系情况,在双变量回归分析中,可以确定两个自变量之间是否存在线性联系,以及确定这种关系有何特性。
SPSS中双变量线性回归分析可以实现以下功能:(1)获取变量本身的描述统计量;(2)计算变量之间的相关系数和线性回归方程;(3)建立变量的拟合曲线;(4)计算变量之间的线性关系的估计值;3、多变量回归多变量回归也称多元回归,即多个自变量和一个因变量之间的关系。
它可以确定不同变量之间的关系,从而推断自变量与因变量之间的关系。
(09)第9章 一元线性回归(2011年)

变量之间是否存在关系? 如果存在,它们之间是什么样的关系? 变量之间的关系强度如何? 样本所反映的变量之间的关系能否代表总体 变量之间的关系?
9-9 *
9.1 变量间的关系 9.1.1 变量间是什么样的关系?
统计学 STATIS TICS
函数关系
(第四版) 1. 是一一对应的确定关系 2. 设有两个变量 x 和 y ,变量 y y 随变量 x 一起变化,并完 全依赖于 x ,当变量 x 取某 个数值时, y 依确定的关系 取相应的值,则称 y 是 x 的 函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量 x 3. 各观测点落在一条线上
y 是 x 的线性函数(部分)加上误差项 线性部分反映了由于 x 的变化而引起的 y 的变化 误差项 是随机变量 反映了除 x 和 y 之间的线性关系之外的随机因素 对 y 的影响 是不能由 x 和 y 之间的线性关系所解释的变异性 0 和 1 称为模型的参数
9 - 30 *
统 计 学 数据分析 (方法与案例)
作者 贾俊平
统计学 STATIS TICS
(第四版)
统计名言
不要过于教条地对待研究的结果, 尤其当数据的质量受到怀疑时。
——Damodar N.Gujarati
9-2 *
第 9 章 一元线性回归
9.1 9.2 9.3 9.4 变量间关系的度量 一元线性回归的估计和检验 利用回归方程进行预测 用残差检验模型的假定
9-7
*
第 9 章 一元线性回归
9.1 变量间的关系
9.1.1 变量间是什么样的关系? 9.1.2 用散点图描述相关关系 9.1.3 用相关系数度量关系强度
SPSS线性回归分析

SPSS分析技术:线性回归分析相关分析可以揭示事物之间共同变化的一致性程度,但它仅仅只是反映出了一种相关关系,并没有揭示出变量之间准确的可以运算的控制关系,也就是函数关系,不能解决针对未来的分析与预测问题。
回归分析就是分析变量之间隐藏的内在规律,并建立变量之间函数变化关系的一种分析方法,回归分析的目标就是建立由一个因变量和若干自变量构成的回归方程式,使变量之间的相互控制关系通过这个方程式描述出来。
回归方程式不仅能够解释现在个案内部隐藏的规律,明确每个自变量对因变量的作用程度。
而且,基于有效的回归方程,还能形成更有意义的数学方面的预测关系。
因此,回归分析是一种分析因素变量对因变量作用强度的归因分析,它还是预测分析的重要基础。
回归分析类型回归分析根据自变量个数,自变量幂次以及变量类型可以分为很多类型,常用的类型有:线性回归;曲线回归;二元Logistic回归技术;线性回归原理回归分析就是建立变量的数学模型,建立起衡量数据联系强度的指标,并通过指标检验其符合的程度。
线性回归分析中,如果仅有一个自变量,可以建立一元线性模型。
如果存在多个自变量,则需要建立多元线性回归模型。
线性回归的过程就是把各个自变量和因变量的个案值带入到回归方程式当中,通过逐步迭代与拟合,最终找出回归方程式中的各个系数,构造出一个能够尽可能体现自变量与因变量关系的函数式。
在一元线性回归中,回归方程的确立就是逐步确定唯一自变量的系数和常数,并使方程能够符合绝大多数个案的取值特点。
在多元线性回归中,除了要确定各个自变量的系数和常数外,还要分析方程内的每个自变量是否是真正必须的,把回归方程中的非必需自变量剔除。
名词解释线性回归方程:一次函数式,用于描述因变量与自变量之间的内在关系。
根据自变量的个数,可以分为一元线性回归方程和多元线性回归方程。
观测值:参与回归分析的因变量的实际取值。
对参与线性回归分析的多个个案来讲,它们在因变量上的取值,就是观测值。
《统计分析与SPSS的应用(第五版)》课后练习答案(第9章)
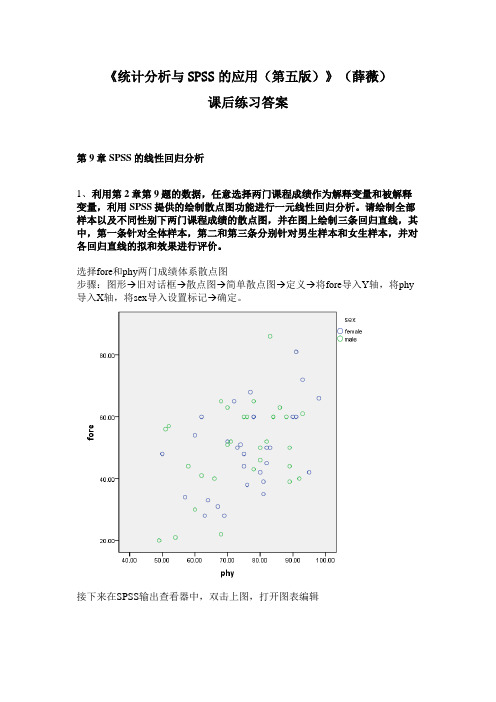
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy 导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
spss多元线性回归分析结果解读

spss多元线性回归分析结果解读SPSS多元线性回归分析结果解读1. 引言多元线性回归分析是一种常用的统计分析方法,用于研究多个自变量对因变量的影响程度及相关性。
SPSS是一个强大的统计分析软件,可以进行多元线性回归分析并提供详细的结果解读。
本文将通过解读SPSS多元线性回归分析结果,帮助读者理解分析结果并做出合理的判断。
2. 数据收集与变量说明在进行多元线性回归分析之前,首先需要收集所需的数据,并明确变量的含义。
例如,假设我们正在研究学生的考试成绩与他们的学习时间、家庭背景、社会经济地位等因素之间的关系。
收集到的数据包括每个学生的考试成绩作为因变量,以及学习时间、家庭背景、社会经济地位等作为自变量。
变量说明应当明确每个变量的测量方式和含义。
3. 描述性统计分析在进行多元线性回归分析之前,我们可以首先对数据进行描述性统计分析,以了解各个变量的分布情况。
SPSS提供了丰富的描述性统计方法,如均值、标准差、最小值、最大值等。
通过描述性统计分析,我们可以获得每个变量的分布情况,如平均值、方差等。
4. 相关性分析多元线性回归的前提是自变量和因变量之间存在一定的相关性。
因此,在进行回归分析之前,通常需要进行相关性分析来验证自变量和因变量之间的关系。
SPSS提供了相关性分析的功能,我们可以得到每对变量之间的相关系数以及其显著性水平。
5. 多元线性回归模型完成了描述性统计分析和相关性分析后,我们可以构建多元线性回归模型。
SPSS提供了简单易用的界面,我们只需要选择因变量和自变量,然后点击进行回归分析。
在SPSS中,我们可以选择不同的回归方法,如逐步回归、前向回归、后向回归等。
6. 回归结果解读在进行多元线性回归分析后,SPSS将提供详细的回归结果。
我们可以看到每个自变量的系数、标准误差、t值、显著性水平等指标。
系数表示自变量与因变量之间的关系程度,标准误差表示估计系数的不确定性,t值表示系数的显著性,显著性水平则表示系数是否显著。
用SPSS做回归分析

用SPSS做回归分析回归分析是一种统计方法,用于研究两个或多个变量之间的关系,并预测一个或多个因变量如何随着一个或多个自变量的变化而变化。
SPSS(统计软件包的统计产品与服务)是一种流行的统计分析软件,广泛应用于研究、教育和业务领域。
要进行回归分析,首先需要确定研究中的因变量和自变量。
因变量是被研究者感兴趣的目标变量,而自变量是可能影响因变量的变量。
例如,在研究投资回报率时,投资回报率可能是因变量,而投资额、行业类型和利率可能是自变量。
在SPSS中进行回归分析的步骤如下:1.打开SPSS软件,并导入数据:首先打开SPSS软件,然后点击“打开文件”按钮导入数据文件。
确保数据文件包含因变量和自变量的值。
2.选择回归分析方法:在SPSS中,有多种类型的回归分析可供选择。
最常见的是简单线性回归和多元回归。
简单线性回归适用于只有一个自变量的情况,而多元回归适用于有多个自变量的情况。
3.设置因变量和自变量:SPSS中的回归分析工具要求用户指定因变量和自变量。
选择适当的变量,并将其移动到正确的框中。
4.运行回归分析:点击“运行”按钮开始进行回归分析。
SPSS将计算适当的统计结果,包括回归方程、相关系数、误差项等。
这些结果可以帮助解释自变量如何影响因变量。
5.解释结果:在完成回归分析后,需要解释得到的统计结果。
回归方程表示因变量与自变量之间的关系。
相关系数表示自变量和因变量之间的相关性。
误差项表示回归方程无法解释的变异。
6.进行模型诊断:完成回归分析后,还应进行模型诊断。
模型诊断包括检查模型的假设、残差的正态性、残差的方差齐性等。
SPSS提供了多种图形和统计工具,可用于评估回归模型的质量。
回归分析是一种强大的统计分析方法,可用于解释变量之间的关系,并预测因变量的值。
SPSS作为一种广泛使用的统计软件,可用于执行回归分析,并提供了丰富的功能和工具,可帮助研究者更好地理解和解释数据。
通过了解回归分析的步骤和SPSS的基本操作,可以更好地利用这种方法来分析数据。
SPSS的线性回归分析
线性回归方程的预测
(一)点估计
y0
(二)区间估计 300
200
领 导(管 理)人 数( y)
x0为xi的均值时,预 测区间最小,精度最
100
高.x0越远离均值,预 测区间越大,精度越
低.
0
200
400
600
800
1000
1200
1400
1600
1800
普通职工数(x)
18
多元线性回归分析
(一)多元线性回归方程 多元回归方程: y= β0 +β1x1+β2x2+...+βkxk
– β1、β2、βk为偏回归系数。 – β1表示在其他自变量保持不变的情况下,自变量x1变动一个
单位所引起的因变量y的平均变动
(二)多元线性回归分析的主要问题
– 回归方程的检验 – 自变量筛选 – 多重共线性问题
19
多元线性回归方程的检验
(一)拟和优度检验:
(1)判定系数R2:
R21n n k11S SS ST ER21因均 变方 量误 的差 样
n
n
(yˆi y)2
(yi yˆ)2
R2
i1 n
1
i1 n
(yi y)2
(yi y)2
i1
i1
– R2体现了回归方程所能解释的因变量变差的比例;1-R2则体 现了因变量总变差中,回归方程所无法解释的比例。
– R2越接近于1,则说明回归平方和占了因变量总变差平方和 的绝大部分比例,因变量的变差主要由自变量的不同取值造 成,回归方程对样本数据点拟合得好
27
线性回归分析中的共线性检测
(一)共线性带来的主要问题
线性回归spss
线性回归spss线性回归是一种数学方法,可以用来预测一个变量(称为因变量)的变化情况。
它的基本思想是:可以建立一个函数,这个函数可以用另一个变量(称为自变量)来表示。
例如,假设我们想预测一个学生的成绩,我们可以建立一个函数,它用学生的学习时间来表示学生的成绩,这就是线性回归方法。
线性回归统计分析软件SPSSSPSS(Statistical Package for Social Sciences)是IBM公司开发的一款非常强大的数据分析软件,可以用来进行线性回归分析。
SPSS包括许多数据分析工具,如分类分析、回归分析、多元统计分析、t检验等,其中线性回归分析就是其中一种,可以用来检验两种变量之间的回归关系。
下面将介绍如何使用SPSS进行线性回归分析。
线性回归分析的基本原理线性回归分析的基本原理是确定一个目标变量Y和一个或多个自变量X之间的回归关系。
其中,Y是因变量,表示被预测变量;X是自变量,表示用于预测Y的变量,可以由一个或多个变量组成。
回归分析的目的是确定Y和X之间的关系,这种关系的数学表达式称为回归方程。
使用SPSS进行线性回归分析使用SPSS进行线性回归分析可以通过以下步骤完成:1.先,在SPSS中打开我们的数据集,然后在“数据”菜单中点击“回归”,然后在“线性回归”选项中点击“线性回归”。
2.弹出的窗口中,点击“因变量”,确定需要进行线性回归分析预测的目标变量。
3.后点击“自变量”,确定用于预测变量Y的自变量X。
4.击“设置”,勾选回归分析需要的统计检验,比如,假设检验、相关性分析等,所有的检验要求都可以在这里完成。
5.后,点击“确定”,SPSS会自动计算出回归系数、假设检验结果和其它分析结果。
结论以上就是关于线性回归SPSS的分析,SPSS是一款强大、功能齐全的数据分析软件,可以方便的进行线性回归分析工作。
线性回归分析可以用来预测一个变量的变化情况,并且可以确定变量之间的回归回归关系,是一种有用的数学分析方法。
SPSS线性回归分析
c. Dependent Variable: R's Occupational Prestige Score (1980)
.339
R's Federal Income Tax
.006
R's Occupational Prestige Score (1980)
.
Age of Respondent
.487
Highest Year of School Co mp l ete d
.000
Highest Year School Completed, Father
.000
Highest Year School Completed, Mother
.001
Highest Year School Completed, Spouse
.000
R's Federal Income Tax
.458
R's Occupational Prestige Score (1980)
.009
F Change 149.650 4.403
df1 1 1
Du rb i n -W df2 Sig. F Change atson
330
.000
329
.037
1.955
a. Predictors: (Constant), Highest Year of School Completed
b. Predictors: (Constant), Highest Year of School Completed, Age of Respondent
用F统计量的值,同上
选择此项不显示回 归方程中常数项。
Options 对话框
《统计分析和SPSS的应用(第五版)》课后练习答案解析(第9章)
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
主要包括回归方程的拟合优度检验、显著性检验、回归系数的显著性检验、残差分析等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章SPSS的线性回归分析 学习目标 1. 掌握线型回归分析的主要目标,了解回归方程的最小二乘法估计的基本设计思路。 2. 熟练掌握线性回归分析的具体操作,能够读懂基本分析结果,掌握计算结果之间的数量关系,并能够写出回归方程、对回归方程进行各种统计检验。 3. 了解多元线性回归分析哦那个自变量筛选的主要策略,能够结合筛选策略对相应分析进行说明。 4. 了解SPSS残差分析和多重共线性检验的基本操作,并能够分析结果。 9.1 回归分析概述 9.1.1 什么是回归分析 回归分析是一种应用极为广泛的数量分析方法。它用于分析事物间的统计关系,侧重考虑变量之间的数量变化规律,并通过回归方程的形式描述和反应这种关系,帮助人们准确把握受其他一个或多个变量影响的程度,进而为预测提供科学依据。
“回归”一词是英国统计学家F·Galton在研究父亲身高和其成年儿子的身高关系时提出的。从大量的父亲身高和其成年儿子数据的散点图中,F·Galton天才地发现了一条贯穿其中的直线,它能够描述父亲身高和其成年儿子身高之间的关系,并可用于预测某身高父亲其成年儿子的平均身高。他的研究发现:如果父亲的身高很高,那么她的儿子也会比较高,但不会像他父亲那么高;如果父亲的身高很矮,那么她的儿子也会比较矮,但不会像他父亲那
么矮。他们会趋向于子辈身高的平均值。F·Galton将这种现象称为“回归”,将那条贯穿于系的数量分析关系的数量分析方法称为回归分析。 正如上述F·Galton研究父亲身高与儿子身高关系问题那样,回归分析的核心目的是找到回归线,涉及包括如何得到回归线、如何描述回归线、回归线是否可用于预测等问题。 9·1·2 如何得到回归线 利用样本数据获得回归线通常可采用两类方法:第一,局部平均法;第二,函数拟合。 一、局部平均 局部平均的含义可借用父亲和儿子的身高关系的例子来理解。如果收集到n对父亲和儿子身高的数据(xi,yi)(i=1,2,„,n),可以对它们绘制散点图、计算基本描述统计量。现在得到一个父亲身高数据(x0),于是其儿子身高的预测值可以是:
第一, 子辈身高的平均值—y。显然这个预测是不准的,原因没有考虑父亲身高(x0)的作用。
第二, 父亲身高为x0的所有儿子身高的平均值—y0.。该预测较第一种方法显然要准确得多。 第三, 如果在获得的数据中没有父亲身高为x0的样本数据,可以考虑计算父亲身高为x0左右的一个较小区间内的儿子身高的平均值。
按照这种思路在散点图上不难得到一系列(xi,—yi)(j表示散点图有左往右的第j个小区间)对应的数据点。如果这些点足够多,则可以得到一条光滑的曲线,它们将是上述提到的回归线的近似线。可见,回归线是局部平均的结果。利用回归线做预测是对当x=x0时y的平均值的预测。 二、函数拟合 利用局部平均得到的回归线应在样本量足够大时才能实现,然而通常样本量可能无法达到预期的数量,此时多采用函数拟合的方式得到回归线。函数拟合的基本思路是: 首先,通过散点图观察变量之间的关系,得到回归线形状(线性关系或非线性关系)的感性认知,并确定一个能够反应和拟合这种认知且最简洁的(参数最少的)数学函数(线性函数或非线性函数),即回归模型。 最后,回归方程中的参数是在样本数据的基础上得到的。由于抽样随机性的存在,估计出的回归方程未必是事物总体间数量关系的真实体现,因此需要对回归方程进行各种检验,判断该方程是否真实地反应了事物总体间的统计关系,能否用与预测,并最终得到由回归方程确定的回归近似线。可见,函数拟合方式较局部平均具有更强的可操作性,因而得到广泛采纳。 9.1.3 回归分析的一般步骤 回归分析的一般步骤如下: 1. 确定回归方程中的解释变量和被解释变量 由于回归分析用于分析一个事物如何随其他事物的变化而变化,因此回归分析的的第一步应是确定哪个事物是需要被解释的,即哪个变量是被解释变量(记为y);哪些事物是用于解释其他变量的,即那些变量是解释变量(记为x)。回归分析正是要建立y与x的回归方程,并在给定x的条件下,通过回归方程预测y的平均值。这点是有别于相关分析的。例如,父亲身高关于成年儿子身高的回归分析与成年儿子关于父亲身高是完全不同的。 2. 确定回归模型 根据函数拟合方式,通过观察散点图确定应通过哪种数学模型来概括回归线。如果被解释变量和解释变量之间存在线性关系,则应进行线性回归分析,建立线性回归模型;繁殖如果被解释变量和解释变量之间存在非线性关系,则应进行非线性回归分析,建立非线性回归模型。 3. 建立回归方程 根据收集到的样本数据以及前步所确定的回归模型,在一定的统计拟合准则下估计出模型中的各个参数,得到一个确定的回归方程。 4. 对回归方程进行各种检验 前面已经提到,由于回归方程是在样本数据基础上得到的,回归方程是否真实地事物总体间的统计关系以及回归方程能否用与预测等都需要进行检验。 5. 利用回归方程进行预测 建立回归方程的目的之一是根据回归方程对事物的未来发展趋势进行预测。 利用SPSS会自动进行计算并给出最佳模型。 9.2 线性回归分析和线性回归模型 观察被解释变量y和一个或多个解释变量xi的散点图,当发现y与xi之间呈现出显著地线性关系,则应采用线性回归分析的方法,建立y与xi的线性回归模型。在线性回归分析中,根据模型中解释变量的个数,可将现行回归模型分成一元线性回归模型和多元线性回归模型,相应的分析称为一元线性回归分析和多元线性回归分析。 9.2.1 一元线性回归模型 一元线性回归模型是指只有一个解释变量的线性回归模型,用于揭示被解释变量与另一个解释变量之间的线性关系。 一元线性回归的数学模型为: y=β0+β1x+ε (9.1) 式(9.1)表明:被解释变量y的变化可以由两个部分解释。第一,由解释变量x引起的y的线性变化部分,即y=β0+β1x;第二,有其他随机因素引起的y的变化部分,即ε。 由此可以看出一元线性回归模型是被解释变量和解释变量间非一一对应的统计关系的良好诠释,即当x给定后y的值并非唯一,但它们之间又通过β0和β1保持密切的线性相关关。β0和β1都是模型中的未知参数,β0和β1分别称为回归常数和回归系数,ε称为随机误差,是一个随机变量,当满足两个前提条件,即 E(ε)=0
Var(ε)=2 (9.2) 式(9.2)表明:随机误差的期望应为0,随机误差的方差应为一个特定的值。如果对式(9.1)两边求期望,则有 E(y)=β0+β1x (9.3) 式(9.3)称为一元线性回归方程,它表明x和y之间的统计关系是在平均意义下表现的,即当x的值给定后利用回归模型计算得到的y值是一个平均值,助于前面讨论的局部平均是相一致的。也就是说,例如,如果父亲的身高x给定了,得到的儿子的身高y是特定“儿子群”身高的平均值。 对式(9.3)的一元线性回归方程中的未知参数β0和β1进行估计是一元线性回归分析的核心任务之一。由于参数估计的工作是基于样本数据的,由此得到的参数只是参数真值β0
和β1的估计值,记为^0和^1,于是有 ^y=^0+^1x (9.4)
式(9.4)称为一元线性经验回归方程。从几何意义上讲,一元线性回归经验方程是二维
平面上的一条直线,即回归直线。其中,^0是回归直线在y轴上的截距,^1为回归直线的斜率,它表示解释变量x每变动一个单位所引起的被解释变量y的平均变动数量。 现实社会经济现象中,某一事物(被解释变量)总会收到多方面因素(多个解释变量)的影响。一元 线性回归分析是在不考虑其他影响因素或在认为其他影响因素确定的条件下,分析一个解释变量是如何线性影响被解释变量的,因而是比较理想化的分析。 9.2.2 多元线性回归模型 多元线性回归模型是指含有多个解释变量的线性回归模型,用于揭示被解释变量与其他多个解释变量之间的线性关系。 多元线性回归的数学模型是: Y=β0+β1x1+β2x2+„+βpxp+ε 式(9.5)是一个p元线性回归模型,其中有p个解释变量。它表明被解释变量y的变化可由两个部分解释。第一,由p个解释变量x的变化引起的y的线性变化部分,即Y=β0+β
1x1+β2x2+„+βpxp;第二,由其他随机因素引起的y的变化部分,即ε0β0,β1,,„,β
pxp;参数,分别称为回归常数和偏回归系数,ε称为随机误差,也是一个随机变量,同样满足式(9.2)的要求。如果对式(9.5)两边求期望,则有 E(y)=β0+β1x1+β2x2+„+βpxp (9.6) 式(9.6)称为多元线性回归方程。估计多元线性回归方程中的未知参数β0,β1,,„,βp是多元线性回归分析的核心任务之一。由于参数估计的工作是基于样本数据的,由此得
到的参数只是参数真值β0,β1,,„,βp 的估计值,记为^0,^1„„ ,于是有 xppˆxˆxˆˆ22110
yˆ (9.7)
(9.7)称为多元线性经验回归方程。从几何意义上讲,多元线性回归经验方程是p维空间上的一个超平面,即回归平面。 表示当其他解释变量保持不变时, 每变动一个单位所引起的被解释变量y的平均变量数量 9.2.3 回归参数的普通最小二乘估计 线性回归模型确定后的任务是利用已经收集到的样本数据,根据一定统计拟合准则,对模型中的各个参数进行估计。普通最小二乘就是一种最为常见的统计拟合准则,在该准则下得到的回归参数的估计称为回归参数的普通最小二乘估计。 普通最小二乘估计(ordinary least square estimation ,OLSE)的基本出发点是:应是每个样本点(xi,yi)回归线上的对应点(xi,E(yi))偏差距离的总和最小那么应如何定这个偏差
呢?普通最小二乘将这个偏差距离定义为离差的二次方1,即E(yi))-(yi2偏差距离的总和就转化为离差平方和。 1. 对于一元线性回归方程
Q(β0,β1)=nixyyEiii12n1i2)())(y10i( (9.8)
最小二乘估计是寻找参数β0,β1 的估计值ˆˆ10, ,使式(9.8)达到极小,即 nixyii1210)ˆˆˆˆ0i)(Q(,minnixyii12)(10
2. 对于多元线性回归方程 Q(β0,β1,β2,,„βp)=nixxxyipiii12)...(121110
最小二乘估计是寻找参数 β0,β1,„βp 的估计值 ˆˆˆ10p,, 使式(9.10)达到极小,即 Q(n1i2p210)ˆˆˆˆyˆˆˆˆip1211i10ixxxi(),,,
= min )(2i121110n12xxxyiiii p210,,
