基于BP神经网络的多变量PID解耦控制
(完整word版)基于BP神经网络的自整定PID控制仿真

基于BP神经网络的自整定PID控制仿真一、实验目的1.熟悉神经网络的特征、结构及学习算法。
2.通过实验掌握神经网络自整定PID的工作原理。
3.了解神经网络的结构对控制效果的影响。
4. 掌握用Matlab实现神经网络控制系统仿真的方法。
二、实验设备及条件1.计算机系统2.Matlab仿真软件三、实验原理在工业控制中,PID控制是工业控制中最常用的方法。
这是因为PID控制器结构简单,实现简单,控制效果良好,已得到广泛应用。
但是,PID具有一定的局限性:被控制对象参数随时间变化时,控制器的参数难以自动调整以适应外界环境的变化。
为了使控制器具有较好的自适应性,实现控制器参数的自动调整,可以采用神经网络控制的方法。
利用神经网络的自学习这一特性,并结合传统的PID控制理论,构造神经网络PID控制器,实现控制器参数的自动调整。
基于BP神经网络的PID控制器结构如图4所示。
控制器由两部分组成:一是常规PID控制器,用以直接对对象进行闭环控制,且3个参数在线整定;二是神经网络NN,根据系统的运行状态,学习调整权系数,从而调整PID参数,达到某种性能指标的最优化。
图4中神经网络采用结构为4-5-3型的BP网络。
BP网络是一种单向传播的多层前向网络。
输入节点对应系统的运行状态量,如系统的偏差与偏差变化率,必要时要进行归一化处理。
输入变量的个数取决于被控系统的复杂程度,输出节点对应的是PID的3个可调参数。
由于输出不能为负,所以输出层活化函数取2()(1)()(1)1(1)a k y k y k u k y k -=+-+-非负的Sigmoid 函数,隐含层取正负对称的Sigmoid 函数。
本系统选取的BP 网络结构如图5所示。
网络的学习过程由正向和反向传播两部分组成。
如果输出层不能得到期望输出,那么转入反向传播过程,通过修改各层神经元的权值,使得误差信号最小。
输出层节点分别对应3个可调参数K p 、K i 、K d 。
BP神经网络PID控制
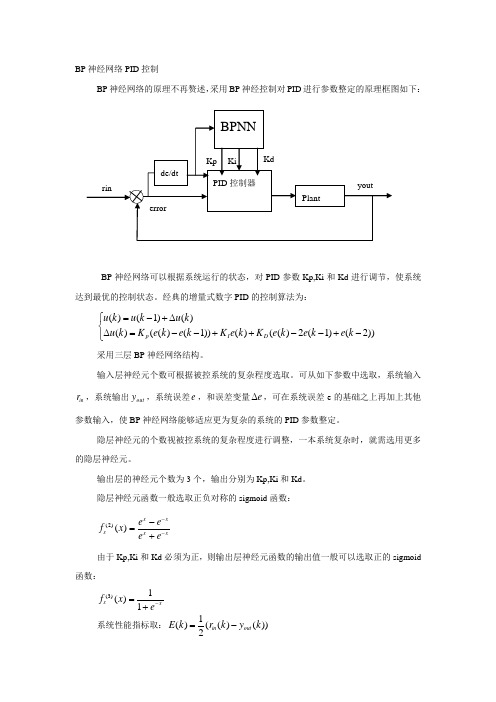
BP 神经网络PID 控制BP 神经网络的原理不再赘述,采用BP 神经控制对PID 进行参数整定的原理框图如下:BP 神经网络可以根据系统运行的状态,对PID 参数Kp,Ki 和Kd 进行调节,使系统达到最优的控制状态。
经典的增量式数字PID 的控制算法为:()(1)()()(()(1))()(()2(1)(2))p I D u k u k u k u k K e k e k K e k K e k e k e k =-+∆⎧⎨∆=--++--+-⎩采用三层BP 神经网络结构。
输入层神经元个数可根据被控系统的复杂程度选取。
可从如下参数中选取,系统输入in r ,系统输出out y ,系统误差e ,和误差变量e ∆,可在系统误差e 的基础之上再加上其他参数输入,使BP 神经网络能够适应更为复杂的系统的PID 参数整定。
隐层神经元的个数视被控系统的复杂程度进行调整,一本系统复杂时,就需选用更多的隐层神经元。
输出层的神经元个数为3个,输出分别为Kp,Ki 和Kd 。
隐层神经元函数一般选取正负对称的sigmoid 函数:(2)()x xsx xe e fx e e ---=+由于Kp,Ki 和Kd 必须为正,则输出层神经元函数的输出值一般可以选取正的sigmoid 函数:(3)1()1s xf x e -=+系统性能指标取:1()(()())2in out E k r k y k =-采用梯度下降法对BP 神经网络的参数进行调整:设输入层的个数为N ,输出向量为(1)O ,隐层个数为H ,输入阵为(2)W ,为H ×N 维向量,输出层的个数为3,输入阵设为(3)W 。
令(1)(1)(1)(1)12[,,,]TN OO O O =设隐层的输入向量为(2)(1)hi W O =,hi 为列向量,第j 个隐层神经元的输入:(2)(1)1Nj ji ii hi w O ==∑,(1,2,j H =)第j 个神经元的输出为(2)()j s j ho f hi =; 输出层的输入(3)(3)I W ho =,输出为(3)(3)(3)()[,,]T s p I D Of I K K K ==按照梯度下降法修正网络权系数,按E(k)的负方向调整系统,并且加一个是搜索加快的收敛全局极小的惯性量:(3)(3)(3)()()(1)oj oj ojE k W k W k W ηα∂∆=-+∆-∂,其中η为学习速率,α为平滑因子; (3)(3)(3)(3)(3)(3)()()()()()()()()()()()oo oj o o oj O k I k E k E k y k u k W y k u k O k I k W k ∂∂∂∂∂∂∆=∂∂∂∆∂∂∂(1,2,3o =,1,2,j H =)其中(3)oj W 为(3)W 的第o 行和第j 列。
基于BP神经网络PID整定原理和算法步骤_精品

基于BP神经网络PID整定原理和算法步骤_精品1.收集实验数据:首先需要收集系统的输入和输出数据,包括输入变量(如温度、压力等)和输出变量(如阀门开度、电机转速等)。
同时,需要记录系统的环境条件,如温度、湿度等。
2.数据预处理:对收集到的数据进行预处理,包括数据清洗、去除异常值等。
确保数据质量的同时,也要注意保持数据的连续性和完整性。
3.构建神经网络:使用BP神经网络构建PID整定模型。
BP神经网络是一种具有前馈和反馈连接的多层感知器,可以用于解决非线性问题。
根据PID控制器的输入和输出关系,设计网络的输入层、隐含层和输出层。
4. 网络训练:使用收集到的实验数据对神经网络进行训练。
训练的目标是使网络的输出尽可能接近实际输出,从而建立输入和输出之间的映射关系。
可以使用误差反向传播算法(Backpropagation)来调整网络的权重和阈值。
5.网络评估:训练完成后,使用预留的一部分数据对网络进行评估。
通过比较网络的输出和实际输出,可以评估网络的准确性和稳定性。
如果评估结果不满意,可以进行网络调整和再训练。
6. PID参数计算:根据已经训练好的神经网络,可以使用PID整定算法计算PID参数值。
常用的PID整定算法包括Ziegler-Nichols方法、Chien-Hrones-Reswick方法等。
根据系统的响应特性和性能指标,选择合适的算法进行参数计算。
7.参数调整和优化:根据实际应用需求,对计算得到的PID参数进行调整和优化。
可以通过仿真和实验验证的方式,不断调整参数,直到满足系统的性能要求。
8.实际应用:将优化后的PID参数应用到实际控制系统中。
根据系统的特点和要求,可以进一步进行参数调整和优化。
同时,需要不断监测和评估系统的性能,并及时调整和优化PID参数。
综上所述,基于BP神经网络的PID整定原理和算法步骤主要包括数据收集、数据预处理、神经网络构建、网络训练、网络评估、PID参数计算、参数调整和优化以及实际应用等步骤。
改进BP神经网络PID多变量解耦控制器的设计

改进BP神经网络PID多变量解耦控制器的设计
李爽;孙盛骐
【期刊名称】《仪器仪表用户》
【年(卷),期】2012(019)005
【摘要】针对多变量系统间的耦合问题,设计了改进的BP神经网络与PID控制器相结合的多变量解耦控制器.在将BP神经网络附加动量项的基础上,还将激活函数进行了改进.利用神经网络的自学习能力,在线调整PID控制器的三个参数,实现了多变量系统的解耦控制.用Matlab软件对一个耦合系统模型进行仿真,结果表明,改进后神经网络PID控制器优于传统神经网络PID控制器,震荡小,系统响应速度快,可以得到满意的解耦效果.
【总页数】3页(P63-65)
【作者】李爽;孙盛骐
【作者单位】沈阳大学信息工程学院,沈阳110044;沈阳大学信息工程学院,沈阳110044
【正文语种】中文
【中图分类】TP391.9
【相关文献】
1.基于忆阻的自适应单神经元多变量解耦PID控制器 [J], 方晓燕;王丽丹;段书凯
2.基于忆阻的自适应单神经元多变量解耦PID控制器 [J], 方晓燕;王丽丹;段书凯;
3.关于多变量PID自适应解耦控制器的设计 [J], 刘伟; 冯向军
4.多变量自校正解耦PID控制器 [J], 余文;柴天佑
5.一种多变量自校正前馈解耦PID控制器及其应用 [J], 张贵军;柴天佑;余文
因版权原因,仅展示原文概要,查看原文内容请购买。
bp神经网络在pid控制器参数整定中的应用

bp神经网络在pid控制器参数整定中的应用
BP神经网络在控制器参数整定中的应用越来越广泛。
BP神经网
络是一种人工神经网络,可以模拟人类神经系统的信息处理功能,用
于复杂系统建模和控制,在PID控制器参数整定中得到了广泛的应用。
一般来说,PID控制器由三部分组成:比例、积分和微分。
根据常
规PID控制调节策略,需要经过多次实验调整参数,以获得最佳控制
效果。
然而,传统的参数调整方法难以满足快速改变的系统和复杂的
控制系统的变化需求,因此,BP神经网络的出现为PID控制参数整定
提供了一种新的思路和手段。
BP神经网络可以用于自动调整PID参数,具有更高的效率和更好
的精度。
通过将系统模型形式化为BP神经网络,可实现基于模型的
PID调节策略,使得调节参数直接从系统模型获得,从而极大地减少参
数的调节时间。
此外,BP神经网络还可以用于故障诊断,如特征提取、特征识别和故障诊断。
可以说,BP神经网络的出现,大大提高了控制
器参数的整定效率和精度。
因此,BP神经网络已成为PID控制器参数整定的重要工具。
它不
仅可以大大提高控制参数调整效率,而且还可以更准确地预测控制系
统的行为。
同时,BP神经网络也可以用于诊断和保护,以确保系统更
加稳定和可靠。
因此,BP神经网络在PID控制器参数整定中应用广泛。
基于神经网络的PID控制

基于神经网络的PID控制课程名称:智能控制任课教师:学生姓名:学号:年月日摘要:本文基于BP神经网络的PID控制方法设计控制器,通过BP神经网络与PID的控制相结合的神经网络控制基本原理和设计来自适应的功能调节PID的的三个参数,并根据被控对象的近似数学模型来输出输入与输出并分析BP神经网络学习速率η,隐层节点数的选择原则及PID参数对控制效果的影响。
计算机的仿真结果表示,基于BP神经网络的PID控制较常规的PID控制具有更好的自适应性,能取得良好的的控制结果。
关键字:BP算法神经网络 PID控制Abstract:In this paper, based on BP neural network PID control method designed controller, through the BP neural network PID control with a combination of neural network control basic principles and design features adaptively adjusting the PID of the three parameters, and based on the controlled object approximate mathematical model to analyze the output and the input and output BP n eural network learning rate η, hidden layer nodes and PID parameter selection principle effect of the control . Computer simulation results indicated that based on BP neural network PID control compared with conventional PID control has better adaptability , can achieve good control results . Keyword:BP algorithms neural networks PID control1引言PID控制是最早发展起来的应用经典控制理论的控制策略之一,由于算法简单,鲁棒性好和可靠性高,被广泛应用于工业过程并取得了良好的控制效果。
基于BP神经网络的PID优化控制研究
基于BP神经网络的PID优化控制研究【摘要】PID控制要取得较好的控制效果,就必须通过调整好比例、积分和微分三种控制的关系。
本文提出一种基于BP神经网络的PID优化控制的方法,充分利用BP神经网络自学习、自适应、强大的泛化能力,弥补PID控制方法学习,适应能力的不足。
将此方法应用于控制直流电机调速系统,仿真结果表明,此方法能提高系统的控制精度,具有良好的鲁棒性。
【关键词】BP神经网络;PID控制;直流电机调速系统1.引言PID控制以其算法简单,鲁棒性好和可靠性高等优点,广泛地应用于工业生产当中,成为衡量各行各业现代化水平的一个重要标志。
随着科学技术的发展,生产工艺的日益复杂化,生产系统具有非线性,时变不确定性,在实际生产中,常规PID控制器参数往往整定不良、性能欠佳,对运行工况的适应性很差[1]。
BP神经网络具有良好的自学习、自适应能力和鲁棒性,可以用来处理高维、非线性、强耦合和不确定性的复杂控制系统。
本文结合BP神经网络的优点和传统PID控制的优势,对PID控制器进行优化,使其具有很强的自适应性和鲁棒性。
通过对直流电机调速系统仿真,结果表明,这种方法是有效的。
2.PID控制原理PID是工业生产中最常用的一种控制方式,PID调节器是一种线性调节器,它将给定值r(t)与实际输出值c(t)的偏差的比例(P)、积分(I)、微(D)通过线性组合构成控制量,对控制对象进行控制。
传统的PID控制系统原理框图如图2.1所示,系统主要由PID控制器和被控对象组成。
它根据给定值rin(t)与实际输出值yout(t)构成控制偏差额e(t):图2.1为PID控制系统原理框图。
3.基于BP神经网络的PID整定原理PID控制要取得好的控制效果,就必须通过调整好比例、积分和微分三种控制作用在形成控制量中相互配合又相互制约的关系,这种关系不一定是简单的“线性组合”,而是从变化无穷的非线性组合中找出最佳的关系[2]。
BP神经网络具有良好的自学习、自适应能力和鲁棒性,将PID和BP神经网络结合起来,建立参数自学习的PID控制器。
BP神经网络算法的改进及其在PID控制中的应用研究共3篇
BP神经网络算法的改进及其在PID控制中的应用研究共3篇BP神经网络算法的改进及其在PID控制中的应用研究1随着工业自动化的不断推进和智能化的不断发展,控制理论和算法变得越来越重要。
PID控制算法已成为现代控制中最常用的算法之一。
然而,传统的PID控制算法在某些情况下会出现一些问题,这些问题需要新的解决方案。
因此,本文将探讨BP神经网络算法的改进及其在PID控制中的应用研究。
BP神经网络是一种前向反馈神经网络,它通过反复迭代调整参数来学习训练数据,从而实现分类和回归等任务。
BP神经网络作为一种非线性动态系统,具有自适应性、非线性和强泛化能力等特点。
在控制系统中,BP神经网络可以用于模型预测、模型识别和模型控制等方面。
在控制系统中,PID控制是一种常规的线性控制技术。
然而,传统的PID控制算法存在一些问题,如难以解决非线性系统、难以控制多变量系统等。
为了解决这些问题,人们开始探索将BP神经网络用于控制系统。
BP神经网络可以通过学习训练数据来逼近未知非线性系统,从而实现对系统的控制。
在使用BP神经网络控制系统时,需要进行参数调整来保证网络的准确性和控制效果。
对于传统的BP神经网络,训练过程需要耗费大量的计算时间和计算资源。
因此,人们提出了一些改进的BP神经网络算法,如逆传播算法、快速BP算法和LM算法等。
逆传播算法是一种基于梯度下降的BP神经网络算法,该算法通过不断地调整权重和偏置来实现网络的训练。
快速BP算法是一种改进的逆传播算法,它增加了一些优化步骤,使训练过程更快速和高效。
LM算法是一种基于牛顿法的BP神经网络算法,在训练过程中可以自动调整学习率,从而提高训练的速度和准确性。
在控制系统中,BP神经网络可以用于模型预测、模型识别和模型控制等。
例如,在模型控制方面,可以使用BP神经网络来进行预测,并根据预测结果来调整控制参数,从而实现对系统的更加有效的控制。
此外,在模型识别方面,人们也可以使用BP神经网络精确地识别复杂的非线性系统,实现对系统的更加准确的控制。
基于BP神经网络的PID控制系统设计
基于BP神经网络的PID控制系统设计摘要本文主要研究一个基于神经网络的自适应PID控制系统的设计方法,利用BP神经网络对被控对象进行在线辨识和控制。
基于BP神经网络学习算法设计出两个神经网络模型:一个利用神经网络(NNM)对非线性映射的逼近能力,对被控对象进行辨识,另一个构成具有PID结构的控制器(NNC)。
通过神经网络NNM的在线学习和修正,产生对被控对象输出的预测作用,然后由网络NNC实施控制作用,从而实现对辨识对象的PID控制。
在利用神经网络对系统进行辨识时,选用白噪声信号作为系统的输入信号,以提高系统的辨识精度;另外,为了得到神经网络控制器的初始化权值,本文在自整定过程中采用常规PID控制器整定方法之一的稳定边界法。
在设计过程中运用MATLAB语言工具箱进行编程,并通过SIMULINK动态仿真工具对一阶非线性对象进行了仿真。
仿真结果表明了利用神经网络对系统进行辨识的有效性,并用经辨识所得到的输出值取代系统的实际输出值,利用神经网络NNC对系统进行控制,获得了满意的控制效果。
关键词:神经网络,BP学习算法,自适应,参数优化,辨识1 综述PID调节器从问世至今已历经了半个多世纪,在这几十年中,人们为它的发展和推广做出了巨大的努力,使之成为工业过程控制中主要的和可靠的技术工具。
近几十年来,现代控制理论迅速发展,出现了许多先进的控制算法,但到目前为止,即使在微处理技术迅速发展的今天,过程控制中大部分控制规律都未能离开PID,这充分说明PID控制仍具有很强的生命力。
过程工业控制中实际应用最多的仍是常规的PID控制算法,这是因为PID控制具有结构简单、容易实现、控制效果好和鲁棒性强等特点,且PID算法原理简明,参数物理意义明确,理论分析体系完整,为广大控制工程师所熟悉。
但在生产现场往往由于参数整定不好而使PID控制器控制效果欠佳,整定的好坏不但会影响到控制质量,而且还会影响到控制器的性能。
PID控制中一个至关重要的问题,就是控制器三参数(比例系数、积分时间、微分时间)的整定。
基于BP神经网络的PID控制器设计
基于BP神经⽹络的PID控制器设计基于BP神经⽹络的PID控制器设计班级:21班学号:2014561姓名:常临妍摘要常规PID控制技术是⼯业控制中⼀种常⽤的控制⽅法。
其结构简单、容易实现、控制效果良好,且能对相当⼀些⼯业对象或过程进⾏有效的控制,已得到⼴泛应⽤。
但其局限性在于:当控制对象不同,或被控对象具有复杂的⾮线性特性时,难以建⽴精确的数学模型。
控制器的参数难以⾃动调整以适应外界环境的变化。
且由于对象和环境的不确定性,往往难以达到满意的控制效果。
为了使控制器具有较好的⾃适应性,实现控制器参数的⾃动调整,可以借助BP神经⽹络控制的⽅法。
BP神经⽹络已被证明具有逼近任意连续有界⾮线性函数的能⼒,给⾮线性控制带来了新的思路。
利⽤⼈⼯神经⽹络的⾃适应能⼒,并结合传统的PID控制理论,构造神经⽹络PID控制器,实现控制器参数的⾃动调整。
本⽂研究了基于BP神经⽹络的PID控制器设计,利⽤BP神经⽹络的⾃适应能⼒进⾏在线参数整定。
其实现具有⾃适应性等特点,⽹络的收敛速度快,能够对⾮线性对象有很好的控制,系统的跟踪性能好。
其参数设定⽆需知道被控对象的具体参数及其数学模型,对不同的对象具有适应性。
关键词:PID控制BP神经⽹络控制器设计⼀.绪论1.1神经元⽹络PID的发展历程1934年,美国⼼理学家W.McCulloch和数学家W.Pitts⽤数学模型对神经系统中的神经元进⾏理论建模,建⽴了MP神经元模型。
MP神经元模型⾸次⽤简单的数学模型模仿出⽣物神经元活动功能,并揭⽰了通过神经元的相互连接和简单的数学计算,可以进⾏相当复杂的逻辑运算这⼀事实。
1957年,美国计算机学家F.Rosenblatt提出了著名的感知器模型。
它是⼀个具有连续可调权值⽮量的MP神经⽹络模型,经过训练可达到对⼀定输⼊⽮量模型进⾏识别的⽬的。
1959年,美国⼯程师B.Widrow和M.Hoff提出了⾃适应线性元件。
它与感知器的主要不同之处在于其神经元有⼀个线性激活函数,这允许输出可以是任意值,⽽不仅仅只是像感知器中那样只能取0或1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仪器仪表标准化与计量2005・6
7
薛昊洋 刘红军(华北电力大学自动化系,保定市 071003)Xue Haoyang Liu Hongjun(Automatic Department of North China Electric Power University, Baoding 071003)
基于BP神经网络的多变量PID解耦控制Multivariate Decoupling Control Based on Back Propagation Neural Network
Abstract: Intelligent PID control strategy, which is based on neural network, is according to classical PID control,realized through neural network parameter setting which has self study function for multivariate decoupling control.The structure and the algorithm were given and the real-time simulation results of double variable and strong-coupled time-varying system were shown in the paper. It proved that PID control based on neural network haspreferably self study and self adapting decoupling control ability through simulation. The system, which inosculatesthe decoupler and controler, is easy to implement and applicable for multivariate decoupling control. It makes thedecoupled system have better dynamic behavior and static characteristic. Especially, it makes parameters astringefast when determing initial value of network according to BP control law.Key words: PID Control Neural Network Multivariable System Decoupling Control
【摘 要】基于神经网络实现智能PID控制的策略,它以经典的PID控制为基础,通过神经网络参数整定
实现,进而进行自学,用于多变量系统的解耦控制。本文给出了网络的结构和算法,对一组二变量强耦合时变系统进行了仿真。通过计算机仿真证明了基于神经网络的PID控制器网络结构简单规范具有良好的自学习和自适应解耦控制能力。系统易于实现,融解耦器与控制器于一体,适用于非线性多变量系统的解耦控制。能够使解耦后的系统具有良好的动态和静态性能,特别是依据BP控制规律来确定网络连接权的初值,还具有参数快速收敛的优点。【关键词】PID控制 神经网络 多变量系统 解耦控制
引言多变量控制系统(MIMO)属于高级而又复杂的过程控制系统,从广度和深度上都超过了单变量控制系统。而工业过程控制则要求系统能够安全稳定地运行;有较好的调节性能;能以较小的误差跟踪设定值的变化,或使误差为零。但是,由于系统有多个输入和多个输出,内部结构比较复杂,往往存在有一定程度的耦合作用,因此经常需要对控制系统进行解耦。多变量系统的解耦控制大体可分为三大类:传统解耦控制、自适应解耦控制以及智能解耦控制。传统的多变量系统的解耦控制是采用微分几何的方法,利用状态反馈,将多变量系统化为从外部看完全解耦的线性系统。这种方法要求被控对象必须用精确的数学模型来描述,因此难于实现自适应控制。本文则建立了一种新型的基于BP神经网络的参数自整定多输人多输出神经网络PID控制器,用来对有强耦台的一类多输人多输出系统进行解耦控制。它根据设定的控制规律,通过网络在线调整PID控制器的比例、积分和微分参数,从而利用经典的PID控制算法得到相应各变量的控制量参与控制,并能在该过程中实现解耦控制,而不用给定样本信号进行离线的学习。由于神经网络还可以在指定的紧集上以任意精度逼近解析非线性函数,因此神经网络成为了实现非线性系统自适应控制的有力的工具。1 基于神经网络参数自学习PID解耦控制原理基于神经网络的PID控制属于多层前向神经元网络的范畴。传统的PID调节器具有结构简单、调整方便和参数整定与工程指标联系密切等特点,而神经网络又具有自学习和自适应的能力。若将两者结合,则可以在一定程度解决传统PID调节器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。PID控制要取得好的控制效果,就必须通过调整好比例、积分和微分三种控制作用在形成控制量中相互配合又相互制约的关系,这种关系不一定是简单的线性组合,从变化无穷的非线性组合中可以找出最佳的关系。神经网络所具有的任意非线性表示能力,可以通过对系统性能的学习来实现具有最佳组合的PID控制。而通过PID控制,可实现对多变量系统的解耦控制,控制器由两部分组成[1]:①经典的PID控制器:直接对被控对象过程闭环
收稿日期:2005-06-20
作者简介:薛昊洋(1979-),男,河北保定人,华北电力大学硕士生,研究方向为现代控制理论及应用。
论述与研究仪器仪表标准化与计量2005・6
8
Review and Research控制,并且三个参数kp、ki、kd为再线整定式;②神经网络NN:根据系统的运行状态,调节PID控制器参数,以期达到某种性能指标的最优化。即使输出层神经元的输出状态对应于PID控制器的三个可调参数kp、ki、kd,通过神经网络的自身学习、加权系统调整,从而使其稳定状态对应于某种最优控制律下的PID控制器参数[2]。图1给出了二变量PID解耦控制系统框图:图1 二变量PID解耦控制系统结构示意图该系统由两个增量式数字PID控制器构成,其解耦控制算法为:u1(k)=u1(k-1)+kp1(e1(k)-e1(k-1))+kd1(e1(k)- 2e1(k-1)+e1(k-2))+ki1e1(k)u2(k)=u2(k-1)+kp2(e2(k)-e2(k-1))+kd2(e2(k)- 2e2(k-1)+e2(k-2))+ki2e1(k) (1)其中e1(k)=r1(k)-y1(k) e2(k)=r2(k)-y2(k) (2)kp、ki、kd分别为比例、积分和微分系数。2 基于BP神经网络的PID控制的结构形式采用BP网络可以建立参数kp、ki、kd自学习的PID控制器。基于BP网络的PID控制系统结构如图2所示:图2 BP神经网络结构图神经网络采用一个由3层的BP神经元网络构成的子网络[3],其结构见图2。它有4个输入节点(x1、x2、x3和x4);5个隐含节点,3个输出节点(kp、ki、kd)。输入节点与隐含节点的网络权值为wij,隐含节点与输出节点网络权值为wli。3 基于BP神经网络的前向算法[4]设PID神经网络有M个输入,3个输出(kp、ki、kd),上标(1)(2)(3)分别代表输入层、隐含层和输出层,该PID神经网络在任意采样时刻k的前向计算公式如下所述:3.1 网络输入层网络输入层的输入为Oj(1)=x(j),j=1,2…M (3)3.2 网络隐含层网络隐含层的输入、输出算法如式(4)、(5)所示:
Oi(2)=f(neti(2)(k)),i=1,2…Q (5)式(4)、(5)中wij(2)-隐含层加权系数,隐含层神经元活化函数取正负对称的Sigmoid函数。按照梯度下降法修正网络的权系数,即按E(k)对加权系数的负梯度方向搜索调整,并附加一使搜索快速收敛全局极小的惯性项,隐含层的加权系数算法如式(6)、(7)所示:Vwij(2)(k)=αVwij(2)(k-1)+ηδi(2)Oj(1)(k) (6)
3.3 网络输出层网络隐含层的输入、输出算法如式(8)、(9)所示:
Ol(3)=g(netl3(k)) (9)式中wli(3)-输出层加权系数,输出层神经元活化函数取非负的Sigmoid函数。输出层加权系数的学习算法如式(10)、(11)和(12)所示:
(11)4 基于PID神经网络的多变量解耦控制系统的仿真实例为了检验PID神经网络的多变量解耦控制系统的性能,以下为一个仿真实例。设一个非线性强耦合对象由(13)、(14)方程描述[5]:
(13)(14)设采样时间为1s,给定输入为单位阶跃输入,即
采用基于BP神经网络整定的PID解耦控制,网络结构取4-5-3,
(4)(7)(8)
(12)
(15)
(10)仪器仪表标准化与计量2005・6
9
图3 分量一的PID参数响应曲线图4 分量二的PID参数响应曲线图5 控制器的输入输出响应曲线
网络输入为:I={u(k-1),y(k),error(k),1},学习速率: η=0.5,惯性系数:α=0.05,权值取(+0.5 -0.5)之间的随机数。由仿真结果可知,基于BP神经网络的PID多变量控制器可以对这一类强耦合的非线性多变量对象实现有效的解耦控制,在控制过程中神经元网络同时要进行PID控制器比例、积分和微分系数的在线整定,即实现边控制边学习的特点。图3、图4分别是子网络PID参数在线自调整过程曲线。其控制过程输出曲线见图5。输出量y1的稳态误差小于0.2%,而y2的稳态误差小于0.1%.系统的动态性能很好,网络学习的收敛速度很快。5 结论在仿真过程中,连接权系数初值的选择对系统的调节过程有很大影响。另外,惯性系数和学习速率的选取对保证系统的稳定性有重要的作用。仿真结果表明,基于BP神经网络的PID多变量控制器是一种内含动、静特性的多层前向神经元网络,可以在系统对象参数未知的情况下,通过自身的训练和学习,实现多变量系统的解耦控制,能够基本消除变量之间的耦合作用。而且系统的响应速度快、超调小甚至无超调。与普通PID解耦控制相比,基于BP神经网络整定的PID解耦控制又具有响应速度快、自适应能力强、抗干扰能力强等优点。
参考文献[1] 刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003[2] 柴天佑.多变量自适应解耦控制及应用[M]. 北京:科学出版社,2001[3] Akhyar,S., Omatu,S.. Self-tuning PID control by neural-networks[J]. IEEE Transactions on PowerSystems, Vol 3, 25~29 Oct. 1993:2749~2752[4] 闻新,周露,李翔,张宝伟.MATLAB神经网络仿真与应用[M].北京:科学出版社,2003[5] 陶永华,尹怡欣,葛芦生.新型PID控制及其应用[M].北京:机械工业出版社,1998□
