窄带随机过程1
第6章 窄带随机过程

Z (t ) B(t ) cos[ (t )], 其中 B( t ) 0, ( t ) t ( t ) 。 0
上 海 大 学 通 信 学 院
表达式1: Z ( t ) B( t ) cos[ 0 t ( t )],
B( t ) 0, ( t ) 0 t ( t ) 表达式2: Z ( t ) X ( t ) cos 0 t Y ( t ) sin 0 t
上 海 大 学 通 信 学 院
二、解析信号与希尔伯特变换*
1. 解析信号的引入
S ( f ) s(t )e j 2 f t dt R( f ) jI ( f ) 时域实信号S(t)
S ( f )满足共轭对称性,即,
R( f ) R( f ), 偶函数 S ( f ) S ( f ) I ( f ) I ( f ), 奇函数
上 海 大 学 通 信 学 院
2.解析信号的构造
对给定的时域实信号s(t),设构造的时域复信号为
ˆ(t ) z( t ) s( t ) js
ˆ(t ) 为一由s(t)构造的信号,其构造方法可为, 其中,s
s( t )
即,
h( t )
ˆ s( t )
z( t ) s( t ) js( t ) h( t )
ˆ ( t ) 的互相关函数满足: X
T
T
R X ( t , t )dt
性质5. 平稳随机过程X(t)和其对应的Hilbert变换
ˆ ( ) ˆ RX X ( ) R ( ), R ( ) R ˆ ˆ X X XX
上 海 大 学 通 信 学 院
第6章 窄带随机过程
xˆ
2
(
t
)dt
x
2
(t
)dt
lim 1 T xˆ 2 (t)dt lim 1 T x 2 (t)dt
T 2T T
T 2T T
上 海 大 学 通 信 学 院
上 海 大 学 通 信 学 院
3
2016/10/28
上
海 三、窄带随机过程的性质
大
学
通 问题:若已知Z(t)的功率谱密度 GZ ( ) 或统计特性RZ ( ) 信 (讨论平稳窄带过程),则其B(t)和 (t ) 或X(t) 和Y (t)
性质4.
RX
(
)
1
0 GZ ()cos[( 0 ) ]d
性质5. RX ( ) RY ( )
性质6.
RXY
(
)
1
0 GZ ()sin[( 0 ) ]d
性质7. RY X ( ) RXY ( ), RXY ( ) RXY ( )
上
海
大 学
性质8. RXY (0) E[X(t)Y(t)] 0, RY X (0) 0
(
f
),奇函数
由此可知:时域实信号正、负频域的频谱可互求。
1
2016/10/28
上
海 大
从有效利用信号的角度出发,实信号负频域部分是冗余
学 的,所以只要保留正频域的频谱,记为 S ( f ),即可。
通
信 学
若只取正频域频谱
S ( f ),则
S
(
f
)
S (
f
),即S ( f ) 不满
院 足共轭对称性,且 S ( f ) 时域复信号。
s( t )
h( t )
随机信号分析_第五章_窄带随机过程

定义复指数函数: ~s (t) ae j (t) ae j e j0t a~e j0t 式中 a~ ae j ,称为复包络。 可以看出s(t)是~s (t) 的实部,即:
s(t) Re[~s (t)]
某些情况下,用复指数形式来分析 问题更加简便,可以简化信号和滤波器 的分析。
复信号~s (t) 的频谱为:
1. s(t) Re[~s (t)]
2.
X~ (
)
2 0
X
(
)
0 0
式中X~ ( )为~s (t)的频谱。
可以证明:满足上面要求的 ~s (t) 是 存在的,称为解析信号。把它用解析表 达式表示为:~s (t) s(t) jsˆ(t)
可以推导出: sˆ(t)
1
s( ) d
t
上式称为希尔伯特(Hilbert)变换,记做
0
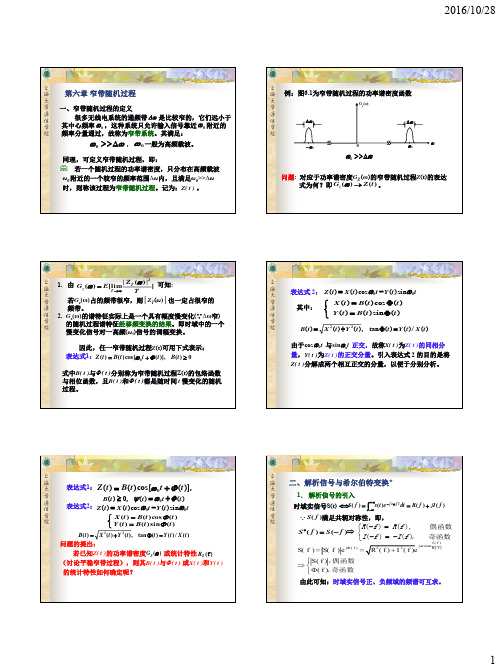
ω ω0-ωc ω0 ω0+ωc
|X~H(ω)|
0
ω0-ωc ω0 ω0+ωc
ω
2. 复指数表示
设s(t)为窄带信号,其频谱为X(ω) 。 定义窄带信号s(t)的复指数函数 ~se (t) 为:
~se (t) A(t)e j[0t (t)] A~(t)e j0t 其中A~(t)=A(t)e j (t) sc (t) jss (t)
用复数表示为:
s(t)=acosφ(t)=a[ejφ(t)+ e-jφ(t)]/2
因为 e j0t ( 0 )
所以s(t)的频谱为:
X(ω)= a[ejθδ(ω-ω0)+e-jθδ(ω+ω0)]/2 |X(ω)|= a[δ(ω-ω0)+δ(ω+ω0)]/2 说明正弦型信号包含正负两种频率成分, 其频谱为对称的两根单一谱线。
第5章-窄带随机过程

第五章 窄带随机过程5.1 窄带随机过程的概念1. 通信工程中的信号频率在通信工程中,如雷达、广播、电视等信号,在传输中信号有相对固定的信号频率。
对于有相对固定频率的信号,其数学表达方法的研究是非常重要的。
2. 窄带随机过程(1) 带通随机过程的定义若随机过程)(t X 的谱密度满足:⎩⎨⎧∆<-=其它0)()(0ωωωωωS S X 则称)(t X 为带通过程。
带通过程的谱密度的图解如下图。
(2) 窄通随机过程的定义若)(t X 为带通过程,且0ωω<<∆,即中心频率过大于谱宽,则称)(t X 为窄通随机过程。
3. 窄带随机过程的解析表达方法之一:莱斯表示法(1)窄带随机过程的莱斯表示定理:任何一个实窄带随机过程)(t X 都可表示为下式:)sin()()cos()()(00t t b t t a t X ωω-=证明:略。
注:证明过程要用到一种重要的数学变换――希尔伯特变换,此变换需掌握。
(2) )(t a 、)(t b 的性质 ①)(t a 、)(t b 都是实随机过程。
②0))(())((==t b E t a E . 。
③)(t a 与)(t b 各自广义平稳,联合平稳,且:)()(ττb a R R =。
④))(())(())((222t X E t b E t a E ==,由此可得方差22b a σσ=。
⑤0)0(=ab R ,这说明)(t a 与)(t b 在同一时刻正交。
⑥)()(ωωb a S S =。
4. 窄带随机过程的解析表达方法之二:准正弦振荡表示法定理:实窄带随机过程)(t X 都可表示为下式:))(cos()()(0t t t A t X Φ+=ω证明:由莱斯表示法有:)()()(22t b t a t A +=, )()()(t a t b arctgt =Φ )(t A 与)(t Φ都是慢变化的随机过程。
慢变化是指)(t A 与)(t Φ随时间变化比)cos(0t ω随时间的变化要缓慢得多。
六.窄带随机过程

(2)
ˆ x(t ) 的希尔伯特变换为 x(t )
ˆ H [ x(t )] x(t )
两次希尔伯特变换相当于连续两次 900 相移,结果 正好是 1800反相
9 2013-7-21
1.2 希尔伯特变换性质(3)
(3)
y(t ) v(t ) * x(t ) 的希尔伯特变换为
ˆ ˆ ˆ y (t ) v (t ) * x (t ) v (t ) * x (t )
1 x (t ) d
反变换
ˆ x( ) ˆ x(t ) H [ x(t )] d t ˆ 1 x(t ) d
1
1
ˆ 1 x(t ) d
5
2013-7-21
CZ1Z2 E (Z1 mZ1 )* (Z2 mZ2 )
15 2013-7-21
1.3 复随机过程
若X与Y分别是实随机变量,定义
Z (t ) X (t ) jY (t )
为复随机变量 均值: 方差:
mZ (t ) mX (t ) jmY (t )
DZ (t ) DX (t ) DY (t )
H ( )
一个典型的确定性窄带信号可表示为 窄带系统
白噪声
X (t )
Y (t )
x 系统示意图 或宽带噪声 ( t ) a ( t ) cos[ 0 t ( t )]
x(t ) y(t ) a(t ) ——幅度调制或包络调制信号
窄带噪声
0
窄带系统传递函数
(t ) ——相位调制信号
1.1 希尔伯特变换
窄带随机过程的两种表达式

窄带随机过程的两种表达式
随机过程是有关概率的一个抽象概念,它指的是一系列随机变化的事件序列,可以通过某种数学形式来描述。
窄带随机过程是指在一定的时间和频率内的随机过程,它是不断变换的快速信号序列,可以被压缩表示为一维或二维的图像。
窄带随机过程的表达式可以主要分为两类:
一、谱密度函数表示法
谱密度函数可以定义为:S(f),是指窄带随机过程中,每一种频率f处的功率谱密度,即根据频率f得到每一次过程的变化情况,它可以用来预测窄带随机过程所属的分布,如正态分布、均方差和偏差等。
举例来说,以正态分布为例,谱密度函数S(f)的表达式可以表示为:S(f) = σ^2 / (2πf^2)
其中,σ代表窄带随机过程的均方差,f为频率。
二、功率谱密度函数表示法
功率谱密度函数可以定义为:P(f),是指窄带随机过程中,随机变量的模方差的函数,它可以用来描述窄带随机过程的功率谱特性,估计窄带
随机信号的能量。
举例来说,功率谱密度函数P(f)的表达式可以表示为:
P(f) = 2πf^2σ^2
其中,σ代表函数的模方差,f为频率。
总的来说,窄带随机过程的两种表达式主要是谱密度函数表达法和功率谱密度函数表达法,它们各有特点,可以根据不同的窄带随机信号类型选择不同的表达方式,以达到最佳的谱性能效果。
窄带随机过程《通信原理》
窄带随机过程
1.窄带随机过程的定义
若随机过程ξ(t)的谱密度集中在中心频率f c附近相对窄的频带范围Δf内,即满足
条件,且f c远离零频率,则称该ξ(t)为窄带随机过程。
2.窄带随机过程的表示
①一般正弦表达式
窄带随机过程的样本的波形如同一个包络和相位随机缓变的正弦波。
即
式中,及分别为窄带随机过程ξ(t)的随机包络和随机相位;为正弦波的中心角频率。
②三角函数展开式
式中,ξc(t)是ξ(t)的同相分量;ξs(t)是ξ(t)的正交分量,则
3.窄带随机过程的统计特性
(1)ξc(t)和ξs(t)的统计特性
一个均值为零的窄带平稳高斯过程ξ(t):
①它的同相分量ξc(t)和正交分量ξs(t)同样是平稳高斯过程;
②ξc(t)和ξs(t)的均值为零,方差相同;
③在同一时刻上得到的ξc和ξs是互不相关的或统计独立的。
(2)的统计特性
一个均值为零、方差为的窄带平稳高斯过程ξ(t):
①包络aξ(t)的一维分布是瑞利分布,相位φξ(t)的一维分布是均匀分布;
②就一维分布而言,aξ(t)与φξ(t)是统计独立的,即。
13第八章窄带随机过程
步骤1 求a(t)和b(t)的联合分布
ˆ (t)= X(t)cosw 0t X(t)sinw 0t ˆ b (t)= -X(t)sinw 0t X(t)cosw 0t
所以: (at , bt ) 的二维概率密度函数为:
f ab (at , bt ) f a (at ) fb (bt ) at2 bt2 = exp{ } 2 2 2 2 At2 1 exp{ 2 } 2 2 2 1
1
X (t )
d X (t )] ˆ ( ) d R X
E[ X (t ) X (t )] 1 d
R ( )
ˆ R XX ˆ ( ) E[ X (t ) X (t )] E[ X (t )( 1
(t),b(t )为另外两个随机过程。
ˆ )sinw t (t)= X(t)cosw 0t X(t 0 ˆ b(t)= -X(t)sinw 0t X(t)cosw 0t 证明:
证明: 若X(t)为实随机过程,则其解析过程为: ˆ X(t)=X(t) jX(t) 用乘e jw0t 上式两端得: ˆ (t)][cos w t j sin w t ] X(t)e jw0t [X(t) jX 0 0 ˆ sin w t ] j[ X(t)sin w t X(t) ˆ [X(t)cos w t X(t) cos w t ]
证明:
例题:求S (t ) sin w0t , w0 >0的希尔伯特变换。 解:
H [sin w0t ] 1
1
第四章 窄带随机过程
(准正弦震荡)
包络 A t 与相位 t 均为慢变化(包含信息)
0
快变(载波)
展开成另一种表达形式:
X t A t cos 0 t t
A t cos t cos 0 t A t sin t sin 0 t
ˆ X t cos t X t sin t
0 0
ˆ RX cos 0 t cos 0 t RX sin 0 t sin 0 t
ˆ RX cos 0 RX sin 0 RAC ( )
解析信号(复信号的一种常见形式)
ˆ z t x t jx t
2 X ( ) Z X sgn X 0
0 0
正频率加倍,负频率清零。复信号没有负频率。
4.1.2 Hilbert变换的性质
2 X
2 AC
2 AS
3.功率谱密度
1 S AC S X 0 S X 0 2
1 sgn 0 S X 0 sgn 0 S X 0 2
用 X (t )及希尔伯特变换 X (t ) 表示 两个正交分量
ˆ AC t X t cos 0 t X t sin 0 t ˆ AS t X t sin 0 t X t cos 0 t
1.均值:零均值
5.互相关
ˆ RAC AS RX sin 0 RX cos 0
ˆ RAS AC RX sin 0 RX cos 0
窄带随机过程
正
交
滤
相频特性为:
()
/ 2
/
2
0 0
波 器
二、希尔伯特变换的性质
(1) H[xˆ(t)] x(t)
(2) H[cos(0t )] sin(0t )
H[sin(0t )] cos(0t )
(3) 如果a(t)是低频信号
H[a(t) cos0t] a(t)sin 0t H[a(t)sin 0t] a(t) cos0t
低频信号
是窄带确知信号,其解析信号为
x%(t) A(t)cos0t+(t) jA(t)sin0t+(t)
A(t)e j0t+ (t) A%(t)e j0t
其中 A%(t) A(t)e j (t) ,称为复包络。
一、确知信号的复信号表示
对解析信号取傅里叶变换,得
X%() X () jX ()
第五章 窄带随机过程
窄带随机过程
5.1 窄带随机过程 5.2 信号的复信号表示 5.3 窄带随机过程的统计特性 5.4 窄带正态随机过程包络和相位的分布
5.1 窄带随机过程
一、希尔伯特变换的定义
假定一实函数x(t),其希尔伯特变换为:
H[x(t)] xˆ(t) 1 x( ) d
t
其反变换为:
4、同相分量和正交分量的统计特性
RY ( ) cos0t cos0 (t ) RYˆY ( ) sin 0t cos0 (t )
RYYˆ ( ) cos0t sin 0 (t ) RYˆ ( ) sin 0t sin 0 (t ) 利用如下关系 RY ( ) RYˆ ( ) RYYˆ ( ) RˆY ( ) RYˆY ( )
具有系统函数为 jsgn 的网络是一个使相位滞 π 后 2 弧度的宽带相移全通网络。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4S X (ω ) ω ≥ 0 ~ S X (ω ) = ω<0 0
例题解析
设低频信号a(t)的频谱为:
A(ω ), A(ω ) = 0,
证明当ω 0〉 ω 2时, ∆
H [a (t ) cos ω0t ] = a (t ) sin ω0t H [a (t ) sin ω0t ] = −a(t ) cos ω0t
Ω
ω0 ± Ω
ω0 + Ω
(或ω0 − Ω)
ω0
希尔伯特变换应用及实现
相移法(难点在移相网络)
v1 =V0 sin Ωt sin ω0 t
V0 sin Ωt
V0 sin ω0 t
v3
V0 cos ω0 t
v 2 =V0 cos Ωt cos ω0 t
实信号、复信号、 实信号、复信号、解析信号
为何引入复信号 实信号与复信号的关系 如何得到,有何特点,与之间存在什么关系
| ω |< ∆ω / 2 其它
窄带随机过程
信息与通信工程学院 叶方
希尔伯特变换
定义
在区间 ( −∞ < t < ∞)内给定实值函数 x(t ) ,它的希 ˆ ) 尔伯特变换记作 x(t (或者记作 H [ x(t )]) 1 ∞ x (τ ) ˆ H [ x (t )] = x (t ) = ∫ dτ π −∞ t − τ
τ = t +τ '
90 o
ω
ω
− 90 o
ω
希尔伯特变换逆变换
ˆ x(t ) = H −1[ x(t )] ˆ 1 ∞ x(t − τ ) 1 dτ = =− ∫ ˆ = h(t ) ∗ x(t )
π
−∞
τ
π∫
∞
ˆ x(t + τ )
−∞
τ
dτ
1 h(t ) = − πt
希尔伯特变换应用及实现
滤波法(难点在于滤波器设计)
ˆ RXX (τ ) = RX (τ ) ˆ
解析过程性质
R XX ( 0 ) = 0 ˆ
ˆ ~ RX (τ ) = 2[ RX (τ ) + jRXX (τ )] = 2[ RX (τ ) + jR(τ )] ˆ
− jS X (ω ) ω ≥ 0 S XX (ω ) = ˆ + jS X (ω ) ω < 0
ˆ x(t ) = −
π∫
1
∞
x(t + τ )
−∞
τdτ =π∫1∞x(t − τ )
−∞
τ
dτ
希尔伯特变换性质
希尔伯特变换相当于一个正交滤波器。
1 ˆ x (t ) = x (t ) ∗ πt
H (ω )
x(t )
h(t ) =
1 πt
ˆ x(t )
H (ω ) = − j sgn(ω )
| H (ω ) | H (ω )
解析过程性质
ˆ 若X (t ) 为实平稳随机过程,则 X (t )也是实平稳 过程,且联合平稳 。 实函数与其希尔伯特变换的相关函数(功率谱) RXˆ (τ ) = RX (τ ) S Xˆ (ω ) = S X (ω ) 相同
ˆ RXX (τ ) = − RX (τ ) ˆ
RXX (τ ) = − RXX (τ ) ˆ ˆ RXX ( −τ ) = − RXX (τ ) ˆ ˆ
解析过程
定义
% 给定任实随机过程 X (t ) ,定义复随机过程X (t )为
% ˆ X (t ) = X (t ) + jX (t )
ˆ (t ) = H [ X (t )] = 1 X
π
∫
∞
−∞
X (τ ) dτ t −τ
~ 称 X (t ) 为实随机过程X (t ) 的复解析过程,简称
解析过程。
