实验二 信号处理的matlab仿真
实验二 二阶系统matlab仿真(dg)

利用simulink进行仿真的步骤:1.打开Matlab软件;2.在Command Window命令行>>后输入simulink并回车或点击窗口上部图标直接进入simulink界面;3.点击File-New-Modle就可以在新的界面上建立系统的仿真模型了;4.在左面的器件模型库中找到所需模型,用鼠标将器件模型拖到建立的界面上,然后用鼠标将它们用连线连起来,系统的仿真模型就建立起来了;5.点击界面上部的图标‘’进行仿真,双击示波器就可以看到仿真结果。
实验要用到的元件模型的图标及解释如下:阶跃信号:在simulink-source中可以找到,双击可以设定阶跃时间。
sum:在simulink-math operations中可以找到,双击可以改变器属性以实现信号相加还是相减;比例环节:在simulink-math operations中可以找到,双击可以改变器属性以改变比例系数;积分环节:在simulink-continues中可以找到;传函的一般数学模型表达形式:在simulink-continues中可以找到,双击可以对传递函数进行更改(通过设定系数)。
示波器:在simulink-sinks中可以找到。
实验二二阶系统的Matlab仿真一、实验目的1、研究二阶系统的特征参数―阻尼比ζ和无阻尼自然频率ωn对系统动态性能的影响。
2、利用simulink工具和MATLAB语句实现二阶系统的仿真。
3、熟悉MATLAB语句对二阶系统传函的表达形式以及阶跃响应的表达形式。
二、实验内容1、simulink仿真(标准二阶系统ωn=1,ζ=0.5)2、用Matlab语句实现二阶系统仿真(1)对于标准二阶系统,当ωn=4,改变ζ值对性能的影响-1<ζ<0(负阻尼)>> step(tf(4^2,[1,2*(-0.5)*4,4^2]))ζ<-1(负阻尼)>> step(tf(4^2,[1,2*(-1.5)*4,4^2]))ζ=0(零阻尼)>> step(tf(4^2,[1,2*0*4,4^2]))0<ζ<1(欠阻尼)>> figure>> step(tf(4^2,[1,2*0.1*4,4^2]))>>hold on>> step(tf(4^2,[1,2*0.2*4,4^2]))>> step(tf(4^2,[1,2*0.3*4,4^2]))>> step(tf(4^2,[1,2*0.4*4,4^2]))>> step(tf(4^2,[1,2*0.5*4,4^2]))>> step(tf(4^2,[1,2*0.6*4,4^2]))>> step(tf(4^2,[1,2*0.7*4,4^2]))>> step(tf(4^2,[1,2*0.8*4,4^2]))>> step(tf(4^2,[1,2*0.9*4,4^2]))ζ=1(临界阻尼)>> figure>> step(tf(4^2,[1,2*1*4,4^2]))ζ>1(过阻尼)>> hold on>> step(tf(4^2,[1,2*2.0*4,4^2]))>> step(tf(4^2,[1,2*4.0*4,4^2]))>> step(tf(4^2,[1,2*8.0*4,4^2]))(2)对于标准二阶系统,当ζ=0.5,改变ωn时的情况:>> figure>> step(tf(1^2,[1,2*0.5*1,1^2])) (ωn=1)>> hold on>> step(tf(2^2,[1,2*0.5*2,2^2])) (ωn=2)>> step(tf(4^2,[1,2*0.5*4,4^2])) (ωn=4)>> step(tf(8^2,[1,2*0.5*8,8^2])) (ωn=8)三、实验报告要求:1、记录由matlab仿真所得到的阶跃响应曲线。
实验2_连续时间信号的Matlab表示与计算
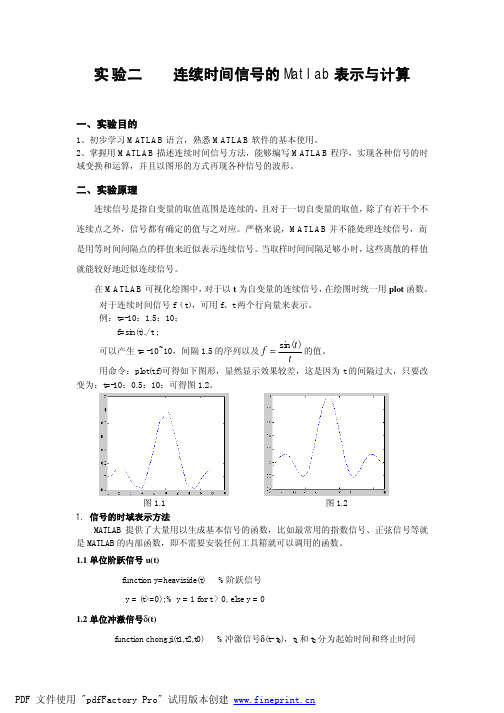
y = rectpuls(t, width)
用以产生一个幅值为 1、宽度为 width、相对于 t=0 点左右对称的矩形波信号。该函数的横 坐标范围由向量 t 决定,是以 t=0 为中心向左右各展开 width/2 的范围。width 的默认值为 1。
用命令:plot(t,f)可得如下图形,显然显示效果较差,这是因为 t 的间隔过大,只要改 变为:t=-10:0.5:10;可得图 1.2。
图 1.1
图 1.2
1. 信号的时域表示方法
MATLAB 提供了大量用以生成基本信号的函数,比如最常用的指数信号、正弦信号等就
是 MATLAB 的内部函数,即不需要安装任何工具箱就可以调用的函数。
1、初步学习 MATLAB 语言,熟悉 MATLAB 软件的基本使用。 2、掌握用 MATLAB 描述连续时间信号方法,能够编写 MATLAB 程序,实现各种信号的时 域变换和运算,并且以图形的方式再现各种信号的波形。
二、实验原理
连续信号是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干个不 连续点之外,信号都有确定的值与之对应。严格来说,MATLAB 并不能处理连续信号,而 是用等时间间隔点的样值来近似表示连续信号。当取样时间间隔足够小时,这些离散的样值 就能较好地近似连续信号。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
图 1-5 抽样函数
图 1-6 矩形波信号
周期性矩形波(方波)信号在 MATLAB 中用 square 函数来表示,其调用形式为:
y=square(t,DUTY)
信号与系统仿真作业

nGDOU-B—11—112广东海洋大学学生实验报告书(学生用表)课程名称课程号学院(系)信息学院专业班级学生姓名学号实验地点04002 实验日期实验一连时间信号的MATLAB表示和连续时间LTI系统的时域分析一、实验目的1.掌握MA TLAB产生常用连续时间信号的编程方法,并熟悉常用连续时间信号的波形和特性;2.运用MATLAB符号求解连续系统的零输入响应和零状态响应;3.运用MATLAB数值求解连续系统的零状态响应;4.运用MATLAB求解连续系统的冲激响应和阶跃响应;5.运用MATLAB卷积积分法求解系统的零状态响应。
二、实验原理1. 连续信号MATLAB实现原理从严格意义上讲,MA TLAB数值计算的方法并不能处理连续时间信号.然而,可用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能够被MATLAB处理,并且能较好地近似表示连续信号.MATLAB提供了大量生成基本信号的函数.比如常用的指数信号、正余弦信号等都是MATLAB的内部函数。
为了表示连续时间信号,需定义某一时间或自变量的范围和取样时间间隔,然后调用该函数计算这些点的函数值,最后画出其波形图.三、实验内容1.实例分析与验证根据以上典型信号的MA TLAB函数,分析与验证下列典型信号MA TLAB程序,并实现各信号波形图的显示,连续信号的图形显示使用连续二维图函数plot().(1)正弦信号:用MA TLAB命令产生正弦信号2sin(2/4)ππ+,并会出时间0≤t≤3的波形图。
程序如下:K=2;w=2*pi ;phi=pi/4;t=0:0.01:3;ft=K*sin (w*t+phi );plot(t,ft ),grid on ;axis ([0,3,-2。
2,2.2])title (’正弦信号’)(2) 抽样信号:用MA TLAB 中的sinc(t)函数命令产生抽样信号Sa(t),并会出时间为66t ππ-≤≤的波形图。
MATLAB信号处理仿真实验

MATLAB信号处理仿真实验1. 引言信号处理是一种广泛应用于各个领域的技术,它涉及到对信号的获取、处理和分析。
MATLAB是一种强大的数学软件,提供了丰富的信号处理工具箱,可以用于信号处理的仿真实验。
本文将介绍如何使用MATLAB进行信号处理仿真实验,并提供详细的步骤和示例。
2. 实验目的本实验旨在通过MATLAB软件进行信号处理仿真,以加深对信号处理原理和算法的理解,并掌握使用MATLAB进行信号处理的基本方法和技巧。
3. 实验步骤3.1 生成信号首先,我们需要生成一个待处理的信号。
可以使用MATLAB提供的信号生成函数,如sine、square和sawtooth等。
以生成一个正弦信号为例,可以使用以下代码:```MATLABfs = 1000; % 采样频率t = 0:1/fs:1; % 时间向量f = 10; % 信号频率x = sin(2*pi*f*t); % 生成正弦信号```3.2 添加噪声为了更真实地摹拟实际信号处理场景,我们可以向生成的信号中添加噪声。
可以使用MATLAB提供的随机噪声生成函数,如randn和awgn等。
以向生成的信号中添加高斯白噪声为例,可以使用以下代码:```MATLABSNR = 10; % 信噪比y = awgn(x, SNR); % 向信号中添加高斯白噪声```3.3 进行滤波处理滤波是信号处理中常用的一种技术,用于去除信号中的噪声或者提取感兴趣的频率成份。
可以使用MATLAB提供的滤波函数,如fir1和butter等。
以设计并应用一个低通滤波器为例,可以使用以下代码:```MATLABorder = 10; % 滤波器阶数cutoff = 0.1; % 截止频率b = fir1(order, cutoff); % 设计低通滤波器filtered_y = filter(b, 1, y); % 应用滤波器```3.4 进行频谱分析频谱分析是信号处理中常用的一种技术,用于分析信号的频率成份。
《基于MATLAB的数字信号处理》实验报告

0.60007.0000-5.4000所以,X=[错误!未找到引用源。
]=[ 0.6000, 7.0000, -5.4000]’实验结果2:K=1.732051实验结果3:三曲线的对比图如下所示:图1.1 三曲线的对比实验二基于MATLAB信号处理实验xlabel('频率/Hz');ylabel('振幅/dB');title('布莱克窗的幅频特性');grid on;subplot(2,1,2);plot(f4,180/pi*unwrap(angle(H4)));xlabel('频率/Hz');ylabel('相位');title('布莱克窗的相频特性');grid on;六、实验结果实验结果2.1:图2-1 x(n)与y(n)的互相关序列图由实验结果可知,x(n)与y(n)的互相关只在区间[-4,8]上有能力,刚好是区间[-3,3]与右移后的区间[-1,5]两端点之和,与结论一致。
且互相关在2处达到最大。
实验结果2.2.1:其表示的差分方程为:y(n)-0.8145y(n-4)=x(n)+x(n-4)实验结果2.2.2:滤波器的幅频和相频图如下所示:图2-2 滤波器的幅频与相频图实验结果2.2.3:由下图实验结果可知,输出信号相对于输入信号有一小小的延迟,基本上x(n)的频点都通过了,滤波器是个梳状filter,正好在想通过的点附近相位为0,也就是附加延迟为0图2-3 滤波器的幅度和相位变化图2-4 两信号波形实验结果2.3:四种带通滤波器的窗函数的频率响应如下所示:图2-5 矩形窗的频率特性图2-6 汉宁窗的频率特性图2-7 海明窗的频率特性图2-8 布莱克曼窗的频率特性图3-1 加噪前、后图像对比图3-2 加椒盐噪声的图像均值滤波前、后的图像对比图3-3 加椒盐噪声的图像中值滤波前、后的图像对比图3-4加高斯噪声的图像均值滤波前、后的图像对比图3-5 加高斯噪声的图像中值滤波前、后的图像对比实验结果3.2:图3-6 原图及重构图像图3-7 程序运行结果由实验结果可知,当DCT变换的系数置0个数小于5时,重构图像与原图像的峰值信噪比为2.768259,重构图像置为0的变换系数的个数个数为:43.708737;当DCT变换的系数置0个数小于10时,重构图像与原图像的峰值信噪比15.922448,重构图像置为0的变换系数的个数个数为:36.110705;当DCT变换的系数置0个数小于5时,重构图像与原图像的峰值信噪比为2.768259,重构图像置为0的变换系数的个数个数为:30.366348;可以发现,在抛弃部分DCT系数后,重构图像时不会带来其画面质量的显著下降,采用这种方法来实现压缩算法时,可以通过修改mask变量中的DCT系数来更好地比较仿真结果。
“数字信号处理”实验报告二

实验报告课程名称:数字信号处理实验任课教师:杨鉴实验名称:离散时间系统的时域分析年级、专业:2015级通信工程学号:**********姓名:***日期:2017 年10 月9 日云南大学信息学院一、实验1.通过MATLAB仿真一些简单的离散时间系统,并研究他们的时域特性。
2.掌握卷积在MATLAB的算法并理解滤波的概念。
二、实验内容1. 假定另一个系统为y[n]=x[n]x[n-1],修改程序P2.3,计算这个系统的输出序列y1[n],y2[n]和y[n]。
比较y[n]和yt[n]。
这两个序列是否相等?该系统是线性系统吗?2. 考虑另一个系统:y[n]=nx[n]+x[n-1],修改程序P2.4,以仿真上面的系统并确定该系统是否为时不变系统。
3.修改程序P2.7,计算长度为15的序列h[n]和长度为10的序列x[n]的卷积,重做问题Q2.28。
h[n]和x[n]的样本值你自己给定。
4.修改程序P2.9,将输入序列改变成扫频正弦序列(长度为301、最低频率为0、最高频率为0.5)。
那个滤波器能更好的抑制输入信号x[n]的高频分量?三、主要算法与程序Q2.11:clf;n = 0:40;a = 2;b = -3;f1=0.1;f2=0.4;x11=[0 cos(2*pi*f1*n) 0];x12=[0 0 cos(2*pi*f1*n)];x21=[0 cos(2*pi*f2*n) 0];x22=[0 0 cos(2*pi*f2*n)];x = a*x11 + b*x21;y1 = x11.*x12;y2 = x21.*x22;xd = a*x12+b*x22;y = x.*xd;yt = a*y1 + b*y2;d = y - yt; % Compute the difference output d[n]% Plot the outputs and the difference signalsubplot(3,1,1)stem([0 n 0],y);ylabel('Amplitude');title('Output Due to Weighted Input: a \cdot x_{1}[n] + b \cdot x_{2}[n]');subplot(3,1,2)stem([0 n 0],yt);ylabel('Amplitude');title('Weighted Output: a \cdot y_{1}[n] + b \cdot y_{2}[n]'); subplot(3,1,3)stem([0 n 0],d);xlabel('Time index n');ylabel('Amplitude');title('Difference Signal');Q2.17:clf;n = 0:40; D = 10;a = 3.0;b = -2;x = a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n);xd = [zeros(1,D) x];nd=0:length(xd)-1;y=(n.*x)+[0 x(1:40)];yd=(nd.*xd)+[0 xd(1:length(xd)-1)];d = y - yd(1+D:41+D);subplot(3,1,1)stem(n,y);ylabel('振幅');title('输出 y[n]'); grid;subplot(3,1,2)stem(n,yd(1:41));ylabel('振幅');title('由于延时输入 x[n-10]的输出'); grid;subplot(3,1,3)stem(n,d);xlabel('时间序号 n'); ylabel('振幅');title('差值信号');grid;Q2.29:clf;h = [3 2 1 -2 1 0 -4 0 3 1 5 4 0 3 5]; % impulse responsex = [1 -2 3 -4 3 2 1 5 6 1]; % input sequencey = conv(h,x);n = 0:23;subplot(2,1,1);stem(n,y);xlabel('时间序号n');ylabel('振幅');title('用卷积得到的输出'); grid;x1 = [x zeros(1,14)];y1 = filter(h,1,x1);subplot(2,1,2);stem(n,y1);xlabel('时间序号 n'); ylabel('振幅');title('由滤波生成的输出'); grid;Q2.35:f=w/2pi=(2a*n+b)/2pi=[0,0.5],所以b=0,a*n<=0.5*pi,当n=300时,a取pi/600。
(完整版)数字信号处理实验二
y = filter(num,den,x,ic);
yt = a*y1 + b*y2;
d = y - yt;
subplot(3,1,1)
stem(n,y);
ylabel('振幅');
title('加权输入: a \cdot x_{1}[n] + b \cdot x_{2}[n]的输出');
subplot(3,1,2)
%扫频信号通过2.1系统:
clf;
n = 0:100;
s1 = cos(2*pi*0.05*n);
s2 = cos(2*pi*0.47*n);
a = pi/2/100;
b = 0;
arg = a*n.*n + b*n;
x = cos(arg);
M = input('滤波器所需的长度=');
num = ones(1,M);
三、实验器材及软件
1.微型计算机1台
2. MATLAB 7.0软件
四、实验原理
1.三点平滑滤波器是一个线性时不变的有限冲激响应系统,将输出延时一个抽样周期,可得到三点平滑滤波器的因果表达式,生成的滤波器表示为
归纳上式可得
此式表示了一个因果M点平滑FIR滤波器。
2.对线性离散时间系统,若y1[n]和y2[n]分别是输入序列x1[n]和x2[n]的响应,则输入
plot(n, y);
axis([0, 100, -2, 2]);
xlabel('时间序号 n'); ylabel('振幅');
数字信号处理第三版用MATLAB上机实验
实验二:时域采样与频域采样一、时域采样1.用MATLAB编程如下:%1时域采样序列分析fs=1000A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=1000;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,1);stem(n,xn);xlabel('n,fs=1000Hz');ylabel('xn');title('xn');subplot(3,2,2);plot(n,abs(Xk));xlabel('k,fs=1000Hz'); title('|X(k)|');%1时域采样序列分析fs=200A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=200;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs);Xk=fft(xn);subplot(3,2,3);stem(n,xn);xlabel('n,fs=200Hz'); ylabel('xn');title('xn');subplot(3,2,4);plot(n,abs(Xk));xlabel('k,fs=200Hz'); title('|X(k)|');%1时域采样序列分析fs=500A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=500;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,5);stem(n,xn);xlabel('n,fs=500Hz');ylabel('xn');title('xn');subplot(3,2,6);plot(n,abs(Xk));xlabel('k,fs=500Hz'); title('|X(k)|');2.经调试结果如下图:20406080-200200n,fs=1000Hzxnxn2040608005001000k,fs=1000Hz|X (k)|51015-2000200n,fs=200Hzx nxn510150100200k,fs=200Hz |X(k)|10203040-2000200n,fs=500Hzx nxn102030400500k,fs=500Hz|X (k)|实验结果说明:对时域信号采样频率必须大于等于模拟信号频率的两倍以上,才 能使采样信号的频谱不产生混叠.fs=200Hz 时,采样信号的频谱产生了混叠,fs=500Hz 和fs=1000Hz 时,大于模拟信号频率的两倍以上,采样信号的频谱不产生混叠。
实验2 用MATLAB进行信号频谱分析 2
实验报告通信工程 1101学号:********* 姓名:李*实验2 用MATLAB 进行信号频谱分析一、实验目的㈠ 初步掌握MATLAB 产生常用离散时间信号的编程方法。
㈡ 学习编写简单的FFT 算法程序,对离散信号进行幅频谱分析。
㈢ 观察离散时间信号频谱的特点。
二、实验原理㈠ 常用的离散时间信号在 MATLAB 语言主要是研究离散信号的。
常用的离散信号有: 1.单位取样序列⎩⎨⎧≠==0001)(n n n δ2.单位阶跃序列⎩⎨⎧<≥=001)(n n n u3.实指数序列R a n a n x n∈∀=;)(4.复指数序列n e n x n j ∀=+)(0)(ωσ5.正(余)弦序列)cos()(0θω+=n n x n ∀ 6.周期序列n N n x n x ∀+=)()(㈡ 离散信号的产生离散信号的图形显示使用stem 指令。
在 MATLAB 中的信号处理工具箱中,主要提供的信号是离散信号。
由于MATLAB 对下标的约定为从1开始递增,例如x=[5,4,3,2,1,0],表示x(1)=5,x(2)=4,X(3)=3…因此要表示一个下标不由1开始的数组x(n),一般应采用两个矢量,如 n=[-3,-2,-1,0,l ,2,3,4,5];x=[1,-l ,3,2,0,4,5,2,1];这表示了一个含9个采样点的矢量:X(n)={x(-3),x(-2),x(-1),x(0),x(1),x(2),x(3),x(4),x(5)}。
1.单位取样序列⎩⎨⎧≠==δ0001)(n n n 这一函数实现的方法有二:方法一:可利用MATLAB 的zeros 函数。
x=zeros(1,N); %建立一个一行N 列的全零数组x(1)=1; %对X (1)赋1 方法二:可借助于关系操作符实现n=1:N;x=[n==1]; %n 等于1时逻辑关系式结果为真,x=1;n 不等于1时为假,x=0如要产生 ⎪⎩⎪⎨⎧≤<<=≤≤=-δ20210100)(10)(n n n n n n n n n n n n则可采用MATLAB 实现:n=n1:n2;x=[(n-n0)==0];%n=n0时逻辑关系式结果为真,x=1;n ≠n0时为假,x=0 2.单位阶跃序列⎩⎨⎧<≥=001)(n n n u这一函数可利用MATLAB 的ones 函数实现: x=ones(1,N);还可借助于关系操作符“>=”来实现。
数字信号处理实验利用MATLAB进行信号分析
实验2 利用MATLAB 进行信号分析实验目的:学习用MATLAB 编程进行信号分析实验内容:1、 数字滤波器的频率响应:数字滤波器的系统函数为:H(z)=21214.013.02.0----++++z z z z ,求其幅频特性和相频特性:2、离散系统零极点图:b =[0.2 0.1 0.3 0.1 0.2]; a=[1.0 -1.1 1.5 -0.7 0.3]; 画出其零极点图3、数字滤波器的冲激响应: b=[0.2 0.1 0.3 0.1 0.2];a=[1.0 -1.1 1.5 -0.7 0.3]; 求滤波器的冲激响应。
4、 计算离散卷积:x=[1 1 1 1 0 0]; y=[2 2 3 4]; 求x(n)*y(n)。
5、 计算离散信号的能量和功率:序列的能量:E=∑∞=02)(n n x =∑∞=0)(*)(n n x n x序列的功率:P=N1∑-=102)(N n n x =N1∑∞=0)(*)(n n x n xx(n)=0.8nu(n),计算前10点的能量占总能量的百分比。
6、 求逆Z 变换:求X(z)=)9.01()9.01(121z z +-- z ﹥0.9的逆Z 变换。
实验要求:打印出程序、图形及运行结果,并分析实验结果。
利用MATLAB 进行信号分析● 数字滤波器的频率响应:例:对一数字滤波器H(z)=21214.013.02.0----++++zz z z ,求其幅频特性和相频特性: a=[1 0.4 1]; b=[0.2 0.3 1]; freqz(b,a,128)● 离散系统零极点图:b =[0.2 0.1 0.3 0.1 0.2]; a=[1.0 -1.1 1.5 -0.7 0.3]; zplane(b,a)● 数字滤波器的冲激响应: b=[0.2 0.1 0.3 0.1 0.2];a=[1.0 -1.1 1.5 -0.7 0.3]; impz(b,a,50)● 计算离散卷积:x=[1 1 1 1 0 0]; y=[2 2 3 4]; z=conv(x,y);stem(0:length(x)+length(y)-2,z)● 计算离散信号的能量和功率:序列的能量:E=∑∞=02)(n n x = ∑∞=0)(*)(n n x n x序列的功率:P=N1∑-=12)(N n n x =N1∑∞=0)(*)(n n x n x例:x(n)=0.8n u(n),计算前10点的能量占总能量的百分比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 T T
T /2
T / 2
x(t ) dt 和 P lim
2
N 1 2 x(n) 。若 P ,则称 x(t)或 x(n) N 2 N 1 n N
为功率有限信号,简称功率信号。 4. Fourier 分析 信号的时域与频域关系可以通过傅里叶变换和傅里叶逆变换获得。 1)连续时间信号的 Fourier 变换: 在 matlab 中给出了能够直接求解傅里叶变换及 其逆变换的函数 fourier 和 ifourier。其中,F=fourier(f)是符号函数 f 的 Fourier 变换,默认返回是关于ω的函数; f=ifourier(f)是函数 F 的 Fourier 逆变换,默认的 独立变量是ω,默认返回是关于 x 的函数。 2)离散时间信号的 Fourier 变换:设 h(n)为以线性时不变系统的单位抽样响应, 定义 H (e )
S ( f )e j 2f df 。
正态随机过程又称高斯过程是一种普遍存在和十分重要的随机过程,在 matlab 中 用 randn 函数实现。在通信信道中的噪声,通常是一种正态随机过程。正态随机过程的 n 维分布仅由各随机分量的数学期望、方差和两两之间的归一化协方差函数所决定。另 外,如果高斯过程中的随机变量之间互不相关,则他们是统计独立的。
0.1t
,0 t 40 及它们的
subplot(4,1,1);plot(t,x1);title('x1')
subplot(4,1,2);plot(t,x2);title('x2') subplot(4,1,3);plot(t,x);title('x') subplot(4,1,4);plot(t,y);title('y')
0.1n
,0 n 30 ,绘出该系统
的频率响应;若输入信号为 x( n) sin(0.2n) 3 cos(0.4n),0 n 30 ,确定该 系统的稳态输出响应。 程序: clear all w=-1:0.001:1; n=0:30; h=sinc(0.2*n); x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n); Hjw=h*(exp(-j*pi).^(n'*w)); Xjw=x*(exp(-j*pi).^(n'*w)); Yjw=Xjw.*Hjw; n1=0:2*length(n)-2; dw=0.001*pi; y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi); y1=conv(x,h); subplot(3,1,1);plot(w,abs(Hjw)) title('H');xlabel('pi 弧度(w)');ylabel('振幅') subplot(3,1,2);plot(w,abs(Xjw)); title('X');xlabel('pi 弧度(w)');ylabel('振幅')
2
x(t ) dt 和
2
如果 E , 称 x(t)或 x(n)为能量有限信号, 简称能量信号;E , E x ( n) 。
则 能 量 无 限 , 往 往 研 究 他 们 的 功 率 。 信 号 x(t) 、 信 号 x(n) 的 功 率 分 别 定 义
P lim
0.1n
, x(n) e 0.2 n ,0 n 40 的卷积。
%产生信号序列 %产生信号序列 %求两信号卷积
subplot(3,1,1);stem(h);title('h') subplot(3,1,2);stem(x);title('x'); subplot(3,1,3);stem(y);title('y')
1 2 3
,试绘出该信号的时域波形f(t)和
%说明t、w为符号变量 %生成函数表达式 %绘出图形 %傅里叶反变换 %绘图
输入并检查程序 运行程序,记录绘图结果 去掉第五行的分号,记录程序执行结果
4.
已知系统的冲激响应函数,求系统输出 程序:一个系统的单位脉冲响应为 h( n) sin(0.2n)e
j
)e jn d
3)离散 Fourier 变换:长序列的离散 Fourier 变换计算量相当大,因此出现了几 种计算 DFT 的高效方法,统称为快速 Fourier 变换(FFT),Matlab 中有 fft 函数实现。 5. 随机信号与随机过程 在通信系统中所遇到的信号及噪声, 大所属均可视为平稳的随机过程。 平稳随机过 程即指它的任何 n 维分布函数或概率密度函数与时间起点无关。也就是说,随机过程 X(t) 在 任 意 一 组 时 刻 t1 t 2 t3 ... t n 且 n 为 任 意 值 时 得 到 的 随 机 变 量 X ti ,
R (t1 , t1 ) R ( ) ,这样的过程称为宽平稳过程。
变换,即
S ( f ) R ( )e j 2f d 。同样,一个平稳随机过程 X(t)的自相关函数可以由功率谱
密度的 Fourier 逆变换得到,即 R ( )
实验二 信号处理的 Matlab 仿真
一、 实验目的:
1. 2. 3. 进一步熟悉 Matlab 操作页面和常用函数的使用; 通过编写简单的 Matlab 程序,对确定信号的时域和频域特性进行分析; 通过编写简单的 Matlab 程序,对随机信号及随机过程进行分析。
二、实验原理:
1. 离散信号 一个信号 x(t)可以是连续时间信号(模拟信号),也可以是离散时间信号(数字信 号)。若 x(t)是李三信号,则 t 仅在时间轴的离散点上取值,此时,应将 x(t)改记为 x(nTs),Ts 表 示 相 邻 两 个 点 之 间 的 时 间 间 隔 , 又 称 抽 样 周 期 , n 取 整 数 , 即
输入程序,并检查是否编译错误 2 运行程序,绘制图形 3 观察图形,描述图形可反映的信息(时域图看不出信号 的周期成分;频域图 可以清除看到,在频率为 60HZ 和 150HZ 处有两个尖峰,即为信号的两个频率分量) 4 通过图形界面给图形增加标题 ( 图 3-1 原始信号的时域波形图, 图 3-2 原始 信号的频谱图). 5 将时域图中的时间轴修订为 0~0.1,频域图横轴范围修订为 0~200,重新获得 图形。
1
程序 2:绘图叠加信号的功率谱,观察不同采样点数是的功率谱图形
%3.1 功率谱估计(Welch 法) ,在上一程序上继续编写,利用上图的带噪原始信号 的傅里叶变换后结果幅值,将幅值平方,即可得功率谱的估计值, Pxx=abs(fft(x,N)).^2/N; %采样点数为 1024, Pxx_short=abs(fft(x,256)).^2/256; %采样点数为 256 figure(3) subplot(2,1,1) plot((0:N-1)/N*fs,10*log10(Pxx)) %绘制估计功率谱, 功率单位 dB, 采样点数 1024 subplot(2,1,2) plot((0:255)/256*fs,10*log10(Pxx_short)*10) %绘制估计功率谱,功率单位 dB,采样点数 256 1 输入程序,并检查是否编译错误 2 运行程序,绘制图形, 3 添加横纵坐标及图形说明 (横坐标 f/Hz,纵坐标 P(f)/dB, 图形说明“采样点数 256” 、 “采样点数 1024” )
t
的时域波形f(t)及相应的幅频特性。
subplot(1,2,1);ezplot(f); F=fourier(f);
subplot(1,2,2);ezplot(abs(F));
1 2 3
输入并检查程序 运行程序,记录绘图结果 去掉第五行的分号,记录程序执行结果
程序2:若某信号的傅里叶变换为 f ( ) e 频谱图。 程序: clear all syms t w; F=pi*exp(-abs(w)); subplot(1,2,1); ezplot(abs(F)); f=ifourier(F,t); subplot(1,2,2); ezplot(f)
三、实验内容:
1. 2. 进一步熟悉Matlab操作页面和常用函数的使用。 熟悉信号间的常用运算如相加、相减、乘积、卷积等,并绘制时域图形。 程序1: 分别画出信号 x1 (t ) sin( 2 0.1t ) 与信号 x2 (t ) e 相加和相乘后得到的信号曲线。 程序: clear all t=0:40; x1=sin(2*pi*0.1*t); x2=exp(-0.1*t); x=x1+x2; y=x1.*x2; %产生信号1 %产生信号2 %信号相加 %信号相乘 %绘图
x(nTs ), n N1 ,...,1,0,1,..., N 2 ,其中 N1、N2 是 n 的取值范围。一般可以把 Ts 归一
化为 1,则 x(nTs)可简记为 x(n)。这样表示的 x(n)仅是整数 n 的函数,所以又称 x(n) 为离散时间序列。 绘制离散时间序列用 stem 函数, stem(n,x),其中抽样时刻为横坐标, 抽样值为纵坐标。 2. 信号间的卷积是求线性时不变系统输出信号的主要方法。 设两序列 x(t)、h(t),则其卷积和定义为 y (t ) x(t ) h(t ) ,matlab 提供了求卷积 函数 conv(x,h),利用此函数可以方便的求得两个信号的卷积。 3. 信号的能量与功率 对连续时间信号 x(t)和离散时间信号 x(n),其能量分别定义为 E
i 1,2,..., n 的联合概率密度函数满足 p ( xt1 , xt2 ,..., xtn ) p ( xt1 t , xt2 t ,..., xtn t ) 。对所有
