09组合图形面积
阴影部分面积
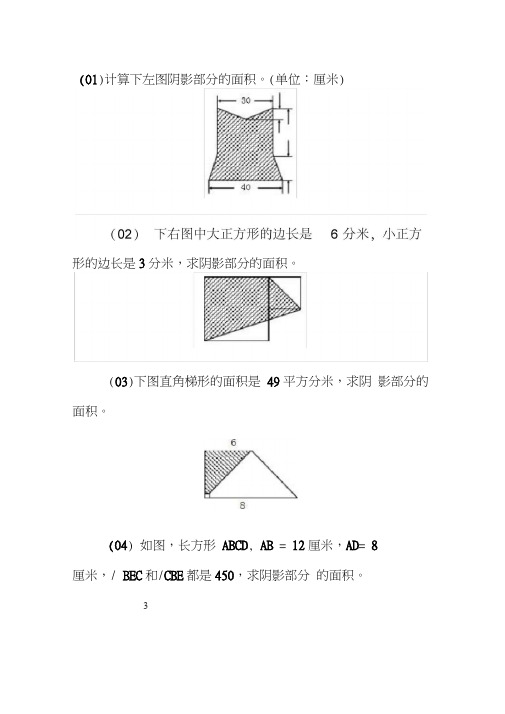
(01)计算下左图阴影部分的面积。
(单位:厘米)形的边长是3分米,求阴影部分的面积。
(03)下图直角梯形的面积是49平方分米,求阴影部分的面积。
(04) 如图,长方形ABCD, AB = 12厘米,AD= 8厘米,/ BEC和/CBE都是450,求阴影部分的面积。
3D C(05)图中,梯形ABCD的面积是50平方厘米,高是5厘米,AB= 8厘米,ABCE是一个平行四边形,求三角形ADE的面积。
(06)如图,求平行四边形中的梯形面积。
(单位:厘米)(07)直角梯形ABCD被划分成一个直角三角形和一个平行四边形,已知AD = 6分米,EC= 4分米,直角三角形CDE的面积是14平方分米,求平行四边形ABED 的面积。
(08)下图正方形ABCF边长为10厘米,阴影部分甲的面积比乙的面积大12平方厘米,求CD的长度。
(09)图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
A 5 DB 12 C(10)在直角三角形ABC中,AD= 7厘米,三角形ADC的面积是35平方厘米,/ BCD和/ BDC都是45 °求直角三角形BCD的面积。
(11)如图,平行四边形ABED的面积为23平方厘米,AD= 5厘米,EC= 4.8厘米,求梯形ABCD的面积。
(12)求梯形中阴影部分的面积。
(单位:厘米)(13)如图,已知AB= 4厘米,EB= 3厘米,长方形的面积是36平方厘米,求三角形AEC的面积。
(14)如下图,在长方形ABCD中,点E是BC的中点,EC= 7.5厘米,三角形CDE的面积是22.5平方厘米,求长方形ABCD的面积。
(15)求下面图形的面积。
(单位:厘米)—十LdiL左一I(16)如右图,已知AB平行DC, AB= 3.2厘米,CD= 4.8厘米,/ ADE= 45 °求四边形ABCD的面积。
(17)如右图,已知BC= 1.1厘米,CE= 1.9厘米,长方形ABCD的面积是1.65平方厘米,求三角形DBE 的面积。
优化“分与合”数学解题策略

优化“分与合”数学解题策略作者:***来源:《广西教育·A版》2021年第04期【摘要】本文論述优化“分与合”的数学解题策略,引导学生在笔算乘法运算法则中,感受“先分后合”的数学转化思想、理解算法、优化计算方法;利用分与合数学解题策略解决平面图形中的复杂问题,为学习高阶数理化知识做铺垫。
【关键词】数学思想分与合建构模型【中图分类号】G 【文献标识码】A【文章编号】0450-9889(2021)13-0139-03数学解题策略是人们为实现数学解题目标而确定的具体方法,是更重要、更高级的思维能力。
和其他事物一样,数学解题策略有着内在的规律性。
在小学阶段,数学教学的根本任务是提高学生的综合素养,而教师指导学生掌握一些数学解题策略,则能帮助学生提高分析问题、解决问题的能力。
以下,笔者就如何培养学生学会用“分与合”的数学解题策略去分析数学问题,谈谈具体的策略。
一、探究笔算乘法的运算法则(一)口算中体现“先分后合”,感受转化的数学思想人教版四年级上册教材中,第四单元《三位数乘两位数》例1充分运用了分与合的数学解题策略,教师要利用好教材,引导学生熟悉这一数学解题方式。
例1.李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。
该城市到北京有多少千米?在学生正确列式“145×12= ”后,笔者先让学生进行口算。
学生经过思考,得出:把12分成10和2。
2×145=290(千米)10×145=1450(千米)290+1450=1740(千米)学生口算的过程就是一种解题策略——先分后合,即把12分成10和2,分别去乘三位数145,然后把两次乘得的积合起来,得出问题的答案。
运用这种策略,也是实施了转化的数学思想,把新知识转化为旧知识,易于学生理解和吸收。
学生在口算过程中体验到了“先分后合”方式给解决问题带来的便利,从中体会到了成功的快乐。
(二)笔算中学习“先分后合”,理解算理、掌握算法笔者引导学生进行三位数乘两位数的笔算方法自主探究,目的是让他们充分利用已有的知识经验(两位数乘两位数)探求新知。
小学五年级数学求阴影部分面积习题

14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。求 平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四
边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
1、下图中,已知阴影部分面积使30平方厘米,AB二15厘米,求图形空
白部分的总面积。
2、右图,一个长方形和一个三角形重叠在一起,已知三角形ADE的面积
比长方形ABCD的面积小4平方厘米,求CE的长。
A4B
D
3、如图,求直角梯形中阴影部分的面积。(单位:厘米)
10
4、下面直角梯形的面积是49平方分米,求阴影部分的面积
5、求整个图形的面积。(单位:厘米)
6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米, 这梯形原来的面积是多少平方厘米?
7、求下面图形中阴影部分的面积。(单位:厘米)
8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部 分面积是60厘米,求图中空白部分的面积。
小学五年级数学求阴影部分面积习题
1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米, 求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴 影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平 方厘米,把它分成一个平行四边形和直角三角形后, 三角形的面积是多少平方厘 米。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分 面积。
(完整版)小学五年级数学求阴影部分面积习题(最新整理)
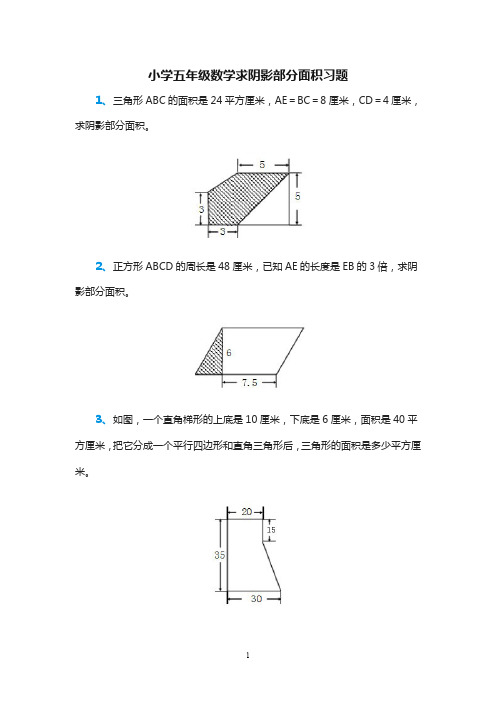
小学五年级数学求阴影部分面积习题 1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米) 6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米? 7、求下面图形中阴影部分的面积。
(单位:厘米) 8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
简单的组合教学反思

简单的组合教学反思简单的组合教学反思1课前,我一直在担心二年级的学生能否理解掌握《简单的排列与组合》这一课。
今天上完这节课时,我是怀着一种轻松愉悦的心情走出教室。
因为,孩子们学得非常的好,这些7岁的孩子不但能理解和掌握《简单的排列与组合》,而且能做到熟练的运用。
在教学例1时:1、让学生拿出数字卡片1、2摆两位数,学生很快的摆出12、21。
2、让学生独立用卡片1、2、3摆两位数,一边摆一边把摆出的数记录在学习纸上。
3、小组交流讨论,谁方法最科学、不会漏掉。
4、让学生到前面的黑板上展示交流小组讨论的结果。
三人到前面展示,其中2名同学的方法是:十位上的数字是1,个位上的数字是2或3,组成的两位数是12,13;十位上的数字是2,个位上的数字是1或3,组成的两位数是21,23;十位上的数字是3,个位上的数字是1或2,组成的两位数是31,32;一名同学的方法是:用数字1、2来摆,可以摆出的数是12、21;用数字1、3来摆,可以摆出的.数是13、31;用数字2、3来摆,可以摆出的数是23、32。
同学们都很赞同这两种方法,于是我给这两种方法称为“2钟法”和“叶氏法”当其他学生学习了这两种方法后,在练习中我又让学生用数字卡片“0、3、9”摆两位数。
我想,学生这时肯定遇到困难了,他们一定会为“03、09”是不是两位数展开争论。
没想到,大部分学生都没有一个是写6个两位数。
用“2钟法”写出了4个数:30、39、90、93“叶氏法”写出03、30、09、90、39、93(学生是把039删去的)。
就这样,这部分让我担心孩子们会学不懂的知识,在孩子们的自主探究、小组合作学习中顺利地学会并做到了熟练的运用,教学效果真的很好。
简单的组合教学反思211月5日我在界湖小学东校区多媒体教室观看了张京菊老师执教的《简单的排列组合》,感触颇深。
这节课中,张老师以小学生熟知的游戏乐园为题材,创设了买票、猜密码的情境。
这样的教学设计比较新颖,符合二年级小学生的年龄心理特点,激发了学生的学习兴趣,同时也切合了本节课的`教学主题。
小学五年级数学求阴影部分面积习题之欧阳治创编

小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD =9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD =4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD为平行四边形,已知梯形面积为 66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
小学五年级数学求阴影部分面积习题
小学五年级数学求阴影部分面积习题
1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴
8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
4
面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD 的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
(单位:厘米)。
(完整版)小学五年级数学求阴影部分面积习题(可编辑修改word版)
小学五年级数学求阴影部分面积习题1、三角形 ABC 的面积是 24 平方厘米,AE=BC=8 厘米,CD=4 厘米,求阴影部分面积。
2、正方形 ABCD 的周长是 48 厘米,已知 AE 的长度是 EB 的 3 倍,求阴影部分面积。
3、如图,一个直角梯形的上底是 10 厘米,下底是 6 厘米,面积是 40 平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是 49 平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加 4 厘米,面积就增加 18 平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是 6 厘米,阴影部分面积是 60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形 ABED 的面积是 30 平方厘米,BE 长 6 厘米,EC 长 4 厘米。
求梯形 ABCD 的面积。
11、图中空白部分是一个面积为 30 平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形 ABCD 中,AB=4 分米。
CD=9 分米,空白部分面积为 10 平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形 DEC 的面积是 2.7 平方米,AD=4.4 米,AB=2 米。
求平行四边形 CDFG 中阴影部分的面积。
15、如图,在梯形 ABCD 中,CD=4 厘米,AB=2DC,AECD 为平行四边形,已知梯形面积为 66 平方厘米,求阴影部分面积。
16、图中三角形 ABC 的面积是 24 平方厘米,AE=BC=8 厘米,CD=4 厘米,求阴影部分的面积。
17、图中空白部分是一个面积为 30 平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是 56 平方厘米,BD=14 厘米,求梯形 ABCD 的面积。
小学五年级数学求阴影部分面积习题之欧阳数创编
小学五年级数学求阴影部分面积习题1、三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分面积。
2、正方形ABCD的周长是48厘米,已知AE的长度是EB的3倍,求阴影部分面积。
3、如图,一个直角梯形的上底是10厘米,下底是6厘米,面积是40平方厘米,把它分成一个平行四边形和直角三角形后,三角形的面积是多少平方厘米。
4、下面直角梯形的面积是49平方分米,求阴影部分的面积。
5、求整个图形的面积。
(单位:厘米)6、下图所示梯形,如果它的上底增加4厘米,面积就增加18平方厘米,这梯形原来的面积是多少平方厘米?7、求下面图形中阴影部分的面积。
(单位:厘米)8、下图由大小不等的两个正方形拼成,小正方形的边长是6厘米,阴影部分面积是60 厘米,求图中空白部分的面积。
9、求正方形中阴影部分的面积。
10、在下图中,已知平行四边形ABED的面积是30平方厘米,BE长6厘米,EC长4厘米。
求梯形ABCD的面积。
11、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
12、如图:在直角梯形ABCD中,AB=4分米。
CD=9分米,空白部分面积为10平方分米,求阴影部分面积。
13、求阴影部分的面积(单位:厘米):14、图中三角形DEC的面积是2.7平方米,AD=4.4米,AB=2米。
求平行四边形CDFG中阴影部分的面积。
15、如图,在梯形ABCD中,CD=4厘米,AB=2DC,AECD 为平行四边形,已知梯形面积为 66平方厘米,求阴影部分面积。
16、图中三角形ABC的面积是24平方厘米,AE=BC=8厘米,CD=4厘米,求阴影部分的面积。
17、图中空白部分是一个面积为30平方厘米的平行四边形,求阴影部分面积。
18、图中,阴影部分的面积是56平方厘米,BD=14厘米,求梯形ABCD的面积。
19、梯形ABCD面积是96平方厘米,AB=6厘米,中位线EF=12厘米,求阴影部分面积。
20、求这个组合图形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金牌教研中心 2013年春季四年级数学09
博学精教 成就学生
1
第九讲 组合图形的周长、面积
主讲老师: 学生姓名:
周长:是指围成这个图形的所有边长的总和。 面积:指物体的表面一平面图形的大小。
长方形的周长=(长+宽)×2 面积=长×宽
正方形的周长=边长×4 面积=边长×边长
对于一些稍复杂一些的,无法直接运用公式.那么我们就要利用拆拼、平移等方法,巧妙地运
用周长公式来求它们的周长。
【典型例题】
1.一个正方形的周长是36厘米,它的面积是多少?
2.求下图的周长和面积.
(单位:米)
3.如图正方形ABCD的边长为4cm,每边被三等分.求图中所有小正方形周长的和.
4.把长130厘米的铁丝围成一个长方形,接头处重合2厘米,要使长比宽多18厘米,长和宽
各是多少厘米?
30
50
60
25
A B
C D
金牌教研中心 2013年春季四年级数学09
博学精教 成就学生
2
随堂大练兵
成绩
1.要在一块周长是24米的正方形空地上种草坪,这块草坪的面积是多少?
2.求下图的周长和面积.(单位:米)
3.宝外小学原来操场长180米,宽60米,今年扩建后,长增加25米,宽增加35米,现在
操场面积是多少?
4.求下图的周长和面积.(单位:厘米)
5.一个正方形,边长是10厘米,边长增加3厘米后,面积增加了多少?
3
3
8
12
12
18
6
18
金牌教研中心 2013年春季四年级数学09
博学精教 成就学生
3
1
1
2
6.一根丝线能围成长12米,宽4米的长方形,现在把它围成一个正方形,正方形的面积是
多少?
7.求下图的周长和面积.(单位:厘米)
8.下图是由若干个相等的正方形组成的“土山”两个字,已知每个正方形的边长是3厘米,这
两个字的周长分别是 、 厘米.
9.一张长方形的纸,长是28厘米,宽是15厘米,先剪下一个最大的正方形,再从余下的纸
片中,再剪下一个最大的正方形,最后余下的长方形周长是多少厘米?
10.下图是一个方形螺线。已知两相邻平行线之间的距离均为1厘米,求螺线的总长度。
5
5
15
15
金牌教研中心 2013年春季四年级数学09
博学精教 成就学生
4
恭喜你,做完了。要检查哦!
*11.一根铁丝长80厘米,围成一个边长为8厘米的正方形,余下的铁丝围成一个长为14厘
米的长方形,这个长方形的宽是多少厘米?
*12.用4个同样大小的长方形和一个小正方形,拼成一个边长是24分米的大正方形,每个长
方形的周长是多少?
*13.一个正方形被分成6个大小、形状完全一样的长方形,每个长方
形的周长是14厘米。原正方形的周长是多少厘米?
