地球物理、地震正演模拟方法
地震波动方程方向行波波场分离正演数值模拟与逆时成像

地震波动方程方向行波波场分离正演数值模拟与逆时成像陈可洋;陈树民;李来林;吴清岭;范兴才;刘振宽【摘要】为了进一步提高对地震波传播规律的认识,将波印廷矢量引入到二维地震波动方程方向行波波场分离正演数值模拟中.根据地震波波印廷矢量的波场数值特征,实现了对全地震波场中左行波、右行波、上行波和下行波波场的自动识别与分离.以均匀介质模型、倾斜界面模型以及Marmousi模型为例,开展了相应的数值模拟实验与逆时成像处理.计算结果表明,该方法准确有效,能够实现任意时刻波场快照中方向行波的波场分离,并合成分别由左行波、右行波、上行波和下行波形成的波场快照与数值模拟记录.该方法简单易行,计算量较小,对实际地震资料中方向行波波场的识别、分离、成像及验证具有一定的应用价值.【期刊名称】《岩性油气藏》【年(卷),期】2014(026)004【总页数】7页(P130-136)【关键词】地震波动方程;正演模拟;单程波;波场分离;波印廷矢量;逆时成像【作者】陈可洋;陈树民;李来林;吴清岭;范兴才;刘振宽【作者单位】中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;中国石油大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;中国石油大庆油田有限责任公司勘探事业部,黑龙江大庆163453【正文语种】中文【中图分类】P631.40 引言地震波正演数值模拟技术一直是国际地球物理学界的热点内容之一。
随着地震波动理论和计算机技术的不断发展,自20世纪60年代以来该项技术便得到了飞速发展,其中采用波动方程的地震波数值模拟技术能更好地保持地震波的几何学、运动学和动力学等特征,因此可达到精确模拟地震波传播规律的目的[1]。
地震模型正演
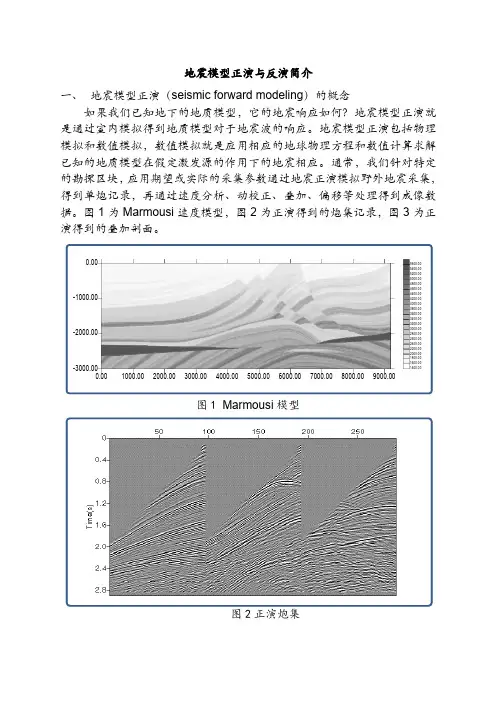
地震模型正演与反演简介一、地震模型正演(seismic forward modeling)的概念如果我们已知地下的地质模型,它的地震响应如何?地震模型正演就是通过室内模拟得到地质模型对于地震波的响应。
地震模型正演包括物理模拟和数值模拟,数值模拟就是应用相应的地球物理方程和数值计算求解已知的地质模型在假定激发源的作用下的地震相应。
通常,我们针对特定的勘探区块,应用期望或实际的采集参数通过地震正演模拟野外地震采集,得到单炮记录,再通过速度分析、动校正、叠加、偏移等处理得到成像数据。
图1为Marmousi速度模型,图2为正演得到的炮集记录,图3为正演得到的叠加剖面。
图1 Marmousi模型图2正演炮集图3 正演叠加剖面二、数值模型正演方法通常,我们提到的模型正演为数值模拟的模型正演,目前常用的数值模拟地震模型正演方法包括基于射线原理的射线追踪法,以及基于波动方程的有限差分法、有限元法、积分方程法、快速傅里叶变换法和拟谱法等。
射线追踪法主要反映地震波的运动学特征,有限差分、有限元法则适合复杂地质构造的正演模拟,积分方程法涉及复杂的数学推导,快速傅里叶变换法在频率域计算得到正演数据。
三、数值模型正演的步骤数值模拟求解地震模型正演问题的步骤主要包括以下三个方面:1) 地质建模,根据研究对象和问题建立地球物理或地质模型;2) 数学建模,根据应用的物理手段和地球物理模型建立相应的数学模型;3) 模拟计算,选择正演计算方法,编写计算程序进行数值模拟计算。
四、什么是地震反演地震反演技术就是充分利用测井、钻井、地质资料提供的丰富的构造、层位、岩性等信息,从常规的地震剖面推导出地下地层的波阻抗、密度、速度、孔隙度、渗透率、沙泥岩百分比、压力等地球物理信息。
反演就是由地震数据得到地质模型,进行储层、油藏研究。
地震资料反演可分为两部分:1)通过有井(绝对)、无井(相对)波阻抗反演得到波阻抗、速度数据体。
2)利用测井、测试资料结合波阻抗、速度数据进行岩性反演,得到孔隙度、渗透率、砂泥百分比、压力等物理数据。
声波介质一次散射波场高斯束Born正演

声波介质一次散射波场高斯束Born正演岳玉波;钱忠平;张旭东;王德营;岳媛媛;常稳【摘要】Born正演是一种常用的地震波场正演模拟方法,也是线性化地震反演的理论基础.在实际应用时,Born正演通常结合常规的地震射线方法进行实现.为了克服常规地震射线方法的弊端,并且保证地震波场的模拟精度和计算效率,本文提出了一种基于高斯束的一阶散射波场Bo rn正演方法.该方法分为两个环节:首先,我们利用高斯束的走时和振幅信息将地下散射点处的反射率映射为地表束中心位置处的局部平面波;然后,我们利用逆倾斜叠加将局部平面波转化为接收点处的时空域散射波场.在具体的实施过程中,我们提出一种以w avelet-bank方式实现的局部平面波合成方法,同现有的算法相比,可以在保持计算精度的同时,大大减少计算时间;此外,我们还利用最速下降法优化了高斯束的迭代循环过程,进一步提高了Born正演的计算效率.两个模型的应用效果证明,本文所提出的高斯束Born正演方法可以精确、高效的实现声波介质一次散射波场的正演模拟,为三维大规模地震波场的正演问题提供了一种切实可行的实现方案.【期刊名称】《地球物理学报》【年(卷),期】2019(062)002【总页数】9页(P648-656)【关键词】一次散射;高斯束;Born近似;声波介质【作者】岳玉波;钱忠平;张旭东;王德营;岳媛媛;常稳【作者单位】东方地球物理公司物探技术研究中心,河北涿州 072751;山东科技大学山东省沉积成矿作用与沉积矿产重点实验室,山东青岛 266590;东方地球物理公司物探技术研究中心,河北涿州 072751;东方地球物理公司物探技术研究中心,河北涿州 072751;山东科技大学山东省沉积成矿作用与沉积矿产重点实验室,山东青岛266590;东方地球物理公司物探技术研究中心,河北涿州 072751;东方地球物理公司物探技术研究中心,河北涿州 072751【正文语种】中文【中图分类】P6310 引言地震波场的正演模拟是勘探地震学的重要研究课题,其不但可以用来认识地下介质的波场传播规律,进而指导地震资料的采集、处理和解释等环节,还可以利用其共轭算子(或者逆算子)来进行地下介质成像和参数反演运算(Tarantola,1984; Bleistein,1987; Beylkin and Burridege,1990; Chapman,2004).目前,地震勘探规模越来越庞大,所面临的地下地质构造也愈加的复杂,在这种背景下发展具备高精度和高效率的波场正演方法具有重要的理论意义和应用价值.现有的地震波场正演模拟方法主要包括两类:一类是波动方程的数值求解方法,包括有限差分法、有限元法、频谱法等(Tessmer, 2000; Virieux et al., 2011).该类方法直接对波动方程进行数值求解,可以计算直达波、折射波、一次反射波和多次波等全部的波场信息,具有很高的波场模拟精度.但是该类方法的计算效率较低,特别是在模拟高频地震波场或者模型速度较低时,为保证计算过程的稳定性而采用的小计算网格往往会导致计算量大幅度增长.因此,较低的计算效率严重地制约了波动方程数值解法在三维大规模地震波场正演时的应用.另一类是射线类方法1983, 2005; 李辉等, 2012),该类方法以波动方程的高频近似解为基础,通过射线追踪来逐步求取每个射线节点的走时和振幅,进而进行一次反射地震波场的合成.常规的射线类算法(如两点射线追踪),计算效率较高,但是其对模型的构造细节不敏感,且存在波场焦散区、阴影区等固有缺陷,致使其波场模拟精度较低.此外,在常规的射线方法中,地下的反射界面是通过离散的样点并结合样条函数进行描述的,当地下构造复杂时,准确的界面描述也是一项很大的难题.射线Born近似或Kirchhoff近似也是常用的地震波场正演方法,具有优于常规射线方法的波场模拟精度(Hudson and Heritage, 1981; Cohen et al., 1986; Jaramillo and Bleistein, 1999; Bleistein et al., 2001),但是该类方法依赖常规的射线追踪来求取地下走时和振幅信息,因此仍然受到常规射线方法局限性的制约,而且在模拟多次走时波场时存在较大的实现难度.针对上述问题,Huang等(2016)提出了一种基于高斯束的地震波场Born正演方法,该方法使用高斯束取代常规的地震射线进行地下散射点走时和振幅信息的计算,在理论上克服了常规射线方法的弊端.他们在实现过程中使用最小虚值走时点来构建等时线,进而通过等时线叠加求取模拟波场.由于高斯束表征的格林函数是一系列高斯束的叠加,仅仅选择最小虚值走时点显然无法代表全部的波场信息,致使文中给出的高斯束Born正演模拟结果同波动方程有限差分正演结果存在较大的差异.此外,他们所提出的算法是逐道进行的,且在频率域中实现,因此计算效率也不存在优势.本文提出了一种新的声波介质高斯束Born正演模拟算法.该方法将Born正演过程分解为两个基本环节:首先,我们利用高斯束的走时和振幅信息,将地下散射点处的反射率函数映射为地表稀疏束中心位置处的局部平面波;然后,我们通过逆倾斜叠加将局部平面波累加到接收点波场中,得到最终的波场正演结果.在实现过程中,我们使用了Hill(2001)和Gray(2005)所提出的最速下降法来减少循环迭代次数,在保证模拟精度的同时,显著地提高了计算效率.此外,我们在平面波合成时,给出了一种wavelet-bank算法,相对于传统的wave-packet算法计算效率提高了数倍.在下文中,我们首先对相关的理论公式进行推导,接下来对具体的计算实现细节进行探讨,最后通过两个数值模型对波场模拟精度和计算效率进行验证.1 方法原理1.1 基于高斯束的Born正演公式在各向同性声波介质中,假设震源和接收点的空间位置矢量分别为xs和xr,那么由震源xs激发,途径地下散射点x,最后到达接收点xr的一次散射地震波场u(xr,xs,ω)可以利用Born正演公式(Tarantola, 1984; Beydoun and Mendes, 1989)来表示:(1)式中,D为地下散射点的集合,G(x,xs,ω)为由震源下行格林函数,G(x,xr,ω)为接收点上行格林函数,F(ω)为频率域的震源函数,m(x)≈2c1(x)/(x)为地下散射点x 处速度扰动c1(x)所引起的地震反射率,c0(x)为该点的背景速度.为了保证格林函数的正则性,并且使正演过程具备处理多次走时波场的能力,我们使用高斯束来计算式(1)中的格林函数,其表达形式为一系列具有不同出射方向的高斯束的叠加(Hill,2001):∬×exp[iω τGB(x,x′)],(2)其中,p=(px,py,pz)为中心射线在出射点x′处的初始射线参数,AGB和τGB分别为高斯束的复值振幅和走时,并且具有如下的形式:AGB(x,x′)=AR(x,x′)+iAI(x,x′),τGB(x,x′)=τR(x,x′)+iτI(x,x′),(3)式中,下标R和I分别代表复数参量的实部和虚部.将式(2)、(3)代入式(1),可以得到以高斯束表征的Born正演公式:∬∬×[AR(xr,xs)+iAI(xr,xs)]exp[iω τR(xr,xs)-ω τI(xr,xs)],(4)其中,AR(xr,xs)和AI(xr,xs)为地下散射点处震源和接收点高斯束振幅乘积的实部和虚部,τR(xr,xs)和τI(xr,xs)为相应的高斯束走时和的实部和虚部,具有如下形式:AR(xr,xs)=AR(x,xr)AR(x,xs)-AI(x,xr)AI(x,xs),AI(xr,xs)=AR(x,xr)AI(x,xs)+AI(x,xr)AR(x,xs),τR(xr,xs)=τR(x,xr)+τR(x,xs),τI(xr,xs)=τI(x,xr)+τI(x,xs).(5)直接利用式(4)进行波场的计算,需要在每个接收点位置计算高斯束.为提高计算效率,我们选择在稀疏的地表束中心位置计算高斯束,并且通过引入一个相移校正量exp[-iωpL·(xr-L)],来近似计算接收点上行格林函数(Gray and Bleistein, 2009;岳玉波等,2012)∬×exp[iω τGB(x,L)-iωpL·(xr-L)\,(6)并且为了减小上述近似的误差,我们在式(4)中引入下述的单位分解公式(岳玉波,2011)(7)得到最终的Born正演公式:∬dpLxdpLyU(L,xs,pL,ω)(8)其中,为束中心间隔,ωr和w0分别为所选择的参考频率和高斯束初始宽度.U(L,xs,pL,ω)为束中心处L所合成的射线参数为pL的局部平面波,具有如下表达形式:∬×[AR(L,xs)+iAI(L,xs)]×exp[iω τR(L,xs)-ω τI(L,xs)].(9)式(8)的作用是将每个束中心处所合成的局部平面波累加到临近的接收点波场中,该式实际上是一个局部逆倾斜叠加过程,因此可以在频率波数域进行高效计算.式(9)的作用是通过高斯束的振幅和走时信息,将地下的反射率映射为束中心处的局部平面波.该式是本文所提出的Born正演方法的核心,其计算过程决定了最终的波场模拟精度和计算效率,因此我们接下来对其进行重点讨论.1.2 多波至模式直接求解式(9),需要对震源和束中心高斯束的所有组合对进行循环计算.在三维情况下,若psx,psy,pLx,pLy的采样数分别为Np,那么需要Np4次的束循环运算(我们称该实现方式为全波至模式),计算量庞大.为了减少计算量,我们应用Hill(2001),Gray(2005)在高斯束偏移中应用的最速下降法对式(9)的计算进行简化,具体的实现过程如下:(1) 首先,我们通过下式将震源和束中心射线参数转化为中心点和偏移距射线参数pm=ps+pL,ph=pL-ps,(10)得到以中心点和偏移距射线参数索引的高斯束组合;(2) 接下来,对于中心点射线参数为的高斯束组合,按照ph进行循环找到使地下散射点处虚值走时最小的高斯束对.假设此时的偏移距射线参数为则该高斯束对中震源高斯束的射线参数为束中心高斯束的射线参数为计算(11)式中的积分,并且将计算结果累加到局部平面波波场中×exp[iω τR(L,xs)-ω τI(L,xs)],(11)式中,为被震源和束中心高斯束同时照明到的地下散射点,行列式detT为应用最速下降法后产生的振幅校正项(Gray and Bleistein, 2009)detT=(12)其中,Qs,QL分别为震源和束中心高斯束所求取的2×2复值动力学射线追踪参数矩阵(Hill, 2001; Gray and Bleistein, 2009),c0(x),c0(L)分别为震源和束中心处的速度.(3) 最后,重复步骤(2)直到所有的中心射线参数处理完成,得到对应不同的接收点射线参数的局部平面波U(L,xs,pL,ω).在计算式(8)后,即可得到最终的Born正演结果.上述实现过程可以称为多波至模式,其可以对地下的大部分波场传播路径进行处理(即使存在多次走时波场),但是所需的束循环次数却由Np4减少为4Np2次.此外,由于高斯束所携带的走时和振幅信息是平滑变化的,求取最小虚部走时的束循环过程可以在稀疏的粗网格上高效的进行.多次波至模式具有比全波至模式高得多的计算效率,而计算精度却损失不大,我们将在模型试算中对此进行验证.1.3 Wavelet-bank算法在将束循环过程进行简化后,我们接下来探讨如何高效的实现式(11)所描述的局部平面波的合成过程.由于式(11)的计算位于整个正演模拟过程的核心位置,其求解过程在很大程度上决定了整个高斯束Born正演的精度和效率.接下来,我们首先对现有的频率域算法和wave-packet算法进行简要的介绍,然后给出一种以wavelet-bank方式实现的时间域高效算法.为了公式表达的简洁,我们将分别用AR,AI来代表式(11)中振幅项的实部和虚部,用τR,τI来代表实部和虚部走时. (1) 频率域算法该算法直接在频率域进行计算,然后利用反傅氏变换求取时间域的局部平面波.由于没有使用任何近似,因此其计算精度是最高的.然而,由于我们需要对每个频率成分进行一次式(11)的循环求解,因此计算量巨大.(2) Wave-packet算法由于频率域算法效率很低,提出了一种wave-packet算法,该方法将频率域的振荡积分转换为了时间域褶积的形式,我们在此直接给出式(11)应用wave-packet 算法后的表达公式(13)其中,是时间域的震源子波,fH(t)为f(t)的希尔伯特变换.由于这两个震源子波项是独立的,我们只需要将地下散射点的反射率通过高斯束的走时和振幅映射叠加到时间域地震道中,待所有的循环计算完成后,将时间域地震道同震源子波项进行褶积即可得到合成的平面波波场.该算法虽然简单直接,但是我们需要将地下单个散射点的反射率m(x)映射到时间域地震道中τR周围的多个时间样点(取决于式中分数项的衰减程度.例如,当τI=5 ms时,时域地震道中|t-τR|≈20 ms的时间样点的振幅项才会衰减为最大值的百分之一).由于散射点的循环位于Born正演的最内层,因此,虽然wave-packet算法的计算效率优于频率域算法,但仍难以令人满意. (3) Wavelet-bank算法我们在此提出一种基于wavelet-bank方式的时间域高效算法.首先,将式(11)通过反傅氏变换转化为时间域:(14)其中,(15)为应用虚部走时对子波频谱进行衰减后的时间域震源子波,为其希尔伯特变换.式(14)只需要将反射率m(x)映射到时间域地震道对应τR的唯一时间样点处,但是每完成一个点的映射我们就需要一次褶积运算,计算效率很低.然而,我们发现式(15)中与虚部走时相关的振幅衰减项只会影响子波的振幅,不会改变子波的相位,因此,我们可以根据所允许的最大虚部走时=5/ωr,创建一个规则采样的虚部走时序列:τI(n)=nΔτI, 0≤n<N,(16)其中,N为离散样点数,ΔτI=/N为采样间隔.然后计算出对应每个序列点τI(n)的震源子波:(17)这样,我们便可以利用线性插值将式(15)表示为:(18)其中,τI(n)=int(τI/ΔτI)×ΔτI,int为取整函数.此时,式(14)便可以表示为:(19)其中, Rn(t),In(t)为:(20)为满足如下条件的地下散射点的集合:(21)W为线性加权系数,根据虚部走时的大小,其取值如下:(22)Wavelet-bank算法的实现过程可以大致概括为:首先,对于地下每一个散射点,根据其对应的实部和虚部走时计算式(20),从而将反射率加权映射到对应的Rn(t),In(t)中;然后,在所有散射点计算完成后,计算式(19)即可得到最终模拟到的局部平面波u(L,xs,pL,t).随着虚部走时的增大,式(15)中的震源子波是单调且平滑衰减的,因此我们不需要选择太大的虚部走时离散样点数N.在实际计算中,我们发现N=10即可完全满足精度的要求.应用wavelet-bank算法,我们只需对地下每个散射点进行两次数据累加运算,此后的褶积运算可以在频率域内高效进行.因此,wavelet-bank算法的计算效率要远高于频率域算法和wave-packet算法.在接下来的模型试算中,我们同样对此进行测试和验证.2 模型试算在本节中,我们将通过两个模型数据进行高斯束Born正演的测试.首先使用一个层状介质模型来对比wavelet-bank算法和现有方法的效率和精度.接下来,使用Marmousi模型测试高斯束Born正演在复杂模型中的应用效果.我们分别计算对应全波至和多波至模式的波场正演结果,并且同具备时间2阶、空间8阶精度的交错网格波动方程有限差分正演结果进行对比.2.1 层状介质模型首先,使用一个层状模型测试wavelet-bank算法的计算效率和精度.图1a展示了所使用的速度模型,该模型横向采样点数为1000,采样间隔为10 m,纵向采样点数为550,采样间隔为5m.图1b为对速度场进行平滑后计算得到的反射率剖面.我们将炮点放在模型表面水平位置5.0 km处并使用主频为20 Hz的雷克子波作为震源,240个接收点均匀的分布在炮点两侧,间隔为20 m(如图1a所示),每个接收道道长为2 s,时间采样间隔为2 ms.我们利用多波至模式进行高斯束Born正演计算,并且在合成局部平面波时分别使用了频率域算法、wave-packet算法和wavelet-bank算法.我们将频率域计算结果作为基准,来比较另外两种算法的精度和效率.图2a、2b、2c分别为应用频率域算法、wave-packet算法和wavelet-bank算法计算得到的单炮正演记录,可以看到三者几乎没有任何的区别.为了进一步对比精度,我们将频率域算法结果d0作为精确解,然后使用函数ε=‖d-d0‖2/‖d0‖2来计算wave-packet或wavelet-bank算法结果d相对于d0的误差.在对比精度的同时,我们还比较了三种方法的计算时间,最终的时间和精度对比结果如表1所示,可以看到wavelet-bank和wave-packet算法的计算精度类似,同频率域算法的相对误差均在1%以内,但是wavelet-bank算法的计算效率却比其他两种方法高得多,大约是wave-packet算法的7倍,是频率域算法的100倍以上.因此,wavelet-bank算法在保证计算精度的同时,极大提高了计算效率.图1 层状介质模型(a) 速度场,地表黑色线段标识了接收点位置,炮点位于接收道中心; (b) 反射率剖面.Fig.1 Multi-layer model(a) The velocity field, wherethe black line segment on the surface marks the recording receivers andthe shot is at the center of the receivers; (b) The corresponding reflectivity profile.图2 应用不同算法得到的单炮记录(a) 频率域算法; (b) Wave-packet算法; (c) Wavelet-bank算法.Fig.2 Shot records simulated with different modeling algorithms(a) Frequency approach; (b) Wave-packet approach; (c) Wavelet-bank approach.在进行波场模拟时,我们采取了高斯束偏移所使用的束宽度、射线参数采样间隔等参数选取准则(Hill, 2001; 岳玉波, 2001).同高斯束偏移类似,高斯束Born正演方法的波场模拟效果对于上述参数的选取并不敏感,具有较高的冗余度.表1 不同算法的精度和效率对比Table 1 The comparison of accuracy and efficiency between different modeling algorithms频率域算法Wave-packet算法Wavelet-bank算法计算时间(s)127.347.331.05相对误差(%)0.000.970.89 2.2 Marmousi模型接下来,使用Marmousi模型验证高斯束Born正演在复杂模型中的应用效果.图3展示了Marmousi模型的速度场,模型横向采样点数为369,采样间隔为20 m,纵向采样点数为375,采样间隔为8 m,相应的反射率剖面如图4所示.在正演时我们同样使用20 Hz的雷克子波作为震源函数,将炮点放置在横向位置为4.4 km 处的地表位置(如图3所示).共有201个接收道,道间隔为20 m,且沿炮点对称分布.可以看到,该炮对地下照明的区域恰好为模型中构造最复杂的部分.我们分别使用全波至和多波至模式并结合wavelet-bank算法进行单炮记录的计算,所得到的结果如图5a和5b所示,可以看到两者的模拟效果基本相同.为了更好的验证高斯束Born正演的波场模拟精度,我们使用有限差分法进行了相同位置处单炮记录的计算,所得到的结果如图5c所示.可以看到,高斯束Born正演结果同有限差分正演结果的波场整体分布特征相似,证明了本文方法在进行复杂模型正演时的有效性.然而,由于Born正演只能模拟一次散射波场,而有限差分法模拟了地下全部的波场信息,因此两者在局部细节上存在一定的差异.对三者的计算时间进行统计,全波至模式为3.89 s、多波至模式为0.67 s、有限差分法为31.29 s,多波至模式具有明显的效率优势.为对比全波至和多波至的差异,我们计算了两者的残差(图5d),并求得两者的相对误差为9.7%.相对于全波至模式,多波至模式结果精度略有损失,但是两者的差异主要在于最速下降法近似对波场整体背景振幅的改变,同时考虑到多波至模式的具有接近于全波至模式6倍的计算效率,因此我们认为上述精度损失完全可以接受.为了进一步验证高斯束Born正演对于复杂模型的模拟效果,我们应用多波至模式模拟了总共135炮的地震记录,并且使用高斯束偏移对模拟记录进行了成像处理,所得到的偏移剖面如图6所示.可以看到,最终的偏移结果准确的恢复了该模型复杂的构造形态,进一步验证了本文所提出的高斯束Born正演算法的正确性和有效性.图3 Marmousi模型速度场地表黑色线段标识了接收点位置,炮点位于接收道中心.Fig.3 The velocity field of Marmousi modelWhere the black line segment on the surface marks the receivers and the shot is at the center of the receivers.图4 Marmousi模型反射率剖面Fig.4 The reflectivity profile of Marmousi model图5 应用不同正演方法得到的单炮记录(a) 全波至模式高斯束Born正演; (b) 多波至模式高斯束Born正演; (c) 有限差分法; (d) 全波至模式(图a)同多波至模式(图b)结果之差.Fig.5 The simulated shot gathers using different modeling methods(a) Full arrival Gaussian beam Born modeling; (b) Most arrival Gaussian beam Born modeling; (c) Finite-difference modeling; (d) The difference between (a) and (b).图6 多波至模式模拟数据的高斯束偏移结果Fig.6 Gaussian beam migration image produced by the simulated data with most arrival mode3 结论本文提出了一种兼具模拟精度和计算效率的声波介质高斯束Born正演方法.该方法使用高斯束作为波场传播算子,不但有效的克服了常规射线方法所具有的阴影区、焦散区等固有缺陷,还具备了模拟多次走时波场的能力,可以实现复杂介质一阶散射地震波场的精确模拟.与此同时,本文还着重探讨了该方法的具体实现过程,给出了一套切实可行的实现方案,在保证波场模拟精度的前提下,极大的提高了计算效率.接下来,我们将进一步探讨弹性各向同性介质中地震波场的Born正演方法.此外,我们还将以本文算法为基础构建相应的共轭算子,进而开展最小二乘高斯束偏移技术的相关研究.References【相关文献】Beydoun W B, Mendes M. 1989. Elastic ray-Born L2-migration/inversion. Geophysical Journal International, 97(1): 151-160.Beylkin G, Burridege R. 1990. Linearized inverse scattering problems in acoustics and elasticity. Wave Motion, 12(1): 15-52.Bleistein N. 1987. On the imaging of reflectors in the earth. Geophysics, 52(7): 931-942. Bleistein N, Cohen J K, Stockwell J W Jr. 2001. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion. New York: Springer.V. 1983. Synthetic body wave seismograms for laterally varying layered structures by the Gaussian beam method. Geophysical Journal International, 73(2): 389-426.V. 2005. Seismic Ray Theory. Cambridge, UK: Cambridge University Press.Chapman C. 2004. Fundamentals of Seismic Wave Propagation. Cambridge, UK: Cambridge University Press.Cohen J K, Hagin F G, Bleistein N. 1986. Three-dimensional Born inversion with an arbitrary reference. Geophysics, 51(8): 1552-1558.Gray S H. 2005. Gaussian beam migration of common-shot records. Geophysics, 70(4):S71-S77.Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration. Geophysics, 74(2): S11-S23.Hill N R. 2001. Prestack Gaussian-beam depth migration. Geophysics, 66(4): 1240-1250. Huang X G, Sun H, Sun J G. 2016. Born modeling for heterogeneous media using the Gaussian beam summation based Green′s function. Journal of Applied Geophysics, 131: 191-201.Hudson J A, Heritage J R. 1981. The use of the Born approximation in seismic scattering problems. Geophysical Journal International, 66(1): 221-240.Jaramillo H H, Bleistein N. 1999. The link of Kirchhoff migrationand demigration to Kirchhoff and Born modeling. Geophysics, 64(6): 1793-1805.Li H, Feng B, Wang H Z. 2012. A new wave field modeling method by using Gaussian Packets. Geophysical Prospecting for Petroleum (in Chinese), 51(4): 327-337.Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266.Tessmer E. 2000. Seismic finite-difference modeling with spatially varying time steps. Geophysics, 65(4): 1290-1293.Virieux J, Calandra H, Plessix R É. 2011. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging. Geophysical Prospecting, 59(5): 794-813.Yue Y B. 2011. Study on Gaussian beam migration in complex medium [Ph. D. thesis] (in Chinese). Qingdao: China University of Petroleum.Yue Y B, Li Z C, Qian Z P, et al. 2012. Amplitude-preserved Gaussian beam migration under complex topographic conditions. Chinese Journal of Geophysics (in Chinese), 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033.附中文参考文献李辉, 冯波, 王华忠. 2012. 波场模拟的高斯波包叠加方法. 石油物探, 51(4): 327-337.岳玉波. 2011. 复杂介质高斯束偏移成像方法研究[博士论文]. 青岛: 中国石油大学.岳玉波, 李振春, 钱忠平等. 2012. 复杂地表条件下保幅高斯束偏移. 地球物理学报, 55(4): 1376-1383, doi: 10.6038/j.issn.0001-5733.2012.04.033.。
《复杂介质地震波正演模拟方法及优化策略》记录

《复杂介质地震波正演模拟方法及优化策略》读书札记1. 内容概括本读书札记主要围绕《复杂介质地震波正演模拟方法及优化策略》聚焦于书中关于复杂介质地震波正演模拟方法的阐述与优化策略的探讨。
在第一部分,本书介绍了地震波正演模拟的基本概念、原理及其在地震研究中的重要性。
阐述了地震波在正演模拟过程中的基本步骤和原理,包括地震波的产生、传播、反射和折射等物理过程。
重点介绍了复杂介质对地震波的影响,包括介质的不均匀性、多相性、孔隙性和裂性等特点,以及这些特性如何影响地震波的传播和模拟结果。
书中详细阐述了复杂介质地震波正演模拟的具体方法,介绍了不同模拟方法的原理、特点和适用场景,如有限元法、有限差分法、边界元法等数值计算方法。
探讨了各种方法的优缺点以及在实际应用中的限制和挑战,在此基础上,详细描述了模型建立、参数设置、计算过程及结果分析等关键步骤。
重点讨论了地震波正演模拟的优化策略,首先分析了影响模拟效率和精度的主要因素,如计算资源、算法优化、并行计算技术等。
提出了针对性的优化策略和方法,包括改进算法、优化模型参数、提高计算效率等。
探讨了在实际应用中如何根据具体情况选择合适的优化策略,以提高模拟的效率和精度。
最后一部分为实践应用与案例分析,书中通过具体案例,展示了复杂介质地震波正演模拟方法在实际地震研究中的应用,包括地质构造分析、地震灾害评估、油气勘探等领域。
通过案例分析,使读者更好地理解和掌握复杂介质地震波正演模拟方法的应用和优化策略。
1.1 研究背景地震波在复杂介质中的传播是地球科学研究的重要基础,对于地震勘探、工程勘察和地震预警等领域具有至关重要的作用。
由于地下介质的复杂性,如非均匀性、各向异性、断裂和渗透性等,使得地震波的正演模拟成为一个极具挑战性的问题。
传统的地震波正演方法往往基于简化假设,如均匀介质、单相介质等,难以准确模拟复杂介质中的地震波传播行为。
发展新的正演模拟方法以更好地描述和预测复杂介质中的地震波传播,对于提高地震勘探和地震预警的准确性具有重要意义。
二维地震正演模拟方法技术研究

二维地震正演模拟方法技术研究一、本文概述随着地球物理学的深入发展和油气勘探的不断推进,二维地震正演模拟方法技术在地震勘探领域的应用越来越广泛。
该技术通过模拟地震波在地下介质中的传播过程,为地震资料解释、储层预测和油气勘探提供重要的理论支撑和实践指导。
本文旨在深入研究二维地震正演模拟方法技术,探讨其基本原理、发展历程以及当前的研究热点和难点,为进一步提高地震勘探的精度和效率提供理论支持和技术保障。
本文将对二维地震正演模拟方法技术的基本概念进行阐述,包括其定义、特点以及应用领域等。
接着,回顾二维地震正演模拟方法技术的发展历程,分析其在不同阶段的主要特点和优缺点。
在此基础上,重点探讨当前二维地震正演模拟方法技术面临的主要挑战和难点,如复杂地质条件下的模拟精度问题、大规模计算的效率问题等。
针对这些挑战和难点,本文将进一步分析现有的解决方案和发展趋势,如基于高性能计算的并行化技术、基于人工智能的反演方法等。
同时,结合具体的应用案例,分析二维地震正演模拟方法技术在油气勘探、矿产资源调查等领域的实际应用效果,以验证其有效性和可靠性。
本文将对二维地震正演模拟方法技术的未来发展进行展望,提出可能的研究方向和应用前景。
通过本文的研究,旨在为推动二维地震正演模拟方法技术的发展和应用提供有益的参考和借鉴。
二、二维地震正演模拟理论基础二维地震正演模拟是地球物理学中一种重要的方法,其理论基础主要基于波动方程和地震波的传播原理。
在二维空间中,地震波的传播受到介质速度、密度、弹性等因素的影响,这些因素决定了波场的空间分布和时间变化。
理解和应用波动方程是二维地震正演模拟的关键。
波动方程是描述波在介质中传播的基本方程,对于地震波而言,常用的波动方程有弹性波方程和声波方程。
在二维正演模拟中,我们通常采用声波方程,因为它相对简单且能够较好地模拟地震波的主要特征。
声波方程描述了声波在弹性介质中的传播规律,包括波速、振幅、相位等参数的变化。
煤炭采空区地震勘探正演模拟

[ 参考文献]
[ 1 ] 陆基孟主编 ,地震勘探原理 ( 上 、下册 )[ M ]. 石油大学 出版社 。2 O O 4年 1 月.
[ 2 ] 周绪文编 ,反射波地震勘探方法 [ M]. 石油工业出版社 , 1 9 8 9 年.
[ 3 ] 宗志 刚,地震勘探方法在探测煤矿采空 区中的应用研究 [ D ]. 中国地质大学 ( 北京 ) ,2 0 0 6年
探 的可行性前提。
3 地震勘探技术及正演模拟方法
地震勘探是应用地球物理勘探的一种方法。通过测量波的传播时间,分析振动特征 ,确
收稿 日期 : 2 o 1 3 —0 2 —1 9
作者简介:李西周 ,男 , 4 1 岁 ,1 9 9 4 年毕业于西安地质学院 ,工程师,长期从事物探勘查工作 。
Ab s t r a c t :G o a l R e c o n n a i s s a n c e i s a h o t s p o t a n d a d i ic f u l t s p o t i n r e c e n t y e a r s .Ap p H c a i f o n o f s e i s - mi c e x p l o r a t i o n t o c o lmi a n e g 0 a f a r e a i s c o n s i d e r e d t o b e a n e f e c i t v e me t h o d . Ba s e d o n e s t a b l i s h -
象。
( 4 ) 采空 煤层 的厚 度及 采 空 区 的宽度 ,对 勘探 结 果 影 响 较 大 ,煤 层 越厚 、采 空 区域 越
大异常特征越 明显 ,但在剖面上须存在较明显的未采区域 ,为标志同相轴的识别提供基础。 ( 5 )地震波在穿越采空区的时候 ,在采空区两侧及下方存 在绕射现象 ,导致下部 同相 轴不连续 ,该特征也可作为采空区识别的参考 因素。 ( 6 )有多层采空存在的区域 ,具有阴影效应 ,由于上部采空的影响,很 难再识别下部 采空 的存 在 。当两层 采 空 区域间距较 大 时 ,下 部采 空 的识别 有所 改善 。 ( 7 )构造复杂区域采空区的识别较 困难 ,尤其是地表起伏较大 的区域 ,很难判断同相 2 采Fra bibliotek 区物性特征
利用正演模拟识别各类地震假象
利用正演模拟识别各类地震假象黄诚;杨飞;李鹏飞【摘要】针对各类地震假象给地震解释人员带来的困扰,本文探讨了正演模拟方法研究假象问题优越性,并从理论方面简单介绍了不同正演模拟方法的优缺点.一般情况下,复杂的地质构造(包括起伏地层类、断层类、低速和高速充填体类、火山岩刺穿类及生物礁类的地质模型)往往在地震剖面上形成假构造,或出现偏离真实构造位置的情况,本文选取波动方程地震正演模拟方法模拟分析了起伏地层类和断层类地震假象的产生,指出了正确的解释方法和依据,对提高复杂研究区地震资料岩性解释的可靠性具有重大意义.【期刊名称】《工程地球物理学报》【年(卷),期】2013(010)004【总页数】4页(P493-496)【关键词】正演;地质模型;起伏地层类;断层类;地震假象【作者】黄诚;杨飞;李鹏飞【作者单位】长江大学油气资源与勘探技术教育部重点实验室,湖北武汉434100;长江大学油气资源与勘探技术教育部重点实验室,湖北武汉434100;长江大学油气资源与勘探技术教育部重点实验室,湖北武汉434100【正文语种】中文【中图分类】P631.41 引言地下地质构造往往是复杂多变的,在地震剖面上容易形成许多假的构造,或出现偏离真实构造位置的情况。
而正演模拟作为一种技术方法,能够帮助解释人员正确认识地下地质构造,直观而有效地解决地震假象给解释工作带来的困扰。
近年来,随着地震勘探技术的发展,要求解决的地质问题也越来越难。
针对复杂地区的勘探问题,国内外众多地球物理学家对地震波在复杂介质中的传播问题进行了研究,各种新的正演计算方法不断涌现,如吴如山等为代表发展了广义屏方法[1],Nielsen 等则研究了基于曲线网格的二维声波方程虚谱法模拟[2]等。
2 地震正演模拟理论地球物理正演是对地质模型进行理论模拟,分为物理模拟和数值模拟两种[3]。
物理模拟是按一定比例制作与实际地质体相对应的地质模型,参照野外探测的情况进行模拟。
地球物理学报视电阻率正演计算程序
地球物理学报视电阻率正演计算程序摘要:一、引言二、地球物理学报视电阻率正演计算程序的概述三、程序的输入参数和输出结果四、程序的优缺点分析五、应用实例六、结论正文:一、引言随着地球物理勘探技术的发展,视电阻率正演计算在地球物理领域中的应用越来越广泛。
地球物理学报视电阻率正演计算程序作为一种重要的地球物理计算工具,为地球物理学家提供了便利。
本文将详细介绍地球物理学报视电阻率正演计算程序的相关内容。
二、地球物理学报视电阻率正演计算程序的概述地球物理学报视电阻率正演计算程序是一种基于地球物理原理的视电阻率正演计算方法。
该程序利用地球物理观测数据(如地震数据、电磁数据等)和地质模型,通过数值模拟方法,计算地下的视电阻率分布。
这种方法可以为地球物理学家提供关于地下地质结构和矿产资源的有效信息。
三、程序的输入参数和输出结果地球物理学报视电阻率正演计算程序需要输入以下参数:地球物理观测数据(如地震数据、电磁数据等)、地质模型、电导率剖面等。
程序运行后,将输出视电阻率分布图、地质结构图等。
四、程序的优缺点分析优点:地球物理学报视电阻率正演计算程序具有较高的计算精度和可靠性,能够为地球物理学家提供准确的地下地质结构信息。
此外,该程序具有较好的适应性,可以应用于多种地球物理勘探领域。
缺点:该程序的运行时间较长,对计算机硬件要求较高。
此外,程序的输入参数和输出结果的解释需要地球物理学家具备一定的专业知识。
五、应用实例地球物理学报视电阻率正演计算程序在我国多个矿产资源勘探项目中发挥了重要作用。
例如,在我国某地热资源勘探项目中,该程序成功地为地球物理学家提供了准确的地下地质结构信息,为地热资源的开发提供了有力支持。
六、结论地球物理学报视电阻率正演计算程序是一种具有广泛应用前景的地球物理计算工具。
该程序能够为地球物理学家提供准确的地下地质结构信息,为地球物理勘探领域的发展做出了重要贡献。
伪谱法地震波正演模拟的多线程并行计算_谢桂生
第20卷 第1期地 球 物 理 学 进 展V ol.20 N o.12005年3月(页码:17~23)P ROG RESS IN G EOP H YSICSM arch 2005伪谱法地震波正演模拟的多线程并行计算谢桂生, 刘 洪, 赵连功(中国科学院地质与地球物理研究所,北京100029)摘 要 地震波的正演模拟,尤其是3D 正演模拟,往往涉及大规模的数据存储和计算,问题的规模往往超出计算机的物理内存,或者计算时间让问题的求解者难以忍受,即使采用目前存储和计算能力很强的计算机,其计算费用仍然是十分昂贵的.本文提出一种基于多线程协同使用多CPU 和计算域分割的正演模拟并行计算技术,使得问题的求解过程得以加快,大大地缩短了用户等待的时间.为了检验我们的并行算法的可行性,文中以傅利叶正演模拟技术为例,给出了声波和3D 各向异性弹性波模拟的例子,并对不同版本(串行、并行)运算效率进行了比较,证实了方法的有效性.关键词 声波,弹性波,各向异性,正演模拟,伪谱法,并行计算,多线程技术中图分类号 P315,P631 文献标识码 A 文章编号 1004-2903(2005)01-0017-07Parallel Algorithm based on the multithread techniquefor pseudospectal modeling of seismic waveXIE Gui -sheng , LIU H ong , ZH AO Lian -go ng(I nstitu te o f Geo logy and Geoph ysics ,Chinese A cademy o f S ciences ,Beijing 100029)A bstract T he modeling of 3D seismic wav efiled is o ften inv olved in mass data sto rage and requires hug e amounts o f co mputer memo ry and computa tion time.Even w hen using current po werful computers ,it is still com putatio nally v er -y intensive.To ove rcome this ,the pa rallel algo rithm fo r 3D wavefiled modeling based o n concurrent use of a number of pro cesso r by the multithread technique has develo ped.T o illustr ate the feasibility o f our parallel algo rithm ,the two examples fo r pseudo spectra l modeling o f seismic wave are given :2D aco ustic and 3D ela stic anisot ropy modeling o f wave pr opagation.Keywords aco ustic w ave ,elastic w ave ,a niso tro py ,modeling ,pseudospec tral technique ,parallel algo rithm ,mul -tithread technique收稿日期 2004-05-20; 修回日期 2004-08-20.基金项目 中国科学院知识创新工程重大项目(编号KZCX1-SW -18)和中科院与海洋石油总公司联合项目资助.作者简介 谢桂生,男,1964年生,江西信丰人,中国科学院地质与地球物理所博士研究生,主要研究方向为地震波理论与成像以及相关方面的研究.(E -mail :xieguisheng @ )0 引 言地震波正演模拟是复杂近地表、崎岖海地、裂缝油藏及时移地震等研究的基础之一.模拟地震波在复杂非均匀介质中的传播,通常采用有限差分、有限元或傅利叶等数值模拟技术.求解同一个问题在相同模拟精度的条件下,有限差分或有限元模拟技术需要较小的网格,因此需要占用较多的内存、更长的计算时间(Fo rgberg ,1987;Daudt 等,1989)[1,2].由于傅利叶模拟技术采用傅利叶变换计算所有的空间导数,从理论上讲其精度是最高的,因此傅利叶模拟技术是非常具有吸引力的地震波正演模拟技术.Ko sloff 等(1982,1988)[3,4]分别将该模拟技术应用于各向同性2D 声波和弹性波的模拟、1988年应用于3D 声波和弹性波的模拟;谢桂生(1994)[5]将其应用于各向异性介质3D 弹性波场的模拟.但是即使采用傅利叶模拟技术,3D 波场模拟、尤其是3D 弹性波波场的模拟也还是非常昂贵,它需要大量的内存和计算时间.为克服这些问题,Reshef (1988b )等[6]在CRAY X -M P 超级计算机上,采用并行傅利叶模拟技术计算3D 弹性波波场;Furumura (1998)等[7,8]给出了一种在各种并行平台下(如:分布式内地 球 物 理 学 进 展20卷存并行计算机、共享内存并行计算机或Cluster网络计算机集群)实现并行傅利叶模拟技术的方案,并实现了3D弹性波波场模拟.并行计算,从硬件的角度看计算机硬件经历了从阵列机(SIM D)、向量机及向量并行机、共享存储的对称多处理器系统(SM P)、分布存储的大规模并行处理系统(M PP)到NUM A(非一致访问的分布共享存储)并行机系统和计算机机群系统(Clus-ters)的演变过程[9—11].因此对于不同架构的并行计算机,并行算法的设计、实现是有差异的.从软件的角度看,并行计算技术可分为以下几个级别:作业级(粗精度)、任务级、子任务级、循环级(中精度)和指令级(细精度)的并行.并行计算的软件架构应针对不同的问题可采用不同级别的设计.本文旨在于提供一种可选择的3D弹性波波场模拟并行计算方案,该方案是以傅利叶模拟技术为基础的.并行算法的实现可采用多种方式,可以是多进程或多线程方式.目前,有一些实验性和商业的并行环境,如PVM、MPI或P4等可供选用,也可以直接利用操作系统级的并行环境.在商业并行编程环境中,并行是以多进程方式还是以多线程方式实现,以及进程或线程的控制过程被隐藏起来,编程人员不必关心;在操作系统级的并行环境中,程序员可以自由选择多进程方式还是多线程方式实现并行算法,但必须编写进程或线程的控制代码.文中首先简短地回顾地震波傅利叶模拟技术,然后给出了并行傅利叶波场模拟方案及算法,并在共享内存并行计算机(SMP)上分别以多线程和多进程协同并行方式实现了该算法,最后给出了声波和3D各向异性弹性波模拟的例子以说明我们的并行算法是可行的.1 地震波正演模拟并行算法1.1 傅利叶地震波正演模拟地震波场的正演模拟归结起来就是在一定的边界条件和初始条件下求解下列偏微分方程 u tt=L u+f x∈Ψ,(1a) u(u,t≤0)=0 x∈Ψ,(1b) u t(x,t≤0)=0 x∈Ψ,(1c) u(x,t)=g(x,t) x∈S,(1d)其中 L≡∑3m,n=1a mn2x m x n+∑3n=1b n xn+c称为二阶线性偏微分算子,u为场量,式中a mn、b n和c为x n的二次连续可微函数,通常与介质的性质有关,g(x,t)为已知的函数,f为源函数,求解域Ψ∈R3,S为Ψ的边界.设u(nΔx),(n=0,…,N-1)与U(mΔk),(m =0,…,N-1;ΔK=2π/(NΔx))为一离散傅利叶变换对,则利用傅利叶变换的性质,对u(nΔx)的空间导数可在波数域通过傅利叶变换精确计算: dd xu(nΔx)=1NΔx∑N-1m=0(imΔk)U(mΔk)e i2πmn N,(2)其中 U(mΔk)=Δx∑N-1n=0u(nΔx)e-i2πmn N,i=-1.对于时间偏微分用下列蛙跳格式积分方案 u t x,l+12=u t x,l-12+Δt u tt(x,l).(3a)u(x,l+1)=u(x,l-1)+Δt u t x,l+12,(3b)其中 u tt(x,l)=∑3m,n=1a mn F-1[k xmk xnF u(x,l)] +∑3m=1b m F-1[-ik xmF u(x,l)]+c u(x,l),(3c)式中F、F-1分别表示正反傅立叶变换,l为正演时间步,Δt为时间积分步长.上式即为在求解域Ψ内傅利叶地震波正演模拟方程.对于各向同性介质的声波方程2Px2+2Py2+2Pz2=1v22Pt2,(4)式中P为标量压力场,v为介质的速度.根据上述的算法,可得各向同性介质的声波正演模拟方程为 P t x,l+12=P t x,l-12+ΔtP tt(x,l),(5a) P(x,l+1)=P(x,l-1)+ΔtP t x,l+12,(5b)其中 P tt(x,l)=v2{F-1[k2x FP]+F-1[k2y F P]+F-1[k2z FP]},(5c)对于各向异性介质,弹性波的传播满足下列方程 üi=σij,j/ρ+f i/ρ,(6a) σij=c ijkl e kl,(6b) e ij=12(u i,j++u j,i),(6c)181期谢桂生,等:伪谱法地震波正演模拟的多线程并行计算式中ρ为介质的密度,c ijkl为介质的弹性常数,u i为位移的第i分量,σij为二阶对称应力张量,e ij为二阶对称应变张量,f i为体力的第i分量,i表示对第i分量的偏导数,表示对时间的导数.其傅利叶正演模拟方程为 u.i x,n+12=u.i x,n-12+Δtüi(x,n),(7a) u.i(x,n+1)=u.i(x,n-1)+Δtu.i x,n+12,(7b)其中 üi(x,n)=∑3j,k,l=1F-1{k x j[A ijkl F-1[k x l Fu k(x,n)]+F-1[k xkF u l(x,n)]]}+f i/ρ,(7c) A ijkl=c ijkl/2ρ.从上述的正演模拟公式中可以看到各空间偏微分项的计算是独立的,因此在此级别上各项的计算可以同时进行.在傅利叶正演模拟方法中,有限模型边界处不会产生反射,但由于用FFT计算空间导数隐含了空间上的周期性,因此在波到达数值网格的边界时出现折返.通常采用吸收边界、边界振幅衰减或者利用波场在空间上的周期性来消除边界折返.1.2 地震波正演模拟的并行算法针对上述的波场模拟方程,我们基于数据和计算域分割的思想,提出了并行傅利叶波场正演模拟算法,在该算法中所有子域的场量计算是同时进行的.设离散后的场量为u(i,j,k),N x、N y和N z分别表示x、y和z方向的网格点数.分析傅利叶地震波正演模拟方程可知,场量对x、y和z方向的导数计算是独立的,因此这三个方向导数的计算可分别用三组CPU完成.在每一组的导数计算中,例如在计算场量u(i,j,k)对x方向的导数时,每一层(j或k为常数)场量u(i,j,k)对x方向的导数计算也是独立的,因此可将场量u(i,j,k)沿y或z方向分成p组(p为该组内CPU的个数),如图1所示.组内每个CPU计算N y N z/p次场量u(i,j,k)对x方向的导数;另两个方向的导数计算也是如此.因此可建立三个存储空间X(i,j,k)、Y(i,j,k)和Z(i,j,k)分别存储场量u(i,j,k)对三个方向导数的计算结果.每个处理器从u(i,j,k)中得到场值,然后利用(2)式计算场值的导数,并将计算的结果分别回送于对应的存储空间X(i,j,k)、Y(i,j,k)或Z(i,j,k)中,最后计算出方程(3c)的结果.实际实现时存储空间X(i,j,k)、Y(i,j,k)和Z(i,j,k)是缓冲空间,仅占用较少的内存.一旦某层的结果计算出,该结果将被取出累加到方程(3c)的结果,下一层计算可重用该缓冲空间.并行模拟算法的代码是用C++语言编写,通过多线程协同方式实现的.图1 计算x或y方向导数时,场量分组的示意图Fig.1 Ex ample of domain partition of the w avefileds w hen they a re calculated fo r calculating the x o r y differentiation下面将给出声波方程和各向异性弹性波方程的并行正演模拟的实例,说明该并行模拟方案是可行的.2 并行模拟的实例这里我们给出了声波方程和各向异性弹性波方程的并行正演模拟的例子.并行正演模拟算法是在共享存储的对称多处理器系统(SMP)上,以操作系统级为平台实现的.为了便于比较,在实现声波方程的并行正演模拟算法时,采用了两种编程模式:多线程方式和多进程方式.由于在共享存储的对称多处理器系统(SM P)中实现上述算法,在多进程方式版本的实现时采用多进程共享内存方式,这样避免了边界网格的处理和进程间的大量数据通讯,与此同时还实现了一个正演模拟的串行版本,以便比较它们的执行效率.2.1 声波方程并行模拟的实例这里我们给出了二维声波模拟算法运行结果的比较.算法的测试采用如图2a所示的速度模型结构,速度模型的网格大小为:10×8m2,网格节点数为:622×492,计算的时间步数为:2501.图2b是零偏移距正演剖面.19地 球 物 理 学 进 展20卷图2 速度模型及其零偏移距正演剖面(a)速度模型(b)零偏移距正演剖面Fig.2 V elo city mo del and zo re-off set sectio n o f modeling(a)Velocity model(b)zore-offset section 表中列出了两种机型的CPU数量和CPU主频的大小,同时给出了三个版本的正演模拟程序在单CPU和多CPU计算机上的运行时间.单CPU计算机的CPU主频为1.2G Hz,多CPU计算机的CPU主频为450M H z,两者主频相差大约2.7倍.三个版本的正演模拟程序在单CPU计算机运行效率显然是串行版本的最高,以串行版本的效率为1(以下比较均以串行版本为准),多线程版本为0.819,多进程版本为0.490.这是由于并行版本有进程间或线程间的通讯开销,尤其是进程版本开销更多所致.表1 不同版本模拟算法运行效率Table1 The ef ficiencies for different modeling algo rithmsCPU算法CPU时间效率Q因子1×1.2GHz串行180.6721216.8线程并行220.6400.819264.8进程并行367.9840.490441.62×450M H z串行556.3131500.7线程并行282.250 1.970254.0进程并行304.594 1.826274.1由于串行版本不能利用多CPU的优势,在单个高CPU主频的计算机上和拥有多个低CPU主频的计算机上运行的时间相差大约3.1倍.但在多CPU计算机上并行版本显示出其优势,运行的效率显然占优,多进程版本效率为1.826,由于多线程版本通讯开销相对多进程版本低,其运行效率达1.970,用时几乎是串行版本的一半.表2 介质参数Table2 Paramters of medium层号ρ(kg/m3)c11=c22/V p(GPa/m/s)c33/V s(GPa/m/s)c44=c55(GPa/m/s)c66(GPa/m/s)c12(GPa/m/s)c13=c23(GPa/m/s) 1225035002350----2281071.853.426.134.3 3.2 1.2 3225035002350----定义CPU主频与CPU使用时间的乘积(称之为Q因子)来初略估计不同CPU主频和CPU数量的机器间程序运行的效率.从表中可以看到在低CPU主频多CPU机上多线程版本运行的效率高于高CPU主频单CPU机相同版本的运行效率,几乎接近于高CPU主频单CPU机上串行版本的效率.2.2 3D各向异性介质弹性波并行模拟的实例并行正演模拟算法的测试采用了三维断层地质201期谢桂生,等:伪谱法地震波正演模拟的多线程并行计算图3 三维断层模型的三视图Fig.3 T ri -sectio n o f 3D fault mo del模型,由三层介质和一垂直断层组成,断层方位近南北向,上下层均为各向同性介质,中间夹一厚度为100m 的各向异性介质层,图3为该模型的三视图,模型的大小为:2.56×2.56×5.12km 3.各层介质的参数见表2.用20×20×20m 3的规则网格离散该模型,网格总节点数为:128×128×256,所需总内存约288M 字节.模拟是在具有主频为450M Hz 的双CPU 机上进行的,一个主频为30H z 的点爆炸震源作用在位置(1500m ,1500m )、深60m 处,计算的时间步数为:1001,耗时约28.5h.图4是不同时刻的波场快照的三视图.可以看到爆炸源在各向同性表层介质中产生的P 波波前,从三个分量上可以看到切向分量为零,这说明模拟程序能够很好地模拟爆炸源.同时也可看到P 波入射到界面时的波的反射与转换,以及透射转换S 的分裂过程,为了更清晰地看到这些现象,图5分别给出了不同时刻不同剖面方向的波场快照放大显示.图4 不同时刻的波场快照三视图(U 为x 分量、V 为y 分量、W 为z 分量)F ig.4 T ri -section of snapshot o f the elastic wav efiled at different time step for 3D fault mo del(U for x -component ,V for y -com ponen t ,W for z -component )21地 球 物 理 学 进 展20卷图5 不同时刻不同方向的波场快照图(U为x分量、V为y分量、W为z分量)Fig.5 Snapsho ts o f the elastic wav efiled at different time step and directio n (U for x-component,V for y-com ponen t,W for z-component)波从各向同性表层介质入射到界面时,产生反射的P波与P-SV转换波,没有切向分量的SH波型转换;当波进入夹层后,我们不仅在径向分量上看到透射的P波与P-S转换波,而且还看到切向分量上出现反射和透射能量,说明S波产生了分裂,这是由于夹层的各向异性所决定的.图5清晰地展现了S波分裂的分裂过程.当波到达垂直断层带时,断点产生的绕射波清晰可见.3 讨 论三维地震波的正演模拟是非常昂贵和耗时的,尤其是应用于3D各向异性弹性波模拟等实际问题.我们给出了一个可选择并行模拟方案,并且在操作系统级的并行环境下实现了地震波正演模拟的并行计算,计算的效率成倍地提高.但也看到算法的实现时,依附于共享存储的对称多处理器系统(SM P),虽然充分地利用了共享存储的优点,但对于更数据规模的模拟计算,由于共享存储器容量的221期谢桂生,等:伪谱法地震波正演模拟的多线程并行计算大小限制,还必需借助于分布存储的大规模并行处理系统或计算机机群系统(Cluste rs机群系统)的并行实现.致 谢 特别感谢中国科学院地质与地球物理所的杨辉博士为本文绘制波场三视图.参 考 文 献(References):[1] Fornb erg B.The pseudospectral meth od:C om parisons w ith fi-nite difference for the elastic w ave equation[J].Geophysics,1987,52:483~501.[2] Dau dt C R,Braile L W,Now ack R N,Chiang C S.A compar-is on of finite difference and Fourier method calcu lations of syn-thetic seismogram s[J].Bu ll S eis S oc Am,1989,79,1210~1230.[3] Kos loff D,Bay sal E.Forw ard modeling by a Fou rier m ethod[J].Geop hysics,1982,47:1402~1412.[4] Reshef M,Kosloff D,Edw ards M,H siung C.Th ree-dimen-sional acous tic model ing by th e Fourier method[J].1988a,Ge-ophy sics,53:1175~1183.[5] 谢桂生.三维各向异性介质中地震波模拟[J].石油物探,1994,33(3):54~58.[6] Reshef M,Kosloff D,Edwards M,Hsiung C.T hree-dimen-sional elastic m odeling by the Fourier method[J].Geop hysics,1988b,53:1184~1193.[7] Tak as hi F,Kennett B L N,H iroshi T.Parallel3-Dpseudospectral simulation of seismic wave propagation[J].Ge-ophysics,1998,63,279~288.[8] Chen H W,M cM ech an G A.3-D ph ysical m odeling andpseudospectral s imulation of seismic common-sou rce data vol-umes[J].Geophysics,Soc of Expl Geophy s,1993,58,121~133.[9] 王宏琳.新一代系统———计算机集成油气勘探系统[J].石油地球物理勘探,1996.[10] 杨辉,高亮,刘洪,李幼铭,范兴才.微机群并行实现M armousi模型叠前深度偏移[J].地球物理学进展,2001,16(3):58~75.[11] 刘礼农,陈树民,高亮,张尔华,刘洪,李幼铭.波动方程三维叠前深度偏移并行计算流程探索[J].地球物理学报,2002,45(增刊):298~306.23。
基于Madagascar的矿山微地震正演模拟
山 西建筑SHANXJ ARCHITECTURE第40卷第6期2 2 2 1 年 3 月Vol. 60 Ne. 6Mvf. 2021・69 •文章编号:1029-6725 (2029) 96-9966-93基于Manaaascor 的矿山微地震正演模拟周项通赵晓阳杨涛(黄河勘测规划设计研究院有限公司,河南郑州450003)摘要:矿山微震监测是一种新型的地球物理方法,通过分析不同复杂程度的矿井层状模型的微震波场特征,能够进一步了解微地震的传播规律。
基于开源地球物理软件Manaaascof ,结合山东菏泽某煤田地层特征,建立不同复杂程度的矿井层状模型进行正演模拟,并对得到的波场快照和地震记录进行了对比分析。
关键词:矿山5微地震5正演,Manaaascof中图分类号:P631 文献标识码:A〔概述矿山微震监测是一种新型的地球物理方法,它主要是在对岩体破裂产生的微地震事件进行捕捉和反演定位的基 础上,结合岩体力学来对岩体损伤演化的过程进行综合分析,从而指导技术人员提前采取措施,阻止灾害事故的发 生。
与传统地震勘探不同的是,矿山微震震源的空间坐标、时间、强度都是未知量,且能量较弱(里氏震级一般在-3〜1之间),大多数微震事件的频率范围为200 He 〜1 502 He,持续时间小于Is 。
高精度的矿山微地震正演模拟是对微震事件进行准确定位的前提,通过分析不同复杂程度的矿井层状模型的微震波场特征,能够了解微地震的传播规律, 对后期的微震事件综合分析具有很好的指导意义。
Madagascrr 是一个开源、功能丰富的地球物理软件,由堪萨斯大学奥斯丁分校的Sergey Fomei 教授在2003年发起并于2005年正式发布。
该软件最大的优点就是提供了一 个很好的开发环境,使用者可以根据需求对软件中已有的成熟模块进行改进并与他人进行交流。
本文基于crr 建立不同复杂程度的矿井层状模型进行正演模拟,并对得到的波场快照和地震记录进行对比分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整理得 解线性矩阵方程式,求取研究区域内各节点的位势Vf,有唯一解。 其精度取决于三角元的尺度
三、积分方程法
不足:积分方程方法涉及较复杂的数学推导 优点:仅需在异常区求出未知场
模 式拟中二,维u表地示电电断位面边,电界f表场节点 示源项。
内节点
3、微分方程离散化,构组差分方程
i k i-1,k
i,k-1 i,k i+1,k
i,k+1
ux,uxx,…和uz,uzz,…分别表示u对x和z的一阶、二阶导数等
含源分区均匀岩石中位函数二维差分方程 无源分区均匀岩石中位函数二维差分方程
2.时间域电磁场的模拟准则
3.模拟模型的种类-4种
导电性溶 液 或固体 作为均匀 介质
导电性 更好的 覆盖
4、物理模报实验装置
5.模型材料
超声波模拟 几何相似性
L为几何尺度,为波长
物理相似性
速度比和密 度比相似
纵、横波速度 比的相似性
地球模型建立的要求:
模型应能够反映主要地质构造和岩石、矿物特征, 具有代表性或普遍性(共性)、针对性(目的性)、 特殊性(特殊问题)
地球物 理模拟
物理模拟
数学 模拟法
概念:将描述各种地球物理场的 方程或表达式及初、边值条件通 过数值方法求出它们的数值解。
相似原理
解析方法 数值 模拟法
正演主要工具
投资大,选材难, 结果真实,
最简捷方便 ,仅适 用少数简单模型
效率高,机时少, 周期短,费用低。
数学模拟方法求解地球物理正演问题的一般步骤:
在各向同性均匀介质、平面波入射假设条件下,标量波动方程
传播问题
在二维情况下,
zz|z=0=ux=0,zx|z=0=uz=0
初始条件 (自由表面)边界条件
2、区域离散化
采用正方形网格元进行网格划分, 步长h;m,n为当前网格节点的横 向及垂向编号;l时间取样号
差分方程式
利用差分方程式,由上至下,由左至右并随时标l增加计算 空间任一点(m,n)的波场um,n,l+1便得到波传播图像, um,0,l是地面直达波和反射波场的合成记录。
下角标dis表示组合前不连接的三角元。对应这两个元的未组合能量写为矩阵
未组合能量
两个三角元连接前、后满足以下关系
下角标con注记已联接,对应连接后的总能量变为
连续近似的势能分布被表示为与元顶点位势向量有关的二次型
5、方程求解计算
记k为网格节点(连接后多个三角形的顶点)的编号,则 Laplace方程的 有限元近似解要将连接网中的势能极小化。——变成了求极值问题 则势能极小化为
第一步,地质建模: 据研究对象和问题建立地球模型 或地质结构模型;
第二步,数学建模: 据使用的物理手段和地球模型建 立相应的数学模型;
第三步,模拟计算: 选择计算方法,编制计算程序, 进行数值计算。
地球模型建立的要求:
模型应能够反映主要地质构造和岩石、矿物特征, 具有代表性或普遍性(共性)、针对性(目的性)、 特殊性(特殊问题)
一次场方程组——可求解
其是电导率为1的均匀介质内的场
定义:二次场为实测场(总场)与一次场之差,并用上角标s表示
整理得二次场方程
二次场方程组
可转换成积分方程,求解
是散射电流,仅在异常体中才存在
表明:二次场可以认为是由异常体中的散射电流Js引起的。
建立二次场方程的积分方程
二次电场可通过将散射电流源Js乘以适当的并矢格林函数G(r,r/), 并对异常体所占的体积做积分而得,
常用微分方程及其泛函 Poisson方程 :
泛函: 非其次Helmhotz方程 :
泛函: 标量波动方程 :
泛函: 频域电磁波似稳电磁场方程 :
泛函:
有限元法解二维Laplace方程举例
1、介质剖分——采用单纯形单剖分元
所谓单纯形,在平面上为三角形,三维空间为四面体 由于三角元以公共边界及顶点连接成网,势的分布在穿过单元 时保持连续。
值越小,计算值与理论值越接近。
矛盾:减小步长h将成倍增加计算节点数目,增加计算机内存需
求和计算时间。降低了效率,增加了费用
解决计算速度与精度矛盾的较好方法:采用变步长,即在
近区将网格分得密些,远区影响较小,可分得稀些。
弹性波场计算举例 1、反射地震中波传播方程
密度不均匀介质弹性波标量波动方程
激发问题
将比例关系代入野外方程得模型参数描述的野外方程
按照模拟准则,要使模拟结果与实际一致,野外和模型磁场满足的波动 方程应完全相同,对比可以写出
模拟准则——参数比例尺
上式两边为响应参数k2r2,亦称综合参数,右端=1,表明:具有相同综合 参数的每个系统必定产生相同的电磁响应 ,与、、及l的具体数值 无关。因此,模拟准则简化为
模型不宜太复杂,否则无法建立相应的数学模型; 或者计算结果太复杂,难以分析、辨认地质特征与地 球物理场特征之间的联系。
常用数值 计算方法
有限差分法 有限元法 积分方程法
计算速度快 微分方程法,适于模拟复 边界刻化好 杂的地质情况
涉及较复杂的数学推导,仅需在异常区求 出未知场,经济,易于处理三维模拟问题
模型的物性参数一 般也应按一定的比例改变; 观测装置要微型化。 缩小模型响应能代表野外实际模型响应
模拟准则:使实际模型场与模拟场具有相同的幅值和规律
一、电磁场物理模拟的基本原理 1.频率域电磁场的模拟准则
野外条件下地 电体参数方程
模型条件下地 电体参数方程
室内模型模拟系统尺寸与野外比例关系为1/l——几何结构比例尺
正演方法
云美厚
河南理工大学资源与环境学院
地球物 理学的 问题
基础
正演 问题
反演 问题
目的
按事物一般原理(或模型)及相关的条 件(初始条件、边界条件)来预测事物 的结果(可由观测可得
据地球物理场的实际观测值(有时也用 理论计算值)定量或定性解释推断地球 内部结构(地质体形态和岩层物性)。
应用地球物理学的基本方程式——阻尼标量波动方程
2、将势场u展成某种简单函数和系数的线性组合 假定,单元内势可用线性(一阶)方程表示,有 V=a+bx+cy 沿三角元边缘势V可以由相应两角点势值线性内插而 来,如果两个三角元共用一条边,则位势在跨单元时 保持连续。 为求各系数,设三个顶点上势为V1,V2,V3
用Cramer准则解线性方程组,求得系数a,b,c的表达式。代回原方程可 得三角元内任一点位势的一阶近似式
其一般只对基本方程中的空间微分算子作逼近,而与时 间微分有关的计算仍然多采用有限差分法。 基本原理:变分原理或最小势能原理
认为:对与势场能量有关的泛函极小化等效于直接解 相应的场的方程
对Laplace方程
势场能量表达式
***满足Laplace方程的势场,同时也是满足势场能量 F(u)取极小的场。
有限差分法采用了直接解方程的办法,有限元法采用了F(u)极小化逼近势场
4、线性方程组的形成与求解
式中[A]是方程组的系数矩阵。其与 物性参数(如电阻率)分布有关; {u}是电位u的列向量,其分量为所 有节点上的电位; {F}是常向量。
当给定电阻率分布(空间分布,模型结构)及边界条件后,解 线性方程式便可求得电位的空间分布
计算精度:主要决定于步长h。一般说来,网格划分越细,即h
基本方程式的有限差分格式 (2D)
有限差分波动方程模拟结果演示实例
地质模型
炮集1 快 照
1 2
3 4
5 6
7
模型边界产生的 假象
蝴蝶结
山顶激发波动方程正演模拟记录
炮集2 快照
1 2
蝴蝶结
3 4
5 6
7
山谷激发波动方程正演模拟记录
二、有限单元法 突出优点:界面刻画能力强。对与复杂介质结构有关的 偏微分方程边值问题的数值计算适应性强。
三角元内任一点位势的一阶近似式
系 数 为
A为三角元的 面积 ,且有
3、单个元内位势能
写成矩阵形式有
至此,对单个元的近似已经完成
4、三角元连接组合求取总势能
整个区域的势能为单个三角元势能之总和。根据最小势能准则,使整个 研究区域势能极小化,就是使所有三角元组合后的势能极小化 两个元组合方法:设一对元在连接前的顶点位势可写成以下列向量
式中,u表示地球物理场的一种,如声场.电磁场的某一分 量等;f(x,t)为源函数;x为空间的一个点;t为时间;系数h和 g对不同场有不同的物理意义。
位场:在场源外区域满足拉普拉斯方程的物理场称为,如 重力场、磁场和稳定场, 如电磁场、弹性波场
求解正 演问题
一般步骤:
(1)区域离散化网格剖分:确立合适网格步长,边界节点定位 步长选择很重要——决定计算精度、速度
(2)微分方程离散化——构建差分方程 边界条件离散化——构建边界条件差分方程 初始条件离散化——构建初始条件差分方程
(4)线性方程组形成与求解
位场计算举例: 1、位场所满足的方程
有源 无源
2、区域网格剖分
有限差分计算必须满足的条件如下:
(1)时间取样率t(t=lt)满足t≤h/c
(2)震源信号的主周期T<10h/c,否则有严重的频散。
(3)由于地下介质无限,而计算网格有限,计算网格 的边界必须是吸收边界。
(4)震源必须作专门处理,即在源点加入f(t) 信号。 有限差分计算的优点与不足:
优点:简明快速 不足:边界刻划能力弱。因只能使用矩形网格,对复杂 的地质构造不能准确地模拟,如,反射地震中常见的倾 斜界面、电法勘探中的局部不规则电性不均匀体等。
