南京盐城2019届高三一模数学试题及答案
江苏省南京市、盐城市2019届高三第二次模拟考试数学试题(WORD解析版)

南京市、盐城市2019届高三年级第二次模拟考试数 学2019.03注意事项:1. 本试卷共4也,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试试卷为120分钟.2. 答题前,请务必将自己的姓名、学校、班级卸载答题卡上.试题的答案写在答题卡上对应题目的答案空格内.考试结束后,交回答题卡.一、填空题:本题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1、已知集合{|13}A x x =<<,{|24}B x x =<<,则A B = .答案:{|14}x x << 考点:并集的运算。
解析:并集,即属于A 或属于B 的部分,故有A B ={|14}x x <<2、若复数2zi a i=+(i 为虚数单位),且实部和虚部相等,则实数a 的值为 . 答案:-2考点:复数的概念与运算。
解析:(2)2z i a i ai =+=-+,实部和虚部相等,所以,a =-23、某药厂选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17),将其按从左到右的顺序分别编号为第一组、,第二组,… …,第五组,右图市根据实验数据制成的频率分布直方图,已知第一组与第二组共有20人,则第三组钟人数为 .答案:18考点:频率分布直方图。
解析:第一、二组的频率为:1×(0.24+0.16)=0.4, 总人数:200.4=50(人),第三组人数:50×1×0.36=18 4、右图是某算法的伪代码,输出的结果S 的值为.答案:16 考点:算法初步。
解析:第1步:i =3,S =4;第2步:i =5,S =9;第3步:i =7,S =16,退出循环,此时S =16。
5、现有5件相同的产品,其中3件合格,2件不合格,从中随机抽检2件,则一件合格,另一件不合格的概率为 . 答案:35考点:古典概型。
南京盐城一模数学试卷及答案.pdf

……………3 分
因为四边形 ABCD 是正方形,对角线 AC 交 BD 于点 O ,
所以点 O 是 AC 的中点,所以 AO OC ,
所以在 ACC1 中,
PC1 PC
AO OC
1.
……………6 分
(2)证明:连结 A1C1 .
因为 ABCD A1B1C1D1 为直四棱柱,所以侧棱 C1C 垂直于底面 ABCD ,
b sin
B
c sin C
可得
AC
sin
3
AB sin C
,所以
AB 2 .
………………7 分
(2)由(1)知
B
3
,所以
A
0,
3
时,
3
A (0,
3
)
,
由
cos
B
A
4 5
即
cos(3
A)
4 5
可得
sin( 3
A)
1
cos2 ( 3
A)
3 5
, ……………10 分
∴ sin
A
sin(
所以 BD 面 ACC1A1 . ……………………………………… …………………………………………12 分 又因为 P CC1, CC1 面ACC1A1 ,所以 P 面ACC1A1 ,又因为 A1 面ACC1A1 ,
所以 A1P 面 ACC1A1,所以 BD A1P .
………………………………………………14 分
最低点的横坐标为π,则ω的值为 ▲ . 6
高三数学试题第 1页(共 4 页)
11.已知 H 是△ABC 的垂心(三角形三条高所在直线的交点),→ AH =1→ AB +1→ AC ,则 cos∠BAC
【精品试题】江苏省盐城中学2019届高三仿真练习(2019.5.30 )数学试题答案解析全国百强校
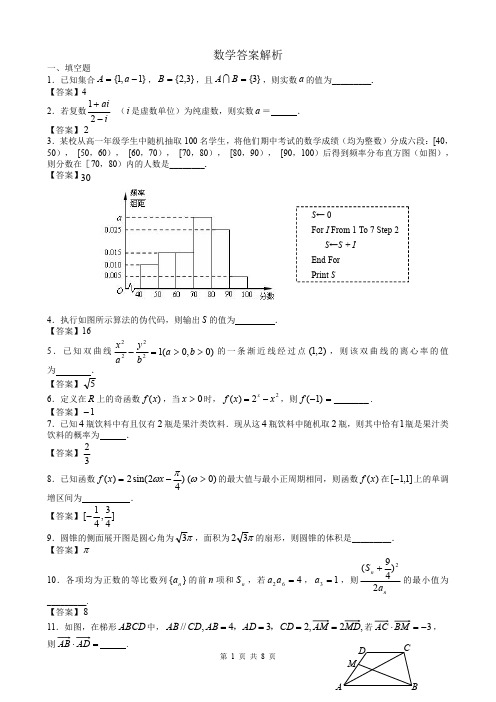
数学答案解析一、填空题1.已知集合}1,1{-=a A ,}3,2{=B ,且}3{=B A ,则实数a 的值为_________.【答案】42.若复数iai-+21(i 是虚数单位)为纯虚数,则实数a =.【答案】23.某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)后得到频率分布直方图(如图),则分数在[70,80)内的人数是________.【答案】304.执行如图所示算法的伪代码,则输出S 的值为.【答案】165.已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线经过点)2,1(,则该双曲线的离心率的值为.【答案】56.定义在R 上的奇函数)(x f ,当0>x 时,22)(x x f x-=,则)1(-f ._______=【答案】1-7.已知4瓶饮料中有且仅有2瓶是果汁类饮料.现从这4瓶饮料中随机取2瓶,则其中恰有1瓶是果汁类饮料的概率为.【答案】328.已知函数)0()42sin(2)(>-=ωπωx x f 的最大值与最小正周期相同,则函数)(x f 在]1,1[-上的单调增区间为.【答案】]43,41[-9.圆锥的侧面展开图是圆心角为π3,面积为π32的扇形,则圆锥的体积是_________.【答案】π10.各项均为正数的等比数列}{n a 的前n 项和n S ,若462=a a ,13=a ,则nn a S 2)49(2+的最小值为_________.【答案】811.如图,在梯形ABCD 中,,2,234,//MD AM CD AD AB CD AB ====,,若3-=⋅BM AC ,则=⋅AD AB .S←0For I From 1To 7Step 2S←S +I End For Print S【答案】2312.已知F 是椭圆()2222:10x y C a b a b +=>>的左焦点,B A ,为椭圆C 的左、右顶点,点P 在椭圆C 上,且PF x ⊥轴,过点A 的直线与线段PF交与点M ,与y 轴交与点E ,直线BM 与y 轴交于点N ,若ON NE 2=,则椭圆C 的离心率为.【答案】2113.若函数⎪⎩⎪⎨⎧>+-≤-=)0(2)0(4)(3x ax x x a e x f x 有三个不同的零点,则实数a 的取值范围是_________.【答案】]4,3(14.在ABC∆中,角C B A ,,的对边分别为c b a ,,,已知52=c ,且C b B b A a B C a sin 25sin sin cos sin 2+-=,点O 满足0=++OC OB OA ,83cos =∠CAO ,则ABC∆的面积为__________.【答案】55二、解答题15.(本小题满分14分)如图,四棱柱1111ABCD A B C D -为长方体,点P 是CD 中点,Q 是11A B 的中点.(Ⅰ)求证:AQ ∥平面1PBC ;(Ⅱ)若1BC CC =,求证:平面11A B C ⊥平面1PBC .解:(Ⅰ)取AB 中点为R ,连接PR ,1B R .由已知点P 是CD 中点,Q 是11A B 的中点可以证得,四边形111AQB R PRB C ,都为平行四边形,所以1AQ B R ∥,11B R PC ∥,所以1AQ PC ∥,··········································4分因为AQ ⊄平面1PBC ,1PC ⊂平面1PBC ,所以AQ ∥平面1PBC .······················································7分(Ⅱ)因为四棱柱1111ABCD A B C D -为长方体,1BC CC =,所以11B C BC ⊥······8分因为11A B ⊥平面11BB C C ,所以11A B ⊥1BC ······9分因为1111A B B C B = ,11A B ⊂平面11A B C,1B C ⊂平面11A B C ,所以1BC ⊥平面11A B C ,·1BC ⊂平面1PBC ,所以平面11A B C ⊥平面1PBC .······14分16.三角形ABC 中,角A 、B 、C 所对边分别为a ,b ,c ,且2sin B =3cos B .(1)若cos A =13,求sin C 的值;P A FO EN M yxr rh(2)若b =7,sin A =3sin C ,求三角形ABC 的面积.解(1)由2sin B =3cos B ,两边平方得2sin 2B =3cos B ,即2(1-cos 2B )=3cos B ,解得cos B =12或cos B =-2(舍去).又B 为三角形内角,则B =π3.因为cos A =13,且A 为三角形内角,则sin A =223,故sin C =sin(B +A )=sin(π3+A )=32cos A +12sin A =3+226.(2)解法一因为sin A =3sin C ,由正弦定理可得a =3c .由余弦定理知:b 2=a 2+c 2-2ac cos B ,则7=9c 2+c 2-3c 2,解得c =1,则a =3.面积S =12ac sin B =334.解法二由sin A =3sin C 得sin(C +B )=3sin C ,即sin(C +π3)=3sin C ,则12sin C +32cos C =3sin C ,即32cos C =52sin C ,故可得tan C =35.又C 为三角形的内角,则sin C =2114.由正弦定理知b sin B =csin C ,则c =1.又sin A =3sin C =32114,故面积S =12bc sin A =334.17.为了在雨季来之前处理好受污染的化工原料,某公司拟建造如图所示的蓄水池密封存放,该蓄水池下方是高为h 的圆柱体,上方是半径为r 的半球体.设计要求,蓄水池总体积为64π33m ,且h ≥2r.经测算,上方半球形部分每平方米建造费用为c(c 为常数且c >3)千元,下方圆柱体的侧面和底面部分平均每平方米建造费用为3千元,设该蓄水池的总建造费用为y 千元.(1)求y 关于r 的函数解析式,并指出该函数的定义域;(2)当该蓄水池的总建造费用y 最小时,求半径r 的值.(1)rr c y ππ128)12(2+-=定义域为(]2,0(2)当293≤<c ,2=r 时总费用最小;当29>c 时31264-=c r 18.如图,在RtΔABC 中,∠A 为直角,AB 边所在直线的方程为x -3y -6=0,点T (-1,1)在直线AC 上,斜边中点为M (2,0).(1)求BC 边所在直线的方程;(2)若动圆P 过点N (-2,0),且与RtΔABC 的外接圆相交所得公共弦长为4,求动圆P 中半径最小的圆方程.解(1)因为AB 边所在直线的方程为x -3y -6=0,AC 与AB 垂直,所以直线AC 的斜率为-3.故AC 边所在直线的方程为y -1=-3(x +1),即3x +y +2=0.设C 为(x 0,-3x 0-2),因为M 为BC 中点,所以B (4-x 0,3x 0+2).xyOT M点B 代入x -3y -6=0,解得x 0=-45,所以C (-45,25).所以BC 所在直线方程为:x +7y -2=0.(2)因为RtΔABC 斜边中点为M (2,0),所以M 为RtΔABC 外接圆的圆心.又AM =22,从而RtΔABC 外接圆的方程为(x -2)2+y 2=8.设P (a ,b ),因为动圆P 过点N ,所以该圆的半径r =(a +2)2+b 2,圆方程为(x -a )2+(y -b )2=r 2.由于⊙P 与⊙M 相交,则公共弦所在直线的方程m 为:(4-2a )x -2by +a 2+b 2-r 2+4=0.因为公共弦长为4,r =22,所以M (2,0)到m 的距离d =2,即|2(4-2a )+a 2+b 2-r 2+4|2(2-a )2+b 2=2,化简得b 2=3a 2-4a ,所以r =(a +2)2+b 2=4a 2+4.当a =0时,r 最小值为2,此时b =0,圆的方程为x 2+y 2=4.19.已知函数xe x x xf 22)(+-=,2)(x a ax e x g x --=。
南京市、盐城市2019届高三年级数学第二次模拟考试参考答案(终稿)

南京市、盐城市2019届高三年级第二次模拟考试 数学参考答案及评分标准 2019.03说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.{ x |1<x <4} 2.-2 3. 18 4. 16 5.356. -4 7.y =±233x 8. 3 9.4+4 3 10.(-2,3) 11.±21 12.2 13.(-9,13) 14.2+12二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)解:(1)由a +b 与a -b 互相垂直,可得(a +b )·(a -b )=a 2-b 2=0,所以cos 2α+λ2sin 2α-1=0. ·································································· 2分 又因为sin 2α+cos 2α=1,所以(λ2-1)sin 2α=0. ····································· 4分 因为0<α<π2,所以sin 2α≠0,所以λ2-1=0.又因为λ>0,所以λ=1. ···································································· 6分 (2)由(1)知a =(cos α,sin α).由a ·b =45,得cos αcos β+sin αsin β=45,即cos(α-β)=45. ···························· 8分因为0<α<β<π2,所以—π2<α-β<0,所以sin(α-β)=-1-cos 2(α-β)=-35. ············································· 10分所以tan(α-β)=sin(α-β) cos(α-β)=-34, ······················································· 12分因此tan α=tan(α-β+β)=tan(α-β)+tan β1-tan(α-β) tan β=12. ···································· 14分16.(本小题满分14分)证明:(1)连接A 1B ,在三棱柱ABC -A 1B 1C 1中,AA 1∥BB 1且AA 1=BB 1, 所以四边形AA 1B 1B 是平行四边形.又因为D 是AB 1的中点,所以D 也是BA 1的中点. ································ 2分在△BA 1C 中,D 和E 分别是BA 1和BC 的中点,所以DE ∥A 1C . 又因为DE ⊄平面ACC 1A 1,A 1C ⊂平面ACC 1A 1,所以DE //平面ACC 1A 1. ···································································· 6分 (2)由(1)知DE ∥A 1C ,因为A 1C ⊥BC 1,所以BC 1⊥DE . ······························· 8分 又因为BC 1⊥AB 1,AB 1∩DE =D ,AB 1,DE ⊂平面ADE ,所以BC 1⊥平面ADE . 又因为AE ⊂平面ADE ,所以AE ⊥BC 1. ············································· 10分 在△ABC 中,AB =AC ,E 是BC 的中点,所以AE ⊥BC .······················· 12分 因为AE ⊥BC 1,AE ⊥BC ,BC 1∩BC =B ,BC 1,BC ⊂平面BCC 1B 1,所以AE ⊥平面BCC 1B 1. ································································· 14分17.(本小题满分14分)解:过O 作OH 垂直于AB ,垂足为H .在直角三角形OHA 中,OA =20,∠OAH =α,所以AH =20cos α,因此AB =2AH =40cos α. ··········································· 4分 由图可知,点P 处观众离点O 处最远. ····················································· 5分 在三角形OAP 中,由余弦定理可知OP 2=OA 2+AP 2-2OA ·AP ·cos(α+2π3) ·········· 7分=400+(40cos α)2-2×20×40cos α·(-12cos α-32sin α)=400(6cos 2α+23sin αcos α+1)=400(3cos2α+3sin2α+4)=8003sin(2α+π3)+1600. ·················································· 10分因为α∈(0,π3),所以当2α=π6时,即α=π12时,(OP 2)max =8003+1600,即(OP )max =203+20.······································· 12分因为203+20<60,所以观众席内每一个观众到舞台O 处的距离都不超过60米. ········································ 13分 答:对于任意α,上述设计方案均能符合要求. ········································· 14分18.(本小题满分16分)解:(1)依题意⎩⎪⎨⎪⎧c a =22,a = 2 ,解得⎩⎨⎧c =1,a =2,所以b 2=a 2-c 2=1,所以椭圆C 的方程为x 22+y 2=1. ···························································· 2分(2)解法1设直线的方程为y =k (x -2),代入椭圆C 的方程,消去y ,得(1+2k 2)x 2-8k 2x +8k 2-2=0.因为直线l 交椭圆C 于两点,所以△=(-8k 2)2-4(1+2k 2)( 8k 2-2)>0,解得-22<k <22. ············································································ 4分设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=8k 21+2k 2,x 1x 2=8k 2-21+2k 2.①设AB 中点为M (x 0,y 0),则有x 0=x 1+x 22=4k 21+2k 2,y 0=k (x 0-2)=-2k1+2k 2. ································ 6分 当k ≠0时,因为QA =QB ,所以QM ⊥l ,即k QM ·k =-2k1+2k 2-0 4k 21+2k 2-m ·k =-1.解得m =2k 21+2k 2. ············································································ 8分当k =0时,可得m =0,符合m =2k 21+2k 2.因此m =2k 21+2k 2.由0≤k 2=m 2(1-m )<12,解得0≤m <12. ············································· 10分②因为点Q 为△F AB 的外心,且F (-1,0),所以QA =QB =QF .由⎩⎪⎨⎪⎧(m +1)2=(x -m )2+y 2,x 22+y 2=1, ······························································ 12分 消去y ,得x 2-4mx -4m =0,所以x 1,x 2也是此方程的两个根,所以x 1+x 2=4m ,x 1x 2=-4m . ························································ 14分 又因为x 1+x 2=8k 21+2k 2,x 1x 2=8k 2-21+2k 2,所以8k 21+2k 2=-8k 2-21+2k 2,解得k 2=18. 所以m =2k 21+2k 2=15. ······································································ 16分解法2①设A (x 1,y 1),B (x 2,y 2),AB 中点为M (x 0,y 0),依题意⎩⎨⎧x 122+y 12=1,x 222+y 22=1,两式作差,得y 1-y 2x 1-x 2×y 0x 0=-12 (x 0≠0).又因为y 1-y 2x 1-x 2=k AB =y 0-0x 0-2,所以y 02=-12x 0(x 0-2).当x 0=0时,y 0=0,符合y 02=-12x 0(x 0-2).(i) ···································· 4分又因为QA =QB ,所以QM ⊥l ,所以(x 0-m )(x 0-2)+(y 0-0)(y 0-0)=0, 即y 02=-(x 0-m )(x 0-2).(ii) ····························································· 6分 由(i) (ii),解得x 0=2m ,因此y 02=2m -2m 2. ········································ 8分 因为直线l 与椭圆C 相交,所以点M 在椭圆C 内,所以(2m )22+(2m -2m 2)<1,解得m <12.又y 02=2m -2m 2≥0,得0≤m ≤1.综上,0≤m <12. ·········································································· 10分②因为点Q 为△F AB 的外心,且F (-1,0),所以QA =QB =QF .由⎩⎪⎨⎪⎧(m +1)2=(x -m )2+y 2,x 22+y 2=1,消去y ,得x 2-4mx -4m =0. (iii) ················· 12分 当y 0≠0时,则直线l 为y =-x 02y 0(x -2),代入椭圆的方程,得(2y 02+x 02)x 2-4x 02x +4x 02-4y 02=0. 将(i)带入上式化得x 2-2x 0x +3x 0-2=0.(iv)当y 0=0时,此时x 0=0,x 1=-2,x 2=2也满足上式. ····················· 14分由①可知m =x 02,代入(iii)化得x 2-2x 0x -2x 0=0.(v)因为(iv)(v)是同一个方程,所以3x 0-2=-2x 0,解得x 0=25,所以m =x 02=15. ············································································ 16分19.(本小题满分16分)解:(1)当a =2时,f (x )=ln x -2x -2x +3,f '(x )=1x -8(x +3)2,则f '(1)=12. 又因为f (1)=0,所以函数f (x )图象在x =1处的切线方程为y =12(x -1),即x -2y -1=0. ·············································································· 2分 (2)因为 f (x )=ln x -2x -2x -1+2a所以f '(x )=1x -4a (x -1+2a )2=x 2-2x +4a 2-4a +1x (x -1+2a )2=(x -1)2+4a 2-4a x (x -1+2a )2, ··········· 4分 且f (1)=0.因为a >0,所以1-2a <1. ①当4a 2-4a ≥0时,即a ≥1时,因为f '(x )>0在区间(1,+∞)上恒成立,所以f (x )在(1,+∞)上单调递增. 当x ∈[1,+∞)时,f (x )≥f (1)=0,所以a ≥1满足条件. ······································································· 6分 ②当4a 2-4a <0时,即0<a <1时,由f '(x )=0,得x 1=1-2a -a 2∈(0,1),x 2=1+2a -a 2∈(1,+∞) 当x ∈(1,x 2)时,f '(x )<0,则f (x )在(1,x 2)上单调递减,所以当x ∈(1,x 2)时,f (x )<f (1)=0,这与x ∈[1,+∞)时,f (x )≥0恒成立矛盾. 所以0<a <1不满足条件.综上,a 的取值范围为[1,+∞). ·························································· 8分 (3)①当a ≥1时,因为f '(x )≥0在区间(0,+∞)上恒成立,所以f (x )在(0,+∞)上单调递增, 所以f (x )不存在极值,所以a ≥1不满足条件. ······································· 9分 ②当 12<a <1时,1-2a <0,所以函数f (x )的定义域为(0, +∞),由f '(x )=0,得x 1=1-2a -a 2∈(0,1),x 2=1+2a -a 2∈(1,+∞)列表如下:由于f (x )在(x 1 ,x 2)是单调减函数,此时极大值大于极小值,不合题意,所以12<a <1不满足条件. ······························································ 11分③当a =12时,由f '(x )=0,得x =2.列表如下:此时f (x )仅存在极小值,不合题意,所以a =12不满足条件.····································································· 12分④当0<a <12时,函数f (x )的定义域为(0,1-2a )∪( 1-2a , +∞),且0<x 1=1-2a -a 2<1-2a ,x 2=1+2a -a 2>1-2a .列表如下:所以f (x )存在极大值f (x 1)和极小值f (x 2),················································ 14分 此时f (x 1)-f (x 2)=ln x 1-2x 1-2x 1-1+2a -ln x 2+2x 2-2x 2-1+2a=ln x 1x 2-4a (x 1-x 2)(x 1-1+2a )( x 2-1+2a )因为0<x 1<1-2a <x 2,所以ln x 1x 2<0,x 1-x 2<0,x 1-1+2a <0,x 2-1+2a >0,所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),所以0<a <12满足条件.综上,所以a 的取值范围为(0,12). ·························································· 16分20.(本小题满分16分)解:(1)因为(a 1a 2)2=a 13a 3,所以a 22=a 1a 3,因此a 1,a 2,a 3成等比数列. ················ 2分设公比为t ,因为a 1,2a 2,3a 3成等差数列,所以4a 2=a 1+3a 3,即4×a 2a 1=1+3×a 3a 1,于是4t =1+3t 2,解得t =1或13,所以a 2a 1=1或13. ················································································· 4分(2)①因为(a 1a 2…a n )2=a 1n +1a n +1n -1,所以(a 1a 2…a n a n +1)2=a 1n +2a n +2n ,两式相除得a n +12=a 1a n +2n a n +1n -1,即a n +1n +1=a 1a n +2n ,(*) ······························ 6分 由(*),得a n +2n +2=a 1a n +3n +1,(**)(*)(**)两式相除得a n +2n +2a n +1n +1=a n +3n +1a n +2n ,即a n +22n +2=a n +1n +1a n +3n +1, 所以a n +22=a n +1a n +3,即a n +12=a n a n +2,n ≥2,n ∈N *, ···························· 8分 由(1)知a 22=a 1a 3,所以a n +12=a n a n +2, n ∈N *,因此数列{a n }为等比数列. ······························································ 10分 ②当0<q ≤2时,由n =1时,可得0<a 1≤1,所以a n =a 1q n -1≤2 n -1,因此a 1+a 2+…+a n ≤1+2+…+2 n -1=2n -1,所以0<q ≤2满足条件. ································································· 12分 当q >2时,由a 1+a 2+…+a n ≤2n-1,得a 1(1-q n )1-q≤2n-1,整理得a 1q n ≤(q -1)2n +a 1-q +1. ···················································· 14分 因为q >2,0<a 1≤1,所以a 1-q +1<0, 因此a 1q n <(q -1)2n ,即(q 2)n <q -1a 1,由于q2>1,因此n <log q 2 q -1a 1,与任意n ∈N *恒成立相矛盾,所以q >2不满足条件.综上,公比q 的取值范围为0<q ≤2. ··············································· 16分南京市、盐城市2019届高三年级第二次模拟考试数学附加题参考答案及评分标准 2019.03说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.21.【选做题】在A 、B 、C 三小题中只能选做2题,每小题10分,共计20分.请在答.题.卡指定区域内......作答.解答应写出文字说明、证明过程或演算步骤. A .选修4—2:矩阵与变换 解:(1)因为A =⎣⎢⎡⎦⎥⎤2b a 3,B =⎣⎢⎡⎦⎥⎤110-1,AB =⎣⎢⎡⎦⎥⎤214 1,所以⎩⎪⎨⎪⎧ 2-b =1,a =4, a -3=1,即⎩⎨⎧b =1,a =4. ·································································· 4分(2)因为|A |=2×3-1×4=2, ······································································ 6分所以A -1=⎣⎢⎢⎡⎦⎥⎥⎤32 -12 -42 22 =⎣⎢⎢⎡⎦⎥⎥⎤32 -12 -21. ··········································· 10分B .选修4—4:坐标系与参数方程解:直线l 的参数方程为⎩⎨⎧x =t ,y =3t +2(t 为参数)化为普通方程为:3x -y +2=0. ······ 2分设P (cos θ,3sin θ) ,则点P 到直线l 的距离d =|3cos θ-3sin θ+2|(3)2+1=|6cos(θ+π4)+2|2, ················ 6分取θ=-π4时,cos(θ+π4)=1,此时d 取最大值,所以距离d 的最大值为6+22. ······························································ 10分C .选修4—5:不等式选讲解:当x ≥12时,有2x -1-x ≥2,得x ≥3. ······················································ 4分当x <12时,有1-2x -x ≥2,得x ≤-13. ··················································· 4分综上,原不等式的解集为{x |x ≥3或x ≤-13}. ··········································· 10分22.(本小题满分10分)解:(1)设“甲从进口A 开始到出口B 经过点C ”为事件M ,甲选中间的路的概率为13,在前面从岔路到达点C 的概率为12,这两步事件相互独立,所以选择从中间一条路走到点C 的概率为P 1=13×12=16. ···························· 2分同理,选择从最右边的道路走到点C 的概率为P 2=13×12=16.因为选择中间道路和最右边道路行走的两个事件彼此互斥, 所以 P (M )=P 1+P 2=16+16=13.答:甲从进口A 开始到出口B 经过点C 的概率13. ····································· 4分(2)随机变量可能的取值X =0,1,2,3,4, ··············································· 5分 则P (X =0)=C 04×(13)0×(23)4=1681, P (X =1)=C 14×(13)1×(23)3=3281, P (X =2)=C 24×(13)2×(23)2=2481, P (X =3)=C 34×(13)3×(23)1=881, P (X =4)=C 44×(13)4×(23)0=181, ························································ 8分 概率分布为:数学期望E (X )=0×1681+1×3281+2×2481+3×881+4×181=43. ······················· 10分23.(本小题满分10分)解:(1)当n =3时,共有6个点,若染红色的点的个数为0个或6个,则T =C 36=20;若染红色的点的个数为1个或5个,则T =C 35=10;若染红色的点的个数为2个或4个,则T =C 34=4;若染红色的点的个数为3,则T =C 33+C 33=2;因此T 的最小值为2. ······································································ 3分(2)首先证明:任意n ,k ∈N *,n ≥k ,有C k n +1>C kn .证明:因为C k n +1-C k n =C k -1n >0,所以C k n +1>C kn .设2n 个点中含有p (p ∈N ,p ≤2n )个染红色的点, ①当p ∈{0,1,2}时,T =C 32n -p ≥C 32n -2=(2n -2)(2n -3)(2n -4)6=4×(n -1)(n -2)(2n -3)6, 因为n ≥4,所以2n -3>n ,于是T >4×n (n -1)(n -2)6=4C 3n >2C 3n . ·············································· 5分②当p ∈{2n -2,2n -1,2n }时,T =C 3p ≥C 32n -2,同上可得T >2C 3n . ········································································· 6分 ③当3≤p ≤2n -3时,T =C 3p +C 32n -p ,设f (p )=C 3p +C 32n -p ,3≤p ≤2n -3, 当3≤p ≤2n -4时,f (p +1)-f (p )=C 3p +1+C 32n -p -1-C 3p -C 32n -p =C 2p -C 22n -p -1, 显然p ≠2n -p -1,当p >2n -p -1即n ≤p ≤2n -4时,f (p +1)>f (p ), 当p <2n -p -1即3≤p ≤n -1时,f (p +1)<f (p ),即f (n )<f (n +1)<…<f (2n -3);f (3)>f (4)>…>f (n );因此f (p )≥f (n )=2C 3n ,即T ≥2C 3n .综上,当n ≥4时,T ≥2C 3n . ················································· 10分。
江苏省南京市、盐城市2019届高三年级第二次模拟考试数学试题

因为0<α<β< ,所以- <α-β<0,
所以sin(α-β)=- =- .(10分)
所以tan(α-β)= =- ,(12分)
因此tanα=tan(α-β+β)= = .(14分)
16.(1) 连结A1B,在三棱柱ABCA1B1C1中,AA1∥BB1且AA1=BB1,
又因为f(1)=0,所以函数f(x)的图象在x=1处的切线方程为y= (x-1),
因为直线l交椭圆C于两点,
所以Δ=(-8k2)2-4(1+2k2)(8k2-2)>0,
解得- <k< .(4分)
设点A(x1,y1),B(x2,y2),
则x1+x2= ,x1x2= .
①设AB的中点为M(x0,y0),
则x0= = ,y0=k(x0-2)=- .(6分)
当k≠0时,因为QA=QB,所以QM⊥l,
B. [选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),曲线C的参数方程为 (θ为参数),P是曲线C上的任意一点.求点P到直线l的距离的最大值.
C. [选修4-5:不等式选讲](本小题满分10分)
解不等式:|2x-1|-x≥2.
【必做题】第22题、第23题,每小题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤.
18.(本小题满分16分)
在平面直角坐标系xOy中,已知椭圆C: + =1(a>b>0)的离心率为 ,且椭圆C短轴的一个顶点到一个焦点的距离等于 .
(1) 求椭圆C的方程;
(2) 设经过点P(2,0)的直线l交椭圆C于A,B两点,点Q(m,0).
江苏省南京市、盐城市2019届高三第三次调研考试(5月)数学附答案

江苏省南京市、盐城市2019届高三模拟考试试卷数 学(满分160分,考试时间120分钟)2019.5一、 填空题:本大题共14小题,每小题5分,共70分.1. 已知集合U ={x|1<x<6,x ∈N },A ={2,3},则∁U A =________.2. 若复数z 满足z(1+i)=1,其中i 为虚数单位,则z 在复平面内对应的点在第________象限.3. 已知某商场在一周内某商品日销售量的茎叶图如图所示,那么这一周该商品日销售量的平均数为________.4. 一个算法的伪代码如图所示,执行此算法,输出S 的值为________.5. 若实数x ,y 满足⎩⎪⎨⎪⎧2x -y +1≥0,2x +y ≥0,x ≤1,则x +3y 的最小值为________.6. 从1,2,3,4,5这5个数字中随机抽取3个不同的数字,则这3个数字经适当排序后能组成等差数列的概率为________.7. 若函数f(x)=⎩⎪⎨⎪⎧2x ,x ≤0,f (x -2),x>0,则f(log 23)=________.8. 已知数列{a n }的前n 项和为S n ,且2S n =3n -1,n ∈N *.若b n =log 3a n ,则b 1+b 2+b 3+b 4的值为________.9. 已知函数f(x)=2sin (ωx +π6),其中ω>0.若x 1,x 2是方程f(x)=2的两个不同的实数根,且|x 1-x 2|的最小值为π,则当x ∈[0,π2]时,f(x)的最小值为________.10. 在平面直角坐标系xOy 中,过双曲线x 2a 2-y 2b2=1(a>0,b>0)的右焦点F 作一条渐近线的平行线,交另一条渐近线于点P.若线段PF 的中点恰好在此双曲线上,则此双曲线的离心率为________.11. 有一个体积为2的长方体,它的长、宽、高依次为a ,b ,1.现将它的长增加1,宽增加2,且体积不变,则所得新长方体高的最大值为________.12. 已知向量a ,b ,c 是同一平面内的三个向量,其中a ,b 是夹角为60°的两个单位向量.若向量c 满足c·(a +2b )=-5,则|c|的最小值为________.13. 在平面直角坐标系xOy 中,已知MN 是圆C :(x -1)2+(y -2)2=2的一条弦,且CM ⊥CN ,P 是MN 的中点.当弦MN 在圆C 上运动时,直线l :x -3y -5=0上存在两点A ,B ,使得∠APB ≥π2恒成立,则线段AB 长度的最小值是________.14. 已知函数f(x)=12x 2-aln x +x -12,对任意x ∈[1,+∞),当f(x)≥mx 恒成立时实数m 的最大值为1,则实数a 的取值范围是________.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤. 15. (本小题满分14分)已知a ,b ,c 分别是△ABC 三个角A ,B ,C 所对的边,且满足acos B +bcos A =ccos Acos C. (1) 求证:A =C ;(2) 若b =2,且BA →·BC →=1,求sin B 的值.16. (本小题满分14分)在四棱锥PABCD 中,PA ⊥平面ABCD ,AD ∥BC ,AB =1,BC =2,∠ABC =60°. (1) 求证:平面PAC ⊥平面PAB ;(2) 设平面PBC ∩平面PAD =l ,求证:BC ∥l.如图,某摩天轮底座中心A与附近的景观内某点B之间的距离AB为160 m.摩天轮与景观之间有一建筑物,此建筑物由一个底面半径为15 m的圆柱体与一个半径为15 m的半球体组成.圆柱的底面中心P在线段AB上,且PB为45 m.半球体球心Q到地面的距离PQ为15 m.把摩天轮看作一个半径为72 m的圆C,且圆C在平面BPQ内,点C到地面的距离CA为75 m.该摩天轮匀速旋转一周需要30 min,若某游客乘坐该摩天轮(把游客看作圆C上一点)旋转一周,求该游客能看到点B的时长.(只考虑此建筑物对游客视线的遮挡)在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a>b>0)过点(1,22),离心率为22.A ,B 分别是椭圆C 的上、下顶点,M 是椭圆C 上异于A ,B 的一点.(1) 求椭圆C 的方程;(2) 若点P 在直线x -y +2=0上,且BP →=3BM →,求△PMA 的面积;(3) 过点M 作斜率为1的直线分别交椭圆C 于另一点N ,交y 轴于点D ,且点D 在线段OA 上(不包括端点O ,A),直线NA 与直线BM 交于点P ,求OD →·OP →的值.已知函数f(x)=ln x +ax+1,a ∈R .(1) 若函数f(x)在x =1处的切线为y =2x +b ,求a ,b 的值;(2) 记g(x)=f(x)+ax ,若函数g(x)在区间(0,12)上有最小值,求实数a 的取值范围;(3) 当a =0时,关于x 的方程f(x)=bx 2有两个不相等的实数根,求实数b 的取值范围.已知数列{a n}的前n项和为S n.若存在正整数r,t,且r<t,使得S r=t,S t=r同时成立,则称数列{a n}为“M(r,t)数列”.(1) 若首项为3,公差为d的等差数列{a n}是“M(r,2r)数列”,求d的值;(2) 已知数列{a n}为等比数列,公比为q.①若数列{a n}为“M(r,2r)数列”,r≤4,求q的值;②若数列{a n}为“M(r,t)数列”,q∈(-1,0),求证:r为奇数,t为偶数.2019届高三模拟考试试卷数学附加题(满分40分,考试时间30分钟)21. 【选做题】 在A ,B ,C 三小题中只能选做两题,每小题10分,共20分.若多做,则按作答的前两题计分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修42:矩阵与变换)已知矩阵M =⎣⎢⎡⎦⎥⎤2112.(1) 求M 2;(2) 求矩阵M 的特征值和特征向量.B. (选修44:坐标系与参数方程)在极坐标系中,直线l 的极坐标方程为ρcos (θ+π3)=1,以极点O 为坐标原点,极轴Ox 所在的直线为x 轴建立平面直角坐标系,曲线C 的参数方程为⎩⎪⎨⎪⎧x =rcos α+2,y =rsin α-1(其中α为参数,r>0).若直线l 与曲线C相交于A ,B 两点,且AB =3,求r 的值.C. (选修45:不等式选讲)若x ,y ,z 为实数,且x 2+4y 2+9z 2=6,求x +2y +6z 的最大值.【必做题】第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. 在平面直线坐标系xOy中,已知抛物线y2=2px(p>0)及点M(2,0),动直线l过点M交抛物线于A,B两点,当l垂直于x轴时,AB=4.(1) 求p的值;(2) 若l与x轴不垂直,设线段AB中点为C,直线l1经过点C且垂直于y轴,直线l2经过点M且垂直于直线l,记l1,l2相交于点P,求证:点P在定直线上.23. 对由0和1这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“010”的最后一个0所在数位是第k(k∈N*,且k≥3)位,则称子串“010”在第k位出现;再继续从第k+1位按从左往右的顺序找子串“010”,若第二个子串“010”的最后一个0所在数位是第k+m位(其中m≥3,且m∈N*),则称子串“010”在第k+m位出现;……;如此不断地重复下去.如:在字符串1 1 0 1 0 1 0 1 0 1 0中,子串“010”在第5位和第9位出现,而不是在第7位和第11位出现.记在n位由0,1组成的所有字符串中,子串“010”在第n位出现的字符串的个数为f(n).(1) 求f(3),f(4)的值;(2) 求证:对任意的正整数n,f(4n+1)是3的倍数.2019届高三模拟考试试卷(南京) 数学参考答案及评分标准1. {4,5}2. 四3. 304. 345. -56. 257. 348. 69. -1 10. 2 11. 14 12. 57713. 210+2 14. (-∞,1]15. (1) 证明:由正弦定理a sin A =b sin B =csin C =2R ,得a =2Rsin A ,b =2Rsin B ,c =2Rsin C ,代入acos B +bcos A =ccos Acos C,得(sin Acos B +sin Bcos A)cos C =sin Ccos A ,(2分)即sin(A +B)cos C =sin Ccos A.因为A +B =π-C ,所以sin (A +B)=sin C ,所以sin Ccos C =sin Ccos A .(4分) 因为C 是△ABC 的内角,所以sin C ≠0,所以cos C =cos A. 因为A ,C 是△ABC 的内角,所以A =C.(6分)(2) 解:由(1)知A =C ,所以a =c ,所以cos B =a 2+c 2-b 22ac =a 2-2a2.(8分)因为BA →·BC →=1,所以a 2cos B =a 2-2=1,所以a 2=3.(10分)所以cos B =13.(12分)因为B ∈(0,π),所以sin B =1-cos 2B =223.(14分)16.证明:(1) 因为PA ⊥平面ABCD ,AC 平面ABCD ,所以PA ⊥AC.(2分) 因为AB =1,BC =2,∠ABC =60°,由余弦定理, 得AC =AB 2+BC 2-2AB·BCcos ∠ABC =12+22-2×1×2cos 60°= 3.(4分) 因为12+(3)2=22,即AB 2+AC 2=BC 2,所以AC ⊥AB.(6分) 因为AC ⊥PA ,且PA ∩AB =A ,PA 平面PAB ,AB平面PAB ,所以AC ⊥平面PAB. 又AC平面PAC ,所以平面PAC ⊥平面PAB.(8分)(2) 因为BC ∥AD ,AD平面PAD ,BC平面PAD ,所以BC ∥平面PAD.(10分)因为BC 平面PBC ,且平面PBC ∩平面PAD =l ,所以BC ∥l.(14分)17. 解:以点B 为坐标原点,BP 所在直线为x 轴,建立如图所示平面直角坐标系,则B(0,0),Q(45,15),C(160,75).过点B 作直线l 与圆Q 相切,与圆C 交于点M ,N , 设直线l 的方程为y =kx ,即kx -y =0,则点Q 到l 的距离为|45k -15|k 2+1=15,解得k =34或k =0(舍去).所以直线l 的方程为y =34x ,即3x -4y =0.(4分)点C(160,75)到直线l 的距离CH =|3×160-4×75|32+(-4)2=36.(6分)在Rt △CHM 中,因为CH =36,CM =72,所以cos ∠MCH =3672=12.(8分)因为∠MCH ∈(0,π2),所以∠MCH =π3,所以∠MCN =2∠MCH =2π3,(12分)所以所用时长为30×2π32π=10 min.(13分)答:该游客能看到点B 的时长为10 min.(14分)18. 解:(1) 因为椭圆过点(1,22),离心率为22,所以1a 2+12b 2=1,b 2a 2=1-e 2=12,解得a 2=2,b 2=1,所以椭圆C 的方程为x22+y 2=1.(2分)(2) 由(1)知B(0,-1),设M(x 0,y 0),P(x ,y). 由BP →=3BM →,得(x ,y +1)=3(x 0,y 0+1),则x =3x 0,y =3y 0+2. 因为P 在直线x -y +2=0上,所以y 0=x 0 ①.(4分)因为M 在椭圆C 上,所以x 202+y 20=1,将①代入上式,得x 20=23.(6分) 所以|x 0|=63,从而|x P |=6,所以S △PMA =S △PAB -S △MAB =12×2×6-12×2×63=263.(8分)(3) (解法1)由(1)知,A(0,1),B(0,-1).设D(0,m),0<m <1,M(x 1,y 1),N(x 2,y 2).因为MN 的斜率为1,所以直线MN 的方程为y =x +m.联立方程组⎩⎪⎨⎪⎧y =x +m ,x 22+y 2=1,消去y ,得3x 2+4mx +2m 2-2=0, 所以x 1+x 2=-4m3,x 1·x 2=2m 2-23. (10分)直线MB 的方程为y =y 1+1x 1x -1,直线NA 的方程为y =y 2-1x 2x +1,联立解得y P =(y 1+1)x 2+(y 2-1)x 1(y 1+1)x 2-(y 2-1)x 1.(12分)将y 1=x 1+m ,y 2=x 2+m 代入,得y P =2x 1x 2+m (x 1+x 2)+x 2-x 1x 1+x 2+m (x 2-x 1)=2·2m 2-23-4m 23+(x 2-x 1)-4m 3+m (x 2-x 1)=-43+(x 2-x 1)-4m 3+m (x 2-x 1)=1m .(14分)所以OD →·OP →=(0,m)·(x P ,y P )=my P =m·1m=1.(16分)(解法2)由(1)知,A(0,1),B(0,-1).设M(x 0,y 0),则x 202+y 20=1. 因为直线MN 的斜率为1,所以直线MN 的方程为y =x -x 0+y 0,则D(0,y 0-x 0).联立方程⎩⎪⎨⎪⎧y =x -x 0+y 0,x 22+y 2=1,消去y ,得3x 2-4(x 0-y 0)x +2(x 0-y 0)2-2=0, 所以x N +x 0=4(x 0-y 0)3,(10分)所以x N =x 0-4y 03,y N =-2x 0+y 03,所以直线NA 的方程为y =y N -1x N x +1=2x 0+y 0+34y 0-x 0x +1,直线MB 的方程为y =y 0+1x 0x -1,联立解得y P =2y 20+x 20+x 0+2y 02y 20-x 20-x 0y 0-2x 0+2y 0.(12分)因为x 202+y 20=1, 所以y P =2+x 0+2y 0(2+x 0+2y 0)(y 0-x 0)=1y 0-x 0,(14分)所以OD →·OP →=(0,y 0-x 0)·(x P ,y P )=(y 0-x 0)1y 0-x 0=1.(16分)19. 解:(1) f′(x)=1x -a x 2,则f′(1)=1-a =2,解得a =-1,则f(x)=ln x -1x+1,此时f(1)=ln 1-1+1=0,则切点坐标为(1,0),代入切线方程,得b =-2, 所以a =-1,b =-2.(2分)(2) g(x)=f(x)+ax =ln x +a x +ax +1,g ′(x)=1x -ax 2+a =ax 2+x -a x 2.①当a =0时,g ′(x)=1x >0,则g(x)在区间(0,12)上为增函数,则g(x)在区间(0,12)上无最小值.(4分)②当a ≠0时,方程ax 2+x -a =0的判别式Δ=1+4a 2>0, 则方程有两个不相等的实数根,设为x 1,x 2,由韦达定理得x 1x 2=-1,则两根一正一负,不妨设x 1<0<x 2. 设函数m(x)=ax 2+x -a(x >0), (i) 若a >0,当x 2∈(0,12)时,m(0)=-a <0,m(12)=a 4+12-a >0,解得0<a <23.此时当x ∈(0,x 2)时,m(x)<0,则g(x)递减;当x ∈(x 2,12)时,m(x)>0,则g(x)递增,当x =x 2时,g(x)取极小值,即为最小值.当x 2≥12时,x ∈(0,12),m(x)<0,则g(x)在(0,12)上单调递减,无最小值.(6分)(ii) 若a <0,当x ∈(0,x 2)时,m(x)>0,则g(x)递增; 当x ∈(x 2,+∞)时,m(x)<0,则g(x)递减,在区间(0,12)上,g(x)不会有最小值.所以a <0不满足条件.综上,当0<a <23时,g(x)在区间(0,12)上有最小值.(8分)(3) 当a =0时,由方程f(x)=bx 2,得ln x +1-bx 2=0.记h(x)=ln x +1-bx 2,x >0,则h′(x)=1x -2bx =-2bx 2+1x.①当b ≤0时,h′(x)>0恒成立,即h(x)在(0,+∞)上为增函数,则函数h(x)至多只有一个零点,即方程f(x)=bx 2至多只有一个实数根, 所以b ≤0不符合题意.(10分) ②当b >0时,当x ∈(0,12b )时,h ′(x)>0,所以函数h(x)递增;当x ∈(12b,+∞)时,h ′(x)<0,所以函数h(x)递减,则h(x)max =h(12b )=ln 12b +12. 要使方程f(x)=bx 2有两个不相等的实数根,则h(12b )=ln 12b +12>0,解得0<b <e2.(12分)(i) 当0<b <e 2时,h(1e )=-be2<0.又(1e )2-(12b )2=2b -e 22be 2<0,则1e <12b, 所以存在唯一的x 1∈(1e ,12b),使得h(x 1)=0.(14分)(ii) h(1b )=ln 1b +1-1b =-ln b +1-1b ,记k(b)=-ln b +1-1b ,0<b <e 2.因为k′(b)=-1b +1b 2=1-b b 2,则k(b)在(0,1)上为增函数,在(1,e2)上为减函数,则k(b)max =k(1)=0,则h(1b)≤0.又(1b )2-(12b )2=2-b 2b 2>0,即1b >12b, 所以存在唯一的x 2∈(12b ,1b],使得h(x 2)=0.综上,当0<b <e2时,方程f(x)=bx 2有两个不相等的实数根.(16分)20. (1) 解:因为{a n }是M(r ,2r)数列,所以S r =2r ,且S 2r =r.由S r =2r ,得3r +r (r -1)2d =2r.因为r >0,所以(r -1)d =-2 (*).由S 2r =r ,得6r +2r (2r -1)2d =r.因为r >0,所以(2r -1)d =-5 (**).由(*)和(**),解得r =3,d =-1.(2分) (2) ①解:(i) 若q =1,则S r =ra 1,S t =ta 1.因为{a n }是M(r ,2r)数列,所以ra 1=2r (*),2ra 1=r (**).由(*)和(**),得a 1=2且a 1=12,矛盾,所以q ≠1.(3分)(ii) 当q ≠1,因为{a n }是M(r ,2r)数列,所以S r =2r ,且S 2r =r , 即a 1(1-q r )1-q =2r (*),a 1(1-q 2r )1-q=r (**).由(*)和(**),得q r =-12.(5分)当r =1时,q =-12;当r =2,4时,无解;当r =3时,q =-132.综上,q =-12或q =-132.(6分)②证明:因为{a n }是M(r ,t)数列,q ∈(-1,0),所以S r =t ,且S t =r , 即a 1(1-q r )1-q =t ,且a 1(1-q t )1-q=r ,两式作商,得1-q r 1-q t =t r,即r(1-q r )=t(1-q t).(8分) (i) 若r 为偶数,t 为奇数,则r(1-|q|r )=t(1+|q|t ).因为r <t ,0<1-|q|r <1,1+|q|t >1,所以r(1-|q|r )<t(1+|q|t ), 这与r(1-|q|r )=t(1+|q|t )矛盾,所以假设不成立.(10分) (ii) 若r 为偶数,t 为偶数,则r(1-|q|r )=t(1-|q|t ). 设函数y =x(1-a x ),0<a <1,则y′=1-a x -xa x ln a.当x>0时,1-a x>0,-xa x ln a>0,所以y=x(1-a x)在(0,+∞)上递增.因为r<t,所以r(1-|q|r)<t(1-|q|t),这与r(1-|q|r)=t(1-|q|t)矛盾,所以假设不成立.(12分)(iii) 若r为奇数,t为奇数,则r(1+|q|r)=t(1+|q|t).设函数y=x(1+a x),0<a<1,则y′=1+a x+xa x ln a.设g(x)=1+a x+xa x ln a,则g′(x)=a x ln a(2+xln a).令g′(x)=0,得x=-2ln a.因为ax>0,ln a<0,所以当x>-2ln a,g′(x)>0,则g(x)在区间(-2ln a ,+∞)上递增;当0<x<-2ln a,g′(x)<0,则g(x)在区间(0,-2ln a)上递减,所以g(x)min=g(-2ln a)=1-a-2 ln a.因为-2ln a>0,所以a-2ln a<1, 所以g(x)min>0,从而g(x)>0在(0,+∞)上恒成立,所以y=x(1+a x),0<a<1在(0,+∞)上单调递增.因为r<t,所以r(1+|q|r)<t(1+|q|t),这与r(1-|q|r)=t(1-|q|t)矛盾,所以假设不成立.(14分) (iv) 若r为奇数,t为偶数.由①知,存在等比数列{a n}为“M(1,2)数列”.综上,r为奇数,t为偶数.(16分)2019届高三模拟考试试卷(南京) 数学附加题参考答案及评分标准21. A. 解:(1) M 2=⎣⎢⎡⎦⎥⎤2112⎣⎢⎡⎦⎥⎤2112=⎣⎢⎡⎦⎥⎤5445.(4分) (2) 矩阵M 的特征多项式为f(λ)=⎪⎪⎪⎪⎪⎪λ-2-1-1λ-2=(λ-1)(λ-3). 令f(λ)=0,解得M 的特征值为λ1=1,λ2=3.(6分)①当λ=1时,⎣⎢⎡⎦⎥⎤2112⎣⎢⎡⎦⎥⎤x y =⎣⎢⎡⎦⎥⎤x y ,得⎩⎪⎨⎪⎧x +y =0,x +y =0. 令x =1,则y =-1,于是矩阵M 的一个特征向量为⎣⎢⎡⎦⎥⎤1-1.(8分)②当λ=3时,⎣⎢⎡⎦⎥⎤2112⎣⎢⎡⎦⎥⎤x y =3⎣⎢⎡⎦⎥⎤x y ,得⎩⎪⎨⎪⎧x -y =0,x -y =0. 令x =1,则y =1,于是矩阵M 的一个特征向量为⎣⎢⎡⎦⎥⎤11. 因此,矩阵M 的特征值为1,3,分别对应一个特征向量为⎣⎢⎡⎦⎥⎤ 1-1,⎣⎢⎡⎦⎥⎤11.(10分)B. 解:直线l 的直角坐标方程为x -3y -2=0.(2分) 曲线C 的普通方程为(x -2)2+(y +1)2=r 2.(4分)因为圆心C(2,-1)到直线l 的距离d =|2+3-2|1+3=32,(6分)所以r =d 2+(AB2)2= 3.(10分)C. 解:由柯西不等式,得[x 2+(2y)2+(3z)2](12+12+22)≥(x +2y +6z)2.(4分) 因为x 2+4y 2+9z 2=6,所以(x +2y +6z)2≤36,(6分) 所以-6≤x +2y +6z ≤6.当且仅当x 1=2y 1=3z2时,不等式取等号,此时x =1,y =12,z =23或 x =-1,y =-12,z =-23,(8分)所以x +2y +6z 的最大值为6.(10分)22. (1) 解:因为l 过M(2,0),且当l 垂直于x 轴时,AB =4,所以抛物线经过点(2,2),代入抛物线方程,得4=2p ×2,解得p =1.(2分) (2) 证明:设直线l 的方程为y =k(x -2)(k ≠0),A(x 1,y 1),B(x 2,y 2).联立⎩⎪⎨⎪⎧y 2=2x ,y =k (x -2),消去x ,得ky 2-2y -4k =0,则y 1+y 2=2k,y 1y 2=-4.(4分)因为点C 为AB 中点,所以y C =y 1+y 22=1k ,则直线l 1的方程为y =1k.(6分)因为直线l 2过点M 且与l 垂直,则直线l 2的方程为y =-1k(x -2).联立⎩⎨⎧y =1k,y =-1k (x -2),(8分)解得⎩⎪⎨⎪⎧x =1,y =1k ,即P(1,1k),所以点P在定直线x=1上.(10分)23. (1) 解:在3位数字符串中,子串“010”在第3位出现有且只有1个,即010,所以f(3)=1.(2分)在4位数字符串中,子串“010”在第4位出现有2个,即0010与1010,所以f(4)=2.(4分)(2) 证明:当n≥5且n∈N*时,当最后3位是010时,前n-3个数位上,每个数位上的数字都有两种可能,即0和1,所以共有2n-3种可能.由于当最后3位是010时,若最后5位是01010,且前n-2位形成的字符串中是子串“010”是在第n-2位出现,此时不满足条件.所以f(n)=2n-3-f(n-2),n≥5且n∈N*.(6分)因为f(3)=1,所以f(5)=3.下面用数学归纳法证明f(4n+1)是3的倍数.①当n=1时,f(5)=3是3的倍数;②假设当n=k(k∈N*)时,f(4k+1)是3的倍数,那么当n=k+1时,f(4(k+1)+1)=f(4k+5)=24k+2-f(4k+3) =24k+2-[24k-f(4k+1)]=3×24k+f(4k+1).(8分)因为f(4k+1)是3的倍数,且3×24k也是3的倍数,所以f(4k+5)是3的倍数.这就是说,当n=k+1时,f(4(k+1)+5)是3的倍数.由①②可知,对任意的正整数n,f(4n+1)是3的倍数.(10分)。
江苏省南京市、盐城市2019届高三第二次模拟考试数学试题及答案
江苏省南京市、盐城市2019届高三第二次模拟考试数学试题及答案一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.函数f(x)=lnx +1-x 的定义域为 ▲ .2.已知复数z 1=-2+i ,z 2=a +2i(i 为虚数单位,a ∈R).若z 1z 2为实数,则a 的值为 ▲ . 3.某地区教育主管部门为了对该地拟考试成绩进行分析,随机抽取了150分到450分之间的2018名学生的成绩,并根据这2018名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 ▲ .4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为 ▲ .5.已知等差数列{a n }的公差d 不为0,且a 1,a 3,a 7成等比数列,则a 1d的值为6.执行如图所示的流程图,则输出的k 的值为 ▲ .7.函数f(x)=Asin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如下图所示,则f(π3)的值为 ▲ . a(第3题图)(第6题图)8.在平面直角坐标系xOy 中,双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线与抛物线y 2=4x 的准线相交于A ,B 两点.若△AOB 的面积为2,则双曲线的离心率为 ▲ .9.表面积为12π的圆柱,当其体积最大时,该圆柱的底面半径与高的比为 ▲ .10.已知|OA →|=1,|OB →|=2,∠AOB =2π3,OC →=12OA →+14OB →,则OA →与OC →的夹角大小为▲ .11.在平面直角坐标系xOy 中,过点P(5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 ▲ .12.已知f(x)是定义在R 上的奇函数,当0≤x ≤1时,f(x)=x 2,当x >1时,f(x +1)=f(x)+f(1),且.若直线y =kx 与函数y =f(x)的图象恰有5个不同的公共点,则实数k 的值为 ▲ .13.在△ABC 中,点D 在边BC 上,且DC =2BD ,AB ∶AD ∶AC =3∶k ∶1,则实数k 的取值范围为 ▲ . 14.设函数f(x)=ax +sinx +cosx .若函数f(x)的图象上存在不同的两点A ,B ,使得曲线y =f(x)在点A ,B 处的切线互相垂直,则实数a 的取值范围为 ▲ . 一、填空题:本大题共14小题,每小题5分,计70分.1.(0,1] 2.4 3.300 4.59 5.2 6.4 7.18. 5 9.12 10.60° 11.1或723 12.22-2 13.(53,73) 14.[-1,1]二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,平面PAB ⊥平面ABCD ,PA ⊥PB , BP =BC ,E 为PC 的中点. (1)求证:AP ∥平面BDE ; (2)求证:BE ⊥平面PAC . 15.证:(1)设AC ∩BD =O ,连结OE .因为ABCD 为矩形,所以O 是AC 的中点.因为E 是PC 中点,所以OE ∥AP . …………………………………………4分 因为AP/⊂平面BDE ,OE ⊂平面BDE ,所以AP ∥平面BDE . …………………………………………6分 (2)因为平面PAB ⊥平面ABCD ,BC ⊥AB ,平面PAB ∩平面ABCD =AB ,所以BC ⊥平面PAB . ………………………………………8分 因为AP ⊂平面PAB ,所以BC ⊥PA .因为PB ⊥PA ,BC ∩PB =B ,BC ,PB ⊂平面PBC ,所以PA ⊥平面PBC . …………………………………………12分 因为BE ⊂平面PBC ,所以PA ⊥BE .因为BP =PC ,且E 为PC 中点,所以BE ⊥PC . 因为PA ∩PC =P ,PA ,PC ⊂平面PAC ,所以BE ⊥平面PAC . …………………………………………14分 PBCDEA(第15题图)16.(本小题满分14分)在平面直角坐标系xOy 中,角α的顶点是坐标原点,始边为x 轴的正半轴,终边与单位圆O 交 于点A(x 1 ,y 1 ),α∈(π4,π2).将角α终边绕原点按逆时针方向旋转π4,交单位圆于点B(x 2,y 2).(1)若x 1=35,求x 2;(2)过A ,B 作x 轴的垂线,垂足分别为C ,D ,记△AOC 及 △BOD 的面积分别为S 1,S 2,且S 1=43S 2,求tan α的值.16.解:(1)解法一:因为x 1=35,y 1>0,所以y 1=1-x 21=45.所以sin α=45,cos α=35.所以x 2=cos(α+π4)=cos αcos π4-sin αsin π4=-210. (6)分解法二:因为x 1=35,y 1>0,所以y 1=1-x 21=45.A(35,45),则OA →=(35,45),…………2分OB →=(x 2,y 2), 因为OA →·OB →=|OA →||OB →|cos ∠AOB ,所以35x 2+45y 2= 2 2 ……4分又x 22+y 22=1,联立消去y 2得50 x 22-302x 2-7=0 解得x 2=-2 10或7210,又x 2<0,所以x 2=- 210. ………………………6分 解法三:因为x 1=35,y 1>0,所以y 1=1-x 21=45. 因此A(35,45),所以tan α=43.………2分 所以tan(α+π4)=1+tan α1-tan α=-7,所以直线OB 的方程为y =-7x ……………4分由⎩⎨⎧y =-7x ,x 2+y 2=1.得x =± 2 10,又x 2<0,所以x 2=- 210. …………………6分(2)S 1=12sin αcos α=-14sin2α. …………………………………………8分因为α∈(π4,π2),所以α+π4∈(π2,3π4). 所以S 2=-12sin(α+π4)cos(α+π4)=-14sin(2α+π2)=-14cos2α.……………………………10分因为S 1=43S 2,所以sin2α=-43cos2α,即tan2α=-43. (12)(第16题图)所以2tan α1-tan 2α=-43,解得tan α=2或tan α=-12. 因为α∈(π4,π2),所以tan α=2.………14分17.(本小题满分14分)如图,经过村庄A 有两条夹角为60°的公路AB ,AC ,根据规划拟在两条公路之间的区域内建一工厂P ,分别在两条公路边上建两个仓库M 、N (异于村庄A),要求PM =PN =MN =2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).解法一:设∠AMN=θ,在△A MN 中,MN sin60°=AMsin(120°-θ).因为MN =2,所以AM =433sin(120°-θ) . ………………………………………2分在△APM 中,cos ∠AMP =cos(60°+θ). …………………………………………6分AP 2=AM 2+MP 2-2 AM ·MP ·cos ∠AMP =163sin 2(120°-θ)+4-2×2×433sin(120°-θ) cos(60°+θ) ………………………………8分=163sin 2(θ+60°)-1633 sin(θ+60°) cos(θ+60°)+4 =83[1-cos (2θ+120°)]-833 sin(2θ+120°)+4 =-83[3sin(2θ+120°)+cos (2θ+120°)]+2032016 APMNBC(第17题图)120°).…………………………………………12分当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值23.答:设计∠AMN为60 时,工厂产生的噪声对居民的影响最小. (14)分解法二(构造直角三角形):设∠PMD=θ,在△PMD中,∵PM=2,∴PD=2sinθ,MD=2cosθ.……………2分在△AMN中,∠ANM=∠PMD=θ,∴MNsin60°=AMsinθ,AM=433sinθ,∴AD=433sinθ+2cosθ,(θ≥π2时,结论也正确).……………6分AP2=AD2+PD2=(433sinθ+2cosθ)2+(2sinθ)2=163sin2θ+833sinθcosθ+4cos2θ+4sin2θ…………………………8分=163·1-cos2θ2+433sin2θ+4=433sin2θ-83cos2θ+203=203+163sin(2θ-π6),θ∈(0,2π3).…………………………12分当且仅当2θ-π6=π2,即θ=π3时,AP2取得最大值12,即AP取得最大值23.此时AM=AN=2,∠PAB=30°…………………………14分解法三:设AM=x,AN=y,∠AMN=α.在△AMN中,因为MN=2,∠MAN=60°,所以MN2=AM2+AN2-2 AM·AN·cos∠MAN,即x2+y2-2xycos60°=x2+y2-xy=4.…………………………………………2分因为MNsin60°=ANsinα,即2sin60°=ysinα,所以sinα=34y,cosα=x2+4-y22×2×x=x2+(x2-xy)4x=2x-y4.…………………………………………6分cos∠AMP=cos(α+60°)=12cosα-32sinα=12·2x-y4-32·34y=APMNBC第17题图D在△AMP 中,AP 2=AM 2+PM 2-2 AM ·PM ·cos ∠AMP , 即AP 2=x 2+4-2×2×x ×x -2y 4=x 2+4-x(x -2y)=4+2xy .………………………………………12分因为x 2+y 2-xy =4,4+xy =x 2+y 2≥2xy ,即xy ≤4. 所以AP 2≤12,即AP ≤2 3.当且仅当x =y =2时,AP 取得最大值23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.………………………………14分解法四(坐标法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系. 设M(x 1,0),N(x 2,3x 2),P(x 0,y 0).∵MN =2,∴(x 1-x 2)2+3x 22=4. …………………………………………2分MN 的中点K(x 1+x 22,32x 2). ∵△MNP 为正三角形,且MN =2.∴PK =3,PK ⊥MN . ∴PK 2=(x 0-x 1+x 22)2+(y 0-32x 2)2=3,k MN ·k PK =-1,即3x 2x 2-x 1·y 0-32x 2x 0-x 1+x 22=-1, …………………………………………6分∴y 0-32x 2=x 1-x 23x 2(x 0-x 1+x 22),∴(y 0-32x 2)2=(x 1-x 2)23x 22(x 0-x 1+x 22)2∴(1+(x 1-x 2)23x 22)(x 0-x 1+x 22)2=3,即43x 22(x 0-x 1+x 22)2=3,∴(x 0-x 1+x 22)2=94x 22.∵x 0-x 1+x 22>0 ∴x 0-x 1+x 22=32x 2, ∴x 0=12x 1+2x 2,∴y 0=32x 1. …………………………………………8分∴AP 2=x 20+y 20=(2x 2+12x 1)2+34x 21=x 21+4x 22+2x 1x 2=4+4x 1x 2≤4+4×2=12, …………………………………………12分答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 解法五(变换法):以AB 所在的直线为x 轴,A 为坐标原点,建立直角坐标系. 设M(x 1,0),N(x 2,3x 2),P(x 0,y 0).∵MN =2,∴(x 1-x 2)2+3x 22=4.即x 21+4x 22=4+2x 1x 2∴4+2x 1x 2≥4x 1x 2,即x 1x 2≤2. …………………4分 ∵△MNP 为正三角形,且MN =2.∴PK =3,PK ⊥MN . MN →顺时针方向旋转60°后得到MP →. MP →=(x 0-x 1,y 0),MN →=(x 2-x 1, 3x 2). ∴⎣⎢⎢⎡⎦⎥⎥⎤12 32-32 12⎣⎢⎢⎡⎦⎥⎥⎤x 2-x 13x 2=⎣⎢⎡⎦⎥⎤x 0-x 1y 0,即x 0-x 1=12(x 2-x 1)+32x 2,y 0=-32(x 2-x 1)+32x 2.∴x 0=2x 2+12x 1,y 0=32x 1. …………………………………………8分∴AP 2=x 20+y 20=(2x 2+12x 1)2+34x 21=x 21+4x 22+2x 1x 2=4+4x 1x 2≤4+4×2=12, …………………………………………12分 即AP ≤23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 解法六(几何法):由运动的相对性,可使△PMN 不动,点A 在运动.由于∠MAN =60°,∴点A 在以MN 为弦的一段圆弧(优弧)上, (4)分 设圆弧所在的圆的圆心为F ,半径为R ,由图形的几何性质知:AP 的最大值为PF +R . …………8分 在△AMN 中,由正弦定理知:MNsin60°=2R ,∴R =23, …………10分∴FM =FN =R =23,又PM =PN ,∴PF 是线段MN 的垂直平分线.设PF 与MN 交于E ,则FE 2=FM 2-ME 2=R 2-12=13.APMNBCF E即FE =33,又PE =3. ……………………………12 ∴PF =43,∴AP 的最大值为PF +R =23.答:设计AM =AN =2 km 时,工厂产生的噪声对居民的影响最小.…………………………14分 18. (本小题满分16分)在平面直角坐标系xOy 中,已知椭圆C ∶x 2a 2+y2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,焦距为2,一条准线方程为x =2.P 为椭圆C 上一点,直线PF 1交椭圆C 于另一点Q .(1)求椭圆C 的方程;(2)若点P 的坐标为(0,b),求过P ,Q ,F 2三点的圆的方程; (3)若F 1P →=λQF 1→,且λ∈[12,2],求OP →·OQ →的最大值.(1)解:由题意得⎩⎪⎨⎪⎧2c =2,a 2c=2, 解得c =1,a 2=2,所以b 2=a 2-c 2=1.所以椭圆的方程为x 22+y 2=1. (2)分(2)因为P(0,1),F 1(-1,0),所以PF 1的方程为x -y +1=0.由⎩⎪⎨⎪⎧x +y +1=0,x 22+y 2=1, 解得⎩⎨⎧x =0,y =1,或⎩⎨⎧x =-43,y =-13,所以点Q 的坐标为(-43,-13). ……………………4分解法一:因为k PF 1·k PF 2=-1,所以△PQF 2为直角三角形. ……………………6分因为QF 2的中点为(-16,-16),QF 2=523,所以圆的方程为(x +16)2+(y +16)2=2518. (8)分解法二:设过P ,Q ,F 2三点的圆为x 2+y 2+Dx +Ey +F =0,则⎩⎨⎧1+E +F =0,1+D +F =0,179-43D -13E +F =0,解得⎩⎪⎨⎪⎧D =13,E =13,F =-43.所以圆的方程为x 2+y 2+13x +13y -43=0. …………………………………………8分(3)解法一:设P(x 1,y 1),Q(x 2,y 2),则F 1P →=(x 1+1,y 1),QF 1→=(-1-x 2,-y 2).因为F 1P →=λQF 1→,所以⎩⎨⎧x 1+1=λ(-1-x 2),y 1=-λy 2,即⎩⎨⎧x 1=-1-λ-λx 2,y 1=-λy 2,所以⎩⎪⎨⎪⎧(-1-λ-λx 2)22+λ2y 22=1,x 222+y 22=1,解得x 2=1-3λ2λ. …………………………………………12分 所以OP →·OQ →=x 1x 2+y 1y 2=x 2(-1-λ-λx 2)-λy 22=-λ2x 22-(1+λ)x 2-λ =-λ2(1-3λ2λ)2-(1+λ)·1-3λ2λ-λ=74-58(λ+1λ) . …………………………………………14分 因为λ∈[12,2],所以λ+1λ≥2 λ·1λ=2,当且仅当λ=1λ,即λ=1时,取等号.所以OP →·OQ →≤12,即OP →·OQ →最大值为12. …………………………………………16分解法二:当PQ 斜率不存在时,在x 22+y 2=1中,令x =-1得y =± 2 2.所以11(1)(222OP OQ ⋅=-⨯-+=,此时11,22λ⎡⎤=∈⎢⎥⎣⎦…………………………2 当PQ 斜率存在时,设为k ,则PQ 的方程是y =k(x +1), 由⎩⎪⎨⎪⎧y =k(x +1),x 22+y 2=1.得(1+2k 2)x 2+4k 2x +2k 2-2=0, 韦达定理 22121222422==k k x x x x --+, (4)设P(x 1,y 1),Q(x 2,y 2) ,则212121212(1)(1)OP OQ x x y y x x k x x ⋅=+=+++22212122222222222(1)()224(1)12122 61215122(12)2k x x k x x k k k k k k k k k k k =++++--=+++++-=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯+=-<+分。
南京市、盐城市2019届高三年级第二次模拟考试数学试卷(含参考答案和评分标准)
1南京市、盐城市2019届高三年级第二次模拟考试数 学2019.03第I 卷(必做题,共160分)一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.) 1.已知集合A ={}13x x <<,B ={}24x x <<,则A B = .2.若复数i 2iza =+(i 为虚数单位),且实部和虚部相等,则实数a 的值为 . 3.某药厂选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17),将其按从左到右的顺序分别编号为第一组,第二组,… ,第五组,右图市根据实验数据制成的频率分布直方图,已知第一组于第二组共有20人,则第三组钟人数为 .第4题 第3题4.右图是某算法的伪代码,输出的结果S 的值为 .5.现有5件相同的产品,其中3件合格,2件不合格,从钟随机抽检2件,则一件合格,另一件不合格的概率为 .6.等差数列{}n a 中,4a =10,前12项的和12S =90,则18a 的值为 .7.在平面直角坐标系xOy 中,已知点A 是抛物线24y x =与双曲线2221(0)4x y b b -=>的一个交点.若抛物线的焦点为F ,且FA =5,则双曲线的渐进线方程为 . 8.若函数()2sin()f x x ωϕ=+(0ω>,0ϕπ<<)的图象经过点(6π,2),且相邻两条对称轴间的距离为2π,则()4f π的值为 .0.360.240.160.081i ← 1S ←While 6i <2i i ←+S i S ←+ End While Pr int S29.已知正四棱锥P —ABCD 的所有棱长都相等,则该正四棱锥的表面积为 . 10.已知函数()f x 是定义在R 上的奇函数,且当x ≥0时,2()5f x x x =-,则不等式(1)f x ->()f x 的解集为 .11.在平面直角坐标系xOy 中,已知点A(﹣1,0),B(5,0).若圆M :22(4)()4x y m -+-=上存在唯一点P ,使得直线PA ,PB 在y 轴上的截距之积为5,则实数m 的值为 . 12.已知AD 是直角三角形ABC 的斜边BC 上的高,点P 在DA 的延长线上,且满足(PB PC)AD +⋅=若ADPB PC ⋅的值为 .13.已知函数330()1230x x f x x x x ⎧+≤⎪=⎨-+>⎪⎩,,,设()1g x kx =+,且函数()()y f x g x =-的图象经过四个象限,则实数k 的取值范围为 .14.在△ABC 中,若sinC =2cosAcosB ,则cos 2A +cos 2B 的最大值为 .二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分)设向量a =(cos α,λsin α),b =(cos β,sin β),其中λ>0,0<α<β<2π,且a b+与a b -相互垂直.(1)求实数λ的值; (2)若a b ⋅=45,且tan β=2,求tan α的值. 16.(本小题满分14分)如图,在三棱锥ABC —A 1B 1C 1中,AB =AC ,A 1C ⊥BC 1,AB 1⊥BC 1,D ,E 分别是AB 1,BC 的中点.(1)求证:DE ∥平面ACC 1A 1; (2)求证:AE ⊥BCC 1B 1.A1。
盐城市2019年普通高校对口单招高三年级第一次调研考试数学试卷含问题详解
(1)求数列 的通项公式;
(2)若数列 满足 ,且 ,求数列 的通项公式;
(3)设 ,求数列 的前n项的和 .
21.(本题满分10分)某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05.
题号
1
2
3
4
5
6
7
8
9
10
答案
第Ⅱ卷(共110分)
二、填空题:(本大题共5小题,每小题4分,共20分,把答案填在题中的横线上)
11.题11图是一个程序框图,若输入x的值为8,则输出的k的值为.
12.某工程的工作明细表如下:
工作代码
紧前工作
工期/天
A
无
2
B
A
3
C
B
2
D
B
1
E
C,D
1
F
E
2
则总工期为_____________天.
(1)求确定k的值;
(2)将2013年该产品的利润y万元表示为技术改革费用m万元的函数(利润=销售金额﹣生产成本﹣技术改革费用);
(3)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
23.(本题满分14分)已知椭圆的中心在原点,一个焦点为F1(0,-2 ),离心率e满足: 成等比数列.
16.(本题满分8分)若复数 在复平面对应的点在第一象限.(1)数a的取值围;(2)解不等式: .
17.(本题满分10分)已知函数 为奇函数,且当 时, .
(1)求m的值;(2)求当 时 的解析式;(3)求 的值.
江苏省南京市、盐城市2019届高三第二次调研模拟考试数学试卷(有答案)
江苏省南京市、盐城市2019届高三第二次调研考试数学试卷2019.03注意事项:1. 本试卷共4也,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试试卷为120分钟.2. 答题前,请务必将自己的姓名、学校、班级卸载答题卡上.试题的答案写在答题卡上对应题目的答案空格内.考试结束后,交回答题卡.一、填空题:本题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.1、已知集合{|13}A x x =<<,{|24}B x x =<<,则A B = .2、若复数2zi a i=+(i 为虚数单位),且实部和虚部相等,则实数a 的值为 . 3、某药厂选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17),将其按从左到右的顺序分别编号为第一组、,第二组,… …,第五组,右图市根据实验数据制成的频率分布直方图,已知第一组于第二组共有20人,则第三组钟人数为 .4、右图是某算法的伪代码,输出的结果S 的值为 .5、现有5件相同的产品,其中3件合格,2件不合格,从钟随机抽检2件,则一件合格,另一件不合格的概率为 .6、等差数列{}n a 中,410a =,前12项的和1290S =,则18a 的值为 .7、在平面直角坐标系xOy 中,已知点A 是抛物线24y x =与双曲线2221(0)4x y b b -=>的一个交点.若抛物线的焦点为F ,且5FA =,则双曲线的渐进线方程为 . 8、若函数()2sin()(0,0)f x x ωϕωϕπ=+><<的图象经过点(,2)6π,且相邻两条对称轴间的距离为2π,则()4f π的值为 .9、已知正四棱锥P ABCD -为 .10、已知函数()f x 是定义在R 上的奇函数,且当0x ≥时,2()5f x x x =-,则不等式(1)f x ->()f x 的解集为 .11、在平面直角坐标系xOy 中,已知点(1,0)A -,(5,0)B .若圆22:(4)()4M x y m -+-=上存在唯一点P ,使得直线PA ,PB 在y 轴上的截距之积为5,则实数m 的值为 .12、已知AD 时直角三角形ABC 的斜边BC 上的高,点P 在DA 的延长线上,且满足()42PB PC AD +⋅=若AD =PB PC ⋅的值为 .13、已知函数3|3|,0,()123,0.x x f x x x x +≤⎧=⎨-+>⎩设()1g x kx =+,且函数()()y f x g x =-的图象经过四个象限,则实数k 的取值范围为 .14、在ABC 中,若sin 2cos cos C A B =,则22cos cos A B +的最大值为 .二、解答题:本答题共6分,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内. 15、(本小题满分14分)设向量(cos ,sin )αλα=a ,(cos ,sin )ββ=b ,其中0λ>,02παβ<<<,且+a b 与-a b 相互垂直. (1)求实数λ的值; (2)若45⋅=a b ,且tan 2β=,求tan α的值.16、(本小题满分14分)如图,在三棱锥111ABC A B C -中,AB AC =,11AC BC ⊥,11AB BC ⊥,D ,E 分别是1AB ,BC 的中点.求证:(1)11DE ACC A 平面;(2)11AE BCC B ⊥平面;17、(本小题满分14分)某公园内有一块以O 为圆心半径为20米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形OAB 区域,其中两个端点A ,B 分别在圆周上;观众席为梯形ABQP 内且在圆O 外的区域,其中AP AB BQ ==,120PAB QBA ∠=∠=,且AB ,PQ 在点O 的同侧.为保证视听效果,要求观众席内每一个观众到舞台O 处的距离都不超过60米.设,(0,)3OAB παα∠=∈.问:对于任意α,上述设计方案是否均能符合要求?18、(本小题满分16分)在平面直角坐标系xOy 中,已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2,且椭圆C (1)求椭圆C 的方程;(2)设经过点(2,0)P 的直线l 交椭圆C 于,A B 两点,点(,0)Q m . ①若对任意直线l 总存在点Q ,使得QA QB =,求实数m 的取值范围; ②设点F 为椭圆C 的左焦点,若点Q 是FAB 的外心,求实数m 的值.19、(本小题满分16分)已知函数22()ln ,012x f x x a x a-=->-+.(1)当2a =时,求函数()f x 的图象在1x =处的切线方程;(2)若对任意[1,)x ∈+∞,不等式()0f x ≥恒成立,求a 的取值范围; (3)若()f x 存在极大值和极小值,且极大值小于极小值,求a 的取值范围.20、(本小题满分16分)已知数列{}n a 各项均为正数,且对任意*n N ∈,都有2111211()n n n n a a a a a +-+=+.(1)若1a ,22a 。
