最新高三数学数列的极限教学讲义ppt
合集下载
高三数学数列极限1(PPT)2-1

•
;相亲 相亲
捕蝇草(Catchfly)属于维管植物的一种,是很受欢迎的食虫植物, 拥有完整的根、茎、叶、花朵和种子。它的叶片是最主要并且明显的部位,拥有捕食昆虫的功能,外观明显的刺毛和红色的无柄腺部位,样貌好似张牙利爪的血盆大口。盆栽可适用于向阳窗 台和阳台观赏,也可专做栽植槽培养;是原产于北美洲的一种多年生草本植物。 据说因为叶片边缘会有规则状的刺毛,那种感觉就像维纳斯的睫毛一般,所以英文名称为Venus Flytrap,在茅膏菜科捕蝇草属中仅此一种,捕蝇草被誉为自然界的肉食植物。 捕蝇草仅存于于美国的南卡罗莱纳州东南方的海岸平原及北卡罗莱纳州的东北角。然而,在原产地的捕蝇草在生存上却受到人类活动的威胁。人口快速增加因而剥夺捕蝇草的生存空间,而且因为人为干预自然野火的发生,使得这些地区开始长出一些小型灌木 ,因而遮蔽捕蝇草的阳光。因此,捕蝇草被试着引入其他地区进行复育,像是新泽西州和加州。在佛罗里达州已顺利归化,而成为很大的族群。 中心部位生长出来,属于轮生的叶子,显连坐状以丛生的形态生长。中央长出来扁平或者细线状好似翅膀形状的是属于叶柄的部分,原生种的叶柄是扁平如叶片一般,因为反而像是叶子,所以也称做假叶。 叶柄的末端带有一个捕虫夹,这才是会捕捉昆虫的叶子的部分,正面分布有许多的无柄腺,一般是红色或者橙色,越接近叶绿的地方的无柄腺就越少,这部分是分泌消化液来分解昆虫或者吸收昆虫的养分的部位。叶绿长有齿状的刺毛,刺毛的基部有分泌腺, 会分泌出粘液,作用是防止昆虫挣脱和叶瓣粘合。这种的叶子拥有捕捉昆虫的特殊功能,和特殊的模样,属于变态叶中的“捕虫叶”。 因为新叶都是从中心产生,故越外层的叶子就越老。在最外层的叶柄基部有时还会产生新的侧芽。捕蝇草的叶柄有两种型态发生,有的捕蝇草叶柄细长,达7~16公分长,而且朝向空中伸展;有的捕蝇无限增大时,无穷数列{an} 的项an无限地趋近于某个常数a(即an-a无限地接近 于0),那么就说数列{an}以a为极限,或者说a是数列 {an}的极限。
数列的极限讲解PPT课件
xn的极限,或者称数列xn收敛于a,记为
lim
n
xn
a,
或xn a (n ).
如果数列没有极限,就说数列是发散的.
注意:1.不等式 xn a 刻划了xn与a的无限接近; 2.N与任意给定的正数 有关.
第9页/共30页
目录 上一页 下一页 退 出
N定义 :
lim
n
xn
a
0, N 0,使n N时, 恒有 xn a .
无限接近于1.
问题: “无限接近”意味着什么?如何用数学语言 刻划它.
xn
1
(1)n1
1 n
1 n
第7页/共30页
目录 上一页 下一页 退 出
给定 1 , 100
由 1 1 , 只要 n 100时, n 100
有
xn
1
1, 100
给定 1 , 1000
只要 n 1000时,
有
xn
1
1, 1000
可以看到, 随着n 趋于无穷, 数列的 通项有以下两种变 化趋势: (1) 通项无限趋近于
一个确定的常数; (2) 通项不趋近于任何确定的常数.
第6页/共30页
问题: 当 n 无限增大时, xn是否无限接近于某一
确定的数值?如果是,如何确定?
通过上面演示实验的观察:
当
n
无限增大时,
xn
1
(1)n1 n
证明
lim
n
xn
C.
证 任给 0, 对于一切自然数n ,
xn C C C 0 成立,
所以,
lim
n
xn
C.
说明:常数列的极限等于同一常数.
小结: 用定义证数列极限存在时,关键是任意给 定 0,寻找N,但不必要求最小的N.
02数列的极限PPT课件

•数列与函数
数列{xn}可以看作自变量为正整数n的函数: xn=f(n), nN .
首页
上页
返回
下页
结束
铃
❖数列极限的通俗定义 当n无限增大时, 如果数列{xn}的一般项xn无限接近
于常数a, 则常数a称为数列{xn}的极限, 或称数列{xn}收 敛a, 记为
例如
首页
上页
返回
下页
结束
铃
当n无限增大时, 如果数列{xn}的一般项xn无限接近 于常数a, 则数列{xn}收敛a.
2. 数列1, -1, 1, -1, , (-1)N1, 的有界性与收敛 如何?
首页
上页
返回
下页
结束
铃Байду номын сангаас
二、收敛数列的性质
❖定理1(极限的唯一性) 如果数列{xn}收敛, 那么它的极限唯一.
❖定理2(收敛数列的有界性)
如果数列{xn}收敛, 那么数列{xn}一定有界. ❖定理3(收敛数列的保号性)
首页
上页
返回
下页
结束
铃
❖数列极限的精确定义
设{xn}为一数列, 如果存在常数a, 对于任意给定的正
数e , 总存在正整数N, 使得当n>N 时, 不等式
|xn-a |<e
都成立, 则称常数a是数列{xn}的极限, 或者称数列{xn}收 敛于a, 记为
如果不存在这样的常数a, 就说数列{xn}没有极限,
•数列的几何意义
数列{xn}可以看作数轴上的一个动点, 它依次取数轴 上的点x1, x2, x3, , xn , .
x1
xn x4 x3 x5 x2
首页
上页
返回
数列{xn}可以看作自变量为正整数n的函数: xn=f(n), nN .
首页
上页
返回
下页
结束
铃
❖数列极限的通俗定义 当n无限增大时, 如果数列{xn}的一般项xn无限接近
于常数a, 则常数a称为数列{xn}的极限, 或称数列{xn}收 敛a, 记为
例如
首页
上页
返回
下页
结束
铃
当n无限增大时, 如果数列{xn}的一般项xn无限接近 于常数a, 则数列{xn}收敛a.
2. 数列1, -1, 1, -1, , (-1)N1, 的有界性与收敛 如何?
首页
上页
返回
下页
结束
铃Байду номын сангаас
二、收敛数列的性质
❖定理1(极限的唯一性) 如果数列{xn}收敛, 那么它的极限唯一.
❖定理2(收敛数列的有界性)
如果数列{xn}收敛, 那么数列{xn}一定有界. ❖定理3(收敛数列的保号性)
首页
上页
返回
下页
结束
铃
❖数列极限的精确定义
设{xn}为一数列, 如果存在常数a, 对于任意给定的正
数e , 总存在正整数N, 使得当n>N 时, 不等式
|xn-a |<e
都成立, 则称常数a是数列{xn}的极限, 或者称数列{xn}收 敛于a, 记为
如果不存在这样的常数a, 就说数列{xn}没有极限,
•数列的几何意义
数列{xn}可以看作数轴上的一个动点, 它依次取数轴 上的点x1, x2, x3, , xn , .
x1
xn x4 x3 x5 x2
首页
上页
返回
数列极限ppt课件

例4 由前面我当 们 n无 看限 到 时 增 : , 大
1 2n
0
1 (1)n 0 n
n n 1
1
数列极限的直观定义—定性描画
普通地, 假设数列{xn} 当 n 时,
xn 可以无限地趋近某个常数 a, 那么称数
列{xn} 当 n 时以 a 为极限, 记
为
nl imxn a.
此时, 也称数列是收敛的.
极限描画的是变量的变化趋势.
讨论数列
(1)n
10 n
当 n无限增大时的变化趋势.
容易看出:
当 n无限增大时,
(1)n 10n
无限地趋近于. 零
U(O,) 0
U(O1,) 1
x1 x3 x2n-1
x2n x4 x2
(
1 10
••• (••• ••••(••• *•••)•••• •••)• • •
数列
统称为单调数列
(2) 数列的有界性
回想一下前面讲过的 函数的有界性的情形
我学过吗 ?
若 M 0 ,使 x I 时 得 ,有 |f ( x ) | M 当 成 , 则称 f(x)在 函区 I数 上间 .有界
y yf(x) M
yM
I (
O
) x
M yM
数列的有界性的定义
若 M 0 ,使 |x n | M 得 ,n N 成 , 立 则称 { x n } 有 数 .否 界 列 { 则 x n } 是 称 无 . 界
若 { x n } 满 x 1 x 2 足 x n ,则 {xn}严格单, 调 记{ 增 为 xn} 加 .
单调减少 若 { x n } 满 x 1 x 2 足 x n ,则 {xn}单调 , 也 增 { 记 xn} 加 .为
高等数学之数列的极限PPT课件

§2 数列的极限
一、概念的引入 二、数列的概念 三、数列极限的定义 四、数列极限的性质
1
一、概念的引入
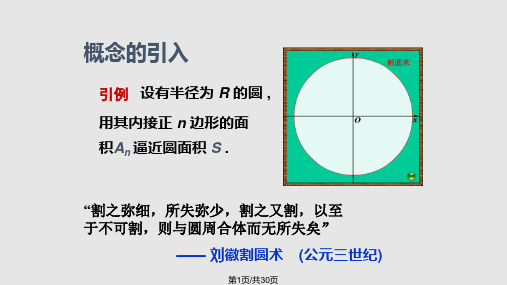
1、割圆术: “割之弥细,所 失弥少,割之又 割,以至于不可 割,则与圆周合 体而无所失矣”
——刘徽
2
正六边形的面积 A1
正十二边形的面积 A 2
R
正62n1形的面积 A n
A 1,A 2,A 3, ,A n,S
随着 n 的无限增大而无限趋于 0 .
4
二、数列的概念
定义:按自然数1,2,3,编号依次排列的一列数
x1 , x2 ,, xn ,
(1)
称为实数列,简称数列.其中的每个数称为数列
的项, xn称为通项(一般项).数列(1)记为{xn }.
例如 2,4,8, ,2n, ;
{2 n }
12,14,18,,21n,;
则对一切 n,皆 自有 xn然 M 数 , 故 xn有.界
推论 无界数列必定发散.
13
例 数x列 n(1)n1.
事实 ,{xn}是 上有 ,但 界却 的 . 发散
注意:有界性是数列收敛的必要条件.
14
3、保号性 定理3 若 ln imxn a, 且a >0( 或a <0),则存在
证 设数 x n k 是 列数 x n 的 列 任一子
ln i m xna,
0 , N 0 , 使 n N 时 , 恒 x n a 有 . 取KN,
则k 当 K时 , n k n k n KN .
xnk a. k l i m xnk a.
证毕.
21
说明: 由此性质可知 , 若数列有两个子数列收敛于不同的极 限 , 则原数列一定发散 . 例如,
一、概念的引入 二、数列的概念 三、数列极限的定义 四、数列极限的性质
1
一、概念的引入
1、割圆术: “割之弥细,所 失弥少,割之又 割,以至于不可 割,则与圆周合 体而无所失矣”
——刘徽
2
正六边形的面积 A1
正十二边形的面积 A 2
R
正62n1形的面积 A n
A 1,A 2,A 3, ,A n,S
随着 n 的无限增大而无限趋于 0 .
4
二、数列的概念
定义:按自然数1,2,3,编号依次排列的一列数
x1 , x2 ,, xn ,
(1)
称为实数列,简称数列.其中的每个数称为数列
的项, xn称为通项(一般项).数列(1)记为{xn }.
例如 2,4,8, ,2n, ;
{2 n }
12,14,18,,21n,;
则对一切 n,皆 自有 xn然 M 数 , 故 xn有.界
推论 无界数列必定发散.
13
例 数x列 n(1)n1.
事实 ,{xn}是 上有 ,但 界却 的 . 发散
注意:有界性是数列收敛的必要条件.
14
3、保号性 定理3 若 ln imxn a, 且a >0( 或a <0),则存在
证 设数 x n k 是 列数 x n 的 列 任一子
ln i m xna,
0 , N 0 , 使 n N 时 , 恒 x n a 有 . 取KN,
则k 当 K时 , n k n k n KN .
xnk a. k l i m xnk a.
证毕.
21
说明: 由此性质可知 , 若数列有两个子数列收敛于不同的极 限 , 则原数列一定发散 . 例如,
高等数学数列的极限PPT课件

其中 : 每一个或任给的; : 至少有一个或存在.
几何解释:
a
2 a
x2 x1 xN 1 a xN 2 x3 x
当n N时, 所有的点 xn都落在(a , a )内,
只有有限个(至多只有N个) 落在其外.
因此:数列的收敛性及其极限与它前面的有限项无关, 改变数列的前有限项,不改变其收敛性和极限
n
n
例3
设xn
C(C为常数),
证明 lim n
xn
C.
证 任给 0 , 对于一切自然数n ,
注意: 数列极限的定义未给出求极限的方法.
例2 证
证明 lim n (1)n1 1.
n
n
xn 1
n (1)n1 1 n
1 n
任给 0,
要 xn 1 ,
只要 1 , n
或n 1 ,
所以, 取N [1], 则当n N时,
就有 n (1)n1 1
n
即lim n (1)n1 1.
S
2、截丈问题:
“一尺之棰,日截其半,万世不竭”
第一天截下的杖长为 X1
1; 2
第二天截下的杖长总和为
X2
1 2
1 22
;
第n天截下的杖长总和为 X n
1 2
1 22
1 2n ;
Xn
1
1 2n
1
二、数列的定义
1. 定义
数列也称为序列
设 f (n) 是以正整数集 Z+ 为定义域的函数.
将 f 的值域 f (Z ) { xn | xn f (n), n N } 中的元素 xn, 按自变量 n 增大的次序排列出来所 得到的一串数:
x1 x2 x3 … xn …
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
进 入 夏 天 ,少 不了一 个热字 当头, 电扇空 调陆续 登场, 每逢此 时,总 会想起 那 一 把 蒲 扇 。蒲扇 ,是记 忆中的 农村, 夏季经 常用的 一件物 品。 记 忆 中 的故 乡 , 每 逢 进 入夏天 ,集市 上最常 见的便 是蒲扇 、凉席 ,不论 男女老 少,个 个手持 一 把 , 忽 闪 忽闪个 不停, 嘴里叨 叨着“ 怎么这 么热” ,于是 三五成 群,聚 在大树 下 , 或 站 着 ,或随 即坐在 石头上 ,手持 那把扇 子,边 唠嗑边 乘凉。 孩子们 却在周 围 跑 跑 跳 跳 ,热得 满头大 汗,不 时听到 “强子 ,别跑 了,快 来我给 你扇扇 ”。孩 子 们 才 不 听 这一套 ,跑个 没完, 直到累 气喘吁 吁,这 才一跑 一踮地 围过了 ,这时 母 亲总是 ,好似 生气的 样子, 边扇边 训,“ 你看热 的,跑 什么? ”此时 这把蒲 扇, 是 那 么 凉 快 ,那么 的温馨 幸福, 有母亲 的味道 ! 蒲 扇 是 中 国传 统工艺 品,在 我 国 已 有 三 千年多 年的历 史。取 材于棕 榈树, 制作简 单,方 便携带 ,且蒲 扇的表 面 光 滑 , 因 而,古 人常会 在上面 作画。 古有棕 扇、葵 扇、蒲 扇、蕉 扇诸名 ,实即 今 日 的 蒲 扇 ,江浙 称之为 芭蕉扇 。六七 十年代 ,人们 最常用 的就是 这种, 似圆非 圆 , 轻 巧 又 便宜的 蒲扇。 蒲 扇 流 传 至今, 我的记 忆中, 它跨越 了半个 世纪, 也 走 过 了 我 们的半 个人生 的轨迹 ,携带 着特有 的念想 ,一年 年,一 天天, 流向长
n→∞
li m
n→∞
n1k=0(k>0);|q|<1
时,li m
n→∞
qn=0.
2.求极限的常用方法和技巧:(1)分式型:分子、分母同除以 n 的最高次
项;
• (2)指数型:分子、分母同除以绝对 值最大的底数的n次方;
• (3)无理型:分子(分母)有理化;
• (4)求和(积)型:先求和(积),再求 极限.
【自以主3n解,答(5】)分(子1)∵有n(理n1+化1).+n(n4+1)+…+
3n-2 n(n+1) =1+4+n…(n++1(3) n-2)
.
=n(n1+1)·n(1+32n-2)
=23(nn- +11)
∴原式=li m
n→∞
23(nn- +11)=32.
(2)∵(3n-1)1(3n+2)
=133n1-1-3n1+2 ∴2×1 5+5×1 8+8×111+…+(3n-1)1(3n+2)
=li m
n→∞
54+542+…+54n-67+762+…+76n 56+652+…+65n-45+542+…+54n
=li m
n→∞
-51n+71n -61n+51n
=li m
n→∞
- -156+n+571n=-1.
• 【答案】 - 1
常见数列极限的求法
求下列极限:
(1)li m
n→∞
n(n1+1)+n(n4+1)+…+n3(nn-+21);
=1321-15+15-18+18-111+…+3n1-1-3n1+2
=1321-3n1+2
∴原式=li m
n→∞
3112-3n1+2=16.
(3)∵1-2121-312…1-n12
=1-121+121-131+13…1-n11+n1
=
1 2
×
3 2
×
2 3
×
4 3
×
3 4
×…×
n-1 n
×
n+1 n
=
n+1
2n
∴原式=li m
n→∞
n2+n1=12.
(4)原式=li m
n→∞
(-- 2)23-n23+n1+3=13.
(5)∵ n2+2n-n
=(
n2+2n-n)( n2+2n+n) n2+2n+n
= n2+2n2n+n=
2 1+n2+1
∴原式=li m
n→∞
1+2 n2+1=1.
1.常用极限:li m C=C;
(2)li m
n→∞
2×1 5+5×1 8+8×111+…+(3n-1)1(3n+2);
(3)li m
n→∞
1-2121-312…1-n12;
(4)li m
n→∞
(-(-2)2n+)n1++33nn+1;
(5)li m ( n2+2n-n).
n→∞
• 【思路点拨】 (1)(2)(3)先求和(积) 再利用法则求极限,(4)分子分母除
∴2aann+-11=22·2n+n+1-1-12+-11=2-2n3+1,
∴li m
n→∞
2aann+-11=2.
• 【答案】 D
4.设等差数列{an}的公差 d 是 2,前 n 项
的和为 Sn,则 li m
n→∞
a2n-Snn2=________.
【解析】
li m
n→∞
a2n-n2 Sn
=
li
)
A.2
B.1
1 C.2 【解析】
D.0
li m
n→∞
nn(n2×+21)=12.
• 【答案】 C
3.把 1+(1+x)+(1+x)2+…+(1+x)n 展
开成关于 x 的多项式,其各项系数为 an,
则 li m
n→∞
2aann+-11等于(
)
1
1
A.4
B.2
C.1
D.2
【解析】 令 x=1 得 an=1+2+22+…+ 2n=1+2(11--22n)=2n+1-1.
n→∞
(3)li m qn=_0__ (|q|<1).
n→∞
1.若 li m
n→∞
1-a an=0,则 a 的取值范围是
()
A.|a|<12
B.a<1
C.a>12
D.a=1
【解析】 1-a a<1⇔1-a a2<1,解得 a>12.
• 【答案】 C
2.li m
n→∞
1+2+3n+2 …+n等于(
长 的 时 间 隧 道,袅
2011届高三数学数列的极限
考 纲 点 击
1.了解数列极限的概念. 2.掌握极限的四则运算法则,
会求某些数列的极限.
热 点 提 示
常见数列极限的求法是高考 常考的内容之一,一般以选
择或填空的形式出现.
3.数列极限的三个基本极限
(1)li m
n→∞
n1=_0__.
(2)li m c=_c__ (c 是常数).
m
n→∞
(2n+a1-2)2-n2
na1+n(n-1)
=li m
n→∞
3n2+4n(2a+1-(a21)-n+1)(na1-2)2=3.
• 【答案】 3
5.li m
n→∞
45-67+542-762+…+54n-76n 56-45+652-542+…+65n-54n
=________.
【解析】 原式
n→∞
li m
n→∞
n1k=0(k>0);|q|<1
时,li m
n→∞
qn=0.
2.求极限的常用方法和技巧:(1)分式型:分子、分母同除以 n 的最高次
项;
• (2)指数型:分子、分母同除以绝对 值最大的底数的n次方;
• (3)无理型:分子(分母)有理化;
• (4)求和(积)型:先求和(积),再求 极限.
【自以主3n解,答(5】)分(子1)∵有n(理n1+化1).+n(n4+1)+…+
3n-2 n(n+1) =1+4+n…(n++1(3) n-2)
.
=n(n1+1)·n(1+32n-2)
=23(nn- +11)
∴原式=li m
n→∞
23(nn- +11)=32.
(2)∵(3n-1)1(3n+2)
=133n1-1-3n1+2 ∴2×1 5+5×1 8+8×111+…+(3n-1)1(3n+2)
=li m
n→∞
54+542+…+54n-67+762+…+76n 56+652+…+65n-45+542+…+54n
=li m
n→∞
-51n+71n -61n+51n
=li m
n→∞
- -156+n+571n=-1.
• 【答案】 - 1
常见数列极限的求法
求下列极限:
(1)li m
n→∞
n(n1+1)+n(n4+1)+…+n3(nn-+21);
=1321-15+15-18+18-111+…+3n1-1-3n1+2
=1321-3n1+2
∴原式=li m
n→∞
3112-3n1+2=16.
(3)∵1-2121-312…1-n12
=1-121+121-131+13…1-n11+n1
=
1 2
×
3 2
×
2 3
×
4 3
×
3 4
×…×
n-1 n
×
n+1 n
=
n+1
2n
∴原式=li m
n→∞
n2+n1=12.
(4)原式=li m
n→∞
(-- 2)23-n23+n1+3=13.
(5)∵ n2+2n-n
=(
n2+2n-n)( n2+2n+n) n2+2n+n
= n2+2n2n+n=
2 1+n2+1
∴原式=li m
n→∞
1+2 n2+1=1.
1.常用极限:li m C=C;
(2)li m
n→∞
2×1 5+5×1 8+8×111+…+(3n-1)1(3n+2);
(3)li m
n→∞
1-2121-312…1-n12;
(4)li m
n→∞
(-(-2)2n+)n1++33nn+1;
(5)li m ( n2+2n-n).
n→∞
• 【思路点拨】 (1)(2)(3)先求和(积) 再利用法则求极限,(4)分子分母除
∴2aann+-11=22·2n+n+1-1-12+-11=2-2n3+1,
∴li m
n→∞
2aann+-11=2.
• 【答案】 D
4.设等差数列{an}的公差 d 是 2,前 n 项
的和为 Sn,则 li m
n→∞
a2n-Snn2=________.
【解析】
li m
n→∞
a2n-n2 Sn
=
li
)
A.2
B.1
1 C.2 【解析】
D.0
li m
n→∞
nn(n2×+21)=12.
• 【答案】 C
3.把 1+(1+x)+(1+x)2+…+(1+x)n 展
开成关于 x 的多项式,其各项系数为 an,
则 li m
n→∞
2aann+-11等于(
)
1
1
A.4
B.2
C.1
D.2
【解析】 令 x=1 得 an=1+2+22+…+ 2n=1+2(11--22n)=2n+1-1.
n→∞
(3)li m qn=_0__ (|q|<1).
n→∞
1.若 li m
n→∞
1-a an=0,则 a 的取值范围是
()
A.|a|<12
B.a<1
C.a>12
D.a=1
【解析】 1-a a<1⇔1-a a2<1,解得 a>12.
• 【答案】 C
2.li m
n→∞
1+2+3n+2 …+n等于(
长 的 时 间 隧 道,袅
2011届高三数学数列的极限
考 纲 点 击
1.了解数列极限的概念. 2.掌握极限的四则运算法则,
会求某些数列的极限.
热 点 提 示
常见数列极限的求法是高考 常考的内容之一,一般以选
择或填空的形式出现.
3.数列极限的三个基本极限
(1)li m
n→∞
n1=_0__.
(2)li m c=_c__ (c 是常数).
m
n→∞
(2n+a1-2)2-n2
na1+n(n-1)
=li m
n→∞
3n2+4n(2a+1-(a21)-n+1)(na1-2)2=3.
• 【答案】 3
5.li m
n→∞
45-67+542-762+…+54n-76n 56-45+652-542+…+65n-54n
=________.
【解析】 原式
