信号与系统课后习题与解答第一章
信号与系统第1章习题解

第1章 习 题 解 答1-1.判断下列信号是否是周期性的,如果是周期性的,试确定其基波周期(1)()⎪⎭⎫⎝⎛+=43cos 2πt t f 解:对于()k Z ∈()222cos 32cos 322cos 333444f t k t k t k t f t ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=++=++=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∴原函数是周期函数,令1k =,则基波周期为23π。
(2)()26sin ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=πt t f解:对于()k Z ∈()()22sin sin 66f t k t k t f t ππππ⎡⎤⎡⎤⎛⎫⎛⎫+=+-=-= ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦∴原函数是周期函数,令1k =,则基波周期为π。
(3)()[]()t u t t f π2cos =解:设其存在周期,令周期为T()()()cos 2f t T t T u t T π+=++⎡⎤⎣⎦在0T ≠的情况下函数不为零的部分发生了平移,故()()f t T f t +≠∴原函数不是周期函数。
(4)())(42π+=t j et f解:对于()k Z ∈())()(())(()224442222j t k j t j t j k f t k eeeef t ππππππ+++++==⨯==∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.求信号())14sin()110cos(2--+=t t t f 的基波周期。
解:cos(101)t +的基波周期为15π, sin(41)t -的基波周期为12π二者的最小公倍数为π,故())14sin()110cos(2--+=t t t f 的基波周期为π。
1-3.设()3,0<=t t f , 对以下每个信号确定其值一定为零的t 值区间。
(1)()t f -1 (2)()()t f t f -+-21 (3))()(t f t f --21 (4)()t f 3 (5)()3tf解:(1)()t f -1为()f t 反折后向右平移一个单位得到,故当()2t >-时()10f t -= (2)()2f t -为()f t 反折后向右平移两个单位得到,故当()1t >-时()20f t -=。
信号与系统第三版郑君里课后习题答案

信号与系统第三版郑君里课后习题答案第一章习题参考解1,判刑下列信号的类型解:()sin[()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x e d τττ--∞=⎰ 连续、模拟、非周期、功率型信号。
()(2y n x n =) 离散、模拟、非周期、功率型信号。
()()y n nx n = 离散、模拟、非周期、功率型信号。
1-6,示意画出下列各信号的波形,并判断其类型。
(1) 0()sin()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()tx t Ae -= 连续、模拟、非周期、只是一个函数,不是物理量。
(3) ()cos 0t x t e t t -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5kx k k =≥ 离散、模拟、非周期、能量型 (6) 0().j kx k eΩ= 离散、模拟、周期、功率型()sin[()];()()()(2);()()tt y t A x t y t x ed y n x n y n nx n τττ--∞====⎰1-6题,1-4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1-6 5-6题 n=0:pi/10:2*pi; y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill '),title('(0.8)^n'),grid n1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill '),title('exp[2*pi*n1'),grid subplot(4,1,4),stem(n1,sin(2*pi*n1),'fill '),title('sin2pin1'),grid subplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1-8,判断下列系统的类型。
信号与系统PPT电子书陈生谭版课后习题答案

1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
解:
(1)
is
(t)
=
i(t
)
+
ic
(t )
+
iR
(t )
=
i (t )
+
Cuc′
(t )
+
1 2
u (t )
----⑴
而 uC (t) = u(t)
对回路①,有:
⎧− ⎩⎨iL
3i(t) (t) =
+ is
LiL′ (t) + u(t) (t) − i(t)
=
0
⇒
u(t)
=
3i(t
)
−
Lis′
(t)
− p 1+ p
−1
3p 0
−p
− p 0 1+ p +1/ p
− p f (t) i2 (t) = 3 p − p
信号与系统第一章习题
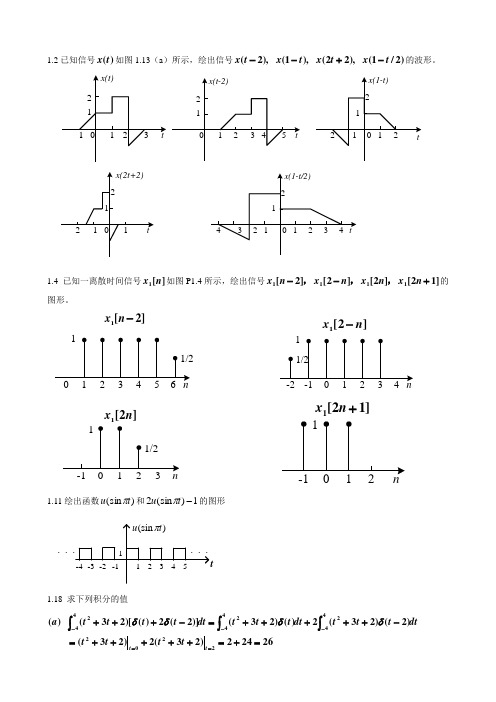
1.2已知信号)(t x 如图1.13(a )所示,绘出信号)2/1(),22(),1(),2(t x t x t x t x -+--的波形。
1.4 已知一离散时间信号][1n x 如图P1.4所示,绘出信号]12[]2[]2[]2[1111+--n x n x n x n x ,,,的图形。
1.11绘出函数)(sin t u π和1)(sin 2-t u π的图形t)(sin t u π1-1123. . .. . .54-2-3-41.18 求下列积分的值26242)23(2)23()2()23(2)()23()]2(2)()[23()(222442442442=+=+++++=-+++++=-+++==---⎰⎰⎰t t t t t t dtt t t dt t tt dt t t t t a δδδδ]2[1-n x]2[1n x-]2[1nx ]12[1+n x651)1()1(0)2()1()()1()5()1()]2()()2()[1()(2202442442442442=+=++++=-++++++=-++++==----⎰⎰⎰⎰t t t t dtt t dt t t dt t t dt t t t t b δδδδδδ12cos1)cos 1()2()cos 1()(2=-=-=--=-⎰ππδπππt t dt t t c4)231()21()21()231()1()1()1()1()23()1()2()1()2()1()23()1()(cos )1(1,23,2,2,23420cos )(23222322222222224321=++++-+-=+++++++=-++-+++++++=+==-=-=====-=-=-----⎰⎰⎰⎰⎰πππππδπδπδπδδπππππππππππππππππππt t t t t t t t dt t t dtt t t dt t t dt t t dt t t t t t t n n t t d 冲击强度均为公式可得它们对应项的由冲击函数的复合函数个根,仅包含取奇数,在积分限内,令:1.21 判断下列每个信号是否是周期的?如果是周期的,试求出它的基波周期。
信号与系统答案 西北工业大学 段哲民 信号与系统1-3章答案
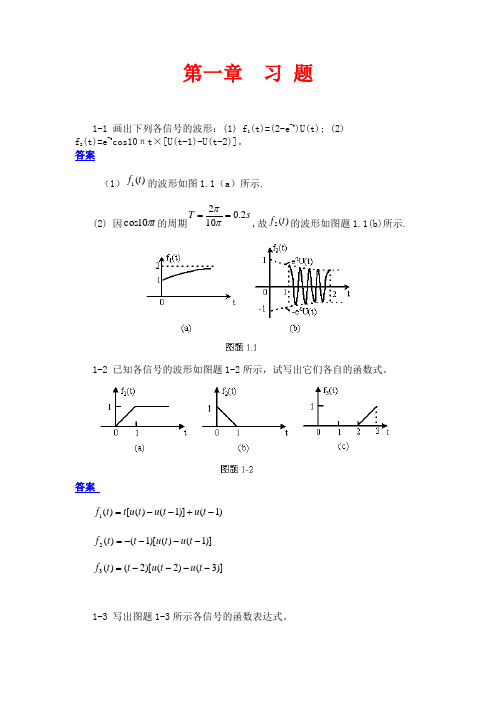
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
信号与系统课后习题参考答案.pdf
-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
(完整版)信号与系统第一章答案
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与系统课后习题答案汇总
第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列,周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sin π的功率为1/2,因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率,其功率为1/2。
信号与系统课后习题参考答案
1.20
解:(a)
x1 (t)
=
cos( 2t )
=
1 2
(e j2t
+
e− j2t
)
则:
y1 (t)
= T{1 (e j2t 2
+ e − j2t )} =
1 (e j3t 2
+ e − j3t ) ;
(b)
x2 (t)
=
cos(2(t
−
1 )) 2
=
1 (e j(2t−1) 2
+ e − j(2t−1) )
-1/2
-1
1 1/2 -2 -1 0 1
1 1 1 x[-n+3]
1/2 n
678 2 34 5
-1/2 -1
(c) x[3n]
1 x[3n]
1/2 n
-4 -3 -2 -1 0 1 2 3 -1/2
7
(d) x[3n+1]
x[n+1]
11 1 1
1/2 1/2
1/2 n
-5 -4 -3 -2 -1 0 1 2 3
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
-5
-4 -3 -2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?
(b)
图1-1 t0
f (t)(a) t0 f (t)1234只取1,2,3,4值
t0 f (t)(c)123
12345678只取1,2,3值
t0 f (t)
(d)12345678
n0
(f)
112345678
只取0,1值 x (n)
n0
112345678
只取-1,1值 x (n)
-1
图1-2 t0 f (t)(a) t0 f (t)(b) k0 f (k)(c) k
0
f (k)(d)12 解 信号分类如下:
))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d21c21
b21a21图1-1所示信号分别为
(a)连续信号(模拟信号); (b)连续(量化)信号; (c)离散信号,数字信号; (d)离散信号; (e)离散信号,数字信号; (f)离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(teat; (2)nTe; (3))cos(n; (4)为任意值)(00)sin(n;
(5)221。 解 由1-1题的分析可知: (1)连续信号; (2)离散信号; (3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T: (1))30t(cos)10t(cos; (2)j10te; (3)2)]8t(5sin[;
(4)为整数)(n)TnTt(u)nTt(u)1(0nn。 解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos(10t)其周期5T1;对于分量cos(30t),其周期15T2。由于5
为21TT、的最小公倍数,所以此信号的周期5T。 (2)由欧拉公式)t(jsin)t(cosetj 即)10t(jsin)10t(cosej10t
得周期5102T。
(3)因为)16t(cos2252252)16t(cos125)8t(5sin2 所以周期8162T。 (4)由于 原函数2)T(2ntT)12n(,11)T(2nt1,2nT n为正整数 其图形如图1-3所示,所以周期为2T。
t0 f (t)
-11
T2T3T4T…
图1-3 1-4对于教材例1-1所示信号,由f(t)求f(-3t-2),但改变运算顺序,先求f(3t)或先求f(-t), 讨论所得结果是否与原例之结果一致。
解 原信号参见例1-1,下面分别用两种不同于例中所示的运算顺序,由f(t)的波形求得f(-3t-2)的波形。 两种方法分别示于图1-4和图1-5中。 tf(3t)103132方法一:倍乘f(-3t)103231反褶tf(-3t-2)1
0132
t
32左移
tf(-t)1
0方法二:
反褶f(-3t)103231倍乘tf(-3t-2)
1
0132
t
32左移
2-1
图1-4
图1-5 1-5 已知f(t),为求)(0attf应按下列那种运算求得正确结果(式中at,0都为正值)? (1))(atf左移0t; (2))(atf右移0t;
(3))(atf左移at0;
(4))(atf右移at0。 解 (1)因为)(atf左移0t,得到的是)()(00atatfttaf,所以采用此种运算不行。 (2)因为)(atf右移0t,得到的是)()(00atatfttaf,所以采用此运算不行。
(3)因为)(atf左移at0,得到的是)()(00tatfattaf,所以采用此运算不行。
(4)因为)(atf右移at0,得到的是)()(00attfattaf,所以采用此运算不行。 1-6 绘出下列各信号的波形: (1))8sin()sin(211tt; (2))8sin()sin(1tt。 解 (1)波形如图1-6所示(图中)8sin()sin(211)(tttf)。 00.511.500.511.52f(t)f(t)
82t82
t
图1-6图1-7(2)波形如图所示1-7(图中)8sin()sin(1)(tttf)。 1-7 绘出下列各信号的波形: (1))4sin()()(tTTtutu;
(2))4sin()2()(2)(tTTtuTtutu。 解 )4sin(tT的周期为2T。 (1)波形如图1-8(a)所示(图中)4sin()()(tTTtutu)。在区间T,0,内,包含有)4sin(tT的两个周期。 01f(t)t图1-8-12TT01f(t)-1T2T(a)(b)t
(2)波形如图1-8(b)所示(图中)4sin()2()(2)(tTTtuTtutu)。在区间TT2,
内是)4sin(tT,相当于将)4sin(tT倒像。
1-8 试将教材中描述图1-15波形的表达式(1-16)和(1-17)改用阶越信号表示。 解 表达式(1-16)为
)(0)(ttaatateee
tf
tttt000当
当
这是一个分段函数。若借助阶越信号,则可将其表示为 )()()(][)()(e)(0)(0)(000ttuetuettueettututfttaatttaatat
]
表达式(1-17)为
)()1(1)1(1)0()1(1)(0)(00tteaea
tteadf
ttaat
att
借助阶越信号,可将其表示为
)(]1[1)()(1)(]1[1)1(1)]()()[1(1)(0)(0)(000ttueatueaattueaeattutueadfttaatttaatatt
1-9 粗略绘出下列各函数式的波形图: (1))()2()(tuetft; (2))()63()(2tueetftt; (3))()55()(3tueetftt; (4))]2()1()[10cos()(tututetft。 解 t0-1
1 f (t)
(d)21 t036 f (t)(b)9 t012 f (t)(a) t0 f (t)(c)123
123图1-9(1)信号波形如图1-9(a)所示。 (2)信号波形如图1-9(b)所示。 (3)信号波形如图1-9(c)所示。 (4)信号波形如图1-9(d)所示。在区间[1,2]包含)10cos(t的5个周期。
1-10 写出如图所示各波形的函数式。
01f(t)t(a)-22t012312f(t)(b)0Tt
f(t)E半周正弦波
(c)图1-10 解 (a)由图1-10(a)可写出
