10.北京理工大学信号与系统精品课程习题及答案.doc
北理工《信号与系统》习题答案第2章答案(纯手写)

xt*)*?23 u.D
k,r*t-^ at+L (aN)
hLt-4nb)
)= qa)(4t*x t&xI
L tt-t1=Gt + z
=) l, 'xt = ({'- e-121 ) u,t*1
btl L ul = + (e-t- u-%) LtLt)
@) | ht ft) = a{m+ cyte
{) a=o
(I C, =l
\ lU Ur= C e-c atrr 7 C,ito;t
,
hnttl:
t
+
O-l) ,at
ht-r{*/-t)+--e "tr;t +e "C.rDt
) i, Lt) = 0o D i,,*t
)l =
dr (-b-A) ryz/L) clx = 1z Lt)x 4, th)
t Crto
-o) (D'-+?/D+zl!/ot=o t flr.o)=1, g'ttro)=z
; ; :t,r,il,Aln= co-m + cro''6 -J
) h,n*)= L'vt-o-'t-tzo
0, kl = d N bt) l,u*) = lw> u u,4,L) = ,f! U
= Lb, ct+t) _ 2 + g *-,., ] *, J -I r/" Lzr) al t -, I-t*r,ol,
-t,-ttt-itUt --;t,e---*rkt) = (+L-t-)tu-'+*wt ) t,LLt)
北理信号与系统本科测试题

综合题一一. 填空题1 .按照信号的能量或功率为有限值,信号可分为和。
2 .一个离散时间系统可由、、等基本部件组成。
3 .如图所示 LTIS ,若, , ,则系统的输出为。
4 .应用卷积积分的方法可以得到系统的。
5 .6 .试写出下列函数的频谱密度函数(a) , 所以(b) , 所以7. x(n) 的离散时间傅立叶变换为 X(e ), 则 y(n)= 的傅立叶变换为8. 果而稳定的 LTI 系统,单位冲击响应为 h(t) , 系统 H(s) 有一极点在 s=-2, 则是9. 知一因果而稳定系统的单位脉冲响应为 h(n),H(z) 是有理的,且, 则10 .二、计算题1 .设三个因果 LTI 系统的级联如图 1 所示,其中冲激响应而总的冲激响应如图 2 所示,求(a)冲激响应(b) 整个系统对输入的响应2 .考虑一个 LTI 系统它对输入的响应为(a) 求该系统的频率响应(b) 确定该系统的冲激响应(c) 求出联系输入、输出的微分方程,并用积分器、相加器和系数相乘器实现该系统。
3 .如图所示,系统(1) 以为状态变量列出其状态方程与输出方程(2) 求状态转移矩阵4.的单边拉氏反变换5.已知信号 x(n) 的傅立叶变换, 求的傅立叶反变换综合题一答案一. 填空题1 .答案:(能量信号,功率信号)2 .答案:(单位延时器、相加器、倍乘器)3 .4 .答案:(零状态响应)5 .答案:6 .答案:(a)7.8.9.10 .二、计算题1 .答案:2 .解 :(a)(b)(c)3 .解 :(1)(2)4.解:(分子阶次与分母阶次相同,降阶)(分母多项式带有重根的部分分式展开法)又因为求单边拉氏变换所得信号为因果信号5.解:综合题二一、填空题1.零状态响应是由和构成的。
2.如图所示,系统总的输入—输出关系为。
3. 散时间信号频谱为 X(e ),如果已知频率范围内的幅谱和相位谱就能够画出全频域的频谱图.4. x(t)=tu(2t-1)的拉氏变换为。
《信号与系统》第五章 北京理工大学

T0 2t m或f 0
x(t ) ~(t )GT0 (t ) x
0 , GT0 (t ) 0, | t | T0 / 2 其它
5.4 周期的离散时间信号的表示 里叶级数
1
离散傅
用复指数序列表示周期的离散时间信号
jk 2n / N , k 0,1,2, 是周期 成谐波关系的复指数序列集 k [n] e 序列,其中每个分量的频率是 0 的整数倍。
2 (
2 2
l)
... bM X (e
j
2 (
2
l)
周期序列的离散 时间傅里叶变换
2
)
c 2 (
0 l N 1 l
l)
c 2 ( 2 / N
1 l 2
l)
...
f (t )
0
t
f s (t )
p(t )
0
Ts
t
t
0
Ts
2 抽样信号的频谱
x(t ) X ( )
x p (t ) X p ( )
抽样信号的频谱
5.2 连续时间信号的离散化
2 抽样信号的频谱
时域抽样定理
1 x p ( ) T
k
X ( k )
s
是周期的连续频率函数以抽样频率 s 为周期重复组成的。
离散时间傅立叶变换
关于傅立叶变换,下列哪个说法是错误的( ) A. 时域是非周期连续的,则频域是非周期连 续的。 B. 时域是周期离散的,则频域也是周期离散 的。 C. 频域不是周期连续的,则时域也不是周期 连续的。 D. 时域是非周期离散的,则频域是周期连续 的
北京理工大学信号与系统信号的频域分析

x(t ) a0 ak cos kw0t bk sin kw0t
k 1 k 1
(3)
其中:
a0
1 2 2 T0 x(t )dt , ak T x(t ) cos kw0tdt , bk T x(t ) sin kw0tdt 0 T0 T0 T0 0
(4)
4、离散非周期时间信号的频域分析
非周期序列 x( n) 可以表示成一组复指数序列的连续和
x ( n)
其中
1 2
X (e
2
j
)e jn d
(15)
X (e j )
n
x ( n )e
jn
(16)
式(16)称为 x( n) 的离散时间傅里叶变换,式(15)和式(16)确立了非周期离散时 间信号 x( n) 及其离散时间傅里叶变换 X (e 称为频谱函数,且 X (e
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
N=20;T=1;a=0.5;A=1;
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
③利用 MATLAB 绘出周期矩形脉冲信号的频谱,观察参数 T 和变 化时对频谱波形的影响。
Answer:频谱包络形状不变,过零点不变,普贤间隔随着 T 变大而缩小。
2、已知 x(t)是如图所示的矩形脉冲信号。 ①求该信号的傅里叶变换; ②利用 MATLAB 绘出矩形脉冲信号的频谱,观察矩形脉冲信号宽 度变化时对频谱波形的影响; ③让矩形脉冲信号的面积始终等于 1,改变矩形脉冲宽度,观察 矩形脉冲信号时域波形和频谱随矩形脉冲宽度的变化趋势。
北京理工大学(已有10试题)

北京理工大学信息科学技术学院自动控制理论1999——2000,2002——2008自动控制理论(非控类)2004电子技术(含模拟、数字部分)1999——2000,2002——2008模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000,2002微机控制与应用技术2002——2008控制工程基础2003——2008物理光学2003——2004,2007——2008应用光学1999——2008,2010(2010为回忆版)波动光学2002大学物理2006——2008精密机械设计2003——2008(其中2003年称“精密机械基础”)激光原理1999——2001,2005——2008电子电路2003——2005,2007——2008电路分析基础1999——2000信号处理导论2003——2008信号与系统1996——2002半导体物理学1999——2008电磁场理论1999——2000,2002——2008微机原理及应用2004——2005电动力学2003——2004理论力学1996——2008(96——98非原版)生物化学1999——2008(注:2007年试卷共11页,缺P5-6页)生物化学(A)2005——2006,2008计算机专业基础(含计算机组织与结构、数据结构)2007计算机技术基础(含计算机组成原理、操作系统和数据结构)2003——2006计算机原理(含操作系统)1999——2002程序设计1999——2000计算机系统结构基础(含计算机组成原理、计算机网络和数据结构)2004——2005 软件理论基础(含离散数学、操作系统、数据结构)1999——2005数据结构与程序设计2004——2008微波技术基础1999——2000晶体管理原理与制造1999——2000机电工程学院电子技术(含模拟、数字部分)1999——2000,2002——2008电子技术基础2007——2008自动控制理论1999——2000,2002——2008自动控制理论(非控类)2004电磁学2005——2008量子力学2005——2008运筹学2001——2008工程力学基础2007——2008流体力学基础2006工程流体力学2005数学物理方程2002——2006数学物理方法2000材料力学1997——1999,2002——2008理论力学1996——2008(96——98非原版)电动力学2003——2004微机控制与应用技术2002——2008控制工程基础2003——2008精密机械设计2003——2008(其中2003年称“精密机械基础”)应用光学1999——2008,2010(2010为回忆版)波动光学2002微机原理及应用2004——2005有机化学1997——2008无机化学(A)2003——2007无机化学(B)2003——2005,2007——2008分析化学2003——2008分析化学(A)2006物理化学2003——2008高分子物理2005——2008高分子化学及高分子物理2003——2004安全系统工程2003——2005,2008工程热力学(不含传热学)2003——2008爆炸与安全技术2005爆炸及其作用2006爆轰理论2003——2005化学2002——2005传感与测试技术2004——2005算法语言1998微波技术基础1999——2000晶体管理原理与制造1999——2000传热学2000应用电子技术2004机械与车辆工程学院电子技术(含模拟、数字部分)1999——2000,2002——2008 电子技术基础2007——2008自动控制理论1999——2000,2002——2008自动控制理论(非控类)2004机械设计2001——2008机械设计原理2001机械制造工程基础2003——2008机械制造工艺学2002理论力学1996——2008(96——98非原版)微机控制与应用技术2002——2008应用光学1999——2008,2010(2010为回忆版)电路分析基础1999——2000模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000,2002精密机械设计2003——2008(其中2003年称“精密机械基础”)控制工程基础2003——2008微机原理及应用2004——2005工程热力学(不含传热学)2003——2008物理化学2003——2008工程力学基础2007——2008流体力学基础2006工程流体力学2005交通运输系统工程学2005,2007——2008微波技术基础1999——2000晶体管理原理与制造1999——2000数字电路与数字信号处理2008材料科学与工程学院物理化学(A)2008高分子物理2005——2008高分子化学及高分子物理2003——2004材料科学基础2003——2007材料力学1997——1999,2002——2008普通化学2008综合化学2008有机化学1997——2008无机化学(A)2003——2007无机化学(B)2003——2005,2007——2008分析化学2003——2008分析化学(A)2006理论力学1996——2008(96——98非原版)电化学原理2003——2006微波技术基础1999——2000晶体管理原理与制造1999——2000化工与环境学院自动控制理论1999——2000,2002——2008自动控制理论(非控类)2004过程控制原理2000——2005,2007——2008化工原理2002——2008有机化学1997——2008无机化学(A)2003——2007无机化学(B)2003——2005,2007——2008分析化学2003——2008分析化学(A)2006物理化学2003——2008电化学原理2003——2006环境微生物学2007——2008工程热力学(不含传热学)2003——2008微波技术基础1999——2000晶体管理原理与制造1999——2000生命科学与技术学院生物化学1999——2008(注:2007年试卷共11页,缺P5-6页)生物化学(A)2005——2006,2008分析化学2003——2008分析化学(A)2006细胞生物学2004——2006微生物学2005——2008分子生物学2007——2008有机化学1997——2008无机化学(A)2003——2007无机化学(B)2003——2005,2007——2008药理学2007信号处理导论2003——2008信号与系统1996——2002电子电路2003——2005,2007——2008物理光学2003——2004,2007——2008应用光学1999——2008,2010(2010为回忆版)波动光学2002信号理论基础2007——2008计算机专业基础(含计算机组织与结构、数据结构)2007计算机技术基础((含计算机组成原理、操作系统和数据结构)2003——2006计算机原理(含操作系统)1999——2002程序设计1999——2000计算机系统结构基础(含计算机组成原理、计算机网络和数据结构)2004——2005 软件理论基础(含离散数学、操作系统、数据结构)1999——2005数据结构与程序设计2004——2008理学院电子技术(含模拟、数字部分)1999——2000,2002——2008大学物理2006——2008数学分析1995,1999——2000,2003——2008高等代数2003——2008电磁学2005——2008量子力学2005——2008电动力学2003——2004普通化学2008综合化学2008无机化学(A)2003——2007无机化学(B)2003——2005,2007——2008分析化学2003——2008分析化学(A)2006物理化学(A)2008物理化学2003——2008有机化学1997——2008理论力学1996——2008(96——98非原版)材料力学1997——1999,2002——2008工程热力学(不含传热学)2003——2008数学物理方程2002——2006数学物理方法2000电路分析基础1999——2000模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000,2002激光原理1999——2001,2005——2008微机控制与应用技术2002——2008爆炸与安全技术2005爆炸及其作用2006电化学原理2003——2006工程力学基础2007——2008流体力学基础2006工程流体力学2005微波技术基础1999——2000晶体管理原理与制造1999——2000管理与经济学院宏微观经济学2008管理学2003——2008(2003,2004名称叫做“管理学基础”。
信号与系统题库答案(完整版)

1 −2( s +1) 1 −2 s e (2) e s +1 s +1 e2 2cos 2 + s sin 2 − s (3) (4) ie s +1 s2 + 4 1 ⎛ 1 1⎞ ⎛ 1 2⎞ (5) 2 [1 − (1 + s )e − s ]e − s (6) ⎜ 2 + ⎟ e − s − ⎜ 2 + ⎟ e −2 s s s⎠ s⎠ ⎝s ⎝s (1)
[3]解 A 点: FA (ω ) =
1 [G1 (ω + ω0 ) + G1 (ω − ω0 )] 2 j B 点: FB (ω ) = [G1 (ω + ω0 ) − G2 (ω − ω0 )] 2 1 C 点: FC (ω ) = [ FA (ω ) + FB (ω )] ⋅ π [δ (ω + ω0 ) + δ (ω − ω0 )] 2π 1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2
1 1 1 j j = [ G1 (ω + 2ω0 ) + G1 (ω ) + G2 (ω + 2ω0 ) − G2 (ω )] 2 2 2 2 2 1 1 1 j j + [ G1 (ω ) + G1 (ω − 2ω0 ) + G2 (ω ) − G2 (ω − 2ω0 )] 2 2 2 2 2
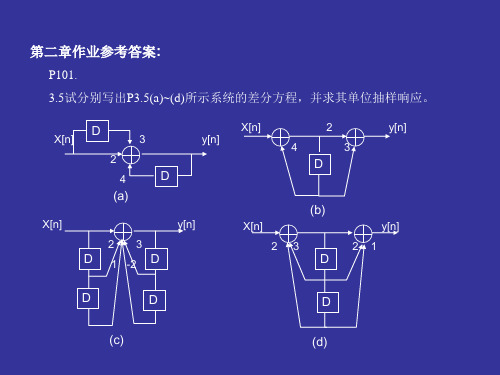
北理工-信号与系统-第三版-第三章-作业参考答案
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
北京理工大学2019-2020-学年-第二学期《信号与系统》期末试题

北京理工大学 2019 - 2020 学年 第二学期
2017 级《信号与系统 B》期末试题 A 卷
班级
学号
姓名
成绩
答题说明: 1. 如无特别说明,试卷中的“系统”均为线性时不变系统; 2. 必须写出解题步骤和必要的文字说明,只写答案不给分。
一、(本题共 60 分,6 道小题,每小题 10 分) 1) 计算卷积 u(t) eatu(t) 。
F
2)已知函数 f t e-3tu(t) ,通过傅里叶变换得出其频谱函数
。
3)若信号
x(
t 2
)
最高角频率为
m
,求对
x(
t) 3
采样的最大时间间隔
Tmax
。
1
4) 线性时不变离散系统的单位抽样响应 hn 1 n u1 n,试判定系统的因果性和
2 稳定性。
5)已知因果序列 x[n] 的y(zt)变换 X (z)
2
5z2 1
1 ,试求 x[n] 的初值 x[0] 和
(z )(z )
32
终值 x[]。
6)知系统函数 Hs
s2 3s 2
,完整见172,7791,836,试判断系统的稳定性,并
8s4 2s3 3s2 s 5 说明是否有
位于 s 平面右半平面上的极点,有几个。 )
二、(本题 10 分)
7)已知某系统 S 由两个子系统 S1 并联而成,子系统 S1 在信号 x1 t cost ut 激 励下的零状态响应为 y1 t Asint ut 。
(a) 求系统 S 的单位冲激响应;
(b) 计算系统 S 在信号 x t ut ut 2 激励下的零状态响应 y t ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图()(A) (B) (C) (D)2 .函数式的值为()( A )0 (B )1 ( C ) 2 (D )3 .已知x(3-2) 的波形如图1 所示,则x (t )的波形应为图()图1 (A)(B)(C)(D)4.已知信号x[n]波形如图2,信号的波形如图()图2 (A)(B)(C) (D)5 .卷积积分等于()(A)(B)-2 (C)(D)-2 (E)-26 .卷积和x[n] u[n-2] 等于()( A )( B )( C )( D )( E )7 .计算卷积的结果为()( A )(B )( C )(D )8 .已知信号x(t) 的波形如图3 所示,则信号的波形如图()图3 (A)(B)(C) (D) 题九图9 .已知信号x (t )如图所示,其表达式为()(A) (B)(C) (D)10 .已知x(t)为原始信号,y(t)为变换后的信号,y(t) 的表达式为()( A )(B )( C )(D )11 .下列函数中()是周期信号( A )(B )( C )( D )( E )12 .函数的基波周期为()。
( A )8 (B )12 (C )16 ( D )2413 .某系统输入—输出关系可表示为,则该系统是()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定14 .某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定15.某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定16.某系统输入—输出关系可表示为,则系统为()系统。
( A )线性( B )时不变( C )无记忆(D )因果( E )稳定17 .某系统输入—输出关系可表示为,则系统为()系统( A )线性( B )时不变( C )无记忆(D )因果()稳定18 .下列系统中,()是可逆系统(A)y[n]=nx[n] (B)y[n]=x[n]x[n-1] (C)y(t)=x(t-4) (D)y(t)=cos[x(t)] (E )y[n]=19 .如图系统的冲激响应为()( A )( B )( C )(D )20 .某系统的输入x (t )与输出y (t )之间有如下关系,则该系统为()(A)线性时变系统(B)线性非时变系统(C)非线性时变系统(D)非线性非时变系统21 .一个LTI 系统在零状态条件下激励与响应的波形如图,则对激励的响应的波形()(A) (B) (C) (D)22. 线形非时变系统的自然(固有)响应就是系统的()( A )零输入响应( B )原有的储能作用引起的响应( C )零状态响应(D )完全的响应中去掉受迫(强制)响应分量后剩余各项之和23 .零输入响应是()( A )全部自由响应( B )部分零状态响应( C )部分自由响应( D )全响应与强迫响应之差24 .下列叙述或等式正确的是()(A) (B)(C)若,则(D)x(t) 和h(t) 是奇函数,则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的,则也是周期的(B) 若是周期的,则也是周期的(C) 若是周期的,则也是周期的(D) 若是周期的,则也是周期的26 .有限长序列经过一个单位序列响应为的离散系统,则零状态响应为()(A) (B)(C) (D)第二章习题1. 某LTI 连续时间系统具有一定的起始状态,已知激励为x (t )时全响应,t 0 ,起始状态不变,激励为时,全响应y (t )=7e +2e ,t 0 ,则系统的零输入响应为()( A )( B )( C )(D )2 .微分方程的解是连续时间系统的()(A) 零输入响应(B) 零状态响应(C) 自由响应(D) 瞬态响应(E)全响应3 .单位阶跃响应是()(A) 零状态响应(B) 瞬态响应(C) 稳态响应(D) 自由响应(E) 强迫响应4 .已知系统如图所示,其中h (t) 为积分器,为单位延时器,h (t) 为倒相器,则总系统的冲激响应h (t) 为()( A )( B )( C )(D )5 .如图所示电路以为响应,其冲激响应h (t) 为()(A) (B)(C) (D)6. 某LTI 系统如图所示,该系统的微分方程为()(A ) (B)(C) (D)7 .已知系统的微分方程, 则求系统单位冲激响应的边界条件h(0 ) 等于()(A) -1 (B) 0 (C) 2 (D) +18 .已知系统的微分方程则系统的单位冲激响应为()(A) (B) (C) (D)9 .已知描述系统的微分方程和初始状态0 值如下;y (0 ) =2 ,, , ,则初始条件0 值为()(A) (B)(C) (D)10 .已知描述系统的微分方程和初始状态0 值如y(t) +6 y (t) +8 y (t) =x (t) +2x (t) ,y (0 ) =1 ,y (0 ) =2 ,x (t) =(t )则初始条件0 值为()。
( A )(B)( C )(D)11 .已知系统微分方程为初始状态为0 ,则系统的阶跃响应为()( A )(B )( C )(D )12 .已知系统具有初始值r(t ),其响应r(t)与激励e(t)有如下关系,其中表示线形系统的有()(A) (B) (C)(D) (E)13.某系统的冲击响应为h(t),输入信号为x(t),系统的零状态响应是()( A )(B )( C )( D )y (t)14 .LTI 系统零状态响应曲线如图所示,则系统的输入响应为()(A) 阶跃信号(B) 正弦信号(C) 冲激信号(D) 斜升信号第三章习题1 .已知离散系统的模拟框图如下,则系统可由()方程表示。
(A)(B)(C)(D)2 .下图所表示的离散系统差分方程为()。
(A)(B)(C)(D)3 .已知离散系统差分方程为y[n+2]-10y[n+1]-24y[n]=7x[n+1]-3x[n],则系统的模拟图为()。
(A)(B)(C) (D)4 .离散时间系统的差分方程为,则系统的单位抽样响应h[n] 为()5 .某离散系统的差分方程为初始条件6 .已知离散系统的差分方程,输入信号()7 .已知差分方程则差分方程的解为()8 .则9.,10 .已知离散时间系统的差分方程为,则系统的单位阶跃响应为()11 .()12 .下列方程的单位抽样响应h[n] 为( )13 .下图所示系统的单位抽样响应h[n] 为( )第四章习题1. 信号如图所示,其三角型付氏级数为()1 2A. n 为奇数B. n 为偶数C. n 为奇数D. n 为偶数2. 锯齿信号x(t) 的付氏级数为( )A. B.C. D.3. 单位冲激序列的频谱为( )A. B.C. D.4. 已知周期信号x(t) 的付氏级数表示式为其单边幅度谱、相位谱为( )5. 周期信号x(t) 内双边频谱如图所示,其三角函数表示式为( )A. B. C. D.5 66. 信号x(t) 如图所示, 其付氏变换为( )A. B.C. D.7. 信号如图所示, 其频谱函数为( )A. B. C. D.7 88. 信号的付氏变换为( )A. B. C. D.9. 信号x(t) 如图所示,其付氏变换为()A. B. C. D.10. 信号,其付氏变换为()A. B. C. D.11. 已知信号频谱如图所示,其原函数为()A. B. C. D.11 1212. 已知信号频谱如图所示,其原函数为()A. B.C. D.13. 已知x(t) X( ) , 则x(t) 为( )A. B. C. D.14. 函数的付氏逆变换( )A. B. C. D.15. 已知如图所示,对应x(t) 为( )A. B. C. D.15 1616. 周期信号x(t) 如图所示,其付氏变换为( )A. B.C. D.17. 周期信号如图所示,其付氏变换为( )A. B.C. D.18. 已知信号其付氏变换为( )A. B.C. D.19. 周期信号x(t) 如图所示,其付氏变换为( )A. ,B. ,C. ,D.17 181920. 的付氏变换为( )A. B. C. D.21. 的付氏变换为( )A. B. C. D.22. 则对应原函数y(t) 为( )A. B. C. D.23. , 的付氏变换为( )A. B. C. D.24. 若a, b 为常数, 且则为( )A. B. C. D.25. 信号的付氏变换为( )A. B.C. D.26. 已知周期函数x(t) 的前周期波形如图所示,若x(t) 是奇函数,只含偶次谐波,则x(t) 在一个函数的波形为( )A B. C. D.27. 如果周期函数满足,则其付氏级数中( )A. 只有余弦项B. 只有奇次谐波项C. 只有正弦项D. 只有偶次谐波项28. 如图所示信号x(t) 的付氏变换, 信号y(t) 的付氏变换为( )A. B. C. D.29. 一个实函数x(t), 已知其付氏变换满足,当x(t) 为偶函数时,函数的表达式为( )A. B. C. D.30. 如图所示信号为周期信号的一个周期,其付氏级数包含( )A. 直流、偶次余弦项B.直流、奇次余弦项B. 直流偶次正弦项 D. 直流奇次正弦项2830第五章习题1 .对频率在6000~7000HZ 之间的信号进行采样,无失真恢复信号的最低采样频率为()A. 3000HZB. 14000HZC. 3500HZD. 1.2kHZ2 .对信号[sinc(100t)] 进行冲激抽样,为了使抽样信号频谱不产生混叠,则奈奎斯特抽样间隔为()A. π /200 s B.π /100 sC. 1/400 sD. 1/200 s3.已知信号x(t)=sinc(100t)+[sinc(50t)] 2 ,对信号x(2t)进行冲激抽样,则奈奎斯特抽样频率为()A. 100 B. 200 C. 50 D. 400 4.已知信号x(t)的频谱X(ω), 对其进行抽样,抽样间隔为T, 则抽样信号的频谱为()A. X(ω-k )B. X(ω-k )C. X(ω- )D. X(ω- )5.已知连续时间信号x(t)=,(β≤π) 的频谱为G (ω),以T=2为抽样间隔,对x(t)进行抽样,得离散时间信号x[2n],则x[2n]的频谱为( )A. B. C. G (ω-π) D.6.下面说法中正确的是( )A. 离散时间信号x[n]的绝对可和是其离散时间傅立叶变换存在的充分条件。
B. 非周期离散时间信号x[n]的偶部:频谱为的实偶函数。
