信号与系统前三章习题课
信号与系统(习题课)

∴ y(t) = e-3t + t e-3t = (1+ t) e-3t
by wky
习题 3-6 (1)
已知系统的微分方程为 y’’(t) +5 y’(t) + 4 y(t) =2 f ’(t) + 5f(t), t >0; 初始状态y(0-) =1,y’(0-) =5, 求系统的零输入响应yx(t)。 解:系统特征方程为 s2+5s+4=0 , 解得特征根 s1=-1, s2=-4
特解 (强迫响应)
比较:完全响应=零输入响应 + 零状态响应 = e-t + (1 - 1/2e-t -1/2e-3t)
by wky
习题 3-4
已知微分方程为 y’(t) + 3 y (t) = f(t),t >0; y(0) =1,
求系统的固有响应(齐次解) yh(t)、强迫响应 (特解) yp(t)和完全响应(全解) y(t) 解:系统特征方程为 s+3=0,
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
2 f(t+2)
f(-3t)
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t by wky
2-10 已知信号波形, 绘出下列信号波形
f(t)
f(-t)
2
2
1
1
-3 -2 -1 0 1 2 3 t -3 -2 -1 0 1 2 3 t
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
信号与线性系统分析习题答案
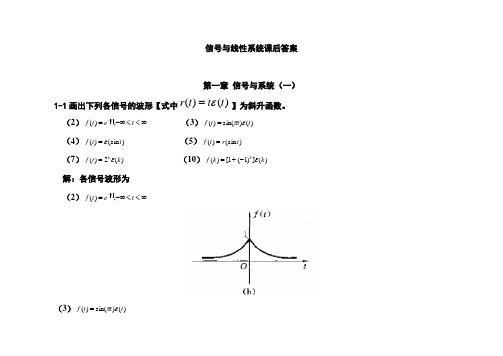
信号与线性系统课后答案第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))tf=r(sin)(t(7))tf kε(k=(2)(10))f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
郑君里《信号与系统》(第3版)(上册)(课后习题 绪 论)【圣才出品】

圣才电子书
(1) ut ut T sin 4π t ;
T
(2) ut 2ut T ut 2T sin 4π t 。
T
解:(1)信号 sin 4π t 的周期为 T ,截取信号 sin 4π t 在区间[0,T]上的波形如
T
2
T
图 1-5(a)所示。
(2)信号 sin 4π t 的周期为 T ,截取信号 sin 4π t 在区间[0,T]上的波形,在区
2
1-3 分别求下列各周期信号的周期 T:
(1) cos10t cos30t;
(2) e j10t ;
(3) 5sin8t2 ;
(4)
1n
ut
nT
ut
nT
T
n为正整数。
|
解:(1)分量 cos(10t) 的周期T1
2 10
5
,分量 cos(30t) 的周期T2
,两者的 15
最小公倍数是 ,所以此信号的周期T 。
eatu(t) 台eatu(t t0 ) eatu(t t0 ) ea(tt0 )u(t t0 )
eatu(t) ea(tt0 )u(t t0 )
(2)表达式(1-17)为
t
(f )d
1
=
a
(1 eat ), (0
t
t0 )
1 a
(1
e at
)
1 a
1
e a (tt0 )
以上各式中 n 为正整数。
解:(1) eat sin(t) 时间、幅值均连续取值,故为连续时间信号(模拟信号);
(2) enT 时间离散、幅值连续,故为离散时间信号(抽样信号);
(3) cos(n ) 时间、幅值均离散,故为离散时间信号(数字信号);
郑君里《信号与系统》(第3版)(上册)(课后习题 傅里叶变换)【圣才出品】

第3章 傅里叶变换3-1 求图3-1所示对称周期矩形信号的傅里叶级数(三角形式与指数形式)。
图3-1解:(1)三角形式由图3-1可知,f(t)为奇函数,故有所以三角形式的傅里叶级数为。
(2)指数形式因所以指数形式的傅里叶级数为。
3-2 周期矩形信号如图3-2所示。
若:重复频率f=5kHz脉宽τ=20μs幅度E=10V求直流分量大小以及基波、二次和三次谐波的有效值。
图3-2解:由图3-2可知,f(x)为偶函数,且f=5kHz,得:所以直流分量为1V基波分量为1sin() 1.3910Vπ=≈二次谐波为2sin( 1.325Vπ=≈三次谐波为。
33sin() 1.2110V π=≈3-3 若周期矩形信号f 1(t )和f 2(t )波形如图3-2所示,f 1(t )的参数为τ=0.5μs,T=1μs,E=1V ;f 2(t )的参数为τ=1.5μs,T=3μs,E=3V ,分别求:(1)f 1(t )的谱线间隔和带宽(第一零点位置)频率单位以kHz 表示;(2)f 2(t )的谱线间隔和带宽;(3)f 1(t )与f 2(t )的基波幅度之比;(4)f 1(t )基波与f 2(t )三次谐波幅度之比。
解:由题3-2的结论可知,f(t)的傅里叶级数可表示为其中,。
(1)f 1(t )的谱线间隔,则带宽:。
(2)f 2(t )的谱线间隔带宽:。
(3)由题3-2可知,所以f 1(t )的基波幅度为:f 2(t )的基波幅度为:故。
(4)的三次谐波幅度为:故。
3-4 求图3-3所示周期三角信号的傅里叶级数并画出频谱图。
图3-3解:由图3-3可知,f(t)为偶函数,故。
bn所以的傅里叶级数可表示为()f t其幅度谱如图3-4所示。
图3-43-5 求图3-5所示半波余弦信号的傅里叶级数。
若E=10V ,f=10kHz ,大致画出幅度谱。
图3-5解:由图3-5可知,f(t)为偶函数,因而b n =0,();所以其傅里叶级数可表示为若E=10V ,,则幅度谱如图3-6所示。
信号与系统课后习题答案(西安电子科技大学)

因此: ⎪⎨x′(t) = y′(t)
即: y′′(t) + 3y′(t) + 2 y(t) = f (t)
⎪⎩x′′(t) = y′′(t)
(d)系统框图等价为:
1.19 设系统的初始状态为 x1(·)和 x2(·),输入为 y(·),完全响应为 y(·),试判断下 列系统的性质(线性/非线性,时变/时不变,因果/非因果,稳定/不稳定)。
−p i2 (t) = 3 p
−p −p
f (t) −p −1 1+ p
−1 −p
=
− p(2 p2 + 3 p + 3) / p − ( p3 + 2 p2 + 2 p + 3)
f (t) =
p(2 p2 + 3 p + 3) f (t) p( p3 + 2 p2 + 2 p + 3)
t
Qτ → 0, f (t) → δ (t)
∫ ∫ ∫ ∴ ∞ f (t)dt = 2K ∞ sin t /τ dt = 2K ∞ sin t /τ d (t /τ ) = −2Kπ = 1
−∞
−∞ t
−∞ t /τ
⇒ K = 1/ 2π
解:(3) f (t) = Ae j5t = A(cos 5t + j sin 5t) ω = 5,T = 2π / ω = 2π / 5
=6+27e-t 十 2e-3t,t≥0 1.26 设有一线性时不变系统,当输入波形如图(a)所示时,系统的零状态响应 yf(t)如图 (b)所示。 (a)试画出输入为 2f(t+4)时,系统零状态响应 yf(t)的波形; (b)画出输入波形如(c)时,系统零状态响应 yf(t) 的波形.
信号与系统习题课(傅里叶变换

才有
F
(ω
)
=
(
1 jω
)2
F
⎡ d2
⎢ ⎣
dt
2
f
( t ) ⎤⎥
⎦
Signals and Systems, Tsinghua University
7
强调
由
F
⎡d ⎢⎣ dt
f
( t )⎤⎥⎦
= Φ(ω)
得到
F
⎡⎣
f
(t )⎤⎦
=
1 jω
Φ (ω )
实际上是引用了FT的积分性质.
因此要考虑 f (−∞) = 0
法二,频移
F(ω) = F0(ω +ω0)+ F(ω −ω0)
求出f0(t)后,
1 F0(ω)
ω
−ω1 0 ω1
[ ] f (t) = f0(t) ejωt +e−jωt =2f0(t)cosω0t
如何求f0S(igt)na?ls
and
定义、对称性、查表。
Systems, Tsinghua University
−2
−1
1
( ) ejω −e−jω ejω +e−jω − ej2ω +e−j2ω
=2
+
jω
ω2
= ......
(1)计算量大;(2)一些函数积分不收敛。
Signals and Systems, Tsinghua University
法二,利用FT的微积分性质
4 1 f(t)
思路:
f
(t
)
d
⎯⎯dt→δ
Φ(0) = 0
Signals and Systems, Tsinghua University
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
