M M C ∞排队系统模型及其应用实例分析
排队模型——精选推荐
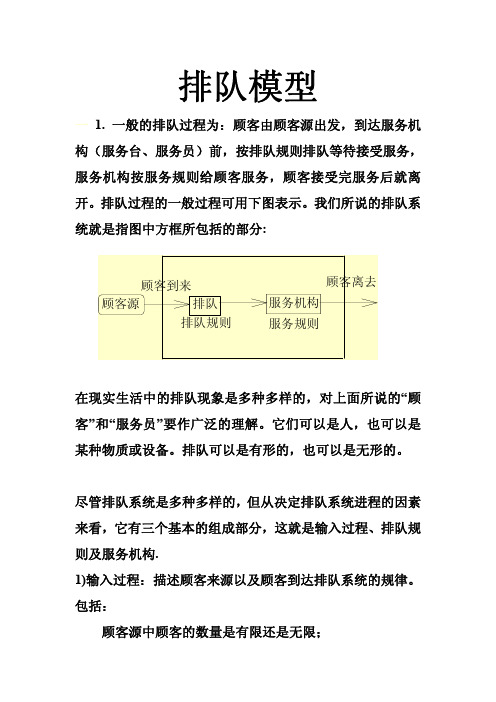
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
第二节无限源的排队系统

S={0,1,2,…},则{N(t);t≥0}是个有限生灭过程,有
λn μn
= =
λ, μ
n = 0,1,2,...,k -1 n =1,2,...,k
ρ= λ, μ
pn
=
(
λ μ
)n
p0
,
n = 0,1,2,...,k
p0
=
1
k
ρn
n=0
=
1, k +1
1- ρ
1 - ρk+1
,
ρ=1 ρ 1
)
,
ρ=1 ρ 1
当ρ≠0时,W=Wq+1/μ
例一
例二
M/M/c/∞系统
平均等待队长
Lq
=
ρc (1 - ρc )2
pc
平均忙的服务台数
c
=
c -1
npn
n=0
+c
n=c
pn
=
λ μ
平均逗留的顾客数
L=
c + Lq
=
ρ+
ρc (1 - ρc )2
pc
平均等待时间
Wq
=
Lq λ
=
pc cμ(1 - ρc
λe
=
λ
-
λpk
=
kλ , k +1 λ(1 - ρk ) 1 - ρk+1
,
ρ=1 ρ 1
M/M/1/k系统 续三
W
=
L λe
=
1
k +1 , 2λ - kρk+1
,
μ - λ λ(1 - ρk )
ρ=1 ρ 1
Wq
=
管理科学教学课件新十三章排队系统分析(下)
可见,k=1时即(M/M/1),k 时即(M/D/1) 注:对于到达与服务均为任意分布的情况,可采用随机模拟的方 法求近似解。
第六节 排队系统最优化
排队系统优化
系统设计优化(静态):如何设计一个系统(如何定,C,服务 规则)使费用最经济(未必最小)。 系统控制优化(动态):一个给定的系统如何运营使目标最优。
目标 : Min z Cs C Cw Ls,
C *是极小点
(单位时间费用最小)
解 : z z (C )是C的离散函数,不能求导,采用边际分析法。
* * z (C ) z (C 1) 应满足 * * z ( C ) z ( C 1) C 化简得:L(C * ) L(C * 1) s L(C * 1) L(C * ) Cw
第五节 M/G/1排队模型
以上讨论了M/M/1和M/M/C系统 ,其 前提均为泊松输入和负指数服务处理,这 类系统的工具是生灭工程状态转移图。在 实际中,有时到达仍为泊松过程 ,但服务 时间并不服从负指数分布,即M/G/1系统 这时不能用生灭过程处理,而主要依据布 拉切克-钦辛公式(P-K公式)。
先解得:
P P0, P2 P P2 , 1 1, P 3 2 3
1 C PC PC 1 ( 再由 Pn 1解出 P0 ,得:
n 0 C n 1 C 1 (C ) 1 (C ) , 1 P0 C C ! 1 n 0 n ! 1 n nC n ! ( ) P0, Pn 1 n ( ) P0, n C n C C !C
……
C C=1
服务台数C C=2 C=3 C=4
第12章 排队模型

一、生灭过程
1.生灭过程的定义
概率为 t o(t ) ;而在 t 内死亡的概率为 t o(t ) ,各个细菌在任何时段内分裂或死亡
(1)假定有一堆细菌,每一细菌在时间
t 内分裂成两个的
都是相互独立的。如果将细菌的分裂或死亡都看成 发生一个事件的话,当 t 足够小时,发生两个或两 个以上事件的概率为 o(t ) 。假定初始时刻细菌的个 数已知,则经过时间t后,细菌变成了多少?这是生 灭过程的例子,不少排队过程是和这个过程相仿的。
第12章
排队模型
§12-1 概述 §12-2 (M/M/1):(∞/∞/FCFS)模型 §12-3 其他马氏过程排队模型 §12-4 两个非马氏排队模型
§12-1
概述
一、排队过程的一般表示
排队系统举例:
到 达 的 顾 客 1.不能运转的机器 2.修理技工 3.病人 4.电话呼唤 5.交件稿 6.提货单 7.到达机场上空的飞机 8.驶入港口的货船 9.上游河水进入水库 10.进入我方阵地的敌机 要求服务内容 修理 领取修配零件 诊断或动手术 通话 打字 提取存货 降落 装(卸)货 放水,调整水位 我方高射炮进行射击 服 务 机 构 修理技工
所以平均停留时间:
Ws E (T )
又因为 T Tq V 所以平均等待时间:
Wq Ws
1
Ws E (T ) E (Tq ) E (V ) Wq 1
1
6.指标参数之间的关系—Little公式
Ls Lq (平均服务台数) W W 1 (平均服务时间) s q Ls Ws , Lq Wq
) p0 ( n C
n 0
C 1
第九章 排队论 (1)

其中Ls、Lq、ws和wq通常称之为重要的运行指标 。它们取值越小,说明系统队长越短,顾客等候时 间越少,因此系统的性能就越好。
我们在稳态下,讨论单服务台排队系统和多服务台 排队系统。
9.2单服务台排队系统分析
本节讨论输入过程为泊松流,服务时间 服从负指数分布的单服务台的排队系统。 其中有:
9.1排队论的基本概念
排队论是通过对服务对象到来及服务时 间的统计研究,得出这些数量指标(等 待时间、排队长度、忙期长短等)的统 计规律,然后根据这些规律来改进服务 系统的结构或重新组织被服务对象,使 得服务系统既能满足服务对象的需要, 又能使服务机构的费用最经济或某些指 标最优。
9.1.1排队过程的一般表示
第9章 排队论
南京航空航天大学
排队是我们在日常生活中经常遇到的现象,例如 病人到医院看病、客户到银行汇款、城市拥堵 路段的汽车排队、电话占线等。排队现象产生 的原因之一是要求服务的数量超过了服务机构 的容量,也就是有部分的服务对象不能立即得 到服务;原因之二是系统服务对象到达和服务 时间均存在随机性。前者可以通过增加服务机 构的容量来解决排队现象,但无休止地增加服 务机构的容量会导致追加投资并可能发生系统 资源长时间闲置。后者,也就是系统服务对象 到达和服务时间均存在随机性,致使无法准确 预测估算排队拥堵的具体情况。所以,在服务 系统中的排队现象几乎不可避免。
标准的M/M/1/∞/∞系统; 有限等待空间系统M/M/1/N/∞; 顾客为有限源系统M/M/1/∞/m。
9.2.1 标准的M/M/1/∞/∞系统
M/M/1系统状态转移图:
系统状态从0转移到l的转移率为λP0, 而系统状态从1转移到0的转移率为μP1。
排队论 第2章PPT课件

出现次数fn
10 28 29 16 10 6 1 100
表9-4
为病人完成手术时 间v(小时)
0.0-0.2 0.2-0.4 0.4-0.6 0.6-0.8 0.8-1.0 1.0-1.2 1.2以上 合计
出现次 数fv
38 25 17 9 6 5 0 100
表9-5
26
1.参数的确定
nfn
算出每小时病人平均到达率= 1 0 0 =2.1(人/小时)
41
例 设船到码头,在港口停留单位时间损失cI元, 进港船只是最简单流,参数为 ,装卸时间服从参数为
的负指数分布,服务费用为
是一个正常数.
求使整个系统总费用损失最小的服务率
解 因为平均队长
的损失费为
服务费用为
所以船在港口停留 因此总费用为
42
求 使F达到最小,先求F的导数
让
解出
因为
最优服务率是
当
它说明服务机构(手术室)有84%的时间是繁忙(被利用),有16 %的时间是空闲的。
27
4.依次算出各指标: 在病房中病人数(期望值)
排队等待病人数(期望值)
Ls
2.1 5.25(人) 2.52.1
L q0 .8 4 5 .2 54 .4 1 (人 )
病人在病房中逗留时间(期望值) Ws 2.51 2.12.5(小 时 )
结
Ls Ws
Ws
Wq
1
Lq Wq
Ls Lq
平均服务 时间
平均在忙的服务 台数/正在接受 服务的顾客数
20
服
4. 系统的忙期与闲期
务
强
度
系统处于空闲状态的概率: P0 1
系统处于繁忙状态的概率: P (n0)1P 0
-数学建模排队论模型[精编文档]
顾客
工人 病人 敌机 机器
服务台
公共汽车 医生 高炮 修理工
排队系统队列除了有形的还有无形的。
在上述顾客-服务台组成的排队系统中,顾客到来 的时刻与服务台进行服务的时间一般来说是随不同 的时机与条件而变化的,往往预先无法确定。因此, 系统的状态是随机的,故而排队论也称随机服务系 统。
最简单流应 x(t) :t 具 0有以下特征称
(1)流具有平衡性
对任何 a 和0 0 t1 t,2 tn x(a ti ) x(a)
的分布只取决于 t1,t2,而,t与n 无关a。
(2)流具有无后效性
(1 i n)
对互不交接的时间区间序列 ai ,bi (1 i, n)
x(bi ) 是x(a一i ) 组相互独立的随机变量。
N
pn
, 1
n0
1
p0
N 1
(1
)
1 N1
1 1
N
n p0 1
n0
1
pn
N 1
(1
)
n
1 N1
1 1
系统的各项指标
N
L
N
npn
n0
2
(N 1) N1
1
1 N1
1 1
Lq
N
(n
n0
1) pn
N 2
N N 1
N N1
1 1 N1
1 1
N 1
排队论模型
排队论模型
一、排队论的基本概念 二、单通道等待制排队问题
(M/M/1排队系统) 三、多通道等待制排队问题
(M/M/c排队系统)
一、排队论的基本概念
(一)排队过程 1.排队系统
十三章四节MMC排队模型
λ
0 1
λ
2
λ
... n-1
n
λ
n+1 ...
µ
λ
C-1 C
2µ
λ
C+1 ... n-1
nµ
λ
n
(n +1)µ
λ
n+1
Cµ
Cµ
Cµ
Cµ
由此列出平衡方程:
λP = µP 0 1 ) n n λP −1 + (n +1 µP +1 = (λ + nµ)P, < C n n λP + CµP = (λ + Cµ)P, ≥ C n n+1 n n-1
3.运行指标
Ls = ∑nP = ∑nP + n n
n=0 n=0 C
∞
C
n=C+1
∑ (n −C)P + ∑ CP
n n=C+1
∞
∞
n
λ = Lq + C − ∑(C − n)P = Lq + n µ n=0 ∞ P ρ C 0 Lq = ∑ (n −C)P = (Cρ) n C! (1− ρ)2 n=C+1
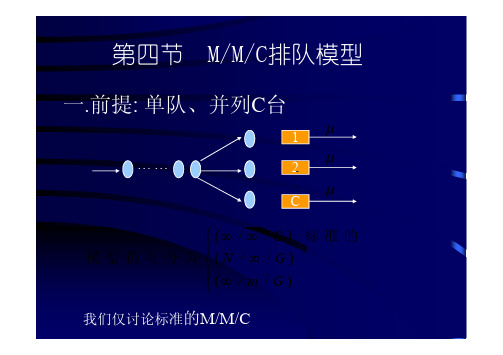
第四节 M/M/C排队模型
一.前提: 单队、并列C台
1 …… 2
µ
µ
µ
⋮
C
准 (∞/ ∞/ G) : 标 的 模 仍 分 (N / ∞/ G) 型 可 为 (∞/ m/ G)
我们仅讨论标准的M/M/C
二.(M/M/C): (∞ / ∞ / G) 系统
/ 1.与(M/M/1/ ∞∞/G)的区别
Ws = Ls
λ
,
W = q
排队模型(掌握mm1,mmc,mm1k)
精选2021版课件
9
三、排队模型的分类(符号表示)
我们采用Kendall记号
顾客相继到达时间间隔分布/服务时间分布/服务 台数目/排队系统允许的最大顾客容量(系统容 量)/顾客总体数量(顾客源数量)/排队规则
说明:如果Kendall记号中略去后3项,表示x/y/z/∞/∞/FCFS 相继到达时间间隔和服务时间分布的符号如下:
λΔt
n
n-2 Pn-2(t) 2
(C)
n-3 …
Pn-3(t) …
3 …
0 P0(t) n
o(Δt)
n n … n
[0, t+Δt ) 概率
Pn(t) ( 1-λΔt+o(Δt)) Pn-1(t)λΔt
o(Δt)
在上述条件下,研究顾客到达数 n 的概率分布
Pn(t+Δt)= Pn(t) ( 1-λΔt+o(Δt))
1)、输入过程(顾客到达的方式)
a、顾客的总体(顾客源)的组成可能是有限的,也 可能是无限的;
b、顾客相继到达的时间间隔可以是确定的,也可以 是随机的,对于随机的情形,要知道单位时间内的 顾客到达数或相继到达的间隔时间的概率分布;
c 、输入过程可以是平稳的(描述相继到达的间隔时 间分布和所含参数(如期望值、方差等)都是与时 间无关的),否则成为非平稳的,我们研究平稳的。
7、稳定状态:limPn(t)→Pn
精选2021版课件
11
四、排队模型的数量指标
8、λn —— 系统有n个顾客时的平均到达率 9、μn ——系统有n个顾客时的平均服务率 10、λ ——对任何n都是常数的平均到达率
11、μ ——对任何n都是常数的平均服务率
12、ρ ——服务强度,或称使用因子,平均到达率与 服务台与平均服务率的乘积的比值
某超市结账柜台排队系统
1.3.1
本文以永辉超市的结账柜台排队系统为原型系统,其属于多队列多服务台排队系统。运用排队论的思想和相关方法对其进行系统仿真。运用多队列多服务台M/M/c/∞/∞排队模型对超市结账柜台排队系统进行分析。对永辉超市进行了数据采集与分析,计算出了相关数据,并且对其进行仿真,以确定合理性,在发现问题后提出改进策略并进行优化。
本文的研究结论可能对相类似的排队系统具有一定的借鉴意义。
关键词超市结账柜台排队系统建模仿真
TitleSimulation and researchon thecheckout counter queuing system ofsupermarket
Abstract
In recent years,thevarioussupermarketshavebrought many conveniences to our life. Butthere aremany reasonsto leadmany supermarket checkout counters queuing system is not very perfect. The long queueorsparecheckout counters and so on.Therefore, the optimization of the supermarket checkout counters queuing systemcan help the supermarket to profoundlyshortenthe check-out time.
目前最主要的研究方法则是从系统仿真、费用优化模型以及排队论算法这三方面对排队系统的优化问题着手。
系统仿真是通过软件建立能反映真实系统规律的仿真模型,对仿真模型进行实验,进行输出数据分析,从而做出系统的方案评价分析。计算机仿真的优势在于对优化模型和原型系统的长期模拟测试[5]。当确定了一个优化方案后,就可以通过软件在计算机中建立起优化模型,然后让优化模型在计算机虚拟环境中运行相对较长的时间,得出一些系统运行的数据量化系统指标,根据这些数据量化系统指标来评判优化方案能否起到优化原型系统的作用。由于计算机仿真对原型系统有较强的模拟能力,因此在一定的条件下计算机仿真可以作为优化方案应用前的检验方法之一[6]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M M C ∞排队系统模型及其应用实例分析
摘要:文章阐述了M/M/C/∞排队系统的理论基础,包括排队论的概念,排队系统的基本组成部分以及排队系统的模型。
在理论分析的基础上,文章以建行某储蓄所M/M/C/∞排队系统为例,对该系统进行分析并提出了最优解决方案。
关键词:排队论;银行储蓄所;M/M/C/∞模型;最优解
1M/M/C/∞排队系统
1.1排队论的概念及排队系统的组成
上世纪20年代,丹麦数学家、电气工程师爱尔朗(A. K. Erlang)在用概率论方法研究电话通话问题时,开创了这门应用数学学科。
排队论主要研究各种系统的排队队长,排队的等待时间及所提供的服务等各种参数,以便求得更好的服务。
研究排队问题实质上就是研究如何平衡等待时间与服务台空闲时间。
目前,排队论已经广泛应用于通信工程、交通运输、生产与库存管理、计算机系统设计、计算机通信网络、军事作战、柔性制造系统和系统可靠性等众多领域。
任意一个排队系统都是由三个基本部分构成,即输入过程、排队规则和服务机构。
①输入过程是描述顾客来源以及顾客按什么规律达到排队系统。
②排队规则描述的顾客到达服务系统时顾客是否愿意排队,以及在排队等待情形下的服务顺序。
③服务机构描述服务台数目及服务规律。
服务机构可分为单服务台和多服务台;接受服务的顾客是成批还是单个的;服务时间服从何种分布。
1.2M/M/C/∞排队模型
①排队系统模型的表示。
目前排队模型的分类采用1953年由D. G. Kendall 提出的分类方法。
他用3个字母组成的符号A/B/C表示排队系统。
为了表示其它特征有时也用4~5个字母来表示如A/B/C/D/E。
其中:A 顾客到达间隔时间的概率分布;B 服务时间的概率分布;C 服务台数目;D 系统容量限制(默认为∞);E 顾客源数目(默认为∞);概率分布的符号表示:M:泊松分布或负指数分布,D:定长分布,Ek:k阶爱尔朗分布,C:一般随机分布。
②排队系统的衡量指标。
—所有服务设施空闲的概率;—系统中的顾客总数;—队列中的顾客总数;—顾客在系统中的停留时间;—顾客在队列中的等待时间。
③M/M/C/∞排队模型。
排队系统模型大体上可以分为简单排队系统,特殊排队系统,休假排队系统及可修排队系统。
纵观所有排队系统的模型,无非是系统的三个组成部分分别为不同情况时,进行的排列组合,并由此导致排队系统的数量指标的计算公式不一致。
无论是何种排队系统,其研究实质都是如何平衡等待时间
与服务台空闲时间,只是等待与服务在不同的实例中被赋予了新的含义。
M/M/C/∞排队模型指顾客的到达规律服从泊松到达,其顾客来源为无限源,服务时间服从负指数时间,服务机构为多服务台。
简单排队系统的求解思路也可以在其它的排队系统中运用。
故现以M/M/C/∞排队系统模型为例进行分析。
2M/M/C/∞排队系统模型应用实例分析
2.1建行某储蓄所M/M/C/∞排队系统基本情况
建行某专业支行现有场地最多可以设置6个单人临柜;支行可提供的工作人员最多6名;每天的期望业务量为600万元,根据测算,每人每天可完成工作量是200万元。
建行总行规定,单笔存取款业务办理时间限制为3分钟以内,顾客到达情况具体选取了顾客到达比较集中有代表性的时间段作了15天的调查统计,频数如表1所示。
每增加一个单人临柜工作间需追加投资10万元。
根据储蓄所工作的特点结合顾客等待服务的期望值给出了排队系统指标的标准参考值为: Po=0.4,Ls=2,Ws=3。
2.2案例分析
一般说来储蓄所顾客到达的过程形成泊松流,而负指数概率分布能较好描述储蓄所排队系统里服务时间的概率分布情况,又知建行每天期望的业务量为600万元,每人每天可完成工作量为200万元,因而服务台数的取值范围为[3,6]。
所以,该储蓄所的排队模型属于M/M/C/∞/∞模型。
解答思路:①确定单位时间平均到达的顾客数;②确定平均服务率;③计算C 分最终确定最佳的服务台数。
④综合投资额。
①计算单位时间平均到达的顾客数λ:λ=nf;根据表1中的数据可求得λ=0.71。
②计算平均服务率μ:题中规定服务的最大的时限为3min,所以可以假设系统一分钟平均处理了0.3个顾客,即平均服务率μ=0.3。
③C分别取3、4、5、6时Po、Lq 、Ls、Wq、Ws的值,并与标准参考值对比:各数量指标的计算公式如下所示:
Po=;
L= Po;
L=L+;W=;W=W+
C分别取3、4、5、6时, Po、Lq 、Ls、Wq、Ws的取值如表2所示。
④确定最佳的服务台数。
对比排队系统指标的标准参考值Po=0.4,Ls =2,Ws=3,可以发现,当C>=4时,满足系统对Po、Ls、Ws 这三项指标的要求。
从直观上看,每增加一个服务台需要多花10万元,而当C取5、6时,各指标的取值情况同C取4时相比,并没有明显的改善,因此服务台应该设置4台。
参考文献:
[1] 唐应辉,唐小我.排队论基础与分析技术[M].北京:科学出版社,2006.
[2] 韩伯棠.管理运筹学(第二版)[M].北京:高等教育出版社, 2005.
[3]张文杰,李学伟,张可明.管理运筹学[M].北京:中国铁道出版社,2000.
[4]徐玖平,胡知能,李军.运筹学(第二版)[M].北京:科学出版社,2003.。
