100测评网高二数学练习卷不等式性质
高二数学不等式练习题

高二数学不等式练习题不等式是数学中常见且重要的概念之一,在数学中有着广泛的应用。
通过解决不等式问题,我们可以提高运算能力,培养逻辑思维,同时也能够加深对不等式概念的理解。
下面是一些高二数学不等式练习题,希望能够帮助大家加深对不等式的理解。
题一:解不等式 2x - 3 > 5,给出解集。
解:首先将不等式转化为一元一次方程,有:2x - 3 = 52x = 5 + 32x = 8x = 8 / 2x = 4然后,我们需要判断解集的范围。
不等式中大于号表示不包含等于的情况,所以解集为 x > 4。
题二:解不等式3x + 2 ≤ 10,给出解集。
解:首先将不等式转化为一元一次方程,有:3x + 2 = 103x = 10 - 23x = 8x = 8 / 3然后,我们需要判断解集的范围。
不等式中小于等于号表示包含等于的情况,所以解集为x ≤ 8 / 3。
题三:解不等式 2x + 1 > x + 5,给出解集。
解:首先将不等式化简,有:2x - x > 5 - 1x > 4所以解集为 x > 4。
题四:解不等式 3x - 4 < 2x + 5,给出解集。
解:首先将不等式化简,有:3x - 2x < 5 + 4x < 9所以解集为 x < 9。
题五:解不等式 -x + 4 ≥ 2x - 3,给出解集。
解:首先将不等式化简,有:-x - 2x ≥ -3 - 4-3x ≥ -7x ≤ 7 / 3所以解集为x ≤ 7 / 3。
通过以上练习题的解析,我们可以发现解不等式的基本方法和技巧。
首先要将不等式化简,并根据不等号的类型来判断解集的范围。
掌握这些基本方法和技巧,对于解决更加复杂的不等式问题将有很大的帮助。
希望以上练习题能够帮助大家更好地理解和掌握不等式的概念和解题方法。
通过不断地练习和思考,我们可以在数学学习中取得更好的成绩。
人教A版高中数学必修5 《不等式的性质与一元二次不等式》专项练习卷(无答案)
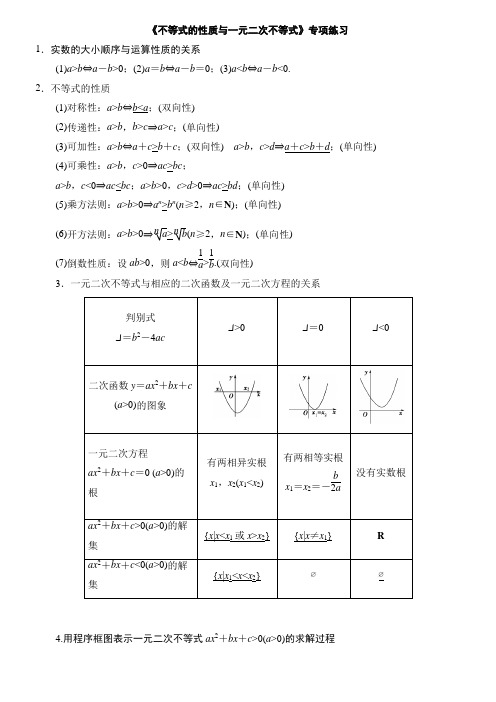
《不等式的性质与一元二次不等式》专项练习1.实数的大小顺序与运算性质的关系(1)a >b ⇔a -b >0;(2)a =b ⇔a -b =0;(3)a <b ⇔a -b <0.2.不等式的性质(1)对称性:a >b ⇔b <a ;(双向性) (2)传递性:a >b ,b >c ⇒a >c ;(单向性)(3)可加性:a >b ⇔a +c >b +c ;(双向性) a >b ,c >d ⇒a +c >b +d ;(单向性)(4)可乘性:a >b ,c >0⇒ac >bc ;a >b ,c <0⇒ac <bc ;a >b >0,c >d >0⇒ac >bd ;(单向性)(5)乘方法则:a >b >0⇒a n >b n (n ≥2,n ∈N );(单向性)(6)开方法则:a >b >0⇒n a >n b (n ≥2,n ∈N );(单向性)(7)倒数性质:设ab >0,则a <b ⇔1a >1b .(双向性)3.一元二次不等式与相应的二次函数及一元二次方程的关系 判别式Δ=b 2-4ac Δ>0 Δ=0 Δ<0二次函数y =ax 2+bx +c(a >0)的图象一元二次方程ax 2+bx +c =0 (a >0)的根有两相异实根 x 1,x 2(x 1<x 2) 有两相等实根 x 1=x 2=-b 2a 没有实数根 ax 2+bx +c >0(a >0)的解集{x |x <x 1或x >x 2} {x |x ≠x 1} R ax 2+bx +c <0(a >0)的解集{x |x 1<x <x 2} ∅ ∅4.用程序框图表示一元二次不等式ax 2+bx +c >0(a >0)的求解过程1.下列四个结论,正确的是( )①a >b ,c <d ⇒a -c >b -d ;②a >b >0,c <d <0⇒ac >bd ;③a >b >0⇒3a >3b ;④a >b >0⇒1a 2>1b 2.A .①②B .②③C .①④D .①③2.若a ,b ∈R ,且a >b ,则下列不等式恒成立的是( )A .a 2>b 2 B.a b >1 C .2a >2b D .lg(a -b )>0 3.不等式-x 2-3x +4>0的解集为________________.(用区间表示)4.若不等式mx 2+2mx +1>0的解集为R ,则m 的取值范围是__________. 5已知x ,y ∈R ,且x >y >0,则( )A.1x -1y >0B .sin x -sin y >0 C.⎝ ⎛⎭⎪⎫12x -⎝ ⎛⎭⎪⎫12y <0 D .ln x +ln y >06.若1a <1b <0,则下列结论不正确的是( )A .a 2<b 2B .ab <b 2C .a +b <0D .|a |+|b |>|a +b |7若角α,β满足-π2<α<β<π,则α-β的取值范围是( )A.⎝ ⎛⎭⎪⎫-3π2,3π2B.⎝ ⎛⎭⎪⎫-3π2,0C.⎝ ⎛⎭⎪⎫0,3π2D.⎝ ⎛⎭⎪⎫-π2,0 8.已知不等式ax 2-bx -1>0的解集是⎩⎨⎧⎭⎬⎫x | -12<x <-13,则不等式x 2-bx -a ≥0的解集是( ) A .{x |2<x <3} B .{x |x ≤2或x ≥3}C.⎩⎨⎧⎭⎬⎫x | 13<x <12D.⎩⎨⎧⎭⎬⎫x | x <13或x >129.已知a >b ,c >d ,且c ,d 不为0,那么下列不等式成立的是( ) A .ad >bcB .ac >bdC .a -c >b -dD .a +c >b +d10.已知函数f (x )=⎩⎨⎧x +2,x ≤0,-x +2,x >0,则不等式f (x )≥x 2的解集为( ) A .[-1,1]B .[-2,2]C .[-2,1]D .[-1,2] 11.不等式-2x 2+x +1>0的解集为__________.12.已知函数f (x )=⎩⎪⎨⎪⎧ 12x +1,x ≤0,-(x -1)2,x >0,则不等式f (x )≥-1的解集是__________.13.若关于x 的不等式4x -2x +1-a ≥0在[1,2]上恒成立,则实数a 的取值范围为________. 14.不等式(a -2)x 2+2(a -2)x -4<0对一切x ∈R 恒成立,则实数a 的取值范围是__________. 15.设函数f (x )=mx 2-mx -1.若对于x ∈[1,3],f (x )<-m +5恒成立,求m 的取值范围.16.解下列不等式:(1)3+2x -x 2≥0; (2)x 2-(a +1)x +a <0.17.对任意的k ∈[-1,1],函数f (x )=x 2+(k -4)x +4-2k 的值恒大于零,则x 的取值范围18.设x <y <0,试比较(x 2+y 2)(x -y )与(x 2-y 2)(x +y )的大小.19.若不等式ax 2+5x -2>0的解集是⎩⎨⎧⎭⎬⎫x | 12<x <2.(1)求实数a 的值; (2)求不等式ax 2-5x +a 2-1>0的解集.20.已知函数f (x )=x 2-2ax -1+a ,a ∈R .(1)若a =2,试求函数y =f (x )x (x >0)的最小值;(2)对于任意的x ∈[0,2],不等式f (x )≤a 成立,试求a 的取值范围.。
高二数学不等式练习题及答案

不等式练习题一、选择题1、若a,b 是任意实数,且a >b,则 ( ) (A )a 2>b 2 (B )a b <1 (C )lg(a-b)>0 (D )(21)a <(21)b 2、下列不等式中成立的是 ( ) (A )lgx+log x 10≥2(x >1) (B )a1+a ≥2 (a ≠0) (C )a 1<b1(a >b) (D )a 21+t ≥a t (t >0,a >0,a ≠1) 3、已知a >0,b >0且a +b =1, 则()11)(1122--ba 的最小值为 ( )(A )6 (B ) 7 (C ) 8 (D ) 94、已给下列不等式(1)x 3+ 3 >2x (x ∈R ); (2) a 5+b 5> a 3b 2+a 2b 3(a ,b ∈R );(3) a 2+b 2≥2(a -b -1), 其中正确的个数为 ( ) (A ) 0个 (B ) 1个 (C ) 2个 (D ) 3个 5、f (n ) =12+n -n , ϕ(n )=n21, g (n ) = n 12--n , n ∈N ,则 ( ) (A ) f (n )<g (n ) <ϕ(n ) (B ) f (n )<ϕ(n )<g (n ) (C ) g (n )<ϕ(n )<g (n ) (D )g (n )<f (n )<ϕ(n )6、设x 2+y 2 = 1, 则x +y ( ) (A ) 有最小值1 (B ) 有最小值2 (C )有最小值-1 (D ) 有最小值-27、不等式|x +5|>3的解集是 ( ) (A){x|-8<x <8} (B){x|-2<x <2}(C){x|x <-2或x >2= (D){x|x <-8或x >-2=8、若a ,b ,c 为任意实数,且a >b ,则下列不等式恒成立的是 ( ) (A)ac >bc (B)|a +c|>|b +c| (C)a 2>b 2 (D)a +c >b +c9、设集合M={x|13-+x x ≤0},N={x|x 2+2x-3≤0},P={x|322)21(-+x x ≥1},则有 ( )(A )M ⊂N=P (B )M ⊂N ⊂P (C )M=P ⊂N (D )M=N=P10、设a,b ∈R,且a+b=3,则2a +2b 的最小值是 ( ) (A )6 (B )42 (C )22 (D )2611、若关于x 的不等式ax 2+bx -2>0的解集是⎪⎭⎫⎝⎛+∞⎪⎭⎫ ⎝⎛-∞-,3121,Y ,则ab 等于( ) (A)-24 (B)24 (C)14 (D)-1412、如果关于x 的不等式(a -2)x 2+2(a -2)x -4<0对一切实数x 恒成立,则实数a 的取值范围是 ( ) (A)]2,(-∞ (B))2,(--∞ (C)]2,2(- (D)(-2,2) 13、设不等式f(x)≥0的解集是[1,2],不等式g(x) ≥0的解集为Φ,则不等式0)()(>x g x f 的解集是 ( ) (A) Φ (B)+∞-∞,2()1,(Y ) (C)[1,2] (D)R14、22+>+x xx x 的解集是 ( ) (A ) (-2,0) (B ) (-2,0) (C ) R (D ) (-∞,-2)∪(0,+ ∞) 15、不等式3331>--x的解集是 ( ) (A ) (-∞,1) (B ) (43,1 ) (C ) (43,1) (D ) R 二、填空题1、若x 与实数列a 1,a 2,…,a n 中各数差的平方和最小,则x=________.2、不等式xxx121log 〈的解集是________. 3、某工厂产量第二年增长率是p 1,第三年增长率是p 2,第四年增长率是p 3且p 1+p 2+p 3=m(定值),那么这三年平均增长率的最大值是________.4、a ≥0,b ≥0,a 2+22b=1,则a 21b +的最大值是________.5、若实数x 、y 满足xy >0且x 2y=2,则xy +x 2的最小值是________.6、x >1时,f(x)=x +11612++x x x 的最小值是________,此时x=________.7、不等式log 4(8x -2x )≤x 的解集是________.8、不等式321141-〉-xx 的解集是________. 9、命题①:关于x 的不等式(a -2)x 2+2(a -2)x -4<0对x ∈R 恒成立;命题②:f(x)=-(1-3a -a 2)x是减函数.若命题①、②至少有一个为真命题,则实数a 的取值范围是________. 10、设A={x|x ≥x1,x ∈R},B={x|12+x <3,x ∈R =,则D=A ∩B=________. 三、解答题1、解不等式:1211922+-+-x x x x ≥7.2、解不等式:x 4-2x 3-3x 2<0.3、解不等式:65592+--x x x ≥-2.4、解不等式:2269x x x -+->3.5、解不等式:232+-x x >x +5.6、若x 2+y 2=1,求(1+xy)(1-xy)的最大、最小值。
高二数学不等式测试及答案

(4)不等式一、选择题(本大题共10小题;每小题5分;共50分) 1.已知c<d ; a > b >0; 下列不等式中必成立的一个是( )A .a +c> b +dB .a -c> b -dC .a d< b cD . db c a > 2.设a 、b ∈R ;且a b<0;则( )A .| a +b|>| a -b|B .| a +b|<| a -b|C .| a -b|<| a |-|b|D .| a -b|<| a |+|b|3.已知命题p:“x > a ”;q:“x ≥a ”;则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .非充分非必要条件4.不等式| x -4|≤3 的整数解的个数是( )A .7B .6C .5D .45.设集合p={ x |-2< x <3};Q={ x | | x +1|>2;x ∈R};则集合P ∪Q=( )A .{ x |-2< x <1}B .{ x |1< x <3}C .{ x |-3< x <3|D .{ x | x <-3 或x >-2}6.若log 3M+log 3N ≥4;则M+N 的最小值是( )A .4B .18C .34D .97.不等式122+<+x x 的解集是( ) A .(-3; -2)∪(0; +∞)B .(-∞; -3)∪(-2; 0)C .(-3; 0)D .(-∞; -3)∪(0; +∞)8.若a < b <0;则下列结论中正确的是( )A. 不等式||1||111b a b a >>和均不成立 B. 不等式||1||111b a a b a >>-和均不成立 C. 不等式22)1()1(11ab b a a b a +>+>-和均不成立 D. 不等式22)1()1(||1||1ab b a b a +>+>和均不成立9.关于x 的不等式a x 2+b x +2>0的解集是}3121|{<<-x x ;则a +b= ( )A .10B .-10C .14D .-1410.已知集合A={ x | | x -1|≤a ; a >0}; B={ x | | x -3|>4};且A ∩B=φ;则a 的取值范围是 ( )A .(0; 2]B .(-∞; 2]C .(7; +∞)D .(- ∞; -1)二、填空题(本大题共4小题;每小题6分;共24分)11.已知sin 2α+sin 2β+sin 2r=1(α、β、r 均为锐角);则cos αcos βcosr 的最大值等于 . 12.若扇形的面积为S ;则半径是 时扇形的周长最小. 13.不等式x x x <-24的解集是 .14.某工厂建造一间地面面积为12m 2的背面靠墙的矩形小房;房屋正面的造价为1200元/ m 2;房屋侧面的造价为800元/ m 2;屋顶的造价为5800元;如果墙高为3 m ;且不计房屋背面的费用;则建造此小房的最低总造价是 元. 三、解答题(本大题共6题;共76分)15.已知0 < x < 1; 0 < a < 1;试比较|)1(log | |)1(log |x x a a +-和的大小.(12分)16.解不等式2931831>⋅+-+x x .(12分)17.锐角三角形△ABC 中;已知边a =1;b=2;求边c 的取值范围.(12分)18.求证:bb aa ba b a +++≤+++111(12分)19.已知21)(x x f += 当a ≠b 时 求证:|||)()(|b a b f a f -<-.(14分)20.从社会效益和经济效益出发;某地投入资金进行生态环境建设;并以此发展旅游产业;根据规划;本年度投入800万元;以后每年投入比上年减少51.本年度当地旅游业收入估计为400万元;由于该项建设对旅游业的促进作用;预计今后的旅游业收入每年会比上年增加.41(Ⅰ)设n 年内(本年度为第一年)总投入为a n 万元;旅游业总收入为b n 万元.写出a n ;b n的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入? (14分)参考答案一.选择题(本大题共10小题;每小题5分;共50分)题号 1 2 3 4 5 6 7 8 9 10 答案BBAADBABDA二.填空题(本大题共4小题;每小题6分;共24分) 11.69212.S 13.]4,2( 14.34600三、解答题(本大题共6题;共76分) 15.(12分)[解法一]:[][])1(log )1(log )1(log )1(log |)1(log | |)1(log |22x x x x x x a a a a a a +---+-=+--xxx a a +--=11log )1(log 2 ∵0 < 1 - x 2 < 1;1110<+-<x x∴011log )1(log 2>+--xx x a a ∴|)1(log | |)1(log |x x a a +>- [解法二]:2111111log 11log )1(log )1(log )1(log )1(log x x x x x x x xx x x a a -+=-=--=-=+-++++)1(log 121x x --=+∵0 < 1 - x 2 < 1; 1 + x > 1; ∴0)1(log 21>--+xx∴1)1(log 121>--+xx ∴|)1(log | |)1(log |x x a a +>-[解法三]:∵0 < x < 1; ∴0 < 1 - x < 1; 1 < 1 + x < 2; ∴0)1(log ,0)1(log <+>-x x a a∴左 - 右 =)1(log )1(log )1(log 2x x x a a a -=++-∵0 < 1 - x 2 < 1; 且0 < a < 1 ∴0)1(log 2>-x a∴|)1(log | |)1(log |x x a a +>-16.(12分)[解析]:原不等式可化为:018329332>+⋅-⋅x x即:0)233)(93(>-⋅-x x解之得:93>x 或323<x ∴x >2或32log 3<x∴不等式的解集为{x |x >2或32log 3<x} 17.(12分)[解析]:因为△ABC 是锐角三角形;且a =1;b=2;c>0; 所以,0cos 0cos 0cos ⎪⎩⎪⎨⎧>>>C BA即;⎪⎪⎪⎩⎪⎪⎪⎨⎧>⇒>⇒>-+=-+<<⇒<⇒>-+=-+>+⇒>-+=-+3302412505041420304142222222222222222c c c c ac b c a c c c ba c a b c c c bc a c b 因此;所求c 的取值范围是(5,3)18.(12分)[证法一]: 当0=+b a 时;不等式显然成立;当0≠+b a 时;由b a b a +≤+<0ba b a +≥+⇒11所以;ba b a ba ba ba b a +++=++≤++=+++11111111bb aa +++≤11[证法二]:要证明原不等式成立;则只需证明:|a +b|(1+|a |)(1+|b|)≤|a |(1+|a +b|)(1+|b|)+|b|(1+|a +b|)(1+|a |); 展开;合并同类项;得:|a +b|≤|a |+2|a b|+|a 2b+a b 2|+|b|; ∵|a +b|≤|a |+|b|; ∴|a +b|≤|a |+2|a b|+|a 2b+a b 2|+|b|成立; 故原不等式成立.19.(14分)[证法一]:1111|11||)()(|222222+++--+=+-+=-b a b a b a b f a f|||||)(||||))((|11||222222b a b a b a b a b a b a b a b a +-+=+-+<+++-=|||||||||)||(|b a b a b a b a -=+-+≤[证法二]:(构造法) 如图:21)(a a f OA +== 21)(b b f OB +==||||b a AB -=由三角形两边之差小于第三边得:|||)()(|b a b f a f -<-20.(14分)[解析]:(Ⅰ)第1年投入为800万元;第2年投入为800×(1-51)万元;......;第n 年投入为800×1)511(--n 万元.所以;n 年内的总投入为1)511(800)511(800800--⨯+⋅⋅⋅+-⨯+=n n a ])54(1[4000n -⨯=第1年旅游业收入为400万元;第2年旅游业收入为400×)411(+万元.......;第n 年旅游业收入为400×1)411(-+n 万元.所以;n 年内的旅游业总收入为1)411(400)411(400400-+⨯+⋅⋅⋅++⨯+=n n b ]1)45[(1600-⨯=n (Ⅱ)设至少经过n 年旅游业的总收入才能超过总投入;由此0>-n n a b即]1)45[(1600-⨯n -])54(1[4000n -⨯>0 化简得n )54(5⨯+n)45(2⨯-7>0设n x )54(=;得5 x 2-7 x +2>0;解之得152><x x 或(不合题意;舍去)即 52)54(<n由此得 5≥n答:至少经过5年旅游业的总收入才能超过总投入.OA Bab1。
高二数学不等式练习题

高二数学不等式练习题高二数学不等式练习一、选择题:本大题共12步题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知关于x的不等式的解集为[-1,0],则a+b的值为()A.-2B.-1C.1D.32.设x、y满足约束条件的最大值为()A.0B.2C.3D.3.已知不等式对任意正实数x,y恒成立,则正实数a的最小值为()A.2B.4C.6D.84.(2009四川卷文)已知,,,为实数,且>.则“>”是“->-”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.某人计划投资不超过10万元,开发甲、乙两个项目,据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.在确保可能的资金亏损不超过1.8万元的条件下,此项目的最大盈利是()A.5万元B.6万元C.7万元D.8万元6.若x、y为实数,且x+2y=4,则的最小值为()A.18B.12C.2D.47.关于x的不等式的解集为(,1),则关于x的不等式的解集为()A.B.(-1,2)C.(1,2)D.8.(2009山东卷理)设x,y满足约束条件,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则的最小值为()A.B.C.D.49.若不等式x2-2ax+a>0,对x∈R恒成立,则关于t的不等式<1的解为()A.110.若x<0,则2+3x+4x的最大值是()A.2+43B.2±43C.2-43D.以上都不对11.若,则下列不等式:①;②;③;④中,正确的不等式有()A.1个B.2个C.3个D.4个12.若a是1+2b与1-2b的等比中项,则的最大值为()A.B.C.D.二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横一上.13.设m为实数,若的取值范围是.14.若正数a、b满足ab=a+b+3,则ab的取值范围是.15.(2009安徽卷文)不等式组所表示的平面区域的面积等于.16.不等式的解集是.三、解答题:本大题共6小题,共74分,解答应写出文字说明.证明过程或演算步骤.17.(本小题满分12分)已知函数的定义域为R,求实数m的取值范围.18.(本小题满分12分)2009年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.7万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?19.(本小题满分12分)函数f(x)=x2+ax+3,当x∈[-2,2]时f(x)≥a恒成立,求a的取值范围20.(本小题满分12分)据统计,某市的工业垃圾若不回收处理,每吨约占地4平方米,2002年,环保部门共回收处理了100吨工业垃圾,且以后垃圾回收处理量每年递增20%(工业垃圾经回收处理后,不再占用土地面积).(Ⅰ)2007年能回收处理多少吨工业垃圾?(精确到1吨)(Ⅱ)从2002年到2015年底,可节约土地多少平方米(精确到1m2)(参考数据:1.24≈2.11.55=2.51.26=3.01.213≈10.71.214≈12.8)。
高二数学不等式练习题及答案1

不等式练习题(一)1、若a>b ;下列不等式中一定成立的是( )A 、b a 11<B 、1<ab C 、22a b > D 、0lg()a b -> 2、若-1<a<b<1;则下列不等式中成立的是( )A 、-2<a-b<0B 、-2<a-b<-1C 、-1<a-b<0D 、-1<a-b<13、与不等式1232≥--x x 同解的不等式是( ) A 、01≥-x B 、0232≥+-x x C 、lg (232+-x x )>0 D 、02123≥--+-x x x x 210ax bx ++>的解集为{}21x x -<<;则,a b 的值为( )11221 D.122.,.,.,A a b B a b C a b a b =-=-=-=-==-== 5.方程2210()mx m x m -++=有两个不相等的实数解;则m 的取值范围是( )1110000444....A m B m C m m D m m >->-<<><>或或 223121(),()f x x x g x x x =-+=+-;则(),()f x g x 的大小关系是( ).()().()().()().A f x g x B f x g x C f x g x D >=<随x 的值变化而变化 7、不等式x x 283)31(2-->的解集是8.若 0112,,x y ≤≤-≤≤则4z x y =+的最小值为_______;最大值为_______. 240x ax ++<的解集为空集;则a 的取值范围是_______________.10、已知14x y -<+<且23x y <-<;则 23z x y =-的取值范围是__________.11.(1)已知函数231()log ()f x ax ax =-+的定义域为R ;求实数a 的取值范围;(2)已知函数231()log ()f x ax ax =-+的值域为R ;求实数a 的取值范围;12、已知不等式250ax x b -+>解集是{}32x x -<<-;求不等式250bx x a -+<的解集13.已知函数22222()()y a x a x =-+--的图象在x 轴下方;求实数a 的取值范围.14.解关于x 的不等式222ax x ax -≥-不等式练习题一 参考答案 1-6 C A D C C A 7.{}24x x -<< 8.-4;9 9. {}44a a -≤≤ 10.(3;8) 1110424.()()a a ≤<≥{}111223.x x x <->-或 13.(学案62页11题){}02a a <≤14.0a =时;{}1x x ≤- 0a >时;{}21x x x a ≤-≥或 20a -<<时; {}21x x a≤≤- 2a =-时;{}1x x =-2a <-时;{}21x x a-≤≤。
高二数学不等式的证明练习题
高二数学不等式的证明练习题2016高二数学不等式的证明练习题导语:作为心智脂肪储备起来的知识并无用处,只有变成了心智肌肉才有用。
下面是小编为是大家整理的,数学知识点,希望对大家有所帮,欢迎阅读,仅供参考,更多相关的知识,请关该CNFLA学习网。
一、选择题(每小题4分,共40分,每小题只有一个选项符合题意)1. 下列平面图形中与空间的平行六面体作为类比对象较合适的是( )A. 三角形B. 梯形C. 平行四边形D. 矩形2. 分析法是从要证的结论出发,寻求使它成立的`( )A. 充分条件B. 必要条件C. 充要条件D. 既不充分又不必要条件3. 下面几种推理过程是演绎推理的是( )A. 两条直线平行,同旁内角互补,由此若[∠A],[∠B]是两条平行直线被第三条直线所截得的同旁内角,则[∠A+∠B=180°]B. 某校高三(1)班有55人,高三(2)班有54人,高三(3)班有52人,由此得出高三所有班人数超过50人C. 由平面三角形的性质,推测空间四面体的性质D. 在数列[an]中,[a1=1,an=12(an-1+an+1)] ([n]≥2),由此归纳出[an]的通项公式4. 应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用( )①结论相反判断,即假设②原命题的条件③公理、定理、定义等④原结论A. ①②B. ①②④C. ①②③D. ②③5. 用数学归纳法证明不等式[1+12+14+…+12n-1][>12764(n∈N?)]成立,其初始值至少应取( )A. 7B. 8C. 9D. 106. 用反证法证明命题“已知[x∈R],[a=x2-1],[b=2x+2],则[a,b]中至少有一个不小于0”反设正确的是( )A. 假设[a,b]都不大于0B. 假设[a,b]至多有一个大于0C. 假设[a,b]都大于0D. 假设[a,b]都小于07.如果命题[P(n)]对[n=k]成立,则它对[n=k+1]也成立,现已知[P(n)]对[n=4]不成立,则下列结论正确的是( )A. [P(n)]对[n∈N*]成立B. [P(n)]对[n>4]且[n∈N*]成立C. [P(n)]对[nD. [P(n)]对[n≤4]且[n∈N*]不成立8.若把正整数按下图所示的规律排序,则从2013到2015年的箭头方向依次为( )1 4 → 5 8 → 9 12↓ ↑ ↓ ↑ ↓ ↑ …2 →3 6 → 7 10 → 11A. ↓→B. →↓C. ↑→D. →↑9. 为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图:明文[加密密钥密码]密文[发送]密文[解密密钥密码]明文. 现在加密密钥为[y=loga(x+2)],如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得到明文为( )A.12B.13C.14D.1510. 记凸[k]边形的内角和为[f(k)],则[f(k+1)-f(k)]等于( )A. [32π]B. [π]C. [32π]D. [2π]二、填空题(每小题4分,共16分)11. 观察下列不等式:[1+122 12. 数式[1+11+…]中省略号“…”代表无限重复,但原式是一个固定值,可以用如下方法求得:令原式[=t],则1+[1t=t,则t2-t-1=0,]取正值[t=5+12],用类似方法可得[2+2+2+…]= .13. 用数学归纳法证明“1+2+3+…+[n]+…+3+2+1=[n2(n∈N*)]”时,从[n=k]到[n=k+1]时,该式左边应添加的代数式是 .14. 将连续整数1,2,…,25填入5行5列的表格中,使每一行的数字从左到右都成递增数列,则第三列各数之和的最小值为,最大值为 .三、解答题(共4小题,44分)15. (10分)设[x≥1,y≥1,]证明[x+y+1xy≤1x][+1y+xy].16. (10分)设[a3+b3=2],求证[a+b≤2.]17. (12分)用数学归纳法证明[42n+1]+[3n+2]能被13整除,其中[n∈N*].18. (12分)已知数列[an]满足[an+1=12an2-12nan+1]([n∈N+])且[a1=3].(1)计算[a2,a3,a4]的值,由此猜想数列[an]的通项公式,并给出证明;(2)求证:当[n≥2]时,[ann≥4nn.]。
高二数学 不等式的性质同步练习 理 人教版
..
DOC版.
高二数学 不等式的性质同步练习 理 人教版
(答题时间:30分钟)
1. 已知0a,01b,下面不等式成立的是( )
A. 2ababa B. aabab2
C. 2abaab D. aabab2
2. 下列命题中正确的是( )
A. 22bcacba B. bacbca
C. baabba11033 D. baabba11022
3. 若角、满足22,则的取值范围是( )
A. 0 B.
C. 02 D. 22
4. x、y、z均为大于1的负数,则一定有( )
A. 0222zyx B. 1xyz
C. 3zyx D. 1)(2xyz
5. 正数a、b、c满足cbda,cbda则( )
A. bcad B. bcad C. bcad D. ad、bc大小不确定
6. 03log3logba,则有( )
A. 10ba B. ba1 C. 10ab D. ab1
7. 121a,21aA,21aB,aC11,aD11,则有( )
A. DCBA B. DBAC
C. DBCA D. DCAB
..
DOC版.
【试题答案】
1. D 2. C 3. A 4. B 5. C 6. B 7. B
100测评网高二数学练习卷二项式定理
典型例题一例1 在二项式nx x ⎪⎭⎫ ⎝⎛+421的展开式中,前三项的系数成等差数列,求展开式中所有有理项.分析:此题是典型的特定项问题,涉及到前三项的系数及有理项,能够通过抓通项公式解决.解:二项式的展开式的通项公式为:4324121C 21)(C rn r r n rr n r n r x x x T --+=⎪⎭⎫ ⎝⎛=前三项的.2,1,0=r得系数为:)1(8141C ,2121C ,123121-=====n n t n t t n n, 由已知:)1(8112312-+=+=n n n t t t ,∴8=n 通项公式为1431681,82,1,021C +-+==r r r r r T r xT 为有理项,故r 316-是4的倍数,∴.8,4,0=r依次取得有理项为228889448541256121C ,83521C ,x x T x x T x T =====-. 说明:此题通过抓特定项知足的条件,利用通项公式求出了r 的取值,取得了有理项.类似地,1003)32(+的展开式中有多少项是有理项?能够通过抓通项中r 的取值,取得共有17项.典型例题二例2 求10321⎪⎭⎫ ⎝⎛-x x 的展开式中,系数绝对值最大的项和系数最大的项. 分析:此题仍然属于抓通项公式解决特定项的问题,可是系数的绝对值的最大值或系数的最大值,需要对所有项的系数的转变规律进行研究.由于系数的绝对值都是正数,咱们能够用作商来研究系数绝对值的转变情形,另外各项系数正负交替,又便于用系数绝对值的大小转变抓系数的最大值.解:展开式的通项公式为:65301012)1(C r rr rr xT --+⋅⋅-=系数的绝对值为r r-⋅2C 10,记为1+r t .用前后两项系数的绝对值作商得:.)1(210!102)!10(!)!9()!1(!10C 2C 2C 2C 1011010)1(11012+-=⋅-⨯-⋅+==⋅⋅=+-+-+++r r r r r r t t rr r r r r r r 令1)1(210≥+-r r 得:38≤r 即0=r 、1、2时,上述不等式成立.因此,系数的绝对值从第1项到第4项增加,以后逐项减小. 系数绝对值最大的项为第4项,2525334104152)1(C x x T -=-=-.从系数绝对值的转变情形及系数的正负交替,只要比较第3项与第5项的系数,.8105162102C ,4452C 4410522103==⋅==⋅=--t t 因此,系数最大的项为第5项,3558105x t =. 典型例题三例3 已知7722107)21(x a x a x a a x ++++=- ,求:(1)7321a a a a ++++ ;(2)7531a a a a +++;(3)6420a a a a +++.分析:此题是有关展开式系数和的问题,通过对等式中字母的赋值,往往会取得此类问题的结果.字母常常取的值有0、1、-1等.解:(1)取0=x 可得10=a ,取1=x 得1)1(7710-=-=+++a a a . ∴27321-=++++a a a a .(2)取1-=x 得77632103=-++-+-a a a a a a , 记75316420,a a a a B a a a a A +++=+++=. ∴73,1=--=+B A B A .可得1094)31(21,1093)13(2177-=+-==-=B A 从而10947531-=+++a a a a .(3)从(2)的计算已知10936420=+++a a a a .说明:赋值法不仅能够用来求二项展开式的系数和,关于展开式为多项式的代数式的系数和大多数也能用此方式解决,如:65)21()1(x x -⋅+的展开式中各项的系数和为多少?能够看到65)21()1(x x -+的展开式仍是多项式,令1=x ,即得各项系数和为32)1(265=-.再比如:n n n x a x a x a a x x 2222102)1(++++=++ ,那么n a a a a 2420++++ 等于多少?此题能够由取1=x 取得各项系数和,取1-=x 取得奇数项系数和减去偶数项系数和,两式相加可得)13(21220+=+++nn a a a .另外,为了赋值的需要,有时需要用一个新的二项式替换原先二项式,只要它们的系数等同即可.如:n x x )log 2(2+的展开式中各项的系数和是多少?咱们能够用一个更简单的二项式n x )21(+代替原先的二项式,它们的系数并非改变,令1=x 便得各项系数和为n 3.典型例题四例4 (1)求103)1()1(x x +-展开式中5x 的系数;(2)求6)21(++xx 展开式中的常数项.分析:此题的两小题都不是二项式展开,但能够转化为二项式展开的问题,(1)能够视为两个二项展开式相乘;(2)能够通过代数式变形转化为二项式.解:(1)103)1()1(x x +-展开式中的5x 能够看成以下几种方式取得,然后归并同类项:用3)1(x -展开式中的常数项乘以10)1(x +展开式中的5x 项,能够取得5510C x ;用3)1(x -展开式中的一次项乘以10)1(x +展开式中的4x 项可取得54104410C 3)C )(3(x x x -=-;用3)1(x -中的2x 乘以10)1(x +展开式中的3x 可取得531033102C 3C 3x x x =⋅;用 3)1(x -中的3x 项乘以10)1(x +展开式中的2x 项可取得521022103C C 3x x x -=⋅-,归并同类项得5x 项为:5521031041051063)C C 3C C (x x -=-+-.(2)2121⎪⎪⎭⎫ ⎝⎛+=++x x x x 1251)21(⎪⎪⎭⎫⎝⎛+=++x x x x . 由121⎪⎪⎭⎫ ⎝⎛+x x 展开式的通项公式rr rr r r x x T --+=⎪⎭⎫ ⎝⎛=61212121C 1)2(C ,可得展开式的常数项为924C 612=.说明:问题(2)中将非二项式通过因式分解转化为二项式解决.这时咱们还能够通过归并项转化为二项式展开的问题来解决.典型例题五例5 求62)1(x x -+展开式中5x 的系数.分析:62)1(x x -+不是二项式,咱们能够通过22)1(1x x x x -+=-+或)(12x x -+把它看成二项式展开.解:方式一:[]6262)1()1(x x x x -+=-+-+++-+=44256)1(15)1(6)1(x x x x x其中含5x 的项为55145355566C 15C 6C x x x x =+-.含5x 项的系数为6.方式二:[]6262)(1)1(x x x x -+=-+62524232222)()(6)(15)(20)(15)(61x x x x x x x x x x x x -+-+-+-+-+-+=其中含5x 的项为555566)4(15)3(20x x x x =+-+-. ∴5x 项的系数为6.方式3:此题还可通过把62)1(x x -+看成6个21x x -+相乘,每一个因式各取一项相乘可取得乘积的一项,5x 项可由以下几种可能取得.5个因式中取x ,一个取1取得556C x .3个因式中取x ,一个取2x -,两个取1取得)(C C 231336x x -⋅⋅. 1个因式中取x ,两个取2x -,三个取1取得222516)(C C x x -⋅⋅.归并同类项为5525161336566)C C C C (C x x =+-,5x 项的系数为6.典型例题六例6 求证:(1)1212C C 2C -⋅=+++n n n n n n n ; (2))12(11C 11C 31C 21C 1210-+=++++++n n n n n n n n . 分析:二项式系数的性质事实上是组合数的性质,咱们能够用二项式系数的性质来证明一些组合数的等式或求一些组合数式子的值.解决这两个小题的关键是通过组合数公式将等式左侧各项转变的等数固定下来,从而利用二项式系数性质nn n n n n 2C C C C 210=++++ .解:(1)11C )!()!1()!1()!()!1(!)!(!!C --=+--⋅=--=-⋅=k n kn n k n k n n k n k n k n k n k k∴左侧111101C C C ----+++=n n n n n n n=⋅=+++=-----11111012)C C C (n n n n n n n 右边. (2))!()!1(!)!(!!11C 11k n k n k n k n k k k n--=-⋅+=+ 11C 11)!()!1()!1(11+++=-++⋅+=k n n k n k n n . ∴左侧112111C 11C 11C 11++++++++++=n n n n n n n =-+=++++=+++++)12(11)C C (C 111112111n n n n n n n 右边. 说明:此题的两个小题都是通过变换转化成二项式系数之和,再用二项式系数的性质求解.另外,有些组合数的式子能够直接作为某个二项式的展开式,但这需要逆用二项式定理才能完成,因此需认真观看,咱们能够看下面的例子:求10C 2C 2C 2C 22108107910810109+++++ 的结果.认真观看能够发觉该组合数的式与10)21(+的展开式接近,但要注意:10101099102210110010102C 2C 2C 2C C )21(⋅+⋅++⋅+⋅+=+ 10101091092102C 2C 2C 21021++++⨯+= )C 2C 2C 210(21101099108210+++++=从而能够取得:)13(21C 2C 2C 21010101099108210-=++++ . 典型例题七例7 利用二项式定理证明:98322--+n n 是64的倍数.分析:64是8的平方,问题相当于证明98322--+n n 是28的倍数,为了使问题向二项式定理切近,变形1122)18(93++++==n n n ,将其展开后各项含有k 8,与28的倍数联系起来.解:∵98322--+n n98)18(98911--+=--=++n n n n9818C 8C 8C 81211111--+⋅+⋅++⋅+=+-+++n nn n n n n n 981)1(88C 8C 8211111--+++⋅++⋅+=-+++n n n n n n n 2111118C 8C 8⋅++⋅+=-+++n n n n n64)C 8C 8(112111⋅++⋅+=-+-++n n n n n 是64的倍数.说明:利用此题的方式和技术不仅能够用来证明整除问题,而且能够用此方程求一些复杂的指数式除以一个数的余数.典型例题八例8 展开52232⎪⎭⎫ ⎝⎛-x x .分析1:用二项式定理展开式.解法1:52232⎪⎭⎫ ⎝⎛-x x2232524150250523)2(23)2(23)2(⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=x x C x x C x x C52554245322352323)2(23)2(⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+x C x x C x x C 10742532243840513518012032x x x x x x -+-+-= 分析2:对较繁杂的式子,先化简再用二项式定理展开.解法2:10535232)34(232x x x x -=⎪⎭⎫ ⎝⎛- 233254315530510)3()4()3()4()4([321-+-+=x C x C x C x])3()3()4()3()4(5554134532335-+-+-+C x C x C)243716204320576038401024(321369121510-+-+-=x x x x x x10742532243840513518012032x x x x x x -+-+-=. 说明:记准、记熟二项式n b a )(+的展开式,是解答好与二项式定理有关问题的前提条件.对较复杂的二项式,有时先化简再展开会更简便.典型例题九例9 假设将10)(z y x ++展开为多项式,通过归并同类项后它的项数为( ). A .11 B .33 C .55 D .66 分析:10)(z y x ++看做二项式10])[(z y x ++展开.解:咱们把z y x ++看成z y x ++)(,按二项式展开,共有11“项”,即∑=-⋅+=++=++10010101010)(])[()(k k k kz y x C z y x z y x .这时,由于“和”中各项z 的指数各不相同,因此再将各个二项式ky x -+10)(展开,不同的乘积k k k z y x C ⋅+-1010)((10,,1,0 =k )展开后,都可不能显现同类项. 下面,再别离考虑每一个乘积k k k z y x C ⋅+-1010)((10,,1,0 =k ). 其中每一个乘积展开后的项数由ky x -+10)(决定,而且各项中x 和y 的指数都不相同,也可不能显现同类项. 故原式展开后的总项数为66191011=++++ , ∴应选D .典型例题十例10 假设nx x ⎪⎭⎫⎝⎛-+21的展开式的常数项为20-,求n .分析:题中0≠x ,当0>x 时,把三项式nx x ⎪⎭⎫⎝⎛-+21转化为nnx x x x 2121⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+;当0<x 时,同理nn nx x x x 21)1(21⎪⎭⎫ ⎝⎛----=⎪⎭⎫⎝⎛-+.然后写出通项,令含x 的幂指数为零,进而解出n .解:当0>x 时nn x x x x 2121⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+,其通项为rn r n r r rn r n r x C xx C T 222221)()1()1()(--+-=-=, 令022=-r n ,得r n =,∴展开式的常数项为nn n C 2)1(-;当0<x 时,nn n x x x x 21)1(21⎪⎭⎫ ⎝⎛----=⎪⎭⎫⎝⎛-+,同理可得,展开式的常数项为nn n C 2)1(-. 不管哪一种情形,常数项均为n n n C 2)1(-.令20)1(2-=-n n n C ,以 ,3,2,1=n ,逐个代入,得3=n .典型例题十一例11 1031⎪⎭⎫ ⎝⎛+x x 的展开式的第3项小于第4项,那么x 的取值范围是______________.分析:第一运用通项公式写出展开式的第3项和第4项,再依照题设列出不等式即可.解:使1031⎪⎭⎫ ⎝⎛+x x 成心义,必需0>x ; 依题意,有43T T <,即3373102382101)(1)(⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛x x C x x C .∴31123891012910xx ⨯⨯⨯⨯⨯<⨯⨯(∵0>x ).解得5648980<<x .∴x 的取值范围是⎭⎬⎫⎩⎨⎧<<5648980x x . ∴应填:5648980<<x . 典型例题十二例12 已知n xx)1(2log +的展开式中有持续三项的系数之比为321∶∶,这三项是第几项?假设展开式的倒数第二项为112,求x 的值.解:设持续三项是第k 、1+k 、2+k 项(+∈N k 且1>k ),那么有32111∶∶∶∶=+-k n k n k n C C C ,即321!)1)(1(!!)(!!!)1)(1(!∶∶∶∶=--+-+--k n k n k n k n k n k n .∴321)1(1)(1)1)((1∶∶∶∶=+-+--k k k n k k n k n .∴⎪⎪⎩⎪⎪⎨⎧=-+=+-⇒⎪⎪⎩⎪⎪⎨⎧=-+=+---32)()1(21132)()1(21)1)(()(k n k k n k k n k k k k n k n k n k 14=⇒n ,5=k 所求持续三项为第5、6、7三项.又由已知,1122log 1314=xxC .即82log =x x .两边取以2为底的对数,3)(log 22=x ,3log 2±=x , ∴32=x ,或32-=x .说明:当题目中已知二项展开式的某些项或某几项之间的关系时,常利用二项式通项,依照已知条件列出某些等式或不等式进行求解.典型例题十三例13 nx )21(+的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.分析:依照已知条件可求出n ,再依照n 的奇偶性;确信二项式系数最大的项.解:556)2(x C T n =,667)2(x C T n =,依题意有8226655=⇒=n C C n n .∴8)21(x +的展开式中,二项式系数最大的项为444851120)2(x x C T ==.设第1+r 项系数最大,那么有65222211881188≤≤⇒⎪⎩⎪⎨⎧⋅≥⋅⋅≥⋅++--r C C C C r r r r r r r r . ∴5=r 或6=r (∵{}8,,2,1,0 ∈r ). ∴系娄最大的项为:561792x T =,671792x T =.说明:(1)求二项式系数最大的项,依照二项式系数的性质,n 为奇数时中间两项的二项式系数最大,n 为偶数时,中间一项的二项式系数最大.(2)求展开式中系数最大项与求二项式系数最大项是不同的,需依照各项系数的正、负转变情形,一样采纳列不等式,解不等式的方式求得.典型例题十四例14 设n m x x x f )1()1()(+++=(+∈N n m ,),假设其展开式中关于x 的一次项的系数和为11,问n m ,为何值时,含2x 项的系数取最小值?并求那个最小值.分析:依照已知条件取得2x 的系数关于n 的二次表达式,然后利用二次函数性质探讨最小值问题.解:1111=+=+m n C C n m .211)(21222222-+=-+-=+n m n n m m C C nm499)211(55112211022+-=+-=-=n n n mn . ∵+∈N n ,∴5=n 或6,6=m 或5时,2x 项系数最小,最小值为25.说明:二次函数499)211(2+-=x y 的对称轴方程为211=x ,即5.5=x ,由于5、6距5.5等距离,且对+∈N n ,5、6距5.5最近,因此499)211(2+-n 的最小值在5=n 或6=n 处取得.典型例题十五例15 若0166777)13(a x a x a x a x ++++=- ,求(1) 721a a a +++ ;(2) 7531a a a a +++;(3) 6420a a a a +++. 解:(1)令0=x ,那么10-=a ,令1=x ,那么128270167==++++a a a a . ① ∴129721=+++a a a .(2)令1-=x ,那么701234567)4(-=+-+-+-+-a a a a a a a a ② 由2②①-得:8256]4128[2177531=--=+++)(a a a a (3)由2②①+得: 6420a a a a +++][210123456701234567)()(a a a a a a a a a a a a a a a a +-+-+-+-++++++++= 8128])4(128[217-=-+=. 说明:(1)本解法依照问题恒等式特点来用“特殊值”法.这是一种重要的方式,它适用于恒等式.(2)一样地,关于多项式n n n x a x a x a a q px x g ++++=+= 2210)()(,)(x g 的各项的系数和为)1(g :)(x g 的奇数项的系数和为)]1()1([21-+g g .)(x g 的偶数项的系数和为)]1()1([21--g g .典型例题十六例16 填空:(1) 3230-除以7的余数_____________;(2) 155555+除以8的余数是________________.分析(1):将302分解成含7的因数,然后用二项式定理展开,不含7的项确实是余数.解:3230-3)2(103-=3)8(10-= 3)17(10-+=37771010910911010010-++++=C C C C 2]77[791081109010-+++⨯=C C C又∵余数不能为负数,需转化为正数 ∴3230-除以7的余数为5 ∴应填:5分析(2):将5555写成55)156(-,然后利用二项式定理展开. 解:155555+15)156(55+-=15565656555554555415555055+-++-=C C C C容易看出该式只有14155555=+-C 不能被8整除,因此155555+除以8的余数,即14除以8的余数,故余数为6.∴应填:6.典型例题十七例17 求证:关于+∈N n ,111111+⎪⎭⎫ ⎝⎛++<⎪⎭⎫ ⎝⎛+n n n n .证明:nn ⎪⎭⎫⎝⎛+11展开式的通项rr n r r nr n r p n C T !11=⋅=+ r r r n n n n r )1()2)(1(!1+---=)11()21)(11(!1nr n n r ----=. 1111+⎪⎭⎫ ⎝⎛++n n 展开式的通项rr n r r n r n r A n CT)1(!)1(11'1+=+⋅=++ )111()121)(111(!1+--+-+-=n r n n r . 由二项式展开式的通项明显看出'11++<r r T T ,因此111111+⎪⎭⎫ ⎝⎛++<⎪⎭⎫ ⎝⎛+n n n n .说明:此题的两个二项式中的两项为正项,且有一项相同,证明时,依照题设特点,采纳比较通项大小的方式完本钱题证明.典型例题十八例18 在52)23(++x x 的展开式中x 的系数为( ).A .160B .240C .360D .800分析:此题考查二项式定理的通项公式的运用.应想方法将三项式转化为二项式求解. 解法1:由5252]2)3[()23(++=++x x x x ,得k k k k x x C T 2)3(5251⋅+=-+k k kx x C -+⋅⋅=525)3(2.再一次利用通项公式得,rk r r k k k r xC C T ---+⋅⋅⋅=21055132, 那个地址50≤≤k ,k r -≤≤50. 令1210=--r k ,即92=+r k .因此1=r ,4=k ,由此取得x 的系数为24032445=⋅⋅C .解法2:由5552)2()1()23(++=++x x x x ,知5)1(+x 的展开式中x 的系数为45C , 常数项为1,5)2(+x 的展开式中x 的系数为4452⋅C ,常数项为52.因此原式中x 的系数为24022445545=⋅+⋅C C . 解法3:将52)23(++x x 看做5个三项式相乘,展开式中x 的系数确实是从其中一个三项式中取x 3的系数3, 从另外4个三项式中取常数项相乘所得的积,即2402344415=⋅⋅⋅C C . ∴应选B .典型例题十九例19 已知92⎪⎪⎭⎫⎝⎛-x x a 的展开式中3x 的系数为49,常数a 的值为___________. 分析:利用二项式的通项公式.解:在92⎪⎪⎭⎫⎝⎛-x x a 的展开式中, 通项公式为=⎪⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛=-+rrr r x x a C T 299192329921)1(--⋅⎪⎭⎫ ⎝⎛⋅-r r r r r x a C . 依照题设,3923=-r ,因此8=r .代入通项公式,得39169ax T =. 依照题意,49169=a ,因此4=a . ∴应填:4.典型例题二十例20 (1)求证:n n n n n n C C C )2(3)1(333133221-=-++⋅-⋅+-(2)假设443322104)32(x a x a x a x a a x ++++=+,求2312420)()(a a a a a +-++的值.分析:(1)注意观看n n n n n n x C x C x C x ++++=+ 2211)1(的系数、指数特点,即可通过赋值法取得证明.(2)注意到)()()(432102312420a a a a a a a a a a ++++=+-++)(43210a a a a a +-+-⋅,再用赋值法求之.解:(1)在公式n n n n n n x C x C x C x ++++=+ 2211)1(中令3-=x ,即有 n n n n n n C C C )3()3()3(1)31(2211-++-+-+=-n n n n C C 3)1(331221⋅-+-⋅+⋅-=∴等式得证.(2)在展开式443322104)32(x a x a x a x a a x ++++=+中, 令1=x ,得443210)32(+=++++x a a a a a ; 令1-=x ,得443210)32(+-=+-+-a a a a a .∴原式)()(4321043210a a a a a a a a a a +-+-⋅++++=1)32()32(44=+-⋅+=.说明:注意“赋值法”在证明或求值中的应用.赋值法的模式是,在某二项展开式,如n n n x a x a x a a bx a ++++=+ 2210)(或b a C a C b a n n n n n 110)(-+=+222b a C n n -+ n n n b C ++ 中,对任意的A x ∈(A b a ∈,)该式恒成立,那么对A 中的特殊值,该工也必然成立.特殊值x 如何选取,没有一成不变的规律,需视具体情形而定,其灵活性较强.一样取1,1,0-=x 较多.一样地,多项式)(x f 的各项系数和为)1(f ,奇数项系数和为)]1()1([21--f f ,偶次项系数和为)]1()1([21-+f f .二项式系数的性质n n n n n n C C C C 2210=++++ 及15314202-=+++=+++n n n n n n n C C C C C C 的证明确实是赋值法应用的范例.典型例题二十一例21 假设+∈N n ,求证明:3724332+-+n n 能被64整除.分析:考虑先将323+n 拆成与8的倍数有关的和式,再用二项式定理展开.解:3724332+-+n n37243322+-⋅=+n n 3724931+-⋅=+n n3724)18(31+-+⋅=+n n3724]8888[311112111101+-+⋅++⋅+⋅+⋅⋅=+++-++++n C C C C C n n n n n n n n n n 3724]18)1(888[3121111+-+⋅+++⋅+⋅+⋅=-+++n n C C n n n n n 3724)]98(8888[3211121111+-++⋅++⋅+⋅+⋅=-+-+++n n C C C n n n n n n n 3724)98(3]888[831132121112+-+⋅+++⋅+⋅+⋅=-+-+-+-n n C C C n n n n n n n 64]888[6433212111++⋅+⋅+⋅=-+-+- n n n n n C C , ∵18-n ,2118-+⋅n n C ,3218-+⋅n n C ,…均为自然数,∴上式各项均为64的整数倍. ∴原式能被64整除.说明:用二项式定理证明整除问题,大体上确实是这一模式,先将某项凑成与除数有关的和式,再展开证之.该类题也可用数学归纳法证明,但不如用二项式定理证明简捷.典型例题二十二例22 已知n x x )3(232+的展开式各项系数和比它的二项式系数和大992.(1)求展开式中二项式系数最大的项; (2)求展开式中系数最大的项.分析:先由条件列方程求出n .(1)需考虑二项式系数的性质;(2)需列不等式确信r . 解:令1=x 得展开式的各项系数之和为n n 22)31(=+,而展开式的二项式系数的和为n n n n n n C C C C 2210=++++ ,∴有992222=-n n.∴5=n .(1)∵5=n ,故展开式共有6,其中二项式系数最大的项为第三、第四两项. ∴62233225390)3()(x x x C T =⋅=,32232232354270)3()(x x x C T =⋅=.(2)设展开式中第1+r 项的系数最大.341052532513)3()(r rr rrr r xC x x C T +-+⋅⋅=⋅⋅=,故有⎪⎩⎪⎨⎧⋅≥⋅⋅≥⋅++--115511553333r r r r r r r r C C C C 即⎪⎪⎩⎪⎪⎨⎧+≥--≥.1351,613r r r r解得2927≤≤r .∵N r ∈, ∴4=r ,即展开式中第5项的系数最大.32642132455405)3()(x x x C T =⋅⋅=说明:展开式中二项式系数最大的项与系数最大的项是两个不同的概念,因此其求法亦不同.前者用二项式系数的性质直接得出,后者要列不等式组;解不等式组时可能会求出几个r ,这时还必需算出相应项的系数后再比较大小.典型例题二十三例23 求证:(1) pn m m p n p m n p m n C C C C C C C +-=+++0110 ;(2) 1144220242333--+⋅=++++n n n n n n n n C C C C (K n 2=,*N n ∈)分析:(1)注意到两列二项式两乘后系数的特点,可构造一个函数;也可用构造一个组合问题的两种不同解法找到思路.(2)同上构造函数,赋值.证明:(1)(法1)∵n m n m x x x )1()1()1(+⋅+=++,∴)1()1()1(221221nn n n n m m m m m n m x C x C x C x C x C x C x ++++⋅++++=++ .∴此式左右两边展开式中Px 的系数必相等.左侧Px 的系数是p n m C +,右边Px 的系数是 022110mp n p m n p m n p m n C C C C C C C C ⋅++⋅+⋅+⋅-- , ∴pn m m p n p m n p m n p m n C C C C C C C C C +--=⋅++⋅+⋅+⋅022110 .等式成立.(法2)假想有下面一个问题:要从n m +个不同元素中掏出P 个元素,共有多少种取法?该问题可有两种解法.一种解法是明显的,即直接由组合数公式可得出结论:有p n m C +种不同取法.第二种解法,可将n m +个元素分成两组,第一组有m 个元素,第二组有n 个元素,那么从n m +个元素中掏出P 个元素,可看成由这两组元素中别离掏出的元素组成,取法可分成1+P 类:从第一组取P 个,第二组不取,有0n p m C C ⋅种取法;从第一组取1-P 个,从第二组取1个,有11n p m C C ⋅-种取法,…,第一组不取,从第二组取P 个.因此取法总数是p n m n p m n p m n p m C C C C C C C C ⋅++⋅+⋅+⋅--022110 .而该问题的这两种解法答案应是一致的,故有pn m m p n p m n p m n p m n C C C C C C C C C +--=⋅++⋅+⋅+⋅022110 .(2)∵n 为偶数,∴nn nn n n nC C C C 333)31(221++++=+ ;nnn n n n n C C C C 333)31(2210+-+-=- . 两式相加得)333(22444220nn n n n n n n C C C C ++++=+ , ∴114422242333--+⋅=++++n n nn nn n n C C C C .说明:构造函数赋值法,构造问题双解法,拆项法、倒序相加法都是证明一些组合数恒等式(或求和)的经常使用方式.本卷由《100测评网》整理上传,专注于中小学生学业检测、练习与提升.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. 典型例题一
例1 比较33x与x3的大小,其中Rx. 解:xx3)3(2 332xx,
3)23(])23(3[222xx,
43)23(2x,
043,
∴ xx332. 说明:由例1可以看出实数比较大小的依据是:①baba0; ②baba0;③baba0.
典型例题二
例2 比较16x与24xx的大小,其中Rx 解:)()1(246xxx 1246xxx,
)1()1(224xxx,
)1)(1(42xx,
)1)(1)(1(222xxx,
)1()1(222xx,
∴ 当1x时,2461xxx; 当1x时,.1246xxx 说明:两个实数比较大小,通常用作差法来进行,其一般步骤是:第一步:作差;第二步:变形,常采用配方,因式分解等恒等变形手段;第三步:定号,贵州省是能确定是大于0,还是等于0,还是小于0.最后得结论.概括为“三步,—结论”,这里的“变形”一步最为关键. 欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. 典型例题三
例3 Rx,比较)12)(1(2xxx与)21(x(12xx)的大小. 分析:直接作差需要将)12)(1(2xxx与)21(x(12xx)展开,过程复杂,式子冗长,可否考虑根据两个式子特点,予以变形,再作差. 解:∵)12)(1(2xxx=)1(x(122xxx)
)1(2)1)(1(2xxxxx,
)1)(211()1)(21(22xxxxxx )1(21)1)(1(22xxxxx,
∴ )1)(21()12)(1(22xxxxxx 021)1(21)1(212xxxx.
则有Rx时,)12)(1(2xxx)21(x(12xx)恒成立. 说明:有的确问题直接作差不容易判断其符号,这时可根据两式的特点考虑先变形,到比较易于判断符号时,再作差,予以比较,如此例就是先变形后,再作差.
典型例题四
例4 设Rx,比较x11与x1的大小. 解:作差xxxx1)1(112, 1)当0x时,即012xx, ∴ xx111; 2)当01x,即1x时,012xx, ∴xx111; 3)当01x但0x,即01x或0x时,012xx, 欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. ∴xx111. 说明:如本题作差,变形,变形到最简形式时,由于式中含有字母,不能定号,必须对字母根据式子具体特点分类讨论才能定号.此时要注意分类合理恰当.
典型例题五
例5 比较1618与1816的大小 分析:两个数是幂的形式,比较大小一般采用作商法。
解:1616162161816)289()21()89(161)1618(1618
.1618,016,1)289()1,0(28918161816<><
说明:求商法比大小的变形要围绕与1比大小进行. 典型例题六
例6 设0,0>>ba,且ba,比较:baba与abba的大小。 分析:比较大小一般方法是求差法或求商法,利用不等式的性质进行变形,然后确定大小。
解:baabbaabbababababa)( 当0>>ba时,0,1>>baba,1)(>baba 当0>>ab时,0,10<<<baba1)(>baba
1)(>baba即1>abbababa,
又0>abba,abaababa> 说明:求商法的基本步骤是:①求商,②变形,③与1比大小从而确定两个数的大小. 典型例题七
例7 实数dcba、、、满足条件:①dcba,;②0cbca;③欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. 0dbda,则有( )
A.bdca B.dbac C.dbca D.bdac (天津市2001年南开中学期末试题) 分析:先由条件②③分析出ba、与dc、的关系,根据条件利用①用数轴数形结合比出大小.
解:∵0cbca,∴ba、与c同侧
∵0dbda,∴ba、与d异侧 ∵dcba, ∴把dcba、、、标在数轴上,只有下面一种情况
由此得出bdac,∴此题选D. 说明:比较大小时可以借助于数轴,利用推出的一些结论在数轴上标出它们的相对位置,这样容易看出几个数之间的大小关系,尤其是比较的个数较多时适用.
典型例题八
例8 已知①11ba;②31ba,求:ba3的取值范围. 分析:此题是给代数式的字母的范围,求另外代数式的范围.分为两步来进行:(1)利用待定系数法将代数式ba3用ba和ba表示.(2)利用不等式性质及题目条件确定ba3的范围.
解:设:byxayxbaybaxba)()()()(3
2113yxyxyx
由①+②×2得:231)(2)(21baba 即:731ba.
说明:此题的一种典型错误做法,如下: ,31,11baba420a,即:20a
02413,11babba
即:02b 欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. 830,20,630baba 此解法的错误原因是因为a与b是两个相互联系,相互制约的量,而不是各自独立的,当ba取到最大值或最小值时,ba不一定能取到最值,所以用以上方法可能扩大变量的范围. 避免出错的方法是通过待定系数法“整体代入”,见解题过程.
典型例题九 例9 判断下列各命题的真假,并说明理由. (1)若22bcac,则.ba
(2)若ba,则.11ba (3)若0,cba,则.bcac (4)若dcba,,则.dbca (5)若caba,0,则.2bca (6)若Nmba,,则.mmba 分析:利用不等式的性质来判断命题的真假.
解:(1)0222cbcacbabcacc22201,是真命题.
(2)可用赋值法:2,3ba,有ba11,是假命题. 也可这样说明:ababba11, ∵ ba,只能确定0ab, 但ab的符号无法确定,从而ba11的符号确定不了,所以ba11无法得到,实际上有:
.110,baabba .110,baabba
(3)与(2)类似,由babcaccba011,从而bcacba是假命题. 欢迎登录100测评网www.100ceping.com进行学习检测,有效提高学习成绩. (4)取特殊值:.3,2,1,5dcba 有dbca,∴ 是假命题. 定理3的推论是同向不等式可相加,但同向不等式相减不一定成立.只有异向不等式
可相减,即.,dbcadcba
(5)bcabcabbcaabaaba22000, ∴是真命题. (6)定理4成立的条件为必须是正数. 举反例:
2,4,3mba,则有.mmba
说明:在利用不等式的性质解题时,一定要注意性质定理成立的条件.要说明一个命题是假命题可通过举反例.
典型例题十
例10 求证:.0,011,bababa 分析:把已知的大小关系转化为差数的正负,再利用不等式的性质完成推理. 证明:利用不等式的性质,得
00011110ababbaabba
baba
.0,0异号,baba
ba
典型例题十一 例11 若dcba,,则下面不等式中成立的一个是( ) (A)cbda (B)bdac (C)dbca (D)bcad 解:由不等式的性质知:(A)、(B)、(C)成立的条件都不充分,所以选(D),其实(D) 正是异向不等式相减的结果.
.bcadcddcbaba
