南京理工大学机械设计基础上——解析法设计凸轮的轮廓曲线
机械设计教案:凸轮机构的认识与盘形凸轮轮廓的设计
授课教案No任务3.1 凸轮机构的认识一、复习10分钟复习上次课学习内容二、教师导课与课程学习:(1)学习提示,教师介绍本任务的学习内容。
15分钟本项目以直动从动件的盘形凸轮机构为例,在从动件等速运动、等加速等减速运动、余弦加速度运动(简谐运动)规律条件下,分析了凸轮机构中存在的柔性冲击与刚性冲击。
教师介绍本任务的学习内容:凸轮机构的分类;常用术语;从动件的运动规律;凸轮机构的结构形式;常用材料及热处理(2)分小组学习: 40分钟3.1.1常用设备中的凸轮机构1. 凸轮机构的组成如图所示的凸轮机构是由凸轮、从动件和机架等三个基本构件组成的机构。
2.凸轮机构应用实例自动钻床进给机构、冲床凸轮机构等。
3.1.2凸轮机构的分类凸轮机构的类型很多,按凸轮和从动件的形状及其运动形式的不同,凸轮机构的分类方法有以下几种:1.按凸轮形状分类(1)盘形凸轮(2)移动凸轮。
(3)圆柱凸轮2.按从动件形式分类(1)尖顶从动件(2)滚子从动件(3)平底从动件从动件的结构形式3.按从动件的运动形式分类学生发言汇报、记录学习笔记学生发言汇报并记录学习笔记阅读教材和PPT、分组讨论、撰写发言提纲、学生发言汇报,课,记录学习笔记No(1)直动从动件直动从动件指相对于机架作直线往复移动的从动件,如图3.1.1中所示。
直动从动件又分为对心直动从动件和偏置直动从动件。
(2)摆动从动件:绕某一固定转动中心摆动的从动件。
4.按凸轮与从动件的锁合方式分类 (1)力锁合利用从动件的重力、弹簧力或其他外力使从动件与凸轮轮廓保持接触,(2)形锁合利用从动件和凸轮特殊的几何形状来维持接触,例如圆柱凸轮机构是利用滚子与凸轮凹槽两侧面的配合来实现形锁合。
3.1.3凸轮机构的常用术语如下:1.凸轮基圆与基圆半径b r2.凸轮的转角δ凸轮相对于某一位置转过的角度,称为凸轮转角δ。
具体包括推程运动角0δ、远停程运动角S δ回程运动角0′δ和近停程运动角Sδ'。
最新机械基础教案(劳动版)——第十一讲 盘形凸轮轮廓曲线的确定
第十一讲
学时:2学时
课题:3.3 盘形凸轮轮廓曲线的确定目的任务:掌握凸轮廓线的设计方法。
重点:凸轮廓线的设计方法
难点:反转法原理
教学方法:利用动画演示反转法原理。
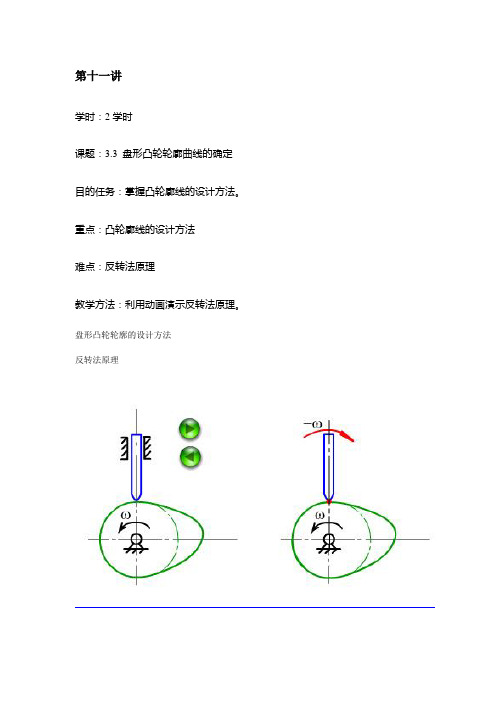
盘形凸轮轮廓的设计方法
反转法原理
在设计凸轮廓线时,可假设凸轮静止不动,而使推杆相对于凸轮作反转运动;同时又在其导轨内作预期运动,作出推杆在这种复合运动中的一系列位置,则其尖顶的轨迹就是所要求的凸轮廓线。
这就是凸轮廓线设计方法的反转法原理。
图解法设计凸轮轮廓曲线
一、尖顶对心移动从动件盘形凸轮轮廓的设计
二、滚子对心移动从动件盘形凸轮轮廓的设计
思考题:上述凸轮的实际廓线能否通过由理论廓线沿径向减去滚子半径得到?(即等距线)
小结
作业:P87 3-7 3-8。
移动从动件盘形凸轮轮廓曲线的图解设计

设计方法:
1.图解法 2.解析法
设计一般精度凸轮时常被采用图解法。而设计高精度 凸轮,则必须用解析法,但计算复杂。本节主要讨论 图解法。
基本原理:
反转法原理
移动从动件盘形凸轮 轮廓曲线的图解设计
反转法原理 :
反转法原理 :
设想给凸轮机构加上一个绕凸轮轴心并与凸轮角速度等值 反向的角速度。根据相对运动原理,机构中各构件间的相对 运动并不改变,但凸轮已视为静止,而从动件则被看成随同 导路以角速度绕点转动,同时沿导路按预定运动规律作往复 移动。从动件尖顶的运动轨迹即为凸轮的轮廓。这就是图解 法绘制凸轮轮廓曲线的原理,称为“反转法”。
通过推广“公司+基地+农户”的产业化发展模式,将产品的产、供、销链紧紧联系在一起,公司按照市场的需要,与农民签订《种植/
取[ ]=35°~45° 养殖收购合同》,由公司给农民提供市场信息、资金、技术和良种等服务,采用欧盟良好农业规范(GLOBALG.
在结构空间允许条件下,可适当将基圆半径取大些,以利于改善机构的传力性能,减少磨损和减少凸轮廓线的制造误差。
反转法设计凸轮轮廓曲 线的方法和步骤
1.对心尖顶移动从动件盘形凸轮轮廓曲线的设计
2.对心滚子移动从动件盘形凸轮轮廓曲线的设计
3.偏置尖顶移动从动件盘形凸轮轮廓曲线的设计
对心尖顶移动从动件盘形凸轮轮廓曲线的设计
已知,如图
1.选与位移线图一致的比 例作凸轮的基圆 ;
基圆半径R b
2.将基圆分成与位移线图 中相对应的等份;
3.分别自基圆圆周向外量 取从动件位移线图中相 应的位移量 ;
4.光滑连接各点即为所求 的凸轮轮廓。
对心滚子移动从动件盘形凸轮轮廓曲线的设计
凸轮设计步骤

所属标签:产品外观设计根据使用要求确定了凸轮机构的类型、基本参数以及从动件运动规律后,即可进行凸轮轮廓曲线的设计。
设计方法有几何法和解析法,两者所依据的设计原理基本相同。
几何法简便、直观,但作图误差较大,难以获得凸轮轮廓曲线上各点的精确坐标,所以按几何法所得轮廓数据加工的凸轮只能应用于低速或不重要的场合。
对于高速凸轮或精确度要求较高的凸轮,必须建立凸轮理论轮廓曲线、实际轮廓曲线以及加工刀具中心轨迹的坐标方程,并精确地计算出凸轮轮廓曲线或刀具运动轨迹上各点的坐标值,以适合在数控机床上加工。
圆柱凸轮的廓线虽属空间曲线,但由于圆柱面可展成平面,所以也可以借用平面盘形凸轮轮廓曲线的设计方法设计圆柱凸轮的展开轮廓。
下面时间财富网的小编分别介绍用几何法和解析法设计凸轮轮廓曲线的原理和步骤。
1 几何法反转法设计原理:以尖底偏置直动从动件盘形凸轮机构为例:凸轮机构工作时,凸轮和从动件都在运动。
为了在图纸上画出凸轮轮廓曲线,应当使凸轮与图纸平面相对静止,为此,可采用如下的反转法:使整个机构以角速度(-w)绕O转动,其结果是从动件与凸轮的相对运动并不改变,但凸轮固定不动,机架和从动件一方面以角速度(-w)绕O转动,同时从动件又以原有运动规律相对机架往复运动。
根据这种关系,不难求出一系列从动件尖底的位置。
由于尖底始终与凸轮轮廓接触,所以反转后尖底的运动轨迹就是凸轮轮廓曲线。
1). 直动从动件盘形凸轮机构尖底偏置直动从动件盘形凸轮机构:已知从动件位移线图,凸轮以等角速w顺时针回转,其基圆半径为r0,从动件导路偏距为e,要求绘出此凸轮的轮廓曲线。
运用反转法绘制尖底直动从动件盘形凸轮机构凸轮轮廓曲线的方法和步骤如下:1) 以r0为半径作基圆,以e为半径作偏距圆,点K为从动件导路线与偏距圆的切点,导路线与基圆的交点B0(C0)便是从动件尖底的初始位置。
2) 将位移线图s-f的推程运动角和回程运动角分别作若干等分(图中各为四等分)。
机械设计基础第4章

第四章凸轮机构在各种机器中,尤其是自动化机器中,为实现各种复杂的运动要求,常采用凸轮机构,其设计比较简便。
只要将凸轮的轮廓曲线按照从动件的运规律设计出来,从动件就能较准确的实现预定的运动规律。
本章将着重研究盘状凸轮轮廓曲线绘制的基本方法和凸轮设计中的相关问题。
§4—1 凸轮机构的应用与分类一、凸轮机构的应用凸轮机构的组成凸轮是一个具有曲线轮廓或凹槽的构件。
凸轮通常作等速转动,但也有作往复摆动或移动的。
从动件是被凸轮直接推动的构件。
凸轮机构就是由凸轮、从动件和机架三个主要构件所组成的高副机构。
图4-1所示为内燃机配气凸轮机构。
当具有一定曲线轮廓的凸轮1以等角速度回转时,它的轮廓迫使从动作2(阀杆)按内燃机工作循环的要求启闭阀门。
图4-2为自动机床上控制刀架运动的凸轮机构。
当圆柱凸轮1回转时,凸轮凹槽侧面迫使杆2运动,以驱动刀架运动。
凹槽的形状将决定刀架的运动规律。
内燃机,配气机构凸轮一般作连续等速转动,从动件可作连续或间歇的往复运动或摆动。
凸轮机构广泛用于自动化和半自动化机械中作为控制机构。
但凸轮轮廓与从动件间为点、线接触而易磨损,所以不宜承受重载或冲击载荷。
凸轮机构的特点1)优点:只要适当地设计出凸轮的轮廓曲线,就可以使推杆得到各种预期的运动规律,且机构简单紧凑。
2)缺点:凸轮廓线与推杆之间为点、线接触,易磨损,所以凸轮机构多用在传力不大的场合。
二、凸轮机构的分类凸轮机构的类型很多,通常按凸轮和从动件的形状、运动形式分类。
⒈按凸轮的形状分类(1)盘形凸轮它是凸轮的最基本型式。
这种凸轮是一个绕固定轴转动并且具有变化半径的盘形零件,如图4-1。
(2)移动凸轮当盘形凸轮的回转中心趋于无穷远时,凸轮相对机架作直线运动,这种凸轮称为移动凸轮。
在以上两种凸轮机构中,凸轮与从动件之间的相对运动均为平面运动,故又统称为平面凸轮机构。
(3)圆柱凸轮(圆柱凸轮是一个在圆柱面上开有曲线凹槽,或是在圆柱端面上作出曲线轮廓的构件,它可看作是将移动凸轮卷于圆柱体上形成的。
3.2凸轮轮廓设计ppt课件

一、凸轮廓线设计方法的基本原理
反转原理:
给整个凸轮机构施以-ω时,不影响各构件之间
的相对运动,此时,凸轮将静止,而从动件尖顶复合
运动的轨迹即凸轮的轮廓曲线。
-ω 1
依据此原理可以用几何作图的方法 3’
设计凸轮的轮廓曲线,
2’
2
1’
ω 1 2 潘存云教授
O
33
设计:潘存云
二、直动从动件盘形凸轮轮廓的绘制
若不满足此条件时:
增大r0 减小rr
4.平底尺寸l 的确定 作图法确定: l=2lmax+(5~7)mm
ω
1’ 2’
3’
同理,当导路位于中心左侧时,有:
OP= v/ω = [ds/dt] / [dδ/dt] =[ds/dδ]
∴ CP = ds/dδ
n
+ etgα=(OP+e)/BC
s
B
Dα
=(ds/dδ+e)/(s0+s) 其中: s0= r20 - e2
s0 ω r0
O 潘存云教授
P
C
设计:潘存云
n
∴ tgα = ds/dδ + e
正确偏置:导路位于与凸轮旋转方向ω相反的位置。 注意:用偏置法可减小推程压力角,但同时增大了回
程压力角,故偏距 e 不能太大。
错误偏置
n
αB
ω 设潘计存:云潘教存云授
o
e Pn
正确偏置
n B
α
ω0 P 潘存云教授 en
对心布置有:tgα=ds/dδ/ (r0+s)
设计时要求: α≤[α] 于是有:
1.对心直动尖顶从动件盘形凸轮 已知凸轮的基圆半径r0,角速度ω和 从动件的运动规律,设计该凸轮轮 廓曲线。
8次课凸轮轮廓曲线的设计
课时授课计划第8 次课【教学课题】:§4-3 凸轮轮廓曲线的设计【教学目的】:掌握凸轮轮廓曲线的设计方法,设计步骤。
【教学重点及处理方法】:凸轮轮廓曲线的设计方法,设计步骤。
处理方法:详细讲解【教学难点及处理方法】:反转法的原理。
处理方法:比较讲解【教学方法】: 讲授法【教具】:三角板【时间分配】:引入新课5min新课80 min 小结、作业5min第八次课【提示启发引出新课】由前面可知,凸轮轮廓曲线的形状决定了从动件的运动规律,而从动件的运动规律又要满足一定的工作要求。
因此,在设计凸轮轮廓曲线之前,要根据工作要求选择适当的从动件运动规律,然后再考虑凸轮安装空间的尺寸大小及确定凸轮的基圆半径。
最后进行凸轮轮廓曲线的设计。
凸轮轮廓曲线的设计的方法有作图法和解析法。
【新课内容】§ 4-3凸轮轮廓曲线的设计一、作图法设计凸轮轮廓曲线1、凸轮轮廓的设计原理和方法基本原理是反转原理,其方法是反转法。
反转原理是假想给整个凸轮机构加上一个与凸轮角速度大小相等、方向相反的角速度-,并不改变凸轮与从动件之间的相对运动关系。
所以反转以后尖顶复合运动的轨迹就是凸轮的轮廓曲线。
反转法是利用反转原理来设计凸轮轮廓曲线的方法。
2、对心尖顶移动从动件盘形凸轮轮廓曲线设计已知:从动件位移曲线s (t),基圆半径r b,凸轮等角速度逆时针回转。
作图步骤如下:1)以0为圆心,r b为半径作基圆2)将位移曲线的推程角°、回程角2分别若干等份。
3)B D开始按- 方向取0、!、2和3,并将各阶段的凸轮转角分别等分,得到一系列径向线。
4)径向线上自基圆开始量取与位移相等的点。
5)将各点连成光滑的曲线即为所求。
3、对心滚子从动件设计方法:1)将滚子中心看作尖顶,然后按尖顶推杆凸轮廓线的设计方法确定滚子中心的轨迹,称其为凸轮的理论廓线;2)以理论廓线上各点为圆心,以滚子半径rr为半径,作一系列圆;3)再作此圆族的包络线,即为凸轮工作廓线(实际廓线)H210°1102 984 764、对心平底从动件设计方法:1)将平底与推杆导路与推杆的交点A视为推杆尖顶然后确定出点A在反转中各位置1'、2'、…。
机械设计基础----凸轮机构设计(第三章)
-ω
ω
步骤:
1)—5 ) 同上
1 3 5 78
O
6) 以理论轮廓曲线上各点为圆心,滚子半径 rs为半径作一系列滚子圆,过滚子圆作一 内包络线,即为滚子从动件凸轮的实际轮 廓曲线。 注意:凸轮基圆仍为理论轮廓的基圆。
实际轮廓
理论轮廓
凸轮轮廓曲线的设计
四、摆动从动件盘形凸轮机构
摆动从动件凸轮机构中, 已知凸轮的基圆半径r0,角速 度ω,摆杆长度l以及摆杆回转 中心与凸轮回转中心的距离d, d 摆杆角位移方程。 设计该凸轮轮廓曲线。 A8
●从动件的加速度:
v2
由运动线图可知: 在行程起点、中点和终点,存在加 a2 4hω2/δt2 速度突变,但突变为有限值,引起的惯 性力为有限值,在机构中产生有限冲击, 称为柔性冲击。 ∴等加速等减速运动规律可用于中、低速轻载场合。
d
从动件常用运动规律
位移线图的几何作图法:由s2 与 t2的关系作图。
0 1
4Байду номын сангаас9 4 1 0 1 2
s
3
4
5
6
s
3’ 2’ 1’
h/2
h/2
6 d
O
1 2 3 4 5 dt
从动件常用运动规律
四、余弦加速度运动规律
又称简谐运动规律,从动件加速度 按余弦规律变化。
s 5 6
4 3 2 1 1 h
推程中从动件位移: s2=h[1-cos(πδ/δt)]/2 加速度曲线为一余弦曲线。 由其运动线图可知: 在行程的起始和终止处加速 度有突变,但突变为有限值, 故产生柔性冲击。
3.1 凸轮机构的应用和分类 3.2 从动件的运动规律 3.3 盘状凸轮轮廓的设计 3.4 设计凸轮机构应注意的问题
南京理工大学-研究生入学考试大纲-812机械原理
《机械原理》研究生考试大纲
一、复习参考书
1、机械设计基础(上). 王华坤、范元勋编,兵器工业出版社,2001.8
2、机械原理. 郑文伟等. 高等教育出版社. 6、7版
二、复习要点
第一章绪论
1.机械原理的研究对象,机械、机器、机构
2.机械原理课程的内容
3.机械原理课程的地位与作用
第二章平面机械结构分析
1.研究机构结构分析的目的
2.平面运动副及其分类
3.平面机构运动简图
4.平面机构的自由度
重点:平面机构自由度的计算
第三章平面机构的运动分析
1.研究机构运动分析的目的和方法
2.速度瞬心法及其在机构速度分析上的应用
3.用相对运动图解法对机构进行运动分析
重点:瞬心法、相对运动图解法对机构进行运动分析
第四章平面连杆机构及其设计
1.平面连杆机构的应用及其设计的基本问题
2.平面四杆机构的基本型式及其演化
3.平面四杆机构的主要工作特征;有存在曲柄条件、行程速度变化系数、压力角、传动角、死点
4.平面四杆机构的图解法设计
重点:平面四杆机构的工作特征,压力角、传动角、行程速度变化系数的概念与计算
—1—。
机械设计基础-凸轮反转法(PPT35页)
依据此原理可以用几何作图的方法 设计凸轮的轮廓曲线,例如:
尖顶凸轮绘制动画 滚子凸轮绘制动画
2、用作图法设计凸轮廓线
-ω ω
偏置直动尖顶推杆凸轮机构中,已知凸
轮的基圆半径r0,角速度ω和推杆的运动规律
e
和偏心距e,设计该凸轮轮廓曲线。
-ω
ωA
8’ 7’ 5’ 3’ 1’
1 3 5 78
9’ 11’ 12’
ω -V
v
v
B
R
2πR V=ωR
6)直动推杆圆柱凸轮机构 已知:圆柱凸轮的半径R ,从动
件的运动规律,设计该圆柱凸轮机构。
ω
s
3’ 4’ 5’
2’
6’
1’
7’
δ
12 3 4 5 67 8
-V
4’
3’
5’
v
2’
6’
β 1’
7’β'
s
12
34
5
6
7β" 8
2πR V=ωR R
7)摆动推杆圆柱凸轮机构
实际轮廓为B’点的坐标: x’=x - rrcosθ y’= y - rrsinθ
式中“-”对应于内等距线,“+”对应于外等距线。
(x’,y’)n rr θ
(x, y) θ n (x’,y’)
每一个成功者都有一个开始。勇于开始,才能找到成
•
1、
功的路 。2020/10/152020/10/15Thursday, October 15, 2020
13’ 14’
9 11 13 15
15’
13’ 12’
15 14’14
13 12
11 10
kk9k1k0k1181kk21k73k14k61k055k4kk3k21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4—4 用解析法设计凸轮的轮廓曲线
一、滚子从动件盘形凸轮
1.理论轮廓曲线方程
(1)直动从动件盘形凸轮机构
图示偏置直动滚子从动件盘形凸轮机构。求凸轮理论廓线的方程,反转法给整个机构一个绕
凸轮轴心O的公共角速度-ω,这时凸轮将固定不动,而从动件将沿-ω方向转过角度,滚
子中心将位于B点。B点的坐标,亦即理论廓线的方程为:
sin)(cossincos)(00ssey
essx
(4-15)
22
0ersa
,ra为理论廓线的基圆半径,对于对心从动件凸轮机构,因e=0,所以s0=ra
sin)(cos)(sry
srx
a
a
(4-16)
(2)摆动从动件盘形凸轮机构
图所示为摆动滚子从动件盘形凸轮机构。仍用反转法使凸轮固定不动,而从动件沿-ω
方向转过角度,滚子中心将位于B点。B点的坐标,亦即理论廓线的方程为:
)sin(sin)cos(cos00lay
lax
(4-17)
ψ0为从动件的起始位置与轴心连线OA0之间的夹角。
alrrlaT2
)(arccos20220
(4-18)
在设计凸轮廓线时,通常e、r0、rT、a、l等是已知的尺寸,而s和ψ是的函数,它
们分别由已选定的位移方程s=s()和角位移方程ψ=ψ()确定。
2.实际廓线方程
滚子从动件盘形凸轮的实际廓线是圆心在理论廓线上的一族滚子圆的包络线。由微分几
何可知,包络线的方程为:
0),,(0),,(1111yx
f
yxf
(4-20)
式中x1、y1为凸轮实际廓线上点的直角坐标。
对于滚子从动件凸轮,由于产生包络线(即实际廓线)的曲线族是一族滚子圆,其圆心
在理论廓线上,圆心的坐标由式(4-15)~(4-17)确定,所以由(4-20)有:
0)()(),,(2212111Tryyxxyxf
0)(2)(2),,(1111ddyyyddxxxyxf
式(a)和(b)联立求解x1和y1,即得滚子从动件盘形凸轮的实际廓线参数方程:
221221//ddyddxddxryy
ddyd
dx
ddy
rxx
T
T
(4-21)
上面的一组加减号表示一根外包络廓线,下面的一组加减号表示另一根内包络廓线。
3、刀具中心轨迹方程
加工凸轮廓线时,采用直径和滚子相同的刀具。刀具中心轨迹方程就是理论廓线方程。
如果采用直径大于滚子的铣刀、砂轮等加工凸轮轮廓曲线,或者在线切割机上用钼丝等加工
凸轮廓线,这时刀具中心不在理论廓线上。刀具中心轨迹曲线(图中虚线所示)是一条与实
际廓线处处相差刀具半径的等距曲线,在rc>rT时(图4-23(a)),刀具中心轨迹将是以理论
廓线上各点为圆心,以rc-rT为半径的一族假想滚子圆的外包络线;在rc
络线。只要将式(4-21)中的rT用|rc-rT|代替,就得到刀具中心轨迹的参数方程:
222222/||/||ddyddxddxrryy
ddyd
dx
ddy
rrxx
Tc
Tc
(4-22)
式中x2、y2为刀具中心轨迹的直角坐标,当rc>rT时,取上面的一组加减号;rc
