〖word版本〗人教版八年级数学上册期中综合能力检测题部分附答案共3份
人教版2024-2025学年八年级数学上册期中试卷(解析版)

2024-2025八年级上册期中模拟试卷一、填空题(本题满分30分,每小题3分)1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A. B. C. D.【答案】D【解析】【分析】利用轴对称图形的概念可得答案.【详解】解:A .不是轴对称图形,故此选项不合题意;B .不是轴对称图形,故此选项不合题意;C .不是轴对称图形,故此选项不合题意;D .是轴对称图形,故此选项符合题意;故选:D .【点睛】本题主要考查了轴对称图形,关键是掌握如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.2. 已知长为a ,b ,c 的三条线段首尾顺次相接组成一个三角形.若7a =,9b =,则c 的取值范围是( ) A. 2>cB. 16c <C. 216c ≤≤D. 216c <<【答案】D【解析】【分析】根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,进行求解即可.【详解】解:∵长为a ,b ,c 的三条线段首尾顺次相接组成一个三角形,7a =,9b =, ∴b a c a b −<<+,即:9779c −<<+,∴216c <<;故选D .【点睛】本题考查三角形的三边关系.熟练掌握两边之和大于第三边,两边之差小于第三边,是解题的关键.3. 如图,ACE △≌DBF ,若11cm AD =,5cm =BC ,则AB 长为( )A. 6cmB. 7cmC. 4cmD. 3cm【答案】D【解析】 【分析】根据全等三角形的性质得到AC BD =,结合图形计算,得到答案.【详解】解:ACE ≌DBF ,AC BD ∴=,AC BC BD BC ∴−=−,即AB CD =,11cm AD = ,5cm =BC ,()11523cm AB ∴=−÷=,故选D .【点睛】本题考查全等三角形的性质,线段的和与差.掌握全等三角形的对应边相等是解题的关键. 4. 下列命题:①经过一点有且只有一条直线;②线段垂直平分线上的点到这条线段两端的距离相等;③有两边及其一角对应相等的两个三角形全等;④等腰三角形底边上的高线和中线重合.其中是真命题的有( )A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】根据直线、线段垂直平分线的性质、三角形全等的判定、等腰三角形的性质逐个判断即可得.【详解】解:①经过一点有无数条直线;则这个命题是假命题;②线段垂直平分线上的点到这条线段两端的距离相等;则这个命题是真命题;③有两边及其夹角对应相等的两个三角形全等;则这个命题是假命题;④等腰三角形底边上的高线和中线重合;则这个命题是真命题;综上,是真命题的有2个,故选:B .【点睛】本题考查了直线、线段垂直平分线的性质、三角形全等的判定、等腰三角形的性质,熟练掌握各判定定理与性质是解题关键.5. 如图,四边形ABCD 是轴对称图形,BD 所在的直线是它的对称轴, 1.6 cm AB =, 2.3 cm CD =,则四边形ABCD 的周长为( )A. 3.9cmB. 7.8cmC. 4cmD. 4.6cm【答案】B【解析】 【分析】本题考查了轴对称的性质,熟记性质得到相等的边是解题的关键.根据轴对称图形的性质得出 1.6cm AB BC ==, 2.3cm CD AD ==,进而求出即可.【详解】∵四边形ABCD 是轴对称图形,BD 所在的直线是它的对称轴, 1.6cm AB =, 2.3cm CD =, ∴ 1.6cm AB BC ==, 2.3cm CDAD ==, 则四边形ABCD 的周长为:1.6 1.6 2.3 2.37.8cm +++=.故选:B .6. 如图,CD ,CE ,CF 分别是ABC 的高、角平分线、中线,则下列各式中错误的是( )A. 2AB BF =B. 12ACE ACB ∠=∠C. AE BE =D. CD BE ⊥【答案】C【解析】 【分析】本题考查了三角形的角平分线、中线和高,从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线,三角形一边的中点与此边所对顶点的连线叫做三角形的中线,依此即可求解,熟悉它们的定义和性质是解题的关键.【详解】解:∵CD ,CE ,CF 分别是ABC 的高、角平分线、中线,∴CD BE ⊥,12ACE ACB ∠=∠,2AB BF =,无法确定AE BE =,故选:C .7. 如图90B C ∠=∠=°,AD AE =,添加下列条件后不能..使ABD ECA △≌△的是( )A. 2AD BD =B. BD AC =C. =90DAE ∠°D. AB EC =【答案】A【解析】 【分析】要判断能不能使ABD ECA △≌△,主要看添加上条件后能否符合全等三角形判定方法所要求的条件即可.【详解】解:A .添加2AD BD =,无法证明ABD ECA △≌△,故此选项符合题意;B .添加BD AC =,可以利用HL 证明ABD ECA △≌△,故此选项不符合题意;C .添加=90DAE ∠°,可以利用AAS 证明ABD ECA △≌△,故此选项不符合题意;D .添加AB EC =,可以利用HL 证明ABD ECA △≌△,故此选项不符合题意;故选:A .AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等.8. 一个正多边形的边长是3,从一个顶点可以引出4条对角线,则这个正多边形的周长是( )A. 12B. 15C. 18D. 21【答案】D【解析】【分析】由n 边形从一个顶点出发可引出()3n −条对角线,可求出多边形的边数即可解答.【详解】解:∵经过多边形的一个顶点有4条对角线,∴这个多边形有437+=条边, ∴此正多边形的周长为3721×=,故选:D .【点睛】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.熟记n 边形从一个顶点出发可引出()3n −条对角线是解题的关键.9. 如图,在ABC 中,AB AC =,AB 的垂直平分线交AC 于点P ,若10cm AB =,6cm BC ,则PBC △的周长等于( )A. 16cmB. 12cmC. 8cmD. 20cm【答案】A【解析】 【分析】先求出10cm AC =,再根据线段垂直平分线的性质可得PA PB =,从而可得PB PC BC PA PC BC AC BC ++=++=+,由此即可得.【详解】解:AB AC = ,10cm AB =,10cm AC ∴=,AB 的垂直平分线交AC 于点P ,PA PB ∴=,6cm BC = ,PBC ∴△的周长为16cm PB PC BC PA PC BC AC BC ++=++=+=,故选:A .【点睛】本题主要考查了线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解题关键. 10. 如图,在ABC 中,BD 为AC 边上的中线,已知8BC =,5AB =,BCD △的周长为20,则ABD △的周长为( )A. 17B. 23C. 25D. 28【答案】A【解析】 【分析】根据三角形中线的性质可得AD CD =,进而根据三角形周长可得12BD AD +=,进而即可求解.【详解】解:∵在ABC 中,BD 为AC 边上的中线,∴AD CD =,8BC =,5AB =,BCD △的周长为20,20812BD AD ∴+−,∴ABD △的周长为51217AB BD AD ++=+=.故选A【点睛】本题考查了三角形中线的性质,掌握三角形中线的性质是解题的关键.11. 四盏灯笼的位置如图.已知A ,B ,C ,D 的坐标分别是()1,1−−,()1,1-,()2,1−,()3.2,1−,平移y 轴右侧的一盏灯笼,使得y 轴两侧的灯笼对称,则平移的方法可以是( )A. 将B 向左平移4.2个单位B. 将C 向左平移4个单位C. 将D 向左平移5.2个单位D. 将C 向左平移4.2个单位【答案】C【解析】 【分析】注意到A ,B 关于y 轴对称,只需要C ,D 关于y 轴对称即可,可以将点()2,1C −向左平移到()3.2,1−−,平移5.2个单位,或可以将()3.2,1D −向左平移到()2,1−−,平移5.2个单位.【详解】解:∵A ,B ,C ,D 这四个点的纵坐标都是1−,∴这四个点在一条直线上,这条直线平行于x 轴,∵()1,1A −−,()1,1B −,∴A ,B 关于y 轴对称,只需要C ,D 关于y 轴对称即可,∵()2,1C −,()3.2,1D −,∴可以将点()2,1C −向左平移到()3.2,1−−,平移5.2个单位,或可以将()3.2,1D −向左平移到()2,1−−,平移5.2个单位,故选:C .【点睛】本题考查了生活中的平移现象,关于y 轴对称的点的坐标,注意关于y 轴对称的点的坐标,横坐标互为相反数,纵坐标不变.12. 如图,在ABC ∆中,90A ∠=°,4AB =,3AC =,点O 为AB 的中点,点M 为ABC 内一动点且2OM =,点N 为OM 的中点,当BN CM +最小时,则ACM ∠的度数为( )A 15°B. 30°C. 45°D. 60°【答案】C【解析】 【分析】取OB 的中点D ,连接DM ,证明BON MOD ≌可得BN DM =,从而可判断当点D ,M ,C 共线时BN CM DM CM +=+最短,然后证明ACD 是等腰直角三角形即可.【详解】如图1,取OB 的中点D ,连接DM .∵4AB =,点O 为AB 中点,∴2AO BO ==,∵2OM =,∴OB OM =.∵D 是OB 的中点,点N 为OM 的中点,∴1ODON ==, ∵BON MOD ∠=∠,∴()SAS BON MOD ≌,∴BN DM =,∴BN CM DM CM +=+,∴当点D ,M ,C 共线时BN CM DM CM +=+最短.如图2,.的∵2,1OA OD ==, ∴3AD =,∵3AC =∴AD AC =.∵90A ∠=°,∴ACD 是等腰直角三角形,∴45ACD ∠=°. 故选C .【点睛】本题考查了全等三角形的判定与性质,两点之间线段最短,等腰直角三角形的判定与性质,正确作出辅助线是解答本题的关键.二.填空题(本题满分24分,每小题3分)13. 正五边形每个内角的度数为______.【答案】108°##108度【解析】分析】本题主要考查了正多边形内角和定理,外角和定理:方法一:先根据多边形的内角和公式()2180n −⋅°求出内角和,然后除以5即可;方法二:先根据正多边形的每一个外角等于外角和除以边数,再根据每一个内角与相邻的外角是邻补角列式计算即可得解.【详解】解:方法一:正五边形的内角和为()52180540−×°=°, ∴正五边形的一个内角度数为5405108°÷=°;方法二:正五边形一个外角的度数为360572°÷=°,∴正五边形的一个内角度数为18072108°−°=°;∴正五边形每个内角的度数为108°.故答案为:108°.【点评】本题考查了正多边形的内角与外角的关系,注意两种方法的使用,通常利用外角和与每一个外角的关系先求外角的度数更简单一些.【14. 若等腰三角形的一个内角为36°,则这个等腰三角形顶角的度数为_____________.【答案】36°或108°【解析】【分析】等腰三角形的一个内角是36°,则该角可能是底角,也可能是顶角,注意分情况讨论.【详解】解:分两种情况:当36°的角是底角时,则顶角度数为180°−36°×2=108°;当36°的角是顶角时,则顶角为36°.故答案为:36°或108°.【点睛】本题考查了等腰三角形的性质及三角形的内角和定理;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,也是解答问题的关键.15. 点P (1,-2)关于y 轴的对称点的坐标是_________.【答案】()1,2−−【解析】【分析】根据若点(),a b 关于y 轴对称的点的坐标为(),a b −,据此可求解.【详解】解:点P (1,-2)关于y 轴的对称点的坐标是()1,2−−;故答案为()1,2−−.关键.16. 过12边形的一个顶点可以画对角线的条数是____.【答案】9【解析】【分析】根据对角线的定义,得出过多边形的一个顶点可以画对角线的条数的规律,代入求解即可.【详解】解:根据对角线的定义可知,多边形的一个顶点可以与自身以及相邻的两个点以外的()3n − 个点形成对角线当12n = ,31239n −=−=故答案:9.【点睛】本题考查了多边形的对角线问题,掌握过多边形的一个顶点的对角线条数与边数的关系是解题的关键.17. 如图,点D 在BC 上,AB AC CD ==,AD BD =,则BAC ∠=_____. 为【答案】108°##108度【解析】【分析】本题考查了等边对等角、三角形外角的定义及性质、三角形内角和定理,由等边对等角得出ABC ACB BAD ∠=∠=∠,结合三角形外角的定义及性质得出2CAD CDA ABD ∠=∠=∠,再由三角形内角和定理计算得出36ABC ACB BAD ∠=∠=∠=°,从而推出272DAC BAD ∠=∠=°,即可得解.【详解】解:∵AD BD =,∴ABD BAD ∠=∠,∵AB AC CD ==,∴A ABC CB =∠∠,CAD CDA ∠=∠,∴ABC ACB BAD ∠=∠=∠,∵2CDA BAD ABD ABD ∠=∠+∠=∠,∴2CAD CDA ABD ∠=∠=∠, ∵225180CAD CDA ACD ABD ABD ACD ABD ∠+∠+∠∠+∠+∠∠°,∴ABC ACB BAD ∠=∠=∠=°∴272DAC BAD ∠=∠=°,∴108BAC DAC BAD ∠=∠+∠=°,故答案为:108°.18. 如图,在ABC 中,按以下步骤作图:①分别以点B 和C 为圆心,以大于12BC 的长为半径作弧,两弧相交于点M 和N ;②作直线MN ,分别交边AB BC ,于点D 和E ,连接CD .若90BCA ∠=°,8AB =,则CD 的长为_______.【答案】4【解析】【分析】本题考查了基本作图−作线段的垂直平分线,线段垂直平分线的性质“线段垂直平分线上点到线段两端点的距离相等”,直角三角形斜边中线的性质“直角三角形斜边中线等于斜边的一半”.根据线段垂直平分线的性质即可得到BD CD =,再利用直角三角形斜边中线的性质求解即可.【详解】解:连接CD .由作图知,MN 是线段BC 的垂直平分线,∴BD CD =,∴B BCD ∠=∠,∵90BCA ∠=°,∴90B A BCD ACD ∠+∠=°=∠+∠,∴ACD A ∠=∠,∴CD AD =,∵8AB =, ∴142CD AB ==. 故答案为:4.三. 解答题(本大题满分62分)19. 如图,B D BC DC ∠=∠=,.求证:AB AD =.【答案】见解析【解析】【分析】连接BD ,根据等腰三角形的性质得CBD CDB ∠=∠,再根据等腰三角形的判定定理,即可得到结论.本题主要考查等腰三角形的判定和性质定理,添加辅助线,构造等腰三角形,是解题的关键.【详解】证明:连接BD ,∵BC DC =,∴CBD CDB ∠=∠, ∵ABC ADC ∠=∠,∴ABC CBD ADC CDB ∠−∠=∠−∠,∴ABD ADB ∠=∠,∴AB AD =.20. 如图,在ABC 中,AB AC =,P 是边BC 的中点,PD AB PE AC ⊥⊥,,垂足分别为D ,E .求证:PD PE =.【答案】见解析【解析】【分析】利用AAS 证明PBD PCE ≌即可.本题考查了三角形全等的判定和性质,熟练掌握三角形全等的判定是解题的关键.【详解】证明:∵PD AB PE AC ⊥⊥,,∴90PDB PEC ∠=∠=°,∵AB AC =,∴B C ∠=∠,∵P 是边BC 的中点,∴PB PC =,∵PDB PEC B C PB PC ∠=∠ ∠=∠ =,∴PBD PCE ≌,∴PD PE =.21. 如图,ABC 中,16cm AC =,DE 为AB 的垂直平分线,交AC 于点E ,BCE 的周长为26cm ,求BC 的长.【答案】10cm BC =【解析】【分析】本题考查了线段垂直平分线的性质、三角形的周长,由线段垂直平分线的性质得出AE BE =,由BCE 的周长为26cm 得出()26cm BC AC +=,即可得解,熟练掌握线段垂直平分线的性质是解此题的关键.【详解】解:∵DE 垂直平分AB∴AED BED ≌,∴AE BE =,∵BCE 的周长为26cm ,∴()26cm BC CE BE BC CE AE BC AC ++=++=+=,∵16cm AC =,∴10cm BC =.22. 如图所示,等边三角形ABC 中,AD BC ⊥,垂足为D ,点E 在线段AD 上,45EBC ∠=°,求ACE ∠的度数.【答案】15ACE ∠=°.【解析】【分析】此题考查了等边三角形的性质、线段垂直平分线的性质等知识.根据等边三角形的性质可得ACB ∠的度数,并证得AD 是BC 的垂直平分线,利用线段垂直平分线性质定理可得BE CE =,再由等腰三角形的性质可求得ECB ∠的度数,即可求得结论.【详解】解:∵ABC 是等边三角形,AD BC ⊥,∴60ACB ∠=°,BD CD =,∴AD 是BC 的重直平分线,点E 在线段AD 上,∴BE CE =.∵45EBC ∠=°,∴45ECB EBC ∠=∠=°,∴604515ACE ACB ECB ∠=∠−∠=°−°=°.23. 在 ABC 中,CD ⊥AB 于D ,CE 是∠ACB 的平分线,∠A =20°,∠B =60°.求∠BCD 和∠ECD 的度数.【答案】∠BCD =30°,∠ECD =20°【解析】【分析】由CD ⊥AB 与∠B =60°,根据两锐角互余,即可求得∠BCD 的度数,又由∠A =20°,∠B =60°,求得∠ACB 的度数,由CE 是∠ACB 的平分线,可求得∠ACE 的度数,然后根据三角形外角的性质,求得∠CEB 的度数.【详解】∵CD ⊥AB ,∴∠CDB =90°,∵∠B =60°,∴∠BCD =90°﹣∠B =90°﹣60°=30°;∵∠A =20°,∠B =60°,∠A+∠B+∠ACB =180°,∴∠ACB =100°,∵CE 是∠ACB 的平分线,∴∠ACE =12∠ACB =50°, ∴∠CEB =∠A+∠ACE =20°+50°=70°,∠ECD =90°﹣70°=20°,∴∠BCD =30°,∠ECD =20°.【点睛】本题考查了三角形的外角性质,角平分线,直角三角形两锐角互余等知识点,灵活运用外角定理是快速解题的关键.24. ABC 在平面直角坐标系中的位置如图所示.(1)将ABC 先向下平移4个单位长度,再向右平移3个单位长度,画出平移后的111A B C △,并写出顶点1A ,1B ,1C 的坐标;(2)计算111A B C △的面积.【答案】(1)见解析,()11,1A −,()10.2B −,()12,3C −(2)1.5【解析】【分析】(1)利用点平移的坐标变换规律写出点1A ,1B ,1C 的坐标,然后描点即可;(2)用一个矩形的面积分别减去三个直角三角形的面积去计算111A B C △的面积.【小问1详解】∵将ABC 先向下平移4个单位长度,再向右平移3个单位长度,且()2,3A −,()3,2B −,()1,1C −∴()11,1A −,()10.2B −,()12,3C −,111A B C △如下图所示,【小问2详解】111A B C △的面积为:11122112112 1.5222×−××−××−××=. 【点睛】本题考查了作图与平移变换:作图时要先找到图形关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.25. 如图(1) ABC 和 DEC 都是等腰直角三角形,其中∠ACB =∠DCE =90°,BC =AC ,EC =DC ,点E 在 ABC 内部,直线AD 与BE 交于点F ,线段AF 、BF 、CF 之间存在怎么样的数量关系?(1)先将问题特殊化如图2,当点D 、F 重合时,直接写出线段AF 、BF 、CF 之间的数量关系式: ;(2)再探究一般情况如图1,当点D 、F 不重合时,证明(1)中的结论仍然成立.(3)如图3,若 ABC 和 DEC 都是含30°的直角三角形,若∠ACB =∠DCE =90°,∠BAC =∠EDC =30°,点E 在 ABC 内部,直线AD 、BE 交于点F ,直接写出一个等式,表示线段AF 、BF 、CF 之间的数量关系.【答案】(1)BF -AFCF的(2)见解析 (3)BF 【解析】【分析】(1)证明△ACD ≌△BCE (SAS ),则△CDE 为等腰直角三角形,故DE =EF CF ,进而求解; (2)由(1)知,△ACD ≌△BCE (SAS ),再证明△BCG ≌△ACF (ASA ),得到△GCF 为等腰直角三角形,则GF ,即可求解;问题拓展:证明△BCE ∽△CAD 和△BGC ∽△AFC ,得到BGBC GC AF AC CF ===,则,BG AF GC FC =,进而求解. 【小问1详解】结论:BF -AF ;理由:∵∠ACD +∠ACE =90°,∠ACE +∠BCE =90°,∴∠BCE =∠ACD ,∵BC =AC ,EC =DC ,∴△ACD ≌△BCE (SAS ),∴BE =AD ,∠EBC =∠CAD ,而点D 、F 重合,故BE =AD =AF ,而△CDE 为等腰直角三角形,故DE =EF CF ,则BF =BD =BE +ED =AF CF ;即BF -AF CF ;故答案为:BF -AF CF ;【小问2详解】如图(1),由(1)知,△ACD ≌△BCE (SAS ),∴∠CAF =∠CBE ,BE =AD ,过点C 作CG ⊥CF 交BF 于点G ,∵∠ACF +∠ACG =90°,∠ACG +∠GCB =90°,∴∠ACF =∠BCG ,∵∠CAF =∠CBE ,BC =AC ,∴△BCG ≌△ACF (ASA ),∴GC =FC ,BG =AF ,故△GCF 为等腰直角三角形,则GF CF ,则BF =BG +GF =AF CF ,即BF -AF CF ;【小问3详解】结论:BF AF FC =+. 理由:∵△ABC 和△DEC 都是含30°的直角三角形,∴,BC AC EC =,∴BCEC ACCD == ∵∠ACB =∠DCE ,∴∠BCE =∠ACD ,∴△BCE ∽△ACD ,∴∠CAD =∠CBE ,过点C 作CG ⊥CF 交BF 于点G ,由(2)知,∠BCG =∠ACF ,∴△BGC ∽△AFC ,∴BGBC GC AF AC CF===,则,,BG AF GC FC =,在Rt △CGF 中,GF ==,FG =则=+=+BF BG GF AF FC ,即BF AF FC =+. 理等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题.26. 在平面直角坐标系中,点A 在x 轴正半轴上,点B 在y 轴正半轴上,∠ABC =90°,且AB BC =.(1)如图(1),(5,0)A ,(0,2)B ,点C 在第三象限,请直接写出点C 的坐标;(2)如图(2),BC 与x 轴交于点D ,AC 与y 轴交于点E ,若点D 为BC 的中点,求证:ADB CDE ∠=∠;(3)如图(3),(,0)A a ,M 在AC 延长线上,过点(,)M m a −作MN x ⊥轴于点N ,探究线段BM ,AN ,OB 之间的关系,并证明你的结论.【答案】(1)(2,3)C −−; (2)证明见解析; (3)AN BM OB =+.证明见解析.【解析】【分析】(1)过C 作CR y ⊥轴于R ,证明(AAS)AOB BRC ≌,得到5,2BRAO CR OB ====,即可得到答案;(2)作BF 平分ABC ∠交AD 于F 点,证明(SAS)CED BFD ≌即可得到结论; (3)在ON 上取一点H ,使NH BO =,证明(SAS)ABM MHA ≌,根据全等三角形的性质即可得出结论.【小问1详解】解:过C 作CR y ⊥轴于R ,如图1所示:则90BRC ∠=°, (5,0)A ,(0,2)B ,5,2OA OB ∴==,90AOB ABC BRC ∠=∠=∠=° , 90ABO CBR ∴∠+∠=°, 90CBR BCR ∠+∠=°, ABO BCR ∴∠=∠,AB BC = ,(AAS)AOB BRC ∴ ≌, 5,2BR AO CR OB ∴====, 3OR BR OB ∴=−=, (2,3)C ∴−−;【小问2详解】解:证明:作BF 平分ABC ∠交AD 于F 点,,90AB BC CBA =∠=° ,45C BAC DBF ABF ∴∠=∠=∠=∠=°,90CBE ABO BAF ABO ∠+∠=∠+∠=° ,CBE BAF ∴∠=∠,在BCE 和ABF △中,CBE BAF BC BABCE ABF ∠=∠ = ∠=∠, (ASA)BCE ABF ∴ ≌,CE BF ∴=,点D 为BC 的中点,CD BD ∴=,在CED △和BFD △中,CD BD C DBF CE BF = ∠=∠ =, (SAS)CED BFD ∴ ≌,CDE ADB ∴∠=∠;【小问3详解】解:AN BM OB =+.证明:在ON 上取一点H ,使NH BO =,如图3所示:(,0)A a ,AO a ∴=,MN x ⊥ 轴于G ,(,)M m a −,ON m MN a ∴=−=,AO MN ∴=,90AOB HNM ∠=∠=° ,(SAS)ABO MHN ∴ ≌,,BAO NMH AB HM ∴∠=∠=,AHG MHN ∠=∠ ,90ANM AGM ∴∠=∠=°,90,ABC BC AB ∠=°= ,45BAC ∴∠=°,AGM ∴ 是等腰直角三角形,45BAM GMA ∴∠=∠=°,又,AB HMAM MA == , (SAS)ABM MHA ∴ ≌,BM HA ∴=,AN AH NH =+ ,AN BM OB ∴=+.【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定和性质,坐标与图形性质,直角三角形的性质,熟练掌握等腰直角三角形的判定与性质,正确做出辅助线,构造全等三角形是解题的关键.。
人教版八年级数学(上册)期中检测卷(附参考答案)
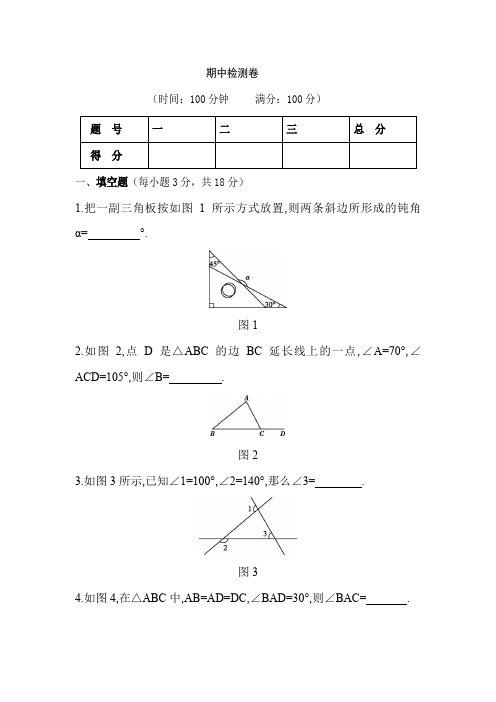
期中检测卷(时间:100分钟 满分:100分)一、填空题(每小题3分,共18分)1.把一副三角板按如图1所示方式放置,则两条斜边所形成的钝角α= °.图12.如图2,点D 是△ABC 的边BC 延长线上的一点,∠A=70°,∠ACD=105°,则∠B= .图23.如图3所示,已知∠1=100°,∠2=140°,那么∠3= .图34.如图4,在△ABC 中,AB=AD=DC ,∠BAD=30°,则∠BAC=.图45.如图5,在△ABC中,AB=5 cm,AC=3 cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为cm.图56.如图6,有两个长度相等的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面的夹角∠ABC与∠DFE的度数和是度.图6二、选择题(每小题3分,共24分)7.下面是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中是轴对称图形的有()图7A.1个B.2个C.3个D.4个8.下列长度的三条线段能组成三角形的是()A.1,2,3.5B.4,5,9C.20,15,8D.5,15,89.如图8所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是()图8A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短10.等腰三角形的一边为3,另一边为8,则这个三角形的周长为()A.11B.14C.19D.14或1911.点M(1,2)关于y轴对称的点的坐标为()A.(-1,2)B.(-1,-2)C.(1,-2)D.(2,-1)12.如图9所示,已知AB=AC=BD,那么()图9A.∠1=∠2B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1-∠2=180°13.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是()A.6B.7C.8D.914.如图10所示是跷跷板的示意图,支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角(即∠A’OA)是()图10A.80°B.60°C.40°D.20°三、解答题(满分58分)15.(6分)小强和小勇想利用课本上学过的知识来进行台球比赛:小强把白球放在如图11所示的位置,想通过击打白球撞击黑球,使黑球撞AC边后反弹进F洞.想想看,小强这样打,黑球能进F洞吗?请用画图的方法验证你的判断,并说出理由.图1116.(6分)如图12,在方格纸中画出△ABC关于直线MN对称的△A1B1C1.图1217.(6分)已知,如图13所示,AE是∠BAC的平分线,∠1=∠D.求证:∠1=∠2.图1318.(8分)如图14所示,直线CF垂直平分AD于点E,AB=BC=CD=AD,BA的延长线交CF于点F,连接AC.(1)图中有几对全等三角形,请把它们都写出来;(2)证明:△ABC是等边三角形.图1419.(7分)如图15所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:△BEC≌△CDA.图1520.(8分)如图16所示,在平面直角坐标系中,Rt△ABC的三个顶点坐标分别为A(-3,0),B(-3,-3),C(-1,-3).(1)求Rt△ABC的面积;(2)在图中作出△ABC关于x轴对称的△DEF,并写出D,E,F的坐标.图1621.(8分)如图17所示,在△ABC中,∠B=60°,∠C=20°,AD为△ABC 的高,AE为△ABC的角平分线.(1)求∠EAD的度数;(2)寻找∠DAE与∠B,∠C的关系并说明理由.图1722.(9分)如图18所示,八年级(6)班的小毛站在河边的A点处,观察河对面(正北方向)点B处的一棵小树,他很想知道自己距离这棵树有多远.可是身边没有测量工具,于是他运用本学期学到的数学知识,设计了如下方案:先向正东方向走了30步到达电线杆C,接着再向东走了30步到达D 处,然后向正南方向继续行走,当看到电线杆C、小树B与自己现在所处的位置E在同一条直线上时,小毛向正南方向恰好走了40步.(1)根据题意,画出测量的路线图;(2)如果小毛的一步大约0.5米,试计算出A,B两点的距离约为多少?并说明理由.图1823.(12分)八年级(1)班同学上数学活动课,利用角尺平分一个角(如图19所示).设计了如下方案:①∠AOB是一个任意角,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.②∠AOB是一个任意角,在边OA,OB上分别取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.(1)方案①、方案②是否可行?若可行,请证明;若不可行,请说明理由.(2)在方案①PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.图19参考答案1.1652.35°3.60°4.67.5°5.86.907.B8.C9.A10.C11.A12.D13.B14.C15.略16.解:如图所示:①过点A作AD⊥MN,延长AD使AD=A1D;②过点B作BE⊥MN,延长BE使B1E=BE;③过点C作CF⊥MN,延长CF使CF=C1F;④连接A1,B1,C1即可得到△ABC关于直线MN对称的△A1B1C1.17.证明:∵∠1=∠D,∴AE∥DC(同位角相等,两直线平行).∴∠EAC=∠2(两直线平行,内错角相等).∵AE是∠BAC的平分线,∴∠1=∠EAC,∴∠1=∠2.18.解:(1)图中有四对全等三角形,分别为△ABC≌△CDA,△AEF≌△DEC,△DEC≌△AEC,△AEF≌△AEC.(2)证明:∵CF垂直平分AD,∴AC=CD.又∵AB=BC=CD=DA,∴AB=BC=AC.∴△ABC为等边三角形.19.证明:∵BE⊥CE于E,AD⊥CE于D,∴∠BEC=∠CDA=90°.在Rt△BEC中,∠BCE+∠CBE=90°,在Rt△BCA中,∠BCE+∠ACD=90°.∴∠CBE=∠ACD.在△BEC和△CDA中,∠⎧∴△BEC≌△CDA(AAS). 20.解:(1)S△ABC=12AB×BC=12×3×2=3;(2)所画图形如下所示,其中△DEF即为所求,D,E,F的坐标分别为D(-3,0),E(-3,3),F(-1,3). 21.解:(1)∵在△ABC中,∠BAC=180°-∠C-∠B=180°-20°-60°=100°.又∵AE为△ABC的角平分线,∴∠EAB=∠BAC=50°.在Rt△ABD中,∠BAD=90°-∠B=90°-60°=30°,∴∠EAD=∠EAB-∠BAD=50°-30°=20°.(2)根据(1)可以得到:∠EAB=∠BAC=(180°-∠B-∠C),∠BAD=90°-∠B,则∠DAE=∠EAB-∠BAD=(180°-∠B-∠C)-(90°-∠B)=(∠B-∠C).22.解:(1)DE 的长就是所求.(2)在△ABC 和△DEC 中,∠⎧所以△ABC ≌△DEC (ASA ).所以AB=DE.又因为DE 为40步,且每一步大约0.5米,所以AB 的长约为40×0.5=20(米).23.解:(1)方案①不可行.缺少证明三角形全等的条件.方案②可行.证明:在△OPM 和△OPN 中,∴△OPM ≌△OPN (SSS ).∴∠AOP=∠BOP (全等三角形的对应角相等).∴OP 是∠AOB 的平分线.(2)解:当∠AOB 是直角时,此方案可行. ∵四边形的内角和为360°,又PM ⊥OA ,PN ⊥OB ,∴∠OMP=∠ONP=90°.又∠MPN=90°,∴∠AOB=90°.∵若PM⊥OA,PN⊥OB,且PM=PN,∴OP为∠AOB的平分线.(到角两边距离相等的点在这个角的角平分线上),当∠AOB不为直角时,此方案不可行.。
人教版八年级数学上册期中检测试卷(二)【测试范围:11.1-13.4】【含答案】

2024-2025学年八年级上学期(人教版)期中数学检测试卷(二)一、选择题(本题包括10小题,每小题3分,共30分。
每小题只有1个选项符合题意)1.下列交通标志中,属于轴对称图形的是( )A .B .C .D .2.以下列每组三条线段为边,能组成三角形的是( )A .1、1、2B .2、2、4C .4、4、9D .6、6、103.如图,∠1=100°,∠2=145°,那么∠3=( ).A .55°B .65°C .75°D .85°4.如图所示,将含角45°角的直角三角板与含60°角的直角三角板叠放在一起,若295Ð=°,则1Ð的度数为( )A .95°B .85°C .70°D .50°5.在平面直角坐标系中,点()2,3P -关于y 轴对称的点的坐标为( )A .()2,3--B .()2,3-C .()3,2--D .()3,2-6.佩佩在“黄娥古镇”研学时学习扎染技术,得到了一个内角和为1080°的正多边形图案,这个正多边形的每个外角为( )A .36°B .40°C .45°D .60°7.将一个含30°角的三角尺和直尺如图放置,若150Ð=°,则2Ð的度数是( )A .30°B .40°C .50°D .60°8.如图,在△ABC 中,AB =AC ,D 是BC 的中点,AC 的垂直平分线交AC ,AD ,AB 于点E ,O ,F ,则图中全等三角形的对数是( )A .1对B .2对C .3对D .4对9.如图,在ABC V 中,AB AC =,130BAC Ð=°,DA AC ^,则ADB =∠( )A .100°B .115°C .130°D .145°10.如图,ACE DBF V V ≌,点A ,B ,C ,D 在同一直线上,3AB =,2BC =,则BD 的长为( )A .3B .4C .5D .6二、填空题(本题包括8小题,每空3分,共24分)11.一木工师傅现有两根木条,木条的长分别为40 cm 和30 cm ,他要选择第三根木条,将它们钉成一个三角形木架.设第三根木条长为x cm ,则x 的取值范围是 .12.如图,直线a b P ,直线l a ^,1120Ð=°,则2Ð= °.13.如图,已知AC BD ^于点P ,AP CP =,请增加一个条件,使ABP V ≌(CDP V 不能添加辅助线),你增加的条件是 .14.如图,在ABC V 中,AD AE 、分别是边BC 上的中线与高,2AE =,ABC V 的面积是6,则BD 的长是 .15.平板电脑是我们日常生活中经常使用的电子产品,它的很多保护壳还兼具支架功能,有一种如图所示,平板电脑放在上面就可以很方便地使用了,这是利用了三角形的 .16.如图,已知PA ⊥ON 于A ,PB ⊥OM 于B ,且PA=PB ,∠MON=50°,∠OPC=30°,则∠PCA= .17.如图,在等腰三角形ABC 中,AD 是底边BC 上的高线,CE AB ^于点E ,交AD 于点F .若45BAC Ð=°,8AF =,则BD 的长为 .18.如图,已知ABC V 中,20 cm AB AC ==,16 cm BC =,点D 是AB 的中点,点P 在线段BC 上以2 cm/s 的速度由B 点向C 点运动,同时点Q 在线段CA 上由A 点向C 点运动.当BPD △与CQP V 全等时,点Q 的速度为 .三、解答题(本题包括8小题,共66分)19.如图,在ABC V 和AED △中,AB AE =,BAE CAD Ð=Ð,AC AD =.求证:ABC AED ≌△△.20.如图,在直角坐标系中,ABC V 的三个顶点的坐标分别为()()()151240A B C -,,,,,.(1)请在图中画出ABC V 关于y 轴对称的A B C ¢¢¢V ,并写出A ¢点的坐标;(2)求ABC V 的面积;(3)在y 轴上画出点P ,使PA PC +的值最小,保留作图痕迹.21.如图,在等边三角形ABC 中,AD ⊥BC 于点D ,以AD 为一边向右作等边三角形ADE ,DE 与AC 交于点F.(1)试判断DF 与EF 的数量关系,并给出证明;(2)若CF 的长为2 cm ,试求等边三角形ABC 的边长.22.如图,点D 在ABC V 的边AB 上,DF 经过边AC 的中点E ,且EF DE =.求证CF AB ∥.23.如图,在等腰Rt ABC V 中,90ACB Ð=°,D 为BC 的中点,DE AB ^,垂足为E ,过点B 作BF AC P 交DE 的延长线于点F ,连接CF .(1)求证:AD CF ^;(2)连接AF ,试判断ACF V 的形状,并说明理由.24.如图,把ABC V 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,(1)写出图中一对全等的三角形,并写出它们的所有对应角;(2)设AED Ð的度数为x ,ADE Ð的度数为y ,那么1Ð,2Ð的度数分别是多少?(用含有x 或y 的代数式表示)(3)A Ð与12Ð+Ð之间有一种数量关系始终保持不变,请找出这个规律(写过程).25.综合与实践:数学模型可以用来解决一类问题,是数学应用基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在ABC V 和AEF △中,,AB AC AE AF ==,30BAC EAF Ð=Ð=°,连接,BE CF ,延长BE 交CF 于点D .则BE 与CF 的数量关系: ,BDC Ð= °;(2)类比探究:如图2,在ABC V 和AEF △中,,,120AB AC AE AF BAC EAF ==Ð=Ð=°,连接,BE CF ,延长,BE FC 交于点D .请猜想BE 与CF 的数量关系及BDC Ð的度数,并说明理由.【分析】本题主要考查了轴对称图形,根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形可得答案.【详解】解:A.是轴对称图形,故此选项符合题意;B.不是轴对称图形,故此选项不符合题意;C. 不是轴对称图形,故此选项不符合题意;D. 不是轴对称图形,故此选项不符合题意;故选:A.2.D【分析】本题主要考查了三角形的三边关系.根据三角形的三边关系,逐项判断即可求解.【详解】解:A、112+=,不能组成三角形,故本选项不符合题意;B、224+=,不能组成三角形,故本选项不符合题意;+<,不能组成三角形,故本选项不符合题意;C、449+>,能组成三角形,故本选项符合题意;D、6610故选:D.3.B【分析】两条直线相交,邻角互补,求出邻角的度数,再根据三角形内角和定理求解即可.【详解】∵∠1=100°,∠2=145°,∴∠4=180°-∠1=180°-100°=80°,∠5=180°-∠2=180°-145°=35°,∵∠3=180°-∠4-∠5,∴∠3=180°-80°-35°=65°.故选B.【点睛】本题考查相交直线和三角形内角和定理.根据已知角求补角是解题的关键.【分析】本题考查了三角板中角度的求解,三角形外角性质,先根据三角形外角性质求出3Ð的度数,再利用平角定义求解即可.【详解】解:如图,295Ð=°Q ,445Ð=°,324954550\Ð=Ð-Ð=°-°=°,1180603180605070\Ð=°-°-Ð=°--°=°,故选:C .5.A【分析】本题考查了关于y 轴对称的点的坐标.根据“关于y 轴对称的点,横坐标互为相反数,纵坐标相同”解答即可.【详解】解:点()2,3P -关于y 轴对称的点的坐标为()2,3--.故选:A .6.C【分析】本题考查了正多边形的外角,设这个正多边形的边数为n ,先根据内角和求出正多边形的边数,再用外角和360°除以边数即可求解,掌握正多边形的性质是解题的关键.【详解】解:设这个正多边形的边数为n ,则()21801080n -´°=°,∴8n =,∴这个正多边形的每个外角为360845°¸=°,故选:C .7.B【分析】本题考查了对顶角的性质,三角形内角和定理.根据对顶角相等和三角形的内角和定理,即可求解.【详解】解:如图所示,由题意得3150Ð=Ð=°,590Ð=°,24ÐÐ=,∴24180903905040Ð=Ð=°-°-Ð=°-°=°,故选:B .8.D【详解】解:∵AB =AC , D 为BC 中点,∴CD =BD ,∠BDO =∠CDO =90°,∴在△ABD 和△ACD 中,AB AC AD AD BD CD =ìï=íï=î,∴△ABD ≌△ACD ;∵EF 垂直平分AC ,∴OA =OC ,AE=CE ,在△AOE 和△COE 中,OA OC OE OE AE CE =ìï=íï=î,∴△AOE ≌△COE ;在△BOD 和△COD 中,BD CD BDO CDO OD OD =ìïÐ=Ðíï=î,∴△BOD ≌△COD ;在△AOC 和△AOB 中,AC AB OA OA OC OB =ìï=íï=î,∴△AOC ≌△AOB ;所以共有4对全等三角形,故选:D .9.B【分析】本题主要考查了等腰三角形的性质,三角形外角的性质.根据等腰三角形的性质,可得180252BAC C °-ÐÐ==°,再由三角形外角的性质,即可求解.【详解】解:∵AB AC =,130BAC Ð=°,∴180252BAC C °-ÐÐ==°,∵DA AC ^,∴90CAD Ð=°,∴115ADB C CAD =Ð+Ð=°∠.故选:B10.C【分析】本题考查线段的和差,全等三角形的性质.由3AB =,2BC =可得5AC =,进而有全等三角形的性质得到5BD AC ==,即可解答.【详解】解:∵3AB =,2BC =,∴5AC AB BC =+=,∵ACE DBF V V ≌,∴5BD AC ==.故选:C11.10cm<x <70cm【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,即可求第三边长的范围.【详解】三角形的第三边长大于两边之差,小于两边之和,∴x 的取值范围为:10cm 70cm x <<.故答案为:10cm<x <70cm【点睛】本题考查的是三角形三边关系,熟知三角形两边之和大于第三边,两边差小于第三边是解答此题的关键.12.30【分析】本题考查平行线的性质,三角形的外角性质,根据两直线平行,同位角相等,求出3Ð的度数,根据三角形的外角的性质,得到3902Ð=°+Ð,即可求出2Ð的度数.【详解】解:∵a b P ,∴31120Ð=Ð=°,∵l a ^,∴3290Ð=Ð+°,∴230Ð=°;故答案为:30.13.BP DP =或AB CD =或A C Ð=Ð或B D Ð=Ð【分析】要使△ABP ≌△CDP ,已知AC ⊥BD 于点P ,AP=CP ,即一角一边,则我们增加直角边、斜边或另一组角,利用SAS 、HL 、AAS 判定其全等.【详解】解:∵AC ⊥BD 于点P ,AP=CP ,又AB=CD ,∴△ABP ≌△CDP .∴增加的条件是BP=DP 或AB=CD 或∠A=∠C 或∠B=∠D .故填BP=DP 或AB=CD 或∠A=∠C 或∠B=∠D .【点睛】本题考查了直角三角形全等的判定;这是一道考查三角形全等的识别方法的开放性题目,答案可有多种,注意要选择简单的,明显的添加.14.3【分析】本题主要考查了三角形面积计算,三角形中线的性质,先根据三角形中线平分三角形面积得到132ABD ABC S S ==△△,再根据三角形面积计算公式求解即可.【详解】解:∵ABC V 的面积是6,AD 是ABC V 的中线,∴132ABD ABC S S ==△△,∵AE 是ABC V 的高,且2AE =,∴132AE BD ×=,∴3BD =,故答案为:3.15.稳定性【分析】本题考查了三角形的稳定性的应用,根据三角形具有稳定性即可求解,熟练掌握基础知识是解题的关键.【详解】解:这是利用了三角形的稳定性,故答案为:稳定性.16.55°【分析】由“HL ”可证Rt △OAP ≌Rt △OBP ,可得∠AOP =∠BOP =12∠AOB =25°,由外角可求解.【详解】解:∵PA ⊥ON 于A ,PB ⊥OM 于B ,∴∠PAO =∠PBO =90°,∵PA =PB ,OP =OP ,∴Rt △OAP ≌Rt △OBP (HL ),∴∠AOP =∠BOP =12∠AOB =25°,∴∠PCA =∠AOP +∠OPC =55°,故答案为:55°.【点睛】本题考查了全等三角形的判定和性质,证明Rt △OAP ≌Rt △OBP 是本题的关键.17.4【分析】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、三角形的内角和定理,熟练掌握等腰三角形的判定与性质是解答的关键.先根据等腰三角形的性质得到AD BC ^,12BD CD BC ==,再根据等腰三角形的判定和三角形的内角和定理证得AE CE =,EAF ECB Ð=Ð,然后证明()ASA AEF CEB ≌△△得到8BC AF ==即可求解.【详解】解:∵在等腰三角形ABC 中,AD 是底边BC 上的高线,∴AD BC ^,12BD CD BC ==,∴90BAD B Ð+Ð=°,∵CE AB ^,∴90AEC BEC Ð=Ð=°,又45BAC Ð=°,∴9045ACE BAC EAC Ð=°-Ð=°=Ð,90ECB B ÐÐ+=°∴AE CE =,EAF ECB Ð=Ð,∴()ASA AEF CEB ≌△△,∴BC AF =,∵8AF =,∴11422BD BC AF ===,故答案为:4.18.5cm/s 2或14cm/s 3【分析】本题考查了全等三角形性质,分两种情况讨论求解即可,掌握全等三角形的性质是解题的关键.【详解】解:∵20cm AB AC ==,点D 为AB 的中点,∴B C Ð=Ð, ()12010cm 2BD =´=,设点P ,Q 的运动时间为s t ,则2cm BP t =,()162cm PC t =-,①当BD PC =时,16210t -=,解得:3t =,则26cm BP CQ t ===,()20614cm AQ AC CQ =-=-=,故点Q 的运动速度为()14143cm/s 3¸=,②当BP PC =时,10cm CQ BD ==,则10cm AQ AC CQ =-=,∵16cm BC =,∴8cm BP PC ==,∴824t =¸=,故点Q 的运动速度为()5104cm/s 2¸=,∴点Q 的速度为()14cm/s 3或()5cm/s 2,故答案为:()14cm/s 3或()5cm/s 2.19.见解析【分析】本题考查了全等三角形的判定和性质,熟练掌握三角形全等的判定定理是解题关键.利用“SAS ”证明ABC AED ≌△△,即可解决问题.【详解】证明:Q BAE CAD Ð=Ð,\BAE EAC CAD EAC Ð+Ð=Ð+Ð,即BAC EAD Ð=Ð,在ABC V 和AED △中,AB AE BAC EAD AC AD =ìïÐ=Ðíï=î,\()SAS ABC AED V V ≌.20.(1)图见详解,()15A ¢-,(2)10.5(3)图见详解【分析】本题考查了作图−轴对称变换、轴对称−最短路线问题,解决本题的关键是准确画图.(1)根据ABC V 关于y 轴对称的A B C ¢¢¢V ,先画出点A B C ¢¢¢,,,再依次连接,并求出A ¢点的坐标即可;(2)根据网格,以AB 为底,即可求ABC V 的面积;(3)连接A C ¢即可在y 轴上画出点P ,使PA PC +的值最小.【详解】(1)解:如图所示,A B C ¢¢¢V 即为所求;()15A ¢-,;(2)解:17310.52ABC S =´´=△;(3)解:如图,点P为所作.21.(1)DF =EF (2) 8cm【分析】(1)根据等边三角形的每一个角都是60°可得∠BAC=∠DAE=60°,再根据等腰三角形三线合一的性质求出BD=DC,∠BAD=∠DAC=30°,然后得到∠DAC=∠CAE,然后根据等腰三角形三线合一的性质即可得证;(2)求出∠CDF=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答即可.【详解】:(1)DF=EF.理由: ∵△ABC 和△ADE 均是等边三角形,∴∠BAC=∠DAE=60°,∵AD ⊥BC,∴BD=DC,∠BAD=∠DAC=12×60°=30°,∴∠CAE=60°-30°=30°,即∠DAC=∠CAE,∴AC 垂直平分DE,∴DF=EF;(2)在RT △DFC 中, ∵∠FCD=60°, ∠CFD=90°,∴∠CDF=90°-60°=30°,∵CF=2cm,∴DC=4cm,∴BC=2DC=2×4=8cm,即等边三角形ABC 的边长为8cm.(1)DF =EF.证明:∵△ABC 是等边三角形,∴∠BAC =60°,又∵AD ⊥BC ,∴∠DAC =30°.∵△ADE 是等边三角形,∴∠DAE =60°,∴∠DAF =∠EAF =30°,由三线合一知DF =EF (2)BC =2CD =2×2CF =8 cm【点睛】本题考查了等边三角形的性质,等腰三角形三线合一的性质,直角三角形角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键.22.见详解【分析】本题主要考查全等三角形的判定和性质以及平行线的判定,根据题意得AE EC =,即可证明AED CEF V V ≌,有DAE FCE =∠∠成立,根据平行线的判定即可证明结论.【详解】证明:∵点E 为边AC 的中点,∴AE EC =,∵EF DE =,AED CEF Ð=Ð,∴()SAS AED CEF △≌△,∴DAE FCE =∠∠,∴CF AB ∥.23.(1)证明过程见详解(2)ACF V 是等腰三角形,理由见详解【分析】本题主要考查等腰三角形的判定和性质,全等三角形的判定和性质,垂直平分线的判定和性质,(1)根据题意可证BDF V 是等腰直角三角形,则BD BF =,()ACD CBF SAS V V ≌,CAD BCF Ð=Ð,再根据90BCF ACF Ð+Ð=°,90CAD ACF Ð+Ð=°,即可求证;(2)根据(1)的证明可得AD CF =,AB 是DF 的垂直平分线,所以AD AF =,由此即可求解.【详解】(1)证明:∵ABC V 是等腰直角三角形,∴AC BC =,45CAB CBA Ð=Ð=°,∵DE AB ^,即90BED Ð=°,∴45BDE Ð=°,∵BF AC ∥,90ACB Ð=°,∴90CBF Ð=°,∴45BFD BDF Ð=°=Ð,∴BDF V 是等腰直角三角形,则BD BF =,∵点D 为BC 的中点,∴CD DB BF ==,在ACD CBF V V ,中,90AC CB ACD CBF CD BF =ìïÐ=Ð=°íï=î,∴()SAS ACD CBF V V ≌,∴CAD BCF Ð=Ð,∵90BCF ACF ACB Ð+Ð=Ð=°,∴90CAD ACF Ð+Ð=°,∴=90AGC а,∴AD CF ^;(2)解:ACF △是等腰三角形,理由如下,如图所示,连接AF ,由(1)可知,ACD CBF V V ≌,BDF V 是等腰直角三角形,45CBA Ð=°,∴AD CF =,BE 平分DF ,点E 是DF 的中点,即AB 是DF 的垂直平分线,∴AD AF =,∴AF CF =,∴ACF △是等腰三角形.24.(1)ADE A DE ¢△≌△,EAD Ð与EA D ¢Ð、AED Ð与A ED ¢∠、ADE Ð与A DE ¢Ð是对应角(2)11802x Ð=-,21802yÐ=-(3)()1122A Ð=Ð+Ð,证明见解析【分析】此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.(1)根据翻折方法可得ADE A DE ¢△≌△,进而可得出对应角;(2)根据翻折方法可得2,2AEA x ADA y ¢¢Ð=Ð=,再根据平角定义可得11802x Ð=-,21802y Ð=-;(3)首先由11802x Ð=-,21802y Ð=-,可得19012x =°-Ð,19022y =°-Ð,再根据三角形内角和定理可得180A x y Ð=°--,再利用等量代换可得()1122A Ð=Ð+Ð.【详解】(1)解:∵把ABC V 纸片沿DE 折叠,∴ADE A DE ¢△≌△,其中EAD Ð与EA D ¢Ð、AED Ð与A ED ¢∠、ADE Ð与A DE ¢Ð是对应角;(2)∵AED x Ð=,ADE yÐ=∴2,2AEA x ADA y¢¢Ð=Ð=∴11802x Ð=-,21802y Ð=-;(3)()1122A Ð=Ð+Ð.理由:∵11802x Ð=-,21802yÐ=-∴19012x =°-Ð,19022y =°-Ð,∴()11118018090190212222A A x y æöæöÐ=Ð=°--=°-°-Ð-°-Ð=Ð+Ðç÷ç¢÷èøèø.25.(1),30BE CF =°(2),60BE CF BDC =Ð=°,理由见解析【分析】本题考查全等三角形的判定,等腰三角形和等腰直角三角形的性质,熟练掌握全等三角形的判定是解题的关键.(1)根据等腰三角形的性质,利用SAS 证明ABE ACF V V ≌即可得出结论;(2)根据等腰三角形的性质,利用SAS 证明BAE CAF V V ≌即可得出结论.【详解】(1)解:如图1所示,设AC 与BD 交于点O ,∵30BAC EAF Ð=Ð=°,∴BAC CAE EAF CAE Ð+Ð=Ð+Ð,即BAE CAF Ð=Ð,在ABE V 和ACF △中,AB AC BAE CAF AE AF =ìïÐ=Ðíï=î,∴()SAS ABE ACF V V ≌,∴,BE CF ABE ACF =Ð=Ð,∵A OE A B E B A C Ð=Ð+Ð,AOE ACF BDC Ð=Ð+Ð,∴30BDC BAC Ð=Ð=°.故答案为:BE CF =,30;(2),60BE CF BDC =Ð=°,理由如下:∵120BAC EAF Ð=Ð=°,∴BAC EAC EAF EAC Ð-Ð=Ð-Ð,即BAE CAF Ð=Ð,在ABE V 和ACF △中,AB AC BAE CAF AE AF =ìïÐ=Ðíï=î,∴()SAS ABE ACF V V ≌,∴,BE CF AEB AFC =Ð=Ð,∵120,EAF AE AF Ð=°=,∴30AEF AFE Ð=Ð=°,∴()303060BDC BEF EFD AEB AFC Ð=Ð-Ð=Ð+°-Ð-°=°.。
人教版八年级上册数学期中达标测试卷(二)(word版含答案)
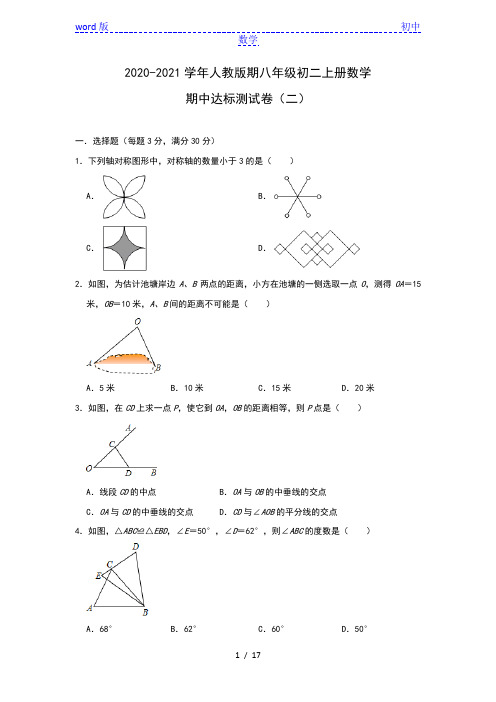
2020-2021学年人教版期八年级初二上册数学期中达标测试卷(二)一.选择题(每题3分,满分30分)1.下列轴对称图形中,对称轴的数量小于3的是()A.B.C.D.2.如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.5米B.10米C.15米D.20米3.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A.线段CD的中点 B.OA与OB的中垂线的交点C.OA与CD的中垂线的交点 D.CD与∠AOB的平分线的交点4.如图,△ABC≌△EBD,∠E=50°,∠D=62°,则∠ABC的度数是()A.68°B.62°C.60°D.50°5.三条公路将A 、B 、C 三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )A .三条高线的交点B .三条中线的交点C .三条角平分线的交点D .三边垂直平分线的交点6.在Rt △ABC 中,∠ACB =60°,DE 是斜边AC 的中垂线,分别交AB 、AC 于D 、E 两点.若BD =2,则AD 的长是( )A .3B .4C .5D .4.57.下列运算正确的是( ) A .a 3•a 4=a 12 B .(a 3)2=a 5 C .(3a 2)3=27a 6D .a 6÷a 3=a 28.要使(﹣6x 3)(x 2+ax ﹣3)的展开式中不含x 4项,则a =( ) A .1B .0C .﹣1D .9.以下运算正确的是( ) A .(ab 3)2=ab 6 B .(﹣3xy )3=﹣9x 3y 3 C .x 3•x 4=x 12D .(3x )2=9x 210.如图,四边形ABCD 中,AD ∥BC ,点E 是CD 的中点,连接AE 、BE ,∠EAD =∠EAB .给出下列五个结论:①BE ⊥AE ;②BE 平分∠ABC ;③AD +BC =AB ;④AB ⊥BC ;⑤△ABC =S 四边形ABCD ; 其中正确的有( )A.2 B.3 C.4 D.5二.填空题(每小题3分,满分15分)11.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则b a的值是.12.腰长为10,腰上的高为8的等腰三角形的底边长为.13.如图,已知△ABC是等边三角形,D是AC边上的任意一点,点B,C,E在同一条直线上,且CE=CD,则∠E=度.14.已知:如图,AD是△ABC的边BC上的中线,AB=6.中线AD=4.则AC的取值范围是.15.如图,在△ABC中,AB=AC,BC=6,△ABC面积为12,AD⊥BC于点D,直线EF垂直平分AB交AB于点E,交BC于点F,P为直线EF上一动点,则△PBD的周长的最小值为.三.解答题16.计算:9(x﹣2)2﹣(3x+2)(3x﹣2)17.将纸片△ABC沿DE折叠使点A落在点A'处【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是;【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为.18.△ABC三顶点A(﹣5,0)、B(﹣2,4)、C(﹣1,﹣2),△A'B'C'与△ABC关于y 轴对称.(1)直接写出A'、B'、C'的坐标;(2)画出△A'B'C';(3)求△ABC的面积.19.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A 运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)(1)运动秒时,AE=DC;(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).20.如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:(1)AM⊥DM;(2)M为BC的中点.21.如图1,△ABD,△ACE都是等边三角形,(1)求证:△ABE≌△ADC;(2)若∠ACD=15°,求∠AEB的度数;(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.22.如图,在四边形ABCD中,∠BAC=∠ACD=90度,AB=CD.(1)判断AD与BC之间有何关系,并说明理由;(2)若AB=5cm,BC=13cm,点P从B点出发,以2cm/s的速度沿BC﹣CD﹣DA运动至A 点停止,则从运动开始经过多少时间,AB=AP?23.观察猜想(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC 上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是,BE+BF=;探究证明(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;拓展延伸(3)如图③,在△ABC中,AB=AC,∠BAC=α,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=α,连接BF,则BE+BF的值是多少?请用含有n,α的式子直接写出结论.参考答案一.选择题1.解:A、有4条对称轴,故本选项不符合题意;B、有6条对称轴,故本选项不符合题意;C、有4条对称轴,故本选项不符合题意;D、有2条对称轴,故本选项符合题意.故选:D.2.解:连接AB,根据三角形的三边关系定理得:15﹣10<AB<15+10,即:5<AB<25,∴A、B间的距离在5和25之间,∴A、B间的距离不可能是5米;故选:A.3.解:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交于点P.故选:D.4.解:∵∠E=50°,∠D=62°,∴∠EBD=180°﹣50°﹣62°=68°,∵△ABC≌△EBD,∴∠ABC=∠EBD=68°,故选:A.5.解:在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,根据角平分线的性质,集贸市场应建在∠A、∠B、∠C的角平分线的交点处.6.解:∵∠ACB=60°,∠B=90°,∴∠A=30°,∵DE是斜边AC的中垂线,∴DA=DC,∴∠ACD=∠A=30°,∵BD=2,∴AD=4,故选:B.7.解:A.a3•a4=a7,故本选项不合题意;B.(a3)2=a6,故本选项不合题意;C.(3a2)3=27a6,正确,故选项C符合题意;D.a6÷a3=a3,故本选项不合题意.故选:C.8.解:原式=﹣6x5﹣6ax4+18x3,由展开式不含x4项,得到a=0,故选:B.9.解:A.(ab3)2=a2b6,故原运算错误;B.(﹣3xy)3=﹣27x3y3,故原运算错误;C.x3•x4=x7,故原运算错误;D.(3x)2=9x2,运算正确.故选:D.10.解:延长AE交BC延长线于M,∵AD∥BC,∴∠DAE=∠M,∵∠EAD=∠EAB,∴∠EAB=∠M,∴AB=BM,∵E为CD中点,∴DE=EC,∴△DAE∽△CME,∴==,∴AD=CM,AE=EM,∴AD+BC=AB,∵AB=BM,AE=EM,∴BE⊥AE;BE平分∠ABC;∴∠ABE=∠CBE,连接AC,∵AD≠BC,∴S△ABC ≠S△ADC,∴S△ABC=S四边形ABCD错误;∵AD≠BC,AE平分∠DAB,BE平分∠ABC,∴∠DAE=∠EAB,∠ABE=∠CBE,∴不能推出AB⊥BC,即①②③正确;④⑤错误;故选:B.二.填空题(共5小题,满分15分,每小题3分)11.解:∵点M(a,b)与点N(3,﹣1)关于x轴对称,∴a=3,b=1,故答案为:1.12.解:①:如图1:当AB=AC=10,CD=8时,则AD==6,∴BD=4,∴BC==4,∴此时底边长为4;②如图2:当AB=AC=10,CD=8时,则AD==6,∴BD=16,∴BC=8,∴此时底边长为8.故答案为:4或8.13.解:∵△ABC是等边三角形,∴∠ACB=60°,∵CE=CD,∴∠E=∠CDE,∵∠ACB=∠E+∠CDE,∴∠E==30°,故答案为30.14.解:延长AD至E,使DE=AD,连接CE.∵BD=CD,∠ADB=∠EDC,AD=DE,∴△ABD≌△ECD(SAS),∴CE=AB.在△ACE中,AE﹣EC<AC<AE+EC,∴8﹣6<AC<8+6,即2<AC<14,故答案为:2<AC<14.15.解:如图,连接PA.∵AB=AC,AD⊥BC,∴BD=DC=3,=•BC•AD=12,∵S△ABC∴AD=4,∵EF垂直平分AB,∴PB=PA,∴PB+PD=PA+PD,∵PA+PD≥AD,∴PA+PD≥4,∴PA+PD的最小值为4,∴△PBD的最小值为4+3=7,故答案为7.三.解答题(共8小题)16.解:原式=9(x2﹣4x+4)﹣(9x2﹣4)=9x2﹣36x+36﹣9x2+4=﹣36x+40.17.解:(1)如图①,∠1=2∠A.理由如下:由折叠知识可得:∠EA′D=∠A;∵∠1=∠A+∠EA′D,∴∠1=2∠A.(2)如图②,2∠A=∠1+∠2.理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,∠A+∠A′+∠A′DA+∠A′EA=360°,∴∠A′+∠A=∠1+∠2,由折叠知识可得:∠A=∠A′,∴2∠A=∠1+∠2.(3)如图③,∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,∴∠1=∠A+∠A′+∠2=2∠A+∠2,∴2∠A=∠1﹣∠2=56°,解得∠A=28°.故答案为:∠1=2∠A;28°.18.解:(1)A'(﹣5,0)、B'(﹣2,4)、C'(﹣1,﹣2);(2)如图所示,△A'B'C'即为所求.(3)△ABC的面积为4×6﹣×1×6﹣×2×4﹣×3×4=24﹣3﹣4﹣6=11.19.解:(1)由题可得,BD=CE=2t,∴CD=12﹣2t,AE=8﹣2t,∴当AE=DC,时,8﹣2t=(12﹣2t),解得t=3,故答案为:3;(2)当△ABD≌△DCE成立时,AB=CD=8,∴12﹣2t=8,解得t=2,∴运动2秒时,△ABD≌△DCE能成立;(3)当△ABD≌△DCE时,∠CDE=∠BAD,又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,∴∠ADE=∠B,又∵∠BAC=α,AB=AC,∴∠ADE=∠B=(180°﹣α)=90°﹣α.故答案为:90°﹣α.20.解:(1)∵AB∥CD,∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM;(2)作NM⊥AD交AD于N,∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM,即M为BC的中点.21.(1)证明:∵△ABD,△ACE都是等边三角形∴AB=AD,AE=AC∠DAB=∠EAC=60°∴∠DAC=∠BAE,在△ABE和△ADC中∴,∴△ABE≌△ADC;(2)由(1)知△ABE≌△ADC∴∠AEB=∠ACD∵∠ACD=15°∴∠AEB=15°;(3)同上可证:△ABE≌△ADC∴∠AEB=∠ACD又∵∠ACD=60°∴∠AEB=60°∵∠EAC=60°∴∠AEB=∠EAC∴AC∥BE.22.解:(1)AD=BC,AD∥BC理由如下:∵∠BAC=∠ACD=90°,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,∴AD=BC,AD∥BC;(2)当点P在BC上时,在Rt△ABC中,∠BAC=90°,AC=12,设经过ts时,AB=AP.过A作AE⊥BC,垂足为E,则AE=,在Rt△ABE中,BE=,∴BP=2BE=时,△ABP为等腰三角形,t==(秒);当点P在AD上时,P点运动距离为13+5+8=26(cm),t==13(秒).综上所述,当t=秒或13秒时,△ABP为等腰三角形.23.解:(1)如图①中,∵∠EAF=∠BAC=90°,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△BAF≌△CAE,∴∠ABF=∠C,BF=CE,∵AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠FBE=∠ABF+∠ABC=90°,BC=BE+EC=BE+BF,故答案为:BF⊥BE,BC.(2)如图②中,作DH∥AC交BC于H.∵DH∥AC,∴∠BDH=∠A=90°,△DBH是等腰直角三角形,由(1)可知,BF⊥BE,BF+BE=BH,∵AB=AC=3,AD=1,∴BD=DH=2,∴BH=2,∴BF+BE=BH=2;(3)如图③中,作DH∥AC交BC的延长线于H,作DM⊥BC于M.∵AC∥DH,∴∠ACB=∠H,∠BDH=∠BAC=α,∵AB=AC,∴∠ABC=∠ACB∴∠DBH=∠H,∴DB=DH,∵∠EDF=∠BDH=α,∴∠BDF=∠HDE,∵DF=DE,DB=DH,∴△BDF≌△HDE,∴BF=EH,∴BF+BE=EH+BE=BH,∵DB=DH,DM⊥BH,∴BM=MH,∠BDM=∠HDM,∴BM=MH=BD•sin.∴BF+BE=BH=2n•sin.。
人教版八年级上册数学 期中精选试卷同步检测(Word版 含答案)
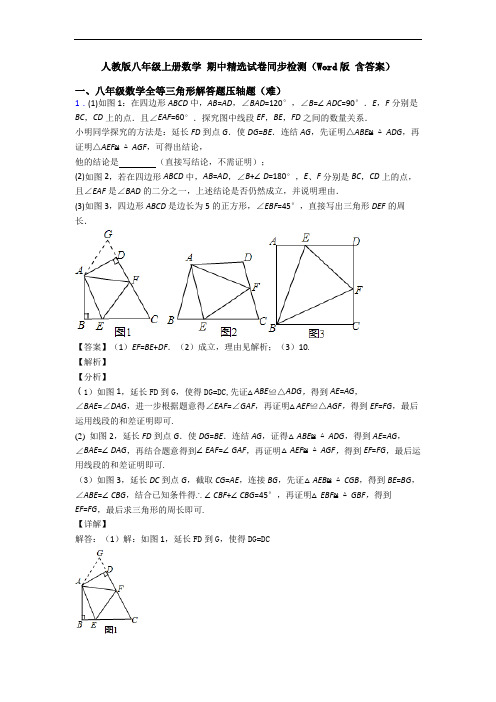
人教版八年级上册数学 期中精选试卷同步检测(Word版 含答案) 一、八年级数学全等三角形解答题压轴题(难) 1.(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是
BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论, 他的结论是 (直接写结论,不需证明); (2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,
且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由. (3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周
长.
【答案】(1)EF=BE+DF.(2)成立,理由见解析;(3)10. 【解析】 【分析】 (1)如图1,延长FD到G,使得DG=DC,先证△ABE≌△ADG,得到AE=AG,
∠BAE=∠DAG,进一步根据题意得∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可. (2) 如图2,延长FD到点G.使DG=BE.连结AG,证得△ABE≌△ADG,得到AE=AG,
∠BAE=∠DAG,再结合题意得到∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可. (3)如图3,延长DC到点G,截取CG=AE,连接BG,先证△AEB≌△CGB,得到BE=BG,∠ABE=∠CBG,结合已知条件得∴∠CBF+∠CBG=45°,再证明△EBF≌△GBF,得到EF=FG,最后求三角形的周长即可.
【详解】 解答:(1)解:如图1,延长FD到G,使得DG=DC 在△ABE和△ADG中, ∵DCDGBADGABAD
人教版八年级数学上册期中综合检测试卷(含解析答案)

期中综合检测(第十一至第十三章)(120分钟120分)一、选择题(每小题3分,共30分)1.下列交通指示标识中,不是轴对称图形的是( )【解析】选C.A.是轴对称图形,故本选项不符合题意;B.是轴对称图形,故本选项不符合题意;C.不是轴对称图形,故本选项符合题意;D.是轴对称图形,故本选项不符合题意.【变式训练】以下微信图标不是轴对称图形的是( )【解析】选D.观察各图形,其中选项A,B,C中的微信图标,均能沿着图形中间竖直的一条直线折叠后两侧部分能够完全重合,故它们都是轴对称图形,且只有一条对称轴;选项D中的微信图标“S”部分无法找到一条直线沿其折叠后使两侧部分重合,它不是轴对称图形.2.如图,下列条件中,不能证明△ABD≌△ACD的是( )A.BD=DC,AB=ACB.∠ADB=∠ADCC.∠B=∠C,∠BAD=∠CADD.∠B=∠C,BD=DC【解析】选B.根据“SSS”利用选项A可以证明△ABD≌△ACD;根据“AAS”利用选项C可以证明△ABD≌△ACD;连接BC,利用选项D的条件可知∠DBC=∠DCB,∴∠DBC+∠ABD=∠DCB+∠ACD,即∠ABC=∠ACB,∴AB=AC,∵AB=AC,BD=DC,AD=AD,∴△ABD≌△ACD.3.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )A.50°B.30°C.20°D.15°【解析】选C.由题意得∠4=∠2=40°,由外角定理得∠4=∠1+∠3,∴∠3=∠4-∠1=40°-20°=20°.4.(2016·毕节中考)到三角形三个顶点的距离都相等的点是这个三角形的( )A.三条高的交点B.三条角平分线的交点C.三条中线的交点D.三条边的垂直平分线的交点【解析】选D.依题意,知这个点到三角形每边的两个端点的距离相等,所以,它是三条边的垂直平分线的交点.5.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC= ( )A. B.2C.3D.+2【解题指南】根据直角三角形中,30°角所对的边是斜边的一半,可求得BD 的长,再根据角平分线上的点到角两边的距离相等可得到DE=DC,从而可求出BC的长.【解析】选C.∵DE⊥AB于点E,DE=1,∠B=30°,∴BD=2,∵AD是角平分线,DE⊥AB于点E,∠C=90°,∴DE=DC=1,∴BC=BD+DC=3.6. (2016·邵阳中考)如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )A.AC>BCB.AC=BCC.∠A>∠ABCD.∠A=∠ABC【解题指南】解答本题的两个关键点:(1)根据等腰三角形的两个底角相等,由AD=BD得到∠A=∠ABD,所以∠ABC>∠A,则对C,D选项进行判断.(2)根据大边对大角可对A,B选项进行判断.【解析】选A.∵AD=BD,∴∠A=∠ABD,∴∠ABC>∠A,所以C选项和D选项错误;根据在三角形中大角对大边,∴AC>BC,所以A选项正确;B选项错误.7.已知点M(1-2m,m-1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )【解题指南】根据关于x轴对称的点的坐标特点列出关于m的不等式组,解不等式组求得m的解集.【解析】选A.由题意知点M在第四象限,∴∴m<0.5.8.如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )A.50°B.60°C.70°D.80°【解析】选B.∵在三角形ABC中,∠ACB=90°,∠B=50°,∴∠A=180°-∠ACB-∠B=40°,由旋转的性质可知:BC=B′C,∴∠B=∠BB′C=50°,∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,∴∠ACB′=10°, ∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°.9.如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=65°,则∠BDF等于( )A.65°B.50°C.60°D.57.5°【解析】选B.∵△DEF是△DEA沿直线DE翻折变换而来,∴AD=DF,∵D是AB边的中点, ∴AD=BD,∴BD=DF,∴∠B=∠BFD,∵∠B=65°,∴∠BDF=180°-∠B-∠BFD=180°-65°-65°=50°.10.(2016·枣庄中考)如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP 的长不可能是( )A.3B.4C.5.5D.10【解题指南】解答本题的三个关键问题:(1)根据翻折后重合的图形全等,可知AC′=AC,求出AC′长.(2)根据三角形面积公式,可求得△ABC′边AC′上的高.(3)根据垂线段最短,即可做出正确选择.【解析】选A.如图:过B作BN⊥AC于点N,BM⊥AD于点M,∵将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,∴∠C′AB=∠CAB,∴BN=BM,∵△ABC的面积等于6,边AC=3,∴×AC×BN=6,∴BN=4,∴BM=4,即点B到AD的最短距离是4,∴BP的长不小于4,即只有选项A的3不可能为BP的长.二、填空题(每小题3分,共24分)11.一个三角形的两边长分别是2和3,若它的第三边长为奇数,则这个三角形的周长为________.【解题指南】首先设第三边长为x,根据三角形的三边关系可得3-2<x<3+2,然后再确定x的值,进而可得周长.【解析】设第三边长为x,∵两边长分别是2和3,∴3-2<x<3+2,即1<x<5,∵第三边长为奇数,∴x=3,∴这个三角形的周长为2+3+3=8.答案:812.如图所示,△ABC中,∠A=90°,BD是角平分线,DE⊥BC,垂足是E,AC=10cm,CD=6cm,则DE的长为________cm.【解析】∵∠A=90°,BD是角平分线,DE⊥BC,∴DE=AD(角的平分线上的点到角的两边的距离相等),∵AD=AC-CD=10-6=4(cm),∴DE=4cm.答案:413.(2015·巴中中考)若a,b,c为三角形的三边,且a,b满足+(b-2)2=0,则第三边c的取值范围是________.【解题指南】由非负数的非负性,解得a,b的值.根据三角形的三边关系可确定第三边c的取值范围.【解析】∵a,b满足+(b-2)2=0,∴a=3(舍去负值),b=2.∵a,b,c为三角形的三边,∴a-b<c<a+b.即1<c<5.答案:1<c<514.如图,AC与BD相交于点O,且AB=CD,请添加一个条件____________,使得△ABO≌△CDO.【解析】∵AC与BD相交于点O,∴∠AOB=∠COD,又∵AB=CD,所以添加∠A=∠C或∠B=∠D,利用AAS可判定△ABO≌△CDO,也可添加AB∥CD,利用平行线的性质得出∠A=∠C或∠B=∠D,再判定△ABO≌△CDO.答案:∠A=∠C(或AB∥CD或∠B=∠D)15.如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了__________米.【解析】由题意得360°÷36°=10,则他第一次回到出发地A点时,一共走了12×10=120(米).答案:12016.(2017·贵阳模拟)如图,a∥b,∠1+∠2=75°,则∠3+∠4=________.【解题指南】本题考查了平行线的性质和三角形的内角和定理;掌握这些性质是解题的关键.先根据平行线的性质得到角相等,再根据三角形内角得到∠1、∠2、∠3、∠4的和是180°,然后把∠1+∠2看作整体代入求解.【解析】如图,∵a∥b,∴∠3=∠5.根据三角形内角和定理,得∠1+∠2+∠5+∠4=180°,∴∠1+∠2+∠3+∠4=180°.∵∠1+∠2=75°,∴∠3+∠4=180°-75°=105°.答案:105°17.(2016·荆门中考)两个全等的三角尺重叠摆放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转到△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=______cm.【解析】∵△ACB≌△DCE,∠ACB=∠DCE=90°,∠B=30°.∴AC=DC,∠D=∠CAB=60°,∴△ADC是等边三角形,∴∠DCA=60°,∴∠ACF=30°,∴∠AFC=90°.∵AB=8cm,∴AC=4cm,∴CF=2cm.答案:218.在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠.若EF的长度为a,则△DEF的周长为________(用含a的式子表示).【解题指南】本题考查了直角三角形的折叠问题,解题的关键是轴对称的性质判断△DEF的形状,先由第1次折叠得到∠AED=60°,再由第2次折叠得到∠DFE=60°,进而判断△DEF是等边三角形.【解析】由折叠可知,△DEF是等边三角形,因为EF= a,所以△DEF的周长为3a.答案:3a三、解答题(共66分)19.(8分)如图,在△ABC中.(1)画出BC边上的高AD和中线AE.(2)若∠B=30°,∠ACB=130°,求∠BAD和∠CAD的度数.【解析】(1)如图所示:(2)∵AD 是△ABC 的高,∴∠ADB=90°. ∵∠ACB=130°, ∴∠ACD=180°-130°=50°. 又∵三角形的内角和等于 180°, ∴∠BAD=180°-30°-90°=60°, ∠CAD=180°-50°-90°=40°. 20. (6 分)如图,△ABC,△CDE 均是等腰直角三角形,∠ACB= ∠DCE=90°,点 E 在 AB 上,求证:△CDA≌△CEB.【 解 题 指 南 】 解 答 本 题 的 三 个 关 键 :(1) 由 等 腰 三 角 形 的 性 质 可 知 BC=AC,EC=CD,∠ACB=∠DCE. (2)利用等式的基本性质,可得∠ECB=∠DCA. (3)利用 SAS 证两个三角形全等. 【证明】∵∠ACB=∠DCE=90°, ∴∠ACB-∠ACE=∠DCE-∠ACE 即∠ECB=∠DCA, 又∵△ABC,△CDE 均是等腰直角三角形,∴BC=AC,EC=CD,∴△CDA≌△CEB(SAS). 【变式训练】 已知,如图所示, AB=AC,BD=CD,DE⊥AB 于点 E,DF⊥AC 于点 F,求证:DE=DF.【证明】连接 AD, ∵AB=AC,BD=CD,AD=AD, ∴△ABD≌△ACD, ∴∠BAD=∠CAD, ∴AD 是∠EAF 的平分线, 又∵DE⊥AB,DF⊥AC, ∴DE=DF. 【一题多解】证△ABD≌△ACD 得∠ACD=∠ABD, ∴∠DCF=∠DBE. 又∵∠DFC=∠DEB=90°,DC=DB. ∴△DFC≌△DEB,∴DE=DF. 21.(6 分 ) 如 图 , 在 直 角 坐 标 系 中 ,A,B,C,D 各 点 的 坐 标 分 别 为 (-7,7),(-7,1), (-3,1),(-1,4). (1)在给出的图形中,画出四边形 ABCD 关于 y 轴对称的四边形 A1B1C1D1(不写 作法). (2)写出点 A1 和 C1 的坐标. (3)求四边形 A1B1C1D1 的面积.【解析】(1)画图如图.(2)由(1)可得 A1(7,7),C1(3,1).(3)=6×6-[(6×3÷2+2×3÷2)]=24.【方法技巧】作轴对称图形三步骤1.先确定图形的关键点.2.利用轴对称性质作出关键点的对称点.3.按原图形中的方式顺次连接对称点.22.(8 分)如图,在六边形 ABCDEF 中,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,求∠F 的度数.【解析】如图,连接 AC, ∵CD∥AF,∴∠DCA+∠CAF=180°, ∵AB⊥BC,∴∠BCA+∠BAC=90°,∴ ∠ BCD+∠ BAF=∠BCA+ ∠ DCA+∠ BAC+∠ CAF=270° ,∴∠BAF=270 ° -∠ BCD=270°-124°=146°, ∵六边形的内角和=(6-2)×180°=720°. ∴∠F=720°-2×146°-90°-124°-80°=134°.【方法技巧】本题是考查多边形的内角和、平行线的性质、直角三角形两 锐角互余的性质的综合题,运用整体思想把∠BCD 与∠BAF,∠CAF 与∠DCA, ∠BCA 与∠BAC 分别看成一个整体是解题的关键. 23. (8 分)(2017·河南实中质检)如图,已知△ABC 是等边三角形,过点 B 作 BD⊥BC,过 A 作 AD⊥BD,垂足为 D,若△ABC 的周长为 12,求 AD 的长.【解析】∵BD⊥BC,在等边三角形 ABC 中,∠ABC=60°, ∴∠ABD=90°-60°=30°. 又∵AD⊥BD,即△ABD 是直角三角形,∴∠ABD 所对的直角边 AD 是斜边 AB 的一半. ∵等边三角形 ABC 的周长为 12, ∴其边长 AB=4.∴AD= AB=2.24.(8 分)如图,在△ABC 中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB. (2)AF=2CD. 【解题指南】(1)由垂直得到互为余角的角,从而有∠EAF=∠ECB,利用角边 角定理即可证得△AEF≌△CEB. (2)利用全等三角形的对应边相等,以及等腰三角形的三线合一的性质即 可得出 AF=BC,BC=2CD,即可得出 AF=2CD. 【证明】(1)∵AD⊥BC,∴∠B+∠BAD=90°. ∵CE⊥AB,∴∠B+∠BCE=90°. ∴∠EAF=∠ECB. 在△AEF 和△CEB 中,∴△AEF≌△CEB. (2)∵△AEF≌△CEB,∴AF=BC. ∵AB=AC,AD⊥BC,∴CD=BD,BC=2CD.∴AF=2CD. 25. (10 分)(2016·荆门中考)如图,在 Rt△ABC 中,∠ACB=90°,点 D,E 分 别在 AB,AC 上,CE=BC,连接 CD,将线段 CD 绕点 C 按顺时针方向旋转 90°后 得 CF,连接 EF.(1)补充完成图形. (2)若 EF∥CD,求证:∠BDC=90°. 【解析】(1)所补图形如图所示(2)∵∠BCA=∠DCF=90°, ∴∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ECF. 又 CB=CE,CD=CF, ∴△BCD≌△ECF.∴∠B=∠CEF. ∵CD∥EF,∴∠DCA=∠CEF.∴∠B=∠DCA. ∵∠BCD+∠DCA=90°,∴∠BCD+∠B=90°.∴∠BDC=90°. 26.(12 分)(2016·北京中考)在等边△ABC 中,(1)如图 1,P,Q 是 BC 边上两点,AP=AQ,∠BAP=20°,求∠AQB 的度数. (2)点 P,Q 是 BC 边上的两个动点(不与点 B,C 重合),点 P 在点 Q 的左侧,且 AP=AQ,点 Q 关于直线 AC 的对称点为 M,连接 AM,PM. ①依题意将图 2 补全; ②小茹通过观察、实验,提出猜想:在点 P,Q 运动的过程中,始终有 PA=PM.小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种 想法: 想法 1:要证 PA=PM,只需证△APM 是等边三角形. 想法 2:在 BA 上取一点 N,使得 BN=BP,要证 PA=PM,只需证△ANP≌△PCM. 想法 3:将线段 BP 绕点 B 顺时针旋转 60°,得到线段 BK,要证 PA=PM,只需 证 PA=CK,PM=CK. …… 请你参考上面的想法,帮助小茹证明 PA=PM(一种方法即可).【解析】(1)∵AP=AQ,∴∠APQ=∠AQP, ∴∠APB=∠AQC, 又∵∠B=∠C=60°,∴∠BAP=∠CAQ=20°, ∴∠PAQ=∠BAC-∠BAP-∠CAQ=60°-20°-20°=20°, ∴∠BAQ=∠BAP+∠PAQ=40°, 又∵∠B=60°,∴∠AQB=180°-∠B-∠BAQ=80°. (2)①如图;②利用想法 1 证明:首先应该证明△APB≌△AQC, 得到∠BAP=∠CAQ,然后由∠CAQ=∠CAM 得到∠CAM=∠BAP, 进而得到∠PAM=60°; 接着利用∠MCA=∠QCA=∠PBA=60°,AB=AC,∠CAM=∠BAP, 得到△APB≌△AMC,从而得到 AP=AM,所以△APM 是等边三角形,进而得到 PA=PM. (利用其他想法证明也可以) 想法 2:辅助线如下:在 AB 上取一点 N,使 BN=BP,连接 PN,CM. ∵△ABC 是等边三角形,∴∠B=∠ACB=60°,BA=BC=AC, ∴△BPN 是等边三角形,AN=PC,BP=NP,∠BNP=60°, ∴∠ANP=120°. 由轴对称知 CM=CQ,∠ACM=∠ACB=60°, ∴∠PCM=120°. 由(1)知,∠APB=∠AQC,∴△ABP≌△ACQ(AAS), ∴BP=QC,∴NP=CM, ∴△ANP≌△PCM(SAS),∴AP=PM.想法 3(后面学习):辅助线如下:将线段 BP 绕点 B 顺时针旋转 60°,得到线 段 BK,连接 PK,KC,CM. 则△BPK 是等边三角形,∴∠ABP=∠CBK=60°, 又 AB=CB,BP=BK, ∴△ABP≌△CBK(SAS),∴PA=KC①; 由轴对称知∠ACB=∠ACM,CQ=CM, 又∵∠ACB=60°,∴∠MCP=120°,∵△BPK 是等边三角形, ∴∠PBK=∠BKP=60°,BP=PK. ∵在△BKC 中,∠CBK+∠BKC+∠BCK=180°, ∴∠PKC+∠PCK=60°,∴∠PKC+∠PCK+∠PCM=180°,∴PK∥CM. 由想法 2 知,BP=QC,∴PK=CM,∴四边形 PKCM 是平行四边形, ∴KC=PM②,由①②知 PA=PM.。
人教版八年级数学上册期中综合检测试卷(含解析答案)
期中综合检测 (第十一至第十三章) (120分钟 120分) 一、选择题(每小题3分,共30分) 1.下列交通指示标识中,不是轴对称图形的是( )
【解析】选C.A.是轴对称图形,故本选项不符合题意; B.是轴对称图形,故本选项不符合题意; C.不是轴对称图形,故本选项符合题意; D.是轴对称图形,故本选项不符合题意. 【变式训练】 以下微信图标不是轴对称图形的是( )
【解析】选D.观察各图形,其中选项A,B,C中的微信图标,均能沿着图形中间竖直的一条直线折叠后两侧部分能够完全重合,故它们都是轴对称图形,且只有一条对称轴;选项D中的微信图标“S”部分无法找到一条直线沿其折叠后使两侧部分重合,它不是轴对称图形. 2.如图,下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC 【解析】选B.根据“SSS”利用选项A可以证明△ABD≌△ACD;根据“AAS”利用选项C可以证明△ABD≌△ACD;连接BC,利用选项D的条件可知∠DBC=∠DCB,∴∠DBC+∠ABD=∠DCB+∠ACD,即∠ABC=∠ACB,∴AB=AC,∵AB=AC,BD=DC,AD=AD,∴△ABD≌△ACD. 3.如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则 ∠3等于( )
A.50° B.30° C.20° D.15° 【解析】选C.由题意得∠4=∠2=40°,由外角定理得∠4=∠1+∠3,∴∠3=∠4-∠1=40°-20°=20°.
4.(2016·毕节中考)到三角形三个顶点的距离都相等的点是这个三角形的 ( ) A.三条高的交点 B.三条角平分线的交点 C.三条中线的交点 D.三条边的垂直平分线的交点 【解析】选D.依题意,知这个点到三角形每边的两个端点的距离相等,所以,它是三条边的垂直平分线的交点. 5.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC= ( ) A. B.2 C.3 D.+2 【解题指南】根据直角三角形中,30°角所对的边是斜边的一半,可求得BD的长,再根据角平分线上的点到角两边的距离相等可得到DE=DC,从而可求出BC的长. 【解析】选C.∵DE⊥AB于点E,DE=1,∠B=30°, ∴BD=2,∵AD是角平分线,DE⊥AB于点E,∠C=90°, ∴DE=DC=1,∴BC=BD+DC=3. 6. (2016·邵阳中考)如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
人教版数学八年级上册 期中精选试卷综合测试卷(word含答案)
人教版数学八年级上册期中精选试卷综合测试卷(word含答案)一、八年级数学全等三角形解答题压轴题(难)1.在平面直角坐标系中,直线AB分别交x轴,y轴于A(a,0),B(0,b),且满足a2+b2+4a﹣8b+20=0.(1)求a,b的值;(2)点P在直线AB的右侧;且∠APB=45°,①若点P在x轴上(图1),则点P的坐标为;②若△ABP为直角三角形,求P点的坐标.【答案】(1)a=﹣2,b=4;(2)①(4,0);②P点坐标为(4,2),(2,﹣2).【解析】【分析】(1)利用非负数的性质解决问题即可.(2)①根据等腰直角三角形的性质即可解决问题.②分两种情形:如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.分别利用全等三角形的性质解决问题即可.【详解】(1)∵a2+4a+4+b2﹣8b+16=0∴(a+2)2+(b﹣4)2=0∴a=﹣2,b=4.(2)①如图1中,∵∠APB=45°,∠POB=90°,∴OP=OB=4,∴P(4,0).故答案为(4,0).②∵a=﹣2,b=4∴OA=2OB=4又∵△ABP为直角三角形,∠APB=45°∴只有两种情况,∠ABP=90°或∠BAP=90°①如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.∴∠PCB=∠BOA=90°,又∵∠APB=45°,∴∠BAP=∠APB=45°,∴BA=BP,又∵∠ABO+∠OBP=∠OBP+∠BPC=90°,∴∠ABO=∠BPC,∴△ABO≌△BPC(AAS),∴PC=OB=4,BC=OA=2,∴OC=OB﹣BC=4﹣2=2,∴P(4,2).②如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.∴∠PDA=∠AOB=90°,又∵∠APB=45°,∴∠ABP=∠APB=45°,∴AP=AB,又∵∠BAD+∠DAP=90°,∠DPA+∠DAP=90°,∴∠BAD=∠DPA,∴△BAO≌△APP(AAS),∴PD=OA=2,AD=OB=4,∴OD=AD﹣0A=4﹣2=2,∴P(2,﹣2).综上述,P点坐标为(4,2),(2,﹣2).【点睛】本题属于三角形综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题.2.如图,在ABC ∆中,903, 7C AC BC ∠=︒==,,点D 是BC 边上的动点,连接AD ,以AD 为斜边在AD 的下方作等腰直角三角形ADE .(1)填空:ABC ∆的面积等于 ;(2)连接CE ,求证:CE 是ACB ∠的平分线;(3)点O 在BC 边上,且1CO =, 当D 从点O 出发运动至点B 停止时,求点E 相应的运动路程.【答案】(1)212;(2)证明见解析;(3)32【解析】【分析】 (1)根据直角三角形的面积计算公式直接计算可得; (2)如图所示作出辅助线,证明△AEM ≌△DEN (AAS ),得到ME=NE ,即可利用角平分线的判定证明;(3)由(2)可知点E 在∠ACB 的平分线上,当点D 向点B 运动时,点E 的路径为一条直线,再根据全等三角形的性质得出CN=1()2AC CD +,根据CD 的长度计算出CE 的长度即可.【详解】解:(1)903, 7C AC BC ∠=︒==, ∴112137222ABC S AC BC =⨯=⨯⨯=, 故答案为:212 (2)连接CE ,过点E 作EM ⊥AC 于点M ,作EN ⊥BC 于点N ,∴∠EMA=∠END=90°,又∵∠ACB=90°,∴∠MEN=90°,∴∠MED+∠DEN=90°,∵△ADE是等腰直角三角形∴∠AED=90°,AE=DE∴∠AEM+∠MED=90°,∴∠AEM=∠DEN∴在△AEM与△DEN中,∠EMA=∠END=90°,∠AEM=∠DEN,AE=DE∴△AEM≌△DEN(AAS)∴ME=NE∴点E在∠ACB的平分线上,即CE是ACB∠的平分线(3)由(2)可知,点E在∠ACB的平分线上,∴当点D向点B运动时,点E的路径为一条直线,∵△AEM≌△DEN∴AM=DN,即AC-CM=CN-CD在Rt△CME与Rt△CNE中,CE=CE,ME=NE,∴Rt△CME≌Rt△CNE(HL)∴CM=CN∴CN=1() 2AC CD+,又∵∠MCE=∠NCE=45°,∠CME=90°,∴22) CN AC CD=+,当AC=3,CD=CO=1时,CE=2(31)22 2+=当AC=3,CD=CB=7时,CE=2(37)2 2+=∴点E的运动路程为:522232=【点睛】本题考查了全等三角形的综合证明题,涉及角平分线的判定,几何中动点问题,全等三角形的性质与判定,解题的关键是综合运用上述知识点.3.如图1,Rt△ABC中,∠A=90°,AB=AC,点D是BC边的中点连接AD,则易证AD=BD=CD,即AD=12BC;如图2,若将题中AB=AC这个条件删去,此时AD仍然等于12BC.理由如下:延长AD到H,使得AH=2AD,连接CH,先证得△ABD≌△CHD,此时若能证得△ABC≌△CHA,即可证得AH=BC,此时AD=12BC,由此可见倍长过中点的线段是我们三角形证明中常用的方法.(1)请你先证明△ABC≌△CHA,并用一句话总结题中的结论;(2)现将图1中△ABC折叠(如图3),点A与点D重合,折痕为EF,此时不难看出△BDE和△CDF都是等腰直角三角形.BE=DE,CF=DF.由勾股定理可知DE2+DF2=EF2,因此BE2+CF2=EF2,若图2中△ABC也进行这样的折叠(如图4),此时线段BE、CF、EF还有这样的关系式吗?若有,请证明;若没有,请举反例.(3)在(2)的条件下,将图3中的△DEF绕着点D旋转(如图5),射线DE、DF分别交AB、AC于点E、F,此时(2)中结论还成立吗?请说明理由.图4中的△DEF也这样旋转(如图6),直接写出上面的关系式是否成立.【答案】(1)详见解析;(2)有这样分关系式;(3)EF2=BE2+CF2.【解析】【分析】(1)想办法证明AB∥CH,推出∠BAC=∠ACH,再利用SAS证明△ABC≌△CHA即可.(2)有这样分关系式.如图4中,延长ED到H山顶DH=DE.证明△EDB≌△HD (SAS),推出∠B=∠HCD,BE=CH,∠FCH=90°,利用勾股定理,线段的垂直平分线的性质即可解决问题.(3)图5,图6中,上面的关系式仍然成立.【详解】(1)证明:如图2中,∵BD=DC,∠ADB=∠HDC,AD=HD,∴△ADB≌△HDC(SAS),∴∠B=∠HCD,AB=CH,∴AB∥CH,∴∠BAC+∠ACH=180°,∵∠BAC=90°,∴∠ACH=∠BAC=90°,∵AC=CA,∴△BAC≌△HCA(SAS),∴AH=BC,∴AD=DH=BD=DC,∴AD=12 BC.结论:直角三角形斜边上的中线等于斜边的一半.(2)解:有这样分关系式.理由:如图4中,延长ED到H山顶DH=DE.∵ED=DH,∠EDB=∠HDC,DB=DC,∴△EDB≌△HDC(SAS),∴∠B=∠HCD,BE=CH,∵∠B +∠ACB =90°,∴∠ACB +∠HCD =90°,∴∠FCH =90°,∴FH 2=CF 2+CH 2,∵DF ⊥EH ,ED =DH ,∴EF =FH ,∴EF 2=BE 2+CF 2.(3)图5,图6中,上面的关系式仍然成立.结论:EF 2=BE 2+CF 2.证明方法类似(2).【点睛】本题属于几何变换综合题,考查了旋转变换,翻折变换,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.4.如图,在ABC ∆中,5BC = ,高AD 、BE 相交于点O , 23BD CD =,且AE BE = . (1)求线段 AO 的长;(2)动点 P 从点 O 出发,沿线段 OA 以每秒 1 个单位长度的速度向终点 A 运动,动点 Q 从 点 B 出发沿射线BC 以每秒 4 个单位长度的速度运动,,P Q 两点同时出发,当点 P 到达 A 点时,,P Q 两点同时停止运动.设点 P 的运动时间为 t 秒,POQ ∆的面积为 S ,请用含t 的式子表示 S ,并直接写出相应的 t 的取值范围;(3)在(2)的条件下,点 F 是直线AC 上的一点且 CF BO =.是否存在t 值,使以点 ,,B O P 为顶 点的三角形与以点 ,,F C Q 为顶点的三角形全等?若存在,请直接写出符合条件的 t 值; 若不存在,请说明理由.【答案】(1)5;(2)①当点Q 在线段BD 上时,24QD t =-,t 的取值范围是102t <<;②当点Q 在射线DC 上时,42QD t =-,,t 的取值范围是152t <≤;(3)存在,1t =或53. 【解析】【分析】(1)只要证明△AOE ≌△BCE 即可解决问题;(2)分两种情形讨论求解即可①当点Q 在线段BD 上时,QD=2-4t ,②当点Q 在射线DC 上时,DQ=4t-2时;(3)分两种情形求解即可①如图2中,当OP=CQ 时,BOP ≌△FCQ .②如图3中,当OP=CQ 时,△BOP ≌△FCQ ;【详解】解:(1)∵AD 是高,∴90ADC ∠=∵BE 是高,∴90AEB BEC ∠=∠=∴90EAO ACD ∠+∠=,90EBC ECB ∠+∠=,∴EAO EBC ∠=∠在AOE ∆和BCE ∆中,EAO EBC AE BEAEO BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AOE ∆≌BCE ∆∴5AO BC ==;(2)∵23BD CD =,=5BC ∴=2BD ,=3CD ,根据题意,OP t =,4BQ t =,①当点Q 在线段BD 上时,24QD t =-,∴21(24)22S t t t t =-=-+,t 的取值范围是102t <<. ②当点Q 在射线DC 上时,42QD t =-, ∴21(42)22S t t t t =-=-,t 的取值范围是152t <≤ (3)存在.①如图2中,当OP=CQ 时,∵OB=CF ,∠POB=∠FCQ ,∴△BOP ≌△FCQ .∴CQ=OP ,∴5-4t ═t ,解得t=1,②如图3中,当OP=CQ 时,∵OB=CF ,∠POB=∠FCQ ,∴△BOP ≌△FCQ .∴CQ=OP ,∴4t-5=t ,解得t=53. 综上所述,t=1或53s 时,△BOP 与△FCQ 全等. 【点睛】 本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5.在等边ABC 中,点D 是边BC 上一点.作射线AD ,点B 关于射线AD 的对称点为点E .连接CE 并延长,交射线AD 于点F .(1)如图,连接AE ,①AE 与AC 的数量关系是__________;②设BAF α∠=,用α表示BCF ∠的大小;(2)如图,用等式表示线段AF ,CF ,EF 之间的数量关系,并证明.【答案】(1) ①AB=AE ;②∠BCF=α;(2) AF-EF=CF ,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由轴对称性,得:AE=AB,∠BAF=∠EAF=α,由ABC是等边三角形,得AB=AC,∠BAC=∠ACB=60°,再根据等腰三角形的性质和三角形内角和等于180°,即可求解;(2)作∠FCG=60°交AD于点G,连接BF,易证∆FCG是等边三角形,得GF=FC,再证∆ACG≅∆BCF(SAS),从而得AG=BF,进而可得到结论.【详解】(1)①∵点B关于射线AD的对称点为点E,∴AB和AE关于射线AD的对称,∴AB=AE.故答案是:AB=AE;②∵点B关于射线AD的对称点为点E,∴AE=AB,∠BAF=∠EAF=α,∵ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,∴∠EAC=60°-2α,AE=AC,∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦,∴∠BCF=∠ACE-∠ACB=60α+-60°=α.(2)AF-EF=CF,理由如下:作∠FCG=60°交AD于点G,连接BF,∵∠BAF=∠BCF=α,∠ADB=∠CDF,∴∠ABC=∠AFC=60°,∴∆FCG是等边三角形,∴GF=FC,∵ABC是等边三角形,∴BC=AC,∠ACB=60°,∴∠ACG=∠BCF=α.在∆ACG和∆BCF中,∵CA CBACG BCF CG CF=⎧⎪∠=∠⎨⎪=⎩,∴∆ACG≅∆BCF(SAS),∴AG=BF,∵点B关于射线AD的对称点为点E,∴AG=BF=EF,∵AF-AG=GF,∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.二、八年级数学轴对称解答题压轴题(难)6.(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC 中,若AB=12,AC=8,求BC边上的中线AD的取值范围.同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是.解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.【答案】(1)2<AD<10;(2)见解析(3)为直角三角形,理由见解析.【解析】【分析】(1)根据△ADC≌△EDB,得到BE=AC=8,再根据三角形的构成三角形得到AE的取值,再根据D为AE中点得到AD的取值;(2)延长AF到H,使AF=HF,故△ADF≌△HCF,AH=2AF,由AB⊥AC,AD⊥AE,得到∠BAE+∠CAD=180°,又∠ACH+∠CAH+∠AHC=180°,根据∠D=∠FCH,∠DAF=∠CHF,得到∠ACH+∠CAD=180°,故∠BAE= ACH,再根据AB=AC,AD=AE即可利用SAS证明△BAE≌△ACH,故BE=AH,故可证明BE=2AF.(3)延长FD到点G,使DG=FD,连结GA,GE,证明△DBF≌△DAG,故得到FD=GD,BF=AG,由DE⊥DF,得到EF=EG,再求出∠EAG=90°,利用勾股定理即可求解.【详解】(1)∵△ADC≌△EDB,∴BE=AC=8,∵AB=12,∴12-8<AE<12+8,即4<AE<20,∵D为AE中点∴2<AD<10;(2)延长AF到H,使AF=HF,由题意得△ADF≌△HCF,故AH=2AF,∵AB⊥AC,AD⊥AE,∴∠BAE+∠CAD=180°,又∠ACH+∠CAH+∠AHC=180°,∵∠D=∠FCH,∠DAF=∠CHF,∴∠ACH+∠CAD=180°,故∠BAE= ACH,又AB=AC,AD=AE∴△BAE≌△ACH(SAS),故BE=AH,又AH=2AF∴BE= 2AF.(3)以线段AE、BF、EF为边的三角形为直角三角形,理由如下:延长FD到点G,使DG=FD,连结GA,GE,由题意得△DBF≌△ADG,∴FD=GD,BF=AG,∵DE⊥DF,∴DE垂直平分GF,∴EF=EG,∵∠C=90°,∴∠B+∠CAB=90°,又∠B=∠DAG,∴∠DAG +∠CAB=90°∴∠EAG=90°,故EG 2=AE 2+AG 2,∵EF=EG, BF=AG∴EF 2=AE 2+BF 2,则以线段AE 、BF 、EF 为边的三角形为直角三角形.【点睛】此题主要考查全等三角形的判定与性质,解题的关键是根据题意作出辅助线,根据垂直平分线与勾股定理进行求解.7.在等边ABC ∆中,点O 在BC 边上,点D 在AC 的延长线上且OA OD =.(1)如图1,若点O 为BC 中点,求COD ∠的度数;(2)如图2,若点O 为BC 上任意一点,求证AD AB BO =+.(3)如图3,若点O 为BC 上任意一点,点D 关于直线BC 的对称点为点P ,连接,AP OP ,请判断AOP ∆的形状,并说明理由.【答案】(1)30;(2)见解析;(3)AOP ∆是等边三角形,理由见解析.【解析】【分析】(1)根据三角形的等边三角形的性质可求1302CAO BAC ∠=∠=︒且,90AO BC AOC ⊥∠=︒,根据OA OD =,等腰三角形的性质得到D ∠的度数,再通过内角和定理求AOD ∠,即可求出COD ∠的度数.(2)过O 作//OE AB ,OE 交AD 于E 先证明COE ∆为等边三角形,再根据等边三角形的性质求120AEO ∠=︒,120DCO ∠=︒,再证明()AOE DOC AAS ∆≅∆,得到CD EA =,再通过证明得到EA BO =、AB AC =通过,又因为AD AC CD =+,通过等量代换即可得到答案.(3)通过作辅助线先证明()ODF OPF SAS ∆≅∆,得到OP OD =,又因为OA OD =,得到AO=OP ,证得AOP ∆为等腰三角形,如解析辅助线,由(2)可知得AOE DOC ∆≅∆得到AOE DOC ∠=∠,通过角的关系得到60AOP COE ∠=∠=°,即可证得AOP ∆是等边三角形.【详解】(1)∵ABC ∆为等边三角形∴60BAC ∠=︒∵O 为BC 中点∴1302CAO BAC ∠=∠=︒ 且,90AO BC AOC ⊥∠=︒∵OA OD =∴AOD ∆中,30D CAO ∠=∠=︒∴180120AOD D CAO ∠=︒-∠-∠=︒∴30COD AOD AOC ∠=∠-∠=︒(2)过O 作//OE AB ,OE 交AD 于E∵//OE AB∴60EOC ABC ∠=∠=︒60CEO CAB ∠=∠=︒∴COE ∆为等边三角形∴OE OC CE ==180120AEO CEO ∠=︒-∠=︒180120DCO ACB ∠=︒-∠=︒又∵OA OD =∴EAO CDO ∠=∠在AOE ∆和COD ∆中AOE DOCEAO CDOOA OD∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AOE DOC AAS∆≅∆∴CD EA=∵EA AC CE=-BO BC CO=-∴EA BO=∴BO CD=,∵AB AC=,AD AC CD=+∴AD AB BO=+(3)AOP∆为等边三角形证明过程如下:连接,PC PD,延长OC交PD于F ∵P D、关于OC对称∴,90 PF DF PFO DFO=∠=∠=︒在ODF∆与OPF∆中,PF DFPFO DFOOF OF=⎧⎪∠=∠⎨⎪=⎩∴()ODF OPF SAS∆≅∆∴OP OD=,POC DOC∠=∠∵OA OD=∴AO=OP∴AOP∆为等腰三角形过O作//OE AB,OE交AD于E 由(2)得AOE DOC∆≅∆∴AOE DOC ∠=∠又∵POC DOC ∠=∠∴AOE POF ∠=∠∴AOE POE POF POE ∠+∠=∠+∠即AOP COE ∠=∠∵AB ∥OE ,∠B=60°∴60COE B ∠=∠=︒∴60AOP COE ∠=∠=°∴AOP ∆是等边三角形.【点睛】本题是考查了全等三角形和等边三角形的综合性问题,灵活应用全等三角形的性质得到边与角的关系,以及等边三角形的性质是解答此题的关键.8.如图1,在ABC 中,90BAC ∠=︒,点D 为AC 边上一点,连接BD ,点E 为BD 上一点,连接CE ,CED ABD ∠=∠,过点A 作AG CE ⊥,垂足为G ,交ED 于点F .(1)求证:2FAD ABD ∠=∠;(2)如图2,若AC CE =,点D 为AC 的中点,求证:AB AC =;(3)在(2)的条件下,如图3,若3EF =,求线段DF 的长.【答案】(1)详见解析;(2)详见解析;(3)6【解析】【分析】(1)根据直角三角形的性质可得90ADB ABD ∠=︒-∠,90EFG CED ∠=︒-∠,然后根据三角形的内角和和已知条件即可推出结论;(2)根据直角三角形的性质和已知条件可得AFD ADF ∠=∠,进而可得AF AD =,BFA CDE ∠=∠,然后即可根据AAS 证明ABF ∆≌CED ∆,可得AB CE =,进一步即可证得结论;(3)连接AE ,过点A 作AH AE ⊥交BD 延长线于点H ,连接CH ,如图4.先根据已知条件、三角形的内角和定理和三角形的外角性质推出45AED ∠=︒,进而可得AE AH =,然后即可根据SAS 证明△ABE ≌△ACH ,进一步即可推出90CHD ∠=︒,过点A 作AK ED ⊥于K ,易证△AKD ≌△CHD ,可得DK DH =,然后即可根据等腰三角形的性质推得DF =2EF ,问题即得解决.【详解】(1)证明:如图1,90BAC ∠=︒,90ADB ABD ∴∠=︒-∠,AG CE ⊥,90FGE ∴∠=︒,90EFG AFD CED ∴∠=∠=︒-∠,180FAD AFD ADF CED ABD ∴∠=︒-∠-∠=∠+∠,CED ABD ∠=∠,2FAD ABD ∴∠=∠;(2)证明:如图2,90AFD CED ∠=︒-∠,90ADB ABD ∠=︒-∠,CED ABD ∠=∠,AFD ADF ∴∠=∠,AF AD ∴=,BFA CDE ∠=∠,∵点D 为AC 的中点,∴AD=CD ,AF CD ∴=,ABF ∴∆≌CED ∆(AAS ),AB CE ∴=,CE AC =,AB AC ∴=;(3)解:连接AE ,过点A 作AH AE ⊥交BD 延长线于点H ,连接CH ,如图4. 90BAC ∠=︒,BAE CAH ∴∠=∠,设ABD CED α∠=∠=,则2,902FAD ACG αα∠=∠=︒-,CA CE =,45AEC EAC α∴∠=∠=︒+,45AED ∴∠=︒,45AHE ∴∠=︒,AE AH ∴=,AB AC =,∴△ABE ≌△ACH (SAS ),135AEB AHC ∴∠=∠=︒,90CHD ∴∠=︒,过点A 作AK ED ⊥于K ,90AKD CHD ∴∠=∠=︒,AD CD =,ADK CDH ∠=∠,∴△AKD ≌△CHD (AAS ),DK DH ∴=,∵,,AK DF AF AD AE AH ⊥==,,FK DK EK HK ∴==,3DH EF ∴==,6DF ∴=.【点睛】本题考查了直角三角形的性质、三角形的内角和定理、三角形的外角性质、等腰直角三角形的判定和性质、全等三角形的判定和性质以及等腰三角形的性质等知识,考查的知识点多、综合性强、难度较大,正确添加辅助线、构造等腰直角三角形和全等三角形的模型、灵活应用上述知识是解题的关键.=. 9.已知ABC为等边三角形,E为射线AC上一点,D为射线CB上一点,AD DE=时,AD是ABC的中线吗?请说明(1)如图1,当点E在AC的延长线上且CD CE理由;AB BD AE之间的数量关系,请说明理(2)如图2,当点E在AC的延长线上时,写出,,由;(3)如图3,当点D在线段CB的延长线上,点E在线段AC上时,请直接写出AB BD AE的数量关系.,,+=,理由详见【答案】(1)AD是ABC的中线,理由详见解析;(2)AB BD AE=+.解析;(3)AB AE BD【解析】【分析】(1)利用△ABC是等边三角形及CD=CE可得∠CDE=∠E=30°,利用AD=DE,证明∠CAD=∠E =30°,即可解决问题.(2)在AB上取BH=BD,连接DH,证明AHD≌△DCE得出DH=CE,得出AE=AB+BD,(3)在AB上取AF=AE,连接DF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB=BD+AE.【详解】(1)解:如图1,结论:AD是△ABC的中线.理由如下:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠B=∠ACB=60°,∵CD=CE,∴∠CDE=∠E,∵∠ACD=∠CDE+∠E=60°,∴∠E=30°,∵DA=DE,∴∠DAC=∠E=30°,∵∠BAC=60°,∴∠DAB=∠CAD,∵AB=AC,∴BD=DC,∴AD是△ABC的中线.(2)结论:AB+BD=AE,理由如下:如图2,在AB上取BH=BD,连接DH,∵BH=BD,∠B=60°,∴△BDH为等边三角形,AB-BH=BC-BD,∴∠BHD=60°,BD=DH,AH=DC,∵AD=DE,∴∠E=∠CAD,∴∠BAC-∠CAD=∠ACB-∠E∴∠BAD=∠CDE,∵∠BHD=60°,∠ACB=60°,∴180°-∠BHD=180°-∠ACB,∴∠AHD=∠DCE,∴在△AHD和△DCE,BAD CDEAHD DCEAD DE∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AHD≌△DCE(AAS),∴DH=CE,∴BD=CE,∴AE=AC+CE=AB+BD.(3)结论:AB=BD+AE,理由如下:如图3,在AB上取AF=AE,连接DF,∵△ABC为等边三角形,∴∠BAC=∠ABC=60°,∴△AFE是等边三角形,∴∠FAE=∠FEA=∠AFE=60°,∴EF∥BC,∴∠EDB=∠DEF,∵AD=DE,∴∠DEA=∠DAE,∴∠DEF=∠DAF,∵DF=DF,AF=EF,在△AFD和△EFD中,AD DEDF DFAF EF=⎧⎪=⎨⎪=⎩,∴△AFD≌△EFD(SSS)∴∠ADF=∠EDF,∠DAF=∠DEF,∴∠FDB=∠EDF+∠EDB,∠DFB=∠DAF+∠ADF,∵∠EDB=∠DEF,∴∠FDB=∠DFB,∴DB=BF,∵AB=AF+FB,∴AB=BD+AE.【点睛】本题属于三角形综合题,考查了全等三角形的判定与性质及等边三角形的判定与性质,解题的关键是正确作出辅助线,运用三角形全等找出对应的线段.10.如图,在 ABC 中,已知 AB AC =,AD 是 BC 边上的中线,点 E 是 AB 边上一动点,点 P 是 AD 上的一个动点.(1)若 37BAD ∠=,求 ACB ∠ 的度数;(2)若 6BC =,4AD =,5AB =,且 CE AB ⊥ 时,求 CE 的长;(3)在(2)的条件下,请直接写出 BP EP + 的最小值.【答案】(1)53ACB ∠=.(2)245CE =.(3) 245. 【解析】【分析】(1)由已知得出三角形ABC 是等腰三角形,ACB ABC ∠∠=,AD 是BC 边的中线,有AD BC ⊥,求出ABC ∠的度数,即可得出ACB ∠的度数.(2)根据三角形ABC 的面积可得出CE 的长 (3)连接CP ,有BP=CP ,BP+EP=EP+CP ,当点E ,P ,C 在同一条直线上时BP+EP 有最小值,即CE 的长度. 【详解】解:(1)AB AC =, ACB ABC ∴∠=∠, AD 是 BC 边上的中线, 90ADB ∴∠=,37BAD ∠=,903753ABC ∴∠=-=, 53ACB ∴∠=.(2)CE AB ⊥,1122ABC S BC AD AB CE ∴=⋅=⋅, 6BC =,4=AD ,5AB =,245CE ∴=. (3) 245【点睛】本题考查的知识点主要有等腰三角形的“三线合一”,三角形的面积公式等,充分利用等腰三角形的“三线合一”是解题的关键.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.如图1是一个长为4a 、宽为b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出2()a b +、2()a b -、ab 之间的等量关系是______;(2)根据(1)中的结论,若5x y +=,94x y ⋅=,则x y -=______; (3)拓展应用:若22(2019)(2020)7m m -+-=,求(2019)(2020)m m --的值.【答案】(1)22()()4a b a b ab +=-+;(2)4,-4:(3)-3【解析】【分析】(1)观察图2,大正方形由4个矩形和一个小正方形组成,根据面积即可得到他们之间的关系.(2)由(1)的结论可得(x-y) ²=16,然后利用平方根的定义求解即可.(3)从已知等式的左边看,左边配成两数和的平方来求解.【详解】解:(1)由题可得,大正方形的面积2()a b =+,大正方形的面积2()4a b ab =-+,∴22()()4a b a b ab +=-+,(2)∵22()()4x y x y xy +=-+, ∴229()()4254164x y x y xy -=+-=-⨯=, ∴4x y -=或-4, (3)∵22(2019)(2020)7m m -+-=,又2(20192020)m m -+-22(2019)(2020)2(2019)(2020)m m m m =-+-+--∴172(2019)(2020)m m =+--∴(2019)(2020)3m m --=-故答案为:(1)22()()4a b a b ab +=-+;(2) 4,-4:(3)-3【点睛】本题通过观察图形发现规律,并运用规律求值,使问题简单化是解题关键.12.阅读下列材料:1637年笛卡尔在其《几何学》中,首次应用“待定系数法”将四次方程分解为两个二次方程求解,并最早给出因式分解定理.他认为:对于一个高于二次的关于x 的多项式,“x a =是该多项式值为0时的一个解”与“这个多项式一定可以分解为(x a -)与另一个整式的乘积”可互相推导成立.例如:分解因式3223x x +-.∵1x =是32230x x +-=的一个解,∴3223x x +-可以分解为()1x -与另一个整式的乘积.设()()322231x x x ax bx c +-=-++ 而()()()()2321x ax bx c ax b a x c b x c -++=+-+--,则有 1203a b a c b c =⎧⎪-=⎪⎨-=⎪⎪-=-⎩,得133a b c =⎧⎪=⎨⎪=⎩,从而()()32223133x x x x x +-=-++ 运用材料提供的方法,解答以下问题:(1)①运用上述方法分解因式323x x ++时,猜想出3230x x ++=的一个解为_______(只填写一个即可),则323x x ++可以分解为_______与另一个整式的乘积;②分解因式323x x ++;(2)若1x -与2x +都是多项式32x mx nx p +++的因式,求m n -的值.【答案】(1)①:x=-1;(x+1);②3223=(1)(3)x x x x x +++-+;(2)3【解析】【分析】(1)①计算当x=-1时,方程成立,则323x x ++必有一个因式为(x+1),即可作答; ②根据待定系数法原理先设另一个多项式,然后根据多项式乘多项式的计算即可求得结论;(2))设32=(1)(2)x mx mx p x x M +++-+(其中M 为二次整式),由材料可知,x=1,x=-2是方程320x mx nx p +++=的解,然后列方程组求解即可.【详解】解:(1)①323x x ++,观察知,显然x=-1时,原式=0,则3230x x ++=的一个解为x=-1;原式可分解为(x+1)与另一个整式的积.故答案为:x=-1;(x+1)②设另一个因式为(x 2+ax+b ),(x+1)(x 2+ax+b )=x 3+ax 2+bx+x 2+ax+b=x 3+(a+1)x 2+(a+b )x+b∴a+1=0 ,a=-1, b=3∴多项式的另一因式为x 2-x+3.∴3223=(1)(3)x x x x x +++-+.(2)设32=(1)(2)x mx nx p x x M +++-+(其中M 为二次整式),由材料可知,x=1,x=-2是方程320x mx nx p +++=的解, ∴可得108420m n p m n p +++=⎧⎨-+-+=⎩①②, ∴②-①,得m-n=3∴m n -的值为3.【点睛】本题考查了分解因式,正确理解题意,利用待定系数法和多项式乘多项式的计算法则求解是解题的关键.13.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x 2﹣4x +1)(x 2﹣4x +7)+9进行因式分解的过程. 解:设x 2﹣4x =y原式=(y +1)(y +7)+9(第一步)=y 2+8y +16(第二步)=(y +4)2(第三步)=(x 2﹣4x +4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的 ;A .提取公因式法B .平方差公式法C .完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ;(3)请你用换元法对多项式(x 2+2x )(x 2+2x +2)+1进行因式分解.【答案】(1)C ;(2)(x ﹣2)4;(3)(x +1)4.【解析】【分析】(1)根据完全平方公式进行分解因式;(2)最后再利用完全平方公式将结果分解到不能分解为止;(3)根据材料,用换元法进行分解因式.【详解】(1)故选C;(2)(x2﹣4x+1)(x2﹣4x+7)+9,设x2﹣4x=y,则:原式=(y+1)(y+7)+9=y2+8y+16=(y+4)2=(x2﹣4x+4)2=(x﹣2)4.故答案为:(x﹣2)4;(3)设x2+2x=y,原式=y(y+2)+1=y2+2y+1=(y+1)2=(x2+2x+1)2=(x+1)4.【点睛】本题考查了因式分解﹣换元法,公式法,也是阅读材料问题,熟练掌握利用公式法分解因式是解题的关键.14.材料阅读:若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“完美数”.例如:因为13=32+22,所以13是“完美数”;再如:因为a2+2ab+2b2=(a+b)2+b2(a、b是正整数),所以a2+2ab+2b2也是“完美数”.(1)请你写出一个大于20小于30的“完美数”,并判断53是否为“完美数”;(2)试判断(x2+9y2)·(4y2+x2)(x、y是正整数)是否为“完美数”,并说明理由.【答案】(1)25,53是完美数; (2)是,理由见解析.【解析】【分析】(1)根据“完美数”的定义判断即可;(2)根据多项式的乘法法则计算出结果后,根据“完美数”的定义判断即可.【详解】(1)25=4²+3²,∵53=49+4=7²+2²,∴53是“完美数”;(2)(x²+9y²)⋅(4y²+x²)是“完美数”,(x²+9y²)⋅(4y²+x²)=4x2y²+364y+4x+9x²y²=13x²y²+364y+4x=(6y²+x²) ²+x²y²,∴(x²+9y²)⋅(4y²+x²)是“完美数”.【点睛】本题考查了因式分解的应用,正确的理解新概念“完美数”是解题的关键.15.观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×=×25;②×396=693×.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.【答案】解:(1)①275;572.②63;36.(2)“数字对称等式”一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a),证明见解析.【解析】【分析】根据题意可得三位数中间的数等于两数的和,根据这一规律然后进行填空,从而得出答案;根据题意得出一般性的规律,然后根据多项式的计算法则进行说明理由.【详解】(1)①275,572; ②63,36;(2)“数字对称等式”一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).证明如下:∵左边两位数的十位数字为a,个位数字为b,∴左边的两位数是10a+b,三位数是100b+10(a+b)+a,右边的两位数是10b+a,三位数是100a+10(a+b)+b,∴左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b+10a+10b+a)=(10a+b)(110b+11a)=11(10a+b)(10b+a),右边=[100a+10(a+b)+b]×(10b+a)=(100a+10a+10b+b)(10b+a)=(110a+11b)(10b+a)=11(10a+b)(10b+a),∴左边=右边.∴“数字对称等式”一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).考点:规律题四、八年级数学分式解答题压轴题(难)16.已知:方程﹣=﹣的解是x=,方程﹣=﹣的解是x=,试猜想:(1)方程+=+的解;(2)方程﹣=﹣的解(a 、b 、c 、d 表示不同的数).【答案】(1)x =4;(2)x =. 【解析】通过解题目中已知的两个方程的过程可以归纳出方程的解与方程中的常数之间的关系,利用这个关系可得出两个方程的解. 解:解方程﹣=﹣,先左右两边分别通分可得:,化简可得:,整理可得:2x =15﹣8,解得:x =,这里的7即为(﹣3)×(﹣5)﹣(﹣2)×(﹣4),这里的2即为[﹣2+(﹣4)]﹣[﹣3+(﹣5)]; 解方程﹣=﹣,先左右两边分别为通分可得:,化简可得:, 解得:x =, 这里的11即为(﹣7)×(﹣5)﹣(﹣4)×(﹣6),这里的2即为[﹣4+(﹣6)]﹣[﹣7+(﹣5)];所以可总结出规律:方程解的分子为右边两个分中的常数项的积减去左边两个分母中的常数项的积,解的分母为左边两个分母中的常数项的差减去右边两个分母中常数项的差. (1)先把方程分为两边差的形式:方程﹣=﹣,由所总结的规律可知方程解的分子为:(﹣1)×(﹣6)﹣(﹣7)×(﹣2)=﹣8,分母为[﹣7+(﹣2)]﹣[﹣6+(﹣1)]=﹣2,所以方程的解为x ==4;(2)由所总结的规律可知方程解的分子为:cd ﹣ab ,分母为(a +b )﹣(c +d ),所以方程的解为x =.17.阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当0a >,0b >时,∵2()20a b a ab b =-≥,∴2a b ab +≥,当且仅当a b =时取等号.请利用上述结论解决以下问题:(1)当0x >时,1x x +的最小值为_______;当0x <时,1x x+的最大值为__________. (2)当0x >时,求2316x x y x++=的最小值. (3)如图,四边形ABCD 的对角线AC ,BD 相交于点O ,△AOB 、△COD 的面积分别为4和9,求四边形ABCD 面积的最小值.【答案】(1)2,-2;(2)11;(3)25【解析】【分析】(1)当x >0时,按照公式ab a=b 时取等号)来计算即可;x <0时,由于-x >0,-1x>0,则也可以按照公式ab a=b 时取等号)来计算; (2)将2316x x y x++=的分子分别除以分母,展开,将含x 的项用题中所给公式求得最小值,再加上常数即可;(3)设S △BOC =x ,已知S △AOB =4,S △COD =9,则由等高三角形可知:S △BOC :S △COD =S △AOB :S △AOD ,用含x 的式子表示出S △AOD ,四边形ABCD 的面积用含x 的代数式表示出来,再按照题中所给公式求得最小值,加上常数即可.【详解】解:(1)当x >0时,112x x x x +≥⋅= 当x <0时,11x x x x ⎛⎫+=--- ⎪⎝⎭ ∵()1122x x x x ⎛⎫--≥-⋅-= ⎪⎝⎭∴12x x ⎛⎫---≤- ⎪⎝⎭ ∴当0x >时,1x x +的最小值为2;当0x <时,1x x+的最大值为-2; (2)由2316163x x y x x x++==++ ∵x >0,∴163311y x x =++≥= 当16x x= 时,最小值为11; (3)设S △BOC =x ,已知S △AOB =4,S △COD =9则由等高三角形可知:S △BOC :S △COD =S △AOB :S △AOD∴x :9=4:S △AOD∴:S △AOD =36x∴四边形ABCD 面积=4+9+x+361325x ≥+= 当且仅当x=6时取等号,即四边形ABCD 面积的最小值为25.【点睛】本题考查了配方法在最值问题中的应用,同时本题还考查了分式化简和等高三角形的性质,本题难度中等略大.18.为响应“绿色出行”的号召,小王上班由自驾车改为乘坐公交车.已知小王家距离上班地点27km ,他乘坐公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的2倍还多9km .他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的37. (1)小王用自驾车上班平均每小时行驶多少千米?(2)上周五,小王上班时先步行了6km ,然后乘公交车前往,共用43小时到达.求他步行的速度.【答案】(1)小王用自驾车上班平均每小时行驶27km ;(2)小王步行的速度为每小时6km .【解析】【分析】(1))设小王用自驾车上班平均每小时行驶xkm ,则他乘坐公交车上班平均每小时行驶()29x km +.再利用乘公交车的方式平均每小时行驶的路程比他自用驾SS 式平均每小时行驶的路程的2倍还多9千米和乘公交车所用时间是自驾车方式所用时间的37,列方程求解即可;(2)设小王步行的速度为每小时ykm ,然后根据“步行时间+乘公交时间=小时”列方程解答即可.【详解】解(1)设小王用自驾车上班平均每小时行驶xkm ,则他乘坐公交车上班平均每小时行驶()29x km +.根据题意得:27327297x x=⋅+ 解得:27x =经检验,27x =是原方程的解且符合题意.所以小王用自驾车上班平均每小时行驶27km ;(2)由(1)知:小王乘坐公交车上班平均每小时行驶29227963x +=⨯+=(km ); 设小王步行的速度为每小时ykm ,根据题意得:62764633y -+= 解得:6y =.经检验:6y =是原方程的解且符合题意所以小王步行的速度为每小时6km .【点睛】本题考查了分式方程的应用,解答的关键在于弄清题意、找到等量关系、列出分式方程并解答.19.某小麦改良品种后平均每公顷增加产量a 吨,原来产m 吨小麦的一块土地,现在小麦的总产量增加了20吨.(1)当a =0.8,m =100时,原来和现在小麦的平均每公顷产量各是多少?(2)请直接接写出原来小麦的平均每公顷产量是 吨,现在小麦的平均每公顷产量是 吨;(用含a 、m 的式于表示)(3)在这块土地上,小麦的改良品种成熟后,甲组收割完需n 小时,乙组比甲组少用0.5小时就能收割完,求两组一起收割完这块麦田需要多少小时?【答案】(1)原来和现在小麦的平均每公顷产量各是4吨,4.8吨;(2)20ma ,+2020ma a ;(3)两组一起收割完这块麦田需要2241n n n --小时. 【解析】【分析】(1)设原来小麦平均每公顷产量是x 吨,根据题意列出分式方程求解并验根即可;(2)设原来小麦平均每公顷产量是y 吨,根据题意列出分式方程求解并验根即可;(3)由题意得知,工作总量为m+20,甲的工作效率为:20m n +,乙的工作效率为:200.5m n +-,再由工作总量除以甲乙的工作效率和即可得出工作时间. 【详解】解:(1)设原来平均每公顷产量是x 吨,则现在平均每公顷产量是(x +0.8)吨, 根据题意可得:100100200.8x x +=+。
人教版八年级数学上册期中综合能力检测题(二)
期中综合能力检测题(附答案)时间:100分钟满分:120分一.选择题(共10小题,满分30分)1.下列图形为轴对称图形的为()A.B.C.D.2.下列各线段中,能与长为4,6的两线段组成三角形的是()A.2 B.8 C.10 D.123.下列各图中,正确画出AC边上的高的是()A.B.C.D.4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是()A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE5.如图,底边BC为,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为()A.B.C.D.6.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ =PQ,PR=PS,则这四个结论中正确的有()①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.A.4个B.3个C.2个D.1个7.已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:①如果添加条件“AB=AC”,那么△ABC是等边三角形;②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.上述说法中,正确的有()A.3个B.2个C.1个D.0个8.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是()A.5cm B.6cm C.7cm D.8cm9.等腰直角三角形的斜边为2,则这个三角形的面积为()A.2 B.1 C.2D.l10.如图,等腰三角形ABC底边BC的长为4cm,面积为12cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为()A.5cm B.6cm C.8cm D.10cm二.填空题(共6小题,满分18分)11.已知点M(x,3)与点N(﹣2,y)关于x轴对称,则3x+2y=.12.一个多边形的每一个外角为30°,那么这个多边形的边数为.13.如图所示:已知∠ACB=∠DBC,请你补充一个条件:,使得△ABC≌△DCB.14.如图,在△ABC中,∠C=46°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是.15.如图,△ABC沿DE折叠,点A落在边BC上的点A1处,连接AA1,△ABC的周长为C△ABC=8.给出下列结论:①AE=A1E;②∠BAC=∠EA1D;③DE垂直平分AA1;④C+C=8.正确结论的序号是.16.如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是边BC的三等分点,连接AD、AC.则下列结论正确的是.①BD=AD;②∠CAD=90°;③若AB=6,则AE=2;④△ADE是等边三角形.三.解答题(共9小题,满分72分)17.(8分)如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).(2)直接写出(1)中F点的坐标为.(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为.(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为.(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.18.(8分)探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.19.(8分)如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC 上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)(1)运动秒时,AE=DC;(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).20.(8分)如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.(1)若∠AFD=155°,求∠EDF的度数;(2)若点F是AC的中点,求证:∠CFD=∠B.21.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE,(1)求证:AB=AC(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.22.(8分)已知:如图,在△ABC中,AB=AC,∠A=60°,求证:△ABC是等边三角形.23.(8分)在数学课上,老师提出如下问题:已知:∠α,直线l和l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.小刚的做法如下:①以∠α的顶点O为圆心,任意长为半径作弧,交两边于M,N;以A为圆心,同样长为半径作弧,交直线l于点P;②以P为圆心,MN的长为半径作弧,两弧交于点Q,作射线AQ;③以B为圆心,任意长为半径作弧,交直线l于E,F;④分别以E,F为圆心,大于EF长为半径作弧,两弧在直线l上方交于点G,作射线BG;⑤射线AQ与射线BG交于点C.Rt△ABC即为所求.(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:连接PQ.在△OMN和△AQP中,∵ON=AP,NM=PQ,OM=AQ,∴△OMN≌△AQP().(填写推理依据)∴∠PAQ=∠O=α.∵CE=CF,BE=BF,∴CB⊥EF().(填写推理依据)24.(8分)如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB、BE于点D、G,垂足为H,CD⊥AB,CD交BE于点F.(1)求证:△BDF≌△CDA,并写出BF与AC的数量关系.(2)若DF=DG,求证:①BE平分∠ABC;②CE=BF.25.(8分)(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE ⊥直线m,垂足分别为D,E.求证:DE=BD+CE;(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由;(3)如图3,在(2)的条件下,若a=120°,且△ACF为等边三角形,试判断△DEF的形状,并说明理由.参考答案一.选择题1.解:A、不是轴对称图形,故此选项不合题意;B、不是轴对称图形,故此选项不合题意;C、不是轴对称图形,故此选项不合题意;D、是轴对称图形,故此选项符合题意.故选:D.2.解:设组成三角形的第三边长为x,由题意得:6﹣4<x<6+4,即:2<x<10,故选:B.3.解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.故选:D.4.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,故A、B、C正确;AD的对应边是AE而非DE,所以D错误.故选:D.5.解:过A作AF⊥BC于F,∵AB=AC,∠A=120°,∴∠B=∠C=30°,BF=CF=2,∵cos30°=,∴AB=AC=4,∵DE垂直平分AB,∴BE=AE,∴AE+CE=BC=4,∴△ACE的周长=AC+AE+CE=AC+BC=4+4,故选:B.6.解:(1)PA平分∠BAC.∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴△APR≌△APS,∴∠PAR=∠PAS,∴PA平分∠BAC;(2)由(1)中的全等也可得AS=AR;(3)∵AQ=PR,∴∠1=∠APQ,∴∠PQS=∠1+∠APQ=2∠1,又∵PA平分∠BAC,∴∠BAC=2∠1,∴∠PQS=∠BAC,∴PQ∥AR;(4)∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP,∵PR=PS,∴△BRP不一定全等与△CSP(只具备一角一边的两三角形不一定全等).故选:B.7.解:①若添加的条件为AB=AC,由∠A=60°,利用有一个角为60°的等腰三角形为等边三角形可得出△ABC为等边三角形;②若添加条件为∠B=∠C,又∵∠A=60°,∴∠B=∠C=60°,∴∠A=∠B=∠C,则△ABC为等边三角形;③若添加的条件为边AB、BC上的高相等,如图所示:已知:∠BAC=60°,AE⊥BC,CD⊥AB,且AE=CD,求证:△ABC为等边三角形.证明:∵AE⊥BC,CD⊥AB,∴∠ADC=∠AEC=90°,在Rt△ADC和Rt△CEA中,,∴Rt△ADC≌Rt△CEA(HL),∴∠ACE=∠BAC=60°,∴∠BAC=∠B=∠ACB=60°,∴AB=AC=BC,即△ABC为等边三角形,综上,正确的说法有3个.故选:A.8.解:∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,∴DC=DE,AC=AE,∴△DEB的周长=DE+BE+BD=BE+DC+BD=BE+BC=BE+AE=AB=6cm.故选:B.9.解:设AC=BC=x,由勾股定理得:x2+x2=22,∴x=,∴△ABC的面积是AC×BC=××=1.故选:B.10.解:如图,连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=BC•AD=×4×AD=12,解得AD=6cm,∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8cm.故选:C.二.填空题11.解:∵点M(x,3)与点N(﹣2,y)关于x轴对称,∴x=﹣2,y=﹣3,∴3x+2y=3×(﹣2)+2×(﹣3)=﹣6﹣6=﹣12.故答案为:﹣12.12.解:多边形的边数:360°÷30°=12,则这个多边形的边数为12.故答案为:12.13.解:添加条件:AC=BD,∵在△ABC和△DCB中,∴△ABC≌△DCB(SAS),故答案为:AC=BD.14.解:由折叠的性质得:∠D=∠C=46°,根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+92°,则∠1﹣∠2=92°.故答案为:92°.15.解:∵△ABC沿DE折叠,点A落在边BC上的点A1处,∴AE=A1E,AD=A1D,∠BAC=∠EA1D,故①②正确,∴DE垂直平分AA1,故③正确,∵△ABC的周长为C△ABC=8,∴AB+AC+BC=8,∵C+C=BE+A1E+A1B+CD+A1D+CA1=BE+AE+BC+AD+DC=AB+AC+BC,∴C+C=8,故④正确,故答案为:①②③④.16.解:作AM⊥BC于M,DN⊥AB于N,如图所示:设AB=AC=6,∵∠BAC=120°,∴∠B=∠C=30°,∴AM=AB=3,∴BM=CM=AM=3,∴BC=2BM=6,∵点D、E是边BC的三等分点,∴BD=DE=CD=2,∴DN=BD=,∴BN=DN=3=AB,∴AN=BN,∵DN⊥AB,∴BD=AD,①正确;∴∠DAN=∠B=30°,同理:CE=AE,∠CAE=∠C=30°,∴AD=DE=AE=2,△ADE是等边三角形,③错误,④正确,∴∠DAE=60°,∴∠CAD=60°+30°=90°,②正确;故答案为:①②④.三.解答题(共9小题,满分64分)17.解:(1)如图,△DEF即为所求.(2)点F的坐标(4,3).故答案为(4,3).(3)∵C(﹣4,3),直线l为y=﹣2,∴点C关于直线l的对称点C′(﹣4,﹣7).(4)延长CB交y轴于点P,此时PC﹣PB的值最大,P(0,﹣1),故答案为(0,﹣1).(5)作点M关于x轴的对称点M′,连接CM′交x轴于点Q,连接QM,此时QM+QC的值最小.18.解:(1)∵∠ADC是△ABD的外角,∴∠ADC=∠BAD+∠B=105°,∠DAE=∠BAC﹣∠BAD=30°,∴∠ADE=∠AED=75°,∴∠CDE=105°﹣75°=30°;(2)∠BAD=2∠CDE,理由如下:设∠BAD=x,∴∠ADC=∠BAD+∠B=45°+x,∠DAE=∠BAC﹣∠BAD=90°﹣x,∴∠ADE=∠AED=,∴∠CDE=45°+x﹣=x,∴∠BAD=2∠CDE;(3)设∠BAD=x,∴∠ADC=∠BAD+∠B=∠B+x,∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,∴∠ADE=∠AED=∠C+x,∴∠CDE=∠B+x﹣(∠C+x)=x,∴∠BAD=2∠CDE.19.解:(1)由题可得,BD=CE=2t,∴CD=12﹣2t,AE=8﹣2t,∴当AE=DC,时,8﹣2t=(12﹣2t),解得t=3,故答案为:3;(2)当△ABD≌△DCE成立时,AB=CD=8,∴12﹣2t=8,解得t=2,∴运动2秒时,△ABD≌△DCE能成立;(3)当△ABD≌△DCE时,∠CDE=∠BAD,又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,∴∠ADE=∠B,又∵∠BAC=α,AB=AC,∴∠ADE=∠B=(180°﹣α)=90°﹣α.故答案为:90°﹣α.20.解:(1)∵∠AFD=155°,∴∠DFC=25°,∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°,在Rt△FDC中,∴∠C=90°﹣25°=65°,∵AB=BC,∴∠C=∠A=65°,∴∠EDF=360°﹣65°﹣155°﹣90°=50°.(2)连接BF∵AB=BC,且点F是AC的中点,∴BF⊥AC,∠ABF=∠CBF=∠ABC,∴∠CFD+∠BFD=90°,∠CBF+∠BFD=90°,∴∠CFD=∠CBF,∴∠CFD=∠ABC.21.证明:(1)过点A作AF⊥BC于点F,∵AD=AE,∴DF=EF,∵BD=CE,∴BF=CF,∴AB=AC.(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,22.证明:∵AB=AC,∴∠C=∠B.又∵∠A+∠B+∠C=180°,∠A=60°,∴∠B=∠C=60°=∠A,∴△ABC是等边三角形.23.解:(1)如图所示:△ABC即为所求.(2)在△OMN和△AQP中,∵ON=AP,NM=PQ,OM=AQ,∴△OMN≌△AQP(SSS),∴∠PAQ=∠O=α.∵CE=CF,BE=BF,∴CB⊥EF(等腰三角形三线合一).故答案为:SSS,等腰三角形三线合一.24.(1))证明:∵DH垂直平分BC,∴BD=CD,∵BE⊥AC,BA⊥CD,∴∠A+∠DBF=90°,∠DBF+∠DFB=90°,∴∠A=∠DFB,在△ADC和△FDB中∴△ADC≌△FDB(AAS),∴BF=AC;(2)证明:①∵DF=DG,∴∠DGF=∠DFG,∵∠BGH=∠DGF,∴∠DGF=∠DFG,∵∠DBF+∠DFB=90°,∠FBC+∠BGH=90°,∴∠DBF=∠FBC,∴BE平分∠ABC;②在△ABE和△CBE中∴△ABE≌△CBE(ASA),∴AE=CE,∴AC=2CE,∵BF=AC,∴CE=BF.25.证明:(1)∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在△ADB和△CEA中,∵,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,∵在△ADB和△CEA中,∵,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.(3)△DEF为等边三角形,理由如下:由(2)知△ADB≌△CEA,BD=AE,∠DBA=∠CAE,∵△ACF为等边三角形,∴∠CAF=60°,AF=AC,又∵AB=AC,∴AB=AF,∵∠BAC=120°,∴∠BAF=60°,∴△ABF是等边三角形,∴∠ABF=60°,BF=AF,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠EAF,∵BF=AF,∴△BDF≌△AEF(AAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.。
人教版八年级数学上册期中综合能力检测题(二)及答案
期中综合能力检测题(二)时间:100分钟满分:120分一.选择题(共10小题,满分30分)1.下列图形为轴对称图形的为()A.B.C.D.2.下列各线段中,能与长为4,6的两线段组成三角形的是()A.2 B.8 C.10 D.123.下列各图中,正确画出AC边上的高的是()A.B.C.D.4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是()A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE5.如图,底边BC为,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE 的周长为()A.B.C.D.6.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则这四个结论中正确的有()①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.A.4个B.3个C.2个D.1个7.已知:在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法:①如果添加条件“AB=AC”,那么△ABC是等边三角形;②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.上述说法中,正确的有()A.3个B.2个C.1个D.0个8.如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是()A.5cm B.6cm C.7cm D.8cm9.等腰直角三角形的斜边为2,则这个三角形的面积为()A.2 B.1 C.2D.l10.如图,等腰三角形ABC底边BC的长为4cm,面积为12cm2,腰AB的垂直平分线EF 交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM 的周长最小值为()A.5cm B.6cm C.8cm D.10cm二.填空题(共6小题,满分18分)11.已知点M(x,3)与点N(﹣2,y)关于x轴对称,则3x+2y=.12.一个多边形的每一个外角为30°,那么这个多边形的边数为.13.如图所示:已知∠ACB=∠DBC,请你补充一个条件:,使得△ABC≌△DCB.14.如图,在△ABC中,∠C=46°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1﹣∠2的度数是.15.如图,△ABC沿DE折叠,点A落在边BC上的点A1处,连接AA1,△ABC的周长为C△ABC=8.给出下列结论:①AE=A1E;②∠BAC=∠EA1D;③DE垂直平分AA1;④C+C=8.正确结论的序号是.16.如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是边BC的三等分点,连接AD、AC.则下列结论正确的是.①BD=AD;②∠CAD=90°;③若AB=6,则AE=2;④△ADE是等边三角形.三.解答题(共9小题,满分72分)17.(8分)如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).(2)直接写出(1)中F点的坐标为.(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为.(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为.(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.18.(8分)探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E 在AC边上,且∠ADE=∠AED,连接DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE 的数量关系.19.(8分)如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)(1)运动秒时,AE=DC;(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).20.(8分)如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.(1)若∠AFD=155°,求∠EDF的度数;(2)若点F是AC的中点,求证:∠CFD=∠B.21.(8分)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE,(1)求证:AB=AC(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.22.(8分)已知:如图,在△ABC中,AB=AC,∠A=60°,求证:△ABC是等边三角形.23.(8分)在数学课上,老师提出如下问题:已知:∠α,直线l和l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.小刚的做法如下:①以∠α的顶点O为圆心,任意长为半径作弧,交两边于M,N;以A为圆心,同样长为半径作弧,交直线l于点P;②以P为圆心,MN的长为半径作弧,两弧交于点Q,作射线AQ;③以B为圆心,任意长为半径作弧,交直线l于E,F;④分别以E,F为圆心,大于EF长为半径作弧,两弧在直线l上方交于点G,作射线BG;⑤射线AQ与射线BG交于点C.Rt△ABC即为所求.(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:连接PQ.在△OMN和△AQP中,∵ON=AP,NM=PQ,OM=AQ,∴△OMN≌△AQP().(填写推理依据)∴∠PAQ=∠O=α.∵CE=CF,BE=BF,∴CB⊥EF().(填写推理依据)24.(8分)如图,在△ABC中,BE⊥AC于点E,BC的垂直平分线分别交AB、BE于点D、G,垂足为H,CD⊥AB,CD交BE于点F.(1)求证:△BDF≌△CDA,并写出BF与AC的数量关系.(2)若DF=DG,求证:①BE平分∠ABC;②CE=BF.25.(8分)(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE 是否成立?若成立,请你给出证明;若不成立,请说明理由;(3)如图3,在(2)的条件下,若a=120°,且△ACF为等边三角形,试判断△DEF 的形状,并说明理由.参考答案一.选择题1.解:A、不是轴对称图形,故此选项不合题意;B、不是轴对称图形,故此选项不合题意;C、不是轴对称图形,故此选项不合题意;D、是轴对称图形,故此选项符合题意.故选:D.2.解:设组成三角形的第三边长为x,由题意得:6﹣4<x<6+4,即:2<x<10,故选:B.3.解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.故选:D.4.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,故A、B、C正确;AD的对应边是AE而非DE,所以D错误.故选:D.5.解:过A作AF⊥BC于F,∵AB=AC,∠A=120°,∴∠B=∠C=30°,BF=CF=2,∵cos30°=,∴AB=AC=4,∵DE垂直平分AB,∴BE=AE,∴AE+CE=BC=4,∴△ACE的周长=AC+AE+CE=AC+BC=4+4,故选:B.6.解:(1)PA平分∠BAC.∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴△APR≌△APS,∴∠PAR=∠PAS,∴PA平分∠BAC;(2)由(1)中的全等也可得AS=AR;(3)∵AQ=PR,∴∠1=∠APQ,∴∠PQS=∠1+∠APQ=2∠1,又∵PA平分∠BAC,∴∠BAC=2∠1,∴∠PQS=∠BAC,∴PQ∥AR;(4)∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP,∵PR=PS,∴△BRP不一定全等与△CSP(只具备一角一边的两三角形不一定全等).故选:B.7.解:①若添加的条件为AB=AC,由∠A=60°,利用有一个角为60°的等腰三角形为等边三角形可得出△ABC为等边三角形;②若添加条件为∠B=∠C,又∵∠A=60°,∴∠B=∠C=60°,∴∠A=∠B=∠C,则△ABC为等边三角形;③若添加的条件为边AB、BC上的高相等,如图所示:已知:∠BAC=60°,AE⊥BC,CD⊥AB,且AE=CD,求证:△ABC为等边三角形.证明:∵AE⊥BC,CD⊥AB,∴∠ADC=∠AEC=90°,在Rt△ADC和Rt△CEA中,,∴Rt△ADC≌Rt△CEA(HL),∴∠ACE=∠BAC=60°,∴∠BAC=∠B=∠ACB=60°,∴AB=AC=BC,即△ABC为等边三角形,综上,正确的说法有3个.故选:A.8.解:∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,∴DC=DE,AC=AE,∴△DEB的周长=DE+BE+BD=BE+DC+BD=BE+BC=BE+AE=AB=6cm.故选:B.9.解:设AC=BC=x,由勾股定理得:x2+x2=22,∴x=,∴△ABC的面积是AC×BC=××=1.故选:B.10.解:如图,连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S=BC•AD=×4×AD=12,△ABC解得AD=6cm,∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8cm.故选:C.二.填空题11.解:∵点M(x,3)与点N(﹣2,y)关于x轴对称,∴x=﹣2,y=﹣3,∴3x+2y=3×(﹣2)+2×(﹣3)=﹣6﹣6=﹣12.故答案为:﹣12.12.解:多边形的边数:360°÷30°=12,则这个多边形的边数为12.故答案为:12.13.解:添加条件:AC=BD,∵在△ABC和△DCB中,∴△ABC≌△DCB(SAS),故答案为:AC=BD.14.解:由折叠的性质得:∠D=∠C=46°,根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+92°,则∠1﹣∠2=92°.故答案为:92°.15.解:∵△ABC沿DE折叠,点A落在边BC上的点A1处,∴AE=A1E,AD=A1D,∠BAC=∠EA1D,故①②正确,∴DE垂直平分AA1,故③正确,∵△ABC的周长为C=8,△ABC∴AB+AC+BC=8,∵C+C=BE+A1E+A1B+CD+A1D+CA1=BE+AE+BC+AD+DC=AB+AC+BC,∴C+C=8,故④正确,故答案为:①②③④.16.解:作AM⊥BC于M,DN⊥AB于N,如图所示:设AB=AC=6,∵∠BAC=120°,∴∠B=∠C=30°,∴AM=AB=3,∴BM=CM=AM=3,∴BC=2BM=6,∵点D、E是边BC的三等分点,∴BD=DE=CD=2,∴DN=BD=,∴BN=DN=3=AB,∴AN=BN,∵DN⊥AB,∴BD=AD,①正确;∴∠DAN=∠B=30°,同理:CE=AE,∠CAE=∠C=30°,∴AD=DE=AE=2,△ADE是等边三角形,③错误,④正确,∴∠DAE=60°,∴∠CAD=60°+30°=90°,②正确;故答案为:①②④.三.解答题(共9小题,满分64分)17.解:(1)如图,△DEF即为所求.(2)点F的坐标(4,3).故答案为(4,3).(3)∵C(﹣4,3),直线l为y=﹣2,∴点C关于直线l的对称点C′(﹣4,﹣7).(4)延长CB交y轴于点P,此时PC﹣PB的值最大,P(0,﹣1),故答案为(0,﹣1).(5)作点M关于x轴的对称点M′,连接CM′交x轴于点Q,连接QM,此时QM+QC 的值最小.18.解:(1)∵∠ADC是△ABD的外角,∴∠ADC=∠BAD+∠B=105°,∠DAE=∠BAC﹣∠BAD=30°,∴∠ADE=∠AED=75°,∴∠CDE=105°﹣75°=30°;(2)∠BAD=2∠CDE,理由如下:设∠BAD=x,∴∠ADC=∠BAD+∠B=45°+x,∠DAE=∠BAC﹣∠BAD=90°﹣x,∴∠ADE=∠AED=,∴∠CDE=45°+x﹣=x,∴∠BAD=2∠CDE;(3)设∠BAD=x,∴∠ADC=∠BAD+∠B=∠B+x,∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,∴∠ADE=∠AED=∠C+x,∴∠CDE=∠B+x﹣(∠C+x)=x,∴∠BAD=2∠CDE.19.解:(1)由题可得,BD=CE=2t,∴CD=12﹣2t,AE=8﹣2t,∴当AE=DC,时,8﹣2t=(12﹣2t),解得t=3,故答案为:3;(2)当△ABD≌△DCE成立时,AB=CD=8,∴12﹣2t=8,解得t=2,∴运动2秒时,△ABD≌△DCE能成立;(3)当△ABD≌△DCE时,∠CDE=∠BAD,又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,∴∠ADE=∠B,又∵∠BAC=α,AB=AC,∴∠ADE=∠B=(180°﹣α)=90°﹣α.故答案为:90°﹣α.20.解:(1)∵∠AFD=155°,∴∠DFC=25°,∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°,在Rt△FDC中,∴∠C=90°﹣25°=65°,∵AB=BC,∴∠C=∠A=65°,∴∠EDF=360°﹣65°﹣155°﹣90°=50°.(2)连接BF∵AB=BC,且点F是AC的中点,∴BF⊥AC,∠ABF=∠CBF=∠ABC,∴∠CFD+∠BFD=90°,∠CBF+∠BFD=90°,∴∠CFD=∠CBF,∴∠CFD=∠ABC.21.证明:(1)过点A作AF⊥BC于点F,∵AD=AE,∴DF=EF,∵BD=CE,∴BF=CF,∴AB=AC.(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,22.证明:∵AB=AC,∴∠C=∠B.又∵∠A+∠B+∠C=180°,∠A=60°,∴∠B=∠C=60°=∠A,∴△ABC是等边三角形.23.解:(1)如图所示:△ABC即为所求.(2)在△OMN和△AQP中,∵ON=AP,NM=PQ,OM=AQ,∴△OMN≌△AQP(SSS),∴∠PAQ=∠O=α.∵CE=CF,BE=BF,∴CB⊥EF(等腰三角形三线合一).故答案为:SSS,等腰三角形三线合一.24.(1))证明:∵DH垂直平分BC,∴BD=CD,∵BE⊥AC,BA⊥CD,∴∠A+∠DBF=90°,∠DBF+∠DFB=90°,∴∠A=∠DFB,在△ADC和△FDB中∴△ADC≌△FDB(AAS),∴BF=AC;(2)证明:①∵DF=DG,∴∠DGF=∠DFG,∵∠BGH=∠DGF,∴∠DGF=∠DFG,∵∠DBF+∠DFB=90°,∠FBC+∠BGH=90°,∴∠DBF=∠FBC,②在△ABE和△CBE中∴△ABE≌△CBE(ASA),∴AE=CE,∴AC=2CE,∵BF=AC,∴CE=BF.25.证明:(1)∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在△ADB和△CEA中,∵,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∵在△ADB和△CEA中,∵,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.(3)△DEF为等边三角形,理由如下:由(2)知△ADB≌△CEA,BD=AE,∠DBA=∠CAE,∵△ACF为等边三角形,∴∠CAF=60°,AF=AC,又∵AB=AC,∴AB=AF,∵∠BAC=120°,∴∠BAF=60°,∴△ABF是等边三角形,∴∠ABF=60°,BF=AF,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠EAF,∵BF=AF,∴△BDF≌△AEF(AAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安居区2020年下期期中八年级文化素质监测 数学试卷(附答案)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分总分150分。考试时间120分钟 第Ⅰ卷(选择题,满分54分)
一选择题(每小题3分,18小题共54分) 1、16的平方根是( ) A.﹣4 B.±2 C.±4 D.4
2、下列各数:722,39,5.12,327,0,25.0,3.1415926,π,23,2.181181118…(两个8之间1的个数逐次多1).其中是无理数的有( )个. A、1 B、2 C、3 D、4 3、下列说法错误的是( ) A.25的平方根是5 B.﹣6是36的平方根 C.﹣1的立方根是﹣1 D.-8的立方根是-2 4、下列运算正确的是( ) A.(﹣1)2020=﹣1 B.﹣22=4 C.=﹣3 D.=±4 5、下列运算正确的是( ) A.3x·93xx B.(x3)2=x5 C.x3÷03xx D.(2x)2=2x2 6、下列各式中,计算正确的是( ) A.x(2x﹣1)=2x2﹣1 B.(a+2b)(a﹣2b)=a2﹣4b2 C.(a+2)2=a2+4 D.(x+2)(x﹣3)=x2+x﹣6 7、下列等式由左边到右边的变形中,因式分解正确的是( ) A.m2﹣8m+16=(m﹣4)2 B.4x3y2+6x3y=x3y(4y+6) C.x2+2x+1=x(x+2)+1 D.(a+b)(a﹣b)=a2﹣b2 8、若实数x,y满足|x﹣3|+=0,则(x+y)3的平方根为( ) A.4 B.8 C.±4 D.±8 9、若34x,97y,则23xy=( )
A.494 B.74 C.43 D.167 10、下列多项式中不是完全平方式的是( ) A.a2﹣12a+36 B.x2﹣x+41 C.x2+4x﹣4 D.x2+2xy+y2 11、若4x2+(k﹣3)x+16是个完全平方式,则k的值是( ) A.11或﹣5 B.7 C.﹣13或19 D.﹣1或7 12、若(x﹣a)(x+6)的展开式中不含有x的一次项,则a的值是( ) A.0 B.6 C.﹣6 D.6或﹣6
13、计算201923×202032的结果是( ) A. B. C. D. /14、若2xy,2xy,则11xy的值是( ) A.1 B.1 C.5 D.3
15、若x+y=6,x2+y2=20,求x﹣y的值是( ) A.4 B.﹣4 C.2 D.±2 16、下列命题中,真命题是( ) A.两个锐角的和一定是钝角 B.相等的角是对顶角 C.一个三角形中至少有两个锐角 D.带根号的数一定是无理数 17、如图,边长为a的大正方形剪去一个边长为b的小正方形后,将剩余部分通过割补拼成新的图形.根据图形能验证的等式为( )
A.222)(baba B.))((22bababa C.2222)(bababa D.2222)(bababa 18、将实数按如图方式进行有规律排列,则第19行的第37个数是( )
A.19 B.﹣19 C. D.﹣ 第Ⅱ卷(非选择题,满分96分)
二、填空题(每小题4分,8小题共32分) 19、计算:6323)(xxx ▲ 。. 20、分解因式:822m=_____▲ ______. 21、如果一个数的平方根是2m+5与m-2,那么这个数是 ▲ . 22、已知322622yxyx且,则yx33____▲ ______ 23、若13的整数部分为a,小数部分为b,求132ba的值 ▲ . 24、在如图所示的数轴上,点C与点B关于点A对称,C、A两点对应的实数分别是5和1,则点B对应的实数为 ▲
25、将4个数a,b,c,d排成两行,两边各加一条竖直线记成a bc d,定义a bc d=bcad若
x+1 1-x
1-x x+1=8,则x=________. 26、如图,有一个长为20m,宽为10m的长方形草地,在草地中间有两条的小路,两条小路的任何地方宽度都是1m那么这片草地的面积是 ▲ 平方米。 三计算(每小题6分共12分) 27、分解因式:①24xx 28、分解因式 ②22242yxyx
29、计算:(每题8分,共计16分) (1) 计算:21163×91383 . (2)张老师给同学们出了一道题:当x=2020,y=2019时,求xyyxyxyx2222÷yx2的值.题目出完后,小明说:“老师给的条件y=2019是多余的.”小兵说:“不多余,不给这个条件,就不能求出结果.”你认为他们谁说得有道理?并说明你的理由.
30、先化简,再求值2)1()2)(1(xxx,其中x=21.(8分) 31、阅读下面的材料,解决问题.(8分) 例题:若0962222nnmnm,求m和n的值. 解:∵0962222nnmnm ∴0962222nnnmnm ∴0322nnm ∴m+n=0,n–3=0, ∴m=–3,n=3. 问题: (1)已知a,b,c是△ABC的三边长,且满足4181022baba求c的取值范围.
32、(10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下: ×xyxyyxxy2132122 (1)求所捂的多项式; (2)若x=32,y=21,求所捂多项式的值. 33、(10分)已知化简qxxpxx3822的结果中不含2x项和3x项. (1)求p,q的值. (2)qpxx322是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由. 安居区2020年下期期中八年级文化素质监测 数学试卷答案
一:选择题(共54分)
二:填空题(共32分) 19题 3x 20 题 222mm 21 题: 9 2 2 题:12 23题: 6 24 题:52 25题: 2 26题: 180
三计算(每小题6分共12分) 分解:原式题3...).........1(.2722xx )1)(1(2xxx..............6分
28题、解原式=分3.......).........2(222yxyx 分6..................)(22yx 29、计算:(每题8分,共计16分)
(1) 计算:21163×91383 .
解原式=2143×32×31.....................4分 =1143.........................................6分 =9........................................................8分 (2)解:小明说得有道理....................................................................................1分
(3)理由如下:原式)222(322223yxyxyxyx÷yx2.........................4分 yx3÷yx2....................................................................................6分
x.................................................................................................7分
所以该式子的结果与y的值无关,即小明说得有道理.(8分)..............................8分
题号 1 2 3 4 5 6 7 8 9 选项 B D A C C B A D B 题号 10 11 12 13 14 15 16 17 18 选项 C C B A D D C B A 30、(8分) 解原式=)12(2222xxxxx.......................4分 =122322xxxx...................................5分 =15x.................................................................6分
当21x
15x=5×121.................................................7分
23............................................................8分
31、(8分)) 解:(1)∵4181022baba
∴0168251022bbaa.........................................3分 ∴04522ba...........................................................5分 ∴a=5,b=4..................................................................................6分 因为a,b,c是三角形三边,根据三角形三边的关系可得 ∴132、(10分)
解(1)根据题意得:多项式=)213(22xyxyyx÷xy21......................3分 =126yx..........................................................6分 解(2)当x=32,y=21,时 126yx=6×232×121...................8分 =114......................................9分 =4................................................10分 33、(10分)
qxpqxpqxpx8248331234)原式解(....................2分
∵结果中不含2x项和3x项,∴08303pqp.....................................................4分
