动点产生的线段和差问题
初中几何中线段和差的最大值与最小值模型解析

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm B mA Bmn mnnmnnnm(4)台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)一个动点,一个定点:(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:m nmnm nmm2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
无锡新领航教育2012年全国中考数学(100套)压轴题分类解析汇编专题6:由运动产生的线段和差问题

无锡新领航教育
2012年全国中考数学(100套)压轴题分类解析汇编
专题6:由运动产生的线段和差问题
1.(2012北京市8分)在平面直角坐标系xoy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”, 给出如下定义:
若∣x 1-x 2∣≥∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣x 1-x 2∣;
若∣x 1-x 2∣<∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣y 1-y 2∣.
例如:点P 1(1,2),点P 2(3,5),因为∣1-3∣<∣2-5∣,所以点P 1与点P 2的“非常距离”为 ∣2-5∣=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A 1
(0)2-,,B 为y 轴上的一个动点, ①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标;
②直接写出点A 与点B 的“非常距离”的最小值;
(2)已知C 是直线3
y x 34=+上的一个动点,
①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标; ②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最 小值及相应的点E 和点C 的坐标。
【答案】解:(1)①(0,-2)或(0,2)。
②21。
(2)①设C 坐标为003x x 34⎛
⎫+ ⎪⎝⎭,,如图,过点C 作
CP ⊥x 轴于点P ,作CQ ⊥y 轴于点Q 。
由“非常距离”的定义知,当OP=DQ 时,点C 与点
D 的“非常距离”最小,。
初中几何中线段和与差最值问题

v1.0可编辑可修改初中几何中线段和(差)的最值问题、两条线段和的最小值。
基本图形解析:)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1 )点A B在直线m两侧:(2)点A B在直线同侧:*A'2、在直线m n上分别找两点P、Q,使PA+PQ+Q最小。
(1)两个点都在直线外侧:B(2)一个点在内侧,一个点在外侧:QB' (3)两个点都在内侧:m22(4 )、台球两次碰壁模型变式一:已知点 A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得变式二:已知点A 位于直线m,n 的内侧,在直线m二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B )1、两点在直线两侧:2、两点在直线同侧:围成的四边形ADEB 周长最短.n 分别上求点P 、Q 点PA+PQ+Q 周长最短.A"33(二)动点在圆上运动点B 在O O 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1、点与圆在直线两侧:三)、已知A B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定 在直线m 上要求P 、Q 两点,使得PA+PQ+Q 的值最小。
(原理用平移知识解)(1 )点A 、B 在直线m 两侧:A■- m作法:过A 点作AC// m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为 P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:2、点与圆在直 m线同侧:基础题1.如图1, / AOB45。
,P是/ AOB^一点,PO1Q, Q R分别是OA 0B上的动点,求厶PQR周长的最小值为 _____________________________分别是AD和AB上的动点,贝U BM+M的最小值为___________________________3、如图3,在锐角三角形ABC中,AB=5j2,/ BAC=45 BAC的平分线交BC于D, M N分别是AD和AB上的动点,贝U BM+MN勺最小值是______________ 。
中考数学之_线段和(差)的最值问题
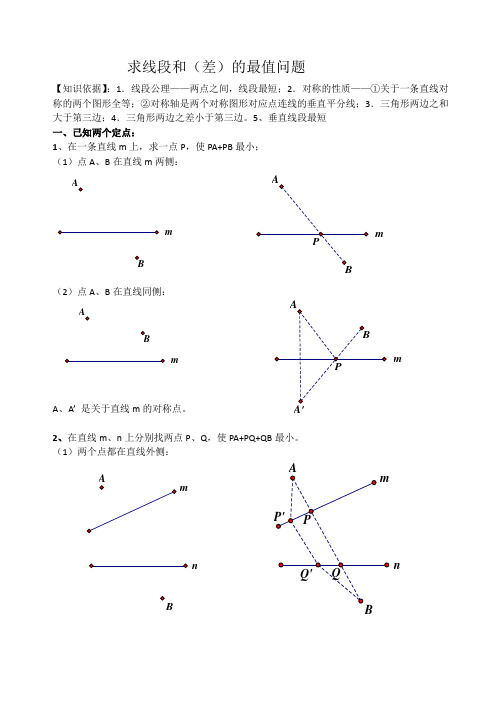
求线段和(差)的最值问题【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。
5、垂直线段最短 一、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:mm ABm ABm n mn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.nm Annnm二、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:m nm nm nmmmmm三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左移动PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:四、求两线段差的最大值问题(运用三角形两边之差小于第三边) 1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P ,此时PB=PB ’,PA-PB 最大值为AB ’BmmmmQ m Q一、在线段之和的最值问题中酝酿与构建,借用线段公理求解例1(湖北荆门)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN =30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )A 2BC 1D 2解析:PA+PB的线段之和最小值求法的依据是“平面几何中,两点之间线段最短”的数学模型与原理,故可作B关于MN的对称点是H,连接AH交MN于点P,AH的长就是PA+PB的线段之和的最小值,借助圆圆周角定理,可知根据∠AOH=90°,巧妙构造Rt△OAH,根据题意运用勾股定理可求出AH=,所以PA+PB的最小值为故选B。
(完整版)初中几何中线段和与差最值问题

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小; (1 )点A B在直线m两侧:■: m(2)点A B在直线同侧:2、在直线m n上分别找两点P、Q,(1)两个点都在直线外侧: 使PA+PQ+Q最小。
BPA'B(2)一个点在内侧,一个点在外侧:Q (3)两个点都在内侧:B'B'* 2(4 )、台球两次碰壁模型变式一:已知点 A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得 围成的四边形ADEB 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1两点在直线两侧:(二)动点在圆上运动点B 在O O 上运动,在直线 m 上找一点P ,使PA+PB 最小(在图中画出点 P 和点B ) 1点与圆在直线两侧:变式二:已知点 A 位于直线m,n 的内侧,在直线 m n 分别上求点 周长最短.P 、Q 点 PA+PQ+QA 2、两点在直线同侧:-:mP'A"B'2、点与圆在直线同侧:三)、已知A B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定在直线m上要求P、Q两点,使得PA+PQ+Q的值最小。
(原理用平移知识解)(1 )点A、B在直线m两侧:A■作法:过A点作AC// m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。
B'(2)点A B在直线m同侧:1.如图1, / AOB45。
,P是/ AOB^一点,PO10, Q R分别是OA 0B上的动点,求厶PQR周长的最小值为______________________________2、如图2,在锐角三角形ABC中,AB=4』^, / BAC=45,/ BAC的平分线交BC于点D, M,N分别是AD和AB上的动点,贝U BM+M的最小值为 ___________________________ .3、如图3,在锐角三角形ABC中,AB=5j2,/ BAC=45 BAC的平分线交BC于D, M N分别是AD和AB上的动点,贝U BM+MN勺最小值是______________ 。
中考复习线段(和差)最值与动点轨迹问题(教师版)

线段最值与轨迹长度问题(江岸模三)1、如图,已知△ABC中,∠ACB=90°,AC=BC=2,将边AC绕A点逆时针旋转得到AC′,E 为BC′的中点,则CE的最大值为。
取AB的中点,用斜边中线和中位线(2018四校3月联考)2、在平面直角坐标系,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8时,则点Q的运动路径长为。
82知识点常见特殊图形的性质【知识梳理】1、等边三角形的性质2、(特殊)平行四边形的性质3、圆的相关性质4、相似三角形的性质与判定5、锐角三角函数的性质【例题精讲一】线段(和差)最值问题例1. (2017硚口模三)1、如图,A(3,0),动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为。
(2017考霸四调模拟一)2、在平面直角坐标系中,点O为坐标原点,A(3,0)、B(33,0)、C(0,5),点D在直角坐标系中,且∠ADB=60°,则线段CD的长的最大值为()A.24-D.234+32+C.272-B.27(2017东西湖6月)3、如图,在平面直角坐标系中,点A (4,0)、B (4,4),点P 在半径为2的⊙O 上运动,则21AP +BP 的最小值是 。
【课堂练习】(2017青山模一)1、如图,在Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠PAB =∠PBC ,则线段CP 长的最小值为 。
(2017硚口四调模拟)2、如图,△ABC 中,AB =5,AC =3,BC =4,D 是BC 边上一动点,BE ⊥AD ,交其延长线于E ,EF ⊥AC ,交其延长线于F ,则AF 的最大值为 。
(2017外校题六)3、如图,A(0,6),B(8,0),点C是y轴上一动点,则12AC+BC最小值为。
完整word版,初中几何中线段和与差最值问题
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mm B mA Bmn mnn mnnn m(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:m nmnm nmm2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:作法:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:练习题 1.如图1,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为.2、如图2,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N分别是AD 和AB 上的动点,则BM+MN 的最小值为 .3、如图3,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是 。
最新中考数学之_线段和(差)的最值问题
求线段和(差)的最值问题【知识依据】:1.线段公理——两点之间,线段最短;2.对称的性质——①关于一条直线对称的两个图形全等;②对称轴是两个对称图形对应点连线的垂直平分线;3.三角形两边之和大于第三边;4.三角形两边之差小于第三边。
5、垂直线段最短 一、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:mm ABm ABm n mn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.nm Annnm二、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:m nm nm nmmmmm三、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左移动PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:四、求两线段差的最大值问题(运用三角形两边之差小于第三边) 1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B ’,连接AB ’交点直线m 于P,此时PB=PB ’,PA-PB 最大值为AB ’BmmmmQ m Q一、在线段之和的最值问题中酝酿与构建,借用线段公理求解例1 (湖北荆门)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN =30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )A 2BC 1D 2解析:PA+PB的线段之和最小值求法的依据是“平面几何中,两点之间线段最短”的数学模型与原理,故可作B关于MN的对称点是H,连接AH交MN于点P,AH的长就是PA+PB的线段之和的最小值,借助圆圆周角定理,可知根据∠AOH=90°,巧妙构造Rt△OAH,根据题意运用勾股定理可求出AH=,所以PA+PB的最小值为故选B。
初中几何中线段和和差最值问题
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:一)、已知两个定点:1、在一条直线m上,求一点P,使PA+PB最小;(1 )点A B在直线m两侧:AA. \*V%;-------------- *----------- * mP乂-- ---------------------------- -mBB(2)点A B在直线同侧:m A4B*------------------------------- • m2、在直线m n上分别找两点P、Q,使PA+PQ+Q最小。
(1 )两个点都在直线外侧:AQ' Q(2) —个点在内侧,一个点在外侧:(3)两个点都在内侧:B'(4 )、台球两次碰壁模型变式一:已知点A、B位于直线m,n的内侧,在直线n、v1.0可编辑可修改m分别上求点D E点,使得围成的四边形ADEB周长最短.变式二:已知点A位于直线m,n的内侧,在直线m二)、一个动点,一个定点:(一)动点在直线上运动:点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点1、两点在直线两侧:‘A An分别上求点P、Q点PA+PQ+Q周长最短.P和点B)2、两点在直线同侧:(二)动点在圆上运动点B在O O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)1、点与圆在直线两侧:2、点与圆在直线同侧:mPA'n*■ / ■三)、已知A B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定在直线m上要求P、Q两点,使得PA+PQ+Q的值最小。
(原理用平移知识解)(1 )点A、B在直线m两侧:A-■ -------- ■P QeB作法:过A点作AC// m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。
(2)点A、B在直线m同侧:B'练习题1.如图1, / AOB45。
中考数学压轴题分类解析汇编:由运动产生的线段和差问题
中考数学压轴题分类解析汇编由运动产生的线段和差问题4. (2012湖北恩施8分)如图,已知抛物线y=﹣x 2+bx+c 与一直线相交于A (﹣1,0),C (2,3)两点,与y 轴交于点N .其顶点为D .(1)抛物线及直线AC 的函数关系式;(2)设点M (3,m ),求使MN+MD 的值最小时m 的值;(3)若抛物线的对称轴与直线AC 相交于点B ,E 为直线AC 上的任意一点,过点E 作EF ∥BD 交抛物线于点F ,以B ,D ,E ,F 为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由;(4)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值.【答案】解:(1)由抛物线y=﹣x 2+bx+c 过点A (﹣1,0)及C (2,3)得,1b+c=04+2b+c=3--⎧⎨-⎩,解得b=2c=3⎧⎨⎩。
∴抛物线的函数关系式为2y x 2x 3=-++。
设直线AC 的函数关系式为y=kx+n ,由直线AC 过点A (﹣1,0)及C (2,3)得k+n=02k+n=3-⎧⎨⎩,解得k=1n=1⎧⎨⎩。
∴直线AC 的函数关系式为y=x+1。
(2)作N 点关于直线x=3的对称点N′,令x=0,得y=3,即N (0,3)。
∴N′(6, 3)由()22y x 2x 3=x 1+4=-++--得D (1,4)。
设直线DN′的函数关系式为y=sx+t ,则 6s+t=3s+t=4⎧⎨⎩,解得1s=521t=5⎧-⎪⎪⎨⎪⎪⎩。
∴故直线DN′的函数关系式为121y x 55=-+。
根据轴对称的性质和三角形三边关系,知当M (3,m )在直线DN′上时,MN+MD 的值最小, ∴12118m 3=555=-⨯+。
∴使MN+MD 的值最小时m 的值为185。
(3)由(1)、(2)得D (1,4),B (1,2),①当BD 为平行四边形对角线时,由B 、C 、D 、N 的坐标知,四边形BCDN是平行四边形,此时,点E 与点C 重合,即E (2,3)。
