因动点产生的线段和差问题专项讲解
初中几何中线段和差最大值最小值典型分析最全

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
mmm mABm(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:nmnnmnnnm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:m nmnmnm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度mmmm恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:QQP练习题1.如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值为.Q2、如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为.3、如图,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC 边上一点.若AE=2,EM+CM的最小值为 .5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF 直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC 上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2(B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
二次函数-因动点产生的线段和差问题经典例题.doc

二次函数-因动点产生的线段和差问题例1、在平面直角坐标系中,已知点J(-2,0), 〃(0,4),点、E 在0B 上,且上OAE= Z OBA.(1) 如图L,求点E 的坐标;(2) 如图2,将△昇加沿/轴向右平移得到ZUF O f ,连结"B 、BE' .① 设曲'=加其中0<刃<2,使用含刃的式子表示木用+加S 并求出使才用+3F 彳取得最小值时点用的坐标;② 当彳B+BE'取得最小值时,求点F 的坐标(直接写出结果即可).思路点拨1. 图形在平移的过程中・,对应点的连线平行且相等,EE 1 =AA f =/〃.2. 求彳$的最小值,第一感觉是用勾股定理列关于/〃的式子.3. 求才B+BE'的最小值,第一感觉是典型的“牛喝水”问题一一轴对称,两点之间 线段最短.满分解答(1) 由 ZOAE=ZOBA, ZAOE=ZBOA,得[\AOEs\BOA.rri ., AO BO m u 2 4所以——=—.因此一=一・OE OA 0E 2解得0E=\.所以00,1).(2) ①如图3,在Rt △才 加屮,OB=4, OA 1 =2—刃,所以才 仔=16+(2— 〃 在 Rt △应F 中,BE=3, EE' =m,所以 BE' 2=^+m ・所以"I^+BE' 2=16+(2-/7?)2 + 9+/W 2=2(/»-1)2+27.图2所以当〃尸1时,A 1Ef 2取得•最小值,最小值为27. 此时点彳是昇0的中点,点F 向右平移了 1个单位,所以E 1(1,1).考点伸展第(2)②题这样解:如图4-,过点〃作y 轴的垂线厶作点E'关于直线1的对称点 所以彳 B+BE' =A f R+BE'三点共线时,A r B+BE' f取得最小值,最小值为线段才E'在 Rt △川 O' E f '中,A r O' =2, O f =7,所以川 F '=后. 当才、B 、三点共线时,也=竺1.所以!1 = 1.BO E'O4 7解得m = -.此时£*(-,1). 77当才、B 、E f例2、如图1,在平面直角坐标系中,抛物线y=ax+bx+c经过/(一2, —4 )、0(0, 0)、M2, 0)三点.(1)求抛物线『=ax^+bx+c的解析式;(2)若点〃是该抛物线对称轴上的一点,求加/+〃”的最小值.图1答案(1) y = _討+ z (2)AM+ OM的最小值为4血.例3、如图1,在平面直角坐•标系中,抛物线尸=一#+2/+3与/轴交于爪B 两点、, 与y 轴交于点C 点〃是抛物线的顶点.(1) 求直线的解析式及〃、〃两点的坐标;(2) 点”是*轴上的一个动点,过"作直线〃/力。
线段和差最值问题解题技巧

线段和差最值问题解题技巧
1. 嘿,你知道吗?平移线段有时就像变魔术一样神奇!比如在这个问题里,把这两条线段平移到一起,你看,是不是一下子就找到答案啦!
2. 哇塞,利用对称性质来解决线段和差最值问题,那可真是绝了呀!就像给问题找到了一把万能钥匙。
比如这个图形,通过对称,一下子就柳暗花明了呢!
3. 哎呀呀,有时候转换思维超重要的啦!别死磕一种方法呀,就像走不通的路咱就换一条呗。
像这个例子,转换一下思考角度,答案不就出来啦!
4. 嘿,当遇到难题不要慌,想想三角形三边关系呀!这就好比给你指了一条明路。
比如看到这样的条件,马上想起三边关系,难题迎刃而解咯!
5. 哇哦,构造辅助线简直就是秘密武器呀!就如同给问题搭了一座桥。
像这个情况,构造出合适的辅助线,一下子就突破难关啦!
6. 哈哈,把复杂问题简单化,不就轻松多了吗?就像把一大团乱麻理清楚。
看这个例子,简单化之后,答案显而易见呀!
7. 哟呵,关注特殊点和特殊位置呀,这可是关键呢!如同发现了宝藏的线索。
像这个情况,抓住特殊点,难题瞬间攻克啦!
8. 嘿呀,寻找等量关系也很重要呀,就像在迷宫里找到了正确的路线。
看看这个例子,一旦找到等量关系,答案就水到渠成啦!
9. 最后我想说,掌握了这些解题技巧,遇到线段和差最值问题根本不用怕呀!它们就是我们的得力助手,能让我们在数学的海洋里畅游无阻呀!。
压轴题专题——因动点产生的线段和差问题
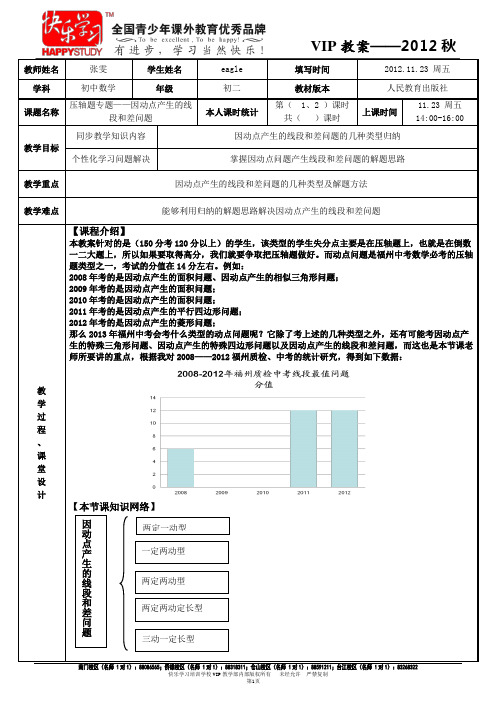
教师姓名张雯学生姓名eagle 填写时间2012.11.23 周五学科初中数学年级初二教材版本人民教育出版社课题名称压轴题专题——因动点产生的线段和差问题本人课时统计第( 1、2 )课时共()课时上课时间11.23 周五14:00-16:00教学目标同步教学知识内容因动点产生的线段和差问题的几种类型归纳个性化学习问题解决掌握因动点问题产生线段和差问题的解题思路教学重点因动点产生的线段和差问题的几种类型及解题方法教学难点能够利用归纳的解题思路解决因动点产生的线段和差问题教学过程、课堂设计【课程介绍】本教案针对的是(150分考120分以上)的学生,该类型的学生失分点主要是在压轴题上,也就是在倒数一二大题上,所以如果要取得高分,我们就要争取把压轴题做好。
而动点问题是福州中考数学必考的压轴题类型之一,考试的分值在14分左右。
例如:2008年考的是因动点产生的面积问题、因动点产生的相似三角形问题;2009年考的是因动点产生的面积问题;2010年考的是因动点产生的面积问题;2011年考的是因动点产生的平行四边形问题;2012年考的是因动点产生的菱形问题;那么2013年福州中考会考什么类型的动点问题呢?它除了考上述的几种类型之外,还有可能考因动点产生的特殊三角形问题、因动点产生的特殊四边形问题以及因动点产生的线段和差问题,而这也是本节课老师所要讲的重点,根据我对2008——2012福州质检、中考的统计研究,得到如下数据:【本节课知识网络】因动点产生的线段和差问题两定一动型一定两动型两定两动型两定两动定长型三动一定长型xyOx =1第25题AC B【题型一】两定一动型1.和的最小值例题.已知:在l 上求作一点M ,使得AM +BM 最小.解析:取两定点中的一个定点做动点所在直线的对称点,连接该点与另一定点交动点所在直线的点即为所求的点,满足和最小!练习.(聊城市中考)如图,已知抛物线()20y ax bx c a =++≠的对称轴为x =1,且抛物线经过()1,0A -()0,3C -两点,与x 轴交于另一点B .(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x =1上求一点M ,使点M 到点A 的距离与到点C 的距离之和最小,并求出此时点M的坐标;2.差最大例题.在l 上求作一点M ,使得|AM -BM |最大;(1)两定点在同侧(2)两定点在异侧练习.(福州市2012年质检22)如图,已知抛物线243y x bx c =++经过()()3,0,0,4A B 两点, (1)求此抛物线的解析式(2)若点D是第二象限内一点,以点D为圆心的圆分别于x轴,y轴,直线AB相交于点E,F,H。
第一讲线段和差中的动点
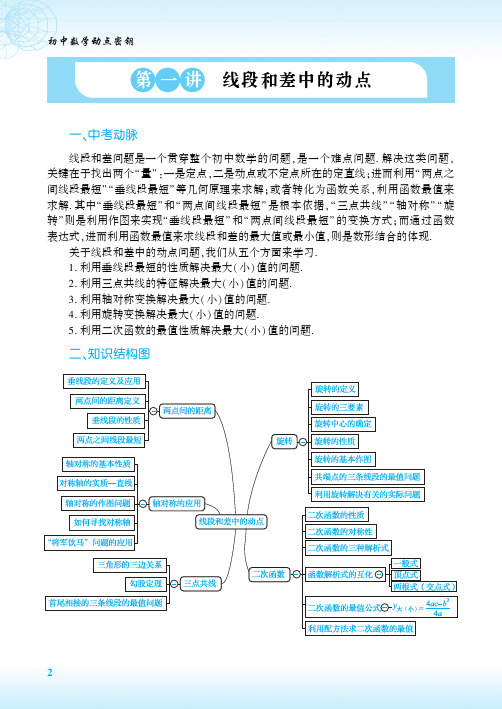
故答案为 3.
变式 1. 如下图所示,在△ABC 中,AB = 10,AC = 8,BC = 6,经过点 C 且与边 AB 相 切的动圆与 CB,CA 分别相交于点 E,F,则线段 EF 长度的最小值是 .
8
第一讲 线段和差中的动点
变式 2. 如下图所示,在 Rt△AOB 中,OA = OB = 3 2,☉O 的半径为 1,点 P 是 AB 边上的 动 点, 过 点 P 作 ☉O 的 一 条 切 线 PQ ( 点 Q 为 切 点) , 则 切 线 PQ 的 最 小 值 为 .
关于线段和差中的动点问题,我们从五个方面来学习. 1. 利用垂线段最短的性质解决最大(小)值的问题. 2. 利用三点共线的特征解决最大(小)值的问题. 3. 利用轴对称变换解决最大(小)值的问题. 4. 利用旋转变换解决最大(小)值的问题. 5. 利用二次函数的最值性质解决最大(小)值的问题.
二、知识结构图
∵ 在 Rt△ADB 中,∠ABC = 45°,AB = 2 2,
∴ AD = BD = 2,即此时圆的直径为 2,
由圆周角定理可知∠EOH =
1 2
∠EOF
= ∠BAC
= 60°,
∴
在
Rt△EOH 中,EH = OE·sin∠EOH = 1
×
3 2
=
23 ,
由垂径定理可知 EF = 2EH = 3,
考频:4 星 难度:3 星 错误率:70%
欲求 EF 的最小值,需要把 EF 进行转化,如何转化? 根据已知条件可以判断四边 形 ECFP 是矩形,EF 是矩形的对角线,它又有什么特点? 等于什么? 哪条线段有最小 值? 于是,联想到点到直线的距离最短为 .
连接 PC.
高考数学_浅析动点到两个定点的距离之和(差)的最值

浅析动点到两个定点的距离之和(差)的最值江苏省泰州市民兴实验中学马永华在高三复习过程中经常碰到有关求某曲线上的一个动点到两定点的距离之和(差)的最值.许多同学在面对此类问题时感到束手无策,无从下手。
本文就此类最值问题常见题型作初步探索。
一、直线上的动点到直线外两个定点的距离之和(差)的最值.例1(1)已知点A(1,1),点B(3,-2),P是x轴上任意一点,则PA+PB的最小值为,此时点P的坐标为;(2)已知点A(1,1),点B(3,2),P是x轴上任意一点,则PB-PA的最大值为,此时点P的坐标为.解析:(1)如图1,当点P在x轴上运动时,PA+PB?AB(当且仅当A,P,B三点共线时等号成立)∴(PA+PB)min =AB=此时,点P的坐标为(2)如图2,当点P在x轴上运动时,PB- PA ?AB(当且仅当A,P,B三点共线时等号成立)∴(PB-PA)max =AB=此时,点P的坐标为变题:(1)已知点A(1,1),点B(3,2),P是x轴上任意一点,则PA+PB的最小值为,此时点P的坐标为;解析:(1)如图3,作点B关于x轴的对称点B?(3,-2),则有PB=PB?当点P在x轴上运动时,PA+PB=PA+PB??AB?(当且仅当A,P,B?三点共线时等号成立)∴(PA+PB)min =AB?=此时,点P的坐标为(2)已知点A(1,1),点B(3,-2),P是x轴上任意一点,则PB-PA的最大值为,此时点P的坐标为.解析:(2)如图4,作点B关于x轴的对称点B?,则有PB=PB?当点P在x轴上运动时,PB- PA= PB?- PA ?AB?(当且仅当A,P,B?三点共线时等号成立)∴(PB-PA)max =AB?=此时,点P的坐标为归纳:①当两定点位于直线的异侧时可求得动点到两定点的距离之和的最小值;②当两定点位于直线的同侧时可求得动点到两定点的距离之和的绝对值的最大值.若不满足①②时,可利用对称性将两定点变换到直线的同(异)侧,再进行求解.如变题的方法.例2函数的值域为.解析:将函数进行化简得:即为动点P(x,0)到两定点A(1,1)、B(3,-2)的距离之和.由例1可知:该值域为二、圆锥曲线上的动点到两个定点的距离之和(差)的最值.(一)直接求解或利用椭圆(或双曲线)的定义进行适当转化后求解.例3(1)已知A(4,0)和B(2,2),M是椭圆上的动点,则MA-MB的范围是;解析:(1)如图5,在∆MAB中有MA-MB<AB,当M,A,B三点共线且MB>MA即点M位于M2处时,有MA-MB=AB,所以MA-MB?AB;同理在∆MAB中有MB-MA?AB,即MB-MA?-AB(当点M位于M1处时等号成立)综上所述:-AB?MA-MB?AB(2)已知A(4,0)和B(2,2),M是椭圆上的动点,则MA+MB的最大值是.解析:(2) 如图6,因为点A恰为椭圆的右焦点,所以由椭圆的定义可得MA+MB=10-MF+MB(F为椭圆的左焦点),同(1)可得MB-MF?BF(当且仅当点M位于点M4处时,等号成立)所以(MA+MB)max =(10-MF+MB)max=10+BF=10+点评:因为点A,B都在椭圆的内部(即两定点都在曲线的同侧),故可直接求出动点M到两定点A,B的距离之差的最值;若要求动点M到两定点A,B的距离之和的最值(其中A恰为焦点),需要利用椭圆的定义转化为动点M到两定点F,B的距离之差的最值(点F为另一焦点).例4(1)已知F是双曲线的左焦点,A(4,1),P是双曲线右支上的动点,则PA+PF的最小值为;解析:(1)如图7,在∆PAB中有PA+PF>AB,当P,A,F三点共线即点P位于P1处时,有PA+PF=AF,所以(PA+PF)min=AF=.(2)已知F是双曲线的左焦点,A(1,4),P是双曲线右支上的动点,则PA+PF 的最小值为.解析:(2)如图8,设F2是双曲线的右焦点,由双曲线的定义可得PA+PF=PA+2a+PF2=8+ PA+PF2?8+AF2(当P,A,F2三点共线即点P位于P2处时等号成立),所以(PA+PF)min=8+AF2=13.点评:本题需要特别关注点与双曲线的位置关系,两定点一定要在动点的轨迹(曲线)的异侧.(二)利用圆锥曲线的统一定义将圆锥曲线上的动点到焦点的距离与到相应准线的距离进行互化后进行求解.例5(1)已知点A(2,2),F是椭圆的右焦点,P是椭圆上的动点,则PF+PA的最小值是,此时,点的坐标为;解析:如图9,设点P到右准线的距离为PP?,由圆锥曲线的统一定义可知,即(当且仅当A,P,P?三点共线,即点P位于点P1处时取等号)此时点P的坐标为P(,2).(2)已知点A(5,2),F是双曲线的右焦点,P是双曲线上的动点,则PF+PA 的最小值是,此时点的坐标为.解析:如图10,设点P到右准线的距离为PP?,由圆锥曲线的统一定义可知,即(当且仅当A,P,P?三点共线,即点P位于点P1处时取等号)此时点P的坐标为P(,2)点评:此类最显著的特征是动点与焦点距离前有系数,可以利用圆锥曲线的统一定义将动点到焦点的距离转化为到相应准线的距离.例6(1)抛物线的焦点为F,A(4,-2)为一定点,在抛物线上找一点M,当MA+MF为最小值时,点M的坐标为;解析:如图11,为抛物线的准线,MM?为点M到准线的距离.利用抛物线的定义:MF=MM?,可得MA+MF= MA+MM??AM?(当且仅当A,M,M?三点共线时等号成立,即当点M在M?处时等号成立)此时点M的坐标为M(,-2)(2)P为抛物线上任一点,A(3,4)为一定点,过P作PP?垂直y轴于点P?,则AP+ PP?的最小值为.解析:如图12,延长PP?交抛物线的准线于点P??,由抛物线的定义:PP?=PF,所以AP+ PP?= AP+ PP??-1= AP+PF-1?AF-1(当且仅当A,P,F三点共线时等号成立,即当点P位于P1处时等号成立)点评:本题需要注意两点:①定点所在位置是抛物线的内部还是外部;②利用抛物线的定义将动点(在抛物线上)到焦点与到准线的距离进行互化.。
2019年中考数学复习1.7因动点产生的线段和差问题
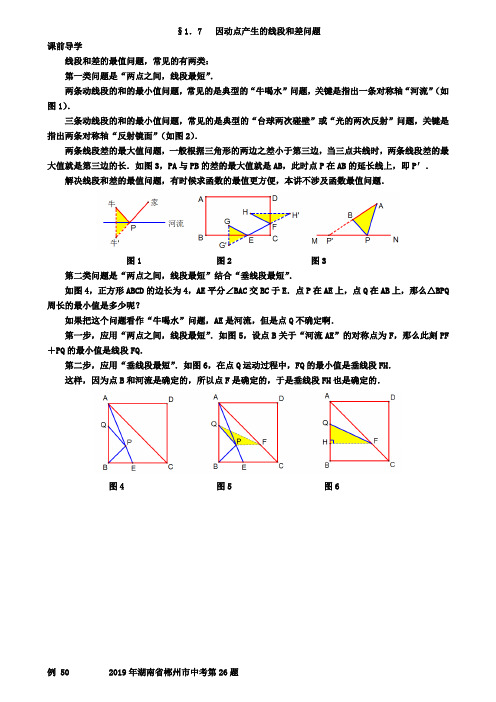
§1.7 因动点产生的线段和差问题课前导学线段和差的最值问题,常见的有两类:第一类问题是“两点之间,线段最短”.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1 图2 图3第二类问题是“两点之间,线段最短”结合“垂线段最短”.如图4,正方形ABCD的边长为4,AE平分∠BAC交BC于E.点P在AE上,点Q在AB上,那么△BPQ 周长的最小值是多少呢?如果把这个问题看作“牛喝水”问题,AE是河流,但是点Q不确定啊.第一步,应用“两点之间,线段最短”.如图5,设点B关于“河流AE”的对称点为F,那么此刻PF +PQ的最小值是线段FQ.第二步,应用“垂线段最短”.如图6,在点Q运动过程中,FQ的最小值是垂线段FH.这样,因为点B和河流是确定的,所以点F是确定的,于是垂线段FH也是确定的.图4 图5 图6例 50 2019年湖南省郴州市中考第26题已知抛物线y =ax 2+bx +c 经过A(-1, 0)、B(2, 0)、C(0, 2)三点. (1)求这条抛物线的解析式;(2)如图1,点P 是第一象限内此抛物线上的一个动点,当点P 运动到什么位置时,四边形ABPC 的面积最大?求出此时点P 的坐标;(3)如图2,设线段AC 的垂直平分线交x 轴于点E ,垂足为D ,M 为抛物线的顶点,那么在直线DE 上是否存在一点G ,使△CMG 的周长最小?若存在,请求出点G 的坐标;若不存在,请说明理由.图1 图2动感体验请打开几何画板文件名“14郴州26”,拖动点P 运动,可以体验到,当点P 运动到CB 的中点的正上方时,四边形ABPC 的面积最大.拖动点G 运动,可以体验到,当A 、G 、M 三点共线时,GC +GM 最小,△CMG 的周长最小. 思路点拨1.设交点式求抛物线的解析式比较简便.2.连结OP ,把四边形ABPC 的面积分割为三个三角形的面积和.3.第(3)题先用几何说理确定点G 的位置,再用代数计算求解点G 的坐标. 图文解析(1)因为抛物线与x 轴交于A(-1, 0)、B(2, 0)两点,设y =a(x +1)(x -2). 代入点C(0, 2),可得a =-1.所以这条抛物线的解析式为y =-(x +1)(x -2)=-x 2+x +2. (2)如图3,连结OP .设点P 的坐标为(x,-x 2+x +2). 由于S △AOC =1,S △POC =x ,S △POB =-x 2+x +2,所以S 四边形ABPC =S △AOC +S △POC +S △POB =-x 2+2x +3=-(x -1)2+4. 因此当x =1时,四边形ABPC 的面积最大,最大值为4.此时P(1, 2). (3)第一步,几何说理,确定点G 的位置:如图4,在△CMG 中,CM 为定值,因此当GC +GM 最小时,△CMG 的周长最小. 由于GA =GC ,因此当GA +GM 最小时,GC +GM 最小. 当点G 落在AM 上时,GA +GM 最小(如图5).图3 图4 图5 第二步,代数计算,求解点G 的坐标:如图6,AC =cos ∠CAO =AD AO AE AC ==52AE ==,E 3(,0)2.如图7,由y =-x 2+x +2=219()24x --+,得M 19()24,. 由A(-1, 0)、M 19()24,,得直线AM 的解析式为3322y x =+.作GH ⊥x 轴于H .设点G 的坐标为33(,)22x x +.由于tan ∠GEH =tan ∠ACO =12,所以12GH EH =,即EH =2GH .所以3332()222x x -=+.解得38x =-.所以G 315(,)816-.图6 图7 图8考点伸展第(2)题求四边形ABPC 的面积,也可以连结BC (如图8).因为△ABC 的面积是定值,因此当△PCB 的面积最大时,四边形ABPC 的面积也最大. 过点P 作x 轴的垂线,交CB 于F .因为△PCF 与△PBF 有公共底边PF ,高的和等于C 、B 两点间的水平距离,所以当PF 最大时,△PCB 的面积最大.设点P(x,-x 2+x +2),F(x,-x +2),那么PF =-x 2+2x . 当x =1时,PF 最大.此时P(1, 2).例 51 2019年湖南省湘西州中考第25题如图1,抛物线y =ax 2+bx +c 关于y 轴对称,它的顶点在坐标原点O ,点B 4(2)3-,和点C(-3,-3)均在抛物线上,点F 3(0)4-,在y 轴上,过点3(0)4,作直线l 与x 轴平行.(1)求抛物线的解析式和直线BC 的解析式;(2)设点D(x, y)是线段BC 上的一个动点(点D 不与B 、C 重合),过点D 作x 轴的垂线,与抛物线交于点G ,设线段GD 的长为h ,求h 与x 之间的函数关系式,并求出当x 为何值时,线段GD 的长度h 最大,最大长度h 的值是多少?(3)若点P(m, n)是抛物线上位于第三象限的一个动点,连结PF 并延长,交抛物线于另一点Q ,过点Q 作QS ⊥l ,垂足为S ,过点P 作PN ⊥l ,垂足为N ,试判断△FNS 的形状,并说明理由;(4)若点A(-2, t)在线段BC 上,点M 为抛物线上的一个动点,连结AF ,当点M 在何位置时,MF +MA 的值最小.请直接写出此时点M 的坐标与MF +MA 的最小值.图1动感体验请打开几何画板文件名“14湘西25”,点击屏幕左下方的按钮(2),拖动点D 在BC 上运动,可以体验到,当点D 是BC 的中点时,GD 最大.点击按钮(3),拖动点P 运动,可以体验到,△FNS 保持直角三角形的形状.点击按钮(4),拖动点M 运动,可以体验到,ME 与MF 保持相等,当AE 是垂线段时,ME +MA 最小. 思路点拨1.第(2)题用x 表示G 、D 两点的纵坐标,GD 的长就转化为关于x 的二次函数. 2.第(3)题是典型结论:抛物线上任意一点到直线l 的距离等于它与点F 间的距离. 3.第(4)题要经过两步说理,得到MF +MA 的最小值是点A 到l 的垂线段长. 图文解析(1)因为抛物线的顶点在坐标原点,所以y =ax 2.代入点C(-3,-3),得13a =-.所以抛物线的解析式为213y x =-.设直线BC 的解析式为y =kx +b ,代入B 4(2)3-,、C(-3,-3),得42,33 3.k b k b ⎧+=-⎪⎨⎪-+=-⎩ 解得13k =,b =-2.所以直线BC 的解析式为123y x =-.(2)由于点D 、G 分别在直线BC 和抛物线上,所以D 1(,2)3x x -,G 21(,)3x x -. 所以h =GD =211(2)33x x ---=21125(+)+3212x -.因此当12x=-时,h取得最大值,最大值为2512.(3)如图2,设点3(0)4,为H.设直线PQ的解析式为34y kx=-.联立直线PQ:34y kx=-与抛物线213y x=-,消去y,得21334x kx+-=.所以x1·x2=94-.它的几何意义是HS·HN=94.又因为HF=32.所以HF2=HS·HN.所以HF HSHN HF=.所以tan∠1=tan∠2.所以∠1=∠2.又因为∠1与∠3互余,所以∠2与∠3互余.所以△FNS是直角三角形.(4)MF+MA的最小值是83,此时点M的坐标是4(2,)3--.图2 图3 图4考点伸展第(3)题也可以通过计算得到PF=PN.同理得到QF=QS.这样我们就可以根据“等边对等角”及“两直线平行,内错角相等”,得到∠NFC=90°.应用这个结论,就容易解答第(4)题:如图3,作ME⊥l于E,那么MF=ME.当ME+MA的值最小时,MF+MA的值也最小.当A、M、E三点共线时,ME+MA的值最小,最小值为AE.而AE的最小值为点A到l的垂线段,即AE⊥l时,AE最小(如图4).2019-2020学年数学中考模拟试卷一、选择题1.方程x 2+6x ﹣5=0的左边配成完全平方后所得方程为( ) A .(x+3)2=14 B .(x ﹣3)2=14 C .(x+3)2=4 D .(x ﹣3)2=4 2.已知P (x ,y )是直线y =1322x -上的点,则4y ﹣2x+3的值为( ) A .3B .﹣3C .1D .03.已知二次函数y =x 2﹣4x+a ,下列说法错误的是( ) A .当x <1时,y 随x 的增大而减小 B .若图象与x 轴有交点,则a≤4C .当a =3时,不等式x 2﹣4x+a >0的解集是1<x <3D .若将图象向上平移1个单位,再向左平移3个单位后过点(1,﹣2),则a =﹣34.如图,已知a ∥b ,点A 在直线a 上,点B 、C 在直线b 上,∠1=120°,∠2=50°,则∠3为( )A .70°B .60°C .45°D .30°5.已知直线y =kx ﹣2经过点(3,1),则这条直线还经过下面哪个点( ) A .(2,0) B .(0,2)C .(1,3)D .(3,﹣1)6.若代数式42x -的值与0(1)-互为相反数,则x =( ) A .1B .2C .2-D .47.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的13,应从乙队调多少人去甲队?如果设应从乙队调x 人到甲队,列出的方程正确的是( ) A .1(96)723x x -=- B .196723x x ⨯-=-C .1(96)723x x+=-D .196(72)3x x +=- 8.如图是L 型钢材的截面,5个同学分别列出了计算它的截面积的算式,甲:()ac b c c +-;乙:()a c c bc -+;丙:2ac bc c +-;丁:()()ab a c b c ---;戊:()()a c c b c c -+-.你认为他们之中正确的是( )A .只有甲和乙B .只有丙和丁C .甲、乙、丙和丁D .甲、乙、丙、丁和戊9.已知ABC △,D 是AC 上一点,用尺规在AB 上确定一点E ,使ADE ∽ABC △,则符合要求的作图痕迹是( )A. B. C.D.10.转动A 、B 两个盘当指针分别指向红色和蓝色时称为配紫色成功。
“线段和差最值问题”专题学习 ppt

专题学习
1、如图,直线L外有点A与点B,点P是L 上一 动点,当PA+PB最小时,试确定点P的位置.
2、如图,射线AC外有一点B,点P是射线AC 上一动点,当PB + 1 PA最小时,试确定点 P
2 的位置.
◆如图,平面直角坐标系中,OA =2, 点P为 x 轴正半轴上一动点, ∠POA=30 °. 求:OP+2PA的最小值。分别是y轴与x轴上的动点, 当 MC+MN — 2 AN最小时,试确定动
2
点M、N 的位置,并求 MC+MN — 2 AN
2
的最小值。
◆如图,射线AC外有一点B,点P是射线AC 上一动点,
当PB — 1 PA 最小时,试确定点 P 的位置. 2
◆如图,点A在第一象限,点B在x轴正半轴上,点M、N分别是y轴与x轴上
的动点,当 MA+MN + 1 BN最小时,试在坐标系中确定动点M、N 的位置。 2
【思考】如图,抛物线 y x2 2x 3 与x轴交于A、B两点,抛物线的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因动点产生的线段和差问题专项讲解
线段和差的最值问题,常见的有两类:
第一类问题是“两点之间,线段最短”.
两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).
三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).
两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.
解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.
图1 图2 图3
第二类问题是“两点之间,线段最短”结合“垂线段最短”.
如图4,正方形ABCD的边长为4,AE平分∠BAC交BC于E.点P在AE上,点Q在AB上,那么△BPQ周长的最小值是多少呢?
如果把这个问题看作“牛喝水”问题,AE是河流,但是点Q不确定啊.
第一步,应用“两点之间,线段最短”.如图5,设点B关于“河流AE”的对称点为F,那么此刻PF+PQ的最小值是线段FQ.
第二步,应用“垂线段最短”.如图6,在点Q运动过程中,FQ的最小值是垂线段FH.这样,因为点B和河流是确定的,所以点F是确定的,于是垂线段FH也是确定的.
图4 图5 图6
已知抛物线y=ax2+bx+c经过A(-1, 0)、B(2, 0)、C(0, 2)三点.
(1)求这条抛物线的解析式;
(2)如图1,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
(3)如图2,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
图1 图2
拖动点P运动,可以体验到,当点P运动到CB的中点的正上方时,四边形ABPC的面积最大.拖动点G运动,可以体验到,当A、G、M三点共线时,GC+GM最小,△CMG 的周长最小.
思路点拨
1.设交点式求抛物线的解析式比较简便.
2.连结OP,把四边形ABPC的面积分割为三个三角形的面积和.
3.第(3)题先用几何说理确定点G的位置,再用代数计算求解点G的坐标.
图文解析
(1)因为抛物线与x轴交于A(-1, 0)、B(2, 0)两点,设y=a(x+1)(x-2).
代入点C(0, 2),可得a=-1.
所以这条抛物线的解析式为y=-(x+1)(x-2)=-x2+x+2.
(2)如图3,连结OP.设点P的坐标为(x,-x2+x+2).
由于S△AOC=1,S△POC=x,S△POB=-x2+x+2,
所以S四边形ABPC=S△AOC+S△POC+S△POB=-x2+2x+3=-(x-1)2+4.
因此当x=1时,四边形ABPC的面积最大,最大值为4.此时P(1, 2).
(3)第一步,几何说理,确定点G的位置:
如图4,在△CMG中,CM为定值,因此当GC+GM最小时,△CMG的周长最小.
由于GA =GC ,因此当GA +GM 最小时,GC +GM 最小. 当点G 落在AM 上时,GA +GM 最小(如图5).
图3 图4 图5
第二步,代数计算,求解点G 的坐标:
如图6,5AC =,cos ∠CAO =
5
AD AO AE AC ==,所以552AE AD ==,E 3(,0)2. 如图7,由y =-x 2+x +2=219()24x --+,得M 19()24
,. 由A (-1, 0)、M 19()24,,得直线AM 的解析式为3322
y x =+. 作GH ⊥x 轴于H .设点G 的坐标为33(,)22
x x +. 由于tan ∠GEH =tan ∠ACO =12,所以12
GH EH =,即EH =2GH . 所以3332()222x x -=+.解得38x =-.所以G 315(,)816-.
图6 图7 图8
考点伸展
第(2)题求四边形ABPC 的面积,也可以连结BC (如图8).
因为△ABC 的面积是定值,因此当△PCB 的面积最大时,四边形ABPC 的面积也最大. 过点P 作x 轴的垂线,交CB 于F .
因为△PCF 与△PBF 有公共底边PF ,高的和等于C 、B 两点间的水平距离,所以当PF 最大时,△PCB 的面积最大.
设点P (x ,-x 2+x +2),F (x ,-x +2),那么PF =-x 2+2x .
当x =1时,PF 最大.此时P (1, 2).
如图1,抛物线y =ax 2+bx +c 关于y 轴对称,它的顶点在坐标原点O ,点B 4(2)3-,和点C (-3,-3)均在抛物线上,点F 3(0)4-,在y 轴上,过点3(0)4
,作直线l 与x 轴平行.
(1)求抛物线的解析式和直线BC 的解析式;
(2)设点D (x , y )是线段BC 上的一个动点(点D 不与B 、C 重合),过点D 作x 轴的垂线,与抛物线交于点G ,设线段GD 的长为h ,求h 与x 之间的函数关系式,并求出当x 为何值时,线段GD 的长度h 最大,最大长度h 的值是多少?
(3)若点P (m , n )是抛物线上位于第三象限的一个动点,连结PF 并延长,交抛物线于另一点Q ,过点Q 作QS ⊥l ,垂足为S ,过点P 作PN ⊥l ,垂足为N ,试判断△FNS 的形状,并说明理由;
(4)若点A (-2, t )在线段BC 上,点M 为抛物线上的一个动点,连结AF ,当点M 在何位置时,MF +MA 的值最小.请直接写出此时点M 的坐标与MF +MA 的最小值.
图1
拖动点D 在BC 上运动,可以体验到,当点D 是BC 的中点时,GD 最大.点击按钮(3),拖动点P 运动,可以体验到,△FNS 保持直角三角形的形状.点击按钮(4),拖动点M 运动,可以体验到,ME 与MF 保持相等,当AE 是垂线段时,ME +MA 最小.
思路点拨
1.第(2)题用x 表示G 、D 两点的纵坐标,GD 的长就转化为关于x 的二次函数.
2.第(3)题是典型结论:抛物线上任意一点到直线l 的距离等于它与点F 间的距离.
3.第(4)题要经过两步说理,得到MF +MA 的最小值是点A 到l 的垂线段长.
图文解析
(1)因为抛物线的顶点在坐标原点,所以y =ax 2.
代入点C (-3,-3),得1
3a =-.所以抛物线的解析式为213
y x =-.
设直线BC 的解析式为y =kx +b ,代入B 4(2)3-,、C (-3,-3)
,得42,33 3.
k b k b ⎧+=-⎪⎨⎪-+=-⎩ 解得13k =
,b =-2.所以直线BC 的解析式为123y x =-.
(2)由于点D 、G 分别在直线BC 和抛物线上,所以D 1
(,2)3x x -,G 21(,)3
x x -. 所以h =GD =211(2)33x x ---=21125(+)+
3212
x -. 因此当12x =-时,h 取得最大值,最大值为2512
. (3)如图2,设点3(0)4,为H .设直线PQ 的解析式为34
y kx =-. 联立直线PQ :34y kx =-与抛物线213y x =-,消去y ,得213034
x kx +-=. 所以x 1·x 2=94-.它的几何意义是HS ·HN =94
. 又因为HF =32.所以HF 2=HS ·HN .所以HF HS HN HF =. 所以tan ∠1=tan ∠2.所以∠1=∠2.
又因为∠1与∠3互余,所以∠2与∠3互余.所以△FNS 是直角三角形.
(4)MF +MA 的最小值是8
3,此时点M 的坐标是4(2,)3
--.
图2 图3 图4
考点伸展
第(3)题也可以通过计算得到PF =PN .同理得到QF =QS .这样我们就可以根据“等边对等角”及“两直线平行,内错角相等”,得到∠NFC =90°.
应用这个结论,就容易解答第(4)题:
如图3,作ME ⊥l 于E ,那么MF =ME .
当ME+MA的值最小时,MF+MA的值也最小.
当A、M、E三点共线时,ME+MA的值最小,最小值为AE.
而AE的最小值为点A到l的垂线段,即AE⊥l时,AE最小(如图4).。
