美式期权二叉树定价及MATLAB程序
期权的定价方法概述及利用matlab计算期权价格

期权的定价方法概述及利用matlab计算期权价格摘要期权是功能最多、最激动人心的融衍生工具之一。
期权定价问题一直是金融数学当中最复杂的问题之一,简要介绍几种基本的期权定价理论,并利用matlab金融工具箱计算出香港恒生指数期权的价格并与实际价格进行比较,指出可能导致偏差的一些原因。
关键词期权定价;MATLAB;B-S模型1 期权概述期权是一种独特的衍生金融产品,实质上是将权利和义务分开进行定价,使得权利的受让人在规定时间内对于是否进行交易,行使其权利具有选择权,而义务方必须履行其义务。
它使买方能够避免坏的结果,同时,又能从好的结果中获益。
2 期权的定价模型2.1 二项式期权定价模型设:S0=股票现行价格,u=股价上行乘数,d=股价下行乘数,r=无风险利率,C0=期权现行价格,Cu=股价上行时期权的到期日价值,Cd=股价下行时期权的到期日价值,X=期权的执行价格,H=套期保值比率,则二项式定价模型为:u=1+上升百分比=d=1+下降百分比=其中:e是自然对数;σ为标的资产连续复利收益率的标准差;t为以年表示的时段长度。
2.2 Black—Scholes期权定价模型1)假设条件B-S微分方程的推导是建立在以下假设的基础上的:①股价遵循预期收益率μ和标准差σ为常数的马尔科夫随机过程;②允许使用全部所得卖空衍生证券;③没有交易费用或税金,且所有证券高度可分;④在衍生证券的有效期内没有支付红利;⑤不存在无风险的套利机会;⑥证券交易是连续的,股票价格连续平滑变动;⑦无风险利率r为常数,能够用同一利率借入或贷出资金;⑧只能在交割日执行期权。
2)Black—Scholes期权定价公式C=SN(d1)-Xe-rTN(d2)P=C-X+Xe-rT=Xe-rT · N(-d2)-S · N(-d1),式中:C表示买入期权的价格;S表示标的资产的现行市场价格;r表示无风险利率(以连续复利率计算);σ表示标的资产的价格波动率;X表示看涨期权的执行价格;T表示距离期权到期日的时间(以年表示);t表示现在的时间;N(x)表示标准正态分布变量的累积概率分布函数。
期权定价公式的二叉树推导与分析

期权定价公式的二叉树推导与分析期权作为金融衍生品的重要组成部分,对于投资者和风险管理师来说具有重要意义。
期权的价值取决于多种因素,包括标的资产的价格、行权价格、剩余到期时间、无风险利率、波动率等。
期权的定价是金融领域的一个重要问题,准确的期权定价可以帮助投资者更好地进行投资决策和风险管理。
本文将介绍期权的定价公式,并通过二叉树的方法推导期权的价格,最后对各种情况下期权定价的计算方法与特点进行分析。
期权的定价公式是由费雪·布莱克、迈伦·斯科尔斯和罗伯特·默顿提出的布莱克-斯科尔斯模型。
该模型基于一些假设,例如无摩擦市场、无套利机会等,通过 Black-Scholes方程求解期权的定价。
具体公式如下:C = SₐN(d1) - XₐN(d2)其中, C为期权的公允价值; Sₐ为标的资产当前的价格; Xₐ为期权的行权价格; N(d1)和 N(d2)分别为正态分布变量的累积分布函数;d1和 d2分别为: d1 = (ln(Sₐ/Xₐ) + (r + σ²/2)T) / (σ√T) d2 = d1 - σ√T T为期权的剩余到期时间,以年为单位; r为无风险利率;σ为标的资产的年波动率。
二叉树方法是一种常用的期权定价模型,它可以用来推导期权的预期价格。
二叉树方法的思路是将期权的到期时间划分为若干个时间段,并假设标的资产在每个时间段内只有两种可能的价格,即上涨或下跌。
基于这个假设,我们可以构建一个二叉树来描述标的资产的价格变动情况。
假设初始时刻为 t0,标的资产的价格为 S0,行权价格为 X。
在每个时间段Δt内,标的资产的价格有两种可能的变化:上涨到 Su = S0 × u,或者下跌到 Sd = S0 × d,其中 u > 1,d < 1,u和 d分别为标的资产的上涨和下跌因子。
假设该期权的剩余到期时间为 T,共分为 n个时间段。
那么在 t0时,该期权的预期价格为:C0 = ∑CN(d1, d2, u, d) × (u × S0 - X)^+ ×Δt其中, N(d1, d2, u, d)为风险中性概率; (u × S0 - X)^+表示当标的资产价格上涨时,取 u × S0 - X,否则取 0;Δt为每个时间段的时间长度。
基于MATLAB的美式期权定价的教学思考

基于MATLAB的美式期权定价的教学思考
宋丽平
【期刊名称】《廊坊师范学院学报(自然科学版)》
【年(卷),期】2014(014)004
【摘要】以二叉树方法和有限差分方法为例,探讨如何利用MATLAB进行美式期权定价的教学.首先对数值方法的原理进行简介,然后利用MATLAB进行编程计算,这样可以提高学生的学习兴趣.
【总页数】4页(P118-121)
【作者】宋丽平
【作者单位】莆田学院,福建莆田351100
【正文语种】中文
【中图分类】O241.8
【相关文献】
1.基于三叉树模型的美式期权定价及其Matlab算法 [J], 董丽沙;王湘玉
2.运用Matlab基于LSM方法对美式期权定价的新探究 [J], 刘海永;严红
3.Matlab与Visual C++混合编程在美式期权定价中的应用 [J], 廖小漩;王孔敬
4.Matlab与Visual C++混合编程在美式期权定价中的应用 [J], 廖小漩;王孔敬
5.基于MATLAB的美式期权定价的教学思考 [J], 宋丽平
因版权原因,仅展示原文概要,查看原文内容请购买。
期权定价理论及其Matlab实现过程

这里 :
d =— ( ( / + (+s / )( O l I S t X) r 2 n ) 2 T
-
— —
收录 日期:0 2年 4月 1 21 7日
期望回报率 , 8为股 票价格波动率 , 为无 r
风险 资产 收益率且 有 0 rm:W ( << d D是标 格 :
其三 , 田素华 (0 2 研究 了境 内外交 高, 20) 从而导致高抑价现象 的出现 。周孝华 的文 献基本上 是从宏观 的制度层 面讨论 叉上市企业 的 IO价格差异 ,发现 A股 等 (O5 也 以换手率和 看涨指标 作为投 这一 问题 , P 2O) 很少有 人从抑价 形成 的微观机
金
资
期权 定价理 论及其 Ma a t b实现过程 l
口丈 /罗 琰
( 南京审计学院数学与统计学院 江苏 ・ ) 南京
[ 提要] 期权定价理论 是现代金 融 融定量分析提供 了强有力的数学工具。
为: [ a( ① 一 ,) , 龟 m xS X o3 其中壹 表示风险
中性条件下的期望值 。 根据风险中性定价 原理 , 不付红利欧式看涨期权价格 C等于 现 值, 即:
关键 词:a b 教学实践 gta ; J
基金项 目:国家 自然科学 基金项 目
(0 7 7 ;教育部 人文 社科青 年项 目 7 9 1 3) 0
( Y C H 8 1 JZ 1 ) 2 2
I nC 无风 险资产价格 R ( t )服从如 下方 获得无风险收益率 。因此 , S D的分 布 只要将 m换成 r 即可 : 程:
明和梁洪昀 (0 1 加入了换手率因素 , 2o) 发 原因。然而 , 这只 能表 明某些敏感 因素对 [】 2 曹凤岐 , 董秀 良. 国 IO定价合理性 我 P
期权定价的二叉树模型
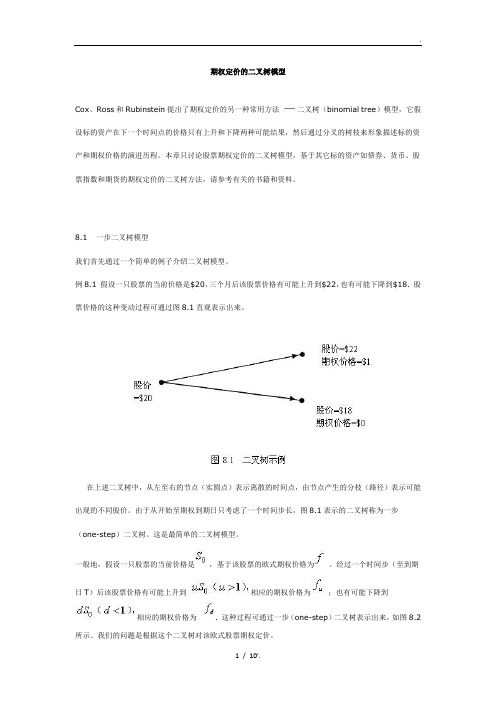
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树(binomial tree)模型,它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果,然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。
本章只讨论股票期权定价的二叉树模型,基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法,请参考有关的书籍和资料。
8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。
例8.1 假设一只股票的当前价格是$20,三个月后该股票价格有可能上升到$22,也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。
在上述二叉树中,从左至右的节点(实圆点)表示离散的时间点,由节点产生的分枝(路径)表示可能出现的不同股价。
由于从开始至期权到期日只考虑了一个时间步长,图8.1表示的二叉树称为一步(one-step)二叉树。
这是最简单的二叉树模型。
一般地,假设一只股票的当前价格是,基于该股票的欧式期权价格为。
经过一个时间步(至到期日T)后该股票价格有可能上升到相应的期权价格为;也有可能下降到相应的期权价格为. 这种过程可通过一步(one-step)二叉树表示出来,如图8.2所示。
我们的问题是根据这个二叉树对该欧式股票期权定价。
为了对该欧式股票期权定价,我们采用无套利(no arbitrage)假设,即市场上无套利机会存在。
构造一个该股票和期权的组合(portfolio),组合中有股的多头股票和1股空头期权。
如果该股票价格上升到,则该组合在期权到期日的价值为;如果该股票价格下降到,则该组合在期权到期日的价值为。
根据无套利假设,该组合在股票上升和下降两种状态下的价值应该相等,即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。
在这种情况下,该组合是无风险的。
以表示无风险利率,则该组合的现值(the present value)为,又注意到该组合的当前价值是,故有即将(8.1)代入上式,可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是,由于我们是在无套利(no arbitrage)假设下讨论欧式股票期权的定价,因此无风险利率应该满足: .现在回到前面的例子中,假设相应的期权是一个敲定价为$21,到期日为三个月的欧式看涨权,无风险的年利率为12%,求该期权的当前价值。
二叉树看涨期权

针对以某一发行美式看跌期权的公司为例,应用二叉树模型为其定价。
2010年12月20日该股票价格为26元,标的股票到期的行权价格为20元,无风险收益率为0.0217,权证存续期为10个月,波动率的标准差为0.35,不发放红利,该权证12月20日的收盘价为2.55元。
看跌不发红利股票价格为26元,标的股票到期的行权价格为20元,无风险收益率为0.0217,权证存续期为10个月,波动率的标准差为0.35程序:function price = AmPutLattice(S0,K,r,T,sigma,N)% Precompute invariant quantitiesdeltaT = T/N;u=exp(sigma * sqrt(deltaT));d=1/u;p=(exp(r*deltaT) - d)/(u-d);discount = exp(-r*deltaT);p_u = discount*p;p_d = discount*(1-p);% set up S valuesSVals = zeros(2*N+1,1);SVals(N+1) = S0;for i=1:NSVals(N+1+i) = u*SVals(N+i);SVals(N+1-i) = d*SVals(N+2-i);end% set up terminal valuesPVals = zeros(2*N+1,1);for i=1:2:2*N+1PVals(i) = max(K-SVals(i),0);end% work backwardsfor tau=1:Nfor i= (tau+1):2:(2*N+1-tau)hold = p_u*PVals(i+1) + p_d*PVals(i-1);PVals(i) = max(hold, K-SVals(i));endendprice = PVals(N+1);调用方式:price = AmPutLattice(S0,K,r,T,sigma,N) 结果为:>> price=AmPutLattice(58,50,0.025,7/12,0.45,100)。
期权定价的数值方法
金融计算与编程
上海财经大学金融学院 曹志广
直接调用 c=latticeeucall(52,50,0.1,6/12,0.2,500)得到:c= 5.5644 直接调用 p=latticeeuput(52,50,0.1,6/12,0.2,100)得到:p=1.1308; 直接调用 p=latticeeuput(52,50,0.1,6/12,0.2,200)得到:p=1.1240; 直接调用 p=latticeeuput(52,50,0.1,6/12,0.2,500)得到:p=1.1259 由以上计算可以看出:随着二叉树阶段数的增加,即时间间隔 ∆t 的减少,二叉树模型 的计算结果与期权价格的解析解也逐步接近。
T T T − r∆t
u = eσ
, d = e −σ
∆t
p=
e r∆t − d = 0.5076 u−d
∆t
股票价格的运动如图所示,期权的二叉树图如图所示。
u = eσ
= 1.1224, d = e −σ
∆t
= 0.8909
2
金融计算与编程
上海财经大学金融学院 曹志广
股票价格的运动
股票价格的运动
金融计算与编程
上海财经大学金融学院 曹志广
lattice(i+1,j+1)=exp(-r*deltaT)*(p*lattice(i+2,j+2)+(1-p)*lattice(i+2,j+1)); end end price=lattice(1,1);
function [price,lattice]=latticeamcall(S0,K,r,T,sigma,N) deltaT=T/N;u=exp(sigma*sqrt(deltaT)); d=1/u;p=(exp(r*deltaT)-d)/(u-d); lattice=zeros(N+1,N+1); for j=0:N lattice(N+1,j+1)=max(0,(S0*(u^j)*(d^(N-j))-K)); end for i=N-1:-1:0 for j=0:i lattice(i+1,j+1)=max(exp(-r*deltaT)*(p*lattice(i+2,j+2)+(1-p)*lattice(i+2,j+1)),-K+S0*u^j*d^ (i-j)); end end price=lattice(1,1); function [price,lattice]=latticeamput(S0,K,r,T,sigma,N) deltaT=T/N;u=exp(sigma*sqrt(deltaT)); d=1/u;p=(exp(r*deltaT)-d)/(u-d); lattice=zeros(N+1,N+1); for j=0:N lattice(N+1,j+1)=max(0,-(S0*(u^j)*(d^(N-j))-K)); end for i=N-1:-1:0 for j=0:i lattice(i+1,j+1)=max(exp(-r*deltaT)*(p*lattice(i+2,j+2)+(1-p)*lattice(i+2,j+1)),K-S0*u^j*d^( i-j)); end end price=lattice(1,1);
期权定价-二叉树模型
期权定价-二叉树模型期权定价是金融市场中的重要内容,它是根据期权的特点和市场条件来确定期权价格的过程。
二叉树模型是一种常用的期权定价方法之一,其基本思想是将时间离散化,并通过构建一个二叉树来模拟标的资产价格的变动。
在二叉树模型中,每个节点代表了一个特定的时刻,而每个节点之间的关系是通过上涨和下跌两种情况进行连接的。
通过调整上涨和下跌的幅度,可以模拟出不同标的资产的价格变动情况。
期权的定价在二叉树模型中可以通过回溯法进行计算。
首先,在最后一个节点上,根据期权的特点以及市场条件来确定期权的价值。
然后,逐步向前回溯,通过考虑不同的路径来计算每个节点上的期权价值。
在回溯过程中,需要考虑每个节点的两个子节点的权重,即上涨和下跌的概率。
这可以根据市场条件来确定,通常是基于历史数据进行估计。
然后,在回溯过程中,可以根据节点上的期权价值和子节点的权重来计算每个节点的期权价格。
通过不断回溯,最终可以得到期权的初始价值,即在当前市场条件下,期权价格应该是多少。
这个初始价值可以用作参考,帮助投资者做出合理的投资决策。
需要注意的是,二叉树模型是一个简化的模型,它有一些假设和限制。
首先,它假设标的资产的价格只有上涨和下跌两种情况,而忽略了其他可能的情况。
其次,它假设市场条件在整个期权有效期内保持不变,而实际情况可能是变化的。
因此,在使用二叉树模型进行期权定价时,需要注意这些假设和限制。
总而言之,期权定价是金融市场中的重要内容,二叉树模型是一种常用的定价方法。
通过构建二叉树模型,并根据回溯法计算每个节点上的期权价值,可以得到期权的初始价格。
然而,需要注意二叉树模型的假设和限制,并结合实际情况进行综合分析和判断。
期权定价是金融市场中的重要内容,其旨在确定期权的合理价格。
期权是一种金融工具,赋予购买者在期权到期时以约定价格购买或出售标的资产的权利。
很多投资者都希望能够在市场上买入或者卖出期权,以便于在未来某个时刻获得利润。
因此,了解期权的合理价格对投资者来说至关重要。
美式期权价格公式
美式期权价格公式美式期权是一种可以在到期日前任意时间行使的期权合约,与欧式期权相比,具有更高的灵活性。
因此,为了计算美式期权的价格,我们需要使用不同的公式。
美式期权的价格可以通过两种方法进行计算:理论定价方法和模拟方法。
下面我们将介绍具体的美式期权定价公式,包括Black-Scholes期权定价模型、树模型(二叉树和三叉树)和蒙特卡洛模拟方法。
1. Black-Scholes期权定价模型Black-Scholes期权定价模型是最常见的对欧式期权进行定价的模型。
然而,对于美式期权,Black-Scholes模型并不适用。
美式期权的特点是可以在到期日前任意时间行使,因此在到期前,股价可能会有剧烈波动。
这种情况下,使用Black-Scholes模型来计算美式期权的价格会导致低估。
2.树模型(二叉树和三叉树)树模型是一种常用的计算美式期权价格的方法。
树模型基于假设股价会按照指数过程增长,并根据风险中性概率构建一个期权价格的二叉或三叉树。
对于二叉树模型,可以根据不同的参数(股价、期权价格、无风险利率等)构建一棵二叉树,并通过回溯计算每个节点的期权价格。
通过比较每个节点的预期回报和早期执行的收益,可以决定何时行使期权。
类似地,三叉树模型也是一种计算美式期权价格的有效方法。
三叉树模型在二叉树模型的基础上增加了一个附加节点,使得股价有三种可能的变动。
这样可以更准确地估计股价的变动范围,提高美式期权价格的准确性。
3.蒙特卡洛模拟方法蒙特卡洛模拟方法是一种基于随机模拟的计算美式期权价格的方法。
该方法通过生成大量的随机路径,以确定期权价格的期望值。
在蒙特卡洛模拟中,我们首先需要设定一个股价的路径模型,如几何布朗运动模型。
然后,通过生成多条随机路径,计算每条路径对应的期权价格,并取平均值作为期权价格的估计值。
蒙特卡洛模拟方法的优点在于可以处理复杂的期权合约和多种因素的影响,但由于需要生成大量路径进行模拟,计算速度可能较慢。
二叉树期权定价模型
两步二叉树模型
24.2 22 20 18 16.2 • 每步长为3个月
2012-1-4 陕西科技大学理学院 14
19.8
欧式看涨期权的估值
D
22 20 1.2823
A
B
24.2 3.2 19.8 0.0 16.2 0.0
2.0257 18 0.0
C
E
• 在节点 B的价值 = e–0.12´0.25(0.6523´3.2 + 0.3477´0) = 2.0257 • 在节点 A的价值 = e–0.12´0.25(0.6523´2.0257 + 0.3477´0) = 1.2823
1.二叉树期权定价模型 二叉树期权定价模型
把期权的有效期分为很多很小的时间间隔 ∆t 并假设在每一个时间间隔 内证券 ∆t 价格只有两种运动的可能: 价格只有两种运动的可能:
,
1、从开始的 S 上升到原先的 u 倍,即到达 Su 2、下降到原先的 d 倍,即 Sd 。 如图5.1所示。 5.1所示 其中 u > 1 d < 1.如图5.1所示。价格上升的概率假设为 1− p 。
ƒu − fd ∆ = Su − Sd
2012-1-4 陕西科技大学理学院 8
推广到一般情形
(continued)
• 组合在时刻 T的价值为 Su ∆ – ƒu • 组合在时刻0的价值为 (Su ∆ – ƒu )e–rT • 组合在时刻0 的价值又可以表达 为S∆–f • 从而 ƒ = S ∆ – (Su ∆ – ƒu )e–rT
二叉树方法的一般定价过程-以无收益证券的美式看跌期权为例 二叉树方法的一般定价过程-
2012-1-4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
美式期权二叉树定价及MATLAB程序
美式期权二叉树定价及MATLAB程序
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们
对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(美式期权二叉树定价及
MATLAB程序)的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,
这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以
下为美式期权二叉树定价及MATLAB程序的全部内容。
美式期权二叉树定价及MATLAB程序
金融随机分析课程
美式期权的二叉树定价
1、对于连续随机游走:
可以用离散格随机游走模型来表示,即标的资产的价格只在离散时间点,2
,3,…,N取值,表示很小但非无穷小的时间步长;如果标的资产在时刻m
的价格为,那么在时刻(m+1)其价格有两种可能的值:和,
并且标的资产的价格从上升到的概率为p。
2、风险中性假设在风险中性条件下,随机微分方程:
其中的可以用r来表示.即
风险中性条件下,在时刻m衍生证券的价格是其在时刻(m+1)的期望值按
照无风险利率r贴现所得到的,即。
3、期权的计算
期权的计算是从二叉树图的末端(时刻T)开始向后倒退进行的。T时刻期权
的价值已知。对于一个看涨期权来说,有
对于一个看跌期权来说,有
其中,n=0,1,2,…,N, K为执行价格。
在风险中性条件下,时刻的每个结点上的期权值都可以用T时刻期权价
值的期望值在时间内用利率r贴现求出;同理,时刻的每个结点的期权值
可以用时刻的期望值在时间内用利率r贴现求出,其它结点依次类推。
而如果对于美式期权,必须检查二叉树图的每个结点,以确定提前执行是否比
继续持有时间更为有利。最后,向后倒推通过所有结点就求出了当前时刻的期权
价值。
下面对美式期权定价问题进行研究:
美式看涨期权被提前执行时,其内涵价值为
n=0,1,2,…,m
SdZSdtdS
t
tttt
tmSt
)1(uuSm)1(ddS
m
mSm
uS
SdZSdtdS
SdZrSdtdS
tmVt
][1mtrmVeEV
N
n
V
)0,max(KSVNnNn
)0,max(NnNnSKV
tT
ttT2
tTt
t
0
V
)0,max(KSVmnmn
美式期权二叉树定价及MATLAB程序
对于看跌期权来说,有
n=0,1,2,…,m
在m时刻从节点(m,n)向(m+1)时刻的结点(m+1,n+1)移动的概率为p;
向(m+1)时刻的结点(m+1,n)移动的概率为1-p.
假设期权不提前执行,有:
若期权提前执行,必须与内涵价值相比较。那么,对于看涨期权,有
对于看跌期权,有
4、计算美式看涨期权的价格的Matlab实现(基于具体的算例)
Matlab程序如下:
%输入具体参数
S0=100; %当前股价
K=105; %执行价格
r=0。05; %利率
T=1; %期权有效期
sigma=0。3; %波动率
q=0.02; %红利率
n=1000; %步数
dt=T/n; %时间步长
%计算二叉树各参数
u=exp(sigma*sqrt(dt)); %计算上升比率
d=1/u; %计算下降比率
p=(exp((r—q)*dt)-d)/(u-d); %计算上升的概率
%构造二叉树矩阵,i表示行数,j表示列数,Sx为股价矩阵,fx为期权的内在价值
for j=1:n+1
for i=1:j
Sx(i,j)=S0*(u^(j-i))*(d^(i—1));
)0,max(mnmnSKV
tt
t
])1([111mnmntrmnVppVeV
]})1([),0,max{max(111mnmntrmnmnVppVeKSV
]})1([),0,max{max(111mnmntrmnmnVppVeSKV
美式期权二叉树定价及MATLAB程序
fx(i,j)=max(Sx(i,j)-K,0);
end;
end;
%计算美式期权价格矩阵Afx和欧式期权价格矩阵Efx
for i=1:n+1 %到期时(j=n+1)期权价格
Afx(i,n+1)=fx(i,n+1);
Efx(i,n+1)=fx(i,n+1);
end;
for jj=1:n %倒推前面各期(j=n-1,n-2,…,1)期权价格
j=n+1—jj;
for i=1:j
Efx(i,j)=exp(—r*dt)*(p*Efx(i,j+1)+(1—p)*Efx(i+1,
j+1));
Afx(i,j)=max(exp(—r*dt)*(p*Afx(i,j+1)+(1-p)*Afx(i+1,
j+1)),fx(i,j));
end;
end;
%输出结果
AmeOptionPrice=Afx(1,1)
ErouOptionPrice=Efx(1,1)
AmeOptionPrice = 10。89434691587509
ErouOptionPrice = 10。89432408424911
