23个基本测试函数蚁群算法

合集下载

蚁群算法——精选推荐

蚁群算法⼀、蚁群算法简介蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法，它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出，并⾸先使⽤在解决TSP（旅⾏商问题）上。

之后，⼜系统研究了蚁群算法的基本原理和数学模型.⼆、蚁群算法原理1、蚂蚁在路径上释放信息素。

2、碰到还没⾛过的路⼝，就随机挑选⼀条路⾛。

同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反⽐。

后来的蚂蚁再次碰到该路⼝时，就选择信息素浓度较⾼路径。

4、最优路径上的信息素浓度越来越⼤。

5、最终蚁群找到最优寻⾷路径。

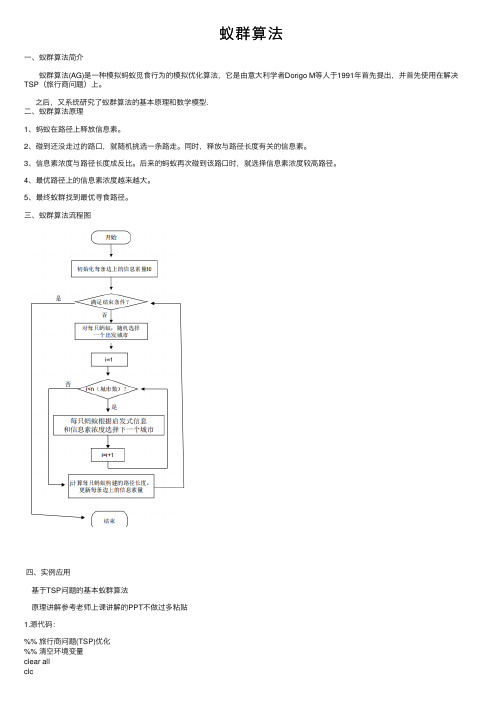
三、蚁群算法流程图四、实例应⽤基于TSP问题的基本蚁群算法原理讲解参考⽼师上课讲解的PPT不做过多粘贴1.源代码：%% 旅⾏商问题(TSP)优化%% 清空环境变量clear allclc%% 导⼊数据citys = ceil(rand(50,2)*50000)%load newcitys.mat%% 计算城市间相互距离fprintf('Computing Distance Matrix... \n');n = size(citys,1);D = zeros(n,n);for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endendend%% 初始化参数fprintf('Initializing Parameters... \n');m = 50; % 蚂蚁数量alpha = 1; % 信息素重要程度因⼦beta = 5; % 启发函数重要程度因⼦rho = 0.05; % 信息素挥发因⼦Q = 1; % 常系数Eta = 1./D; % 启发函数Tau = ones(n,n); % 信息素矩阵Table = zeros(m,n); % 路径记录表iter = 1; % 迭代次数初值iter_max = 150; % 最⼤迭代次数Route_best = zeros(iter_max,n); % 各代最佳路径Length_best = zeros(iter_max,1); % 各代最佳路径的长度Length_ave = zeros(iter_max,1); % 各代路径的平均长度%% 迭代寻找最佳路径figure;while iter <= iter_maxfprintf('迭代第%d次\n',iter);% 随机产⽣各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start;% 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; endP = P/sum(P);% 轮盘赌法选择下⼀个访问城市Pc = cumsum(P);target_index = find(Pc >= rand);target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length;Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); endDelta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1，清空路径记录表% figure;%最佳路径的迭代变化过程[Shortest_Length,index] = min(Length_best(1:iter));Shortest_Route = Route_best(index,:);plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');pause(0.3);iter = iter + 1;Table = zeros(m,n);% endend%% 结果显⽰[Shortest_Length,index] = min(Length_best);Shortest_Route = Route_best(index,:);disp(['最短距离:' num2str(Shortest_Length)]);disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);endtext(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');xlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])figure(2)plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')legend('最短距离','平均距离')xlabel('迭代次数')ylabel('距离')title('各代最短距离与平均距离对⽐')运⾏结果：利⽤函数citys = ceil(rand(50,2)*50000) 随机产⽣五⼗个城市坐标2.研究信息素重要程度因⼦alpha, 启发函数重要程度因⼦beta,信息素挥发因⼦rho对结果的影响为了保证变量唯⼀我重新设置五⼗个城市信息进⾏实验在原来设值运⾏结果：实验结果可知当迭代到120次趋于稳定2.1 alpha值对实验结果影响（1）当alpha=4时运⾏结果实验结果可知当迭代到48次左右趋于稳定（2）当alpha=8时运⾏结果：有图可知迭代40次左右趋于稳定，搜索性较⼩（3）当alpha= 0.5运⾏结果：有图可知迭代到140次左右趋于稳定（4）当alpha=0.2时运⾏结果：结果趋于110次左右稳定所以如果信息素因⼦值设置过⼤，则容易使随机搜索性减弱；其值过⼩容易过早陷⼊局部最优2.2 beta值对实验影响（1）当 beta=8时运⾏结果结果迭代75次左右趋于稳定（2）当 beta=1时运⾏结果：结果迭代130次左右趋于稳定所以beta如果值设置过⼤，虽然收敛速度加快，但是易陷⼊局部最优；其值过⼩，蚁群易陷⼊纯粹的随机搜索，很难找到最优解2.3 rho值对实验结果影响(1)当rho=3时运⾏结果：结果迭代75次左右趋于稳定（2）当rho=0.05运⾏结果：结果迭代125次左右趋于稳定所以如果rho取值过⼤时，容易影响随机性和全局最优性；反之，收敛速度降低总结：蚁群算法对于参数的敏感程度较⾼，参数设置的好，算法的结果也就好，参数设置的不好则运⾏结果也就不好，所以通常得到的只是局部最优解。

蚁群算法PPT课件

Macro Dorigo
2021/7/1
3
基本原理
Nest
Food
Obstacle
图1 蚂蚁正常行进，突然环境改变，增加了障碍物
2021/7/1
4
基本原理
Nest
Food
Obstacle
图2 蚂蚁以等同概率选择各条路径较短路径信息素浓度高，选择该路径的蚂蚁增多
2021/7/1
5
基本原理
E
t=0
迭代次数 t_max 4784 1999 806 8950 6665 884 3650 2214 948 1802
程序运行时间 time 99.0466 123.0078 458.4601 148.2777 381.1539 499.8319 88.1896 149.1128 495.0127 134.2481
LumerE和FaietaB通过在Denurbourg的基本分类模型中引入数据对象之间相似度的概念，提出了 LF聚类分析算法，并成功的将其应用到数据分析中。
2021/7/1
11
基于蚂蚁觅食行为和信息素的聚类分析模型
蚂蚁在觅食的过程中，能够分为搜索食物和搬运食物两个环节。每个蚂蚁在运动过程中都将会在其所经过的路径上留下信息素，而且能够感知到信息素的存在及其强度，比较倾向于向信息素强度高的方向移动，同样信息素自身也会随着时间的流逝而挥发，显然某一路径上经过的蚂蚁数目越多，那么其信息素就越强，以后的蚂蚁选择该路径的可能性就比较高，整个蚁群的行为表现出了信息正反馈现象。
2021/7/1
Z
蚁群聚类结果 (R=100,t=1000)
3500
3000
2500
2000

蚁群算法——精选推荐

蚁群算法蚁群算法⽬录1 蚁群算法基本思想 (1)1.1蚁群算法简介 (1)1.2蚁群⾏为分析 (1)1.3蚁群算法解决优化问题的基本思想 (2)1.4蚁群算法的特点 (2)2 蚁群算法解决TSP问题 (3)2.1关于TSP (3)2.2蚁群算法解决TSP问题基本原理 (3)2.3蚁群算法解决TSP问题基本步骤 (5)3 案例 (6)3.1问题描述 (6)3.2解题思路及步骤 (6)3.3MATLB程序实现 (7)3.1.1 清空环境 (7)3.2.2 导⼊数据 (7)3.3.3 计算城市间相互距离 (7)3.3.4 初始化参数 (7)3.3.5 迭代寻找最佳路径 (7)3.3.6 结果显⽰ (7)3.3.7 绘图 (7)1 蚁群算法基本思想1.1 蚁群算法简介蚁群算法（ant colony algrothrim，ACA）是由意⼤利学者多⾥⼽（Dorigo M）、马聂佐（Maniezzo V ）等⼈于20世纪90初从⽣物进化的机制中受到启发，通过模拟⾃然界蚂蚁搜索路径的⾏为，提出来的⼀种新型的模拟进化算法。

该算法⽤蚁群在搜索⾷物源的过程中所体现出来的寻优能⼒来解决⼀些系统优化中的困难问题，其算法的基本思想是模仿蚂蚁依赖信息素，通过蚂蚁间正反馈的⽅法来引导每个蚂蚁的⾏动。

蚁群算法能够被⽤于解决⼤多数优化问题或者能够转化为优化求解的问题，现在其应⽤领域已扩展到多⽬标优化、数据分类、数据聚类、模式识别、电信QoS管理、⽣物系统建模、流程规划、信号处理、机器⼈控制、决策⽀持以及仿真和系统辩识等⽅⾯。

蚁群算法是群智能理论研究领域的⼀种主要算法。

1.2 蚁群⾏为分析Bm=20t=0 m=10m=10t=11.3 蚁群算法解决优化问题的基本思想⽤蚂蚁的⾏⾛路径表⽰待优化问题的可⾏解，整个蚂蚁群体的所有路径构成待优化问题的解空间。

路径较短的蚂蚁释放的信息量较多，随着时间的推进，较短路径上积累的信息浓度逐渐增⾼，选择该路径的蚂蚁个数愈来愈多。

基本蚁群算法

摘要许多实际工程问题可以抽象为相应的组合优化问题，TSP问题是作为所有组合优化问题的范例而存在的，它已成为并将继续成为测试组合优化新算法的标准问题。

从理论上讲，使用穷举法可以求解出TSP问题的最优解；但是对现有的计算机来说，让它在如此庞大的搜索空间中寻求最优解，几乎是不可能的。

所以，各种求TSP问题近似解的算法应运而生了，本文所描述的蚁群算法（AC）也在其中。

目前已出现了很多的启发式算法，而蚁群算法作为一种新型的启发式算法，已成功地应用于求解TSP问题。

蚂蚁通过分泌信息素来加强较好路径上信息素的浓度，同时按照路径上的信息素浓度来选择下一步的路径：好的路径将会被越来越多的蚂蚁选择，因此更多的信息素将会覆盖较好的路径；最终所有的蚂蚁都集中到了好的路径上。

蚂蚁的这种基于信息素的正反馈原理正是整个算法的关键所在。

本文介绍了基本蚁群算法概念、原理及蚁群算法的特点，再根据蚁群算法的缺点做出了优化。

采用轮盘赌选择代替了基本框架中通过启发式函数和信息素选择路径，改进蚁群算法的信息素传递参数，让整个算法更快速的找到最优解。

其次，采用最大最小优化系统限制最大值和最小值，让整个系统更快收敛，得到最优解。

关键字：蚁群算法，TSP问题，启发式函数，轮盘算法，最大最小优化ABSTRACTMany practical engineering problems can be abstracted as corresponding combinatorial optimization problem, TSP problem is an example of all as a combinatorial optimization problem, it has become and will continue to be a new combinatorial optimization algorithm of standard test problems. In theory, using the exhaustion method can solve the TSP problem optimal solution; But for the existing computer, let it in such a large search space to seek the optimal solution, it is almost impossible. So, all kinds of algorithm arises at the historic moment, the approximate solution of the TSP problem described in this paper, ant colony algorithm (AC) is among them.Has appeared a lot of heuristic algorithm and ant colony algorithm as a kind of new heuristic algorithm, has been successfully used in solving TSP problems. Ant secretion by pheromones to strengthen the good path pheromone concentration, at the same time according to the path to choose the next path pheromone concentration: good paths will be more and more ants to choose, so that more information will cover good path; Eventually all the ants on a good path. This positive feedback based on the pheromone of ant principle is the key to the whole algorithm.This paper introduces the basic concept of ant colony algorithm, principle and characteristics of ant colony algorithm, according to the disadvantages of ant colony algorithm optimization. Adopting roulette selection instead of the basic framework by heuristic function and choose path pheromone, pheromone passing parameters of improved ant colony algorithm, make the whole algorithm find the optimal solution more quickly. Second, limiting the maximum and the minimum maximum minimum optimization system, make the whole system faster convergence and the optimal solution is obtained.Keywords: ant colony algorithm, the TSP problem, a heuristic function, roulette algorithm, maximum_minimum optimization目录摘要 (1)ABSTRACT (2)第1章绪论 (5)1.1 研究目的和意义 (5)1.2 国内外研究现状 (6)1.2.1 国外研究现状 (6)1.2.2 国内研究现状 (7)1.3 本文研究内容 (7)（1）基本蚁群算法 (8)（2）蚁群算法的优化 (8)（3）蚁群算法在TSP问题中的应用 (8)1.4 开发环境与工具 (8)1.5 论文的组织结构 (8)第2章蚁群算法 (9)2.1 蚁群算法简介 (9)2.2 蚁群算法的原理 (10)2.2.1 蚂蚁觅食规则 (10)2.2.2 蚂蚁移动规则 (11)2.2.3 蚂蚁避障规则 (11)2.2.4 蚂蚁撒信息素规则 (11)2.3 蚁群算法的特点及优缺点 (11)2.3.1 蚁群算法的特点 (11)2.3.2 蚁群算法的优点 (12)2.3.3 蚁群算法的缺点 (13)2.5 蚁群算法的核心函数 (13)（1）初始化 (13)（2）选择下一个城市，返回城市编号 (14)（3）更新环境信息素 (16)（4）检查终止条件 (17)（5）输出最优值 (17)2.6 蚁群算法的参数分析 (17)2.6.1 蚂蚁数量N_ANT_COUNT (17)2.6.2 启发因子 (18)2.6.3 期望启发因子 (18)2.6.4 信息素挥发度 (19)2.6.5 总信息量（DBQ） (19)第3章改进的蚁群算法 (20)3.1 轮盘赌选择 (21)3.1.1 轮盘赌选择基本思想 (21)3.1.2 轮盘赌选择工作过程 (21)3.2 MAX_MIN ACO (23)3.2.1 MAX_MIN算法的框架结构 (23)3.2.2 MAX_MIN 算法流程图 (25)第4章蚁群算法在车辆路径问题中的应用 (26)4.1 车辆路径问题简介 (26)4.1.1 车辆路径问题定义 (26)4.1.2 车辆路径问题分类 (27)4.2 车辆路径问题的求解算法 (28)4.2.1 精确算法 (28)4.2.2 启发式算法 (29)4.3 蚁群算法解决车辆路径问题 (30)4.4 数值实验结果及分析 (31)4.4.1 轮盘赌选择优化前后数据对比 (32)4.4.2 MAX_MIN算法改进前后数据对比 (33)第5章总结与展望 (34)参考文献 (35)第1章绪论TSP问题是一种特殊的车辆路径问题，是作为所有组合优化问题的范例而存在的，它已成为并将继续成为测试组合优化新算法的标准问题。

蚁群算法——精选推荐

蚁群算法%% 蚁群算法求函数极值% 初始化clear all; %清除所有变量close all; %清图clc; %清屏m = 20; %蚂蚁个数G = 200; %最⼤迭代次数Rho = 0.9; %信息素蒸发系数P0 = 0.2; %转移概率常数XMAX = 7; %搜素变量x最⼤值XMIN = 1; %搜素变量x最⼩值YMAX = 7; %搜素变量y最⼤值YMIN = 1; %搜素变量y最⼩值%% 随机设置蚂蚁初始位置for i = 1:mX(i,1) = (XMIN +(XMAX-XMIN)*rand);X(i,2) = (YMIN +(YMAX-YMIN)*rand);Tau(i) = func(X(i,1),X(i,2));endstep = 0.1;for NC = 1:Glamda = 1/NC;[Tau_best,BestIndex] = max(Tau);% 计算状态转移概率for i = 1:mP(NC,i) =(Tau(BestIndex)-Tau(i))/Tau(BestIndex); end% 位置更新for i = 1:m%局部搜素if P(NC,i) < P0temp1 = X(i,1)+(2*rand-1)*step*lamda;temp2 = X(i,2)+(2*rand-1)*step*lamda;else%全局搜索temp1 = X(i,1)+(XMAX-XMIN)*(rand-0.5);temp2 = X(i,2)+(YMAX-YMIN)*(rand-0.5);end% 边界处理if temp1 < XMINtemp1 = XMIN;endif temp1 > XMAXtemp1 = XMAX;endif temp2 < YMINtemp2 = YMIN;endif temp2 > YMAXtemp2 = YMAX;end% 判断蚂蚁是否移动if func(temp1,temp2) > func(X(i,1),X(i,2))X(i,1) = temp1;X(i,2) = temp2;endend% 更新信息素for i = 1:mTau(i) = (1-Rho)*Tau(i)+func(X(i,1),X(i,2)); end[value ,index] = max(Tau);trace(NC) = func(X(index,1),X(index,2));end[max_value,max_index] = max(Tau);maxX = X(max_index,1)maxY = X(max_index,2)maxValue = func(X(max_index,1),X(max_index,2)) figure plot(trace)xlabel('搜索次数')ylabel('适应度值')title('适应度进化曲线') function value = func(x,y) value = x^2+y^2;end。

蚁群算法ppt课件

10
2 简化旳蚂蚁寻食过程
假设蚂蚁每经过一处所留下旳信息素为一种单位，则经过36个时间单位后，全部开始一起出发旳蚂蚁都经过不同途径从D点取得了食物，此时ABD 旳路线来回了2趟，每一处旳信息素为4个单位，而 ACD旳路线来回了一趟，每一处旳信息素为2个单位，其比值为2：1。
寻找食物旳过程继续进行，则按信息素旳指导，蚁群在ABD路线上增派一只蚂蚁（共2只），而ACD路线上依然为一只蚂蚁。再经过36个时间单位后，两条线路上旳信息素单位积累为12和4，比值为3：1。
8
2 简化旳蚂蚁寻食过程
蚂蚁从A点出发，速度相同，食物在D点，可能随机选择路线 ABD或ACD。假设初始时每条分配路线一只蚂蚁，每个时间单位行走一步，本图为经过9个时间单位时旳情形：走ABD旳蚂蚁到达终点，而走ACD旳蚂蚁刚好走到C点，为二分之一旅程。
9
2 简化旳蚂蚁寻食过程
本图为从开始算起，经过18个时间单位时旳情形：走ABD旳蚂蚁到达终点后得到食物又返回了起点A，而走ACD旳蚂蚁刚好走到D点。
若按以上规则继续，蚁群在ABD路线上再增派一只蚂蚁（共3只），而 ACD路线上依然为一只蚂蚁。再经过36个时间单位后，两条线路上旳信息素单位积累为24和6，比值为4：1。
若继续进行，则按信息素旳指导，最终全部旳蚂蚁会放弃ACD路线，而都选择ABD路线。这也就是前面所提到旳正反馈效应。
11
3 自然蚁群与人工蚁群算法
15
5 初始旳蚁群优化算法—基于图旳蚁群系统（GBAS）
初始旳蚁群算法是基于图旳蚁群算法，graph-based
ant system,简称为GBAS，是由Gutjahr W J在2023年
旳Future Generation Computing Systems提出旳.

《蚁群算法介绍》课件

总结词
输出最优解和相关性能指标。
详细描述
这一步是将最优解和相关性能指标输出，以便于对算法的性能进行分析和评估。
04
蚁群算法的性能分析
收敛性分析
收敛速度
蚁群算法在优化问题中的收敛速度取决于初始信息素分布、蚂蚁数量、迭代次数等因素。
最优解质量
蚁群算法在某些问题上可能找到全局最优解，但在其他问题上可能只能找到近似最优解。
VS
详细描述
这一步是生成初始解的过程，需要按照设定的规则，将蚂蚁随机放置在解空间中，并初始化每条路径上的信息素。
迭代优化
总结词
通过蚂蚁的移动和信息素的更新，不断优化解的质量。
详细描述
这一步是蚁群算法的核心部分，通过模拟蚂蚁的移动和信息素的更新机制，不断迭代优化解的质量，最终找到最优解。
结果
多目标优化问题的蚁群算法
针对多目标优化问题，蚁群算法需要进行相应的改进。
VS
多目标优化问题要求算法在满足多个冲突目标的同时找到最优解。这需要对蚁群算法进行相应的调整，以适应多目标优化的特性。例如，可以通过引入权重因子来平衡各个目标之间的矛盾，或者采用非支配排序方法对解进行分层处理，以便更好地处理多目标优化问题。
蚁群算法的优化目标
寻找最短路径
蚁群算法的主要目标是找到起点到终点之间的最短路径，这在实际应用中可用于解决如旅行商问题、车辆路径问题等优化问题。
平衡搜索与探索
蚁群算法需要在搜索和探索之间取得平衡，以避免陷入局部最优解，提高算法的全局搜索能力。
03
蚁群算法的实现步骤
问题建模
总结词
将实际问题抽象为蚁群算法能够解决的问题模型。
蚂蚁根据局部信息素浓度选择移动方向，倾向于选择信息素浓度较高的路径。

蚁群算法的讲解

群内间接通信的物质。由于较短路径上蚂蚁的往返时间比较短，单位时间内经过该
路径的蚂蚁多，所以信息素的积累速度比较长路径快。因此，当后续蚂蚁在路口时
，就能感知先前蚂蚁留下的信息，并倾向于选择一条较短的路径前行。这种正反馈
机制使得越来越多的蚂蚁在巢穴与食物之间的最短路径上行进。由于其他路径上的
信息素会随着时间蒸发，最终所有的蚂蚁都在最优路径上行进。
TSP作为应用实例提出的。
TSP 问题（Traveling Salesman Problem，旅行商问题）
是数学领域中著名问题之一。
问题概述：假设有一个旅行商人要拜访n个城市，他必须
选择所要走的路径，路径的限制是每个城市只能拜访一次，
而且最后要回到原来出发的城市。路径的选择目标是要求得
的路径路程为所有路径之中的最小值。TSP问题是一个NP问
整数，表示算法已经收敛，不再需要继续；
4. 目标值控制规则，给定优化问题（目标最小化）的一
个下界和一个误差值，当算法得到的目标值同下界之
差小于给定的误差值时，算法终止。
71
例 1 旅行商问题（TSP 问题）假设有一个旅行商人
要拜访全国 31 个省会城市，他需要选择所要走的路
径，路径的限制是每个城市只能拜访一次，而且最
后要回到原来出发的城市。路径的选择要求是：所
选路径的路程为所有路径之中的最小值。全国 31 个
省会城市的坐标为 [1304 2312; 3639 1315; 4177
2244; 3712 1399; 3488 1535; 3326 1556; 3238
1229; 4196 1004; 4312 790; 4386 570; 3007 1970;
致、有形的结构。经过“演化”，有些死亡，有些静止，有些

《蚁群算法》PPT

图像边缘检测
Thank you so much for your time,and have a nice day.
可选路径较少，使种群陷入局部最优。
信息素重要程度因子
蚂蚁选择以前已经走过的路可能性较大，会使蚁群的搜索范围减小容易过早的收
容易使随机搜索性减弱。
敛,使种群陷入局部最优。
启发函数重要程度因子虽然收敛速度加快,但是易陷入局部最优
蚁群易陷入纯粹的随机搜索，很难找到最优解
信息素挥发因子
各路径上信息素含量差别较小，收敛速信息素挥发较快,容易导致较优路径被排除度降低
2.并行的算法
每只蚂蚁搜索的过程彼此独立，仅通过信息激素进行通信。在问题空间的多点同时开始进行独立的解搜索，不仅增加了算法的可靠性,也使得算法具有较强的全局搜索能力。
3
蚁群算法的基本步骤
1）初始化参数；2）构建解空间；3）更新信息素；4）判断终止与迭代。
3 蚁群算法的基本步骤
优化问题与蚂蚁寻找食物的关系
0.04
0.04
0.92 到城市1 到城市3 到城市5
3.3 更新信息素
蚂蚁访问完所有城市之后，进行信息素的更新。信息素的更新包括挥发和蚂蚁的产生，由以下公式决定：
第 t+1 次循环后城市 i 到城市j上的信息素含量
信息素残留系数=1-信息素挥发因子
ij (t 1) (1 ) ij (t) ij , (0 1)
2.2 蚁群算法的特点
1.自组织的算法
自组织:组织力或组织指令是来自于系统的内部。在抽象意义上讲，自组织就是在没有外界作用下使得系统嫡减小的过程(即是系统从无序到有序的变化过程)。

蚁群算法详细讲解课件

信息素增量
蚂蚁在移动过程中会根据路径的长度和信息素浓度等因素来决定释放多少信息素。一般来说，路径越短、信息素浓度越高，蚂蚁释放的信息素就越少。
参数选择与调整
参数敏感性分析
在蚁群算法中，参数的选择对算法的性能和结果有很大的影响。因此，需要对算法的参数进行敏感性分析，了解参数变化对算法性能的影响。
起源与发展
起源
蚁群算法最初受到对自然界中蚂蚁觅食行为的研究启发，观察到蚂蚁通过信息素传递路径信息，能够找到最短或最优的路径。
发展
蚁群算法经过多年的研究和发展，已经逐渐完善和改进，包括引入启发式信息、多种群并行计算等技术，提高了算法的效率和稳定性。
应用领域
01
02
03
04
组合优化问题
蚁群算法在组合优化问题中应用广泛，如旅行商问题、车辆
参数调整
蚁群算法中的参数对算法性能有很大影响，如何根据不同问题调整参数是一个挑战。
理论支撑
目前蚁群算法的理论支撑还不够完善，需要进一步深入研究其数学基础和原理。
应用领域的拓展
组合优化问题
01
蚁群算法在组合优化问题中有广泛应用，但仍需进一步探索其
在其他类型问题中的应用。
多目标优化问题
02
目前蚁群算法在多目标优化问题中的应用还比较少，需要加强
增强
蚂蚁经过的路径上信息素浓度会增加。
竞争
不同蚂蚁对信息素的贡献不同，根据贡献调整信息素浓度。
蚂蚁系统的集体行为
自组织
蚂蚁通过个体行为形成整体有序状态，无需中央控制。
协同工作
蚂蚁之间相互协作，共同完成目标任务。
优化搜索
通过信息素传递和蚂蚁的移动规则，逐渐找到最优路径。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

23个基本测试函数蚁群算法
蚁群算法是一种模拟蚂蚁行为的启发式算法，它通过模拟蚁群寻找食物的行为，来解决各种优化问题。

蚁群算法的核心思想是通过信息交流和反馈机制来寻找问题的最优解。

本文将介绍蚁群算法的基本原理，并以23个基本测试函数为例，展示蚁群算法在解决优化问题中的应用。

1. 算法简介
蚁群算法最早由意大利学者Dorigo在1992年提出，其灵感来自于观察蚂蚁在寻找食物时的行为。

蚁群算法将问题抽象成一个图论模型，其中蚂蚁代表解空间中的候选解，信息素则代表蚂蚁之间的信息交流。

蚂蚁根据信息素的浓度和距离选择路径，并在路径上释放信息素，从而影响其他蚂蚁的选择。

通过多次迭代，蚂蚁群体逐渐收敛于最优解。

2. 蚁群算法的基本步骤
蚁群算法主要包括初始化、路径选择、信息素更新和收敛判断等步骤。

2.1 初始化
在蚁群算法中，需要初始化蚂蚁的位置和信息素的浓度。

蚂蚁的初始位置可以随机选择或者根据问题的特点进行设置。

信息素的初始浓度通常设置为一个较小的常数。

2.2 路径选择
在路径选择阶段，蚂蚁根据信息素的浓度和距离选择路径。

通常情况下，信息素浓度较高的路径会有更多的蚂蚁选择，但也存在一定的随机性，以保证算法能够全局搜索。

2.3 信息素更新
在信息素更新阶段，蚂蚁根据问题的优化目标更新路径上的信息素。

通常情况下，蚂蚁在路径上释放的信息素与路径的优化程度成正比。

信息素的更新规则可以根据具体问题进行设计。

2.4 收敛判断
在每轮迭代之后，需要判断算法是否收敛。

通常情况下，可以通过设定一个停止准则来判断算法是否继续迭代。

常用的停止准则包括迭代次数、目标函数值的变化幅度等。

3. 蚁群算法在优化问题中的应用
蚁群算法在解决各种优化问题中具有广泛的应用。

下面以23个基本测试函数为例，展示蚁群算法在不同问题中的应用。

3.1 球面函数
球面函数是一个简单的优化问题，目标是找到一个全局最小值。

蚁群算法通过信息素的交流和反馈机制，可以在搜索空间中快速找到最优解。

3.2 Rosenbrock函数
Rosenbrock函数是一个经典的非凸优化问题，目标是找到一个全局最小值。

蚁群算法通过多次迭代和信息素的更新，可以逐渐收敛到最优解。

3.3 Ackley函数
Ackley函数是一个具有多个局部最小值的优化问题，目标是找到一个全局最小值。