最新-八年级数学 相似三角形形探究题一 北师大版 精品
北师大版八年级数学下册第四单元相似图形测试题1[1]
![北师大版八年级数学下册第四单元相似图形测试题1[1]](https://img.taocdn.com/s3/m/30131acf8bd63186bcebbce5.png)
一、 选择题1、若32=y x ,则3x ﹣2y=( )A 、3B 、2C 、1D 、02、若点C 是线段AB 的黄金分割点,且AB=2,则AC=( ) A 、15- B 、53- C 、215- D 、15-或53-3、下列图形中相似的多边形是( )A 、所有的矩形B 、所有的菱形C 、所有的等腰梯形D 、所有的正方形4、△ABC 的三边长分别是102、、2,△A ′B ′C ′的两边长分别为1和5,若△ABC ∽△A ′B ′C ′,则△A ′B ′C ′的第三边长为( )A 、22B 、2C 、2D 、225、甲、乙两地相距3.5km ,画在地图上的距离为7cm ,则这张地图的比例尺为( ) A 、2:1 B 、1:50000 C 、1:2 D 、50000:16下列各组中的四条线段成比例的是( )A.a =2,b =3,c =2,d =3B.a =4,b =6,c =5,d =10C.a =2,b =5,c =23,d =15D.a =2,b =3,c =4,d =1 7.已知线段a 、b 、c 、d 满足ab =cd ,把它改写成比例式,错误的是( )A.a ∶d =c ∶bB.a ∶b =c ∶dC.d ∶a =b ∶cD.a ∶c =d ∶b 8.若ac =bd ,则下列各式一定成立的是( )A.dc b a = B.c cb d d a +=+ C.cd ba =22D.da cd ab = 9.已知点M 将线段AB 黄金分割(AM >BM ),则下列各式中不正确的是( )A.AM ∶B M =AB ∶AMB.AM =215-AB C.BM =215-AB D.AM ≈0.618AB 二、 填空题1、正方形的对角线与边长的比为2、若52=-y y x ,则y x =3、已知线段AB ,延长AB 到C ,使BC=3AB ,则BC/AC=4、电视节目主持人主持节目时,站在舞台的黄金分割点处最自然得体,舞台AB 长为20m ,试计算主持人应走到离A 点至少 m 点再走 m ,也处在比较得体的位置。
八年级数学下册 相似三角形第12讲训练试题(无答案) 北师大版

相似三角形解题方法指导(四)知识回顾一网打尽Ⅰ. 梳理知识1.三角形相似的条件(1) ,(2) ,(3) 。
2.如何寻找和发现相似三角形两个三角形相似,一般说来必须具备下列六种图形之一:只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决.①相似三角形的三边,三角 .②相似三角形的,与都等于相似比.③相似三角形周长之比等于,相似三角形面积之比等于 .①相似多边形的对应边,对应角 .②相似多边形的对角线之比、周长之比都等于 .(1)相似变换:保持图形的形状不变的几何变换叫做相似变换(2)位似变换①位似图形:如果两个图形不仅是图形,而且每组对应点所在的直线都,那么这样的两个图形叫做位似图形,这个点叫做,这时的相似比又称为 .②位似图形的性质:位似图形上任意一对对应点到的距离之比等于位似比.5.相似三角形的应用——测量旗杆的高度(利用阳光下的影子;利用标杆;利用镜子的反射.)知识要点基础练习一、选择题1.如图1,△ABC中,CD⊥AB于D,DE⊥AC于E,图中与△ADE相似的三角形有( )图1 图2 图3 图4A.1个B.2个C.3个D.4个2.下列能使三角形一定相似的是( )A.两边对应成比例的三角形B.两边分别成比例的直角三角形C.两边对应成比例的等腰三角形D.两直角边对应成比例的直角三角形3.如图2,下列条件不能判别△ACD ∽△ABC 的是( )A.∠ADC =∠ACBB.∠ACD =∠BC.AC 2=AD ·AB D.CDADBC AC5.已知在△ABC 中,∠ACB =90°,CD ⊥AB 于D ,若BC =5,CD =3,则AD 等于( )A.2.25B.2.5C.2.75D.36.如图3,铁道口的栏道木短臂长1米,长臂长16米,当短臂下降0.5米时,长臂的端点升高________米( )A.11.25B.6.6C.8D.10.57.一个地图上标准比例尺是1∶300000,图上有一条形区域,其面积约为24 cm 2,则这块区域的实际面积约为( )平方千米( )A.2160B.216C.72D.10.728.如图4,将△ADE 绕正方形ABCD 的顶点A 顺时针旋转90°得△ABF ,连结EF 交AB 于H ,则下列结论错误的是( )A.AE ⊥AFB.EF ∶A F =2∶1C.AF 2=FH ·FE D.FB ∶FC=HB ∶EC9.如图5,把一个矩形纸片ABCD 沿AD 和BC 的中点连线EF 对折,要使矩形AEFB 与原矩形相似,则原矩形长与宽的比为( )A.2∶1B.3∶1C.2∶1D.4∶1图5 图6 图7 图810.如图6,在△ABC 中,D 、E 分别是边AB 、AC 的中点,△ADE 和四边形BCED 的面积分别记为S 1、S 2,那么21S S 的值为( ) A.21 B.41 C.31 D.32 11.如图7,在Rt △ABC 中,AD 为斜边BC 上的高,若S △CAD =3S △ABD ,则AB ∶AC 等于( )A.1∶3B.1∶4C.1∶3D.1∶212.顺次连结三角形三边的中点,所成的三角形与原三角形对应高的比是( )A.1∶4B.1∶3C.1∶2D.1∶213.△ABC ∽△A ′B ′C ′,相似比是2∶3,那么△A ′B ′C ′与△ABC 面积的比是( )A.4∶9B.9∶4C.2∶3D.3∶214.将一个五边形改成与它相似的五边形,如果面积扩大为原来的9倍,那么周长扩大为原来的( )A.9倍B.3倍C.81倍D.18倍 15.在△ABC 中,DE ∥BC ,交AB 于D ,交AC 于E ,且AD ∶DB =1∶2,则下列结论正确的是( )A.BC DE =21 B.BC DE =31 C.的周长的周长ABC ADE ∆∆=21 D.ABC ADE S S ∆∆=3116.如图8,ABCD 中,AE ∶ED =1∶2,S △AEF =6 cm 2,则S △CBF 等于( )A.12 cm2B.24 cm 2C.54 cm2D.15 cm 2典型例题 方法指导(1).如图1,△中,=9,=6,点D 在AB 上,且AD =3,点E 在AC 上,如果连接DE ,使△ADE 与原三角形相似,那么AE =________.(2)垂直于地面的竹竿的影长为12米,其顶端到其影子顶端的距离为13米,如果此时测得某小树的影长为6米,则树高________米.(3)如图2,若OA ∶OD =OB ∶OC =n ,则x =________(用a ,b ,n 表示).图2 图3 图1(4).如图3,在△ABC 中,若∠A =90°,正方形DEFG 内接于△ABC ,则图中与△ABC 相似的三角形有________________.1、如图1,在Rt △ABC 中,∠C =90°,MN ⊥AB 于M ,AM =8 cm ,AC =54AB ,则AN =________.图1 图2 图32、如图2,∠ABC =∠CDB =90°,AC =a ,BC =b ,(1)当BD 与a 、b 之间满足关系式________时,△ABC ∽△CDB ;(2)当BD 与a 、b 之间满足关系________时,△ABC ∽△BD C.3、若△ABC ∽△A ′B ′C ′,AB =4,BC =5,AC =6,△A ′B ′C ′的最大边长为15,那么它们的相似比是________,△A ′B ′C ′的周长是________.4、两个相似三角形的相似比为2∶3,它们周长的差是25,那么较大三角形的周长是________.5、如图3,在ABCD 中,延长AB 到E ,使BE =21AB ,延长CD 到F ,使DF =DC ,EF 交BC 于G ,交AD 于H ,则△BEG 与△CFG 的面积之比是________.1、△∽△′B ′C ′,相似比是3∶4,△ABC 的周长是27 cm ,则△A ′B ′C ′的周长为________.2、两个相似多边形对应边的比为3∶2,小多边形的面积为32 cm 2,那么大多边形的面积为________.3、若两个三角形相似,且它们的最大边分别为6 cm 和8 cm ,它们的周长之和为35 cm ,则较小的三角形的周长为________.4已知,如图2,A ′B ′∥AB ,B ′C ′∥BC ,且OA ′∶A ′A =4∶3,则△ABC 与________是位似图形,位似比为________;△OAB 与________是位似图形,位似比为________.如图,△ABC 是一块锐角三角形余料,其中BC =12 cm ,高AD =8 cm ,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,问这个正方形材料的边长是多少?如图,在Rt ΔABC 中,∠C=90°,AC=4,BC=3.(1)如图(1),四边形DEFG 为ABC 的内接正方形,求正方形的边长.(2)如图(2),三角形内有并排的两个相等的正方形,它们组成的矩形内接于ΔABC ,求正方形的边长.(3)如图(3),三角形内有并排的三个相等的正方形,它们组成的矩形内接于ΔABC ,求正方形的边长.(4) 如图(4),三角形内有并排的n 个相等的正方形,它们组成的矩形内接于ΔABC ,请写出正方形的边长.如图,四边形ABCD 是平行四边形,AE ⊥BC 于E ,AF ⊥CD 于F. (1)ΔABE 与ΔADF 相似吗?说明理由. (2)ΔAEF 与ΔABC 相似吗?说说你的理由.已知:如图(1)E 为平行四边形ABCD 边CD 延长线上的一点,连结BE 交AC 于O ,求证:OE OF BO ∙=2注意:(1)在证明时,常常把等积式转化成比例式.(2)证明比例式时常利用中间比来证明.(3)当证明的比例式中的线段在同一直线上时,常采用相等的线段,相等的比,相等的等积式来代换相应的量. 1、如图,在正方形ABCD 对角线上任意取点E ,AE 延长线交CD 于F ,交BC 延长线于G ,求证:EC 2=EF ·EG 。
2022年北师大版数学《三边成比例的两个三角形相似》配套精品练习(附答案)

第3课时 三边成比例的两个三角形相似1、已知两数4和8,试写出第三个数,使这三个数中,其中一个数是其余两数的比例中项,第三个数是 (只需写出一个即可).2、在△ABC 中,AB=8,AC=6,点D 在AC 上,且AD=2,若要在AB 上找一点E ,使△ADE 与原三角形相似,那么AE= 。
3、如图,在△ABC 中,点D 在AB 上,请再添一个适当的条件,使△ADC ∽△ACB ,那么可添加的条件是 4、已知D 、E 分别是ΔABC 的边AB 、AC 上的点,请你添加一个条件, 使ΔABC 与ΔAED 相似. (只需添加一个你认为适当的条件即可).5、下列说法:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有等腰直角三角形都相似;④所有的直角三角形都相似.其中正确的是 (把你认为正确的说法的序号都填上).6、如图,在直角坐标系中有两点A(4,0)、B(0,2),如果点C 在x 轴上(C 与A 不重合),当点C 的坐标为 或 时,使得由点B 、O 、C 组成的三角形与 ΔAOB 相似(至少写出两个满足条件的点的坐标).7、下列命题中正确的是 ( )①三边对应成比例的两个三角形相似②二边对应成比例且一个角对应相等的两个三角形相似 ③一个锐角对应相等的两个直角三角形相似 ④一个角对应相等的两个等腰三角形相似A 、①③B 、①④C 、①②④D 、①③④8、如图,已知DE ∥BC ,EF ∥AB ,则下列比例式中错误的是( )A ACAE ABAD = B FBEA CFCE = C BDAD BCDE = D CBCF ABEF =9、如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使ΔABE和ΔACD相似的是()A. ∠B=∠CB. ∠ADC=∠AEBC. BE=CD,AB=ACD. AD∶AC=AE∶AB10、在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有()A ΔADE∽ΔAEFB ΔECF∽ΔAEFC ΔADE∽ΔECFD ΔAEF∽ΔABF11、如图,E是平行四边形ABCD的边BC的延长线上的一点,连结AE交CD于F,则图中共有相似三角形()A 1对B 2对C 3对D 4对12、如图,在大小为4×4的正方形网格中,是相似三角形的是()①②③④A.①和②B.②和③C.①和③D.②和④.13、如图,在正方形网格上有6个斜三角形:①ΔABC,②ΔBCD,③ΔBDE,④ΔBFG,⑤ΔFGH,⑥Δ②~⑥中,与三角形①相似的是()(A)②③④(B)③④⑤(C)④⑤⑥(D)②③⑥14、在方格纸中,每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A 1B 1C 1,使ΔA 1B 1C 1与格点三角形ABC 相似(相似比不为1).15、如图,ΔABC 中,BC=a .(1)若AD 1=31AB ,AE 1=31AC ,则D 1E 1= ;(2)若D 1D 2=31D 1B ,E 1E 2=31E 1C ,则D 2E 2= ;(3)若D 2D 3=31D 2B ,E 2E 3=31E 2C ,则D 3E 3= ;……(4)若D n -1D n =31D n -1B ,E n -1E n =31E n -1C ,则D n E n = .16、如图,ΔABC 与ΔADB 中,∠ABC=∠ADB=90°,AC=5cm ,AB=4cm ,如果图中的两个直角三角形相似,求AD 的长.17、已知:如图,在正方形ABCD 中,P 是BC 上的点,且BP=3PC , Q 是CD 的中点.ΔADQ 与ΔQCP 是否相似?为什么?《第5章 二元一次方程组》一、选择题1.下列各方程组中,属于二元一次方程组的是( )A.B.C.D.2.如果是二元一次方程组的解,那么a,b的值是()A.B.C.D.3.如果二元一次方程组的解是二元一次方程3x﹣5y﹣7=0的一个解,那么a值是()A.3 B.5 C.7 D.94.如果a2b3与a x+1b x+y是同类项,则x,y的值是()A.B.C.D.5.在等式y=kx+b中,当x=0时,y=﹣1;当x=﹣1时,y=0,则这个等式是()A.y=﹣x﹣1 B.y=﹣x C.y=﹣x+1 D.y=x+16.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有()A.6种B.7种C.8种D.9种7.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是18岁”.如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,下列方程组正确的是()A.B.C. D.8.如图,直线AB:y=x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是()A.(3,)B.(8,5) C.(4,3) D.(,)9.小明和小莉出生于2000年12月份,他们的生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期和是22,那么小莉的生日是()A.15号B.16号C.17号D.18号10.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是()A.310元B.300元C.290元D.280元二、填空题11.已知方程2m﹣3n=15中m与n互为相反数,那么m=______,n=______.12.已知(2x+3y﹣4)2+|x+3y﹣7|=0,则x=______,y=______.13.如果直线y=2x+3与直线y=3x﹣2b的交点在x轴上,那么b的值为______.14.如图,若直线l1与l2相交于点P,则根据图象可得,二元一次方程组的解是______.15.某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有______人参观.16.小明解方程组的解为,由于不小心,滴上了两滴墨水,刚好遮住了两数■和★,请你帮她找回这两个数,■=______,★=______.17.已知方程组,则y与x之间的关系式为______.18.某车间每天可以生产甲种零件600个或乙种零件300个或丙种零件500个,这三种零件各一个可以配成一套,现要在63天的生产中,使生产的三种零件全部配套,这个车间应安排______天生产甲种零件,______天生产乙种零件,______天生产丙种零件,才能使生产出来的零件配套.三、解答题19.解方程组:(1)(2).20.2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?21.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为.乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么;(2)求出原方程组的正确解.22.在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(1)求出图中格点四边形DEFG对应的S,N,L的值.(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.23.小明的爸爸骑摩托车带着小明在公路上匀速行驶,小明第一次注意到路边里程碑上的数时,发现它是一个两位数且它的两个数字之和为9,刚好过一个小时,他发现路边里程碑上的数恰好是第一次看到的个位和十位数字颠倒后得到的,又过3小时,他发现里程碑上的数字比第一次看到的两位数中间多个0,你知道小明爸爸骑摩托车的速度是多少吗?24.某同学在A,B两家超市发现他看中的随身听的单价相同,书包单价也相同.随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.(1)求该同学看中的随身听和书包的单价各是多少元?(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用).但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?25.为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金.已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:月份销售额销售额(单位:元)1月2月3月4月5月6月小李(A公司)11600 12800 14000 15200 16400 17600 小张(B公司7400 9200 11000 12800 14600 16400 (1)请问小李与小张3月份的工资各是多少?(2)小李1~6月份的销售额y1与月份x的函数关系式是y1=1200x+10400,小张1~6月份的销售额y2也是月份x的一次函数,请求出y2与x的函数关系式;(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资.《第5章二元一次方程组》参考答案一、选择题1.下列各方程组中,属于二元一次方程组的是()A.B.C.D.【解答】解:A、xy不是一次,是二次,不是二元一次方程组,故此选项错误;B、是3元,不是二元一次方程组,故此选项错误;C、是二元一次方程组,故此选项正确;D、是分式,不是二元一次方程组,故此选项错误;故选:C.2.如果是二元一次方程组的解,那么a,b的值是()A.B.C.D.【解答】解:将x=1,y=2代入方程组得:,①×2﹣②得:3b=3,即b=0,将b=1代入①得:a=1,则.故选B.3.如果二元一次方程组的解是二元一次方程3x﹣5y﹣7=0的一个解,那么a值是()A.3 B.5 C.7 D.9【解答】解:由①+②,可得2x=4a,∴x=2a,将x=2a代入①,得y=2a﹣a=a,∵二元一次方程组的解是二元一次方程的一个解,∴将代入方程3x﹣5y﹣7=0,可得6a﹣5a﹣7=0,∴a=7故选C.4.如果a2b3与a x+1b x+y是同类项,则x,y的值是()A.B.C.D.【解答】解:∵a2b3与a x+1b x+y是同类项,∴,解得.故选C.5.在等式y=kx+b中,当x=0时,y=﹣1;当x=﹣1时,y=0,则这个等式是()A.y=﹣x﹣1 B.y=﹣x C.y=﹣x+1 D.y=x+1【解答】解:在y=kx+b中,当x=0时,y=﹣1;当x=﹣1时,y=0.所以,解得b=﹣1,k=﹣1.代入等式y=kx+b得y=﹣x﹣1.故选A.6.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有()A.6种B.7种C.8种D.9种【解答】解:设兑换成10元x张,20元的零钱y元,由题意得:10x+20y=100,整理得:x+2y=10,方程的整数解为:,,,,,,因此兑换方案有6种,故选:A.7.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是18岁”.如果现在弟弟的年龄是x岁,哥哥的年龄是y岁,下列方程组正确的是()A.B.C. D.【解答】解:设现在弟弟的年龄是x岁,哥哥的年龄是y岁,由题意得.故选:D.8.如图,直线AB:y=x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是()A.(3,)B.(8,5) C.(4,3) D.(,)【解答】解:由直线AB:y=x+1分别与x轴、y轴交于点A,点B,可知A,B的坐标分别是(﹣2,0),(0,1),由直线CD:y=x+b分别与x轴,y轴交于点C,点D,可知D的坐标是(0,b),C的坐标是(﹣b,0),根据S△ABD=4,得BD•OA=8,∵OA=2,∴BD=4,那么D的坐标就是(0,﹣3),C的坐标就应该是(3,0),CD的函数式应该是y=x﹣3,P点的坐标满足方程组,解得,即P的坐标是(8,5).故选B.9.小明和小莉出生于2000年12月份,他们的生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期和是22,那么小莉的生日是()A.15号B.16号C.17号D.18号【解答】解:设小明的生日是12月份的x号,小莉的生日是12月份的y号,则或或或,解得,(不是整数,舍去)或或(不是整数,舍去)或(不合题意,舍去).综上所述,小莉的生日是18号.故选:D.10.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售时的收入是()A.310元B.300元C.290元D.280元【解答】解:设y=kx+b,由图知,直线过(1,800)(2,1300),代入得:,解之得:∴y=500x+300,当x=0时,y=300.即营销人员没有销售时的收入是300元.故选:B.二、填空题11.已知方程2m﹣3n=15中m与n互为相反数,那么m=3,n=﹣3.【解答】解:∵m与n互为相反数,∴m=﹣n.将m=﹣n代入2m﹣3n=15得;﹣2n﹣3n=15,解得n=﹣3.∴m=3故答案为:3,﹣3.12.已知(2x+3y﹣4)2+|x+3y﹣7|=0,则x=﹣3,y=.【解答】解:由(2x+3y﹣4)2+|x+3y﹣7|=0,得,解得.13.如果直线y=2x+3与直线y=3x﹣2b的交点在x轴上,那么b的值为﹣.【解答】解:当y=0时,2x+3=0,解得x=﹣,则直线y=2x+3与x轴的交点坐标为(﹣,0),把(﹣,0)代入y=3x﹣2b得3×(﹣)﹣2b=0,解得b=﹣.故答案为﹣.14.如图,若直线l1与l2相交于点P,则根据图象可得,二元一次方程组的解是.【解答】解:根据题意知,二元一次方程组的解就是直线l1与l2的交点P的坐标,又∵P(2,1),∴原方程组的解是:;故答案是:.15.某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有9000人参观.【解答】解:设每周参观人数y人与票价x元之间的关系式为y=kx+b,由题意,得,解得:,∴这个函数关系式为:y=﹣500x+12000.当x=6时,y=﹣500x+12000=9000.所以如果门票价格定为6元,那么本周大约有9000人参观.故答案为:9000.16.小明解方程组的解为,由于不小心,滴上了两滴墨水,刚好遮住了两数■和★,请你帮她找回这两个数,■=9,★=﹣3.【解答】解:将x=4代入3x﹣y=15,得y=﹣3.将x,y的值代第一个方程,得3x+y=3×4﹣3=9.所以■表示的数为9,★表示的数为﹣3,故答案为:9,﹣3.17.已知方程组,则y与x之间的关系式为y=﹣6.【解答】解:,由①得:t=③,③代入②得:y=﹣5=﹣6.故答案为:y=﹣618.某车间每天可以生产甲种零件600个或乙种零件300个或丙种零件500个,这三种零件各一个可以配成一套,现要在63天的生产中,使生产的三种零件全部配套,这个车间应安排15天生产甲种零件,30天生产乙种零件,18天生产丙种零件,才能使生产出来的零件配套.【解答】解:设生产甲种零件应当用x天,生产乙种零件用y天.则生产丙种零件需z天.则,解得,即:生产甲种零件应当15天,生产乙种零件应当用30天,生产丙种零件应当用18天.故答案是:15;30;18.三、解答题19.解方程组:(1)(2).【解答】解:(1)把①代入②得:5x+6x﹣14=8,即x=2,把x=2代入①得:y=﹣1,则方程组的解为;(2)①+②得:5x+2y=16④,②+③得:3x+4y=18⑥,⑤×2﹣⑥得:7x=14,即x=2,把x=2代入④得:y=3,把x=2,y=3代入③得:z=1,则方程组的解为.20.2014年世界杯足球赛在巴西举行,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元,其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?【解答】解:设小李预定了小组赛和淘汰赛的球票各x张,y张,由题意得,,解得:.答:小李预定的小组赛和淘汰赛的球票各8张,2张.21.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为.乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么;(2)求出原方程组的正确解.【解答】解:(1)将代入原方程组得解得.将代入原方程组得,解得,∴甲把a看成﹣,乙把b看成了.(2)由(1)可知原方程组中a=﹣1,b=10.故原方程组为,解得.22.在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(1)求出图中格点四边形DEFG对应的S,N,L的值.(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.【解答】解:(1)观察图形,可得S=3,N=1,L=6;(2)根据格点三角形ABC及格点四边形DEFG中的S、N、L的值可得,,解得,∴S=N+L﹣1,将N=82,L=38代入可得S=82+×38﹣1=100.23.小明的爸爸骑摩托车带着小明在公路上匀速行驶,小明第一次注意到路边里程碑上的数时,发现它是一个两位数且它的两个数字之和为9,刚好过一个小时,他发现路边里程碑上的数恰好是第一次看到的个位和十位数字颠倒后得到的,又过3小时,他发现里程碑上的数字比第一次看到的两位数中间多个0,你知道小明爸爸骑摩托车的速度是多少吗?【解答】解:小明第一次注意到路边里程碑上的两位数的十位数字为x,个位数字为y,根据题意,得解得,即小明第一次注意到路边里程碑上的数字为27,1小时后小明看到的程碑上的数字为72,72﹣27=45(千米/小时),所以小明爸爸骑摩托车的速度是45千米/小时.24.某同学在A,B两家超市发现他看中的随身听的单价相同,书包单价也相同.随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.(1)求该同学看中的随身听和书包的单价各是多少元?(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用).但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?【解答】解:(1)设书包单价为x元,则随身听的单价为(4x﹣8)元.根据题意,得4x﹣8+x=452,解得:x=92,4x﹣8=4×92﹣8=360.答:书包单价为92元,随身听的单价为360元.(2)在超市A购买随身听与书包各一件需花费现金:452×80%=361.6(元).因为361.6<400,所以可以选择超市A购买.在超市B可花费现金360元购买随身听,再利用得到的90元返券,加上2元现金购买书包,总计花费现金:360+2=362(元).因为362<400,所以也可以选择在B超市购买.因为362>361.6,所以在超市A购买更省钱.25.为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金.已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:月份销售额销售额(单位:元)1月2月3月4月5月6月小李(A公司)11600 12800 14000 15200 16400 17600小张(B公司7400 9200 11000 12800 14600 16400(1)请问小李与小张3月份的工资各是多少?(2)小李1~6月份的销售额y1与月份x的函数关系式是y1=1200x+10400,小张1~6月份的销售额y2也是月份x的一次函数,请求出y2与x的函数关系式;(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资.【解答】解:(1)小李3月份工资=2000+2%×14000=2280(元),小张3月份工资=1600+4%×11000=2040(元).(2)设y2=kx+b,取表中的两对数(1,7400),(2,9200)代入解析式,得解得即y2=1800x+5600.(3)小李的工资w1=2000+2%(1200x+10400)=24x+2208,小张的工资w2=1600+4%(1800x+5600)=72x+1824.当小张的工资w2>w1时,即72x+1824>24x+2208解得x>8.答:从9月份起,小张的工资高于小李的工资.。
2022年北师大版数学《相似三角形的判定 课后练习二及详解》配套精品练习(附答案)
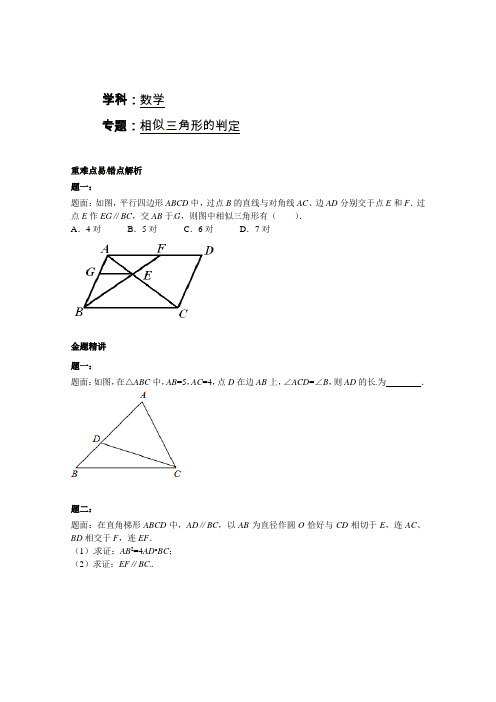
学科:数学专题:相似三角形的判定重难点易错点解析题一:题面:如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有().A.4对B.5对C.6对D.7对金题精讲题一:题面:如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为.题二:题面:在直角梯形ABCD中,AD∥BC,以AB为直径作圆O恰好与CD相切于E,连AC、BD相交于F,连EF.(1)求证:AB2=4AD•BC;(2)求证:EF∥BC.满分冲刺题一:题面:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,12DCCF.求AE的长.题二:题面:如图,在正方形ABCD中,F是CD上一点,AE⊥AF,点E在CB的延长线上,EF交AB于点G.求证:DF•FC=BG•EC.题三:题面:如图,已知边长为2的正方形ABCD中,E为CD的中点,P为BC上的一点,问题:添加一个条件,使得△ABP与以E、C、P为顶点的三角形相似,共有几种添加方法?课后练习详解重难点易错点解析题一:答案:B.详解:根据平行四边形的性质,平行的性质和相似三角形的判定可得:△AGE∽△ABC,△BGE∽△BAF,△AEF∽△CEB,△ACB∽△CAD,△AGE∽△CDA,5对.故选B.金题精讲题一:答案:.详解:∵∠ACD=∠B,∠A=∠A,∴△ABC∽△ACD.∴AD AC AC AB=.又∵AB=5,AC=4,∴445AD=,解得AD.题二:答案:AB2=4AD•BC;EF∥BC.详解:证明:(1)作DH⊥BC于H,如图,∵梯形ABCD为直角梯形,且AD∥BC,∴四边形ABHD为矩形,∴DH=AB,AD=BH,∴CH=CB-AD,∵以AB为直径作圆O恰好与CD相切于E,∴DA、CB都是⊙O的切线,∴DE=DA,CE=CB,∴DC=DA+CB,在Rt△DHC中,DH2=DC2-CH2,∴AB2=(AD+BC)2-(BC-AD)2,∴AB2=4AD•BC;(2)∵AD∥BC,∴△FDA∽△FBC,∴AD DF BC FB=,而DE=AD,EC=BC,∴DE DF EC FB=,∴EF∥BC.满分冲刺题一:答案:5232-.详解:∵四边形ABCD是矩形,∴∠A=∠D=90°,DC=AB=4,∵CF⊥EF,∴∠EFC=90°.∴∠AFE+∠DFC=90°,∵∠AEF+∠AFE=90°,∴∠AEF=∠DFC,∴△AEF∽△DFC.∴AE AF DF DC=,∵12DCCF=,DC=4,∴∠DFC=30°,∴443tan30tan30DCFD===︒︒,∴1043AF=-,∴5232AF FDAECD-==.题二:答案:DF•FC=BG•EC.详解:∵∠EAB+∠BAF=90°,∠DAF+∠BAF=90°,∴∠BAE=∠DAF,∴tan∠BAE=tan∠DAF,∵AB=AD,∴DF=BE,又∵AB∥CD,∴BE BG EC FC=,∴BE•FC=BG•EC,∴DF•FC=BG•EC.题三:答案:只有一种方法在BC上的一点使得BP=43.详解:如图设BP=x,若△ABP∽△ECP,得AB EC BP CP=,即212x x=-,解得x=43.若△PBA∽△ECP,得BP ECBA CP=,即122xx=-,化简得x2-2x+2=0,此方程无解,故不存在综上,只有一种方法在BC上的一点使得BP=43.(或延长AB至M,使BM=BA,连接EM,交BC与点P,则P就是符合条件的点)第七章平行线的证明周周测3一、单选题1、如图,△ABC中,∠ACB=90°, ∠A=30°,AC的中垂线交AC于E.交AB于D,则图中60°的角共有( )A、6个B、5个C、4个D、3个2、下列说法中正确的是( )A、原命题是真命题,则它的逆命题不一定是真命题B、原命题是真命题,则它的逆命题不是命题C、每个定理都有逆定理D、只有真命题才有逆命题3、下列命题是假命题的是( )A、如果a∥b,b∥c,那么a∥cB、锐角三角形中最大的角一定大于或等于60°C、两条直线被第三条直线所截,内错角相等D、矩形的对角线相等且互相平分4、如图,在梯形ABCD中,AB∥CD,AD=DC=CB,若,则A、130°B、125°C、115°D、50°5、如图,AB∥CD,∠D=∠E=35°,则∠B的度数为()A、60°B、65°C、70°D、75°6、下列条件中,能判定△ABC为直角三角形的是()A、∠A=2∠B=3∠CB、∠A+∠B=2∠CC、∠A=∠B=30°D、∠A=∠B=∠C7、下列四个命题,其中真命题有()(1)有理数乘以无理数一定是无理数;(2)顺次联结等腰梯形各边中点所得的四边形是菱形;(3)在同圆中,相等的弦所对的弧也相等;(4)如果正九边形的半径为a,那么边心距为a•sin20°.A、1个B、2个C、3个D、4个8、下列命题:①等腰三角形的角平分线、中线和高重合,②等腰三角形两腰上的高相等;③等腰三角形的最小边是底边;④等边三角形的高、中线、角平分线都相等;⑤等腰三角形都是锐角三角形.其中正确的有()A、1个B、2个C、3个D、4个9、下列命题中,真命题是()A、周长相等的锐角三角形都全等B、周长相等的直角三角形都全等C、周长相等的钝角三角形都全等D、周长相等的等腰直角三角形都全等10、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为()A、80B、50C、30D、20二、填空题11、命题“三角形的一个外角等于和它不相邻的两个内角的和”的条件是________,结论________.12、如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于________.13、已知命题“如果一个四边形是平行四边形,那么这个四边形是旋转对称图形.”,写出它的逆命题是 ________,该逆命题是 ________命题(填“真”或“假”).14、如图,AB∥CD,∠A=56°,∠C=27°,则∠E的度数为________.15、写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:________.16、已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为________.17、一个三角形的三个外角之比为5:4:3,则这个三角形内角中最大的角是________度.18、如图,在ABCD中,CH⊥AD于点H,CH与BD的交点为E.如果,,那么________三、解答题(共5题;共29分)19、如图,已知∠ABC=52°,∠ACB=60°,BO,CO分别是∠ABC和∠ACB的平分线,EF过点O,且平行于BC,求∠BOC的度数.20、如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.21、已知△ABC中,∠A=105°,∠B比∠C大15°,求:∠B,∠C的度数.22、如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.23、已知:如图,E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
北师大版八年级下册4.5相似三角形课件PPT

判断
1 两个全等三角形相似, 2 两个直角三角形相似 3 两个等腰直角三角形相似 4两个等腰三角形相似 5有一个角是30度的直角三角形 相似
比一比 找异同
对应边 对应角
全等三角形 相似三角形
相等 相等
成比例 相等
动动手,练一练
例、1 如图,有一块呈三角形形状的草坪,其中
所以: ∠AED=∠ACB=40°
所以:
在△ADE中,
AE DE , AC BC
∠ADE+ ∠AED+ ∠A=180°
即
50Байду номын сангаас
即: ∠ADE+ 40° + 45° =180° 50 30
DE 70
所以 ∠ADE=95°
所以 DE 50 70 43 .75 cm 50 30
在例2的条件下,图中有哪些 线段成比例?图中有互相平 行的线段吗?
北师大版《数学》八年级 下册
做 一做,谁最快!
1所有的矩形都相似 2所有的菱形都相似 3有一个角是60度的菱形都相似 4所有的正三角形都相似
5所有的正六边形都相似 6边数相同的正多边形都相似
引出问题:这个三角形形状的草坪,其中一边长20
米,在小朋友的画板上,这条边画了5厘米,其他两 边都是14米,小朋友在画板上应画多长?
x 20 33
22
30
48
n°
3a
10 2a 50°y
45°
85° 45° m°
动脑筋 例2 如图,已知
⊿ABC∽⊿ADE,AE=50cm,EC=30cm, BC=70cm,
C
∠BAC=45度, ∠ACB=40度
北师大版-数学-八年级下册--名师e线-用好相似三角形的性质

用好相似三角形的性质山东 田珍一、相似三角形的性质1.相似三角形(或多边形)的周长比等于相似比.2.相似三角形(或多边形)的面积比等于相似比的平方.3.相似三角形对应中线的比,对应角平分线的比,对应高的比都等于相似比.注意:(1)除了上面的三个性质外,还有相似三角形的对应边成比例,对应边的比等于相似比.(2)要特别注意相似三角形(或多边形)的面积的比是等于相似比的平方,不能与其他的性质相混淆.二、典例分析例1 已知△ABC ∽△A ′B ′C ′,AD 是△ABC 的中线,A ′D ′是△A ′B ′C ′的中线,若21''=D A AD ,且△ABC 的周长为60 cm ,则△A ′B ′C ′的周长为______. 分析:因为△ABC ∽△A ′B ′C ′,所以它们的周长比等于它们的相似比,对应中线的比等于相似比,据此列出方程即可求解.解:因为△ABC ∽△A ′B ′C ′,所以相似比=21''=D A AD . 即21'''=∆∆周长周长C B A ABC . 因为△ABC 的周长为60 cm ,故△A ′B ′C ′的周长=2×60=120(cm ).跟踪训练1 已知△ABC 与△A ′B ′C ′相似,23''''''===C A AC C B BC B A AB ,且△ABC 的周长为21 cm ,求△A ′B ′C ′的周长.例2 如图,在梯形ABCD 中,AD ∥BC ,S △ADO ∶S △ABO =1∶2,则S △ADO ∶S △BOC 等于【 】A.1∶3B.1∶4C.1∶5D.1∶6分析:由观察,可知△ADO 与△ABO 是分别以DO 、BO 为底且高相等的两个三角形,所以由S △ADO ∶S △ABO =1∶2,可得21=BO DO .又因为AD ∥BC ,所以△ADO ∽△CBO.根据“相似三角形的面积比等于相似比的平方”,得CBO ADO S S ∆∆=(BO DO )2=41. 解:选B.跟踪训练2 已知△ABC 与△A ′B ′C ′的相似比为73,且S △ABC =9 cm 2,求△A ′B ′C ′的面积.例3 如图,电灯M 在横杆CD 的正上方,CD 在灯光下的影子为AB ,AB ∥CD ,CD =3 m ,AB=7 m ,点M 到AB的距离是5 m ,则点M 到CD 的距离是【 】 A.157 m B.76 m C.715 m D.510 m 分析:点M 到CD 的距离即为△MCD 的高,而点M 到AB 的距离即为△MAB 的高,由AB ∥CD ,可得△MCD ∽△MAB ,根据相似三角形的性质“相似三角形的对应边上高的比等于相似比”即可求出点M 到CD 的距离.解:设点M 到CD 的距离为x cm.因为AB ∥CD ,所以△MCD ∽△MAB.则根据“相似三角形对应边上高的比等于相似比”,可得573x ,解得x=715.故选C. 跟踪训练3 如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶B 、C 刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是_____米.答案1.14(cm )2.49 cm 23.60。
八年级数学下册 第四章 4.5相似三角形学案(无答案) 北师大版
§4.5相似三角形【学习目标】1.掌握相似三角形的定义、表示方法,并能根据定义判断两个三角形是否相似.2.能根据相似比进行计算.【学习重点】1.相似三角形的定义及运用.【学前准备】1.什么是相似多边形?什么是相似比?2.相似多边形指的是哪些多边形?包括相似三角形吗?【师生探究合作交流】1.相似三角形的定义及记法因为相似三角形是相似多边形中的一类,因此,相似三角形的定义可仿照相似多边形的定义给出,你可以吗?相似三角形定义是:_____________________________________________.如△ABC与△DEF相似,记作________________________.其中对应顶点要写在对应位置,如A与D,B与E,C与F相对应.AB∶DE=相似比.2.想一想如果△ABC∽△DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢?解:由相似多边形的性质可知,对应角对应相等,对应边对应成比例.所以∠A=____, ____=∠E, ∠C=____;.AB∶DE=________=________AB即==DE【议一议】(1)两个全等三角形一定相似吗?为什么?两个全等三角形________相似,因为它们的对应角_______,对应边_______,相似比=_______。
(2)两个直角三角形一定相似吗?两个等腰直角三角形呢?为什么?两个直角三角形________相似。
原因或举例说明:两个等腰直角三角形________相似. 因为它们的各角对应_______,各边对应________,所以,所有的等腰直角三角形_______(3)两个等腰三角形一定相似吗?两个等边三角形呢?为什么?(说明理由)3.例题例1.如图,有一块呈三角形形状的草坪,其中一边的长是30m,在这个草坪的图纸上,这条边长6 cm,其他两边的长都是5cm,求该草坪其他两边的实际长度.例2. 已知△ABC∽△ADE, AE=60cm, EC=30cm , BC=80cm, ∠BAC=55°, ∠ACB=42°,求:(1)∠AED和∠ADE的度数;(2)DE的长. CEA D B4.想一想在例2的条件下,图中有哪些线段成比例?图中有互相平行的线段吗?试一试!你用了______分钟(真棒!)【小试牛刀】1.随堂练习1、2【小结】1.相似三角形定义:2.相似三角形表示法:【今日作业】1.已知△ABC∽△DEF,AB=4cm,BC=4cm,CA=2cm,EF=8cm,求线段DE,DF的长。
最新-八年级数学下册 相似图形之相似三角形课件 北师大版 精品
法.请大家回忆一下.
(1)各角对应相等,各边对应成比例的两
个多边形叫做
.
相似多边形对应边的比叫做
.
(2)五边形与五边形相似,记作
回答
(1)各角对应相等,各边对应成比例的两
个多边形叫做
.
相似多边形对应边的比叫做
.
(2)五边形与五边形相似,记作
由上节课学习的内容,你能不能给 相似三角形下个定义?试试看。
定义
三角对应相等,三边对应成 定义 比例的两个三角形叫做相似
三角形.
相似三角形有哪些性质?
示意图
C
回答
A
B
如果△ABC ∽ △DEF,那么哪些角是对应 角?哪些边是对应边?对应角有什么关系? 对应边呢?
C
回答
A
B
△ABC与△DEF相似,记作△ABC ∽ △DEF 。
其中对应顶点要写在对应位置,如A与D,B与E,C与F 相对应。 ∠A和∠E,∠B和∠F,∠C和∠D对应相等,即
X
X
所以,草坪其他两边的实际长度都是14m
例2.如图2,已知△ABC ∽ △ADE,AE = 50cm,EC = 30cm,BC = 70cm,∠A = 45°,∠C = 40°,求:(1) ∠AED和∠ADE的度数;(2)DE的长.
解答
例2.如图2,已知△ABC ∽ △ADE,AE = 50cm,EC = 30cm,BC = 70cm,∠A = 45°,∠C = 40°,求:(1) ∠AED和∠ADE的度数;(2)DE的长.
回答 判断:以下说法是否正确,为什么?请说说你的理由 (1)两个全等三角形一定相似。(√ ) (2)两个直角三角形一定相似。( × ) (3)两个等腰直角三角形一定相似。( √ ) (4)两个等腰三角形一定相似。( × ) (5)两个等边三角形一定相似。( √ )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.△ABC 中,AB=AC ,D 是AB 上一点,使AD=DC=BC 且BD=2,则BC 的长是2.如右图,把一个矩形剪去一个正方形,若所剩矩形与原矩形相似,则原矩形长边与短边的比是( )3 .如图梯形的一条对角线BD 分中位线EF 所成两条线段的比是2:1,则DO :OM :MB=( )4. 已知:a b c b c a c a b k cab+-+-+-===, 则直线y=kx-k 与坐标轴围成的 三角形的面积是5.如图, 正方形ABCD 中,E 为AB 中点,F 为CD 延长线上一点,且∠FEC=∠FCE ,EF 交AD 于P ,.FG ⊥EC.,求证:S △AEP =4S △PDF6.已知:DE ∥BC ,S △BOC =32S △ABC 求:S △ADE+:S △ABC7.如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC8. △ABC 中,DE ∥FG ∥BC ,且AD :DF :FB=3:2:1,则S △ADE :S 四边形DFGE :S 四边形FBCG9.(1)阅读下列材料,补全证明过程:如图,矩形ABCD 中,AC 、BD 相交于点O ,OE ⊥BC 于E ,连接DE 交OC 于点F ,作FG ⊥BC 于G ,求证:点G 是线段BC 的一个三等分点(2)请你仿照上面的画法,在原图上画出BC 的一个四等分点10.如图,在Rt △ABC 中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC 上距离B 点3㎝的点P 为中心,把这个三角形按逆时针方向旋转90º至△DEF ,则旋转前11. 如图,已知点D 是等边三角形ABC 的BC 边上一点,把△ABC 向下折叠,折痕为MN ,使A 点落在D 处,若BD :DC=m :n ,则AM :12.图:D 是AC 的三等分点.E 是BC 的四等分点,BD 、AE 交于点F ,则AF :FE= ; BF :FD= ;CPGFE DC BA ABCD C在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等分点.已知:如图,等边△ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等分点.已知:如图,等边△ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等已知:如图,等边△ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等分点.已知:如图,等边△ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等分点.已知:如图,等边△ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒,当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.1)设△EGA的面积是S,写出S与t的函数关系式;2)当t为何值时,AB⊥GH;3)请你证明△GFH的面积为定值;4)当t为何值时,点F和点C是线段BH的三等分点.(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(1)阅读下列材料,补全证明过程:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连接DE交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点(2)请你仿照上面的画法,在原图上画出BC的一个四等分点如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt△ABC中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC上距离B点3㎝的点P为中心,把这个三角形按逆时针方向旋转90º至△DEF,则旋转前后两如图,在Rt △ABC 中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC 上距离B 点3㎝的点P 为中心,把这个三角形按逆时针方向旋转90º至△DEF ,则旋转前后两如图,在Rt △ABC 中,∠A=90º,AB=3㎝,AC=4㎝,以斜边BC 上距离B 点3㎝的点P 为中心,把这个三角形按逆时针方向旋转90º至△DEF ,则旋转前后两如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
求证:AG=51AC如图,在□ABCD 中,E 为AB 的中点,点F 在AD 上,AF=21DF 。
