Chapter 3 几何光学§ 3-1 抛物面镜成像§ 3-.
第三章几何光学球面反射折射物像公式
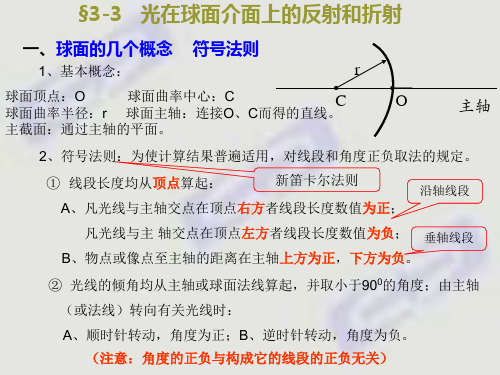
例3.4:
一个折射率为1.6的玻璃哑铃,长20cm,两端的曲率半径为 2cm。若在 离哑铃左端5cm处的轴上有一物点,试求像的位置和性质。
[解]:两次折射成像问题。
n
P
O1
n
P’1 n` O 2
1、P为物, 对球面O1折射成像P1’
已知 : s1 5cm , r1 2cm , n 1, n ' 1.6 n n n n 由折射成像公式 ' r1 s1 s1
沿轴线段
A、凡光线与主轴交点在顶点右方者线段长度数值为正; 凡光线与主 轴交点在顶点左方者线段长度数值为负; B、物点或像点至主轴的距离在主轴上方为正,下方为负。 ② 光线的倾角均从主轴或球面法线算起,并取小于900的角度;由主轴 (或法线)转向有关光线时: A、顺时针转动,角度为正;B、逆时针转动,角度为负。 (注意:角度的正负与构成它的线段的正负无关)
2
r
2
s r
'
2
2 r s ' r cos
光程 PAP ' nl nl ' n
r 2 r s 2 2 r r s cos r
2
n
s r
'
2
2 r s r cos
1、高斯公式:
球面反射 : f ' f 1 1 2 ' s s r
六、理想成象的两个普适公式
n' n n' n 将物像公式 ' 变形为 : s s r n' n r r ' ' ' f f n n n n 1 1 ' ' s s s s
第三章几何光学薄透镜

This solar-thermal electric plant in the Mojave Desert uses long rows of parabolic mirrors to focus the sun’s rays on oil-filled pipes,which are located at the focal point of each mirror.
按照波动理论,产生全反射时除反射波外,在光疏介 质中并非完全不存在透射波,只不过它沿界面方向传 播,且其振幅在垂直界面方向按指数衰减,透入深度 只有波长量级,称为倏逝波,或隐失波。
但平均来说,光波的能量全部返回光密介质, 在光疏介质中并不形成透射光。
临界角(2 sinic n1 n1 n1 2.42 (n1 n2 )
Light rays emanating from the bee’s body enter the tube and, in part, are guided around the 90 degrees turn via TIR, eventually exiting through the front surface and allowing you to see the bee.
2、光在平面上的折射
Refraction
n1 sin1 n2 sin 2
A beam of light is refracted as it enters a tank of water.
3、光束单心性的破坏
出射光束不能保持单心性
第三章-几何光学
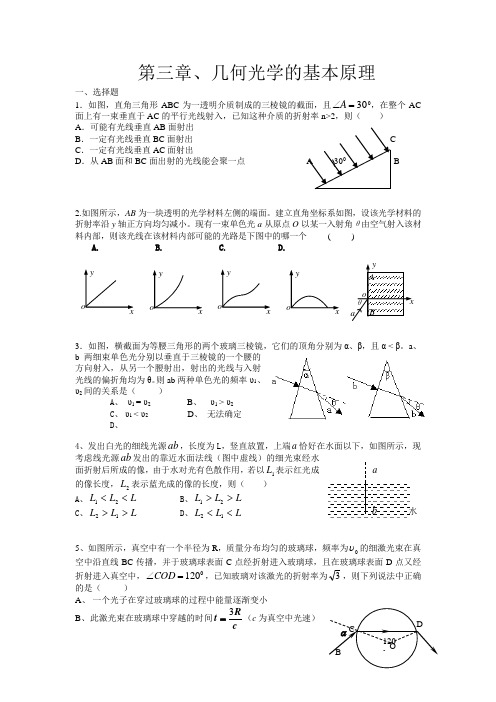
第三章、几何光学的基本原理一、选择题1.如图,直角三角形ABC 为一透明介质制成的三棱镜的截面,且30=∠A 0,在整个AC 面上有一束垂直于AC 的平行光线射入,已知这种介质的折射率n>2,则( ) A .可能有光线垂直AB 面射出 B .一定有光线垂直BC 面射出 CC .一定有光线垂直AC 面射出D .从AB 面和BC 面出射的光线能会聚一点 A 300 B2.如图所示,AB 为一块透明的光学材料左侧的端面。
建立直角坐标系如图,设该光学材料的折射率沿y 轴正方向均匀减小。
现有一束单色光a 从原点O 以某一入射角θ由空气射入该材料内部,则该光线在该材料内部可能的光路是下图中的哪一个 ( )A. B. C. D.3.如图,横截面为等腰三角形的两个玻璃三棱镜,它们的顶角分别为α、β,且α < β。
a 、b 两细束单色光分别以垂直于三棱镜的一个腰的方向射入,从另一个腰射出,射出的光线与入射光线的偏折角均为θ。
则ab 两种单色光的频率υ1、υ2间的关系是( )A 、 υ1 = υ2B 、 υ1 > υ2C 、 υ1 < υ2D 、 无法确定 D 、4、发出白光的细线光源ab ,长度为L ,竖直放置,上端a 恰好在水面以下,如图所示,现考虑线光源ab 发出的靠近水面法线(图中虚线)的细光束经水面折射后所成的像,由于水对光有色散作用,若以1L 表示红光成的像长度,2L 表示蓝光成的像的长度,则( ) A 、L L L <<21B 、L L L >>21C 、L L L >>12D 、L L L <<125、如图所示,真空中有一个半径为R ,质量分布均匀的玻璃球,频率为0υ的细激光束在真空中沿直线BC 传播,并于玻璃球表面C 点经折射进入玻璃球,且在玻璃球表面D 点又经折射进入真空中,0120=∠COD ,已知玻璃对该激光的折射率为3,则下列说法中正确的是( )A 、 一个光子在穿过玻璃球的过程中能量逐渐变小B 、 此激光束在玻璃球中穿越的时间cRt 3=(c 为真空中光速) 水 a b O CDB α1200y a θ xo A ByxoyxoyxoyxoC 、 改变入射角α的大小,细激光可能在玻璃球的内表面发生全反射D 、 图中的激光束的入射角045=α6、如图所示,两束单色光A 、B 自空气射向玻璃,经折射形成复合光束C ,则下列说法中正确的是:( )A 、 A 光子的能量比B 光子的能量大 B 、 在空气中,A 光的波长比B 光的波长短C 、 在玻璃中,A 光的光速小于B 光的光速D 、 玻璃对A 光的临界角大于对B 光的临界角7、如图所示,激光液面控制仪的原理是:固定的一束光AO 以入射角i 照射到液面上,反射光OB 射到水平的光屏上,屏上用一定的装置将光信号转变为电信号,电信号输入控制系统用以控制液面高度,如果发现光点B 在屏上向右移动了Δs 的距离到B ˊ,则可知液面升降的情况是( )A 、 升高了2S ∆·tan i B .降低了2S ∆·tan i D 、 升高了2S ∆·cot i D 、 降低了2S∆·cot i8.人类对光的本性的认识经历了曲折的过程。
几何光学3

几何光学
符号法则:
为了从一具体情况出发导出物像的一般关 系,必须对有关参量规定一套符号规则。 ⅰ°物设点入Q射到光顶从点左A到的右距离QA称为物距,用s表示 。 实物,s > 0,虚物,s < 0。 ⅱ°对像反点射Q镜′到、A折的射距镜离一Q样′A,称左为正像右距负,。用s′表示。 实像,s′>0,虚像,s′<0。 对反射镜, 左正右负;对折射镜, 左负右正。
GanNan Normal University
School of Physics and Electronic Information Science
虚实 象象 (( 物物 )) :: 无有 实实 际际 光光 线线 会会 聚聚 (( 发发 出出 )) 的的 点点
几何光学
成像实例
GanNan Normal University
几何光学
四、物像之间的等光程性 虚光程 物点Q和像点Q′之间的光程都相等。---等光程性
Q
Q′
QQ′间分布有无数条实际光线 ,由费马 原理,其光程应取极值或恒定,都取极大或极 小是不可能的,唯一的可能就是取恒定值,即 光程相等。
GanNan Normal University
School of Physics and Electronic Information Science
Ⅴ、从光轴(或球面的法线)转到光线的方向逆时 钟时交角u为正,顺时钟时u为负,并取小于 π /2的角度。对于反射光线则相反。
Ⅵ、在光路图中,标绝对值。
几何光学
GanNan Normal University
School of Physics and Electronic Information Science
第三章几何光学的基本原理

2.波面:光传播中,位相相同的空间点所构成的平面或曲面。
说明: ① 波面即等相面,也是一种抽象的数学模型。 ② 波面为平面的光波称为平面光波(如平行光束);为球面的 称为球面光波(如点光源所发光波);为柱面的称为柱面光波
(如缝光源所发光波)
No Image
3.光线与波面的关系
在各向同性介质中,光线总是与波面法线方向重合。即光线与波 面总是垂直的。 平面波 球面波 柱面波
第3章 几何光学的基本原理 引 言
• 光的干涉、衍射现象,说明光是一种电磁波;光的传播过程就是 无穷次波的相干迭加;光的行为可用其时空周期性——波长、振幅和 位相来描述。因此,波动光学从光的本性出发,精确地描述了光现象。
• 事实上,在很多情况下,不考虑光的波动性,不用光的时空周期性, 而代之以简单的几何方法,就可得到与实际基本相符的结论(如光的 在所研究的对象中,若其几何的尺寸远 反射、折射成像等)。 远大于所用光波的波长(如对一定大小
沿光程为最小值、最大值或恒定值的路程传播。
B ds A n
2、表达式:
n ds极值
A
B
3.说明:
或 : n ds 0
A
B
①意义:费马原理是几何光学的基本原理,用以描绘光在空间两定点间的传 播规律。
②用途:A.可以推证反射定律、折射定律等实验定律。由此反证了费马原理 的正确性. B.推求理想成象公式。
No Image
第3章 几何光学的基本原理
§3.1 基本概念及基本实验定律
一、光线与波面
1.光线:形象表示光的传播方向的几何线。
说明:① 同力学中的质点一样,光线仅是一种抽象的数学模型。 它具有光能,有长度,有起点、终点,但无粗细之分,仅 代表光的传播方向。任何想从实际装置(如无限小的孔) 中得到“光线”的想法均是徒劳的。 ② 光束:无数光线构成光束。 ③ 光沿光线方向传播时,位相不断改变。
光学第三章几何光学的基本原理

§3.4 光在平面介面上的反射和折射
光学纤维
保持物、像在几何形状上的相似性,是理想成像的基本要求。保持光 束的单心性是保持形状相似从而实现理想成像的保证。所以,研究成像问 题就归结为研究如何保持光束单心性问题。 一般情况下,光在介面上反射和折射后,其单心性不再保持。但只要 满足适当的条件,可以近似地得到保持。接下来的两节,主要研究在不同 介面反射、折射时,光束单心性的保持情况。
0 2 n12 n2
n2 sin ic n 1
2 故 : i sin 1 n12 n2
x x1
y
2 1
x2 x
n2 x2 x
2
y
2 2
同理:也可证 明反射定律。
n1 A'C n2 CB ' n1 sin i1 n2 sin i2 0 AC CB Y n2 sin i2 n2 sin i1
由于反射、折射定律是实 验定律,是公认的正确的 结论,所以,费马原理是 正确的。
3.光线与波面的关系
在各向同性介质中,光线总是与波面法线方向重合。即光线与波 面总是垂直的。 平面波 球面波 柱面波
二、几何光学的基本实验定律
1.直线传播定律:在均匀介质中,光总是沿直线传播的。 2.反射定律: ① 反射线在入射线和法线决定的平面内;
i1 i
' 1
② 反射线、入射线分居法线两侧; ' ③ 1 1
i i
i2
n1 n2
3.折射定律: ① 折射线在入射线和法线决定的平面内; ② 折射线、入射线分居法线两侧; ③
i1 i
' 1
n2 sin i2 n1 sin i1
第三章几何光学薄透镜作图求像法

2、透镜作图求像的原理
透镜作图求像的原理是利用焦点、焦平面和光心的性质:
(1)光心:入射光线入射到光心,出射光线从光心 出射并保持原来的传播方向。 (2)焦点:平行于光轴的光线入射到光学系统,出射
的会聚光线的顶点;或平行于光轴的出射光线所对应的入
射的发散光线的顶点。 (3)焦平面:平行光线入射到光学系统后,出射光线必 相交于第二焦平面(像方焦平面)上的一点。
P
F
F
O
P
2、轴上物点的作图方法
(1)第一焦平面作图法 中学及书本上的作图方法只针对同种介质,是一种特殊
情况。本方法既适用于同种介质,也适用于不同介质。
P
P
F
O
F
对于薄凹透镜的作图请同学们自己练习。
(2)第二焦平面的作图方法
P
F
O F
P
对于薄凸透镜的作图请同学们自己练习。 (3)以上作图方法的文字表述请同学自己总结并会熟练 使用。
第一焦平面(物方焦平面)上的一点发出的光线经
光学系统后,其出射光线一定是平行光线。
(三)薄透镜作图求像的方法 1、轴外物点的作图方法 (1)同种介质中:透镜两侧的折射率相同
一般采用三条典型光线作图,实际作图只需作二条即可。
P
F O
F
P
(2)不同介质中:透镜两侧的折射率不相同 两条典型光线作图即可。
【习题3.11】有一折射率为1.5半径为4cm的玻璃球,物体在 距球表面6cm处,求:1)像离球心之距离;2)像的横向 放大率。
解:(逐次求像法)
(1)由球面折射成像公式可得物体发出的光束经第一个球
面(凸球面)折射所成像的位置
n n n n s s r 1.5 1 1.5 1 s 6 4 s 36cm
第三章 几何光学的基本原理

第三章几何光学的基本原理干涉和衍射现象揭示了光的波动性。
光既然具有波动性,那么,所有光学现象都应该能用波动概念来解释,包括光的直线传播现象在内。
但是直线传播,尤其是反射,折射成像等问题,如果不用波长、相位等波动的概念,而代之以光线和波面等概念,并用几何学方法来研究将更为方便。
这就是几何光学的研究内容。
由于这只有在波面线度远比波长大时才适用,因此本章所讲述的内容仅以成像的一级近似理论为限,因为这种近似有很大的实用意义。
3.1 光线的概念3.1.1 光线与波面“光线”只能表示光的传播方向,不可以误认为是从实际光束中借助于有孔光阑分出的一个狭窄部分,那么,在极限情况下,选用任意小的孔,就能得到像几何线那样的所谓“光线”,但是由于衍射作用,实际上要分出任意窄的光束是不可能的。
通过半径为R的圆孔的实际光束,其传播范围不可比避免的要扩大,其角宽度由衍射角θ∝λ/R决定[见(2-23)?的情况下,由衍射引起的扩大已不显著,光的传播过程才不用以次波叠式]。
只有在R l加的原理来分析,而只用光线来表示光的传播方向。
我们说“光束由无数光线构成”,不过是说明光沿着无数不同的方向传播罢了。
光波在介质中沿着光线传播时,相位不断地改变,但是同一波面上所有点的相位是相同的。
在各向同性介质中,光的传播方向总是和波面的法向方向相重合。
在许多实际情况中,人们经常考虑的只是光的传播方向问题,而不去考虑相位。
这时波面就只是垂直于光线的几何平面或曲面。
在这种极限情况下,实际上是把光线和波面都看做是抽像的数学概念。
对许多实际问题,特别是光学技术成像和照明工程等问题,借助于上述光线(有时用波面)的概念,并应用某些基本实验定律及几何定律,就可以进行所有必要的计算而不必涉及光的本性问题。
这部分以几何定律和某些基本实验定律为基础的光学称为几何光学(或光线光学)。
反映光的波动性的那部分光学称为波动光学。
在第1、2章波动光学中主要考虑的是波长、振幅和相位;这一章几何光学所考虑的主要将是光线和波面。
