江苏省张家港市第一中学2018-2019年八年级数学下学期期中复习综合试题四(无答案) 苏科版

合集下载

江苏省张家港市第一中学八年级数学下学期测试题(第十四周双休日作业)(无答案) 苏科版

（第５题）（第６题）A BC O OBAC DH 江苏省张家港市第一中学2013-2014学年八年级数学下学期测试题（第十四周双休日作业）班级姓名学号一．填空题 1．如图，已知△ABC 内接于⊙O ，BC 是⊙O 的直径，MN 与⊙O 相切，切点为A ，若∠MAB ＝30°，则∠B ＝_______．2．如图，∠APB ＝30°，圆心在边PB 上的⊙O 的半径为1cm ，OP ＝3cm ，若⊙O 沿BP 方向移动，则当⊙O 与PA 相切时，圆心O 移动的距离为_______cm ．3．若⊙O 的半径为8，圆心O 到直线l 的距离为4，则直线l 与⊙O 的位置关系是． 4．如图，点O 是△ABC 的内切圆的圆心，若∠BAC ＝80°，则∠BOC 等于．５.如图，弦CD 垂直于⊙O 直径AB ，垂足为H ，且CD ＝22，BD ＝3，则AB 长为．６.如图，半径为R 的圆内接正三角形的边长是，面积是．７．如图，在△ABC 中，AB ＝2，AC ＝2，若以点A 为圆心，1为半径的圆与边BC 相切于点D ，则∠BAC 的度数是_______．8.⊙O 半径OA =6，∠AOB =90°，则∠AOB 所对的弧AB 的长为．9.直角三角形两直角边为6和8，则这个三角形外接圆半径为，内切圆半径为．10.如图，△ABC 的两边切内切圆于D 、E ，已知∠B = 40°，∠C = 80°，P 是内切圆上异于D 、E 的一个动点，则∠DPE 的度数是．11．如图，AB 是半圆O 的直径，∠BAC=32°，D 为的中点，∠DAC=_____°．12．如图，PA 、PB 是⊙O 是切线，A 、B 为切点，AC 是⊙O 的直径，若∠BAC ＝25°，则∠PAD EC（第10题）＝°_______．13．如图，若AB、AC分别切⊙O于点B、C，延长OB到点D使BD＝OB，连接AD，∠DAC＝72°，则∠ADO等于 .二.选择题14.下列说法正确的是( )A.垂直于半径的直线是圆的切线B.经过三点一定可以作圆C.圆的切线垂直于圆的半径D.每个三角形都有一个内切圆15.如图,已知PA、PB切⊙O于A、B,OP交AB于C,则图中能用字母表示的直角共有( )个 A.3 B.4 C.6 D.5(15) (16) （17）（18）16. 如图,已知圆心角∠AOB为100°,则∠ACB的度数是( )A. 80°B.130°C. 120°D. 100°17.如图，O是正方形ABCD的对角线BD上一点，⊙O边AB，BC都相切，点E，F分别在边AD，DC上．现将△DEF沿着EF对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处．若DE＝2，则正方形ABCD的边长是( ) A．3 B．4 C．22D．2218.如图,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A 的坐标为(0,8),则圆心M的坐标为( ) A .(-4,5) B. (-5,4) C. (5,-4) D. (4,-5)19.如图，在△ABC中，AB＝6，AC＝8，BC＝10，若D，E分别是AC，AB的中点，则以DE为直径的圆与BC的位置关系是 ( )A．相交B．相切C．相离D．无法确定20．已知⊙O的半径为2，若直线l上有一点P满足PO＝2，则直线l与⊙O的位置关系是( )A．相切 B．相离 C．相离或相切 D．相切或相交21.如图，AB为⊙O的直径，C为⊙O外一点，过点C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C＝38°，若点E在AB右侧的半圆周上运动（不与点A，B重合），则∠AED的大小是 ( )A．19°B．38° C．52°D．76°22．如图，AB、AC切⊙O于点B、C，AO交⊙O于点D，过点D作⊙O的切线分别交AB 、AC 于点E 、F ，若OB ＝6，AO ＝10，则△AEF 的周长是 ( ) A ．10 B ．12 C ．14 D ．16三.解答题23.已知△ABC 外切于⊙O,(1)若AB=8,BC=6,AC=4,求 AD 、BE 、CF 的长度。

江苏省苏州市张家港市2018-2019学年八年级下学期数学期末考试试卷及参考答案

经过点D(m,2)和AB边上的点E(3, ).
(k≠0)在第一象限内的图象
（1）求反比例函数的表达式和m的值；（2）将矩形OABC的进行折叠，使点O于点D重合，折痕分别与x轴、y轴正半轴交于点F，G，求折痕FG所在直线的
函数关系式。
参考答案
1.
2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19.
6. 下列说法正确的是（）
A . 某日最低气温是–2℃，最高气温是4℃，则该日气温的极差是2℃ B . 一组数据2，2，3，4，5，5，5，这组数据的众数是2
C . 小丽的三次考试的成绩是116分，120分，126分，则小丽这三次考试平均数是121分 D . 一组数据2，2，3，4，这组数据的中位
3. 一元二次方程
配方后可变形为（）
A.
B.
C.
D.
4. 一只蚂蚁在如图所示的方格地板上随机爬行，每个小方格形状大小完全相同，当蚂蚁停下时，停在地板中阴影部分
的概率为（）
A. B. C. D.
5. 如图，在
中，已知，分别为边，的中点，连结，若
，则
等于（）
A . 70º B . 67. 5º C . 65º D . 60º
26. 已知：如图，在正方形ABCD外取−点E，连接AE、BE、DE.过点A作AE的垂线交DE于点P，已知AE=AP=BE=1.
（1）求证：△APD≌△AEB；（2）连接PC，求线段PC的长度；（3）试求正方形ABCD的面积。 27. 如图,矩形OABC的顶点A.C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=
18. 如图①，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时，△FBC的

江苏省张家港市2018-2019学年八年级下学期期末数学试卷

2018～2019学年第二学期初中期末试卷初二数学 2019.06本试卷由选择题、填空题和解答题三部分组成，共28题，满分130分，考试时间120分钟. 注意事项:1.答题前，考生务必将学校、班级、姓名、考试号等信息填写在答题卡相应的位置上;2.考生答题必须答在答题卡相应的位置上，答在试卷和草稿纸上一律无效.一、选择题(本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案填在答题卡相应的位置上) 1.下列调查中，适合采用普查的是A.夏季冷饮市场上冰激凌的质量B.某本书中的印刷错误C.《舌尖上的中国》第三季的收视率D.公民保护环境的意识 2.下列二次根式中，属于最简二次根式的是A.B. 3.一元二次方程矛2820x x --=配方后可变形为A. 2(4)8x -= B. 2(4)14x -= C. 2(2)6x -= D. 2(2)2x -= 4.一只蚂蚁在如图所示的方格地板上随机爬行，每个小方格形状大小完全相同，当蚂蚁停下时，停在地板中阴影部分的概率为 A.12 B. 45 C. 49 D. 595.如图，在ABC ∆中，已知D ，E 分别为边AB ，AC 的中点，连结DE ，若70C ∠=︒，则AED ∠等于A. 70ºB. 67. 5ºC. 65ºD. 60º6.下列说法正确的是A.某日最低气温是–2℃，最高气温是4℃，则该日气温的极差是2℃B.一组数据2，2，3，4，5，5，5，这组数据的众数是2C.小丽的三次考试的成绩是116分，120分，126分，则小丽这三次考试平均数是121分D.一组数据2，2，3，4，这组数据的中位数是2.5 7.如图，在平行四边形ABCD 中，E ，F 是对角线BD 上不同的两点，连接AE ，CE ，AF ，CF .下列条件中，不能得出四边形AECF 一定是平行四边形的为A. BE DF =B. AE CF =C. //AF CED. BAE DCE ∠=∠8.计算221(1)11x x x -÷+-的结果是 A. 1x - B.1x C. 1x x - D. 1x x - 9.如图，已知一次函数4y kx =-的图像与x 轴，y 轴分别交于A ，B 两点，与反比例函数8y x=在第一象限内的图像交于点C ，且A 为BC 的中点，则一次函数的解析式为 A. 24y x =- B. 44y x =- C. 84y x =- D. 164y x =-10.如图，矩形ABCD 中， AB=8，BC=4，P ，Q 分别是直线AB ，AD 上的两个动点，点E 在边CD 上，2DE =，将DEQ ∆沿EQ 翻折得到FEQ ∆，连接PF ，PC ，则PF PC +的最小值为A. 2-B. 8C. 10D. 2-二、填空题(本大题共8小题，每小题3分，共24分，请将答案填在答题卡相应的位置上)11.x 的取值范围是 . 12.当x = 时，分式2521x x -+的值为0.13.某中学组织八年级学生进行“绿色出行，低碳生活”知识竞赛，为了了解本次竞赛的成绩，把学生成绩分成,,,,A B C D E 五个等级，并绘制如图所示的扇形统计图(不完整)统计成绩，则C 等级所在扇形的圆心角是 º.14.矩形ABCD 的对角线AC 与BD 相交于点O ，4BD =，M ，N 分别是AD ，OD 的中点，则MN 的长度为 . 15.已知关于x 的一元二次方程20x mx n ++=有一个非零实数根n -，则m n -的值为 .16.如图，将矩形ABCD 沿EF 折叠，使点A 落在CD 边上的点G 处，点B 落在点H 处，若30HGC ∠=︒，连接AG ，则AGD ∠= .17.如图，A ，B 是反比例函数6(0)y x x=>图像上的两点，过点A 作//AP y 轴，过点B 作//BP x 轴，交点为P ，连接OA ，OP .若AOP ∆的面积为2，则ABP ∆的面积为 . 18.如图①，点M 从菱形ABCD 的顶点D 出发，沿D C A →→以1 cm/ s 的速度匀速运动到点A .如图②是点M 运动过程中，MAB ∆的面积y ( cm 2)随时间x (s)变化的关系图像，则a 的值为 .三、解答题(本大题共76分.解答时应写出必要的计算或说明过程.并把解答过程填写在答题卡相应的位置上) 19.(本题满分8分)计算:0(2)1)-+; (2)22)+-20.(本题满分8分)解下列方程:(1)(3)10x x -=; (2)2373226x x +=++.21.(本题满分5分)如图，正比例函数2y x =的图像与反比例函数ky x=的图像有一个交点为(2,)P m . (1)求反比例函数ky x=函数表达式; (2)根据图像，直接写出当41x -<<-时，y 的取值范围.22.(本题满分5分)如图，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，且2AB =. (1)菱形ABCD 的周长为； (2)若2BD =，求AC 的长.23.(本题满分6分)某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m 分(60100m ≤≤)，组委会从1000篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表。

江苏省张家港市第一中学八年级数学下册 11 反比例函数复习测试题(无答案)(新版)苏科版

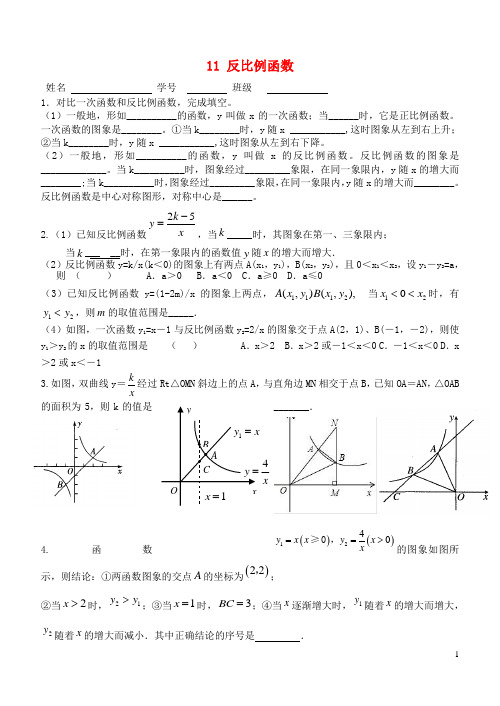
11 反比例函数姓名学号班级 1．对比一次函数和反比例函数，完成填空。

（1）一般地，形如__________的函数，y 叫做x 的一次函数；当______时，它是正比例函数。

一次函数的图象是________。

①当k________时，y 随x ___________,这时图象从左到右上升；②当k________时，y 随x ___________,这时图象从左到右下降。

（2）一般地，形如__________的函数，y 叫做x 的反比例函数。

反比例函数的图象是_____________。

当k__________时，图象经过_________象限，在同一象限内，y 随x 的增大而________;当k__________时，图象经过_________象限，在同一象限内，y 随x 的增大而________。

反比例函数是中心对称图形，对称中心是______。

2.（1）已知反比例函数25k y x -=，当k _____时，其图象在第一、三象限内；当k ___ __时，在第一象限内的函数值y 随x 的增大而增大．（2）反比例函数y=k/x(k ＜0)的图象上有两点A(x 1，y 1)，B(x 2，y 2)，且0＜x 1＜x 2，设y 1－y 2=a ，则（） A ．a ＞0 B ．a ＜0 C ．a ≥0 D ．a ≤0 （3）已知反比例函数y=(1-2m)/x 的图象上两点，1112(,)(,),A x y B x y 当120x x <<时，有12y y <，则m 的取值范围是_____．（4）如图，一次函数y 1=x －1与反比例函数y 2=2/x 的图象交于点A(2，1)、B(－1，－2)，则使y 1＞y 2的x 的取值范围是（） A ．x ＞2 B ．x ＞2或－1＜x ＜0 C ．－1＜x ＜0 D ．x ＞2或x ＜－1 3.如图，双曲线y ＝kx经过Rt △OMN 斜边上的点A ，与直角边MN 相交于点B ，已知OA ＝AN ，△OAB 的面积为5，则k 的值是_______．()()1240y x x y x x ==>≥0，的图象如图所4.函数示，则结论：①两函数图象的交点A 的坐标为()22，；②当2x >时，21y y >；③当1x =时，3BC =；④当x 逐渐增大时，1y 随着x 的增大而增大，2y 随着x 的增大而减小．其中正确结论的序号是．O1y x=xA B C1x =4y x=y5.如图，直线y=kx+b与反比例函数y=k/x(x＜0)的图象相交于点A、点B，与x轴交于点C，其中点A的坐标为(－2，4)，点B的横坐标为－4．(1)试确定反比例函数的关系式； (2)求△AOB的面积．（3）补全双曲线，求出k/x＜kx+b时x的取值范围。

江苏省张家港市2018-2019学年第二学期八年级数学期末试卷

2018～2019学年第二学期初中期末试卷初二数学本试卷由选择题、填空题和解答题三部分组成，共28题，满分130分，考试时间120分钟. 注意事项:1.答题前，考生务必将学校、班级、姓名、考试号等信息填写在答题卡相应的位置上;2.考生答题必须答在答题卡相应的位置上，答在试卷和草稿纸上一律无效.一、选择题(本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案填在答题卡相应的位置上) 1.下列调查中，适合采用普查的是A.夏季冷饮市场上冰激凌的质量B.某本书中的印刷错误C.《舌尖上的中国》第三季的收视率D.公民保护环境的意识 2.下列二次根式中，属于最简二次根式的是A.B. 3.一元二次方程矛2820x x --=配方后可变形为A. 2(4)8x -= B. 2(4)14x -= C. 2(2)6x -= D. 2(2)2x -= 4.一只蚂蚁在如图所示的方格地板上随机爬行，每个小方格形状大小完全相同，当蚂蚁停下时，停在地板中阴影部分的概率为 A.12 B. 45 C. 49 D. 595.如图，在ABC ∆中，已知D ，E 分别为边AB ，AC 的中点，连结DE ，若70C ∠=︒，则AED ∠等于A. 70ºB. 67. 5ºC. 65ºD. 60º6.下列说法正确的是A.某日最低气温是–2℃，最高气温是4℃，则该日气温的极差是2℃B.一组数据2，2，3，4，5，5，5，这组数据的众数是2C.小丽的三次考试的成绩是116分，120分，126分，则小丽这三次考试平均数是121分D.一组数据2，2，3，4，这组数据的中位数是2.57.如图，在平行四边形ABCD 中，E ，F 是对角线BD 上不同的两点，连接AE ，CE ，AF ，CF .下列条件中，不能得出四边形AECF 一定是平行四边形的为A. BE DF =B. AE CF =C. //AF CED. BAE DCE ∠=∠8.计算221(1)11x x x -÷+-的结果是 A. 1x - B.1x C. 1x x - D. 1x x - 9.如图，已知一次函数4y kx =-的图像与x 轴，y 轴分别交于A ，B 两点，与反比例函数8y x=在第一象限内的图像交于点C ，且A 为BC 的中点，则一次函数的解析式为 A. 24y x =- B. 44y x =- C. 84y x =- D. 164y x =-10.如图，矩形ABCD 中， AB=8，BC=4，P ，Q 分别是直线AB ，AD 上的两个动点，点E 在边CD 上，2DE =，将D E Q ∆沿EQ 翻折得到FEQ ∆，连接PF ，PC ，则P F P C +的最小值为A. 2B. 8C. 10D. 2二、填空题(本大题共8小题，每小题3分，共24分，请将答案填在答题卡相应的位置上)11.若式子4有意义，则实数x 的取值范围是 . 12.当x = 时，分式2521x x -+的值为0. 13.某中学组织八年级学生进行“绿色出行，低碳生活”知识竞赛，为了了解本次竞赛的成绩，把学生成绩分成,,,,A B C D E 五个等级，并绘制如图所示的扇形统计图(不完整)统计成绩，则C 等级所在扇形的圆心角是 º.14.矩形ABCD 的对角线AC 与BD 相交于点O ，4BD =，M ，N 分别是AD ，OD 的中点，则MN 的长度为 . 15.已知关于x 的一元二次方程20x mx n ++=有一个非零实数根n -，则m n -的值为 .16.如图，将矩形ABCD 沿EF 折叠，使点A 落在CD 边上的点G 处，点B 落在点H 处，若30HGC ∠=︒，连接AG ，则AGD ∠= .17.如图，A ，B 是反比例函数6(0)y x x=>图像上的两点，过点A 作//AP y 轴，过点B 作//BP x 轴，交点为P ，连接OA ，OP .若AOP ∆的面积为2，则ABP ∆的面积为 . 18.如图①，点M 从菱形ABCD 的顶点D 出发，沿D C A →→以1 cm/ s 的速度匀速运动到点A .如图②是点M 运动过程中，MAB ∆的面积y ( cm 2)随时间x (s)变化的关系图像，则a 的值为 .三、解答题(本大题共76分.解答时应写出必要的计算或说明过程.并把解答过程填写在答题卡相应的位置上) 19.(本题满分8分)计算:(2)1)-+; (2)22)-20.(本题满分8分)解下列方程:(1)(3)10x x -=; (2)2373226x x +=++.21.(本题满分5分)如图，正比例函数2y x =的图像与反比例函数ky x=的图像有一个交点为(2,)P m . (1)求反比例函数ky x=函数表达式; (2)根据图像，直接写出当41x -<<-时，y 的取值范围.22.(本题满分5分)如图，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，且2AB =. (1)菱形ABCD 的周长为； (2)若2BD =，求AC 的长.23.(本题满分6分)某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m 分(60100m ≤≤)，组委会从1000篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表。

张家港市第二中学2018-2019年八年级下期中数学试题

．D．）都在反比例函数的图象9．如图，正方形ABCD 的面积为16，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD ＋PE 的和最小，则这个最小值为（） A ．8 B ．3 C ．4 D ．3210．如图，已知四边形OABC 是菱形，CD ⊥x 轴，垂足为D ，函数y ＝ 4 x的图象经过点C ，且与E 交于点E ．若OD ＝2，则△OCE 的面积为…（） A ．4 B ．4 2 C ．2 D ．2 2第8题第9题第10题二．填空题：(本大题8小题，每小题3分，共24分．将答案填写在答题卷上．)11．反比例函数y=的图象经过点（2，﹣1），则k 的值为． 12．若a 是方程012=-+x x 的一个根，则2335a a +-的值为________． 13．四边形ABCD 中，点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．若四边形EFGH 为菱形，则对角线AC 、BD 应满足条件是． 14．如图，在菱形ABCD 中，∠BAD=70°，AB 的垂直平分线交对角线AC 于点F ，垂足为E ，连接DF ，则∠CDF 等于 °． 15．如图，ABCD 的对角线相交于点O ，且AB ≠AD ，过O 作OE ⊥BD 交BC于点E ．若ABCD 的周长为10cm ，则∆CDE 的周长为 cm ．16．如图，在∆AOB 中，已知C 是AB 的中点，反比例函数ky x=(k ＞0)在第一象限的图像经过A 、C 两点，若∆OAB 面积为6，则k 的值为．第14题第15题第16题17．已知关于x 的一元二次方程01)1(2=++-x x m 有实数根，则 m 的取值范围是．18．如图，在矩形ABCD 中，AD ＝6，AB ＝4，点E 、G 、H 、F 分别在AB 、BC 、CD 、AD 上，且AF ＝CG ＝2，BE ＝DH ＝1，点P 是直线EF 、GH 之间任意一点，连结PE 、PF 、PG 、PH ，则△PEF 和△PGH 的面积和等于．三．解答题：（本大题共11小题，共76分．请将解答过程写在答题卷相应的位置上，解答时应写出必要的计算过程，推演步骤或文字说明．） 19．（ 12分）用适当的方法解下列方程：(1)4(x －1)2＝36； (2) 210x -+=； (3)(3x －1)(x ＋1)＝4； (4)(2x －3)2－3(2x －3)＋2＝0． 20．(6分)△ABC 在平面直角坐标系xOy 中的位置如图所示．(1)作△ABC 关于点C 成中心对称的△A 1B 1C 1； (2)将△A 1B 1C 1向右平移4个单位，作出平移后的△A 2B 2C 2；(3) 将△A 2B 2C 2绕A 1 顺时针旋转90°得 △A ′B ′C ′.21．（4分）已知a ，b ，c 分别是三角形的三边，试判断方程()()220a b x cx a b ++++=的根的情况．22．（4分）已知y 是x 的反比例函数，且当x ＝4，y ＝－1．(1)函数y 与x 之间的函数表达式为； (2)当一3≤x ≤－12时，y 的取值范围是； (3)若x ＞1时，y 的取值范围是； (4) 若y < 2时，x 的取值范围是．23．( 6分)如图将ABCD 的边DC 延长到点E ，使CE =DC ，连接AE ，交BC于点F .（1）求证：△ABF ≌△ECF （2）若∠AFC =2∠D ，连接AC 、BE ，求证：四边形ABEC 是矩形．24．（6分）已知反比例函数y 1=xk的图象与一次函数y 2=ax +b 的图象交于点A （1，4）和点B （m ，﹣2），（1）求这两个函数的关系式；（2）观察图象，写出使得y 1＞y 2成立的自变量x 的取值范围；（3）如果点C 与点A 关于x 轴对称，求△ABC 的面积．25．（ 6分）喝绿茶前需要烧水和泡茶两个工序，即需要将电热水壶中的水烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y(℃)与时间x(min)成一次函数关系；停止加热过了1分钟后，水壶中水的温度y (℃)与时间x （min ）近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃． (1)分别求出图中所对应的函数关系式，并且写出自变量x 的取值范围；(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶，问从水烧开到泡茶需要等待多长时间？26．（5分）如图①，在△ABC 中，CD 是AB 边上的中线，那么△ACD 和△BCD 是“友好三角形”，并且S △ACD =S △BCD ．应用：如图②，在矩形ABCD 中，AB =4，BC =6，点E 在AD 上，点F 在BC 上，AE=BF ，AF 与BE 交于点O ．⑴求证：△AOB 和△AOE 是“友好三角形”；⑵连接OD ，若△AOE 和△DOE 是“友好三角形”，求四边形CDOF 的面积．27．（9分）如图1，在正方形ABCD 中，点E 为BC 上一点，连接DE ，把△DEC 沿DE 折叠得到△DEF ，延长EF 交AB 于G ，连接DG ．(1) 求证：∠EDG=45°．(2) 如图2，E 为BC 的中点，连接BF ． ①求证：BF ∥DE ；②若正方形边长为6，求线段AG 的长． (3) 当BE ︰EC = 时，DE =DG ．A BCDEFG图1CDA BF GE 图228．（本题8分）如图，菱形ABCD的边长为48cm，∠A＝60°，动点P从点A出发，沿着线路AB—BD做匀速运动，动点Q从点D同时出发，沿着线路DC－CB－BA做匀速运动．(1)求BD的长；(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s．经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由，同时求出△AMN的面积；(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为a cm/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a的值．29．（10分）如图1，正方形ABCD中，C(－3，0)，D(0，4) ．过A点作AF⊥y轴于F点，过B点作x轴的垂线交过A点的反比例函数的图像于E点,交x轴于G点。

2018-2019学年第一学期期中考试八年级数学试卷参考答案

(3)连DE，易证△CDE是等腰直角三角形．
∴∠CBE＝ (180°－150°)＝30°－
∴＝30°．…………………………………………………………………………………………12分
20．由题知：点P在第四象限．
∴ 解得a＜－ ……………………………………………………………………………7分
21．(1)证明：∵∠ADE＝∠2＋∠BDE＝∠1Βιβλιοθήκη ∠ACE∴∠BDE＝∠ACE
又∵∠A＝∠B，AE＝BE
∴△ACE≌△BDE，∴AC＝BD．………………………………………………………………………5分
2018--2019学年第一学期期中考试
八年级数学试题参考答案
一、选择题:1．D；2．C；3．A；4．B；5．D；6．A；7．C；8．D；9．B；10．B．
二、填空题:11．10；12．0；13．64º；14．3；15．(4，－4)；16．7．
三、解答题：
17．略．…………………………………………………………………………………………………6分
18．由题知：∠ABD＝2∠DBE＝56º
∴∠BAC＝180º－56º－70º＝54º………………………………………………………………………6分
19．(1)略；………………………………………………………………………………………………4分
(2)A1(8，0)，B1(6，－2)，C1(5，2)…………………………………………………………………7分
(2)由(1)知：△ACE≌△BDE，∴CE＝DE
∴∠C＝∠CDE＝ (180º－40º)＝70º
∴∠BDE＝70º……………………………………………………………………………………………8分
22．(1)易得∠ADE＝∠CDF＝30º，

2018-2019学年江苏省苏州市张家港市八年级(上)期中数学试卷(含详细解析)

2018-2019学年江苏省苏州市张家港市八年级（上）期中数学试卷一、选择题（本大题共有10小题，每小题3分，共30分.）1．（3分）下列标志中，可以看作是轴对称图形的是（）A．B．C．D．2．（3分）一个等腰三角形的两边长分别是3和7，则它的周长为（）A．17B．15C．13D．13或17 3．（3分）下列计算正确的是（）A．=2B．=C．=x D．=x4．（3分）在数0、0.、、、0.1010010001、、中，无理数有（）A．1个B．2个C．3个D．4个5．（3分）下列关于的说法中，错误的是（）A．是无理数B．＜＜C．10的平方根是D．是10的算术平方根6．（3分）若点M（2m﹣1，m+3）在第二象限，则m取值范围是（）A．m＞B．m＜﹣3C．﹣3＜＜D．m＜7．（3分）到三角形三个顶点距离相等的点是（）A．三条边的垂直平分线的交点B．三条高线的交点C．三条边的中线的交点D．三条角平分线的交点8．（3分）如图，D为△ABC内一点，CD平分∠ACB，AE⊥CD，垂足为点D，交BC于点E，∠B=∠BAE，若BC=5，AC=3，则AD的长为（）A．1B．1.5C．2D．2.59．（3分）如图，△ACB和△DCE均为等边三角形，点A、D、E在同一条直线上，连接BE，则∠AEB的度数是（）A．30°B．45°C．60°D．75°10．（3分）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2=21，大正方形的面积为13，则小正方形的面积为（）A．3B．4C．5D．6二、填空题：（本大题共8小题，每小题9分，共24分．）11．（9分）16的平方根是；的立方根是；﹣3的绝对值是．12．（3分）若在实数范围内有意义，则x的取值范围是．13．（3分）一个正数的平方根为﹣m﹣3和2m﹣3，则这个数为．14．（3分）若等腰三角形的一个角为50°，则它的顶角为．15．（3分）已知x＜1，则化简的结果是．16．（3分）点P在第二象限，P到x轴的距离为2，到y轴的距离为3，如把P 向下平移4个单位得到Q，那么点Q的坐标是17．（3分）如图，△ABC中，DE，GF分别是AC，BC的垂直平分线，AD⊥CD，AD=4，BG=5．则△ABC的面积等于．18．（3分）如图，在△ABC中，AB=AC=10，BC=12，AD是角平分线，P，Q分别是AD、AB上的动点，则BP+PQ的最小值为．三、解答题（共9小题，满分70分）19．（8分）求出下列x的值（1）4（x﹣1）2﹣36=0（2）27（x+1）3=﹣6420．（8分）计算（1）﹣（π﹣3）0+（）﹣1（2）﹣|1﹣|21．（8分）在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，3）、（﹣1，1）．（1）请在如图所示的网格平面内作出平面直角坐标系；（2）请作出△ABC关于y轴对称的△A′B′C′；（3）写出点B′的坐标；（4）△ABC的面积．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

经典教育
资料1
江苏省张家港市第一中学2013-2014学年八年级数学下学期期中复习综合试题四

班级姓名学号
1．若反比例函数y＝kx（k为常数，且k≠0）的图象过点（3，－4），则下列各点中也在该图象上的点是 ( )
A．（2，6） B．(－6，-2) C．（－3，4） D．(－3，－4)

2．把分式3xyxy中的x和y都扩大2倍，分式的值（）

A．不变 B．扩大2倍 C．缩小2倍 D．扩大4倍
3．如图，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，
CF⊥BD于点F，连接AF，CE，若DE=BF，则下列结论：①CF=AE；②OE=OF
；③四边

形ABCD是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是（）
A． 4 B． 3 C． 2 D． 1

4．若反比例函数的图象经过点（m，3m），其中m≠0，则此反比例函数图象经过（）

A．第一、三象限 B．第一、二象限 C．第二、四象限 D
．第三、四象限

5．若2224aa＝6，则a的取值范围是( )
A．a＝2 B．－4≤a≤2 C．a≤－4 D．a≥2
6．已知x为整数，且分式1)1(22xx的值为整数，则x可取的值有（）
A．1个 B．2个 C．3个 D．4个
7．图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比
例函数关系如图2所示，等腰直角三角形AEF的斜边EF过
C
点，M为EF的中点，则下列结论正确的是（）

A．当x=3时，EC＜EM B．当y=9时，EC＞EM
C．当x增大时，EC•CF的值增大 D．当y增大时，BE•DF
的值不变

8．如图，A、B、C是反比例函数图象上三点，作直线
l，使A、B、C到直线l的距离之比为3：1：1，则满足条件的直线l共有
（） A．4条 B．3条 C．2条 D．1条

9.使等式313122aaaa成立的实数a的取值范围是

10.如果x满足2310xx，那么代数式21xx_______．
经典教育
资料1
11．当m 时，关于x的方程xxxmx3123的解为正数.

12．已知等式248422aaa，则能使等式成立的a的取值范围为_______．
13.若125a，125b，则a＋b＋ab的值为
14.比较大小：1413 1514
15.如图，矩形ABCD的边AB与y轴平行，顶点A的坐标为(1，2)，点B与点D在反

比例函数y6x (x>0)的图象上，则点C的坐标为_______．
16．如图，矩形ABCD中，E是BC的中点，矩形ABCD的周长是20cm，AE=5cm，则AB的长为
cm
．

17.如图，A、B分别是反比例函数xyxy610，图像上的点过A、B作x轴的垂
线，垂足分别为C、D，连接OB、OA，OA交BD于E点，△BOE的面积为1S，四边形
ACDE的面积为2S，则1S-2S=_____ ___.
18．在平面直角坐标系中，点O是坐标原点，过点A（m，2）的双曲线
k
yx
，且AB与x轴垂直交于点B，且S△AOB=4，则mk的值

是。

19．化简或计算：（1）222baabababab （2）2111211xxxxxx

(3) 112180.53； (4) 222111346yxyxyx
（5）解方程 xxx34231．（6）解方程221211239yyyyy
20.已知m是2的小数部分，求2212mm的值。
经典教育

资料1
21.如图，一次函数y1＝k1x＋2与反比例函数y2＝2kx的图象交于点A(4，m)

和B(－8，－2)，与y轴交于点C．
(1)k1＝_______，k2＝_______；
(2)根据函数图象可知，当y1>y2时，x的取值范围是_______；
(3)过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一
点，设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE＝3：1时，求点P的坐标．

22.为加快某地机场建设，当地政府决定新修一条机场公路，甲、乙两工程队承包此项工程。如果甲工程队
单独施工，则刚好如期完成；如果乙工程队单独施工就要超过6个月才能完成，现在甲、乙两队先共同施工
4个月，剩下的由乙队单独施工，则刚好如期完成。
（1）问原来规定修好这条公路需多长时间？
（2）现在要求提前3个月完成机场公路建设，甲乙合作施工几个月，余下的由乙队单独施工，才能按要求
完工？

23．（1）如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且
CE=CP，连接BP，DE．求证：△BCP≌△DCE
；

（2）直线EP交AD于F，连接BF，FC．点G是FC与
BP的交点．若CD=2PC时，求证：BP⊥CF
；

24.如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点
A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B
匀速运动，当其中一个点到达终点时，

另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，
EF
．

（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，
说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．
经典教育
资料1
25．通过对苏科版八（下）教材一道习题的探索研究，我们知道：一次函数y=x﹣1的图象可以由正比例函
数y=x的图象向右平移1个单位长度得到类似的，函数的图象是由反比例函数
的图象向左平移2个单位长度得到．
灵活运用这一知识解决问题．
如图，已知反比例函数的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（2，2）和点B．
（1）写出点B的坐标，并求a的值；

（2）将函数的图象和直线AB同时向右平移n（n＞0）个
单位长度，

得到的图象分别记为C′和l′，已知图象C′经过点M（2，4）．
①求n的值；
②分别写出平移后的两个图象C′和l′对应的函数关系式；

③直接写出不等式的解集．