材料力学单辉祖第四版答案
完整版材料力学答案单辉祖版全部答案

第二章轴向拉压应力与材料的力学性能13}2-1 试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2 试画图示各杆的轴力图,并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布,集度为q。
A Bq<1aHD题2-2图(a)解:由图2-2a(1)可知,F N(X) 2qa qx 轴力图如图2-2a(2)所示,F N,max 叩图2-2a(b)解:由图2-2b(2)可知,F R qaF N (X1) F R qaF N(X2)F R q(x2 a) 2qa qx2F N,max qa图 2-2b2-3 图示轴向受拉等截面杆,横截面面积A=500mm 2,载荷F=50kN 。
试求图示斜截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题图T ax—50MPa22-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量 E 、比例极限 p 、屈服极限s 、强度极限b 与伸长率 判断该材料属于何种类型(塑性或脆性材料) 。
T -sin2 a 50MPa sin( 100 )49.2MPa2杆内的最大正应力与最大切应力分别为轴力图如图2-2b(2)所示,^maxlOOMPaF 50 103N— A 500 10-6m 2斜截面m-m 的方位角 a 50,故有解:该拉杆横截面上的正应力为1.00 108Pa lOOMPa题2-5解:由题图可以近似确定所求各量。
2 2(T ocos a lOOMPa cos ( 50 ) 41.3MPa A- 220 106PaAe 0.001220 109Pa 220GPa-220MPa ,- 240MPa ,并-440MPa ,3 29.7%该材料属于塑性材料。
2-7 一圆截面杆,材料的应力-应变曲线如题2-6图所示。
若杆径d =10mm , 杆长 I =200mm ,杆端承受轴向拉力 F = 20kN 作用,试计算拉力作用时与卸去 后杆的轴向变形。
《材料力学》答案_材料力学单辉祖答案

《材料力学》答案_材料力学单辉祖答案. 一、单选题(共30道试题,共60分。
)1.厚壁玻璃杯倒入开水发生破裂时,裂纹起始于()A•内壁B.外壁C.壁厚的中间D.整个壁厚正确答案:B满分:2分2.图示结构中,AB杆将发生的变形为()A.弯曲变形B.拉压变形C.弯曲与压缩的组合变形D.弯曲与拉伸的组合变形正确答案:D满分:2分3.关于单元体的定义,下列提法中正确的是()A.单元体的三维尺寸必须是微小的B.单元体是平行六面体C.单元体必须是正方体D. 单元体必须有一对横截面正确答案:A满分:2分4.梁在某一段内作用有向下的分布力时,则在该段内M图是一条()A.上凸曲线;B. 下凸曲线;C. 带有拐点的曲线;D. 斜直线正确答案:A满分:2分5.在相同的交变载荷作用下,构件的横向尺寸增大,其()。
A. 工作应力减小,持久极限提高B.工作应力增大,持久极限降低;C. 工作应力增大,持久极限提高;D. 工作应力减小,持久极限降低。
正确答案:D满分:2分6.在以下措施中()将会降低构件的持久极限A.增加构件表面光洁度B.增加构件表面硬度C.加大构件的几何尺寸D.减缓构件的应力集中正确答案:C满分:2分7.材料的持久极限与试件的()无关A.材料;B. 变形形式;C. 循环特征;D. 最大应力。
正确答案:D满分:2分8.梁在集中力作用的截面处,它的内力图为()A. Q图有突变,M图光滑连续;B. Q图有突变,M图有转折;C. M图有突变,Q图光滑连续;D. M图有突变,Q图有转折。
正确答案:B满分:2分9.空心圆轴的外径为D,内径为d.a = d / D。
其抗扭截面系数为()A B C D A. A B. B C. C D. D正确答案:D满分:2分10.在对称循环的交变应力作用下,构件的疲劳强度条件为公式:若按非对称循环的构件的疲劳强度条件进行了疲劳强度条件校核,则()A.是偏于安全的;B. 是偏于不安全的;C. 是等价的,即非对称循环的构件的疲劳强度条件式也可以用来校核对称循环下的构件疲劳强度 D.不能说明问题,必须按对称循环情况重新校核正确答案:C满分:2分11.关于单元体的定义,下列提法中正确的是()A.单元体的三维尺寸必须是微小的;B. 单元体是平行六面体;C. 单元体必须是正方体;D. 单元体必须有一对横截面。
第四版单辉祖材料力学课后答案

第四版单辉祖材料力学课后答案引言《材料力学》是材料科学与工程专业的一门基础课程,主要介绍了材料的力学性质和力学行为。
本文以《材料力学》第四版的单辉祖所编写的课后习题为题,给出了相应的答案。
通过对这些习题的解答,帮助学生巩固课堂所学的知识,并提供了一些解题思路和方法。
目录•第一章引言•第二章物质的内部力和应力•第三章弹性和塑性力学基础第一章引言1. 什么是材料力学?答案:材料力学是研究物质响应外力作用下的变形和破坏行为的科学。
2. 材料力学的主要内容有哪些?答案:材料力学的主要内容包括静力学、动力学、弹性力学、塑性力学、断裂力学等。
第二章物质的内部力和应力1. 什么是内力?答案:内力是物质内部分子间相互作用所产生的力。
2. 什么是应力?答案:应力是单位面积上的力,表示为单位面积上的力的矢量。
3. 应力的分类有哪些?答案:应力可分为法向应力和切应力两种,法向应力垂直于截面,切应力与截面垂直。
4. 弹性应力-应变关系有哪些?答案:弹性应力-应变关系有胡克定律,即应力与应变成正比。
第三章弹性和塑性力学基础1. 弹性和塑性的区别是什么?答案:弹性是指物体在受到外力作用下发生变形后,外力去除后恢复原状的能力;塑性是指物体在受到外力作用下发生变形后,即使外力去除,物体也不能恢复原状。
2. 什么是弹性模量?答案:弹性模量是描述物质抵抗压缩和拉伸变形能力的指标,表示为物质单位应力与应变的比值。
3. 什么是屈服强度?答案:屈服强度是材料在拉伸过程中,在产生明显塑性变形或显著应力减小时的应力值。
4. 什么是塑性应变?答案:塑性应变是指材料在超过屈服点后产生的应变。
结论本文为《材料力学》第四版单辉祖所编写的课后习题的答案,涵盖了材料力学的部分基础知识。
通过对这些习题的解答,希望能够帮助学生深入理解材料力学的概念和原理,并提供一些解题思路和方法。
通过不断练习,学生能够对材料力学有更深入和全面的认识,为日后的学习和研究打下坚实的基础。
工程力学(静力学与材料力学) 单祖辉 谢传峰合编 课后习题答案

工程力学(静力学与材料力学)单祖辉谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
(a) (b)A(d)(e) 解: AA(a)(b)A(d) (e)1-2 试画出以下各题中AB杆的受力图。
a)b)c)A(c)(c)《工程力学》习题选解工程力学静力学与材料力学(单辉祖谢传锋著) 高等教育出版社课后答案(d)解:B FB(a)(b) (c)BB (e)1-3 试画出以下各题中AB梁的受力图。
F(a)(b) (c)(d)(e) 1《工程力学》习题选解解:D(d)(e)FBx(b)(c)F W1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD;(b) 半拱AB部分;(c) 踏板AB;(d) 杠杆AB;(e) 方板ABCD;(f) 节点B。
解:(a) D (d)(b)(c)(e)(f) W B (b)D(c)FD B2(a)《工程力学》习题选解1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
(b)FC FB (d) (e)FBC (f) W(c)(d) e) 3《工程力学》习题选解解:(a)ATFFBA(b)(c)A A C C(d)’C(e)D D BC’4《工程力学》习题选解2-2 杆AC、BC在C处铰接,另一端均与墙面铰接,如图所示,F1和F2作用在销钉C上,F1=445 N,F2=535 N,不计杆重,试求两杆所受的力。
F1 解:(1) 取节点C为研究对象,画受力图,注意AC、BC都为二力杆,(2) 列平衡方程:AC与BC两杆均受拉。
2-3 水平力F作用在刚架的B点,如图所示。
如不计刚架重量,试求支座A和D 处的约束力。
解:(1) 取整体ABCD为研究对象,受力分析如图,画封闭的力三角形:(2)5 F FD F A D《工程力学》习题选解2-4 在简支梁AB的中点C作用一个倾斜45o的力F,力的大小等于20KN,如图所示。
材料力学答案第四版单辉祖课后答案
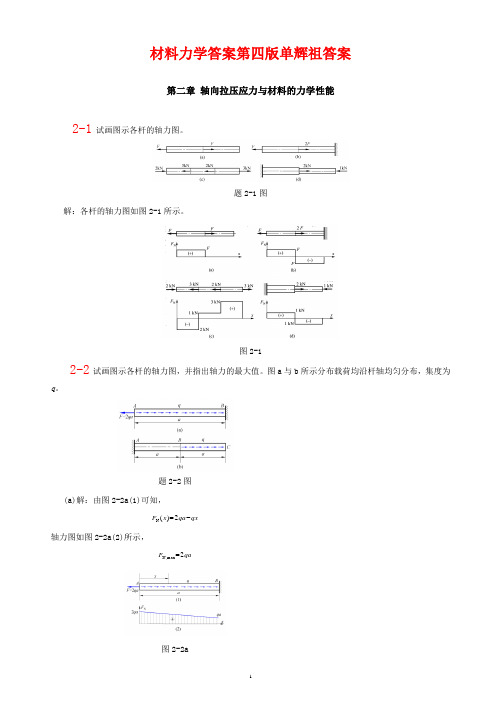
材料力学答案第四版单辉祖答案第二章 轴向拉压应力与材料的力学性能2-1 试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a 与b 所示分布载荷均沿杆轴均匀分布,集度为q 。
题2-2图(a)解:由图2-2a(1)可知,qx qa x F -=2)(N轴力图如图2-2a(2)所示,qa F 2m ax ,N =图2-2a(b)解:由图2-2b(2)可知, qa F =R qa F x F ==R 1N )(22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示,qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N 10508263=⨯=⨯⨯==-A F σ 斜截面m -m 的方位角, 50-=α故有 MPa 3.41)50(cos MPa 100cos 22=-⋅== ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα 杆内的最大正应力与最大切应力分别为 MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa 10220ΔΔ96=⨯=⨯≈=εσE MPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
工程力学(静力学与材料力学)课后习题答案(单辉祖)
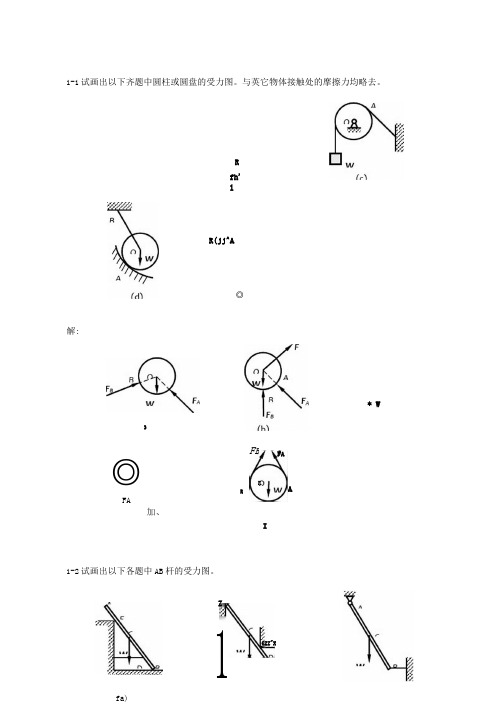
1-1试画出以下齐题中圆柱或圆盘的受力图。
与英它物体接触处的摩擦力均略去。
Rfh'l解:R(jj^A◎3F A* W ◎FA加、F BRInA1-2试画出以下各题中AB杆的受力图。
fa)Z£ZZ"X 11-3试画出以下各题中AB梁的受力图。
解:fd)(etF A◎解:A fZfd) fe)(c)fa)P1-4试画出以下各题中指定物体的受力图。
(a)拱ABCD: (b)半拱AB部分:(c)踏板AB: (d)杠杆AB:(e) 方板ABCD; (0节点B。
s rn1-5试画出以下各题中指窪物体的受力图。
(a)结点A,结点B: (b)圆柱A和B及整体:(c)半拱AB,半拱BC及整体:切刀CEF及整体:2)秤杆AB,秤盘架BCD及整体。
解:(c}rd'iff)(c}(d)杠杆AB,卜 ______ RT I F -. F ]「I]匚「□KF」解:(a) uz(e}F“F-(d)__ 4Vr(e)w2-2杆AGBC 在C 处狡接,另一端均与墙而铁接,如图所示,片和F2作用在销钉C l :, “445N, £=535 N ・不汁杆重.试求两杆所受的力。
解:(1)取节点C 为研究对象,画受力图,注意AG BC 都为二力杆,(2)列平衡方程:4FjX- + FMsin6(r -耳=0 F 揖- Fffc - F^c cos 60" = 0:'=201 N F 肌—164NAC 与BC 两杆均受拉。
2-3水平力F 作用在刚架的6点,如图所示。
如不讣刚架重量,试求支座A 和D 处的约束解:(1)取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:FJ 乩旦丄=乙上BC AB AC 2"4 F 产导小2F2-4在简支梁AB 的中点C 作用一个倾斜45°的力F ,力的大小等于2O KN,如图所示q 若梁的自重不ih 试求两支座的约束力。
材料力学第四版版答案7.docx
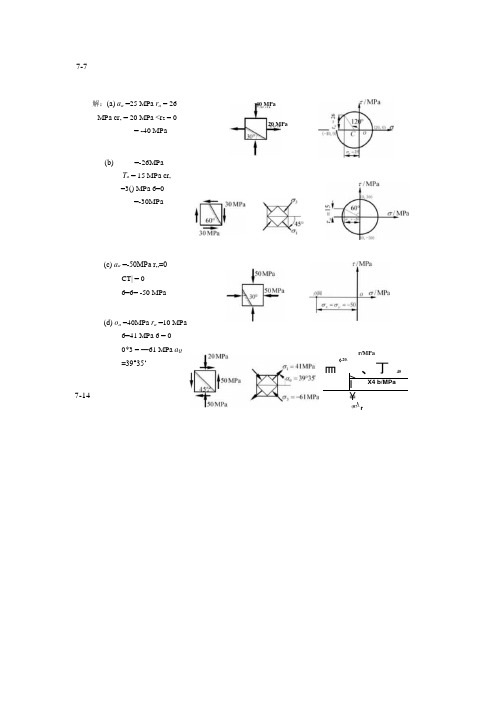
(c) a a =-50MPa r…=0CT| = 0 6=6= -50 MPa(d) o a =40MPa r a =10 MPa6=41 MPa 6 = 0 0*3 = —61 MPa a Q =39°35‘7-7 解:(a) a a =25 MPa r a = 26 MPa cr, = 20 MPa <r 2 = 0= -40 MPa (b) =-26MPa T a = 15 MPa cr, =3() MPa 6=0=-30MPa40 MPa20 MPa7-14(-20.皿、丁40> I X4 b/MPa ¥\ (0?^rr/MPa7-15单元体各面上的应力如图所示。
试用应力圆的儿何关系求主应力及最人切应力。
解:(a)由卩平面内应力值作a, b点,连接"交O•轴得圆心C (5(). 0)应力圆半径心)2+时=44.726 =50+44.7 = 94.7 MPa cr3=50-44.7 = 5.3 MPa (T2 = 50MPa2= 44.7 MPay r/MPa(b)由心平面内应力作g b点,连接血交O•轴丁•(?点,0030.故应力圆半径则: r = >/302 +402 = 506 =30 +50 = 8() MPaa2 =50 MPa a3=-20 MPa= 5() MPa(c)由图7-15 (c)yz平面内应力值作a, b点,圆心为O,半径为50,作应力圆得6 = 5() MPaa2 =-50 MPa6 =-80 MPa50 MPar/MPamax '6 一6 ,二」——=65MPa27-187-19在矩形截面钢拉伸试样的轴向拉力F = 20kN时,测得试样中段B点处与其轴线成30°方向的线应变为a. =3.25x10"。
已知材料的弹性模量£ = 210GPa ,试求泊松比解:F 20X103A " 20x10x10" = 10() MPa CT=a cos2a = —a = 75 MPa4cr|20. = cr cos2a = 25 MPa3.25X10_4 X210X 109 = (75-yx25)x IO6 v = 0.27M c = M n = 690kN- m Fsc 狂=佗 D 右=670 kN7-197-20 D= 120mm,治&hnm 的空心圆轴,两端承受一对扭转力偶矩,如图所示。
材料力学第四版课后答案课件

02 材料力学基础知识
CHAPTER
详细描述
材料力学是工程学科中的一门基础学科,主要研究材料在力作用下的行为,包括材料的 变形、断裂、疲劳等。对于工程师来说,了解材料力学的基本原理和知识是必不可少的
,因为这些原理和知识被广泛应用于各种工程领域,如建筑、机械、航空航天等。
材料力学的基本假设与原理
总结词
材料力学基于一些基本假设和原理,如连续性、均匀 性、各向同性等,通过这些假设和原理来描述材料的 力学行为。
材料力学第四版课后答案课件
目录
CONTENTS
• 材料力学概述 • 材料力学基础知识 • 材料力学基本分析方法 • 材料力学中的能量方法 • 材料力学的应用实例 • 材料力学第四版课后答案解析
01 材料力学概述
CHAPTER
材料力学的定义与重要性
总结词
材料力学是研究材料在力作用下变形、破坏和恢复的学科,对于工程设计和安全至关重 要。
材料力学的发展历程
• 总结词:材料力学的发展经历了多个阶段,从最早的实验观察到现代的数值模拟和智能化技术应用。
• 详细描述:材料力学的发展历程可以追溯到古代,当时的人们通过实践经验积累了一些关于材料性质的认识。然而,真正的材料力学研究始于18世纪,当时的一些科学家开始系统地研 究材料的力学行为。随着科学技术的发展,材料力学的研究也不断深入,涉及到更广泛的应用领域。现代的材料力学研究已经与数学、物理、化学等多个学科交叉融合,形成了许多新 的研究方向和应用领域。同时,随着计算机技术和数值模拟方法的快速发展,现代的材料力学研究也更加依赖于计算机模拟和智能化技术。这些技术的发展为材料力学的研究提供了更 广阔的空间和更深入的认识。
详细描述
材料力学的研究基于一些基本假设和原理。连续性假 设认为材料可以被看作连续的介质,而不是由单个原 子或分子组成。均匀性假设则认为在材料的宏观尺度 上,材料的性质是均匀的,不会因位置的不同而有所 变化。是相同的,不会因方向的不同而有所变化。这些 基本假设和原理为材料力学的研究提供了基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学单辉祖第四版答案
材料力学是工程材料学的重要分支,它研究了材料在外力作用下的力学性能和
行为规律。
单辉祖编著的《材料力学第四版》是该领域的经典教材,其中包含了大量的习题和答案。
本文将针对该教材第四版的答案进行详细解析,帮助读者更好地理解材料力学的相关知识。
第一章,力学基础。
在力学基础这一章节中,主要介绍了向量、坐标系、力的作用点、力的分类等
内容。
在习题答案中,我们需要重点关注向量的运算、坐标系的选择以及力的合成分解等问题。
通过解答这些习题,可以帮助读者建立起对力学基础知识的扎实理解。
第二章,应力。
应力是材料力学中的重要概念,它描述了单位面积上的内力。
在这一章节中,
我们将学习到正应力、剪应力、主应力、最大剪应力等内容。
通过习题答案的解析,我们可以更好地理解应力的计算方法、应力的性质以及应力在材料中的分布规律。
第三章,应变。
应变是材料在外力作用下发生变形的量化描述,它包括线性弹性应变、剪切应变、体积应变等内容。
在习题答案中,我们需要重点关注应变的计算方法、应变与应力的关系以及应变的测量方法等问题。
通过解答这些习题,可以帮助读者深入理解应变的概念和特性。
第四章,弹性力学基本理论。
弹性力学是材料力学中的重要分支,它研究了材料在外力作用下的弹性变形和
恢复性能。
在这一章节中,我们将学习到胡克定律、杨氏模量、泊松比等内容。
通过习题答案的解析,我们可以更好地理解弹性力学的基本理论,掌握弹性参数的计算方法和应用技巧。
第五章,弹性力学应用。
在弹性力学应用这一章节中,我们将学习到梁的弯曲、柱的稳定、薄壁压力容
器等内容。
通过习题答案的解析,我们可以深入理解弹性力学在工程实践中的应用,掌握解决实际工程问题的方法和技巧。
第六章,塑性变形。
塑性变形是材料在超过弹性极限后发生的不可逆变形,它包括屈服、硬化、蠕
变等内容。
在这一章节中,我们将学习到塑性变形的基本特性、塑性材料的力学行为以及塑性变形的计算方法。
通过习题答案的解析,我们可以更好地理解塑性变形的规律和特点,掌握塑性材料的设计和加工原则。
第七章,断裂力学。
断裂力学是材料力学中的重要分支,它研究了材料在外力作用下的断裂行为和
破坏机理。
在这一章节中,我们将学习到裂纹的形成与扩展、断裂韧性、断裂模式等内容。
通过习题答案的解析,我们可以深入理解断裂力学的基本理论,掌握断裂参数的计算方法和应用技巧。
结语。
通过对《材料力学第四版》习题答案的解析,我们可以更好地理解材料力学的
基本概念和理论,掌握解决工程实际问题的方法和技巧。
希望本文能够对读者有所帮助,欢迎大家批评指正。
