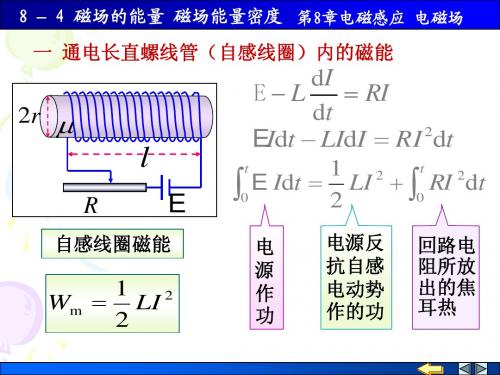
8.4磁场能量 磁场能量密度(8)
磁场的能量 磁场能量密度

磁场的能量
L R
K
当电键打开后,电源已不再向灯泡供应能量了。 它突然闪亮一下,所消耗的能量从哪里来的?
考察在开关合上后的一段时间内,电路中的电 流滋长过程:
由欧姆定律
dI L dt +
ε
L =I R
R
这一方程的解为:
ε
)
I I )
BATTERY
电池
I = R (1 e
= I (1 e
I1
dI dt
M12
1 B2 dV 2
12
I2
1 2 Wm LI 2
, ,
M k L1L 2
磁场能量: Wm v
总磁 能
1 Wm BH d V 2 1 2 1 L 2 m 2 磁场能量密度: 单位体积中储存的磁场能量 wm 磁能密度:
B wm 2
2
总磁能
Wm
V
B dV 2
2
例1 求同轴传输线之磁能 o I 解: B dV = 2 π rl 2r
t
时间内电源提供的部分能量转化为消耗 0 在电阻 R 上的焦耳-楞次热;
1 2
t
RI 2 d t 是
LI 02 是回路中建立电流的暂态过程中电源电动势克
服自感电动势所作的功,这部分功转化为载流回路的 能量; 当回路中的电流达到稳定值后,断开 K1 ,并同时 接通K 2 ,这时回路中的电流按指数规律衰减,此电 流通过电阻时,放出的焦耳-楞次热为
电磁感应 定律
电动势
d m i dt 动 L( v B ) d l
L
大小与方向 非静电力 f 洛 感生电场
无限长直导线磁场能量

无限长直导线磁场能量
无限长直导线的磁场能量可以通过两个方法进行计算:磁场能量密度和磁场能量。
1. 磁场能量密度:
无限长直导线的磁场能量密度可以通过以下公式计算:
\[ U=\frac{1}{2}\mu_0 I^2 \]
其中,U表示单位长度的磁场能量密度,\(\mu_0\)是真空磁导率,I是电流强度。
2. 磁场能量:
磁场能量可以通过以下公式计算:
\[ U = \frac{{\mu_0 I^2 l}}{2\pi} \ln\left(\frac{R}{r}\right) \]
其中,U表示磁场能量,\(\mu_0\)是真空磁导率,I是电流强度,l是导线长度,R是无限大距离(取其为极限),r是导线半径。
需要注意的是,这些公式均是基于理想条件下的无限长直导线,实际情况下,导线的长度和太空中磁场的分布等因素可能会影响到磁场能量的计算结果。
8_4磁场的能量 磁场能量密度1
r < R1 , r > R2 ,
H =0 H =0
µ µ
R2
I R1 < r < R2 , H = 2π r
则
R1 < r < R2
1 1 I 2 2 ) wm = µH = µ ( 2 2π r 2
8 – 4 磁场的能量 磁场能量密度 第8章电磁感应 电磁场
Wm = ∫ wm dV = ∫
V
1 I 2 µI R1 < r < R2 wm = µ ( ) = 2 2 2 2π r 8π r 2 µI
Wm =
∫
V
wm d V =
∫
V
B2 dV 2µ
磁场的能量的计算(对任意载流导体产生的磁场) 磁场的能量的计算(对任意载流导体产生的磁场) 载流导体产生的磁场 1、求 :B ( x . y . z );(载流导体产生) 、 (载流导体产生)
方法
1 B 2、求 : 、 wm =
3、求 : m = 、 W
2
2 µ
,
∫
V
wm d V =
∫
V
B2 dV . 2µ
8 – 4 磁场的能量 磁场能量密度 第8章电磁感应 电磁场
如图同轴电缆,中间充以磁介质 中间充以磁介质,芯线与圆筒上的 例 1 如图同轴电缆 中间充以磁介质 芯线与圆筒上的 电流大小相等、方向相反. 电流大小相等、方向相反 已知 R 1 , R 2 , I , µ , 求单位 长度同轴电缆的磁能和自感. 设金属芯线内的磁场可略. 长度同轴电缆的磁能和自感 设金属芯线内的磁场可略 解 由安培环路定律可求 H
自感线圈磁能
Wm
2
电 源 作 功
电源反 抗自感 电动势 作的功
磁场的能量公式

磁场的能量公式
1. 自感线圈磁场能量公式。
- 对于一个自感系数为L的线圈,当通过的电流为I时,其储存的磁场能量W = (1)/(2)LI^2。
- 推导过程:当电路中的电流I发生变化时,自感电动势E = - L(di)/(dt)。
在建立电流I的过程中,电源克服自感电动势做功,这个功就转化为磁场的能量。
根据能量守恒定律,设电流从0增加到I,电源克服自感电动势做的功W=∫_0^tEidt=∫_0^ILi
di=(1)/(2)LI^2。
2. 磁场能量密度公式。
- 在均匀磁场中,磁场能量密度w=(1)/(2)frac{B^2}{μ},其中B是磁感应强度,μ是磁导率(对于真空μ=μ_0,对于介质μ = μ_rμ_0,μ_r是相对磁导率)。
- 推导过程:对于长直螺线管,内部磁场B=μ nI(n是单位长度的匝数),自感系数L=μ n^2V(V是螺线管的体积)。
根据W=(1)/(2)LI^2,将L和I=(B)/(μ n)代入可得W=(1)/(2)frac{B^2}{μ}V,所以磁场能量密度w = (W)/(V)=(1)/(2)frac{B^2}{μ}。
对于非均匀磁场,可以通过对体积元dV积分W=∫_Vw dV=∫_V(1)/(2)frac{B^2}{μ}dV
来计算磁场的总能量。
高二物理竞赛磁场的能量磁场能量密度PPT(课件)

两边同时对时间进行积分
电源克服自感电动势所做的功
同时为维持I10不变,I10要克服
作功
按照磁场的近距作用观点,磁能也是定域在磁场中的。
dW 1 m 2)维持线圈“1”中电流不变,让线圈“2”中电
在已知自感系数的情况下,应用第一种公式计算较为简单。
w B H m 显然:互感电路中的磁能是克服自感电动势及互感电动势作功的过程中建立的。
S I
磁场能量只能反映空间体积 V 内的总能量,不能反
映磁场的能量分布情况。须引入描写磁场分布的物理
量----能量密度。
能量密度wm(单位体积内的磁场能量):
wm
Wm V体
B2 2
1 H 2 1 BH
2
2
wm
Wm V体
12 – 5 磁场的能量 磁场能量密度 第十二章电磁感应 电磁场
wm2B2 12H2
说明:载流线圈的磁场能量可以用公式
, 也可以用磁场能量密度公式对空间求积分计算。
2)维持线圈“1”中电流不变,让线圈“2”中电
能量密度wm(单位体积内载流长直螺线管为例:
1)线圈“2”开路,让线圈“1”中电流由0
i 2)维持线圈“1”中电流不变,让线圈“2”中电
12 – 5 磁场的能量 磁场能量密度 第十二章电磁感应 电磁场
三、互感磁能
初始状态:
L1 M L2
I1 0 I2 0
电源克服自感电动势所做的功
显然:互感电路中的磁能是克服自感电动势及互感电动势作功的过程中建立的。
1)线圈“2”开路,让线圈“1”中电流由0
稳定状态: 显然:互感电路中的磁能是克服自感电动势及互感电动势作功的过程中建立的。
若电流衰减过程
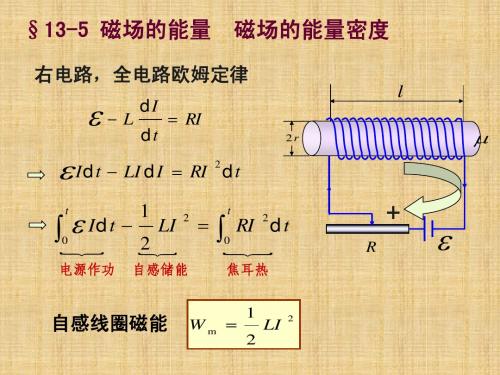
§13-5磁场的能量磁场的能量密度
2
Wm = =
∫ ∫
V
wm d V
µ
⋅ ( 2π rdr ⋅ 1)
µI 2
2 2
8π r 2 R2 µ I =∫ ⋅ dr R1 4 π r R2 µI 2 = ln 4π R1
V
r dr
R2
1 W m = LI 2
2
R2 L= ln 2 π R1
µ
第§13-5节完 13-
Maxell方程组 §13-6 位移电流 Maxell方程组 13麦克斯韦( 麦克斯韦(1831-1879) ) 英国物理学家。 英国物理学家。经典 电磁理论的奠基人, 电磁理论的奠基人, 气体 动理论创始人之一。 动理论创始人之一。①提 出了有旋场、 出了有旋场、位移电流的 概念, 概念, 建立了经典电磁理 论;②预言了以光速传播 的电磁波的存在。 的电磁波的存在。 ③在 气体动理论方面, 气体动理论方面, 提出了 气体分子按速率分布的统 计规律。 计规律。
一 位移电流 全电流安培环路定理
稳恒磁场中,安培环路定理 稳恒磁场中,
∫ H ⋅ dl = ∑ I = ∫ j ⋅ ds
l s
以 L 为边做任意曲面 S1 和 S2
∫LH ⋅ dl = ∫S1 j ⋅ ds = I
S1
-
S2
+ + + +
∫ H ⋅ dl = ∫
L
S2
j ⋅ ds = 0
I
−σ dD +σ + - dt +
∫ D ⋅ ds = ∑ q dφ ∫ E ⋅ d l = − dt
S
l
m
∫ B ⋅ ds = 0 ∫ H ⋅ dl = I + I
磁场的能量磁场能和磁场的能量密度
磁场的能量磁场能和磁场的能量密度磁场是物质中特定区域内部存在的一种物理量,它可以由电流、磁铁等产生。
在物质中,磁场具有能量,磁场的能量密度则是描述磁场能量分布的物理量。
本文将着重探讨磁场的能量以及磁场的能量密度,并从理论和实验两个方面进行论述。
一、磁场的能量磁场的能量是由电流和磁铁等物体产生的。
当电流通过导线时,就会在周围产生一个磁场。
此时,电流所具有的能量会转化为磁场能量。
同样地,磁铁中的磁场也是由磁场的能量驱动的。
磁场的能量主要存在于两种形式,一种是磁场中的储能,另一种是以磁场能量形式储存于物体中。
首先来看磁场中的储能。
当一个点电荷沿曲线移动时,在磁场中要克服磁场的作用才能改变自己的位置。
这就相当于是对磁场做了一定的功。
根据功的定义,功是能量转化的过程中所做的功,因此我们可以得出结论:磁场中的储能等于电荷在磁场中所受到的力与移动距离的乘积,即U=Fl。
其中,U表示储存在磁场中的能量,F表示电荷所受到的磁场力,l表示电荷在磁场中移动的距离。
其次来看以磁场能量形式储存于物体中。
如果在一个磁性物质中存在一个磁场,那么这个磁场会使得物质内部的磁矩发生定向,从而存储了一定的能量。
这部分能量就是以磁场能量的形式储存在物体中。
二、磁场的能量密度磁场的能量密度是指单位体积内磁场能量的大小。
在物质中,磁场的能量密度可以由以下公式表示:ε = (B^2) / (2μ)其中,ε表示磁场的能量密度,B表示磁场的磁感应强度,μ表示真空中的磁导率。
从上述公式可以看出,磁场的能量密度与磁感应强度的平方成正比。
根据磁通连续性定律,磁场的能量是相对稳定的,即磁场的能量密度在整个空间中是保持不变的。
这也意味着,磁场的能量既没有位势能,也没有动能,仅仅以磁场能量密度的形式存在于物体中。
实验上可以通过测量磁场的能量密度来了解磁场的能量分布情况。
一种常用的方法是利用霍尔探测器来测量磁场的磁感应强度,然后根据磁场能量密度的公式计算得出磁场的能量密度。
大学物理简明教学教程(吕金钟)第四章知识题目解析
第四章 电磁学基础静电学部分4.2 解:平衡状态下受力分析 +q 受到的力为:20''41r qq F qq πε=ϖ()()24441lq q F q q πε=ϖ处于平衡状态:()04'=+q q qq F F ϖϖ()0441'412020=+l qq r q q πεπε (1)同理,4q 受到的力为:()()()20'44'41r l q q F q q -=πεϖ()()204441l q q F q q πε=ϖ ()()04'4=+q q q q F F ϖϖ()()()04414'412020=+-l q q r l q q πεπε (2)通过(1)和(2)联立,可得: 3lr =,q q 94'-=4.3 解:根据点电荷的电场公式:r e r q E ϖϖ2041πε=点电荷到场点的距离为:22l r +22041l r qE +=+πε两个正电荷在P 点产生的电场强度关于中垂线对称:θcos 2//+=E E0=⊥E22cos lr r +=θqlq+所以:()232202222021412cos 2l r qrlr r l r qE E +=++==+πεπεθ当l r >>202024121r q r q E πεπε==与点电荷电场分布相似,在很远处,两个正电荷q 组成的电荷系的电场分布,与带电量为2q 的点电荷的电场分布一样。
4.4 解:取一线元θλRd dq =,在圆心处产生场强:20204141R Rd R dq dE θλπεπε==分解,垂直x 方向的分量抵消,沿x 方向 的分量叠加:RR Rd dE x 00202sin 41πελθθλπεπ==⎰⎰方向:沿x 正方向4.5 解:(1)两电荷同号,电场强度为零的点在内侧;(2)两电荷异号,电场强度为零的点在外侧。
4.7 解:线密度为λ,分析半圆部分:θλλrd dl dq ==点电荷电场公式:r e r q E ϖϖ2041πε=在本题中: 241rrd E θλπε=电场分布关于x 轴对称:θθλπεθsin 41sin 2r rd E E x ==,0=y Ex进行积分处理,上限为2π,下限为2π-:rd r r rd E E 000022sin 4sin 41sin πελθθπελθθλπεθππ====⎰⎰⎰方向沿x 轴向右,正方向 分析两个半无限长:)cos (cos 4d sin 4210021θθπελθθπελθθ-===⎰⎰xx dE E x x )sin (sin 4d cos 4120021θθπελθθπελθθ-===⎰⎰xx dE E y y 21πθ=,πθ=2, x E x 04πελ=,xE y 04πελ-= 两个半无限长,关于x 轴对称,在y 方向的分量为0,在x 方向的分量:rr E E x 002422πελπελ=== 在本题中,r 为场点O 到半无限长线的垂直距离。
磁场能量的计算公式
磁场能量的计算公式
磁场能量的计算公式是磁场能量密度乘以体积。
磁场能量密度可以通过磁场能
量的总和除以体积来得到。
根据电磁学原理,磁场能量密度可以由磁场强度H和
磁感应强度B的乘积得到,即磁场能量密度(W)= 1/2 * B * H。
这里的B代表磁
感应强度,单位是特斯拉(T),H代表磁场强度,单位是安培/米(A/m)。
所以,磁场能量(E)= W * V,其中V表示磁场所占据的体积。
通过使用这个公式,我
们可以计算出在给定磁场条件下的磁场能量。
需要注意的是,在实际计算中,我们应该使用合适的单位。
大学物理磁场能量
2. 磁能密度 磁能:
wm
B2
2
1 2
BH
1 2
H 2
Wm V wmdV
( The end)
Wm
1 2
LI 2
11( ( n2nVI ) I2 V2 2
B2
2
V
管内为均匀场,则单位体
自感:L
积内磁场能量为:
I
V
I
wm
Wm V
B2
2
B2
( 可推广 )
Chapter 8. 电磁感应
§8. 5 磁作 场能者量:杨磁茂场田能量密度
P. 10 / 17 .
磁场能量密度(磁能密度):
wm
dWm dV
B2
2
,
B H
wm
B2
2
1 2
BH
1 2
H 2
管内为均匀场,则单位体
积内磁场能量为:
dV B
wm
Wm V
B2
2
B2
( 可推广 )
Chapter 8. 电磁感应
§8. 5 磁作 场能者量:杨磁茂场田能量密度
磁场能量密度(磁能密度):
wm
dWm dV
B2
2
,
B H
P. 11 / 17 .
wm
B2
P. 4 / 17 .
L L L
Chapter 8. 电磁感应
§8. 5 磁作 场能者量:杨磁茂场田能量密度
i2Rdt:焦耳热
-iLdt:磁能 (储存在螺线管 的磁场中)
充电结束后磁场能量:
Wm i Ldt
0
i(L
di
)dt
0
dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Wm V wmdV
I 2
dV
V 8π2 r2
(3)
r dr
R2
单位长度壳层体积元(由磁能密度定):
dV 2π rdr 1
(4)
Wm
R2 I 2 dr I 2 ln R2
R1 4 π r
4π R1
(5)
Wm
1 LI 2 2
(6)
(6)与(5) 比较得:
L ln R2
上述结论表明:任何磁场都具有能量,其能量分 布于场所占据的空间,故(10)式的积分遍布磁场 所占据的全部空间;(9)式对应的磁场能量密度是 为空间点的函数;
例:同轴电缆间充以磁介质,芯线与圆筒上的电流大小
同、方向反。 已知 R1, R2 , I , ,求单位长度电缆
的磁能和自感,设芯线内的磁场可略。
(7)
2π R1
r dr
R2
解:分析:由磁能公式直接
求解。安培环路定律可求H,
再求磁能和自感:
r R1 , H 0
R1 r R2 ,
H I 2π r
(1)
r R2 , H 0
R2
则由磁场能量密度公式得:
wm
1 2
BH
1 2
( 2
I π
r
)2
I
8π 2
2
r
2
R1 r R2 (2)
l
2.电流增长的规律: I I(t)
R
3电.电动路势闭 合L,时同,时电建流立由磁零场逐,渐由增全长电,路线欧圈姆中定产律生可自得感:
L RI
L dI RI
(1)
dt
上式是RL电路中电流随时间的变化规律,随着电流的
增长,线圈中的磁场逐渐建立起来:
Idt LIdI RI 2 dt
8-5.磁场能量 磁场能量密度
已了解到:电场是一种特殊物质,对应一 定能量;磁场也对应一定能量吗?本节专门讨 论该问题:
思路:磁场的建立总是伴有电磁感应现象发生, 故可从能量转换角度,由分析电磁感应现象入手 讨论磁场能量,从 RL 电路电流的增长出发;
1.RL电路:主要由电阻和线圈 2r 串联而成的电路;
(2)
t
Idt
1
LI
2
t RI 2 dt
0
2
0
电 电源反 回路电 2r
源 抗自感 阻放出
作 功
电动势 作功
的焦耳 热
自感线圈磁能:
Wm
1 2
LI 2
(3)
l
R
(4)
由长直螺线管对应的物理量:
L n2V ,
B nI (5)
I
L
得:
Wm
1 LI 2 2
1 2
n 2V
(
B
n
)2
1 B2 V
2
wmV
(6)
磁场能量密度: wm
B2
2
1 H 2
2
1 BH 2
(7)
磁场能量:
Wm
V wmdV
B2 dV
V 2
(8)
磁场能量密度:
1
wm
BH 2
(9)
磁场能量:
1
Wm
V wm dV
B HdV V2
(10)
