捷联惯导初始对准以及姿态解算
捷联惯导与组合导航解读
? 由于在解欧拉角微分方程时，当俯仰角为 90度时， 方程出现奇点，使方程式出现退化现象，因此这 种方法不能用于全姿态飞行器上，尤其是垂直发 射上。相比之下，用四元数微分方程求解姿态矩 阵时，计算量较小，可以全姿态飞行，也可以写 出适合于计算机的递推表达式，因此被广泛用于 捷联姿态计算中。这里介绍四元数在刚体中的应 用，具体到确定姿态矩阵中的应用。
6、制导和控制信息的提取，飞行器的姿态信息既用来 显示也是控制系统最基本的控制信息。此外，飞行 器的角速度和线加速度信息也都是控制飞行器所需 要的信息。这些信息可以从姿态矩阵的元素和陀螺 加速度计的输出中提取出来。
? 1.2.2 姿态矩阵的计算
? 捷联式惯导中，飞行器的地理位置就是地理坐标 系相对地球坐标系的方位。而飞行器的姿态和航 向则是机体坐标系相对地理坐标系的方位关系。 确定两个坐标系之间的方位关系问题，是力学中 的刚体定点转动理论。在刚体定点转动理论中， 描述动坐标系相对参考坐标系方位关系的方法有 多种，我们可以简单的把它们分作三类，即：三 参数法、四参数法和九参数法。
cos ? 0
2
sin ? 0
2
cos ? 0
2
cos ? 0
?
sin ? 0
?
sin
0
22
?
?
sin
0
?
sin
0
22
?
sin ? 0
?
cos
0
22
? cos ? 0 sin ? 0
sin ? 0
2
cos ? 0
2
sin ? 0
2
sin ? 0
? ? ? ? ? ? ? ? ? ?
?2 2 2
2 2 2?
-初始对准
捷联惯导系统的 静基座初始对准1．初始对准惯性导航系统是根据测得的运载体的加速度，经过积分运算求得速度与位置的，因此，必须知道初始速度和初始位置。
此外，在以地理坐标系为导航坐标系的惯导系统中（包括平台式和捷联式），物理平台和数学平台都是测量加速度的基准，而且平台必须准确地跟踪地理坐标系，以避免由平台误差引起加速度测量误差。
在惯性系统加电启动后，平台的三轴指向是任意的，平台一般不在水平面内，又没有确定的方位，因此在系统进入导航工作状态前，必须将平台的指向对准，此过程便称为惯性系统的初始对准。
初始对准的精度直接关系到惯导系统的工作精度，初始对准的时间是惯导系统的重要战术技术指标。
因此，初始对准是惯导系统最重要的关键技术之一。
2．初始对准的分类（1）按对准的阶段来分惯导系统的初始对准一般分为两个阶段：第一阶段为粗对准：对平台进行水平与方位粗调，要求尽快地将平台对准在一定的精度范围内，为后续的对准提供基础，所以要求速度快，精度可以低一些。
第二阶段为精对准：它是在粗对准的基础上进行的，要求在保证对准精度的前提下尽量快。
（2）按对准的轴系来分在以地理坐标系为导航坐标系的情况下，初始对准可分为水平对准和方位对准。
在平台式惯导系统中，物理平台通常先进行水平对准，然后同时进行平台的水平与方位对准。
在捷联式惯导系统中，对数学平台进行对准时，一般情况下水平对准与方位对准是同时进行的。
（3）按基座的运动状态来分按照安装惯导系统所在基座的运动状态可分为静基座对准和动基座对准。
动基座对准通常是在运载体处于运动状态下进行的。
（4）按对准时对外信息的需求来分惯导系统只依靠重力矢量和地球速率矢量通过解析方法实现的初始对准称为自主式对准，此时不需要其它外部信息，自主性强，但精度不高。
非自主对准可通过机电、光学或其它方法将外部参考坐标系引入系统，使平台对准至导航坐标系。
3．初始对准的要求惯导系统不论用于运载体导航还是武器弹药中的制导，都要求初始对准保证必需的准确性与快速性。
捷联惯性导航系统的解算方法ppt课件
的 分量构成的矩阵，则
r rnT n r nT Cnb n rnT r nT Cbn
由于坐标系不动而是矢量转动，它 相应于矢量固定时坐标系方向转动
rn
n
C
n b
r
2010-03-19
方向余弦矩阵微分方程
由矢量相对导数和绝对导数的关系式
dr dt
n
dr dt
b
ω nb r
假定地理坐标系为参考坐标系，作为参考 坐标系认为它在空间是不动的，即
如把OXbYbZb作为动坐标系， ENU作为参考坐标系，则航向 角H，纵摇角（俯仰角）P和横 摇角（横滚角、倾斜角）R。就 是一组欧拉角。
Zb Zb'' U Zb' P
欧拉角没有严格的定义，根 据
需要，可以选用不同的欧拉 角
组。第一次转动，可以绕三 个
轴中的任一个转动，故有3种 可
能，第二次有2种可能，第三 次
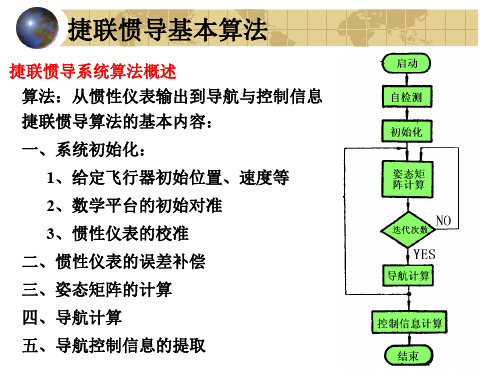
启动
自检 测
初始 化
返回9
姿态
迭 数
代
次阵计 算
N O
YES
导 航 计 控 制 信 息算提 取
3.2 姿态矩阵的计算
捷联式惯导中，载体地理位置就是地理坐标系相对 地球坐标系的方位。而载体的姿态和航向则是载体 坐标系相对于地理坐标系的方位关系。确定两个坐 标系的方位关系问题，是力学中的刚体定点转到理 论。在刚体定点转动理论中，描述动坐标系相对参 考坐标系方位关系的方法有多种。
求解方程可以直接得到航向和姿态信息，
欧 拉角法得到的姿态阵永远是正交阵，用这
个矩 阵将比力fb→fn信息的坐标变换时，变换后的信 息
中不存在非正交误差。因此，用欧拉角法得 到的姿态矩阵无
北航卡尔曼滤波课程-捷联惯导静基座初始对准实验
卡尔曼滤波实验报告捷联惯导静基座初始对准实验一、实验目的① 掌握捷联惯导的构成和基本工作原理； ② 掌握捷联惯导静基座对准的基本工作原理；③ 了解捷联惯导静基座对准时的每个系统状态的可观测性； ④ 了解双位置对准时系统状态的可观测性的变化。
二、实验原理选取状态变量为：[]T EN E N U x y x y z X V V δδεεε=ψψψ∇∇，其中导航坐标系选为东北天坐标系，E V δ为东向速度误差，N V δ为北向速度误差， E ψ为东向姿态误差角 ，N ψ为北向姿态误差角， U ψ为天向姿态误差角， x ∇为东向加速度偏置，y ∇为北向加速度偏置，x ε为东向陀螺漂移，y ε为北向陀螺漂移，z ε为天向陀螺漂移。
则系统的状态模型为：X AX W =+(1)其中，1112212211121321222331323302sin 000002sin 000000000sin cos 0000sin 000000cos 00000000000000000000000000000000000000000000000000000L g C C L g C C L L C C C L C C C L C C C A Ω-⎡⎤⎢⎥-Ω⎢⎥⎢⎥Ω-Ω⎢⎥-Ω⎢⎥⎢⎥Ω=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦[00000]E N E N UT V V W W W W W W δδψψψ=，ED VW W δψ为零均值高斯白噪声，分别为加速度计误差和陀螺漂移的噪声成分，Ω为地球自转角速度，ij C 为姿态矩阵nb C 中的元素，L 为当地纬度。
量测量选取两个水平速度误差：[ ]TE N Z V V δδ=，则量测方程为：10000000000100000000E E N N V X V δηδη⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦(2)即Z HX η=+其中，H 为量测矩阵，[]TEN ηηη=为量测方程的随机噪声状态矢量，为零均值高斯白噪声。
捷联惯导系统算法.ppt
cos
b Ebz
注意事项：当 θ= 90 度时，方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度，所以：
CbE
b ib
E iE
C
E b
或四元数微分方程：
q(t)
(
b ib
b iE
)q(t)
注意事项： 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小，计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量：陀螺仪数字脉冲输出，每个脉冲代表一个角增量
一个采样周期内，陀螺输出脉冲数对应的角增量为：
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述：
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序：
Ψ →θ →γ
捷联惯导系统静基座的高精度初始对准方法
（ ｂ ） ～。
（ ３ ）
就 可获得 粗对 准结 果 ，即姿态矩 阵 ｃ ： 的初 始矩 阵 ：
（ ｇ ） （ ｇ ）
＿＋
ｒ Ｃ Ｃ ｚ
＝
Ｃ ：＝ 【 ｃ ＝ （ ： ）
（ ｒ ） Ｔ
＿
（ ｂ ）
—
Ｉ ｌ Ｃ ： Ｃ 。 ：
ｒ：【 罾 誊×
由于 ｇ系与 ｂ系可通 过矩 阵 Ｃ 进行 转换
（ 誊× ）×香 】 ＝［ ｒ 一 ２ ｒ 一 ３ 】 。
，
（ １ ）
故
ｒ － ｂ
＝
ｃ ： 。
（ ２ ）
ቤተ መጻሕፍቲ ባይዱ
又 由于 与 可 以通 过测 量获 得 ，而 、 、 、 也 都 可 以通 过计 算获 得 ，因此 联立 求解 就可 以
第２ ７卷
第 １期
２ ０ １ ７年 ３月
洛 阳理 工 学 院学 报 （ 自然 科 学 版 ） Ｊ ｏ ｕ ｒ ｎ ａ ｌ ｏ ｆ Ｌ ｕ ｏ ｙ ａ ｎ ｇ Ｉ ｎ ｓ ｔ ｉ ｔ ｕ ｔ ｅ ｏ ｆ Ｓ ｃ ｉ ｅ ｎ ｃ ｅ ａ ｎ ｄ Ｔ ｅ ｃ ｈ ｎ ｏ ｌ ｏ ｇ ｙ （ Ｎ ａ ｔ ｕ ｒ ａ ｌ Ｓ ｃ ｉ ｅ ｎ ｃ ｅ Ｅ ｄ ｉ ｔ ｉ ｏ ｎ ）
Ｖｏ １ ． ２ ７ Ｎｏ ． １ Ｍａ Ｌ ２ ０１ ７
捷 联 惯 导 系统 静 基座 的 高 精 度 初 始 对 准 方 法
王雪瑞 ，周 岩
（ 河南工程 学院 计算机 学院，河南 郑州 ４ ５ １ １ ９ １ ）
摘
要 ：针对捷联惯导 系统静基座初始对 准存在精 度低的 问题 ，通过加 速度 计和 陀螺仪获得 重力 矢量和地球 角
动基座条件下舰载武器捷联惯导系统初始对准研究
动基座条件下舰载武器捷联惯导系统初始对准研究随着现代化舰艇的不断发展，其中一项重要的技术就是舰载武器的捷联惯导系统。
这种系统将惯性导航系统和星载导航系统结合起来，能够提高武器的精度和可靠性，确保击中目标。
而在动基座条件下，捷联惯导系统的初始对准是实现高精度打击的重要前提。
动基座条件下的舰载武器捷联惯导系统与传统型号相比，需要额外考虑动基座的姿态确定和补偿问题。
在舰艇运动状态下，动基座将遇到多种力学干扰，如风浪、航行状态变化等。
为了获得准确的姿态信息，需要考虑惯性方程和传感器的实际误差，同时需要运用数学模型来消除干扰对姿态的影响，确保系统能够快速、准确地对准目标。
捷联惯导系统的初始对准是捷联系统实现高精度打击的重要前提。
捷联惯导系统的精度受多种因素影响，其中最关键的因素之一就是惯性传感器的初始对准误差。
初始对准误差会在系统使用过程中积累，导致系统的误差逐渐扩大，影响武器的精度和可靠性，因而需要采取适当的措施来解决。
在捷联惯导系统的初始对准过程中，主要考虑惯性导航系统和星载导航系统之间的配合和对准误差的消除。
一般情况下，捷联惯导系统会先采用星载导航系统进行粗略定位，再用惯性导航系统进行精细定位，以此来提高系统的定位精度。
但由于星载导航系统的精度受限，粗略定位可能会带来不可避免的误差，而大幅度运动也会导致惯性传感器的零偏误差，使得捷联惯导系统无法准确掌握自身姿态和位置信息，从而影响武器的打击结果。
因此，在动基座条件下，需要采取适当的初始对准方法，以提高捷联惯导系统的精度和可靠性。
传统的捷联惯导系统初始对准方法主要包括三种：心理想象矫正，静停地平线矫正和动基座矫正。
其中心理想象矫正是指利用心理想象方法计算偏差角，并根据偏差角通过动态调整惯性器件的参考坐标系来实现对准。
静停地平线矫正是指在静态条件下使用陀螺仪的水平度进行对准。
动基座矫正是指在动态条件下使用动基座姿态信息进行对准。
然而，这些传统的初始对准方法在动基座情况下都存在一定的局限性和缺陷。
捷联惯导与组合导航系统高精度初始对准技术研究
捷联惯导与组合导航系统高精度初始对准技术研究捷联惯导与组合导航系统高精度初始对准技术研究引言捷联惯导与组合导航系统是一种集捷联惯导和其他导航传感器（如GPS、气压计、陀螺仪等）的优势于一体的导航系统，具有在惯导滞后情况下实现导航信息快速、准确更新的优势。
为了确保导航精度和可靠性，捷联惯导与组合导航系统的初始对准是不可或缺的关键技术之一。
本文将重点探讨捷联惯导与组合导航系统高精度初始对准技术的研究。
一、捷联惯导与组合导航系统概述捷联惯导与组合导航系统是一种通过融合多种导航传感器测量数据来计算导航解的导航系统。
其中，捷联惯导通过惯性导航算法利用加速度计和陀螺仪提供的姿态、速度和位移信息进行导航计算，而组合导航则通过融合GPS和其它传感器的信息来修正惯导的误差，提供更准确的导航结果。
二、初始对准技术的研究现状初始对准技术在捷联惯导与组合导航系统中起到了决定性的作用，对其精度和可靠性具有重大影响。
目前，针对初始对准技术的研究主要集中在以下几个方面：1. 惯性传感器标定：惯导系统的精度和准确性直接依赖于惯性传感器的性能。
因此，对于惯导系统而言，惯性传感器的标定至关重要。
传感器标定主要涉及惯性传感器的误差估计、参数校准和标定方法等。
2. 导航状态估计算法：捷联惯导与组合导航系统的核心是导航状态估计算法。
目前常用的算法包括扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）以及粒子滤波（PF）等。
这些算法通过融合多种传感器的信息，实现对导航状态的准确估计。
3. 高精度传感器融合：为了提高初始对准的精度和可靠性，可以考虑使用更高精度的传感器，如高精度的加速度计和陀螺仪。
此外，对于GPS系统而言，使用双频技术和高精度的差分GPS技术可以进一步提高导航精度。
三、捷联惯导与组合导航系统高精度初始对准技术研究在捷联惯导与组合导航系统高精度初始对准技术的研究中，可以采用以下方法来提高初始对准的精度和可靠性：1. 多目标标定方法：采用多目标标定方法来标定捷联惯导系统中的惯性传感器。