统计学主要计算公式
统计学重要计算及公式
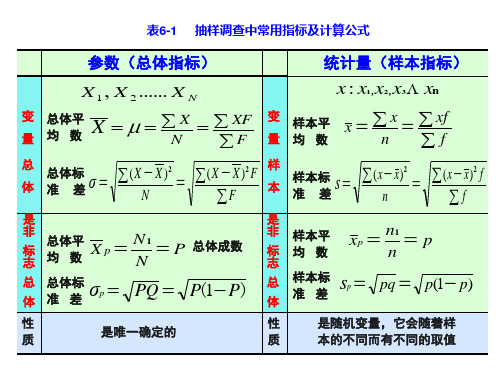
s2 s2 P x-t 2 (n 1) x+t 2 (n 1) 1 = n n
根据t分布性质,在置信水平1- 下总体均值的置信区间为:
x x
或:
x t 2 (n 1) x
s x t (n 1) 2 n
假设检验的类型:双侧检验和单侧检验
2
n 1
2
2
a a
1
a
2
f
1 1
an an
1
f fn-
2
1
fn-
1
环比发展速度和定基发展速度的关系
1.各个时期环比发展速度连乘积等于相应的定基发展
速度;
a1 a 2 a 3 an a 0 a1 a 2 an 1
展速度。
an a0
2.相邻时期的定基发展速度之比等于相应的环比发
x n
x
xf
f
σ (X X ) (X X ) F N F
2 2
( x x )2 ( x x )2 f n f
xp n1 n
总体平 Xp 标 均 数 志 总 总体标 体 准 差 性 质
N1 N
P
பைடு நூலகம்总体成数
标 志 总 体 性 质
p
σp PQ P(1 P)
在置信水平1- 下参数的置信区间为: 或:
x x
x z 2 x
x z
2
s n
2 3、总体服从正态分布、 未知、小样本时 ,均值的区间估计
总体方差未知且是在小样本情况下,则需用样本方差代替总体方差,这时 样本均值经过标准化以后的随机变量则服从自由度为(n-1)的t分布, 可 得到
统计学公式大全

3 i1 N3
峰度
(概念要点)
• 1. 数据分布扁平程度的测度 • 2. 峰度系数=3扁平程度适中 • 3. 偏态系数<3为扁平分布 • 4. 偏态系数>3为尖峰分布 • 5. 计算公式为
K Xi X 4 Fi
4 i1 N 4
时间序列的分类
时间序列
绝对数序列 相对数序列 平均数序列
时期序列 时点序列
线性模型法
(a和b的最小二乘估计)
1. 根据最小二乘法得到求解 a 和 b 的标准方程为
Ynab t tYa tb
t2
解得:b
ntY tY
nt 2 t2
a Y bt
2. 取时间序列的中间时期为原点时有 t=0,上
式可化简为
Y na tY bt 2
a Y
解得:
b
tY t2
增1% 长 绝对环 值 逐 比 = 期 增 增 1长 0 长 0前 速 1量 期 0度 0水
甲企业增长1%绝对值=500/100=5万元 乙企业增长1%绝对值=60/100=0.6万元
时间序列的构成要素与模型
(要点)
1. 构成因素
– 长期趋势 (Secular trend ) – 季节变动 (Seasonal Fluctuation ) – 循环波动 (Cyclical Movement ) – 不规则波动 (Irregular Variations )
3. 平均数时间序列
– 一系列平均数按时间顺序排列而成
绝对数序列的序时平均数
(计算方法)
时期序列
n
•
计算公 式:
Y Y1 Y2
Yn
Yi
i1
n
n
【例11.1】 根据表11.1中的国内生产总值 序列,计算各年度的平均国内生产总值
统计学自由度计算公式

统计学自由度计算公式
统计学自由度是指在进行统计推断时,样本数据可以自由变化的数量。
在不同的统计分析方法中,自由度的计算公式也不同。
以下是一些常见的统计学自由度计算公式:
1. 单因素方差分析的自由度计算公式:
自由度=总体样本数-组数
2. 双因素方差分析的自由度计算公式:
自由度=总体样本数-组数1-组数2+1
3. 卡方检验的自由度计算公式:
自由度=(行数-1)×(列数-1)
4. t检验的自由度计算公式:
自由度=样本量-2
5. F检验的自由度计算公式:
分子自由度=分子样本数-1
分母自由度=分母样本数-1
以上是一些常见的统计学自由度计算公式,希望能对您有所帮助。
- 1 -。
统计学常用公式汇总

《统计学原理》常用公式汇总(一)第三章统计整理a) 组距=上限-下限b) 组中值=(上限+下限)÷2c) 缺下限开口组组中值=上限-1/2邻组组距d) 缺上限开口组组中值=下限+1/2邻组组距第四章综合指标i. 相对指标1.结构相对指标=各组(或部分)总量/总体总量2.比例相对指标=总体中某一部分数值/总体中另一部分数值3.比较相对指标=甲单位某指标值/乙单位同类指标值4.强度相对指标=某种现象总量指标/另一个有联系而性质不同的现象总量指标5.计划完成程度相对指标=实际数/计划数=实际完成程度(%)/计划规定的完成程度(%)ii.平均指标1.简单算术平均数:2.加权算术平均数或iii.变异指标1.全距=最大标志值-最小标志值2.差: 简单σ= ;加权σ=3.差系数:第五章抽样估计1.平均误差:重复抽样:不重复抽样:2.抽样极限误差3.重复抽样条件下:平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下:平均数抽样时必要的样本数目第七章相关分析1.相关系数2.配合回归方程y=a+bx3.估计误:第八章指数分数一、综合指数的计算与分析(1)数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。
( - )此差额说明由于数量指标的变动对价值量指标影响的绝对额。
(2)质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度。
( -)此差额说明由于质量指标的变动对价值量指标影响的绝对额。
加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析:= ×绝对值变动分析:- = ( - )×( -)第九章动态数列分析一、平均发展水平的计算方法:(1)由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算:a.若间断的间隔相等,则采用“首末折半法”计算。
公式为:b.若间断的间隔不等,则应以间隔数为权数进行加权平均计算。
统计学常用公式

统计学常用公式统计学是一门研究数据收集、整理、分析和解释的学科。
在统计学中,公式是非常重要的工具,用于计算和推导各种统计指标和结果。
下面是一些统计学中常用的公式,它们可以帮助我们理解和应用统计学的基本概念和方法。
1. 数据的中心趋势度量在统计分析中,我们经常需要了解数据的中心趋势,即数据的集中程度或平均水平。
以下是几个常用的中心趋势度量公式:- 平均值(Mean):一组数据中所有观测值的总和除以观测值的个数。
- 中位数(Median):将一组数据按照大小排序,位于中间位置的观测值。
- 众数(Mode):出现次数最多的观测值。
- 加权平均值(Weighted Mean):将每个观测值乘以相应的权重,然后求和并除以总的权重和。
2. 数据的离散程度度量除了了解数据集中在哪里,我们还需要了解数据的离散程度,即数据分散的程度。
以下是几个常用的离散程度度量公式:- 方差(Variance):一组数据与其平均值之差的平方的平均值。
- 标准差(Standard Deviation):方差的算术平方根。
- 平均绝对偏差(Mean Absolute Deviation):一组数据与其平均值之差的绝对值的平均值。
3. 数据的相关性度量在统计分析中,我们常常需要了解两个或多个变量之间的相关性。
以下是几个常用的相关性度量公式:- 协方差(Covariance):一组数据中两个变量之间的协方差。
协方差的正负表示两个变量是正相关还是负相关。
- 相关系数(Correlation Coefficient):协方差除以两个变量各自的标准差的乘积。
相关系数的取值范围为-1到1,越接近-1或1表示相关性越强。
4. 抽样误差估计在统计学中,我们通常只能对样本数据进行分析,从而推断总体的特征。
以下是几个常用的抽样误差估计公式:- 样本标准差(Sample Standard Deviation):类似于总体标准差,但在计算时使用样本数据。
- 样本均值(Sample Mean):类似于总体均值,但在计算时使用样本数据。
应用统计学计算公式

应用统计学计算公式
应用统计学计算公式有很多,下面列举几个常见的计算公式:
1. 平均值(均数):计算一组数据的平均值,公式为 sum(x) / n,其中 sum(x)表示所有数据的和,n表示数据的个数。
2. 中位数:计算一组数据的中位数,公式为(排序后的)第
(n+1)/2个数据,如果n为偶数,则中位数为第n/2个和第
(n/2)+1个数据的平均值。
3. 众数:计算一组数据中出现次数最多的数值,可以通过统计每个数值出现的频数,然后选择频数最大的数值作为众数。
4. 方差:用于衡量一组数据的离散程度,公式为 sum((x - mean)^2) / n,其中x表示每个数据,mean表示平均值,n表
示数据的个数。
5. 标准差:是方差的平方根,用于衡量一组数据的离散程度,公式为 sqrt(variance),其中variance表示方差。
6. 相关系数:用于衡量两个变量之间的线性相关性,公式为
cov(x, y) / (std(x) * std(y)),其中cov(x, y)表示x和y的协方差,std(x)和std(y)分别表示x和y的标准差。
7. 回归分析:用于建立一个变量与多个自变量之间的线性关系模型。
最常见的是简单线性回归模型,公式为 y = a + b * x,
其中y是因变量,x是自变量,a和b是回归系数。
以上仅是一些常见的应用统计学计算公式,实际应用中还有很多其他公式和方法。
具体使用哪些公式要根据具体情况来确定。
统计学计算公式
统计学计算公式第4章)(公式计划实际总2-4%100?=∑∑XX K计划任务数为平均数时)(公式计划实际平3-4%100?=X X K(ⅰ)当计划任务数表现为提高率时)(公式计划提高百分数实际提高百分数4-4% 10011?++=Kⅱ)当计划任务数表现为降低率时时间进度=)(公式全期时间截止到本期的累计时间7-4%100?8)-4(%100公式数计划期间计划规定累计数计划期间实际完成累计计划完成程度相对指标?= )(公式水平计划规定末期应达到的平计划末期实际达到的水计划完成程度相对指标9-4%100?=(%100公总体的全部数值总体中某一部分数值结构相对指标?=)11-4(公式总体中另一部分数值总体中某一部分数值比例相对指标=)12-4(公式单位)的同一指标数值同时期乙地区(部门或的某一指标数值甲地区(部门或单位)比较相对指标=)13-4(公式联系的总量指标数值另一性质不同但有一定某一总量指标数值强度相对数=%100?=计划任务数实际完成数计划完成程度相对指标5)-4( %100-11公式计划降低百分数实际降低百分数-=K %100?=全期的计划任务数本期内累计实际完成数计划执行进度14)-4(%100公式该指标基期数值某指标报告期数值动态相对数?=对于分组数据,众数的求解公式为:df f f f f f M m m m m m m ?-+---≈+-+)()(U 1110上限公式: df f f f f f M m m m m m m ?-+---≈+-+)()(U 1110上限公式:对于分组的数值型数据,中位数按照下述公式求解: 对于分组的数值型数据,四分位数按照下述公式求解: LL L L L d f S n L Q ?-+≈-14 u U U U U d f S n L Q ?-+≈-143(1)简单算数平均数 (2)加权算数平均数nxx ni i∑==1∑∑∑∑====?==ki ki iii kki ii ff x f fx x 1111各变量值与算术平均数的离差之与为零。
统计学常用公式
统计学常用公式在我们的日常生活和各种研究领域中,统计学都发挥着至关重要的作用。
它帮助我们从大量的数据中提取有价值的信息、发现规律,并做出合理的推断和决策。
而要进行准确的统计分析,就离不开一系列常用的公式。
接下来,让我们一起了解一些常见的统计学公式。
首先,我们来谈谈平均数。
平均数是最基本也是最常用的统计量之一。
对于一组数据$x_1, x_2, \cdots, x_n$,算术平均数的公式为:$\bar{x} =\frac{x_1 + x_2 +\cdots + x_n}{n}$。
例如,一组学生的考试成绩分别为 85、90、75、80、95,那么这组成绩的平均数就是:$(85 + 90 + 75 + 80 + 95) \div 5 = 85$ 。
平均数能够反映数据的集中趋势,让我们对一组数据的大致水平有一个直观的了解。
方差也是一个重要的统计量,它衡量的是数据的离散程度。
方差的公式为:$S^2 =\frac{\sum_{i=1}^{n}(x_i \bar{x})^2}{n}$。
还是以上面那组学生成绩为例,先算出平均数 85,然后分别计算每个成绩与平均数的差值的平方,再求和并除以 5,就得到了方差。
方差越大,说明数据的离散程度越大,即数据分布越分散;方差越小,数据越集中。
标准差则是方差的平方根,公式为:$S =\sqrt{\frac{\sum_{i=1}^{n}(x_i \bar{x})^2}{n}}$。
标准差与方差的作用类似,但由于它与原始数据的单位相同,所以在实际应用中更加直观。
接下来是样本比例的公式。
在抽样调查中,如果我们关心某个具有特定特征的个体在总体中所占的比例,设样本中具有该特征的个体数为$x$,样本容量为$n$,则样本比例为:$p =\frac{x}{n}$。
再来说说正态分布的概率密度函数公式。
正态分布是一种非常常见的连续型概率分布,其概率密度函数为:$f(x) =\frac{1}{\sigma\sqrt{2\pi}} e^{\frac{(x \mu)^2}{2\sigma^2}}$,其中$\mu$ 是均值,$\sigma$ 是标准差。
统计学常用公式
公式一1. 众数【MODE 】(1) 未分组数据或单变量值分组数据众数的计算未分组数据或单变量值分组数据的众数就是出现次数最多的变量值。
(2) 组距分组数据众数的计算对于组距分组数据,先找出出现次数最多的变量值所在组,即为众数所在组,再根据下面的公式计算计算众数的近似值。
下限公式: 1012M =L++i ∆⨯∆∆ 式中:0M 表示众数;L 表示众数的下线;1∆表示众数组次数与上一组次数之差;2∆表示众数组次数与下一组次数之差;i 表示众数组的组距。
上限公式:2012M =U-+i ∆⨯∆∆ 式中:U 表示众数组的上限。
2.中位数【MEDIAN 】(1)未分组数据中中位数的计算根据未分组数据计算中位数时,要先对数据进行排序,然后确定中位数的位置。
设一组数据按从小到大排序后为12N X X X ,,…,,中位数e M ,为则有:e N+M =X1()2当N 为奇数e N N +1221M =X +X 2⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭ 当N 为偶数(2)分组数据中位数的计算分组数据中位数的计算时,要先根据公式N / 2 确定中位数的位置,并确定中位数所在的组,然后采用下面的公式计算中位数的近似值:式中:e M 表示中位数;L 表示中位数所在组的下限;m-1S 表示中位数所在组以下各组的累计次数;m f 表示中位数所在组的次数;d 表示中位数所在组的组距。
3.均值的计算【AVERAGE 】(1)未经分组均值的计算未经分组数据均值的计算公式为: 112n ++==nii x x x x x n n=∑…(2)分组数据均值计算分组数据均值的计算公式为: 11221121+++==+ki ik k i k kii x f x f x f x f x f f f f==+∑∑+4.几何平均数【GEOMEAN 】几何平均数是N 个变量值乘积的N 次方根,计算公式为: 式中:G 表示几何平均数;∏表示连乘符号。
统计学主要计算公式56793
统计学主要计算公式(第三章)1111k i i ki i k i k i i i f f f f ====⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩⋅∑∑∑∑∑N i i=1i i 一、算术平x 简单x=Nx 均数加权x=频数权数x=x 1i iHiiiim m x m mx x==∑∑∑∑二、调和平均数⎧=⎪⎪⎨⎪=⎪⎩G G 简单x 三、几何平均数加权x11/2/2m e m m e m f S M L i f f S M U if -+⎧-=+⨯⎪⎪⎨-⎪=-⨯⎪⎩∑∑下限公式四、中位数上限公式 10122012d M L i d d d M U i d d ⎧=+⨯⎪+⎪⎨⎪=-⨯⎪+⎩下限公式五、众数上限公式()()x x x x f fAD AD ⎧-⎪⎪⎨-⎪⎪⎩∑∑∑六、平均差简单=N加权=σσσσ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩七、标准差简单加权简捷公式简单加权100%100%AD ADV x V xσσ⎧⨯⎪⎪⎨⎪⨯⎪⎩平均差系数=八、离散系数标准差系数=统计学主要计算公式(第五章)()()11n n s s t t n αααααασσμμμμμμ--⎧±±⎪⎪⎪⎪±±⎨⎪⎪⎪±±⎪⎩222222一、参数估计(随机抽样)1.总体均值估计-单总体正态总体,方差已知=x z =x z 正态总体,方差未知=x =x 非正态总体,足够大=x z =x z()1211211)))pn n p t S S n ααμμμμμμ+-⎧-±⎪⎪⎪⎪-±⎪⎪⎨⎪=⎪⎪⎪⎪-±⎪⎩2122122221222.总体均值之差估计-双总体正态总体,方差已知-=(x x 正态总体,方差未知但相等-=(x x 非正态总体,,n 足够大-=(x x z12ˆˆˆˆP P P P ααα⎧±±⎪⎪⎪⎨⎪⎪-±⎪⎩22111122221223.总体成数估计单总体:np,nq 大于5=p z =p z 双总体(成数之差),n p ,n q 和n p ,n q 大于5-=(p p )z22212222212112221221//n S S S S S S F F αααασσχχσσ--⎧-<<<<⎪⎪⎪⎨⎪<<⎪⎪⎩22224.总体方差估计n-1单总体:双总体(方差之比)221121.11ˆˆˆˆLLh h hh h h st h h h h h N x S NS N Npx p S p q μ==⎧±==⎪⎨⎪⇒⇒⇒⎩∑∑st st st 二、参数估计(其他抽样方式)分层抽样(等比例)均值估计=x x 成数估计x22112.11()1ˆˆrr ibi i i i i x S x x r r x p x p μ==⎧±==-⎪-⎨⎪⇒⇒⎩∑∑整群抽样均值估计=x x 成数估计2200ˆ220000(1ˆˆ2.ˆˆ3.,,,ˆˆ,,,b n n n n n NpqS pqN R n r n r S N R n r n r pqαασσσσσσσ==∆∆+⇒∆⇒∆⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒22x x2x p 2222三、样本容量1.纯随机抽样Z Z 均值估计=重复)(不重复)成数估计分层抽样(等比例)均值估计成数估计整群抽样均值估计成数估计001002001000010000100(1)20010(1)01.(((((n n H H Z Z H H H Z Z H H H Z Z H H H t t H t H H t t H αααααμμμμμμμμμμμμμμμμμμμμ--⎧≠≥>≥<≤-⎪⎩≠≥>≥四、假设检验均值检验正态总体方差已知:=:拒绝双侧):=:拒绝单侧):=:拒绝单侧)正态总体方差未知(单总体):=:拒绝双侧):=:拒绝单侧0010(1)0(30n H H t t H n s αμμμμσ-⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪<≤-⎪⎪⎩⎪≥⇒⎪⎪⎩):=:拒绝单侧)非正态总体,同正态总体方差已知,若方差未知:01211202012112001211200121120(1)2((((nH H Z Z Hx xH H Z Z HH H Z Z HH H t t Hx xt Hααααμμμμμμμμμμμμμμμμ-⎧≠≥⎪>≥<≤-≠≥2.均值之差检验两个正态总体方差已知:=:拒绝双侧):=:拒绝单侧):=:拒绝单侧)两个正态总体方差未知但相等:=:拒绝双侧)(双总体):12112(1)0012112(1)012((nnH t t HH H t t Hn nααμμμμμμμμ--⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎨⎪⎪⎪⎪>≥⎨⎪⎪⎪<≤-⎪⎪⎩⎪⎪⎪⎪⎪⎩p2212=:拒绝单侧):=:拒绝单侧)S两个非正态总体,大,同两个正态总体方差已知,未知用S,S估计001002001000010002120202120(ˆ(((ˆˆ(H H p Z Z Hp pH H p Z Z HH H p Z Z HH H p Z Z HP PZ H H p Z Z HHααααα⎧≠≥⎪-⎪>≥⎨⎪<≤-⎪⎩≠≥->≥111113.成数检验单总体::p=p:p拒绝双侧)Z=:p=p:p拒绝单侧):p=p:p拒绝单侧)两成数之差检验:p=p:p拒绝双侧)=:p=p:p拒绝单侧):p2120(H p Z Z Hα⎧⎪⎪⎨⎪<≤-⎪⎩1=p:p拒绝单侧)01022010200100111122101222122((((1,1)(1,1)(H H Z Z H H H Z Z H H H Z Z H H H F n n F F n n H S F S ααααασσσσχσσσσσσσσσσσσσ-⎧≠≥⎪⎪>≥⎨⎪<≤⎪⎩≠--≤≤--22220022222002222002222224.方差检验(正态总体)单总体::=:拒绝双侧)(n-1)S =:=:拒绝单侧):=:拒绝单侧)两方差之比检验:=:拒绝=011112001111210(1,1)((1,1)(H H F F n n H H H F F n n H αασσσσσσσσ-⎧⎪⎪>≥--⎨⎪<≤--⎪⎩222222222222双侧):=:拒绝单侧):=:拒绝单侧)统计学主要计算公式(第六章)2()()1::(2)xy x yx yx x y y r n xy x y n xy x yr t rt t n ασρσσσσρρρρ--=--===≠=>-∑∑∑∑01一、相关系数1.公式:=2.显著性检验H H 拒绝原假设2222222222222222()ˆ//ˆˆ()()1()()2.ˆ()()()ˆ()n xy x y b n x x a y n b x ny y y y a y b xy ny r y y y y y ny b r y y b x x x x y y ε⎧-=⎪-⎨⎪=-⎩⎧--+-==-=⎪---⎪⎨⎪=-=--=⎪-⎩∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑二、一元线性回归1.模型:y=a+bx+ 拟合优度检验判定系数121122221.ˆ0:0ˆˆ(2):00:0ˆ()/1(2)(1,2)ˆ()/21b b b b b H t t t n H H R y y r n F F F F n y yn r ααβββσσσββ=≠==>-=≠=≠--==≥----∑∑000三、模型显著性检验回归系数b 检验-H :=拒绝原假设2.F 检验H :或H :R 或拒绝原假设002002222ˆ2.)(2)ˆ3.(2)()ˆ()xy xy E y yt n S y yt n S b x x y y αα==±-=±--=-∑∑xy 四、模型估计1.估计标准误S 平均值的估计(特定值的估计统计学主要计算公式(第七章)21222201122112)(1)()2.(1)(1)e e r c ij ij j i ij i i ij H f f k f H H O E n n E E n r c ααχχχχχχχ==⎧⎪-⎨>-⎪⎩⎧⎪⎪⎪-⨯⎨==⎪⎪⎪>--⎩∑∑∑000020一、检验H :服从某种分布:不服从某种分布(如均匀分布)1.拟合优度检验(=拒绝H H :两变量之间独立:两变量之间不独立H :两变量之间没有差别:两变量之间有差别独立性检验拒绝H01210.50.51.ˆ2.p T T H P H P S Z Z H T T U Z Z αασ⎧⎪≠⎪⎪⎨⎪⎪=≥⎪⎩⎧⎪⎪⎪⎨⎪-⎪=⎪⎩p 0二、成对比较检验:=:符号检验小样本:一种符号明显居多,拒绝H p-p 大样本:Z =拒绝H S H :两样本没有显著差别:两个样本有显著差别n(n+1)威尔科克森带符号检验小样本:T=较小的值>T 接受H 2大样本:检验具体公式给出 111221212022(1)(1)22UUU H n n n n n n n n U U H U Z U U Z Z U Z ααασ-++=+=+>⎧-⎪=⎨⎪⎩0A B 三、检验H :两现象没有差异:两现象有差异小样本:U U 较小的接受大的大样本:公式给出检验小的01121220,20b rH H n n r r r r E r n n Z Z ασ<-<<四、游程检验:样本具有随机性,:样本不具有随机性小样本、游程个数r 接受原假设-()大样本、中>检验=010101221:2:3:61(1)i i i i i i i i i i i i is H x y H x y H x y H x y H x y H x y dr r n n α=->-≥∑s 五、等级相关检验()和相互独立,:和相互不独立()和相互独立,:和相互正相关()和相互独立,:和相互负相关小样本<30例假设(2)r 拒绝原假设大样本30 Z 检验 Z =r统计学主要计算公式(第八章)1t tx y y y -⇒⇒一、自相关系数的计算计算公式同一元相关()2110121:0ntt i nti e e H H d eρρ-==-=≠∑∑二、回归模型的自相关检验:=dL d U 2 4-dU 4-d L正相关 不能确定 无自相关 不能确定 负自相关21321211121n n n n n a a a a a a a n a a a a a a f f f a f f a c b ---⎧⎧⎪⎪⎪⎪⎪⎪⎧++++⎪⎪⎪⎪⎪⎨⎪⎪-⎪⎪⎨⎨⎪+++⎪⎪+++⎪⎪⎪⎪⎪⎪++⎪⎩⎩⎪⎪=⎪⎩∑i 12n-11三、动态分析水平指标时期=n 2绝对数间隔相等 =序时平均数时点222间隔不等=相对数、平均数 0)(1)a a a a n n ⎧⎪⎪⎨-⎪⎪+⎩∑n 0i -水平法=n 平均增长量2(总和法= 1X ⎧==⎪⎨⎪⎩四、动态分析速度指标水平法平均发展速度方程法(P298)平均增长速度=平均发展速度-/(/C T S C I T S I T S C I T S C⨯⨯⨯⎧⎨⎩⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯五、时间序列分析分解模型Y=T S C I(乘法模型)长期趋势T 测定:y=a+bt同月平均/总平均季节变动S 测定:(同月平均-趋势增量b )/总平均循环变动的测定:移动平均计算得到)不规则I 的变动: 01'201201101ˆˆˆˆˆˆˆ(1)(1)(1)t t t t tt t t t y y b b t y yb b t b t y ab b b y ya y a a a a -⎧⎪∆=+⎪⎪∆=++⎨⎪⎪=⎪⎩=++++=+-=-+-t t-1t t-1t-2t-nt+1t t 六、时间序列预测一阶差分大致相同,趋势外推法模型测定二阶差分大致相同, (同回归模型)y环比发展速度大体相同,y 自回归预测y(同回归模型)y y y 移动平均n指数平滑y =ay y y 201(1)(1)n a a a a ++-++-t-1t-2t-n-1y y 统计学主要计算公式(第九章)10001101q p q p p q p q⎧=⎪⎪⎨⎪=⎪⎩∑∑∑∑q p 数量指数K 一、综合指数质量指数K000011111q q P p k q p K q p q p K q p k kw K ⎧⎪⎪=⎪⎪⎪=⎨⎪⎪⎪⎪⎪⎩∑∑∑∑∑∑数量指数(加权算术)二、平均数指数质量指数(加权调和)固定权数=w 00111111111111111010///f f f f f f ff f f f f f ff ff f f f f f f f ---⨯∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑101011000三、总平均数指数可变构成指数x x x x 固定构成指数xx xx 结构影响指数xx xx 三者关系可变构成指数=固定构成指数结构影响指数11101100011100100011011111001101111011011100100(p q q p p q p q q p p qp q p q q p q p p q p q A B C A B C A B C A B C A B C A B C A B C A B CA B C A B CA B C ⨯==⨯+-=⨯⨯-=-∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑pq四、指数因素分析两因素:总额指数=数量指数质量指数K 绝对数关系:-=(-)()三因素:绝对数关系:000110100111110)()()A B C A B C A B C A B C A B C +-+-∑∑∑∑∑∑1001001⨯=⨯五、指数应用计算期居民消费价格指数测定通货膨胀率=-基期居民消费价格指数货币购买力指数=居民消费价格指数职工平均工资指数职工实际工资指数=居民消费价格指数职工平均工资指数货币购买力指数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档 标准文案 统计学主要计算公式(第三章)
1111kiikiikikiiiffff
Nii=1ii一、算术平x简单x=Nx均数加权x=频数权数x=x
1iiHiiiimmxmm
xx
二、调和平均数
11inniinffiixx
GG简单x
三、几何平均数加权x
11/2/2memmemfSMLiffSMUif
下限公式
四、中位数上限公式
10
12
20
12
dMLidddMUidd下限公式
五、众数上限公式 实用文档 标准文案 ()()xxxxffADAD
六、平均差
简单=N
加权=
22
22
()()xxxxffxxnnfffxxf
22N七、标准差简单=加权=简捷公式简单=加权=
100%100%ADADVxVx平均差系数=八、离散系数标准差系数=
统计学主要计算公式(第五章) 实用文档
标准文案 11()1()1()1nnNnNssNnttNNnnN
222222一、参数估计(随机抽样)1.总体均值估计-单总体正态总体,方差已知=xz=xz
nn
正态总体,方差未知=x=xnn
非正态总体,足够大=xz=xznn
12
221211212122211221222121112)11)(1)1)2)pnnpnntSnnnSnSSnnSSnnn212
2
2122
22122
2.总体均值之差估计-双总体正态总体,方差已知-=(xxz
正态总体,方差未知但相等-=(xx(
非正态总体,,n足够大-=(xxz
11221212()ˆˆ1ˆˆˆˆˆˆpqpqNnPPnnNpqpqPPnn221111222212
2
3.总体成数估计单总体:np,nq大于5=pz=pz双总体(成数之差),np,nq和np,nq大于5-=(pp)z
实用文档
标准文案 2221122222121122212211//nnSSSSSSSSFF
222222224.总体方差估计n-1n-1
单总体:
双总体(方差之比)
222
1121.()111ˆˆˆˆLLhhhhhhsthhhhhSNnNxSNSnNNNpxpSpq
stst2st二、参数估计(其他抽样方式)分层抽样(等比例)均值估计=xzx
成数估计x
222
112.()11()11ˆˆrrbibiiiiiSRrxSxxrRrrxpxp
2整群抽样均值估计=xzx
成数估计
22000
ˆ220000(1ˆˆ2.ˆˆ3.,,,ˆˆ,,,bnnnnnNpqSpqNRnrnrSNRnrnrpq22xx2xp22
22
三、样本容量1.纯随机抽样ZZ均值估计=重复)(不重复)
成数估计分层抽样(等比例)均值估计成数估计整群抽样均值估计成数估计
实用文档 标准文案 001002
0010000100
00100(1)20010(1)01.(((((nnHHZZHHHZZHHHZZHHHttHtHHttH
00四、假设检验均值检验正态总体方差已知:=:拒绝双侧)x-Z=:=:拒绝单侧)/n:=:拒绝单侧)
正态总体方差未知(单总体)
:=:拒绝双侧)x-=:=:拒绝单侧s/n0010(1)0(30nHHttHns
):=:拒绝单侧)
非正态总体,同正态总体方差已知,若方差未知:
0121120212012112021012112010121120(1)21201((((1npHHZZHxxHHZZHHHZZHnHHttHxxtHSn2
2
2
2
2.均值之差检验两个正态总体方差已知:=:拒绝双侧)
Z=:=:拒绝单侧):=:拒绝单侧)+
n
两个正态总体方差未知但相等:=:拒绝双侧)(双总体)=:1+n12112(1)0012112(1)022121212((1)1)2nnHttHHHttHSSnnnn
12p2212=:拒绝单侧)
:=:拒绝单侧)
(n(nS=
两个非正态总体,大,同两个正态总体方差已知,未知用S,S估计 实用文档
标准文案 001002000100
0000100
021202120212001(ˆ(((ˆˆ(ˆˆˆˆHHpZZHppHHpZZHpqHHpZZHnHHpZZHPPZHHpZZHpqpqHn1111123.成数检验单总体::p=p:p拒绝双侧)Z=:p=p:p拒绝单侧):p=p:p拒绝单侧)两成数之差检验:p=p:p拒绝双侧)=:p=p:p拒绝单侧)+:pn2120(HpZZH1=p:p拒绝单侧)
01022010200100111122101222122((((1,1)(1,1)(HHZZHHHZZHHHZZHHHFnnFFnnHSFS2222002222200
222200
222222
4.方差检验(正态总体)单总体::=:拒绝双侧)(n-1)S=:=:拒绝单侧)
:=:拒绝单侧)
两方差之比检验:=:拒绝=011112001111210(1,1)((1,1)(HHFFnnHHHFFnnH222222222222双侧)
:=:拒绝单侧):=:拒绝单侧)
统计学主要计算公式(第六章) 实用文档 标准文案 22222222
0022()()111()()()()2::(2)1xyxyxyxxyyrnxyxynxyxynrnxxnyyxxyynnntrttnr01
一、相关系数1.公式:=
2.显著性检验HH拒绝原假设
2222222222
222222
2
()ˆ//ˆˆ()()1()()2.ˆ()()()ˆ()nxyxybnxxaynbxnyyyyaybxynyryyyyynybrryybxxxxyy
二、一元线性回归1.模型:y=a+bx+ 拟合优度检验
判定系数
212221122221.ˆ0:0ˆˆ()(2)0:00:0ˆ()/1(2)(1,2)ˆ()/21xybbbSbbHtxnxttnHHRyyrnFFFFnyynr0
00
三、模型显著性检验回归系数b检验
-H:=
拒绝原假设2.F检验H:或H:R
或拒绝原假设
