扬州大学数学科学学院简介
扬州大学各校区学院专业分布情况表
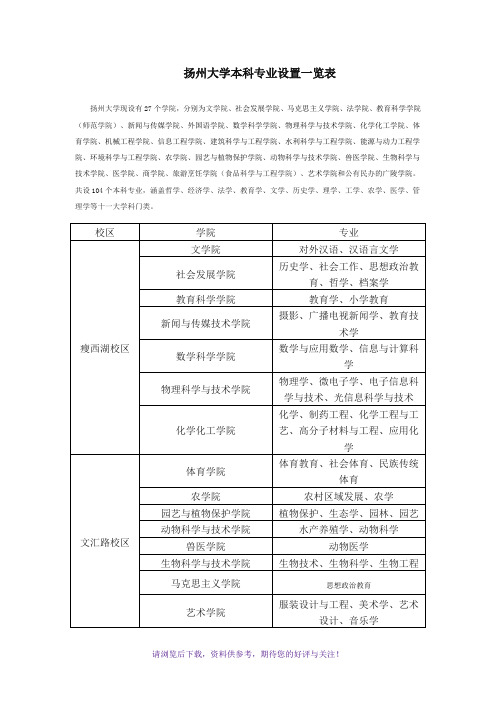
扬州大学本科专业设置一览表
扬州大学现设有27个学院,分别为文学院、社会发展学院、马克思主义学院、法学院、教育科学学院(师范学院)、新闻与传媒学院、外国语学院、数学科学学院、物理科学与技术学院、化学化工学院、体育学院、机械工程学院、信息工程学院、建筑科学与工程学院、水利科学与工程学院、能源与动力工程学院、环境科学与工程学院、农学院、园艺与植物保护学院、动物科学与技术学院、兽医学院、生物科学与技术学院、医学院、商学院、旅游烹饪学院(食品科学与工程学院)、艺术学院和公有民办的广陵学院。
共设104个本科专业,涵盖哲学、经济学、法学、教育学、文学、历史学、理学、工学、农学、医学、管理学等十一大学科门类。
扬州大学数学科学学院《601数学分析》历年考研真题汇编

目 录2016年扬州大学601数学分析考研真题2015年扬州大学601数学分析考研真题2014年扬州大学601数学分析考研真题2011年扬州大学数学分析考研真题2010年扬州大学数学分析考研真题2009年扬州大学数学分析考研真题2008年扬州大学614数学分析考研真题2007年扬州大学数学分析考研真题2006年扬州大学数学分析考研真题2005年扬州大学数学分析考研真题2004年扬州大学数学分析考研真题2003年扬州大学数学分析考研真题2016年扬州大学601数学分析考研真题场州大学2016年硕士研究生招甥贼眦题(j_卷)林倒虬梆铺数学分析融幽嘴OiU邮巍处髀料斯颤麻避场胃楹醐t胃麟勰象辩郡壮觥故;跳勰顺嶙斯-贼入顺勤刎!21幅即刍*我+“■•*"W«}+2!3我尸1山+扃),蛾分4、翱分((扃^砂00$『2炊5、蝴加=湍砰5岫岫,:'谜题供2吩巍5加要求;糊断顶后疏鹏出证毗,融触艮此)’1、数列{姑勉,仇}发能则姒站也撒2、醵/在电雌幼且仅袖/(5)-/(W)nC,3、君导醐倬有限区间雄)上觥财在岫上也觥4、散敏俗岫上可导,贼导醐「在岫上可机三、船顾供80分成3艇吩其余毓10允)1、盼棵义跚血空旦]梆代马60L科耽滁敖学分析漏分15。
分Z、gpO,匕产哗公心,未证:lim姑茁井求该盟值,3+土*3、雌如在翱瓯岫上连婀导,且酬/(沪脯的伽M瓶推:1)/在(M)上-致连续;i2)如心,购沁血虬使得加;3)m,贿在桐务队使(I伽}瑚4)箱潟且/不是制I觥,赡在“(碱,她们洗4、胴如为有躯航M)上如魏.a:<.1)佐阚上融;2)町不何为谶,肘不嘘大催5、段液/在有佩豳(讷上可导,虾岫,Klim—=1,求证;f F/跃赚醐小值.*6、财勤在[。
,2]上站婀导,且典)KI J(O)=/(2)=L求证:7、姬数/在[0』上耳导.求证:1)血,『/(4虹/(1);2)糊有川)=0,M啊/,『/(灿二成),2015年扬州大学601数学分析考研真题4、新在岫上瞰财在岫上零有觇蚀毓扬W 大学2015年硕土册究生踱老试初粼题(三、隐合题(烦分,巍10分)2、糊考察酸侗日在(0』和网上的-致:螂,并翻理岛林僻;项1神;u:_枚掌分折3、收函勤在有限区间岫上连婀导,且冲)=1血北),束证:存敬邸州*-*F使得/饷0.4、斓倾网上聘,。
扬州大学大一高等数学教材

扬州大学大一高等数学教材在扬州大学大一的学习中,高等数学教材是学生必不可少的一部分。
高等数学是一门基础学科,它几乎在所有科学、工程和经济领域都有广泛的应用。
本文将介绍扬州大学大一高等数学教材的内容和特点,以及学生如何有效地学习和应用这门学科。
扬州大学大一高等数学教材的内容丰富多样,主要包括微积分、线性代数和概率论等内容。
其中,微积分是高等数学的核心内容之一。
它主要包括函数的极限、连续性、导数与微分、不定积分和定积分等概念和方法。
通过学习微积分,学生可以了解数学分析的基本思想和方法,培养分析问题和解决问题的能力。
线性代数是高等数学的另一个重要部分。
它主要介绍了向量空间、线性变换、矩阵和行列式等内容。
线性代数是现代数学的基础,在物理学、工程学和计算机科学等领域中有广泛的应用。
通过学习线性代数,学生可以了解向量空间和线性变换的基本性质,掌握矩阵和行列式的运算方法,培养抽象思维和推理能力。
除了微积分和线性代数,高等数学教材还包括概率论的内容。
概率论是研究随机事件的概率和统计规律的数学分支。
它在现代科学和工程技术中有广泛的应用,如金融风险管理、数据分析和信号处理等。
通过学习概率论,学生可以了解概率的基本概念和性质,掌握概率计算的方法和统计规律的应用。
扬州大学大一高等数学教材的特点是理论与实践相结合,重点在于培养学生的数学思维和解决问题的能力。
教材不仅讲解了基本的数学概念和原理,还提供了大量的例题和习题供学生练习和巩固知识。
此外,教材还注重培养学生的数学建模和实际问题解决能力,通过解决实际问题来应用数学的知识和方法。
在学习高等数学的过程中,学生需要掌握一些有效的学习方法和技巧。
首先,学生应该认真听课,做好笔记,并及时复习和总结课堂内容。
其次,学生应多做习题,巩固和应用所学知识。
同时,学生还可以参加讨论组和学习小组,与同学一起合作解决问题,加深理解和记忆。
在学习高等数学的过程中,学生还可以利用互联网和图书馆的资源,查阅相关的参考书和学术资料,扩展知识的广度和深度。
向量背景下动点问题解法例析

→
PQDG = 0ꎬ 3 λ - h = 0ꎬ所以 PQ =
二、多种解法
→ →
→
PQ = ( λ - 1ꎬ4λꎬ 3 λ - h) ꎬ易证DG ⊥平面 ABEFꎬ所以
图 1 图 2
→
3 ) ꎬFQ = ( λꎬ4λꎬ 3 λ) ꎬ所 以 Q ( λ - 1ꎬ4λꎬ 3 λ) ꎬ所 以
→
= 3 ( a + 1) ꎬ故 PQ =
-
a2 + 16 ( a + 1) 2 ꎬ当且仅当 a =
16
3
4 17
ꎬb = 时ꎬ线段 PQ 的长度取得最小值
.
17
17
17
分析 利用动点所在的直线方程ꎬ把原本应设成 Q
( xꎬyꎬz) 中的 yꎬz 用 x 表示出来ꎬ与向量共线法一样达到
参考文献:
向量背景下动点问题解法例析
龙 玲
( 江苏省扬州大学数学科学学院 225000)
摘 要:高考试题中ꎬ向量背景下的动点问题有求最值、存在性、未知参数的值和轨迹等题型ꎬ求出与动点
相关的不定向量、动点坐标是解决此类问题的关键. 对此类问题的解题方法进行整理ꎬ有助于学生快速识别该
类问题并对问题展开不同角度的思考.
收稿日期:2019 - 08 - 05
→
当且仅当 λ =
( λ - 1) 2 + 16λ2 ꎬ
1
3
16 4 3
ꎬ即 P(0ꎬ0ꎬ ) ꎬQ( - ꎬ ꎬ ) 时ꎬ线
17
17
17 17 17
4 17
段 PQ 的长度取得最小值
.
17
作者简介:龙玲ꎬ扬州大学数学科学学院学科教学( 数学) 专业研一在读.
— 46 —
单位矢量变换矩阵的导出及其应用

新
P
坐在标新系坐)标,系其中标的准坐正标交为基(记u,为v,e^wu)、,e^ v在、e^笛w .
空 卡
间 儿
直角坐标系中的坐标为(x,y,z).设新坐标系和笛卡
儿坐标系之间的一一映射(变换)为
T:x = x(u,v,w),y = y(u,v,w),z = z(u,v,w)
(1)
映射 T 的逆映射为
h3 =
x
2 w
+
y
2 w
+
z
2 w
记 ,, ^i ^j k^ 为笛卡儿坐标系中的标准正交基,则从新
坐标系和笛卡儿坐标系的关联式(1),可得到
; 收稿日期: 修回日期:
2018 - 01 - 31
2018 - 05 - 14.
基金项目:江苏高校品牌专业建设工程(PPZY2015B109)、扬州大学教改(YZUJX2016-27C)资助
关键词:正交曲线坐标系;单位矢量;变换矩阵;速度;加速度 ( ) 中图分类号:O 411 文献标识码:A 文章编号:1000 0712 2018 11 0006 03 【 】 DOI 10.16854 / j.cnki.1000 0712.180083
众所周知,除笛卡儿直角坐标系外,在数学、物 理学以及工程技术中,人们还常常根据被研究物体 的几何形状采用其它的坐标系,如球坐标系、柱坐标 系等等. 由于坐标系中单位矢量的空间导数、时间 导数可以用来定量说明质点的运动状态,对它们的 研究一直为科技工作者们所关注[17]. 从文献[2 ]7 不难看到,如果能将不同正交曲线坐标系中单位矢 量之间的变化规律用矩阵进行表示,则在计算单位 矢量的空间导数、时间导数以及质点的速度、加速度 时将非常方便,但遗憾的是上述文献没有从数学上 说明正交曲线坐标系中单位矢量的变换矩阵是如何 导出的,这使得部分学习者认为用变换矩阵求解问 题时计算过程严谨,通用性好,但比较抽象.
瘦西湖校区各专业概述及课程设置介绍-扬州大学图书馆

9
10 11
袁东锦
周正新 朱家生
男
女 男
1950.6.20
1962.3.15 1957.10.23
教授(硕导)
教授(硕导) 副教授(硕导)
大学
本科 本科 博士 学士
扬州师范学院
Ya.Kupala state Universit 扬州师范学院
信息与计算科学 计算数学
数学分析 几何与代数 常微分方程 数学教育
•
信息与计算科学专业
专业课
组合数学 •群与表示论 •伽罗华理论 •数学史 •非线性规划 •数理统计 •多元统计 •代数几何初步 •算法数论 •近代物理讲座 •基础代数 •图论 •微分方程数值解 •数值逼近 •管理与信息系统概论 •符号计算系统 •运筹与优化 •计算机图形学 •计算机网络 •操作系统
软件工程 •线性规划 •决策分析 •近代编码学 •初等数论 •计算机组成原理 •数字信号处理 •离散数学 •Java程序设计 •密码学基础 •理论力学 •流体力学 •实变函数 •泛函分析 •Fourier分析 •小波分析 •金融数学 •随机过程 •控制论
•
专业课程设置情况
数学科学学院
院级公共选修课(数学部分)
数学建模 与数学软件
数学实验
数学分析 选讲
高等代数 选讲
数学科学学院
专业发展及就业方向
毕业生主要在中学从事 数学教学工作。
数学与应用数学
江苏省品牌专业。
全国发行的杂志
《高中数学教与学》月刊 28-151 《初中数学教与学》月刊 28-152
数学科学学院
享受国务院特殊津贴的教师2名
副教授32名
博、硕士生导师22名
师资力量
例谈换元法解题
例谈换元法解题于雯雯(扬州大学数学科学学院ꎬ江苏扬州225009)摘㊀要:随着新课改的进行ꎬ在教学中融入数学的思想方法对学生来说愈加重要.本文从整体的思想㊁新旧元的特点对换元法进行了分类ꎬ旨在提升学生分析问题和解决问题的能力.关键词:换元法ꎻ解题ꎻ整体换元ꎻ新元ꎻ旧元中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)21-0038-03收稿日期:2023-04-25作者简介:于雯雯(1999.11-)ꎬ女ꎬ山东省菏泽人ꎬ硕士研究生在读ꎬ从事数学教学研究.基金项目:扬州大学教学改革研究课题项目 线性代数线上和线下混合式教学研究 (YZUJX2020-D11)㊀㊀罗增儒先生在«数学解题学引论»一书中指出:数学方法的本质在于数学思想的程序化[1].所以我们在解题时需要数学思想和方法的引领ꎬ但同时也需要一些具体的解题程序和技巧.而换元法就是其中一个解题方法ꎬ它在初等数学和高等数学中的应用都十分广泛ꎬ在因式分解㊁解方程㊁证明不等式㊁求函数的值域和定义域㊁解决数列问题等方面中都起着重要的作用.应用换元法解题的基本步骤是引入一个或几个新的元来代替原有的元ꎬ解出新元之后ꎬ再利用新元和旧元的关系恢复原来的元ꎬ以得到原来问题的结果.换元法的基本思想是通过变量代换化繁为简ꎬ化难为易ꎬ化未知为已知ꎬ使问题发生有利的转化ꎬ从而达到解题的目的[2].但不同题目特点不同ꎬ因此解题技巧方法也不同ꎬ故而我们需要基于题目本身的特点寻找解题的方向.通过对以往的文献进行分析发现大部分研究是针对于不同换元法类型与不同题目间的关系ꎬ如付立业的«三角换元法ꎬ巧解高考题»就介绍了某一类换元法在高考题目中的应用ꎻ刘延群的«高中数学换元解题 六法 »介绍了多种换元方法在解题时的应用ꎻ杨小兵的«利用换元法解决一类三根问题»介绍了多种换元法在一类题目中的应用ꎬ这种一对多㊁多对多或多对一的方法固然清晰ꎬ但方法太多并不易于学生选择.因此本文使用分层的思想对换元法进行分类ꎬ旨在使读者对换元法的本质有一个更加清晰的认识ꎬ从而使学生更容易选择合适的换元方法.1从整体的思想来看将题目中的一个或几个式子分别看成一个整体ꎬ用一个或几个新元代换它们ꎬ以此来使复杂的问题清晰化㊁简单化ꎬ从而使问题得到更容易解答的方法叫做整体换元法.一元变量互换性换元㊁分母换元㊁目标换元等都属于整体换元.1.1一元变量互换性换元一元变量互换型换元是在应用整体换元时ꎬ只需引入一个变量ꎬ这个变量所替代的部分往往是一个式子中重复出现的部分ꎬ但有时并不能直接发现题目中重复出现的部分ꎬ此时就需要先对式子进行观察ꎬ寻找各部分之间的关联ꎬ再对问题进行解决ꎬ这也是换元法的难点所在.例1㊀已知f(x)=(1+x+1-x+2)(1-x2+1)ꎬ则f(x)的值域是.分析㊀通过对题目的观察可以发现1+x+1-x在平方后会出现1-x2ꎬ即f(x)=12(1+x+1-x+2)1+x+1-x()2ꎬ变形83后可发现1+x+1-x在式子中重复出现ꎬ故可以考虑令1+x+1-x=tꎬ再进行后续求解.1.2分母换元分母换元法是把分母看成一个整体用新元替换分母的方法.对于一些含有分式的题目ꎬ如果各项分式的分母比较复杂ꎬ直接运算很难找出答案则可以采用分母换元的方法.例2㊀已知xꎬy是正实数ꎬ则4x4x+y+yx+y的最大值是.分析㊀在求解形如cxax+b+mydx+ey的值域时会比较困难ꎬ而对于形如ax+bcx+dx+eymy的式子已经有一个固定的模式来对它求解ꎬ因此可以想办法将题目中的式子转化成第二种式子的形式.本题可设s=4x+yꎬt=x+yꎬ反解出xꎬy再代入原方程进行求解.注㊀本题也可以说是二元变量互换型换元ꎬ所谓二元变量互换型ꎬ是指在应用整体换元时ꎬ需引入两个变量ꎬ并且需要进行变量互换ꎬ即不仅要设s=fxꎬy()ꎬt=gxꎬy()而且要从中求出x=hsꎬt()ꎬy=φsꎬt()然后将其代入求解[3].1.3目标换元将所要求的代数式看成一个新元ꎬ然后与已知的式子建立起联系ꎬ从而得出的新元的值也就是所要求的代数式的值.例3㊀已知关于x的方程x2+2px+2-q2()=0有两个相等的实数根ꎬ则p+q的取值范围是.分析㊀把p+q整体看成一个变元ꎬ反代入原方程ꎬ再利用一元二次方程的性质求解.本题可令p+q=tꎬ则p=t-qꎬ带入原方程得x2+2t-q()x+2-q2()=0ꎬ之后再借助二次方程根与系数的关系进行求解.注㊀先令判别式等于0可得关于pꎬq的二次方程ꎬ这样来看这道题目似乎并没有太大的难度ꎬ但应对开放性拓展性日益增强的题目ꎬ作为教师必须学会引导学生对同一个问题进行多角度的思考ꎬ在 一题多解 的过程中加强学生对数学本质的理解.2从 被换元 的形式来看从 被换元 的形式来看换元法分为:比值换元㊁常数换元㊁根式换元.2.1比值换元如果已知条件为比例式子或者可以看成作比例ꎬ那么用比值代入可使其简化[3].例4㊀已知函数fx()=lnx-ax有两个零点x1ꎬx2x1<x2()求证:x1x2>e2.分析㊀因要求证x1x2>e2且所求式子与a无关ꎬ故而可先将a消去ꎬ即本题可先由lnx1=ax1ꎬlnx2=ax2得出lnx1lnx2=x1x2ꎬ又lnx1-lnx2=lnx1x2ꎬ令x1x2=u即可用u表示出lnx1+lnx2=lnx1x2=u+1u-1lnuꎬ令h(u)=u+1u-1lnu即可借助函数的单调性进行求解.例5㊀已知5x2y2+y4=1xꎬyɪR()ꎬ则x2+y2的最小值是.分析㊀比值换元不但适用于含有比值的题目ꎬ对于含有二元齐次方程的题目同样也可以采用比值换元法.解㊀设xy=kꎬ则5k2y4+y4=1⇒y2=15k2+1x2=k25k2+1ìîíïïïïꎬ故x2+y2=k25k2+1+15k2+1=5k2+1+455k2+1=5k2+15+455k2+1ȡ25k2+15 455k2+1=45.等号成立当且仅当-k=ʃ155.注:比值换元法的基本方法是先找到可以形成比值的式子ꎬ将这个含有双变量的比值形式用一个单变量(如k)来代换ꎬ最后将代换后得到的代数式一步步化简或求值[4].2.2常数换元常数换元法是将常数代入目标关系式进行求解的方法ꎬ通过把目标关系式中的常数换为已知条件中用93字母表示出的常数ꎬ构造关系式进行求解.例6㊀(2021新高考卷Ⅰ)若tanθ=-2ꎬ则sinθ1+sin2θ()sinθ+cosθ=.分析㊀本题也可以直接根据条件求出sinθ和cosθ的值ꎬ再代入求解ꎬ但此时计算起来比较繁琐ꎬ因此可以找出题目中隐藏的常数1ꎬ将所求式子转化为齐次sinθ1+sin2θ()sinθ+cosθ=sinθsin2θ+cos2θ+2sinθcosθ()sinθ+cosθ()sin2θ+cos2θ()=sin3θ+sinθcos2θ+2sin2θcosθsin3θ+sinθcos2θ+sin3θ+sin2θcosθ+cos3θꎬ分子分母同时除以cos3θ即可求解.2.3根式换元当函数中含有根式(根号内通常是多项式或有理分式)ꎬ可以对根式的整体进行换元ꎬ通过两边求幂的方式解出其反函数ꎬ随后根据不同题目的特点进行进一步的求解.例7㊀求函数f(x)=2x+4+1-x的最大值和最小值.分析㊀遇到根式方程常想到平方法ꎬ但有时平方法会使题目变得复杂ꎬ此时就可以采用根式换元的方法.解㊀令u=2x+4ꎬv=1-xuꎬv>0()ꎬ平方可得x=u22-2ꎬx=1-v2ꎻ消去xꎬ得u26+v23=1(uꎬvȡ0)ꎬ之后再令z=u+vꎬ即v=-u+z(z>0)则结合图像即可求得z的取值范围ꎬ即fx()的取值范围.3从新元的特征来看从新元的特征来看换元法可以分为三角换元㊁和差换元.3.1三角换元通过三角换元可以把代数形式转换为三角形式ꎬ达到减元的目的ꎬ同时可以利用三角函数的特殊性质进行求解.一般情况下若题目中的xɪ-1ꎬ1[]或出现形如ax2ʃby2=c的式子时可以采用三角换元.例8㊀设实数xꎬy满足x24-y2=1ꎬ则3x2-2xy的最小值是.分析㊀本题中出现了ax2-by2ꎬ且ax2-by2=1ꎬ故而可以借助公式sec2θ-tan2θ=1进行换元ꎬ从而将本题转化成不等式中常见的题目ꎬ以起到的简化的作用.本题可令x=2secθꎬy=tanθꎬ再代入求解.3.2和差换元若xꎬyɪRꎬ则可设x=a+bꎬy=a-bꎬ这种变换称为和差换元法.一般在解决两数之和为定值的问题或题目中出现含有Ax2ʃAy2的问题时有应用ꎬ注意这里x2与y2的系数相同.例9㊀设实数xꎬy满足x24-y2=1ꎬ则3x2-2xy的最小值是.分析㊀在这里x2和y2的系数不同ꎬ但若将x24当做一个整体即x2æèçöø÷2ꎬ就可发现x2æèçöø÷2与y2的系数相同ꎬ故在设元时可设x2=m+nꎬy=m-nꎬ如此便可达到最大限度的消元.以上介绍了几种常见的换元法ꎬ但值得注意的是在解一道题目时可以不拘泥于一种方法ꎬ我们可以从不同的方向进行观察分析ꎬ就会发现题目具有的不同特征ꎬ进而可以从不同角度出发进行解题ꎬ因此在解题时不一定就必须用某种方法求解某种类型的题目.所谓的方法只是提供一个思考分析甚至是猜想解决问题的方向而已ꎬ要想真正提高解题能力还是需要勤加思考ꎬ多加练习.参考文献:[1]罗增儒.数学解题学引论[M].西安:陕西师范大学出版社ꎬ2008.[2]李明振.数学方法与解题研究[M].上海:上海科技教育出版社ꎬ2022:235-255.[3]孟伟业.整体换元法在解题中的应用[J].数学教学研究ꎬ2016ꎬ35(05):59-63.[4]刘延群.高中数学换元解题 六法 [J].中学数学ꎬ2022(09):81-82ꎬ95.[责任编辑:李㊀璟]04。
数学系专业全国大学最新排名名单
数学系专业全国大学最新排名名单数学系专业全国大学最新排名名单为大家整理出了全国数学类专业大学排行榜,想要了解相关内容的考生和家长可以重点参考。
序号学校名称评估结果1北京大学A+2复旦大学A+3山东大学A+4清华大学A5北京师范大学A6南开大学A7上海交通大学A8中国科学技术大学A9西安交通大学A10吉林大学A-11哈尔滨工业大学A-12同济大学A-13华东师范大学A-14南京大学A-15浙江大学A-16武汉大学A-17中山大学A-18四川大学A-19首都师范大学B+20大连理工大学B+21东北师范大学B+22上海大学B+23苏州大学B+24南京师范大学B+25浙江师范大学B+26厦门大学B+27华中科技大学B+28华中师范大学B+29湘潭大学B+30湖南大学B+31中南大学B+32湖南师范大学B+33华南理工大学B+34华南师范大学B+35重庆大学B+36陕西师范大学B+37兰州大学B+38国防科技大学B+39中国人民大学B40北京工业大学B41河北师范大学B42上海师范大学B43中国矿业大学B44安徽大学B45福州大学B46福建师范大学B47郑州大学B48西南大学B49云南大学B50西北大学B51西北工业大学B52西北师范大学B53新疆大学B54广州大学B55北京交通大学B-56北京科技大学B-57山西大学B-58内蒙古大学B-59华东理工大学B-60南京航空航天大学B-61南京理工大学B-62南京信息工程大学B-63江苏师范大学B-64合肥工业大学B-65江西师范大学B-66山东师范大学B-67曲阜师范大学B-68湖北大学B-69四川师范大学B-70重庆师范大学B-71贵州大学B-72扬州大学B-73宁波大学B-74北方工业大学C+75东北大学C+76辽宁师范大学C+77东华大学C+78江苏大学C+79浙江理工大学C+80杭州师范大学C+81温州大学C+82南昌大学C+83中国海洋大学C+84河南大学C+85河南师范大学C+86暨南大学C+87汕头大学C+88广西大学C+89贵州师范大学C+90宁夏大学C+91中国石油大学C+92中国农业大学C93华北电力大学C94华北理工大学C95中北大学C96吉林师范大学C97哈尔滨理工大学C98哈尔滨师范大学C99上海理工大学C100浙江工业大学C国内顶尖的数学系专业大学简介1、北京大学:北京大学是中国最顶尖的综合性大学之一,其数学学科一直保持着卓越的研究和教学水平。
师范生“学研行”一体化线上教学技能训练模式探索
实裁探索即***************.cn师范生“学研行”一体化线上教学技能训练模式探索陈算荣(扬州大学数学科学学院,江苏扬州225000)摘要:提高师范生线上学习教学技能的积极性、参与性和实效性,需要在教学技能训练的课程设计、实施和评价三个方面进行改革探索。
在课程设计层面,以素养发展为核心目标,构建'‘学研行”一体化的学习模式,创设形式多样和注重体验的学习活动;在教学实施层面,周密策划与落实课前、课中和课后各项学习活动,及时跟踪与反馈学习结果;在评价层面,重视过程中的多维量化评价和多层面互动评价策略。
关键词:生长理念;师范生;教学技能;线上教学;“学研行”一体中图分类号:G65文献标识码:A文章编号:2095-5995(2022)05-0045-06师范生教学技能训练是一门实践性很强的课程,它不仅需要师范生掌握各项教学技能原理,而且需要他们在实践体悟中领会如何将教学技能整合于教学实践应用中,因而微格教学训练是必不可少的课程教学环节。
然而,微格教学训练指导活动通常采用的是线下面对面的方式,难以釆用线上方式进行,那么,在新冠疫情依然肆虐无法组织线下教学的环境下,如何有效利用学校网络综合平台和QQ、钉钉等软件有效开展师范生的线上教学训练将极具挑战性。
在课程设计和实践探索中需要思考和解决的问题有:课程目标应如何确立?何种课程教学模式有利于师范生的技能理论学习和实践训练能在线上实现有机整合?怎样的学习活动有助于师范生获得丰富的学习体验?何种实施和管理策略有助于线上教和学的落实,以及课程目标的达成?怎样的评价体系能更有助于师范生在线上开展技能学习?围绕这一系列问题,在生长理念指引下,以学为中心、以能力为本,实践研究者从课程设计、实施、评价等维度进行整体性思考、构建和实践探索,旨在最大限度地提高师范生在线上实施教学技能训练的成效。
一、基于生长理念的课程设计信息技术的飞速发展和5G时代的到来已宣告教育从互联网诞生之前的传统封闭式学校教育环境中走出,走向一个半开放甚至全开放的社会教育环境中⑷。
数学高考运算能力考查研究
数学高考运算能力考查研究文/庄雅欣摘要:新课程的改革对高考数学产生了一定的影响,本文在鲍建生教授综合难度模型的基础上对近三年高考试卷试题难度进行总体分析,进而对难度变化较大的运算因素从试题数量和试题分值分布进行了剖析,在此基础上为高考试题命制及一线教师教学提出建议。
1 问题提出随着教育的改革,高考也发生了相应的变化,越来越重视学生核心素养的考查。
高中数学核心素养主要包括数学抽象、逻辑推理、数学建模、数学运算、几何直观、数据分析。
核心素养是高中数学教与学过程中主要的发展对象,所以作为高中生的必备技能的运算能力成为数学高考的重要考查内容。
笔者借助综合难度模型对近三年高考理科数学卷进行科学的统计分析,让读者更清楚高考数学试题对数学运算能力的考查。
这一研究能够帮助命题人员明确试题对学生数学运算能力的具体考查,正确把握命题的方向。
同时帮助一线的教育工作者更好地培养学生的运算能力,提高学生的运算思想,以便促进学生的全面发展。
2 研究工具鲍建生在比较研究中英两国初中数学课程综合难度时提出了综合难度模型,他将Noraha提出刻画试题难度的“扩展性问题”的百分比、“实际背景”的题目的百分比、“运算”的题目的百分比、“多步推理”的题目的百分比等四个因素扩展探究、推理、背景、运算和知识含量五个因素建立了综合难度模型。
该模型对五个因素进行了层次等级的划分,对每个层次等级进行赋值,用加权平均的方式对每个因素进行计算得出结果。
计算公式为:其中,分别表示五个难度因素的取值;其中表示第个难度因素的第个水平的题目数量,表示表示第个难度因素的第个水平的权重,他们的和就是题目总的数量。
其中鲍健生教授将运算难度划分为无运算、数值运算、简单符号运算和复杂符号运算四个水平。
高考试卷运算难度的研究能够帮助一线教师明确高考的命题动向,进而更好的培养学生的运算能力。
笔者将利用鲍建生教授在2014年修改后的综合难度模型对近三年高考试卷进行剖析。
3 试题分析根据鲍建生综合难度模型的公式计算出近三年全国Ⅰ卷在综合难度各因素上的加权平均,进而得出近三年全国Ⅰ卷试题综合难度五边形如图1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扬州大学数学科学学院简介
扬州大学数学科学学院前身是扬州师范学院数学系。
始建于1952年,至今已有近60年的办学历史。
现设有数学与应用数学、信息与计算科学两个本科专业,其中数学与应用数学专业(师范类)为江苏省高校品牌专业和国家特色专业建设点,信息与计算科学专业为校品牌特色专业建设点,数学类(含数学与应用数学、信息与计算科学)为江苏省“十二五”重点专业;拥有数学一级学科博士点、统计学一级学科硕士点,基础数学、应用数学、计算数学、概率论与数理统计、运筹与控制、课程与教学论(数学)6个硕士点;基础数学在“九五”、“十五”、“十一五”期间连续被评为省级重点学科,数学被评为江苏省“十二五”一级学科重点学科。
该院师资力量雄厚,师资队伍职称、学历、年龄、学缘结构合理,现有专任教师70人,其中,教授14人、副教授34人,具有博士学位教师23人,博、硕士生导师20人,2人享受国务院特殊津贴,1人被评为教育部“新世纪优秀人才”,1人入选教育部“优秀青年教师资助计划”。
学院从严治教,教学质量稳步提高。
半个世纪以来,已为社会各界培养了大批优秀人才,在省内外有较大影响。
近
年来,该院先后承担了包括国家重点基础研究发展规划项目(973计划)、国家自然科学基金重点项目在内的一大批科研项目。
在微分几何、动力系统、泛函分析、表示论与量子群、编码和密码理论等方向的科学研究处于国内先进水平,在国际上也有一定影响。
该院图书资料室有中外文藏书2万余册,订有中外文专业期刊180余种,为师生的教学科研提供了良好的条件。
该院举办的《高中数学教与学》和《初中数学教与学》两本全国发行的杂志,为促进中学数学教学质量的提高做出了积极贡献,在国内同类杂志中具有较在影响。
半个多世纪来,该院现已经发展成为江苏省,特别是苏中、苏北地区培养从本科、硕士到博士各层次教学人才的重要基地。
该院培养的学生基础扎实,学风纯正,每年均有数十人被保送或考取国内外著名大学深造,在“全国大学生数学建模竞赛”和美国大学生数学建模竞赛等学科竞赛中,屡获佳绩。
学院秉承“坚苦自立”的校训,坚持“学科引领、内涵提升、人才兴院、科技强院、质量立院、科学发展”的理念,坚持以提高质量为主线,以改革创新为动力,以全面提升人
才培养、科学研究、社会服务水平为目标,努力把学院建设成为具有基础数学学科优势和数学应用特色的开放式、教学与研究并重型学院。
