2014高三数学一轮复习:2.5二次函数与幂函数
二次函数与幂函数专题复习
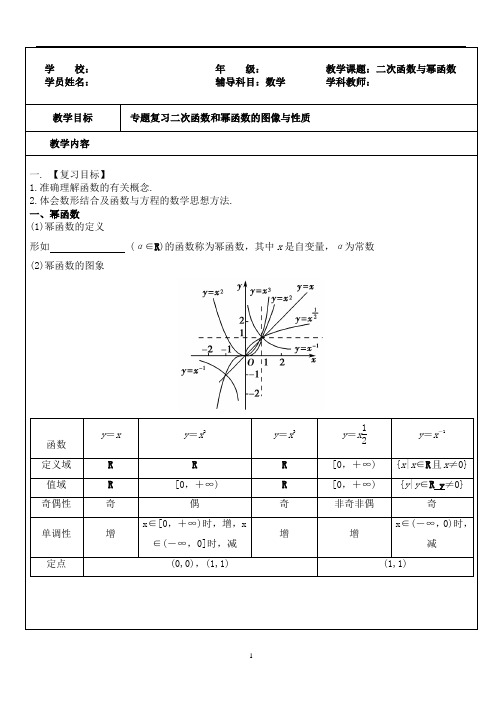
学校:年级:教学课题:二次函数与幂函数学员姓名:辅导科目:数学学科教师:教学目标专题复习二次函数和幂函数的图像与性质教学内容一. 【复习目标】1.准确理解函数的有关概念.2.体会数形结合及函数与方程的数学思想方法.一、幂函数(1)幂函数的定义形如 (α∈R)的函数称为幂函数,其中x是自变量,α为常数(2)幂函数的图象函数y=x y=x2y=x3y=x12y=x-1定义域R R R[0,+∞){x|x∈R且x≠0} 值域R [0,+∞)R[0,+∞){y|y∈R y≠0} 奇偶性奇偶奇非奇非偶奇单调性增x∈[0,+∞)时,增,x∈(-∞,0]时,减增增x∈(-∞,0)时,减定点(0,0),(1,1) (1,1)例1.下列函数中是幂函数的是( )A .y =2x 2B .y =1x 2C .y =x 2+xD .y =-1x例2. (2011·陕西高考)函数y =13x的图象是( )例3.幂函数y =x m 2-2m -3(m ∈Z )的图象关于y 轴对称,且当x >0时,函数是减函数,则m 的值为( ). A .-1<m <3B .0C .1D .2练习:已知点(2,2)在幂函数y =f (x )的图象上,点⎝⎛⎭⎪⎫-2,12在幂函数y =g (x )的图象上,若f (x )=g (x ),则x =________.已知点M ⎝ ⎛⎭⎪⎫33,3在幂函数f (x )的图象上,则f (x )的表达式为( )A .f (x )=x 2B .f (x )=x -2C .f (x )=x 12xD .f (x )=12x-设α∈⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-1,1,12,3,则使函数y =x α的定义域为R 且为奇函数的所有α值为 ( )A .1,3B .-1,1C .-1,3D .-1,1,3对于函数y =x 2,y =x 12有下列说法:①两个函数都是幂函数;②两个函数在第一象限内都单调递增;③它们的图象关于直线y =x 对称;④两个函数都是偶函数;⑤两个函数都经过点(0,0)、(1,1);⑥两个函数的图象都是抛物线型.其中正确的有________.二、二次函数1、二次函数的三种形式【1】【2】【3】2.二次函数的图像和性质二次函数())0(2≠++=a c bx ax x f 的图像是一条抛物线,对称轴的方程为 顶点坐标是( ) 。
高考数学总复习第五节 二次函数与幂函数

返回
考点三 二次函数的图象与性质
[锁定考向]
题点多变型考点——多角探明
高考对二次函数图象与性质进行单独考查的频率较
低.常与一元二次方程、一元二次不等式等知识交汇命题是
高考的热点,多以选择题、填空题的形式出现,考查二次函
数的图象与性质的应用.
常见的命题角度有:
(1)二次函数的单调性问题;
(2)二次函数的最值问题;
∴f(2)=2 -12
=
2 2.
答案:C
返回
)
返回
2.函数 f(x)=(m2-m-1)xm 是幂函数,且在 x∈(0,+∞) 上为增函数,则实数 m 的值为________. 解析:∵f(x)=(m2-m-1)xm 是幂函数, ∴m2-m-1=1,解得 m=-1 或 m=2. 又∵f(x)在(0,+∞)上为增函数, ∴m=2. 答案:2
y=x3
1
y=x 2
y=x-1
_奇__ 非 __奇__非___偶_ _奇__
单调性
(-∞,0)
_增__ 减,(0, _增___ +∞)增
(-∞,0)
_增__ 和(0,+∞)
减
公共点
__(_1_,_1_)__
返回
2.二次函数解析式的三种形式 (1)一般式:f(x)= ax2+bx+c(a≠0) ; (2)顶点式:f(x)= a(x-m)2+n(a≠0) ; (3)零点式:f(x)= a(x-x1)(x-x2)(a≠0) .
(2)若幂函数 y=xα(α∈R )是偶函数,则 α 必为偶数. 当 α 是分数时,一般将其先化为根式,再判断.
(3)若幂函数 y=xα 在(0,+∞)上单调递增,则 α>0, 若在(0,+∞)上单调递减,则 α<0.
高考数学一轮复习第2章函数的概念及基本初等函数Ⅰ第4节二次函数与幂函数课件理新人教A版

第四节 二次函数与幂函数
栏
课 前 ·基 础 巩 固 1
目
导
课 堂 ·考 点 突 破 2
航
3 课 时 ·跟 踪 检 测
[最新考纲]
[考情分析]
[核心素养]
1.了解幂函数的概念.
2.结合函数 y=x,y=x2,y
幂函数一般不单独命题,常与指数、对数
=x3,y=1x,y=x12的图象,函数交汇命题;二次函数的图象与应用仍是 1.逻辑推理
(2)二次函数的图象和性质
解析式
f(x)=ax2+bx+c(a>0)
图象
定义域 值域
(-∞,+∞) 4ac4-a b2,+∞
f(x)=ax2+bx+c(a<0)
(-∞,+∞) -∞,4ac4-a b2
解析式
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
单调性
在-∞,-2ba上单调递减; 在 6 ___-__∞__,__-__2b_a__上单调递增; 在 5 ___-__2b_a_,__+__∞___上单调递 在-2ba,+∞上单调递减 增
考点二 二次函数的图象与性质 |题组突破|
4.如图是二次函数 y=ax2+bx+c 图象的一部分,图象过点 A(-3,0),对称轴为 x =-1.给出下面四个结论:①b2>4ac;②2a-b=1;③a-b+c=0;④5a<b.其中正确的 是( )
A.②④ B.①④ C.②③ D.①③
解析:选 B 因为图象与 x 轴交于两点,所以 b2-4ac>0,即 b2>4ac,①正确;对称 轴为 x=-1,即-2ba=-1,2a-b=0,②错误;结合图象知,当 x=-1 时,y>0,即 a -b+c>0,③错误;由对称轴为 x=-1 知,b=2a.又函数图象开口向下,所以 a<0,所 以 5a<2a,即 5a<b,④正确.故选 B.
高三数学知识点总结9:二次函数和幂函数

(十一)二次函数一.二次函数解析式(1)一般式:).0()(2≠++=a c bx ax x f(2)顶点式:若二次函数的顶点坐标为),,(k h 则其解析式).0()()(2≠+-=a k h x a x f(3)交点式:若二次函数的图象与x 轴的交点为),0,(),0,(21x x 则),)(()(21x x x x a x f --= .0≠a二.二次函数的对称轴(1)对于二次函数)(x f y =的定义域内有21,x x 满足),()(21x f x f =则二次函数的对称轴为.221x x x += (2)对于一般函数)(x f y =对定义域内所有,x 都有)()(x a f x a f -=+成立,那么函数 )(x f y =图像的对称轴方程为:a x =.三.二次函数)0(2≠++=a c bx ax y 在],[n m 上的最值(1)0>a ① 最小值讨论三种情况 1.)(2min m f y m a b =≤-,;2.)2(2min a b f y n a b m -=<-<,;3.)(2min n f y n ab =≥-,. ② 最大值讨论两种情况 1.)(,22max n f y n m a b =+≤-;2.)(22max m f y n m a b =+>-,. (2)0<a ① 最大值讨论三种情况 1.)(2max m f y m a b =≤-,;2.)2(2max a b f y n a b m -=<-<,;3.)(,2max n f y n ab =≥-. ② 最小值讨论两种情况 1.)(,22min n f y n m a b =+≤-;2.)(22min m f y n m a b =+>-,. 四.三个二次的关系一元二次方程的根=一元二次函数的零点=一元二次不等式解集的端点.五.一元二次方程)0(02≠=++a c bx ax 的实根分布(1)数的角度:① 两实根异号等价于0<a c ;② 有两个正根等价于.0,0,0>>-≥∆a c a b ;③ 有两个负根等价于.0,0,0><-≥∆ac a b (2)形的角度:画出满足要求的图像,用“内有无,内无有”(开口内有端点则不需要考虑对称轴和,∆开口内无端点则需要考虑对称轴和.∆)。
【高考复习方案 】2014年高考数学(文,江苏教育版)一轮复习课件:第12讲 函数模型及其应用

返回目录
第12讲
函数模型及其应用
点 面 讲 考 向
[归纳总结] (1)指数函数模型常与增长率相结合进行 考查,在实际问题中有人口增长、银行利率、细胞分裂等 增长问题可以利用指数函数模型来表示. (2)应用指数函数模型时,先设定模型,将已知的相关 数据代入验证,确定参数,从而确定函数模型. (3)对于函数 y=a(1+x)n 通常利用指数运算与对数函 数的性质进行求解.
返回目录
第12讲
双 向 固 基 础
函数模型及其应用
4. 1992 年底世界人口达 54.8 亿, 若人口的年平均增长率 为 x% , 2014 年底世界人口数为 y(亿), 那么 y 与 x 的函数关系 式是____________________.
[答案]
y=54.8(1+x%)22
[解析] 因为 2014-1992=22,所以 y=54.8(1+x%)22.
返回目录
第12讲
函数模型及其应用
点 面 讲 考 向
可见,细胞总数 y 与时间 x(小时)之间的函数关系为 y= 3x 100×(2) ,x∈N*. 3x 3x 10 由 100×(2) >10 ,得(2) >108. 3 8 两边取以 10 为底的对数,得 xlg >8,解得 x> . 2 lg 3-lg 2 8 8 因为 = ≈45.45, lg 3-lg 2 0.477-0.301 所以 x>45.45. 故经过 46 小时,细胞总数超过 1010 个.
ax=300, x=120, 解得 (a+1)(x-12)=300+78. a=2.5.
返回目录
第12讲
双 向 固 基 础
函数模型及其应用
3.某车站有快、慢两种车,始发站距终点站 7.2 km,慢 车到终点站需 16 min,快车比慢车晚发车 3 min,且行驶 10 min 后到达终点站,则在慢车出发________min 后两车相遇, 相遇时距终点站________ km. [答案] 8 3.6
高考数学第一轮复习幂函数图像与性质

幂函数的性质与图像 幂函数及其性质 1、幂函数的定义一般地,形如y x α=(x ∈R )的函数称为幂孙函数,其中x是自变量,α是常数.如11234,,y x y x y x-===等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数. 2、函数的图像(1)y x = (2)12y x= (3)2y x= (4)1y x-= (5)3yx=用描点法在同一坐标系内画出以上五个函数图像,通过观察图像,可以看出幂函数的性质。
3.幂函数性质(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);(2)x >0时,幂函数的图象都通过原点,并且在[0,+∞]上,是增函数(3)α<0时,幂函数的图象在区间(0,+∞)上是减函数.(4)在第一象限内,图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象,在第一象限内,直线1x =的右侧,图象由下至上,指数 . y 轴和直线1x =之间,图象由上至下,指数α .:4. 规律总结1.在研究幂函数的性质时,通常将分式指数幂化为根式形式,负整指数幂化为分式形式再去进行讨论;2.对于幂函数y =αx ,我们首先应该分析函数的定义域、值域和奇偶性,由此确定图象的位置,即所在象限,其次确定曲线的类型,即α<0,0<α<1和α>1三种情况下曲线的基本形状,还要注意α=0,±1三个曲线的形状;对于幂函数在第一象限的图象的大致情况可以用口诀来记忆:“正抛负双,大竖小横”,即α>0(α≠1)时图象是抛物线型;α<0时图象是双曲线型;α>1时图象是竖直抛物线型;0<α<1时图象是横卧抛物线型. 在[0,+∞]上,y x =、2y x=、3y x=、12y x=是增函数, 在(0,+∞)上,1y x -=是减函数。
例1.已知函数()()2531m f x m m x --=--,当 m 为何值时,()f x :(1)是幂函数;(2)是幂函数,且是()0,+∞上的增函数;(3)是正比例函数;(4)是反比例函数;(5)是二次函数;简解:(1)2m =或1m =-(2)1m =-(3)45m =-(4)25m =-(5)1m =-变式训练: 已知函数()()2223m m f x m m x--=+,当 m 为何值时,()f x 在第一象限内它的图像是上升曲线。
二次函数与幂函数典型例题含答案完整版
二次函数与幂函数典型例题含答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】二次函数与幂函数1.求二次函数的解析式.2.求二次函数的值域与最值.3.利用幂函数的图象和性质分析解决有关问题.【复习指导】本节复习时,应从“数”与“形”两个角度来把握二次函数和幂函数的图象和性质,重点解决二次函数在闭区间上的最值问题,此类问题经常与其它知识结合命题,应注重分类讨论思想与数形结合思想的综合应用.基础梳理1.二次函数的基本知识(1)函数f(x)=ax2+bx+c(a≠0)叫做二次函数,它的定义域是R.(2)二次函数f(x)=ax2+bx+c(a≠0)的图象是一条抛物线,对称轴方程为x=-,顶点坐标是.①当a>0时,抛物线开口向上,函数在上递减,在上递增,当x=-时,f(x)=;min②当a<0时,抛物线开口向下,函数在上递增,在上递减,当x=-时,f(x)=.max③二次函数f(x)=ax2+bx+c(a≠0)当Δ=b2-4ac>0时,图象与x轴有两个交点M1(x1,0)、M2(x2,0),|M1M2|=|x1-x2|=.(3)二次函数的解析式的三种形式:①一般式:f(x)=ax2+bx+c(a≠0);②顶点式:f(x)=a(x-m)2+h(a≠0);③两根式:f(x)=a(x-x1)(x-x2)(a≠0).2.幂函数(1)幂函数的定义形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α为常数.(2)幂函数的图象(3)幂函数的性质第一象限一定有图像且过点(1,1);第四象限一定无图像;当幂函数是偶函数时图像分布第一二象限,奇函数时图像分布第一三象限;第一象限图像的变化趋势;当a<0时,递减,a>0时,递增,其中a>1时,递增速度越来越快,0<a<1时,递增速度越来越慢。
二次函数、一元二次方程和一元二次不等式是一个有机的整体,要深刻理解它们之间的相互关系,能用函数与方程、分类讨论、数形结合思想来研究与“三个二次”有关的问题,高考对“三个二次”知道的考查往往渗透在其他知识之中,并且大都出现在解答题中.两种方法二次函数y=f(x)对称轴的判断方法:(1)对于二次函数y=f(x)对定义域内x1,x2,都有f(x1)=f(x2),那么函数y=f(x)图象的对称轴方程为x=;(2)对于二次函数y=f(x)对定义域内所有x,都有f(a+x)=f(a-x)成立,那么函数y=f(x)图象的对称轴方程为x=a(a为常数).两种问题与二次函数有关的不等式恒成立问题:(1)ax2+bx+c>0,a≠0恒成立的充要条件是(2)ax2+bx+c<0,a≠0恒成立的充要条件是双基自测1.下列函数中是幂函数的是( ).A.y=2x2B.y=C.y=x2+x D.y=-2.(2011·九江模拟)已知函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的范围是( ).A.f(1)≥25B.f(1)=25C.f(1)≤25D.f(1)>253.(2011·福建)若关于x的方程x2+mx+1=0,有两个不相等的实数根,则实数m的取值范围是( ).A.(-1,1)B.(-2,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-1)∪(1,+∞)4.(2011·陕西)函数的图象是( ).5.二次函数y=f(x)满足f(3+x)=f(3-x)(x∈R)且f(x)=0有两个实根x1,x,则x1+x2=________.2考向一求二次函数的解析式【例1】已知函数f(x)=x2+mx+n的图象过点(1,3),且f(-1+x)=f(-1-x)对任意实数都成立,函数y=g(x)与y=f(x)的图象关于原点对称.求f(x)与g(x)的解析式.【训练1】已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8.试确定此二次函数的解析式.考向二幂函数的图象和性质【例2】幂函数y=xm2-2m-3(m∈Z)的图象关于y轴对称,且当x>0时,函数是减函数,则m的值为( ).A.-1<m<3 B.0C.1 D.2【训练2】已知点(,2)在幂函数y=f(x)的图象上,点在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________.考向三二次函数的图象与性质【例3】已知函数f(x)=x2-2ax+1,求f(x)在区间[0,2]上的最值.【训练3】已知f(x)=1-(x-a)(x-b)(a<b),m,n是f(x)的零点,且m<n,则a,b,m,n从小到大的顺序是________.双基自测1.(人教A版教材习题改编)下列函数中是幂函数的是( ).A.y=2x2B.y=C.y=x2+x D.y=-解析A,C,D均不符合幂函数的定义.答案B2.(2011·九江模拟)已知函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则f(1)的范围是( ).A.f(1)≥25B.f(1)=25C.f(1)≤25D.f(1)>25解析对称轴x=≤-2,∴m≤-16,∴f(1)=9-m≥25.答案A3.(2011·福建)若关于x的方程x2+mx+1=0,有两个不相等的实数根,则实数m的取值范围是( ).A.(-1,1)B.(-2,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-1)∪(1,+∞)解析依题意判别式Δ=m2-4>0,解得m>2或m<-2.答案C4.(2011·陕西)函数的图象是( ).解析由幂函数的性质知:①图象过(1,1)点,可排除A,D;②当指数0<α<1时为增速较缓的增函数,故可排除C.答案B5.二次函数y=f(x)满足f(3+x)=f(3-x)(x∈R)且f(x)=0有两个实根x1,x,则x1+x2=________.2解析由f(3+x)=f(3-x),知函数y=f(x)的图象关于直线x=3对称,应有=3x1+x2=6.答案 6考向一求二次函数的解析式【例1】已知函数f(x)=x2+mx+n的图象过点(1,3),且f(-1+x)=f(-1-x)对任意实数都成立,函数y=g(x)与y=f(x)的图象关于原点对称.求f(x)与g(x)的解析式.[审题视点]采用待定系数法求f(x),再由f(x)与g(x)的图象关于原点对称,求g(x).解依题意得解得:∴f(x)=x2+2x.设函数y=f(x)图象上的任意一点A(x0,y0),该点关于原点的对称点为B(x,y),则x=-x,y0=-y.∵点A(x0,y0)在函数y=f(x)的图象上,∴y0=x+2x0,∴-y=x2-2x,∴y=-x2+2x,即g(x)=-x2+2x.二次函数解析式的确定,应视具体问题,灵活地选用其形式,再根据题设条件列方程组,即运用待定系数法来求解.在具体问题中,常常会与图象的平移、对称,函数的周期性、奇偶性等知识有机地结合在一起.【训练1】已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8.试确定此二次函数的解析式.解法一利用二次函数的一般式.设f(x)=ax2+bx+c(a≠0).由题意得解之得∴所求二次函数的解析式为y=-4x2+4x+7.法二利用二次函数的顶点式.设f(x)=a(x-m)2+n(a≠0),∵f(2)=f(-1).∴此二次函数的对称轴为x==.∴m=,又根据题意,函数有最大值8,即n=8.∴y=f(x)=a2+8,∵f(2)=-1,∴a2+8=-1,解之得a=-4.∴f(x)=-42+8=-4x2+4x+7.考向二幂函数的图象和性质【例2】幂函数y=xm2-2m-3(m∈Z)的图象关于y轴对称,且当x>0时,函数是减函数,则m的值为( ).A.-1<m<3 B.0C.1 D.2[审题视点]由幂函数的性质可得到幂指数m2-2m-3<0,再结合m是整数,及幂函数是偶函数可得m的值.解析由m2-2m-3<0,得-1<m<3,又m∈Z,∴m=0,1,2.∵m2-2m-3为偶数,经验证m=1符合题意.答案C根据幂函数的单调性先确定指数的取值范围,当α>0时,幂函数在(0,+∞)上为增函数,当α<0时,幂函数在(0,+∞)上为减函数,然后验证函数的奇偶性.【训练2】已知点(,2)在幂函数y=f(x)的图象上,点在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________.解析由题意,设y=f(x)=xα,,则2=()α,得α=2,设y=g(x)=xβ,则=(-)β,得β=-2,由f(x)=g(x),即x2=x-2,解得x=±1.答案±1考向三二次函数的图象与性质【例3】已知函数f(x)=x2-2ax+1,求f(x)在区间[0,2]上的最值.[审题视点]先确定对称轴,再将对称轴分四种情况讨论.解函数f(x)=x2-2ax+1=(x-a)2+1-a2的对称轴是直线x=a,(1)若a<0,f(x)在区间[0,2]上单调递增,当x=0时,f(x)min=f(0)=1;当x=2时,f(x)max=f(2)=5-4a;(2)若0≤a<1,则当x=a时,f(x)min=f(a)=1-a2;当x=2时,f(x)max=f(2)=5-4a;(3)若1≤a<2,则当x=a时,f(x)min=f(a)=1-a2;当x=0时,f(x)max=f(0)=1;(4)若a≥2,则f(x)在区间[0,2]上单调递减,当x=0时,f(x)max=f(0)=1;当x=2时,f(x)min=f(2)=5-4a.解二次函数求最值问题,首先采用配方法,将二次函数化为y=a(x-m)2+n(a≠0)的形式,得顶点(m,n)或对称轴方程x=m,分三个类型:①顶点固定,区间固定;②顶点含参数,区间固定;③顶点固定,区间变动.【训练3】已知f(x)=1-(x-a)(x-b)(a<b),m,n是f(x)的零点,且m<n,则a,b,m,n从小到大的顺序是________.解析由于f(x)=1-(x-a)(x-b)(a<b)的图象是开口向下的抛物线,因为f(a)=f(b)=1>0,f(m)=f(n)=0,可得a∈(m,n),b∈(m,n),所以m<a <b<n.答案m<a<b<n考向四有关二次函数的综合问题【例4】设函数f(x)=ax2-2x+2,对于满足1<x<4的一切x值都有f(x)>0,求实数a的取值范围.[审题视点]通过讨论开口方向和对称轴位置求解.解当a>0时,f(x)=a+2-.∴或或∴或或∴a≥1或<a<1或,即a>;当a<0时,解得a∈;当a=0时,f(x)=-2x+2,f(1)=0,f(4)=-6,∴不合题意.综上可得,实数a的取值范围是a>.含有参数的二次函数与不等式的结合问题是高考的热点,通过围绕二次函数的开口方向、对称轴,不等式的恒成立等基本问题展开,重点考查学生分类讨论的思想、函数与方程的思想,以及分析、解决问题的能力.【训练4】已知二次函数f(x)=ax2+bx+1(a>0),F(x)=若f(-1)=0,且对任意实数x均有f(x)≥0成立.(1)求F(x)的表达式;(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.解(1)∵f(-1)=0,∴a-b+1=0,∴b=a+1,∴f(x)=ax2+(a+1)x+1.∵f(x)≥0恒成立,∴∴∴a=1,从而b=2,∴f(x)=x2+2x+1,∴F(x)=(2)g(x)=x2+2x+1-kx=x2+(2-k)x+1.∵g(x)在[-2,2]上是单调函数,∴≤-2,或≥2,解得k≤-2,或k≥6.所以k的取值范围为k≤-2,或k≥6.规范解答3——如何求解二次函数在某个闭区间上的最值【问题研究】二次函数在闭区间上的最值问题,一定要根据对称轴与区间的相对位置关系确定最值,当函数解析式中含有参数时,要根据参数的取值情况进行分类讨论,避免漏解.【解决方案】对于二次函数f(x)=ax2+bx+c(a≠0)而言,首先确定对称轴,然后与所给区间的位置关系分三类进行讨论.【示例】(本题满分12分)(2011·济南模拟)已知f(x)=-4x2+4ax-4a-a2在区间[0,1]内有最大值-5,求a的值及函数表达式f(x).求二次函数f(x)的对称轴,分对称轴在区间的左侧、中间、右侧讨论.[解答示范]∵f(x)=-42-4a,∴抛物线顶点坐标为.(1分)①当≥1,即a≥2时,f(x)取最大值-4-a2.令-4-a2=-5,得a2=1,a=±1<2(舍去);(4分)②当0<<1,即0<a<2时,x=时,f(x)取最大值为-4a.令-4a=-5,得a=∈(0,2);(7分)③当≤0,即a≤0时,f(x)在[0,1]内递减,∴x=0时,f(x)取最大值为-4a-a2,令-4a-a2=-5,得a2+4a-5=0,解得a=-5或a=1,其中-5∈(-∞,0].(10分)综上所述,a=或a=-5时,f(x)在[0,1]内有最大值-5.∴f(x)=-4x2+5x-或f(x)=-4x2-20x-5.(12分)求解本题易出现的问题是直接利用二次函数的性质——最值在对称轴处取得,忽视对称轴与闭区间的位置关系,不进行分类讨论.【试一试】设函数y=x2-2x,x∈[-2,a],求函数的最小值g(a).[尝试解答] ∵函数y=x2-2x=(x-1)2-1,∴对称轴为直线x=1,而x=1不一定在区间[-2,a]内,应进行讨论.当-2<a<1时,函数在[-2,a]上单调递减,则当x=a时,y min=a2-2a;当a≥1时,函数在[-2,1]上单调递减,在[1,a]上单调递增,则当x=1时,ymin =-1.综上,g(a)=。
高考北师大版数学总复习课件:2.5幂函数
[解析] (1)若 f(x)为正比例函数,则
2 m + m- 1= 1, 2 m + 2m≠ 0
- 1 2 3 2 2 3
-4
1 3
4.下列命题: ①幂函数的图像都经过点(1,1)和点 (0,0); ②幂函数的图像不可能在第四象限; ③ n= 0 时,函数 y= xn 的图像是一条直线; ④幂函数 y= xn,当 n>0 时是增函数; ⑤幂函数 y= xn, 当 n<0 时, 在第一象限内函数值随 x 值的 增大而减小
(3)α <0 时幂函数的图像在区间 (0, +∞ )上是 减函数.在第 一象限内,当 x 从右边趋向于原点时,图像在 y 轴右方无限地 逼近
y轴 ,当 x 趋于+∞时,图像在 x 轴上方无限地逼近
x轴.
(4)当 α 为奇数时,幂函数为 奇函数 ;当 α 为偶数时, 幂函数为 偶函数.
4. 5 个具体幂函数的性质
[答案] B
[解析 ] 依据幂函数的定义, y= 2x2 的系数不是 1, y= x2 + x 是两个函数的和的形式, y= 1 也不同于 y= x0(x≠0),因此 1 这三个都不是幂函数,只有 y= 2符合. x
2. (2012· 陕西宝鸡期末)函数 y= x 是 ( A.奇函数,并且在(0,+∞ )上为增函数 B.偶函数,并且在 (-∞, 0)上为减函数 C.奇函数,并且在(0,+∞ )上为减函数 D.偶函数,并且在(-∞,0)上为增函数
4 5
)
[答案] B
5 4 [解析] y= x = x ,x∈ R,且满足 f(- x)= f(x),故为偶
4 5
4 函数. 又 >0, 所以在第一象限内的图像是单调递增, 因此在 (- 5 ∞, 0)上为减函数.
幂函数与指对数运算课件高三数学一轮复习
幂函数及其应用
1. 概念理解:
幂函数及其应用
2. 函数图象:
幂函数及其应用
2. 函数图象:
幂函数及其应用
3. 二次函数相关: ① 函数解析式
题给条件要看清,方程颇有选择性。
点乘双根法 二三次方程韦达定理
能判断“图象” 能熟练“配方” 能用好“零点”
幂函数及其应用
3. 二次函数相关: ① 函数解析式
朗博同构 1 一元同构:
朗博同构 1 一元同构:
朗博同构 1 一元同构:
朗博同构 2 二元同构:
朗博同构 2 二元同构:
朗博同构 3 同构与切线不等式:
朗博同构 3 同构与切线不等式:
课后小结
1. 幂函数及其图象. 2. 幂的运算性质. 3. 对数的概念及其运算性质. 4.三个二次之间的关系 5.大小比较 6.同构的应用技巧
题给条件要看清,方程颇有选择性。
幂函数及其应用
3. 二次函数相关: ① 函数解析式
题给条件要看清,方程颇有选择性。
幂函数及其应用
3. 二次函数相关:
② 函数值域
定义端点与中点,关注一线点间穿。
幂函数及其应用
3. 二次函数相关:
② 函数值域
定义端点与中点,关注一线点间穿。
幂函数及其应用
3. 二次函数相关:
③ 二次不等式
能否分解要确定,先看开口后比根。
指数与对数运算
1. 对数运算:
指数与对数运算
2.大小比较: 选好中间量,用好单调性
指数与对数运算
2.大小比较: 分参构造新函数,然后再手单调性。
朗博同构
指对共存须同构,看清形式再变形。
朗博同构
构造以后用图象,六个图象必记清。
高中数学讲义 第4节 幂函数与二次函数
第四节幂函数与二次函数课标解读考向预测1.通过具体实例,结合函数y =x,y =x 2,y =x 3,y =x 12,y =x -1的图象,理解它们的变化规律,了解幂函数.2.掌握二次函数的图象与性质(单调性、对称性、顶点、最值等).以幂函数的图象与性质的应用为主,常与指数函数、对数函数交汇命题;以二次函数的图象与性质的应用为主,常与方程、不等式等知识交汇命题,着重考查函数与方程、转化与化归及数形结合思想,题型一般为选择题、填空题,中档难度.预计2025年高考对于幂函数的考查最多出一道选择题,以幂函数的图象和性质应用为主.对于二次函数的考查一般与其他知识综合,题型一般为选择题、填空题,中档难度.必备知识——强基础1.幂函数(1)幂函数的定义一般地,函数01y =x α叫做幂函数,其中x 是自变量,α是常数.(2)在同一坐标系中的五个幂函数的图象(3)幂函数的性质①幂函数在(0,+∞)上都有定义;②当α>0时,幂函数的图象都过点02(0,0)和03(1,1),且在(0,+∞)上单调递增;③当α<0时,幂函数的图象都过点04(1,1),且在(0,+∞)上单调递减;④当α为奇数时,y =x α为05奇函数;当α为偶数时,y =x α为06偶函数.2.二次函数解析式的三种形式一般式:f (x )=ax 2+bx +c (a ≠0);顶点式:f (x )=a (x -h )2+k (a ≠0);两根式:f (x )=a (x -x 1)(x -x 2)(a ≠0).3.二次函数的图象和性质1.概念辨析(正确的打“√”,错误的打“×”)(1)函数y =-x12是幂函数.()(2)当α<0时,幂函数y =x α在定义域内单调递减.()(3)若幂函数y =x α是偶函数,则α为偶数.()(4)若二次函数y =ax 2+bx +c 的两个零点确定,则二次函数的解析式确定.()答案(1)×(2)×(3)×(4)×2.小题热身(1)已知幂函数f (x )f (4)的值是()A .64B .42C.24D.14答案D(2)(北师大版必修第一册1.4.2例4改编)若一次函数y =ax +b 的图象经过第二、三、四象限,则二次函数y =ax 2+bx 的图象可能是()答案C解析因为一次函数y =ax +b 的图象经过第二、三、四象限,所以a <0,b <0,所以二次函数y =ax 2+bx 的图象开口向下,对称轴为直线x =-b2a<0,且过原点.故选C.(3)已知α-2,-1,-12,12,1,2f (x )=x α为奇函数,且在(0,+∞)上单调递增,则α=________.答案1解析由y =x α为奇函数,知α取-1,1,又y =x α在(0,+∞)上单调递增,∴α>0,∴α=1.(4)(人教B 必修第二册4.4例1改编)已知a =0.40.3,b =0.30.3,c =0.30.4,则a ,b ,c 的大小关系是________(用“<”连接).答案c <b <a解析由指数函数、幂函数的单调性可知,0.30.4<0.30.3,0.40.3>0.30.3,即c <b <a .考点探究——提素养考点一幂函数的图象与性质例1(1)若幂函数y =x -1,y =x m 与y =x n 在第一象限内的图象如图所示,则m 与n 的取值情况为()A .-1<m <0<n <1B .-1<n <0<m <12C .-1<m <0<n <12D .-1<n <0<m <1答案D解析幂函数y =x α,当α>0时,y =x α在(0,+∞)上单调递增,且0<α<1时,图象上凸,∴0<m <1.当α<0时,y =x α在(0,+∞)上单调递减.不妨令x =2,由图象得2-1<2n ,则-1<n <0.综上,-1<n <0<m <1.故选D.(2)(2024·江苏连云港海滨中学高三学情检测)若幂函数f (x )=(m 2-2m -2)x -m 2+m +3在(0,+∞)上是减函数,则实数m =________.解析因为幂函数f(x)=(m2-2m-2)x-m2+m+3在(0,+∞)上是减函数,2-2m-2=1,m2+m+3<0.由m2-2m-2=1,得m=-1或m=3.当m=-1时,-m2+m+3=-1-1+3=1>0,所以m=-1舍去;当m=3时,-m2+m+3=-9+3+3=-3<0,符合题意.综上,m=3.【通性通法】(1)幂函数的形式是y=xα(α∈R),其中只有一个参数α,因此只需一个条件即可确定其解析式.(2)对于幂函数的图象,需记住在第一象限内三条线分第一象限为六个区域,即x=1,y=1,y=x所分区域.根据α<0,0<α<1,α=1,α>1的取值确定位置后,其余象限部分由奇偶性决定.(3)在比较幂值的大小时,可结合幂值的特点,选择适当的函数,借助其单调性进行比较.(4)在区间(0,1)上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大图低”),在区间(1,+∞)上,幂函数中指数越大,函数图象越远离x轴(简记为“指大图高”).【巩固迁移】1.(2023·皖淮联考)已知a=2ln2,b=3-0.5,c=2-0.4,则()A.a>b>c B.a>c>bC.c>a>b D.c>b>a答案B解析因为2ln2=ln4>ln e=1,3-0.5<3-0.4<2-0.4<1,所以a>c>b.故选B. 2.(2023·江苏南京高三二模)幂函数f(x)=x a(a∈R)满足:对任意x∈R有f(-x)=f(x),且f(-1)<f(2)<2.写出符合上述条件的一个函数:f(x)=________.答案x 23(答案不唯一)解析取f(x)=x 23,则定义域为R,且f(-x)=(-x)23=x23=f(x),f(-1)=1,f(2)=223=34,满足f(-1)<f(2)<2.故f(x)=x 23满足题意.考点二二次函数的解析式例2已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,则f(x)=________.答案-4x2+4x+7解析解法一(利用“一般式”):设f(x)=ax2+bx+c(a≠0).c=-1,1,8,解得=4,=7.∴所求二次函数的解析式为f (x )=-4x 2+4x +7.解法二(利用“顶点式”):设f (x )=a (x -m )2+n (a ≠0).∵f (2)=f (-1),∴函数图象的对称轴为直线x =2+(-1)2=12,∴m =12.又函数有最大值8,∴n =8,∴y =f (x )=+8.∵f (2)=-1,∴+8=-1,解得a =-4,∴f (x )=-+8=-4x 2+4x +7.解法三(利用“两根式”):由已知得f (x )+1=0的两根为x 1=2,x 2=-1,故可设f (x )+1=a (x -2)(x +1)(a ≠0),即f (x )=ax 2-ax -2a -1.又函数有最大值8,即4a (-2a -1)-(-a )24a=8,解得a =-4.∴所求函数的解析式为f (x )=-4x 2+4x +7.【通性通法】根据已知条件确定二次函数的解析式,一般用待定系数法,选择规律如下:【巩固迁移】3.已知二次函数f (x )=x 2-bx +c 满足f (0)=3,∀x ∈R ,都有f (1+x )=f (1-x )成立,则f (x )=________.答案x 2-2x +3解析由f (0)=3,得c =3,又f (1+x )=f (1-x ),所以函数f (x )的图象关于直线x =1对称,所以b2=1,即b =2,所以f (x )=x 2-2x +3.考点三二次函数的图象与性质(多考向探究)考向1二次函数的图象例3(多选)二次函数y =ax 2+bx +c (a ≠0)的部分图象如图,图象过点A (-3,0),对称轴为直线x =-1,则下列四个结论中正确的是()A.b2>4ac B.2a-b=1C.a-b+c=0D.5a<b答案AD解析因为图象与x轴交于两点,所以b2-4ac>0,即b2>4ac,A正确;对称轴为直线x=-1,即-b2a=-1,2a-b=0,B错误;结合图象,当x=-1时,y>0,即a-b+c>0,C错误;因为2a-b=0,即b=2a,根据抛物线开口向下,知a<0,所以5a<2a,即5a<b,D正确.故选AD.【通性通法】1.识别二次函数图象应学会“三看”2.解决二次函数图象问题的基本方法(1)排除法,抓住函数的特殊性质或特殊点.(2)讨论函数图象,依据图象特征,得到参数间的关系.【巩固迁移】4.设abc>0,二次函数f(x)=ax2+bx+c的图象可能是()答案D解析因为abc >0,二次函数f (x )=ax 2+bx +c ,对于A ,a <0,b <0,c <0,不符合题意;对于B ,a <0,b >0,c >0,不符合题意;对于C ,a >0,b >0,c <0,不符合题意.故选D.考向2二次函数的单调性例4若函数f (x )=x 2+a |x |+2,x ∈R 在区间[3,+∞)和[-2,-1]上均单调递增,则实数a 的取值范围是()A.-113,-3B .[-6,-4]C .[-3,-22]D .[-4,-3]答案B解析∵f (x )为偶函数,∴f (x )在[1,2]上单调递减,在[3,+∞)上单调递增,当x >0时,f (x )=x 2+ax +2,图象的对称轴为直线x =-a 2,∴2≤-a2≤3,解得-6≤a ≤-4.故选B.【通性通法】解决二次函数单调性问题的基本方法(1)二次函数的单调性在其图象对称轴的两侧不同,因此研究二次函数的单调性时要依据其图象的对称轴进行分类讨论.(2)若已知f (x )=ax 2+bx +c (a >0)在区间A 上单调递减(单调递增),则A ∞,⊆-b2a,+即区间A 一定在函数图象的对称轴的左侧(右侧).【巩固迁移】5.若函数f (x )=ax 2+(a -3)x +1在区间[-1,+∞)上单调递减,则实数a 的取值范围为()A .[-3,0)B .(-∞,-3]C .[-2,0]D .[-3,0]答案D解析当a =0时,f (x )=-3x +1在[-1,+∞)上单调递减,满足题意;当a ≠0时,f (x )图象的对称轴为直线x =3-a2a.由f (x )在[-1,+∞)上单调递减,-1,解得-3≤a <0.综上,实数a 的取值范围为[-3,0].故选D.考向3二次函数的最值例5已知函数f (x )=ax 2+2ax +1在区间[-1,2]上有最大值4,则实数a 的值为________.答案38或-3解析f (x )=a (x +1)2+1-a .当a =0时,函数f (x )在区间[-1,2]上的值为常数1,不符合题意,舍去;当a >0时,函数f (x )在区间[-1,2]上单调递增,最大值为f (2)=8a +1=4,解得a =38;当a <0时,函数f (x )在区间[-1,2]上单调递减,最大值为f (-1)=1-a =4,解得a=-3.综上可知,实数a 的值为38或-3.【通性通法】求二次函数在闭区间上最值的类型及策略【巩固迁移】6.设关于x 的方程x 2-2mx +2-m =0(m ∈R )的两个实数根分别是α,β,则α2+β2+5的最小值为________.答案7解析+β=2m ,=2-m ,且Δ=4m 2-4(2-m )≥0,解得m ≤-2或m ≥1,所以α2+β2+5=(α+β)2-2αβ+5=4m 2+2m +1,令f (m )=4m 2+2m +1,而f (m )图象的对称轴为直线m =-14,且m ≤-2或m ≥1,所以f (m )min =f (1)=7.课时作业一、单项选择题1.如图,①②③④对应四个幂函数的图象,其中①对应的幂函数可能是()A .y =x 3B .y =x 2C .y =xD .y =x 58答案D解析根据题中函数图象可得①对应的幂函数y =x α在[0,+∞)上单调递增,且增长速度越来越慢,故α∈(0,1),故D 符合要求.故选D.2.已知幂函数y =f (x )的图象经过点(3,3),则f (x )()A .是偶函数,且在(0,+∞)上是增函数B .是偶函数,且在(0,+∞)上是减函数C .是奇函数,且在(0,+∞)上是减函数D .是非奇非偶函数,且在(0,+∞)上是增函数答案D解析设幂函数的解析式为y =x α,将点(3,3)的坐标代入解析式得3α=3,解得α=12,所以y =x 12,函数的定义域为[0,+∞),是非奇非偶函数,且在(0,+∞)上是增函数.故选D.3.已知函数f (x )=ax 2+bx +c ,其中a >0,c <0,a +b +c =0,则()A .∀x ∈(0,1),都有f (x )>0B .∀x ∈(0,1),都有f (x )<0C .∃x ∈(0,1),使得f (x )=0D .∃x ∈(0,1),使得f (x )>0答案B解析由a >0,c <0,a +b +c =0可知抛物线开口向上,f (0)=c <0,f (1)=a +b +c =0,所以∀x ∈(0,1),都有f (x )<0.故选B.4.(2024·甘肃武威十八中一诊)若函数f (x )=ax 2+2x -1在区间(-∞,6)上单调递增,则实数a 的取值范围是()A.-16,0-16,-16,+∞-16,答案A解析当a =0时,函数f (x )=2x -1在R 上单调递增,即a =0符合题意;当a ≠0时,由二<0,-1a≥6,解得-16≤a <0.综上,实数a 的取值范围是-16,0.故选A.5.(2024·江苏南京高三摸底)已知a=243,b=425,c=2513,d=623,则()A.b<a<d<c B.b<c<a<d C.c<d<b<a D.b<a<c<d 答案D解析由题意得a=243=1613,b=425=1615,c=2513,d=623=3613,因为幂函数y=x13在R上单调递增,所以a<c<d.又因为指数函数y=16x在R上单调递增,所以b<a.故选D. 6.设函数f(x)=x2+x+a(a>0).已知f(m)<0,则()A.f(m+1)≥0B.f(m+1)≤0C.f(m+1)>0D.f(m+1)<0答案C解析因为f(x)图象的对称轴为直线x=-12,f(0)=a>0,所以f(x)的大致图象如图所示,由f(m)<0,得-1<m<0.所以m+1>0.所以f(m+1)>f(0)>0.故选C.7.已知f(x)=ax2+bx+c(a>0),g(x)=f(f(x)),若g(x)的值域为[2,+∞),f(x)的值域为[k,+∞),则实数k的最大值为()A.0B.1C.2D.4答案C解析设t=f(x),由题意可得g(x)=f(t)=at2+bt+c(t≥k),函数y=at2+bt+c,t≥k的图象为y=f(x)的图象的部分,即g(x)的值域为f(x)的值域的子集,即[2,+∞)⊆[k,+∞),可得k≤2,即实数k的最大值为2.故选C.8.已知在(-∞,1]上单调递减的函数f(x)=x2-2tx+1,且对任意的x1,x2∈[0,t+1],都有|f(x1)-f(x2)|≤2,则实数t的取值范围是()A.[-2,2]B.[1,2]C.[2,3]D.[1,2]答案B解析由于f(x)=x2-2tx+1图象的对称轴为直线x=t,又y=f(x)在(-∞,1]上是减函数,所以t≥1,则在区间[0,t+1]上,f(x)max=f(0)=1,f(x)min=f(t)=t2-2t2+1=-t2+1,要使对任意的x1,x2∈[0,t+1],都有|f(x1)-f(x2)|≤2,只需1-(-t2+1)≤2,解得-2≤t≤ 2.又t ≥1,所以1≤t ≤2.故选B.二、多项选择题9.二次函数f (x )=ax 2+bx +c 的图象如图所示,则下列说法正确的是()A .2a +b =0B .4a +2b +c <0C .9a +3b +c <0D .abc <0答案ACD 解析由二次函数图象开口向下知a <0,图象的对称轴为直线x =-b 2a =1,即2a +b =0,故b >0,又因为f (0)=c >0,所以f (2)=f (0)=4a +2b +c >0,f (3)=f (-1)=9a +3b +c <0,abc <0.故选ACD.10.已知幂函数f (x )=(m 2-m -1)x m 2+m -3,对任意x 1,x 2∈(0,+∞),且x 1≠x 2,都满足f (x 1)-f (x 2)x 1-x 2>0,若a ,b ∈R 且f (a )+f (b )<0,则下列结论可能成立的是()A .a +b >0且ab <0B .a +b <0且ab <0C .a +b <0且ab >0D .以上都可能答案BC 解析因为f (x )=(m 2-m -1)x m 2+m -3为幂函数,所以m 2-m -1=1,解得m =2或m =-1.依题意f (x )在(0,+∞)上单调递增,所以m =2,此时f (x )=x 3,因为f (-x )=(-x )3=-x 3=-f (x ),所以f (x )=x 3为奇函数.因为a ,b ∈R 且f (a )+f (b )<0,所以f (a )<f (-b ),又y =f (x )为增函数,所以a <-b ,所以a +b <0.故选BC.三、填空题11.已知函数f (x )为幂函数,且f (4)=12,则当f (a )=4f (a +3)时,实数a =________.答案15解析设f (x )=x α,则4α=12,所以α=-12,因此f (x )=x -12,从而a -12=4(a +3)-12,解得a =15.12.已知二次函数f (x )的图象经过点(4,3),且图象被x 轴截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),则f (x )的解析式为________.答案f (x )=x 2-4x +3解析∵f (2-x )=f (2+x )对任意x ∈R 恒成立,∴f (x )图象的对称轴为直线x =2,又f (x )的图象被x轴截得的线段长为2,∴f(x)=0的两根为1和3,设f(x)的解析式为f(x)=a(x-1)(x-3)(a≠0),∵f(x)的图象过点(4,3),∴3a=3,∴a=1,∴所求函数的解析式为f(x)=(x-1)(x -3),即f(x)=x2-4x+3.13.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x3,若不等式f(-4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是________.答案(-∞,-2)解析由题意知,f(x)在R上是增函数,结合f(-4t)>f(2m+mt2)对任意实数t恒成立,知-4t>2m+mt2对任意实数t恒成立,∴mt2+4t+2m<0对任意实数t恒成立,<0,=16-8m2<0,∴m∈(-∞,-2).14.(2024·浙江台州模拟)已知函数f(x)=(x2-2x-3)(x2+ax+b)是偶函数,则f(x)的值域是________.答案[-16,+∞)解析因为f(x)=(x2-2x-3)(x2+ax+b)=(x-3)(x+1)(x2+ax+b)是偶函数,所以-3)=f(3)=0,=f(-1)=0,代入整理,-3a+b=0,+a+b=0,=2,=-3.所以f(x)=(x2-2x-3)·(x2+2x-3)=(x2-3)2-4x2=x4-10x2+9=(x2-5)2-16≥-16,所以f(x)的值域为[-16,+∞).四、解答题15.(2024·福建百校高三联考)已知幂函数f(x)=(m2+m-1)x m+1在(0,+∞)上是减函数.(1)求f(x)的解析式;(2)若(5-a)1m>(2a-1)1m,求实数a的取值范围.解(1)由幂函数的定义,知m2+m-1=1,即m2+m-2=0,解得m=-2或m=1.因为f(x)在(0,+∞)上是减函数,所以m+1<0,即m<-1,则m=-2.故f(x)=x-1=1x.(2)由(1)可得m=-2,设g(x)=x-12,则g(x)的定义域为(0,+∞),且g(x)在定义域上为减函数,因为(5-a)-12>(2a-1)-12,-a>0,a-1>0,-a<2a-1,解得2<a<5.故实数a的取值范围为(2,5).16.若函数y=x2-4x-4的定义域为[0,a),值域为[-8,-4],则实数a的取值范围为________.答案(2,4]解析函数y=x2-4x-4的图象如图所示,因为函数在[0,a)上的值域为[-8,-4],结合图象可得2<a≤4,故实数a的取值范围为(2,4].17.已知幂函数f(x)=(m-1)2x m2-4m+2在(0,+∞)上单调递增,函数g(x)=2x-3t,对任意x1∈[1,5),总存在x2∈[1,5),使得f(x1)=g(x2),则t的取值范围是________.答案13,73解析因为f(x)=(m-1)2x m2-4m+2为幂函数,则(m-1)2=1,解得m=0或m=2.当m=2时,f(x)=x-2在(0,+∞)上单调递减,舍去,故f(x)=x2.当x∈[1,5)时,f(x)∈[1,25),故g(5)=25-3t≥25,所以t≤73;g(1)=2-3t≤1,所以t≥13.综上所述,t的取值范围是13,73. 18.(2024·福建福州高三模拟)已知二次函数f(x)=ax2-x+2a-1.(1)若f(x)在区间[1,2]上单调递减,求a的取值范围;(2)若a>0,设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.解(1)当a>0时,f(x)=ax2-x+2a-1的图象开口向上,对称轴方程为x=12a,所以f(x)在区间[1,2]2,,解得0<a≤14;当a<0时,f(x)=ax2-x+2a-1的图象开口向下,对称轴方程为x=12a<0,所以f (x )在区间[1,2]上单调递减需满足a <0.综上,a 的取值范围是(-∞,0),14.(2)①当0<12a ≤1,即a ≥12时,f (x )在区间[1,2]上单调递增,此时g (a )=f (1)=3a -2;②当1<12a <2,即14<a <12时,f (x )在区间1,12a 上单调递减,在区间12a,2上单调递增,此时g (a )=2a -14a-1;③当12a ≥2,即0<a ≤14时,f (x )在区间[1,2]上单调递减,此时g (a )=f (2)=6a -3.综上所述,g (a )a-3,a ,14,a -14a-1,aa -2,a ∈12,+。
