思考题3-杨式模量
弹性模量思考题

弹性模量思考题1.拉伸法测金属丝的杨氏弹性模量实验中,在砝码盘中加载时为什么采用正反向取平均值的办法?鉴于金属受外力时存在着弹性滞后效应,即钢丝受到拉伸力作用时,并不能立即伸长到应有的长度Li同样,当钢丝受到的拉伸力一旦减小时,也不能马上缩短到应有的长度Li,仅缩短到.因此,为了消除弹性滞后效应引起的系统误差,测量中应包括增加拉伸力以及对应地减少拉伸力这一对称测量过程.因为只要将相应的增,减测量值取平均,就可以消除滞后量的影响.2. 常见金属材料弹性模量表常用金属材料弹性模量表序号材料名称弹性模量\E\Gpa切变模量\G\Gpa泊松比\μ1 镍铬钢、合金钢206 79.38 0.25~0.32 碳钢196~206 79 0.24~0.283 铸钢172~2102 - 0.34 球墨铸铁140~154 73~76 -5 灰铸铁、白口铸铁113~157 44 0.23~0.276 冷拔纯铜127 48 -7 轧制磷青铜113 41 0.32~0.358 轧制纯铜108 39 0.31~0.349 轧制锰青铜108 39 0.3510 铸铝青铜103 41 -11 冷拔黄铜89~97 34~36 0.32~0.4212 轧制锌82 31 0.2713 硬铝合金70 26 -14 轧制铝68 25~26 0.32~0.3615 铅17 7 0.4216 玻璃55 22 0.2517 混凝土14~23 4.9~15.7 0.1~0.1818 纵纹木材9.8~12 0.5 -19 横纹木材0.5~0.98 0.44~0.64 -20 橡胶0.00784 - 0.4721 电木 1.96~2.94 0.69~2.06 0.35~0.3822 尼龙28.3 10.1 0.423 可锻铸铁152 - -24 拔制铝线69 - -25 大理石55 - -26 花岗石48 - -27 石灰石41 - -28 尼龙1010 1.07 - -29 夹布酚醛塑料4~8.8 - -30 石棉酚醛塑料 1.3 - -31 高压聚乙烯0.15~0.25 - -32 低压聚乙烯0.49~0.78 - -33 聚丙烯 1.32~1.42 - -3.(1)为什么要先加砝码将钢丝拉直?(2)材料相同,但粗细,长度不同的两根金属丝,它们的杨氏模量是否不同?(3)作图法和逐差法处理实验数据各有什么特点?(4)金属丝直径加倍,其他保持不变,试问每1kg砝码所引起的伸长量,将变为原来的几倍? (5)细钢丝的直径是不可能完全均匀的,应该如何测量?我们选用螺旋测微计,为什么不用米尺或游标卡尺测量?在测量中钢丝的长度L只要求测量一次,而直径d要求测量多次,为什么?答:1 防止因钢丝形变而造成测量误差。
杨氏模量的测定-厉华明解读

平台前面的横槽内,后足放在活动金属丝夹具
上,但不可与金属丝相碰.调整平台的上下位
置,使光杠杆前后足位于同一水平面上。
2.光杠杆及望远镜尺组的调节
(1) 外观对准 将望远镜尺放在离光杠杆镜面约为 1.2~ 1.5m处,并使二者在同一高度。 调整光杠杆 镜面与平台面垂直。 望远镜成水平,标尺与 望远镜光轴垂直。
拉伸法测量 金属丝的杨氏模量
朱林彦
太原理工大学
一、实验目的
1. 掌握用静态拉伸法测定金属丝杨氏 模量 的方法。 2. 学习使用光杠杆测微小长度变化的 原理和方法,学会使用望远镜。 3. 学会使用逐差法处理数据。
二、实验仪器
杨氏模量仪、光杠杆、砝码、米尺 (或钢卷尺)、螺旋测微计、望远 镜尺组等。
二、实验仪器
三、实验原理
物体在外力作用下发生形状大小的变化, 称为形变。它可分为弹性形变和塑性形变两 类。在本实验中,只研究弹性形变。最简单 的形变是金属丝或棒受到沿纵向外力作用后 所引起的长度的伸长或缩短,拉伸法就是研 究这种简单弹性形变的方法。
1.基本原理
设有一根长为L、粗细均匀的钢丝,截 面积为S,在外力F的作用下伸长△L。根据 胡克定律,在弹性限度内,应变与应力成 正比,即:
2.光杠杆及望远镜尺组的调节
(2)镜外找像 打开激光器电源,使望远镜上方沿镜筒方向射出 的激光束照到光杠杆镜面,并反射到标尺的中部。 (3)镜内找像 先调望远镜目镜,看清叉丝后,再慢慢调节物镜, 直到看清标尺的像。 (4)细调 观察到标尺像后,再仔细地调节目镜和物镜,使 既能看清叉丝又能看清标尺像,且没有视差。
五、数据记录与处理
次数 荷重 增重 读数 减重 读数 平均值 增4KG 数变化
0 1 2 3 4 5 6 7
(整理)实验报告:杨氏模量的测量

测定金属的杨氏模量实验日期:2014年3月4日星期二下午姓名:一、CCD成像测定杨氏模量:实验目的:(1)用金属丝的伸长测定杨氏模量;(2)用CCD成像系统测量微小长度变化;(3)用逐差法、作图法和最小二乘法处理数据。
实验仪器:测定杨氏模量专用支架,显微镜,CCD CAMERA 型号WAT-308A DC+12V(CCD摄像机,监视器),米尺(带有卡口),螺旋测微器(分度0.01mm,量程0-25mm),电子天平(精度0.01g)实验原理:(1)由胡克定律我们知道在弹性限度内:σ=Eε,其中σ是应力,E为杨氏模量,ε为应变。
那么对于截面积为S,长为L,在力F作用下形变δL时,有如下关系:E=FL SδLF,S,L比较容易测量,但是δL比较微小难以测量,所以实验中用CCD成像进行观察和直接测量。
则由此可以测定杨氏模量E。
(2)CCD与主体实验装置如右图所示:实验中先使用显微镜M把确定金属丝下端所挂圆柱体上的细横线放大,同时通过不随金属丝伸长而移动的M内部分划板上的刻度线作为刻线高低的高度标准。
然后利用CCD成像进行观察。
实验内容与数据处理:1、认识和调节仪器:(1)预热CCD显示屏,调节支架S竖直,调节钳形平台的两边螺丝的松紧,使得钳形平台既可以很好的限制金属丝的转动又不用造成过多的摩擦干扰。
(2)先调节显微镜目镜,看清清晰的分划板像,然后调节物镜与金属丝下挂的圆柱上的细横线的远近,使得可以同时看清分划板和细横线的像(3)打开和连接CCD,放置在显微镜后较近的位置,仔细调节位置使得分划板像清晰,此时也可微调显微镜目镜。
然后调节显微镜的前后位置旋钮,使得细横线也变清晰。
(此时要注意微调显微镜前后的旋钮时要对应移动CCD的前后,保持分划板的清晰)反复调节可以得到分划板和细横线都比较清晰的像。
2、观测金属丝受外力拉伸后的变化:在砝码盘上一次加砝码,质量约为200.0g(需要具体重新测定精确值)。
金属丝伸长后读出对应的读数r i (i=1,2…9),再加上一个略轻砝码,再一次减去砝码,读出r i ′:表中已用逐差法进行计算得到平均加四个砝码产生的伸长量与加的重量。
杨氏模量的测定
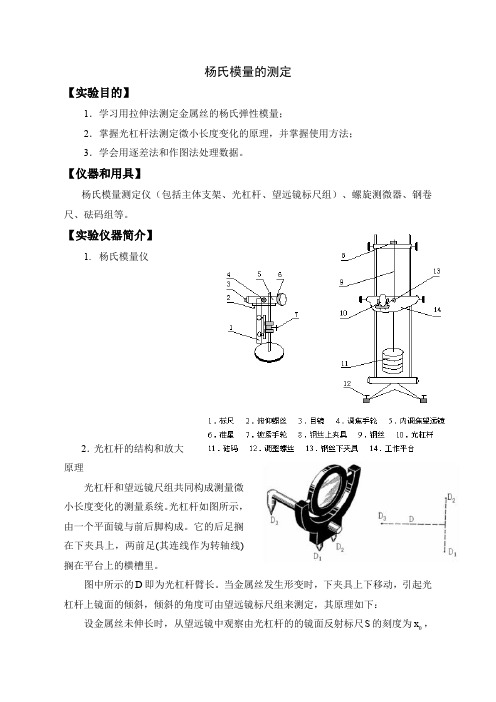
杨氏模量的测定【实验目的】1.学习用拉伸法测定金属丝的杨氏弹性模量;2.掌握光杠杆法测定微小长度变化的原理,并掌握使用方法;3.学会用逐差法和作图法处理数据。
【仪器和用具】杨氏模量测定仪(包括主体支架、光杠杆、望远镜标尺组)、螺旋测微器、钢卷尺、砝码组等。
【实验仪器简介】1. 杨氏模量仪2.光杠杆的结构和放大原理光杠杆和望远镜尺组共同构成测量微小长度变化的测量系统。
光杠杆如图所示,由一个平面镜与前后脚构成。
它的后足搁在下夹具上,两前足(其连线作为转轴线)搁在平台上的横槽里。
图中所示的D即为光杠杆臂长。
当金属丝发生形变时,下夹具上下移动,引起光杠杆上镜面的倾斜,倾斜的角度可由望远镜标尺组来测定,其原理如下:x,设金属丝未伸长时,从望远镜中观察由光杠杆的的镜面反射标尺S的刻度为当金属丝伸长L ∆后,光杠杆镜面由M 转到M '的位置,即转过α角,后足3D 绕两前足尖的连线也转过了α角,如图所示,金属丝伸长L ∆之后,从望远镜读到的标尺刻度为1x ,刻度的变量为:01x x h -=∆。
光杠杆系统的放大原理图当镜面转过α角时,镜面的法线也转过了α角(BOB '∠),则入射光线与反射光线之间的角度应改变α2(BOB ''∠),设镜面到标尺S 的距离为R ,在α角比较小的情况下,由图知:D L tg ∆=≈αα,Rh tg ∆=≈αα22 从上两式中消去α得:h RDL ∆=∆2 因为D R >>,所以用光杠杆测h ∆就能把微小伸长量L ∆放大DR2倍,即利用光杠杆就可把测量微小的长度变化量L ∆转换成测量数值较大的标尺读数变化量h ∆,这就是光杠杆系统的放大原理。
【实验原理】取一粗细均匀的金属丝,长为L ,截面积为42d S π=,d 为截面直径,将其上端固定,下端悬挂质量为m 的砝码,测金属丝内产生单位面积的强力,即应力SF =δ,单位长度的伸长应变LL∆=ε,虎克定理指出,在弹性限度内,应力与应变成正比,即LLyS F ∆= ,称为金属材料的杨氏弹性模量,它完全由材料的性质所决定,是表征材料力学性能的一个物理量。
大学物理实验杨氏模量

L bl 2D
光杠杆的作用在于将微小的伸长量L放大为竖
尺上的位移l, l 叫ΔL 的光杠杆放大量
l 2D
L b
叫光杠杆放大率
l
△L
θ
b
θ θ
D
光杠杆放大原理图
E FL SL
d 2
S 4
L bl 2D
ESFLLdF2
L bl
8Fd2bLlD
4 2D
尺读望远镜组:
测量时,望远镜水平 地对准光杠杆镜架上 的平面反射镜,经光 杠杆平面镜反射的标 尺虚象又成实象于分 划板上,从两条视距 线上可读出标尺像上 的读数,
仪器误/差3
0.683
例 : F 4 如 1 g / 1 个 9 . 8 砝 3 0 0 . 0 码 N 3
二. d,l为多次测量 ,其量不确定度 : 为
k
N
Ni
2
A
i 1
kk 1
B
仪器误差 3
A2B2
0.683
三. 测量结果的不确定度与相对不确定度:
E F 2 L 2 D 2 2 d 2 l N % E F L D d l
实验内容和步骤
1、调节仪器:调节光杠杆和望远镜:
1 调整望远镜水平,光杠杆平面镜竖直 2 调整望远镜与光杠杆平面镜高度相同 3 沿望远镜外侧边沿上方使凹口、瞄准星、
平面镜在同一直线上,左、右移动望远镜 在镜子里找到竖直尺的像;若找不到,可 微调镜子的角度,直到找到为止, 4 旋动望远镜目镜,使十字叉丝清晰;再旋 动聚焦手轮,直到看清竖直尺的像,
实验原理
1、杨氏模量的物理意义:描述材料抵抗形变能 力的物理量,该值越大,材料越不容易变形,
L为其受拉力F后的伸长量
金属杨氏模量的测定实验[试题]
![金属杨氏模量的测定实验[试题]](https://img.taocdn.com/s3/m/a510e717bfd5b9f3f90f76c66137ee06eff94e70.png)
金属杨氏模量的测定杨氏模量是表征固体材料抵抗形变能力的重要物理量,是工程材料重要参数,它反映了材料弹性形变与内应力的关系,它只与材料性质有关,是工程技术中机械构件选材时的重要依据。
本实验采用液压加力拉伸法及利用光杠杆的原理测量金属丝的微小伸长量,从而测定金属材料的杨氏模量。
一、实验目的(1)学会测量杨氏弹性模量的一种方法(2)掌握光杠杆放大法测量微小长度的原理(3)学会用逐差法处理数据二、仪器和量具数显液压杨氏模量仪,光杠杆和标尺望远镜,钢卷尺,螺旋测微计。
三、原理1.拉伸法测量钢丝的杨氏模量任何物体在外力作用下都要产生形变,可分为弹性形变和塑性形变。
弹性形变在外力作用撤除后能恢复原状,而塑性形变则不能恢复原状。
发生弹性形变时,物体内部产生的企图恢复物体原状的力叫做内应力。
对固体来讲,弹性形变又可分为4种:伸长或压缩形变、切变、扭变、弯曲形变。
本实验只研究金属丝沿长度方向受外力作用后的伸长形变。
取长为L ,截面积为S 的均匀金属丝,在两端加外力F 相拉后,则作用在金属丝单位面积上的力SF为正应力,相对伸长LL ∆定义为线应变。
根据胡克定律,物体在弹性限度范围内,应变与应力成正比,其表达式为LLYS F ∆= (1)式中Y 称为杨氏模量,它与金属丝的材料有关,而与外力F 的大小无关。
由于L ∆是一个微小长度变化,故实验常采用光杠杆法进行测量。
2.光杠杆法测量微小长度变化放大法是一种应用十分广泛的测量技术,有机械放大、光放大、电子放大等。
如螺旋测微计是通过机械放大而提高测量精度的,示波器是通过将电子信号放大后进行观测的。
本实验采用的光杠杆法属于光放大。
光杠杆放大原理被广泛地用于许多高灵敏度仪表中,如光电反射式检流计、冲击电流计等。
图1(b)标尺光杠杆如图1(a)、1(b)所示,在等腰三角形板1的三个角上,各有一个尖头螺钉,底边连线上的两个螺钉B和C称为前足尖,顶点上的螺钉A称为后足尖,A到前两足尖的连线BC的垂直距离为b,如图3(a)所示;2为光杠杆倾角调节架;3为光杠杆反射镜。
杨氏模量
【注意事项】
(1)加减砝码时要轻拿轻放,避免使码钩晃动。 (2)同一荷重下的两个读数要记在一起。增重与减重对应同一荷重下读数的平均值才是对应 荷重下的最佳值,它消除了摩擦(圆柱体与圆孔之间的摩擦)与滞后(加减砝码时钢丝伸长与缩短滞 后)等系统误差。
【思考题】
(1)两根材料相同,粗细、长度不同的钢丝,在相同的加载条件下,它们的伸长量是否一样? 杨氏模量是否相同? (2)有一个约 4 cm 长的压电陶瓷双晶片,加直流电压后,一片伸长,另一片收缩。将两片粘 在一起,一端固定,两侧施加几十伏直流电,则活动端将产生几十微米的横向位移,请你设计一
-3-
综合性实验
静态法测量杨氏模量
架上端钢丝上夹头开始到平台夹钢丝的下夹头之间的距离) 。将测量结果填入数据记录表中。 (2)在望远镜中读出加有本底砝码时十字叉丝横线对应的标尺的某一刻度,记为 s 0 ,然后在 此基础上逐个增加砝码,在数据记录表中记下每加一个砝码时十字叉丝横线对应的标尺的刻度
'
s i' ,直到七个砝码加完为止。
1. S 的最佳值及不确定度的计算 (1) . S 的最佳值(用逐差法)
1 1 ; S 2 ( S 5 S1 ) 4 4 1 S4 ( S7 S3 ) ; 4 1 S ( S1 S 2 S 3 S 4 ) 4
S1 ( S 4 S0 )
s( D ) 6
(3). D 平均值的实验标准差: s( D )
(4). 千分尺的的示值极限误差: m 0.004mm (5). 合成不确定度: u( D )
2 2 uB S( D )2 ( uA
m
3
)2
-5-
综合性实验
杨氏模量实验报告
杨氏模量实验报告开展实验自然要写实验报告,杨氏模量实验报告怎样写呢?那么,下面是给大家整理收集的杨氏模量实验报告相关范文,仅供参考。
杨氏模量实验报告1【实验目的】1.1.掌握螺旋测微器的使用方法。
2.学会用光杠杆测量微小伸长量。
3.学会用拉伸法金属丝的杨氏模量的方法。
【实验仪器】杨氏模量测定仪(包括:拉伸仪、光杠杆、望远镜、标尺),水准器,钢卷尺,螺旋测微器,钢直尺。
1、金属丝与支架(装置见图1):金属丝长约0.5米,上端被加紧在支架的上梁上,被夹于一个圆形夹头。
这圆形夹头可以在支架的下梁的圆孔内自由移动。
支架下方有三个可调支脚。
这圆形的气泡水准。
使用时应调节支脚。
由气泡水准判断支架是否处于垂直状态。
这样才能使圆柱形夹头在下梁平台的圆孔转移动时不受摩擦。
2、光杠杆(结构见图2):使用时两前支脚放在支架的下梁平台三角形凹槽内,后支脚放在圆柱形夹头上端平面上。
当钢丝受到拉伸时,随着圆柱夹头下降,光杠杆的后支脚也下降,时平面镜以两前支脚为轴旋转。
图1 图2 图33、望远镜与标尺(装置见图3):望远镜由物镜、目镜、十字分划板组成。
使用实现调节目镜,使看清十字分划板,在调节物镜使看清标尺。
这是表明标尺通过物镜成像在分划板平面上。
由于标尺像与分划板处于同一平面,所以可以消除读书时的视差(即消除眼睛上下移动时标尺像与十字线之间的相对位移)。
标尺是一般的米尺,但中间刻度为0。
【实验原理】1、胡克定律和杨氏弹性模量固体在外力作用下将发生形变,如果外力撤去后相应的形变消失,这种形变称为弹性形变。
如果外力后仍有残余形变,这种形变称为塑性形变。
应力:单位面积上所受到的力(F/S)。
应变:是指在外力作用下的相对形变(相对伸长DL/L)它反映了物体形变的大小。
用公式表达为: (1)2、光杠杆镜尺法测量微小长度的变化在(1)式中,在外力的F的拉伸下,钢丝的伸长量DL是很小的量。
用一般的长度测量仪器无法测量。
在本实验中采用光杠杆镜尺法。
杨氏模量
南昌大学物理实验报告课程名称:大学物理实验名称:杨氏模量学院:信息工程学院专业班级:计算机162班学生姓名:李哲学号:6130116038实验地点:基础实验大楼610座位号:19实验时间:星期五早上9:45一、实验目的:1.学会测量杨氏模量的一种方法,掌握“光杠杆镜”测量微小长度变化的原理.2.学会用“对称测量“消除系统误差”.3.学会如何依实际情况对各个测量量进行误差估算.4.练习用逐差法处理数据二、实验原理:设有一截面为S ,长度为0L 的均匀棒状(或线状)材料,受拉力F 拉伸时,伸长了△L ,其单位面积截面所受到的拉力S F 成为应力,而单位长度的伸长量LL △称为应变.根据胡克定律,在弹性形变范围内,棒状(或线状)固体应变与它所受的应力成正比,即S F =E*0L L△ 其比例系数E 取决于固体材料的性质,反映了材料形变和内应力之间的关系E=S F *0L L△ 称为杨氏模量,它的单位为N*2-m.实验证明,杨氏模量与歪理F 、物体的长度L 和截面积S 的大小无关,只取决于被测物的材料特性,它是表征固体性质的一个物理量.设金属丝的直径为d ,则S=41π2d 杨氏模量可表示为E=L△πd 4FL 2 F 可以由所挂的砝码重量求出,直径d 可以通过螺旋测微器测量,L 可以用米尺等常规的测量器具测量,但△L 由于非常小,用常规的测量方法很难精确测量.本实验将用放大法——“光杠杆镜”来测定。
△L=Db2Δn 式中Δn= |12n n -|,相当于光杠杆镜的长臂端D 的位移. 上式中的bD2叫做光杠杆镜的放大倍数,由于D 远大于b ,所以Δn 远大于△L ,从而获得对微小量的线性放大,提高了△L 的测量精度.这种测量方法被称为放大法.由于该方法具有性能稳定,精度高,而且是线性放大等优点,所以在设计各类测试仪器中有着广泛的应用考虑到金属丝受外力作用时存在着弹性滞后效应,也就是说钢丝受到拉伸力作用时,并不能立即伸长到应有的长度i L (i L =0L +Δi L ),而只能伸长到i L -δi L .同样,当钢丝受到的拉伸力一旦减小时,也不能马上缩短到应有的长度i L ,仅缩短到i L +δi L .因此实验时测出的并不是金属丝应有的伸长或收缩的实际长度.为了消除弹性滞后效应引起的系统误差,测量中应包括增加拉伸力以及对应地减少拉伸力这一对称测量过程,实验中可以采用先增加后减少砝码的办法实验.只要在增减相应重量时,金属丝伸缩量取平均,就可以消除滞后量δi L 的影响.即i L =21[减增L L ]=21[﹙0L +Δi L -δi L ﹚+﹙0L +Δi L +δi L ﹚]==0L +Δi L三、实验仪器:杨氏模量仪测量仪、螺旋测微器、游标卡尺、钢卷尺、望远镜四、实验内容和步骤:1.用2kg 砝码挂在钢丝下端钢丝拉直,调节杨氏模量仪底盘下面的3个底脚螺丝,同事观察放在平台上的水准尺,直至中间平台处于水平状态为止.2.调节光杠杆镜为止.将光杆镜放在平台上,两前脚放在平台横槽内,后脚放在固定钢丝下端圆柱形套管上.3.望远镜调节.将望远镜置于距光杠镜2m 左右处,松开望远镜固定螺钉,上下移动使得望远镜和光杠杆镜的镜面基本等高.从望远镜筒上方沿镜筒轴线瞄准光杠杆镜面,移动望远镜固定架位置,直至可以看到光杠杆镜中标尺的像.然后再从目镜观察,先调节目镜使十字叉丝清晰,最后缓缓旋转调焦手轮,使物镜在镜筒内伸缩,直至从望远镜里可以看到清晰的标尺刻度为止.4.观测伸长变化.以钢丝下挂2kg 砝码时的读数作为开始拉伸的基数0n ,然后每加上1kg 砝码,读取一次数据,这样依次可以得到76543210,,,,,,,n n n n n n n n ,这是钢丝拉伸过程中的读数变化.紧接着再每次撤掉1kg 砝码,读取一次数据,依次得到'0'1'2'3'4'5'6'7,,,,,,,n n n n n n n n ,这是钢丝收缩过程中的读数变化.PS :加减砝码时应轻拿轻放,避免钢丝产生较大幅度振动,加减后要等钢丝渐趋平稳后再读数.5.测量光杠杆镜前后脚距离 b.把光杠杆镜的三只脚在白纸上压出凹痕,用尺画出两前脚的连线,再用游标卡尺量出后脚到该连线的垂直距离6.测量钢丝直径.用螺旋测微器在钢丝的不同部位测3~5次,取其平均值.测量时每次都要注意记下数据和螺旋测微器的零位误差.7.测量光杠杆镜镜面到望远镜附标尺的距离 D.用钢卷尺量出光杠杆镜镜面到望远镜附标尺的距离,作单次测量,并估计误差. 8.用米尺测量钢丝原长0L ,测单次.9.实验中的注意事项:A.钢丝的两端一定要夹紧,一来减少系统误差,二来避免砝码加重后拉脱而砸坏实验装置B.在测读伸长变化的整个过程中,不能碰动望远镜及其安放的桌子,否则重新开始测读C.被测钢丝一定要保持平直,以免将钢丝拉直的过程误测为伸长量,导致测量结果谬误.D.增减砝码时要注意砝码的质量是否都是1kg ,并且不能碰到光杠杆镜.E.望远镜有一定的调焦范围,不能过分用力拧动调焦旋钮.五、实验数据与处理:1.长度的测量:不确定度:22d d S +∆=∆仪,其中1)(21--=∑=n d dS ni id ;结果:=∆+)(mm d d 0.760+0.004mm光杠杆镜臂长:游标卡尺的零位误差 0mm ,示值误差0.02 mm 结果:=∆+)(mm b b 44.22+0.02mm 2、钢丝长度L 和标尺到镜面距离的测量)(mm L L ∆+= 390.0+1.2mm )(mm D D ∆+=960.0+1.2mm3、增减重量时钢丝伸缩量的记录参考数据)4、实验结果的计算:LS FL E ∆=, 其中 241,2d S n D b L π=∆=∆ 故 nb d DFL ∆=08π=1.89)/(10211m N ⨯其中力的单位用N ,长度单位用m 。
实验目的--思考题
1钢丝杨氏模量的测定【实验目的】1.了解静态拉伸法测杨氏模量的方法2.掌握光杠杆放大法测微小长度变化的原理和方法3.学会用逐差法处理数据【思考题】1.材料相同、粗细不同的两根钢丝,其杨氏模量是否相同?2.实验中各长度量采用了不同的长度测量仪器进行测量,选择它们的依据是什么?3.本实验如果从望远镜中看不到标尺的像,应从哪些方面进行调节?标尺像上下清晰度不同应如何调节?4.根据所测数据,能否用作图法或最小二乘法求钢丝的杨氏模量?若能,试简述之。
2固体的导热系数的测定【实验目的】1.学习用稳态法测固体导热系数,了解其测量条件。
2.学习实验中如何将传热速率的测量转化为散热速率的测量方法。
3.学会用作图法处理数据。
【思考题】1. 通过T~t曲线上一点求斜率的随意性很大,给测量带来很大误差,能否将曲线变为一条直线,求直线的斜率?需要保证什么实验条件?2.分析比较原理中提到的两种测量导热系数方法的使用条件及实验中如何保证。
3 惠斯通电桥【实验目的】1.了解惠斯通电桥测电阻的原理,掌握用惠斯通电桥测电阻的方法。
2.了解电桥的灵敏度,学习合理选择实验条件,减小系统误差。
【思考题】1.下列因素是否会使电桥测量的系统误差增大?⑴ 电源电压不太稳定;⑵ 导线电阻;⑶ 检流计没有调好零点;⑷ 检流计灵敏度不够高。
2.从实验结果分析,电桥桥臂比的选择对测量结果有何影响?3.根据实验原理中对系统误差的分析,结合实验结果分析一下,在确定了x R 的大致范围之后,怎样选择r K 和21,R R 能使系统误差尽量减小?4 示波器的使用【实验目的】1.了解示波器的结构和工作原理,掌握示波器的基本使用方法2. 学习示波器显示信号波形及利用波形测信号电压、频率3. 学习示波器显示李萨如图形及利用李萨如图形测频率4.熟悉示波器和信号发生器的面板功能【思考题】1. 如果示波器良好,但由于某些旋钮未调好,荧光屏上看既不到亮点,也看不到扫描线,应怎样操作才能找到亮点?2. 示波器显示波形和显示李萨如图形工作方式有何不同?3. 示波器显示波形时,若波形不稳定,应调节示波器的那些部件使图形稳定?显示李萨如图形时,能否用同样的方法使图形稳定?为什么?5 霍尔效应及应用【实验目的】1.了解霍尔效应,学习利用霍尔效应测量磁场B 的原理和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 “杨氏模量的测定” 思考题参考解答
1、各种不同长度用不同仪器测定,是如何进行的?为什么?
答:本实验中,金属丝长度L用米尺测量,光杠杆与镜尺组间距离D也用米尺测
量;光杠杆常数b用游标卡尺测量;金属丝直径用螺旋测微器测量。
选择测量仪器时,要考虑测量范围和相对误差两个因素,也就是说要考虑仪器的
量程和精度。首先,要考虑测量范围,被测物的长度应在测量仪器的量程之内;
同时还要考虑仪器的精度,尽量减小测量误差,测量仪器的选择要满足所测量的
结果总误差不超过5% 。
2、本实验中哪一个量的测量误差对结果影响最大?试作具体讨论。
答:本实验中,竖尺上的位移l对测量结果影响最大。
提示:用相对误差可以判断某个测量值对整个测量结果的影响大小。
根据相对误差公式:llbbddDDLLFFEE2 (见p83)
可以近似计算各个测量值影响大小,其中:
%278.0360/1gg
F
F
,
%25.140/5.0/mmmmLL
,
%0667.01500/0.1/mmmmDD
%67.14.0/005.0/mmmmdd
%4.22.4/1.0/mmmmll
可见,l对测量结果影响最大。
3、用光杠杆测l变成测l等量,若把ll/称为光杠杆的“放大率”,由(5-21)
知bD/2,能不能增加D减小b来提高,这样有没有好处?有没有限度?
答:由教材p82,(5-23)式得:
DblL2, 即LLbDl2,其中bDl
l2
为光杠杆的“放大率”,
(1) 可以通过增加D减小b来提高,有好处,能够提高测量精度。
(2) 有限度:b太小,则tgbL不能成立;
D
太大,则实验操作会很不方便,会增加实验的成本。
4、采用逐差法处理数据外,能否用作图法求杨氏模量?若能,应怎样作图?
答:可以用作图法求杨氏模量。根据公式(5-24),有ElLDbdF82,将其记做klF,
其中ELDbdk82。可见,对于同一段金属丝,F与l是成正比例关系的。即当
mF
1
时,(m为一个砝码的质量),对应121rrl;mF22时,对应132rrl;…,
依次类推,当mF77时,对应187rrl,以l为横坐标,以F为纵坐标描点作
图,会得到一条直线,求出其斜率k,则ELDbdk82,由此,可以求出E。
