生产运作管理计算例题(2012.02)
生产运作管理考试题型及计算题

考试题型及计算题1. 填空题10分;2. 判断题10分;3. 单项选择题10分;4. 多项选择题12分;5. 简答题18分;6. 计算题40分计算题样题:1.神力公司每年使用24000个齿轮零件,采购价格是每件50元。
公司每采购一次的相关费用为1500元,库存持有成本是每件每年30元。
试用经济订货批量模型确定最佳采购批量,并计算对应的年最低总成本。
2.一产品装配线计划每日出产360件产品,每日用于生产的时间是7.5小时,该装配线各道工序的单件作业时间(分)及紧前工序如下表所示:要求:(1)画出装配线工序先后顺序图。
(2)该装配线节拍是多少。
(3)计算每日装配360件产品所需的最小工作地数。
(4)对该装配线进行平衡,并计算装配线时间损失率,3.某超市近10年月饼的销售情况如下表,已知每盒月饼的进价为C=50元,超市的出售价为P=80元。
若在中秋期间卖不出去,只能按每盒30元(S)降价处理。
试用期望利润最大法为该超市决策:今年应采购多少盒月饼?4.某项工程由10道工序组成,各道工序的作业时间及其相互关系如下表所示:要求:(1)画出网络图。
(2)计算各结点的最早时间与最迟时间。
(3)计算各工序的时差。
(4)找出关键线路并算出该项工程的总工期。
5.根据预测,2012年市场对中原汽车公司生产的某型号特种汽车的需求量为98600辆,每辆该型号特种车的生产成本为86500元,中原公司每天可生产该特种车420辆(生产率),一年按360天计算。
每生产一批次的生产准备费用为3960元,每辆该型号特种车的年维持库存费为600元。
试用经济生产批量模型确定最佳生产批量,并计算对应的年最低总成本。
6.某公司-11月的物流业务量与物流成本资料如下表:若该公司12月份的物流业务量为15万吨,试用一元线性回归模型预测该公司12月的物流成本。
生产与运作管理的计算题
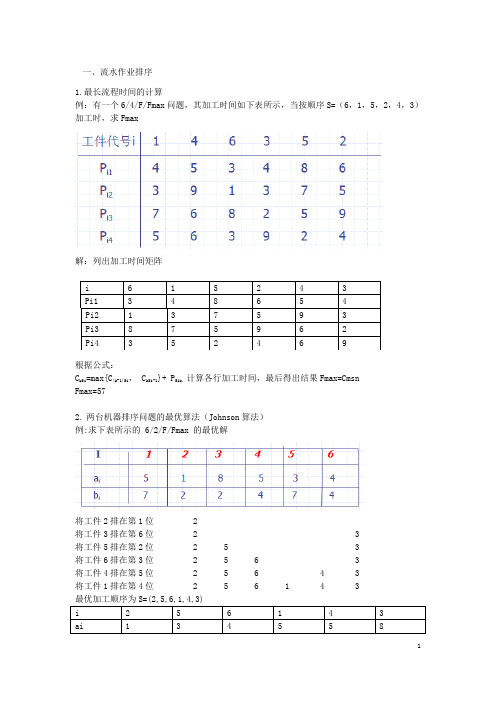
一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出, Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ) 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解:λi= ∑ [k-(3+1)/2]P ik ,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
生产与运作管理的计算题

一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出, Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ) 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解:λi= ∑ [k-(3+1)/2]P ik ,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
考试必备【生产运作管理】经典计算题(带解释和答案)

考试必备【⽣产运作管理】经典计算题(带解释和答案)考试必备【⽣产运作管理】经典计算题(带解释和答案)重⼼法求⼯⼚设置地1、某企业决定在武汉设⽴⼀⽣产基地,数据如下表。
利⽤重⼼法确定该基地的最佳位置。
假设运输量与运输成本存在线性关系(⽆保险费)。
Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=.所以最佳位置为(,)。
1.某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建⽴分部,管理上海市的业务。
假设3家超市的销售额是相同的。
(6.3.24)(1)⽤重⼼法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1.上海分部的最佳位置,也就是3家超市的重⼼坐标,可以这样计算:x=(37+12+29)/3=27y=(61+49+20)/3=(2)如果该企业计划在上海建⽴第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变解:增加⼀家超市后,重⼼坐标将变为:x=(37+12+29+16)/4=y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每⽉平均销售400件,单价180元/件,每次订购费⽤100元,单件年库存保管费⽤是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少(15000元)(2)经济订货批量(EOQ )是多少(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元(2)EOQ=HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=%2、某⾷品⼚每年需要采购3000吨⾯粉⽤于⽣产,每次采购订货⼿续费为300元,每吨产品的年库存成本为20元,请计算该⾷品⼚采购⾯粉的经济订货批量EOQ 。
生产与运作管理的计算题

一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出, Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ) 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解:λi= ∑ [k-(3+1)/2]P ik ,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
生产运作管理习题与案例(DOC 30页)

生产运作管理习题与案例(DOC 30页)部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑《生产运作管理》西安交通大学城市学院管理系2013.09第一部分练习题【练习题1】某玩具厂生产A、B两种玩具,需经过制造车间和装配车间加工。
产品所需的工时、车间可提供的工时及产品的利润如表1-1所示。
试求最大利润的生产计划安排(各生产A、B两种玩具多少台)。
表1-1产品所需的工时、车间可提供的工时及产品的利润表【练习题2】现有甲、乙两个投资方案,甲方案固定投资80万元,生产单位产品变动成本为100元;乙方案固定投资50万元,生产单位产品变动成本为110元,单位产品销售价格均为150元。
要求:(1)若计划产量达到15000件时(产品均能售出),应选择哪个方案?(2)若计划产量超越30000件时(产品均能售出),应选择哪个方案?(3)若采用甲方案,如果增加广告宣传费50万元,可使产品销售量从30000件增至40000件,计算此时的利润为多少?是否划算?(4)若采用甲方案,当产量达到40000件时企业产能发挥为80%,此时有一报价为120元、数量为10000件的订单,企业是否应该接单?为什么?【练习题3】某商贩在A地经营冷饮商品销售已经5年。
已知该产品每箱进价2.5元,售价5元,毛利为每箱2.5元。
若当日进货当日销售不出则报废,每箱残值仅为1元,即每箱赔1.5元。
根据历年同期销售情况,该商贩每天销售量在1000箱~1300箱之间,且有连续5年同期销售资料见表3-1。
表3-1 某商贩连续5年同期销售资料表要求:(1)计算并编制决策分析用表数据;(2)运用期望收益最大化原则求解该商贩的日进货量。
【练习题4】某企业为增强竞争能力,拟订了一个10年发展规划,其初步设计的可行方案有扩建、新建和转包联营三种。
经预测分析后得知未来可能有市场销路好、销路一般、销路差和销路极差四种情况,各方案的投资和可能的年收益见表4-1。
生产与运作管理的计算题
⽣产与运作管理的计算题⼀、流⽔作业排序1.最长流程时间的计算例:有⼀个6/4/F/Fmax问题,其加⼯时间如下表所⽰,当按顺序S=(6,1,5,2,4,3)加⼯时,求Fmax解:列出加⼯时间矩阵根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各⾏加⼯时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所⽰的 6/2/F/Fmax 的最优解将⼯件2排在第1位 2将⼯件3排在第6位 2 3将⼯件5排在第2位 2 5 3将⼯件6排在第3位 2 5 6 3将⼯件4排在第5位 2 5 6 4 3将⼯件1排在第4位 2 5 6 1 4 3最优加⼯顺序为S=(2,5,6,1,4,3)由上表可计算出, Fmax =283.⼀般n/m/F/Fmax问题的最优算法(⼀)Palmar算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi不增的顺序排列⼯件)例:有⼀个4/3/F/Fmax问题,其加⼯时间如下表所⽰,⽤Palmar求解.解:λi= ∑ [k-(3+1)/2]P ik,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λi不增的顺序排列⼯件,得到加⼯顺序(1,2,3,4)和(2,1,3,4),经计算,⼆者都是最优顺序,Fmax=28(⼆)关键⼯件法例:有⼀个4/3/F/Fmax问题,其加⼯时间如下表所⽰,⽤关键⼯件法求解.解:由上表可知,加⼯时间最长的是3号⼯件,Pi1<=Pi3的⼯件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的⼯件为4号⼯件,Sb=(4),这样得到加⼯顺序为(1,2,3,4)。
经计算,Fmax=28⼆、⽣产能⼒的计算(⼀)、对于加⼯装配式⽣产,⽣产能⼒是⼀个模糊的概念。
生产与运作管理的计算题
生产与运作管理的计算题Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵式:C kSi=max{C(k-, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=Cmsn1)SiFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3最优加工顺序为S=(2,5,6,1,4,3)3.一般n/m/F/Fmax问题的最优算法(一)Palmar算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi不增的顺序排列工件)例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用Palmar求解.解:λi= ∑ [k-(3+1)/2]P ik,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λi不增的顺序排列工件,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28(二)关键工件法例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
生产与运作管理的计算题
一、流水作业排序1.最长流程时间的计算例:有一个6/4/F/Fmax问题,其加工时间如下表所示,当按顺序S=(6,1,5,2,4,3)加工时,求Fmax解:列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式:C kSi=max{C(k-1)Si, C kSi-1}+ P Sik,计算各行加工时间,最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法(Johnson算法)例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出, Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法(λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ) 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解:λi= ∑ [k-(3+1)/2]P ik ,k=1,2,3λi=-Pi1+Pi3于是,λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ,得到加工顺序(1,2,3,4)和(2,1,3,4),经计算,二者都是最优顺序,Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解:由上表可知,加工时间最长的是3号工件,Pi1<=Pi3的工件为1和2,按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件,Sb=(4),这样得到加工顺序为(1,2,3,4)。
考试必备【生产运作管理】经典计算题(带解释和参考答案)
考试必备【⽣产运作管理】经典计算题(带解释和参考答案)考试必备【⽣产运作管理】经典计算题(带解释和答案)重⼼法求⼯⼚设置地1、某企业决定在武汉设⽴⼀⽣产基地,数据如下表。
利⽤重⼼法确定该基地的最佳位置。
假设运输量与运输成本存在线性关系(⽆保险费)。
⼯⼚坐标年需求量/件 D1 (2,2) 800 D2 (3,5) 900 D3 (5,4) 200 D4 (8,5) 100解:X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05 Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为(3.05,3.7)。
1. 某跨国连锁超市企业在上海市有3家超市,坐标分别为(37,61)、(12,49)、(29,20)。
现在该企业打算在上海建⽴分部,管理上海市的业务。
假设3家超市的销售额是相同的。
()(1)⽤重⼼法决定上海分部的最佳位置。
解:因为3家超市的销售额相同,可以将他们的销售额假设为1. 上海分部的最佳位置,也就是3家超市的重⼼坐标,可以这样计算: x=(37+12+29)/3=27 y=(61+49+20)/3=43.3(2)如果该企业计划在上海建⽴第四家超市,其坐标为(16,18),那么如果计划通过,上海分部的最佳位置应该作何改变?解:增加⼀家超市后,重⼼坐标将变为: x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装,每⽉平均销售400件,单价180元/件,每次订购费⽤100元,单件年库存保管费⽤是单价的20%,为了减少订货次数,现在每次订货量是800件。
试分析:(1)该服装现在的年库存总成本是多少?(15000元)(2)经济订货批量(EOQ )是多少?(163件) (1)总成本=(800/2)*180*20%+(400*12/800)*100=15000元(2)EOQ =HDS 2=800/)12*400(100*12*400*2=163件(3)EOQ 总成本=(163/2)*180*20%+(400*12/163)*100=5879元(4)年节约额=15000-5879=9121元节约幅度=(9124/15000)*100%=60.81%2、某⾷品⼚每年需要采购3000吨⾯粉⽤于⽣产,每次采购订货⼿续费为300元,每吨产品的年库存成本为20元,请计算该⾷品⼚采购⾯粉的经济订货批量EOQ 。
