2.5 直线与圆的位置关系 课件(共98张PPT) 2023-2024学年苏科数学九年级上册
合集下载
初中数学九年级上册《2.5 直线与圆的位置关系》PPT课件 (11)
经过半径的外端并且垂直于这条半径 的直线是圆的切线。
课堂小结：
如何证明一直线是圆的切线？
1、当已有“切点”时，连接“切点”与圆心， 证垂直。 2、当“切点”不确定时，过圆心作直线的垂线， 证明 d=r.
作业
《南通小题》64页
辅助线提示：当条件中
出现切线时，通常要连接 切点与圆心，可得垂直。
例3 点O是∠DPC的角平分线上的一点，⊙O与 PD相切于A，
求证：PC与⊙O相切.A D
P
O
B
C
辅助线提示：要证r.
课堂小结：
1、切线性质：
圆的切线垂直于经过切点的半径
2、切线的判定定理：
初中数学 九年级(上册)
2.5 直线与圆的位置 关系 （2）
直线和圆的位置关系有哪几种？
图形
公共点 圆心到直线的 的个数 距离d与圆的
半径r的关系
1、直线和圆相离
2、直线和圆相切
3、直线和圆相交
在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm， 以C为圆心，r为半径作圆。
①当 r=3 时， 直线ＡＢ与⊙Ｃ
变式：如图，△ABC内接于⊙O，AB是⊙O的弦，
∠CAD=∠ABC，判断直线AD与⊙O的位置关系，
并说明理由。
B
A 1
D
O C
辅助线提示：要证切线，当已有“切点”时， 连接“切点”与圆心，证垂直。
例2 如图，AB是⊙O的直径，弦AD平分∠BAC， 过点D的切线交AC于点E。
DE与AC有怎样的位置关系？为什么？
;
②当 r=2 时，直线ＡＢ与⊙Ｃ
;
④③当当r r
时，直时线，Ａ线Ｂ段与Ａ⊙ＢＣ与相⊙切Ｃ。有一个公共点。
课堂小结：
如何证明一直线是圆的切线？
1、当已有“切点”时，连接“切点”与圆心， 证垂直。 2、当“切点”不确定时，过圆心作直线的垂线， 证明 d=r.
作业
《南通小题》64页
辅助线提示：当条件中
出现切线时，通常要连接 切点与圆心，可得垂直。
例3 点O是∠DPC的角平分线上的一点，⊙O与 PD相切于A，
求证：PC与⊙O相切.A D
P
O
B
C
辅助线提示：要证r.
课堂小结：
1、切线性质：
圆的切线垂直于经过切点的半径
2、切线的判定定理：
初中数学 九年级(上册)
2.5 直线与圆的位置 关系 （2）
直线和圆的位置关系有哪几种？
图形
公共点 圆心到直线的 的个数 距离d与圆的
半径r的关系
1、直线和圆相离
2、直线和圆相切
3、直线和圆相交
在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm， 以C为圆心，r为半径作圆。
①当 r=3 时， 直线ＡＢ与⊙Ｃ
变式：如图，△ABC内接于⊙O，AB是⊙O的弦，
∠CAD=∠ABC，判断直线AD与⊙O的位置关系，
并说明理由。
B
A 1
D
O C
辅助线提示：要证切线，当已有“切点”时， 连接“切点”与圆心，证垂直。
例2 如图，AB是⊙O的直径，弦AD平分∠BAC， 过点D的切线交AC于点E。
DE与AC有怎样的位置关系？为什么？
;
②当 r=2 时，直线ＡＢ与⊙Ｃ
;
④③当当r r
时，直时线，Ａ线Ｂ段与Ａ⊙ＢＣ与相⊙切Ｃ。有一个公共点。
最新苏科版数学九年级上册《2.5 直线与圆的位置关系》精品课堂教学课件 (19)
B ∠DOE=________
典型例题
例2：如图，四边形ABCD的边AB、BC、CD 、DA和 ⊙O分 别相切于点E、F、G、H，试探究这个四边形ABCD的两组 对边的和有什么数量关系？并说明你的正确性。
A
E
H D
O.
B
G
FC
试问：若图中四边形ABCD是平行四边形， 那么此四边 形还是什么图形？
典型例题
例3：数学课上，数学老师把一个乒乓球放在一个V形架 中，如图是它的平面示意图，CA、CB是⊙O的切线， 切点分别是A、B，某同学通过测量，量得AB=4cm， ∠ACB=600，如何求出乒乓球的直径？
O.
AD
B
C
练习
1.如图AB是⊙O的直径，C为圆上任意一点，过C 的切线分别与过A、B两点的切线交于P、Q，
求证：PO⊥OQ AP
O.1 C
2
B
Q
由分P析A:、PQ、BQ为切线
可∠得1=
1 APC 2
∠2=
1 2
BQC
由AB为直径易得AP//BQ
则有1 2 900
∴PO⊥OQ
练习
2.如图AB是⊙O的直径，C为圆上任意一点，过C A P 的切线分别与过A、B两点的切线交于P、Q，
.C
O
已知AP=1cm，BQ=9cm，求⊙O的半径.
A
O.
P
.
B
（2）如图，从⊙O外一点P作⊙O的两条切线，分别切⊙O 于A，B，在AB 上任取一点C作⊙O的切线分别交PA、PB
于D、E
D A.
①若PA=2，则△PDE的周长为 ______; 若PA=a，则△PDE
P
C
.O 的周长为_______
苏科版九年级数学上册《2.5直线与圆的位置关系(二)》教学课件
O
A
E
B
知识归纳
一、圆的切线：
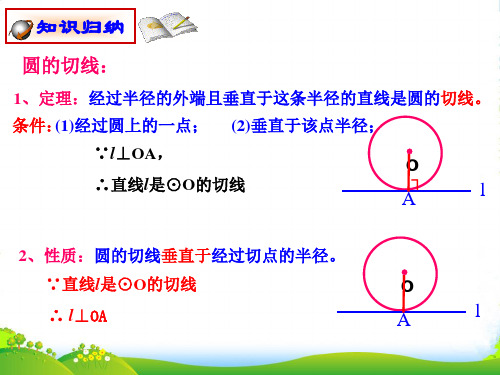
1、定理：经过半径的外端且垂直于这条半径的直线是圆的切线。
条件：(1)经过圆上的一点； (2)垂直于该点半径；
∵l⊥OA，
思考： ∴直线l是⊙O的切线
●
O
┐
A
l
如果直线l是⊙O的切线，点A为切点，那么半径OA与l垂直吗？
2、性质：圆的切线垂直于经过切点的半径。
●
∵直线l是⊙O的切线
1、直线l垂直于半径OA，直线l
是⊙O的切线吗？不是
2、直线l经过半径OA的外端A,直线l
是⊙O的切线吗？ 不是
温馨提示 ：在此定理中，题设是“经过
半径的外端”和“垂直于这条半径”， 两个条件缺一不可，否则就不是圆的切 线，
判定一条直线是圆的切线的三种方法
１、利用定义：与圆有唯一公共点的直线是圆 的切线。
分析：∵PA过⊙O上一点A，要证PA为切 线，只要证PA⊥AO，为此，作 半径AO， 只要证PA⊥AO即可。
课堂练习
7、如图，AB是半圆O的直径，点P在BA的延长线上， PD切⊙O于点C，BD⊥PD，垂足为D，连接BC． （1）求证：BC平分∠P12，求BD的长．
谢谢观赏
You made my day!
我们，还在路上……
A B
课堂练习
4、如图，已知：在△ABC中，AB＝AC，以AB为 直径作⊙O交BC于D，DE⊥AC于E， 求证：DE 是⊙O的切线。
分析：因为DE经过⊙O上的点D，所以要证明 DE为切线，可连结OD， 再证明DE⊥OD。
课堂练习
6、如图，BC为⊙O 直径，△ABC内接于⊙O， P、B、C在一直线上，且PA2＝PB·PC， 求证： PA是⊙O的切线。
2.5 直线与圆的位置关系第2课时切线的判定与性质 苏科版数学九年级上册教学课件
l A
课程讲授
2 切线的性质
我们可以用反证法证明
直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作 一条直径垂直于CD,垂足为M,
则OM<OA,即圆心到直线CD
的距离小于⊙O的半径,因CΒιβλιοθήκη 此,CD与⊙O相交.这与已知条
件“直线与⊙O相切”相矛盾.
所以AB与CD垂直.
B
O
M l
A
D
课程讲授
2 切线的性质
切线的性质定理： 圆的切线垂直于经过切点的_半__径__．
O
l A
课程讲授
2 切线的性质
例1 如图,△ABC 是⊙O的内接三角形，AB是⊙O的直 径，∠CAD=∠ABC.判断直线AD与⊙O的位置关系，并 说明理由.
解：直线AD与⊙O相切.
∵AB是⊙O的直径， ∴∠ACB=90°. ∴∠ABC+∠BAC=90°. 又∵∠CAD=∠ABC，
∴∠ODE=90°， ∴∠AED=90°，即DE⊥AC.
C
E D
A
B
O
课程讲授
2 切线的性质
练一练：如图，AB是⊙O的直径，PA切⊙O于点A， 线段PO交⊙O于点C，连接BC，若∠P=36°，则∠B等
于（ A）
A.27° B.32° C.36° D.54°
随堂练习
1.如图，点P为⊙O外一点，PA为⊙O的切线，A为切点，PO
随堂练习
6.如图，AB是⊙O的直径，点C为⊙O上一点，过点B作
BD⊥CD，垂足为点D，连接BC，BC平分∠ABD.
求证：CD为⊙O的切线.
证明 ∵BC平分∠ABD， ∴∠OBC=∠DBC. ∵OB=OC， ∴∠OBC=∠OCB, ∴∠OCB=∠DBC,
课程讲授
2 切线的性质
我们可以用反证法证明
直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作 一条直径垂直于CD,垂足为M,
则OM<OA,即圆心到直线CD
的距离小于⊙O的半径,因CΒιβλιοθήκη 此,CD与⊙O相交.这与已知条
件“直线与⊙O相切”相矛盾.
所以AB与CD垂直.
B
O
M l
A
D
课程讲授
2 切线的性质
切线的性质定理： 圆的切线垂直于经过切点的_半__径__．
O
l A
课程讲授
2 切线的性质
例1 如图,△ABC 是⊙O的内接三角形，AB是⊙O的直 径，∠CAD=∠ABC.判断直线AD与⊙O的位置关系，并 说明理由.
解：直线AD与⊙O相切.
∵AB是⊙O的直径， ∴∠ACB=90°. ∴∠ABC+∠BAC=90°. 又∵∠CAD=∠ABC，
∴∠ODE=90°， ∴∠AED=90°，即DE⊥AC.
C
E D
A
B
O
课程讲授
2 切线的性质
练一练：如图，AB是⊙O的直径，PA切⊙O于点A， 线段PO交⊙O于点C，连接BC，若∠P=36°，则∠B等
于（ A）
A.27° B.32° C.36° D.54°
随堂练习
1.如图，点P为⊙O外一点，PA为⊙O的切线，A为切点，PO
随堂练习
6.如图，AB是⊙O的直径，点C为⊙O上一点，过点B作
BD⊥CD，垂足为点D，连接BC，BC平分∠ABD.
求证：CD为⊙O的切线.
证明 ∵BC平分∠ABD， ∴∠OBC=∠DBC. ∵OB=OC， ∴∠OBC=∠OCB, ∴∠OCB=∠DBC,
苏科初中九年级上册数学《直线与圆的位置关系》PPT课件 (11)
辅助线提示：当条件中
出现切线时，通常要连接 切点与圆心，可得垂直。
例3 点O是∠DPC的角平分线上的一点，⊙O与 PD相切于A，
求证：PC与⊙O相切. D A
P
O
B
C
辅助线提示：要证切线，当“切点”不确定时， 过圆心作直线的垂线，证明 d=r.
课堂小结：
1、切线性质：
圆的切线垂直于经过切点的半径
2、切线的判定定理：
经过半径的外端并且垂直于这条半径 的直线是圆的切线。
课堂小结：
如何证明一直线是圆的切线？
1、当已有“切点”时，连接“切点”与圆心， 证垂直。
2、当“切点”不确定时，过圆心作直线的垂线， 证明 d=r.
作业
切线性质：
定理： 圆的切线垂直于经过切点的半径
C
D
切线的判定定理：
经过半径的外端并且垂直于这条半径的直线是 圆的切线。
例1 △ABC内接于⊙O，AB是⊙O的直径， ∠CAD=∠ABC，判断直线AD与⊙O的位置关系， 并说明理由.
B
DC
变式：如图，△ABC内接于⊙O，AB是⊙O的弦， ∠CAD=∠ABC，判断直线AD与⊙O的位置关系， 并说明理由。
;
②当 r=2 时，直线ＡＢ与⊙Ｃ
;
③当 r 时，直线ＡＢ与⊙Ｃ相切。
④当 r
时，线段ＡＢ与⊙Ｃ有一个公共点。
操作与探索：
按下面步骤画图： 1、在⊙O上任取一点A，连接OA； 2、过点A作直线 l ，使 l⊥OA;
直线 l 与⊙O位置关系如何? 你能说明理由吗？
切线的判定定理
经过半径的外端并且垂直于这条半径的 直线是圆的切线。
初中数学 九年级(上册)
2.5 直线与圆的位置 关系 （2）
出现切线时，通常要连接 切点与圆心，可得垂直。
例3 点O是∠DPC的角平分线上的一点，⊙O与 PD相切于A，
求证：PC与⊙O相切. D A
P
O
B
C
辅助线提示：要证切线，当“切点”不确定时， 过圆心作直线的垂线，证明 d=r.
课堂小结：
1、切线性质：
圆的切线垂直于经过切点的半径
2、切线的判定定理：
经过半径的外端并且垂直于这条半径 的直线是圆的切线。
课堂小结：
如何证明一直线是圆的切线？
1、当已有“切点”时，连接“切点”与圆心， 证垂直。
2、当“切点”不确定时，过圆心作直线的垂线， 证明 d=r.
作业
切线性质：
定理： 圆的切线垂直于经过切点的半径
C
D
切线的判定定理：
经过半径的外端并且垂直于这条半径的直线是 圆的切线。
例1 △ABC内接于⊙O，AB是⊙O的直径， ∠CAD=∠ABC，判断直线AD与⊙O的位置关系， 并说明理由.
B
DC
变式：如图，△ABC内接于⊙O，AB是⊙O的弦， ∠CAD=∠ABC，判断直线AD与⊙O的位置关系， 并说明理由。
;
②当 r=2 时，直线ＡＢ与⊙Ｃ
;
③当 r 时，直线ＡＢ与⊙Ｃ相切。
④当 r
时，线段ＡＢ与⊙Ｃ有一个公共点。
操作与探索：
按下面步骤画图： 1、在⊙O上任取一点A，连接OA； 2、过点A作直线 l ，使 l⊥OA;
直线 l 与⊙O位置关系如何? 你能说明理由吗？
切线的判定定理
经过半径的外端并且垂直于这条半径的 直线是圆的切线。
初中数学 九年级(上册)
2.5 直线与圆的位置 关系 （2）
苏科版九年级数学上册《2.5直线与圆的位置关系(三)》教学课件
（2）点D、E、F在⊙O上，分别过点D、E、F作 ⊙O的切线
与三角形各边都相切的圆叫做 三角形的内切圆
三角形的内切圆的圆心叫 做三角形的内心
图 23.2.12
这个三角形叫做圆的 外切三角形
三角形的内心就是三角形三条 内角平分线的交点 ，到三角形 三边距离相等.
解决问题
从一块三角形的材料上截下一块圆 形的用料，怎样才能使圆的面积尽 可能最大呢？
s lr
A
2
r rr Or
B
r 2s l
C
例题讲解
例4、已知：如图，E是△ABC的内心，∠A的
平分线交BC于点F，且与△ABC的外接圆相交
于点D
（1）求证：DB=DE
（2）若AD=8，DF：FA=1:3，
求DE的长.
√√
× × √
例题讲解
例5、如图，⊙O是△ABC的内切圆，与AB、 BC、CA分别相切于点D、E、F，∠DEF=45 度．连接BO并延长交AC于点G，AB=4， AG=2． （1）求∠A的度数； （2）求⊙O的半径．
A
F
I
E
B
C D
例题讲解
例2、如图，在△ABC中， ∠A=50 °，点
O是内心，求∠ BOC的度数。
A
如果∠ A=n °，
O
那么∠ BOC=?
B
C
因此：在△ABC中，∠A＝n °，点O是
△ABC的内心，∠BOC＝90 °＋ 1n °
2
例题讲解
例3、已知：一块三角形的白铁片,量得三边 的长分别为5cm , 12cm, 13cm.从这块白铁片 上能剪下最大的圆的半径是多少长? 。
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月下午7时24分21.11.819:24November 8, 2021
与三角形各边都相切的圆叫做 三角形的内切圆
三角形的内切圆的圆心叫 做三角形的内心
图 23.2.12
这个三角形叫做圆的 外切三角形
三角形的内心就是三角形三条 内角平分线的交点 ，到三角形 三边距离相等.
解决问题
从一块三角形的材料上截下一块圆 形的用料，怎样才能使圆的面积尽 可能最大呢？
s lr
A
2
r rr Or
B
r 2s l
C
例题讲解
例4、已知：如图，E是△ABC的内心，∠A的
平分线交BC于点F，且与△ABC的外接圆相交
于点D
（1）求证：DB=DE
（2）若AD=8，DF：FA=1:3，
求DE的长.
√√
× × √
例题讲解
例5、如图，⊙O是△ABC的内切圆，与AB、 BC、CA分别相切于点D、E、F，∠DEF=45 度．连接BO并延长交AC于点G，AB=4， AG=2． （1）求∠A的度数； （2）求⊙O的半径．
A
F
I
E
B
C D
例题讲解
例2、如图，在△ABC中， ∠A=50 °，点
O是内心，求∠ BOC的度数。
A
如果∠ A=n °，
O
那么∠ BOC=?
B
C
因此：在△ABC中，∠A＝n °，点O是
△ABC的内心，∠BOC＝90 °＋ 1n °
2
例题讲解
例3、已知：一块三角形的白铁片,量得三边 的长分别为5cm , 12cm, 13cm.从这块白铁片 上能剪下最大的圆的半径是多少长? 。
6、“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”。2021年11月下午7时24分21.11.819:24November 8, 2021
苏科版九年级数学上册2.5 直线与圆的位置关系(4)课件
O
DO
P
E
点在圆上时，只能画一条切线 ．
2.5 直线与圆的位置关系（4）
请你画一画
点在圆外时．
点在圆外时，可以画两条切线．
2.5 直线与圆的位置关系（4）
请你说一说
在经过圆外一
A
点的切线上，这一
点和切点之间的线
段的长叫做这点到
O·
P
圆的切线长．
切线与切线长的区别与联系：
B
（1）切线是一条与圆相切的直线；
∴OA⊥PA，OB⊥PB 即∠OAP＝∠OBP＝90°．
∵ OA＝OB，OP＝OP．
∴Rt△AOP≌Rt△BOP(HL) ． ∴ PA ＝ PB， ∠OPA＝∠OPB ．
试用文字语言 叙述你所发现 的结论．
2.5 直线与圆的位置关系（4）
请你说一说
切线长定理 从圆外一
B
点引圆的两条切线，它
们的切线长相等，圆心
求⊙O的半径r.
A
6-r
D 6-r
8-r
OF6
r
B 8-r 8 E r C
2.5 直线与圆的位置关系（4）
课堂总结
1．这节课你有哪些收获和困惑？ 2．切线与切线长的区别与联系？
2.5 直线与圆的位置关系（4）
课后作业
1．课本P72第1、2． 2．阅读课本P75～76．
2.5 直线与圆的位置关系（4）
3．如图，如图AB是⊙O的直径，C为圆上任 意一点，过C的切线分别与过A、B两点的切线交 于P、Q，则∠POQ的度数为 90 °.若AP＝2， BQ＝5，则⊙O的半径为 10 .
2.5 直线与圆的位置关系（4）
拓展提升
如图，△ABC中,∠C＝90º，且AC＝6，BC＝8，
初中数学九年级上册《2.5 直线与圆的位置关系》PPT课件 (7)
练习1：已知：如图，△ABC中，AC＝BC，以
BC为直径的⊙O交AB于点D，过点D作DE⊥AC于 点E，交BC的延长线于点F．
求证：（1）AD＝BD；（2）DF是⊙O的切线．
A
D
B O
E
F C
例2.（1）如图，AB是⊙O的直径，直线AT 经过A，且∠CAT=∠B。求证：AT是⊙O的 切线。
O
A
B
练习2：如图，AB=AC，以AB为直径的⊙O交BC 于D，DE⊥AC于E．
求证：DE与⊙O相切．
练习2：如图，AB=AC，以AB为直径的⊙O交BC 于D，DE⊥AC于E．
求证：DE与⊙O相切．
如图，A是⊙O外一点，连OA交⊙O于C，过 ⊙O上一点P作OA的垂线交OA于F，交⊙O于E， 连结PA，若∠FPC=∠CPA，
切线的判定定理：经过半径的外端并且垂直 于这条半径的直线是圆的切线．
练习1 判断下列命题是否正确．
(1)经过半径外端的直线是圆的切线．
(2)垂直于半径的直线是圆的切线．
(3)过直径的外端并且垂直于这条直径的直线是圆 的切线．
(4)和圆有一个公共点的直线是圆的切线．
(5)以等腰三角形的顶点为圆心，底边上的高为半 径的圆与底边相切．
_______________C__________C_____________
O
C
A
D
（ 1）
O
A
D
（ 2）
O
A
D （ 3）
(2)想一想，另外两幅图中的直线CD只要作怎样 的变换就能成为圆的切线？
______________________________________；
______________________________________
苏科版-数学-九年级上册-2.5 直线与圆的位置关系第2课时 课件
解答：（1）证明：连接OD， ∵AD平分∠CAB， ∴∠OAD=∠EAD. ∵OE=OA, ∴∠ODA=∠OAD. ∴∠ODA=∠EAD. ∴OD//AE. ∵∠ODF=∠AEF=90°且D在⊙O上， ∴EF与⊙O相切.
解答：（2）连接BD，作DG⊥AB与G,
∵AB是⊙O的直径，
∴∠ADB=90°,
解：直线AD与⊙O相切 ∵AB是⊙O的直径，∴∠ACB=90°， ∴∠ABC +∠BAC =90° 又∵∠CAD=∠ABC ∴∠CAD +∠BAC =90° 即AD⊥AB. ∴直线AD与⊙O相切（经过半径的外端并且垂直于这条半径 的直线是圆的切线）.
例2 如图2-44，AB是⊙O的直径，弦AD平分∠BAC，过 点D的切线交AC与点E.DE与AC有怎样的位置关系？为什 么？
因此,当半径长为 2 3cm时,AB与⊙C相切. 模型“双垂直三角形”
你可曾认识？
切线性质的应用
1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.
(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这
两个圆与AB分别有怎样的位置关系? 解:(2)由(1)可知,圆心到AB的距离
A D
d= 2 3cm,所以 当r=2cm时,d>r,AB与⊙C相离; 当r=4cm时,d<r,AB与⊙C相交.
解：DE与AC互相垂直. 连接OD. ∵OD=OA， ∴∠ODA=∠OAD. 又∵∠OAD=∠CAD， ∴∠ODA=∠CAD. ∴OD//AC. ∵DE是⊙O的切线， ∴DE⊥OD（圆的切线垂直于经过切点的半径）， 即∠ODE =90° 于是，∠DEA =90°，DE⊥AC.
练习1：如图，AB是⊙O的直径，点C,D在⊙O上，且AD平 分∠CAB,过点D作AC的垂线，与AC的延长线相交于点E， 与AB的延长线相交于点F。 （1）求证：EF与⊙O相切； （2）若AB=6，AD= 4 2，求EF的长。
《直线与圆的位置关系》PPT
（2）
（3）
l
·O
·O
l
·O
l
相离 （4）
相交
相切
·O
相交
l
思考讨论
O
l
相交
O
Al
相切
O
l
相离
上述变化过程中，除了公共点的个数发生了变化， 还有什么量在改变？你能否用数量关系来判别直线 与圆的位置关系？
温馨提示
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线 的距离.
.A
D
l
二、直线与圆的位置关系量化
直线和圆没有公共点,这时我们就说这条直线和圆相离.
一、直线与圆的位置关系（公共点的个数）
1.直线和圆的位置关系有三种(从直线与圆
公共点的个数) 2.用图形表示如下:
有两个公共点
有一个公共点
没有公共点
.o
l
相交
.o
.
.o
l
l
相切
相离
交 点
割 线
切 点
切 线
请你判断
看图判断直线l与⊙O的位置关系.
（1）
O 30°
2.5
MC= 1 OM= 1 x5=2.5
2
2
5M
B
即圆心 M 到OA的距离 d = 2.5 cm.
(1) 当 r = 2 cm 时，有 d > r, 因此⊙M 和 直线OA 相离. (2) 当 r = 4 cm 时，有 d < r, 因此⊙M 和直线O A 相交.
(3) 当 r = 2.5cm 时，有 d = r ，因此⊙M 和直线 OA 相切.
PPT素材：/sucai/ PPT图表：/tubiao/ PPT教程： /powerpoint/ 范文下载：/fanwen/ 教案下载：/jiaoan/ PPT课件：/kejian/
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第 1 页 共 3 页
2.5 直线与圆的位置关系 课件(共98张PPT)
2023-2024学年苏科数学九年级上册
(共98张PPT)
直线与圆的位置关系
新课导入
山水相接的地方出现了一道红霞。过了一会儿，那里出现了太阳的小
半边脸，慢慢儿，一纵一纵地使劲儿向上升。到了最后它终于冲破了
云霞，完全跳出了海面，
操作与思考
在纸上画一个圆，上、下移动直尺，如果将直尺的边缘看作一条直线，
那么在移动直尺的过程中，直线与圆的位置关系发生了怎样的变化
这种位置的变化可以用数量之间的关系来描述吗
答案
按照教材中图形的变化顺序,直线与圆的位置关系分别为:有两个公共
点、有一个公共点、没有公共点.因位置关系的变化而引起的数量关
系的变化依次为:圆心到直线的距离小于半径、圆心到直线的距离等
于半径、圆心到直线的距离大于半径.
OD⊥l，垂足为D，⊥O的半径为r
①中，直线l与⊥O有两个公共点，ODr
于是，我们得到如下结论:
如果⊥O的半径为r，圆心O到直线l的距离为d，那么
第 2 页 共 3 页
直线l与⊥O相交dr
思考与探索(教材第 64 页)
点与圆有3种不同的位置关系，直线与圆也有3种不同的位置关系，
这两者之间有怎样的联系
从图2-37中可以看出，直线l与⊥O的3种位置关系，实质上就是点
D《垂足》与⊥O的3种位置关系
将“直线与圆的位置关系”转化为“点(圆心到直线的垂线段的垂足)与
圆的位置关系”进行研究:
当点(垂足)在圆内时,直线与圆相交
当点(垂足)在圆上时,直线与圆相切
当点(垂足)在圆外时,直线与圆相离.
例1
在⊥ABC中，⊥A=45°,AC=4.以点C为圆心，r为半径的圆与AB所在直
线有怎样的位置关系
(1)r=2 (2)r= (3)r=3
例1答案
解:过点C作CD⊥AB，垂足为D，在Rt⊥ACD中
⊥⊥A=45°
⊥⊥ACD=⊥A,CD – AD
又⊥ ，AC = 4,
⊥ =16, CD=
即圆心C到AB所在直线的距离d=
第 3 页 共 3 页
相离
(1)当r-2时,d>r，⊥C与AB所在直线相离
相切
(2)当r=2V2时d=r ⊥C与AB所在直线相切
相交
(3)当r-3时,dr,所以圆与 AB 所在的直线相离
(2)当r=2.4 时,因为 d=r,所以圆与 AB 所在的直线相切
(3)当r=3时,因为 dR+r;
两圆外切d=R+r;
两圆相交R-rr)
两圆内切d=R-r(R> r)
两圆内含dr)
图形的位置关系决定了相应数量之间的关系，反过来，由数量之间的
关系可以判定图形的位置关系。