线面、面面平行和垂直的八大定理
线面定理性质

线面、面面平行和垂直的定理性质
一、线面平行
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:
二、面面平行
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示:
变形:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示:
(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示:
(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
变形:垂直于同一条直线的两个平面平行
四、面面垂直
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
(如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直)
其他:两个平面相交,如果它们所成的二面角是直角,则这两个平面互相垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
立体几何八个定理
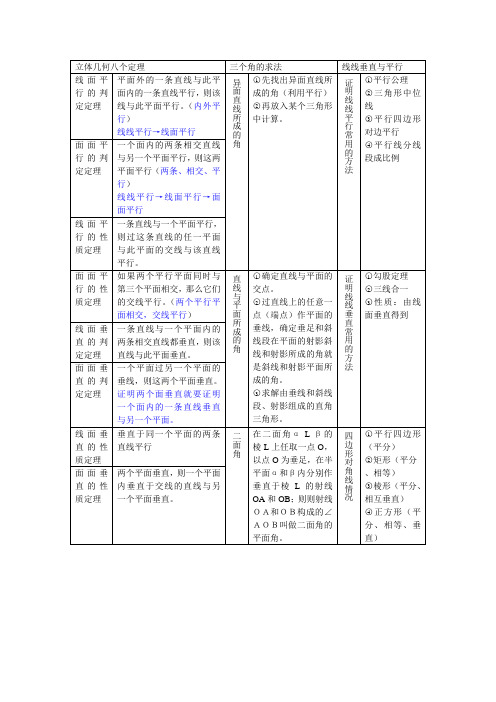
三个角的求法
线线垂直与平行
线面平行的判定定理
平面外的一条直线与此平面内的一条直线平行,则该线与此平面平行。(内外平行)
线线平行→线面平行
异面直线所成的角
先找出异面直线所成的角(利用平行)
再放入某个三角形中计算。
证明线线平行常用的方法
平行公理
三角形中位线
平行四边形对边平行
平行线分线段成比例
四边形对角线情况
平行四边形(平分)
矩形(平分
、相等)
棱形(平分、相互垂直)
正方形(平分直于交线的直线与另一个平面垂直。
面面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。证明两个面垂直就要证明一个面内的一条直线垂直与另一个平面。
线面垂直的性质定理
垂直于同一个平面的两条直线平行
二面角
在二面角α-L-β的棱L上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱L的射线OA和OB;则则射线OA和OB构成的∠AOB叫做二面角的平面角。
面面平行的判定定理
一个面内的两条相交直线与另一个平面平行,则这两平面平行(两条、相交、平行)
线线平行→线面平行→面面平行
线面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
面面平行的性质定理
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。(两个平行平面相交,交线平行)
直线与平面所成的角
确定直线与平面的交点。
过直线上的任意一点(端点)作平面的垂线,确定垂足和斜线段在平面的射影斜线和射影所成的角就是斜线和射影平面所成的角。
求解由垂线和斜线段、射影组成的直角三角形。
证明线线垂直常用的方法
面面平行的性质定理是什么

面面平行的性质定理是什么
面面平行的性质定理:
1、如果两个平面垂直于同一条直线,那么这两个平面平行。
2、如果一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行。
3、如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
扩展资料
一、线线平行
1、同位角相等两直线平行:在同一平面内,两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
2、内错角相等两直线平行:在同一平面内,两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
3、同旁内角互补两直线平行。
二、线面平行
1、利用定义:证明直线与平面无公共点;
2、利用判定定理:从直线与直线平行得到直线与平面平行;
3、利用面面平行的性质:两个平面平行,则一个平面内的'直线必平行于另一个平面。
平行平面间的距离处处相等。
已知:α∥β,AB⊥α,DC⊥α,且A、D∈α,B、C∈β求证:AB=CD证明:连接AD、BC由线面垂直的性质定理可知AB∥CD,那么AB和CD构成了平面ABCD∵平面ABCD∩α=AD,平面ABCD∩β=BC,且α∥β∴AD∥BC(定理2)∴四边形ABCD是平行四边形∴AB=CD。
(完整版)立体几何八大定理
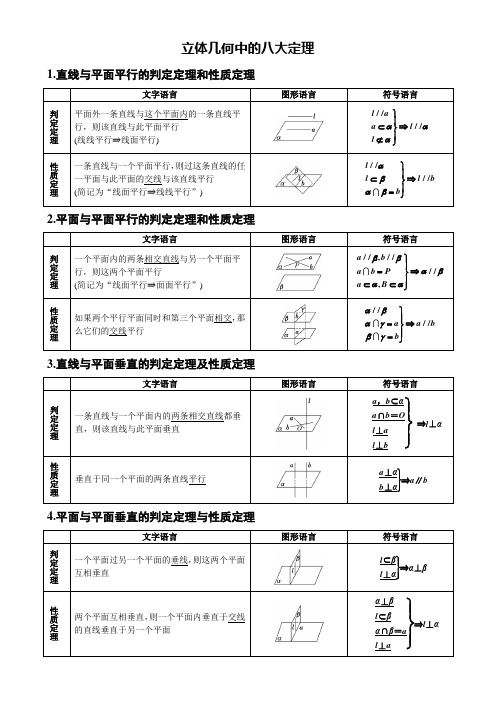
立体几何中的八大定理1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与这个平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)////l aa llααα⎫⎪⊂⇒⎬⎪⊄⎭性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)////ll l bbαβαβ⎫⎪⊂⇒⎬⎪=⎭2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)//,////,a ba b Pa Bββαβαα⎫⎪=⇒⎬⎪⊂⊂⎭性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行////a a bbαβαγβγ⎫⎪=⇒⎬⎪=⎭3.直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a,b⊂αa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b4.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α。
最新高中立体几何八大定理

lmβααba线面位置关系的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行图形语言: 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理:文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行nmAαaαbaBA l βαaβα五、直线与平面垂直的判定定理: 文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言: 符号语言: ,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行 图形语言: 符号语言://a a b b αα⊥⎫⇒⎬⊥⎭作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理: 文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直 2016-2017学年度全等三角形单元测试卷总分:120分; 考试时间:120分钟; 难度系数:0.70 命题人:张少春学校:___________姓名:___________分数:___________一、选择题(共30分,每题3分) 1.下列命题中正确的是( )A .有两条边相等的两个等腰三角形全等B .两腰对应相等的两个等腰三角形全等C .两角对应相等的两个等腰三角形全等D .一边对应相等的两个等边三角形全等 2.面积相等的两个三角形( ) A .必定全等 B .必定不全等 C .不一定全等 D .以上答案都不对3.如图,CE ⊥AB ,DF ⊥AB ,垂足分别为E 、F ,AC ∥DB ,且AC=BD ,那么Rt △AEC ≌Rt △BFC 的理由是( )A .SSSB .AASC .SASD .HL4.如图,在△ABC 中,AB=AC , AD 是∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,则下列说法:①DA 平分∠EDF ;②AE=AF ,DE=DF ;③AD 上任意一点到B 、C 两点的距离相等;④图中共有3对全等三角形,其中正确的有A .4个B .3个C .2个D .1个5.如图,△ABC ≌△AEF ,AB=AE ,∠B=∠E ,则对于结论①AC=AF ,②∠FAB=∠EAB ,③EF=BC ,④∠EAB=∠FAC ,其中正确结论的个数是( )A .1个B .2个C .3个D .4个6.如图,AB ∥CD ,BP 和CP 分别平分∠ABC 和∠DCB ,AD 过点P ,且与AB 垂直.若AD=8,则点P 到BC 的距离是( )A .8B .6C .4D .27.如图,在△ABC 中,∠ACB=90°,BE 平分∠ABC ,DE ⊥第3题第5题第3题第4题。
立体几何平行垂直的判定定理与性质定理总结

1线面平行的判定定理:
如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
2线面平行的性质定理:
一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
3面面平行的判定定理:
如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
4面面平行的性质定理:
两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
. 5线面垂直的判定定理:
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
6线面垂直的性质定理:
垂直于同一个平面的两条直线平行.
7面面垂直的判定定理:
如果一个平面过另一个平面的垂线,那么这两个平面垂直.
8面面垂直的性质定理:
两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.。
立体几何八个定理默写_含答案

2014学年高二数学---1028立体几何“平行、垂直”定理默写给你定理的图形语言,请写出定理的文字语言(即类似原话的叙述)、以及符号语言:文字语言: 符号语言:图形语言:② 面面平行的判定定理——线面平行 则面面平行文字语言: 符号语言: 图形语言:③ 线面平行的性质定理——线面平行 则线线平行文字语言: 符号语言: 图形语言:④ 面面平行的性质定理——面面平行 则线线平行文字语言: 符号语言: 图形语言:▲平行的其它结论:(1) 若面面平行,则一面内任一线平行于另一面。
(2) 等角定理:若两个角的边对应平行,则这两个角相等或互补。
⑤ 线面垂直的判定定理——线线垂直 则线面垂直 文字语言: 符号语言: 图形语言:⑥ 面面垂直的判定定理——线面垂直 则面面垂直文字语言: 符号语言: 图形语言:⑦ 线面垂直的性质定理:(这个还是线面垂直的定义“线面垂直则线线垂直”有用,故用定义代替定理)文字语言: 符号语言: ④ 面面平行的性⑤ 线面垂直的判⑦ 线面垂直的性⑧ 面面垂直的性⑧ 面面垂直的性质定理:面面垂直 则线面垂直文字语言: 符号语言: 图形语言:▲垂直的其它结论:(1)若两平行线中的一条垂直于一面,则另一条也垂直于该面。
(2)若两直线都垂直于一面,则这两直线平行。
(这个是书上的线面垂直性质定理)(3)若两平面垂直,则过一面内一点与另一面垂直的直线,必在该面内。
答案1、八个定理——立体几何的证明的依据、更是证明的思路:① 线面平行的判定定理——线线平行,则线面平行文字语言: 符号语言: 图形语言: 平面外一条直线与此平面 内的一条直线平行,则此直线与此平面平行。
② 面面平行的判定定理——线面平行,则面面平行文字语言: 符号语言: 图形语言: 一个平面内的两条相交 直线与另一个平面平行,则这两个平行平行。
③ 线面平行的性质定理——线面平行,则线线平行文字语言: 符号语言: 图形语言: 一条直线与一个平面平行, 则过这条直线的任一平面与此平面的交线与该直线平行。
立体几何八大定理
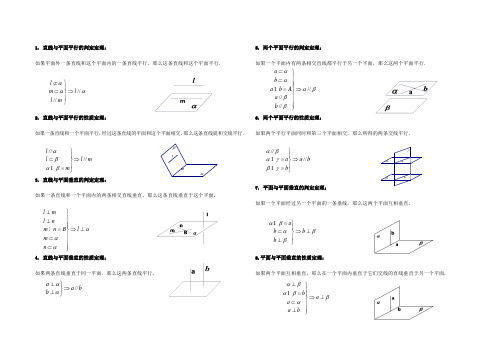
1. 直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.2. 直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.m l m l l ////⇒⎪⎭⎪⎬⎫=⊂βαβα 3. 直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面.l ml n m n B l m n ααα⊥⎫⎪⊥⎪⎪=⇒⊥⎬⎪⊂⎪⊂⎪⎭4. 直线与平面垂直的性质定理:如果两条直线垂直于同一平面,那么这两条直线平行. b a b a //⇒⎭⎬⎫⊥⊥αα5. 两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.6. 两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行.b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα7. 平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.8.平面与平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.βαmlβαββαα//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=⊂⊂b a A b a b aββαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=b b b a ααα////l m l m l ⇒⎪⎭⎪⎬⎫⊂⊄γbaβαβαβαβα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⊥a b a a b。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面、面面平行和垂直的八大定理
一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平
面平行。符合表示: ////ababa
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,
那么这条直线和交线平行。 符号表示:
babaaa////
二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条
相交直线,那么这两个平面平行。
符号表示: //////NnmMbaambn
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示:
dldl////
(更加实用的性质:一个平
面内的任一直线平行另一平面)
三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直
线垂直这个平面。 符号表示: aMcbbaca
$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平
面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:
PAaAoAapooAa
2、性质定理:垂直同一平面的两条直线互相平行。(更加实用的性质是:一个平
面的垂线垂直于该平面内任一直线。)
四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
aa,
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一
个平面。abaab,,,
