山东省淄博市沂源2013届高三第二次模拟数学文试题(word版)
山东省德州市2013届高三第二次模拟考试数学(文)试题 Word版含答案

山东省德州市2013届高三第二次模拟考试数学(文)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟。
注意事项:选择题为四选一题目.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.把正确答案涂在答题卡上.1.设集合U={0,l,2,3,4,5,6},M ={l,3,5},N={2,4,6},则(U M)(UN)=A.{0} B.{1,3,5} C.{2,4,6} D.{0,1,2,3,4,5,6}2.设i为虚数单位,则复数34 12ii-++=A.-1 +2i B.1+2i C.-1-2i D.1-2i 3.在空间中,不同的直线m,n,l,不同的平面,αβ,则下列命题正确的是A.m//α,n∥α,则m∥n B.m//α,m//β,则α//βC.m⊥l,n⊥l,则m∥n D.m⊥α,m⊥β,则α//β4.已知变量x、y满足条件12xyx y≥⎧⎪≤⎨⎪-≤⎩,则x+y的最小值是A.4 B.3 C.2 D.15.已知函数f(x)=4-x2,y=g(x)是定义在R上的奇函数,当x>0时,g(x)=log2x,则函数f(x)·g(x)的大致图象为6.已知sin(2)44πα-=,则sin2α=A .34B .-34C .1516D .-15167.执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为 A .17 B .16 C .10 D .98.若双曲线2x m-y 2=4(m>0)的焦距为8,则它的离心率为A .23B .2C .43D .4159.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为 A .68 B . 68.2 C .68.5D .7510.若对于定义在R 上的函数f (x ),存在常数()t t R ∈,使得f (x+t )+tf (x )=0对任意实数x 均成立,则称f (x )是t 阶回旋函数,则下面命题正确的是 A .f (x )=log a x 是0阶回旋函数 B .f (x )=sin (πx )是1阶回旋函数 C .f (x )=2x 是12-阶回旋函数 D .f (x )=x 2是1阶回旋函数11.给出下列命题:①若a ,b ∈R +,a≠b ,则a 3 +b 3>a 2b+ ab 2;②若a ,b ∈R +,a<b ,则a m ab m b +>+; ③若a ,b ,c ∈R +,则bc ac ab a b c++≥a+b+c ; ④若3x+y=l ,则11423x y+≥+ 其中正确命题的个数为 A .1个 B .2个C .3个D .4个12.已知f (x )为R 上的可导函数,且x ∀∈R ,均有f (x )()f x '>,则有 A .e 2013 f (-2013)<f (0),f (2013)>e 2013f (0) B .e2013f (-2013)< f (0),f (2013)<e 2013f (0) C .e 2013 f (-2013)>f (0),f (2013)>e 2013f (0) D .e 2013 f (-2013)>f (0),f (2013)<e 2013f (0)第Ⅱ卷 (共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题纸的相应位置. 13.为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9), [10,19),[20,29),[30,39),[40,49)五层。
山东省临沂市2013届高三5月模拟(二模)数学理试题(WORD解析版)

临沂市2013年高考模拟试题(二模)理科数学2013.5本试卷分为选择题和非选择题两部分,共4页,满分150分。
考试时间120分钟. 注意事项:1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上.2.第1卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数3i 12i+(i 是虚数单位)的实部是(A )25 (B )25- (C )15 (D )15- 【答案】B【解析】3(12)22112(12)(12)555i i i i i i i i ----===--++-,所以实部是25-,选B. 2.集合{}{}32,log ,,,M a N a b ==若{}1M N = ,则M ∪N =(A ){}0,1,2 (B ){}0,1,3 (C ){}0,2,3 (D ){}1,2,3 【答案】D【解析】因为{}1M N = ,所以3log 1a =,即3a =,所以1b =,即{}{}2,1,3,1M N ==,所以{}2,1,3M N = ,选D.3.某商品的销售量y (件)与销售价格x (元/件)存在线性相关关系,根据一组样本数据(,)(1,2,)i i x y i n =…,,用最小二乘法建立的回归方程为ˆ10200,yx =-+则下列结论正确的是 (A )y 与x 具有正的线性相关关系(B )若r 表示变量y 与x 之间的线性相关系数,则10r =- (C )当销售价格为10元时,销售量为100件 (D )当销售价格为10元时,销售量为100件左右 【答案】D【解析】当销售价格为10元时, ˆ1010200100y=-⨯+=,即销售量为100件左右,选D. 4.平面向量a 与b 的夹角为60°,(2,0),1,==a b 则2+=a b (A )3 (B )23 (C )4 (D )12 【答案】B【解析】因为2,1a b ==,所以1c o s 60212a b a b ⋅=⋅=⨯=,所以2222442441223a a b b +=+⋅+=++== a b ,选B.5.执行如图所示的程序框图,输出的结果是(A )11 (B )12 (C )13 (D )14【答案】C【解析】第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选C.开始0,1,2x y z ===z x y=+y z = x y=z ≤10 是否 输出z结束第5题图6.函数sine()xy x=-π≤≤π的大致图象为【答案】D【解析】因为函数为非奇非偶函数,所以排除A,C.函数的导数为sin'cosxy e x=⋅由sin'cos0xy e x=⋅=,得cos0x=,此时2xπ=或2xπ=-。
山东临沂2013高三5月高考模拟--数学文

2013年高考模拟试题文科数学2013.5本试卷分为选择题和非选择题两部分,共4页,满分150分.考试时间120分钟. 注意事项:1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷 (选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设1i z =+(i 是虚数单位),则22zz+等于(A )1i + (B )1i -+ (C )i - (D )1i --2.已知集合{}0=A y y A B B =∣≥,,则集合B 可能是(A ){}=0y y x ∣≥ (B ){}1=2xyy x ⎛⎫∈ ⎪⎝⎭R ∣,(C ){}=ln 0yy x x ∣,>(D )R3.下列函数中既是偶函数,又在区间0+∞(,)上单调递增的函数是 (A )3y x = (B )||1y x =+(C )21y x =-+ (D )2x y =4.某班共有52人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号同学在样本中,那么样本中还有一个同学的学号是 (A )10 (B )11 (C )12 (D )165.将函数sin y x =的图象向右平移2π个单位长度,再向上平移1个单位长度,则所得的图象对应的解析式为(A )1sin y x =- (B )1sin y x =+ (C )1cos y x =- (D )1cos y x =+ 6.曲线e x y =在点A 处的切线与直线30x y -+=平行,则点A 的坐标为 (A )()11,e -- (B )()0,1(C )()1,e (D )()0,27.阅读如图所示的程序框图,若输入变量n 为100,则输出变量S 为 (A )2500 (B )2550 (C )2600 (D )2650 8.给出如下四个命题:①若“p ∧q ”为假命题,则p ,q 均为假命题;②命题“若a b >,则221a b ->”的否命题为“若a b ≤,则221a b -≤”; ③命题“任意2,10x x ∈+R ≥”的否定是“存在200,10x x ∈+R <”; ④在△ABC 中,“A B >”是“sin sin A B >”的充要条件. 其中不正确...命题的个数是 (A )4 (B )3 (C )2 (D )1 9.设第一象限内的点(,x y )满足2400x y x y --⎧⎨-⎩,,≤≥若目标函数(0,0)z ax by a b =+>>的最大值是4,则11a b+的最小值为(A )3 (B )4 (C )8 (D )9 10.函数ln sin (,0)y x x x =-≠∣∣π<<π且的图象大致是(A ) (B ) (C ) (D )11.多面体MN -ABCD 的底面ABCD 为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则AM 的长(A(B(C(D)12.已知329()6,,()()()02f x x x x abc a b c f a f b f c =-+-===<<且,现给出如下结论:①(0)(1)0f f >;②(0)(1)0f f <;③(0)(2)0f f >;④(0)(2)0f f <.其中正确结论的序号为:(A )①③ (B )①④ (C )②④ (D )②③第7题图2013年高考模拟试题文科数学2013.5第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.把正确答案填写在答题纸给定的横线上.13.若△ABC 的边,,a b c 满足2224a b c +-=,且C =60°,则ab 的值为 . 14.已知圆C :2218x y +=,直线l :4325,x y +=则圆C 上任一点到直线l 的距离小于2的概率为 .15.假设关于某设备的使用年限x 和所支出的维修费y (万元)有如下的统计资料: 使用年限x 2 3 4 5 6 维修费用y 2.2 3.8 5.5 6.5 7.0由资料可知y 和x 呈线性相关关系,由表中数据算出线性回归方程ˆˆˆy bx a=+中的ˆ123,b =. 据此估计,使用年限为10年时的维修费用是 万元. 16.已知双曲线22221(0,0)x y a b a b -=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4,且双曲线的一条渐近线与抛物线准线的交点坐标为(2,1--),则双曲线的焦距为 .三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知2,0(1,sin()),(cos 3sin ),2x x xωωωωπ∈=+=R >,u v 函数1()2=⋅-f x u v 的最小正周期为π.(Ⅰ)求ω的值; (Ⅱ)求函数()f x 在区间[0,]2π上的值域.18.(本小题满分12分)已知点(1,2)是函数()(01)x f x a a a =≠>且的图象上一点,数列{}n a 的前n 项和()1n S f n =-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)将数列{}n a 前2013项中的第3项,第6项,…,第3k 项删去,求数列{}n a 前122013项中剩余项的和.19.(本小题满分12分)如图,AD ⊥平面ABC ,AD ∥CE ,AC =AD =AB =1,∠BAC =90°,凸多面体ABCED 的体积为12,F 为BC 的中点.(Ⅰ)求证:AF ∥平面BDE ;(Ⅱ)求证:平面BDE ⊥平面BCE .20.(本小题满分12分)某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格. (Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.21.(本小题满分12分) 设函数()ln f x x ax =-. (Ⅰ)求()f x 的单调区间; (Ⅱ)若1,()(()1),(1)2a g x x f x x ==+>,且()g x 在区间(,1)k k +内存在极值,求整第19题图第20题图22221(0)x y a b a b+=>>数k 的值.22.(本小题满分14分) 如图,已知椭圆C : 的左、右焦点分别为F 1、F 2,离心率为2,点A 是椭圆上任一点,△AF 1F 2的周长为. (Ⅰ)求椭圆C 的方程;(Ⅱ)过点Q (-4,0)任作一动直线l 交椭圆C 于M ,N 两点,记MQ QN λ=,若在线段MN 上取一点R ,使得MR RN λ=-,则当直线l 转动时,点R 在某一定直线上运动,求该定直线的方程.2013年高考模拟试题文科数学参考答案及评分标准2013.5说明:一、本解答只给出了一种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容参照评分标准酌情赋分.二、当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容与难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确答案应得分数的一半;如果后继部分的解答有较严重的错误或又出现错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分. 一、选择题:(每小题5分,满分60分)1.(A)2.(B)3.(B)4.(D)5.(C)6.(B)7.(B)8.(D)9.(B) 10.(C) 11.(C) 12.(D) 二、填空题:(每小题4分,满分16分) 13. 4 14. 1415. 12.3816. 三、解答题:17.解:(Ⅰ)依据题意,211()(1,sin())(cos )222f x x x x ωωω=-=+⋅-πu v21cos cos2x x x ωωω=⋅-………………………………(1分)1cos 2122221cos 2222x x x x ωωωω+=+-=+sin(2)6x ω=+π.…………………………………………………(4分)0ω>,函数的最小正周期T =π,2222, 1.T ωω∴===∴=πππ………………………………………(6分) (Ⅱ)由(Ⅰ)知()sin(2)6f x x =+π ………………………………(7分)当02x π≤≤时,可得72666x +ππ≤≤π………………………(8分)有1sin(2)126x -+π≤≤…………………………………………(11分) 所以函数()y f x =在[0,]2π上的值域是1[,1]2-………………(12分)18.解:(Ⅰ)把点(1,2)代入函数()x f x a =,得2a =.……………………(1分)()121,n n S f n ∴=-=-…………………………………………(2分)当1n =时,111211;a S ==-=…………………………………(3分)当2n ≥时,1n n n a S S -=-1(21)(21)n n -=---12n -=……………………………………………(5分) 经验证可知1n =时,也适合上式,12n n a -∴=.…………………………………………………………(6分)(Ⅱ)由(Ⅰ)知数列{}n a 为等比数列,公比为2,故其第3项,第6项,…,第2013项也为等比数列,首项31324,a -==公比32012201328,2a ==为其第671项………………………………………………………………(8分)∴此数列的和为67120134(18)4(21)187--=-……………………(10分)又数列{}n a 的前2013项和为2013201320131(12)21,12S ⨯-==--…………………………………(11分) ∴所求剩余项的和为2013201320134(21)3(21)(21)77----=…(12分)19.(Ⅰ)证明:∵AD ⊥平面ABC ,AC ⊂面ABC ,AB ⊂面ABC ,∴AD ⊥AC ,AD ⊥AB , ∵AD ∥CE ,∴CE ⊥AC∴四边形ACED 为直角梯形.……………(1又∵∠BAC =90°,∴AB ⊥AC ,∴AB ⊥面ACED . ………………(2分)∴凸多面体ABCED 的体积13ACED V S AB=⋅⋅111(1)11,322CE =⨯⨯+⨯⨯= 求得CE =2.……………………………………………………(3分)取BE 的中点G ,连结GF ,GD , 则GF ∥EC ,GF12=CE =1,∴GF ∥AD ,GF =AD ,四边形ADGF 为平行四边形,∴AF ∥DG .………………………………………………………(5分) 又∵GD ⊂面BDE ,AF ⊄面BDE ,∴AF ∥平面BDE .………………………………………………(7分) (Ⅱ)证明:∵AB =AC ,F 为BC 的中点,∴AF ⊥BC .………………………………………………………(8分) 由(Ⅰ)知AD ⊥平面ABC ,AD ∥GF ,∴GF ⊥面ABC .∵AF ⊂面ABC ,∴AF ⊥GF . ……………………………………(9分) 又B CG F =F ,∴A F ⊥面B C E .…………………………………(10分)又∵D G ∥A F ,∴D G ⊥面B C E .……………………………(11分) ∵D G ⊂面B D E ,∴面B D E ⊥面B C E .……………………(12分)第19题图20.解:(Ⅰ)设第(1,2,3,4)i i =组的频率为if ,则由频率分布直方图知41(0.0140.030.036)100.2f =-++⨯=…………………………(2分)所以成绩在85分以上的同学的概率P ≈340.03610+0.20.38,22ff ⨯=+= …………………………………(5分) 故这1000名同学中,取得面试资格的约有1000×0.38=380人.…(6分)(Ⅱ)设答对记为1,打错记为0,则所有可能的情况有:甲00乙00,甲00乙10,甲00乙01,甲00乙11,甲10乙00,甲10乙10,甲10乙01, 甲10乙11,甲01乙00,甲01乙10,甲01乙01,甲01乙11,甲11乙00,甲11乙10, 甲11乙01,甲11乙11,共16个………………………………………(9分)甲答对题的个数不少于乙的情况有:甲00乙00,甲10乙00,甲10乙10,甲10乙01,甲01乙00,甲01乙10,甲01乙01, 甲11乙00,甲11乙01,甲11乙10,甲11乙11,共11个……………(11分)故甲比乙优先获得高考加分资格的概率为1116.………………………(12分)21.解:(Ⅰ)由已知110,()ax x f x a x x-'=-=>.…………………………(1分)当0a ≤时,()0,f x '>函数()f x 在(0,)+∞内单调递增;………(2分) 当0a >时,由()0,f x '>得10,ax ->∴10x a<<;……………(3分)由()0,f x '<得10,ax -<∴1x a>.……………………(4分) ∴()f x 在1(0,)a 内单调递增,在1(,)a+∞内单调递减.…………(5分) (Ⅱ)当12a =时,211()(()1)(ln 1)ln (1)22g x x f x x x x x x x x x =+=-+=+-> ∴()ln 2(1),g x x x x '=-+>………………………………………(6分) 令()()ln 2(1)F x g x x x x '==-+>, 则1()10,F x x'=-<∴()F x 在(1,)+∞内单调递减.……………………(8分)∵(1)10,(2)ln 20,F F ==>> (3)(3)l n 332l n 3F g '==-+=-> (4)(4)ln 442ln 420.F g '==-+=-<…………………………(9分) ∴()F x 即()g x '在(3,4)内有零点,即()g x '在(3,4)内存在极值.…………………………………(11分) 又∵()g x 在(,1)k k +上存在极值,且k ∈z ,∴k =3.……………(12分)22.解(Ⅰ)∵△AF 1F 2的周长为4+∴224a c +=+即2a c +=+. ……………………(1分)又c e a ==解得2222,, 1.a cb ac ==-=………………(3分) ∴椭圆C 的方程为221.4x y +=………………………………(4分)(Ⅱ)由题意知,直线l 的斜率必存在,设其方程为1122(4),(,),(,).y k x M x y N x y =+由221,4(4)x y y k x ⎧+=⎪⎨⎪=+⎩得2222(14)326440.k x k x k +++-=…………………………………(6分) 则2212122232644,1414k k x x x x k k --+==++……………………………………(7分)由MQ QN λ=,得1122(4,,)(4,)x y x y λ---=+∴124(4),x x λ--=+∴1244x x λ+=-+.……………………………………(8分)设点R 的坐标为(00,x y ),由MR RN λ=,得01012020(,)(,),x x y y x x y y λ--=---∴0120(),x x x x λ-=--七彩教育网 教学资源分享平台,无需注册、无需登录即可下载七彩教育网 全国最新初中、高中试卷、课件、教案等教学资源免费下载 解得1121221212011224424().41()814x x x x x x x x x x x x x x x λλ++⋅-+++===+-++++………………(10分) 而22121222264432824()24,141414k k x x x x k k k --++=⨯+⨯=-+++ 21222328()88,1414k x x k k -++=+=++ ∴2028141,814k x k -+==-+…………………………………………………(13分) 故点R 在定直线1x =-上. ………………………………………………(14分)。
2013年普通高等学校招生全国统一考试(山东卷)数学试题 (文科) word解析版

2013年普通高等学校招生全国统一考试(山东卷)文科数学参考公式:如果事件B A ,互斥,那么)()()(B P A P B A P +=+一.选择题:本题共12个小题,每题5分,共60分。
1.复数)()2(2为虚数单位i i i z -=,则=||z A .25 B.41C .5 D.5答案C解析z =3-4i i=-4-3i ,所以|z |=(-4)2+(-3)2=5.2.已知集合A ,B 均为全集U ={1,2,3,4}的子集,且∁U (A ∪B )={4},B ={1,2},则A ∩∁U B 等于()A .{3}B .{4}C .{3,4}D .∅答案A解析∵4∈∁U (A ∪B ),∴4∉A ∪B ,又∁U B ={3,4},∴A ∩∁U B ={3}.3.已知函数f (x )为奇函数,且当x >0时,f (x )=x 2+1x ,则f (-1)等于()A .2B .1C .0D .-2答案D解析f (-1)=-f (1)=-2.4.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示,则该四棱锥侧面积和体积分别是()A .45,8B .45,83C .4(5+1),83D .8,8答案B解析该四棱锥的直观图如图,所以侧面积为:4×12×2×5=45,体积为:V =13×2×2×2=83.5.函数f (x )=1-2x +1x +3的定义域为()A .(-3,0]B .(-3,1]C .(-∞,-3)∪(-3,0]D .(-∞,-3)∪(-3,1]答案A解析-2x ≥0,+3>0解得-3<x ≤0.6.执行两次右图所示的程序框图,若第一次输入的a 的值为-1.2,第二次输入的a 的值为1.2,则第一次、第二次输出的a 的值分别为()A .0.2,0.2B .0.2,0.8C .0.8,0.2D .0.8,0.8答案C解析第一次a =-1.2时,输出a =0.8.第二次a =1.2时,输出a =0.2.7.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若B =2A ,a =1,b =3,则c =()A .23B .2 C.2D .1答案B解析由正弦定理得:1sin A =3sin B =3sin 2A =32sin A cos A .所以cos A =32,A =30°,B =60°,C =90°,所以c 2=a 2+b 2=4,所以c =2.8.给定两个命题p 、q ,若﹁p 是q 的必要而不充分条件,则p 是﹁q 的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】因为﹁p 是q 的必要而不充分条件,所以﹁q 是p 的必要而不充分条件,即p 是﹁q 的充分而不必要条件,选A.9.函数y =x cos x +sin x 的图象大致为()答案D 解析因为函数y =x cos x +sin x 为奇函数,所以排除B.取x =π2,排除C ;取x =π,排除A ,故选D.10.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x 表示:则7个剩余分数的方差为()A.1169B.367C .36 D.677答案B解析由题意知87+94+90+91+90+90+x +917=91,解得x =4.所以S 2=17[(87-91)2+(94-91)2+(90-91)2+(91-91)2+(90-91)2+(94-91)2+(91-91)2]=17(16+9+1+0+1+9+0)=367.11.抛物线C 1:y =12p x 2(p >0)的焦点与双曲线C 2:x 23-y 2=1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线,则p =()A.316 B.38 C.233 D.433答案D解析抛物线C 1:y =12p x 2的标准方程为:x 2=2py ,其焦点为双曲线C 2:x 23-y 2=1的右焦点F ′为(2,0),渐近线方程为y =±33x .又y ′=1p x ,所以1p x =33,解得x =33p ,所以点M 由点F 、F ′、M 三点共线可求p =433.12.设正实数x ,y ,z 满足x 2-3xy +4y 2+z =0.则当z xy 取得最小值时,x +2y -z 的最大值为()A .0 B.98C .2 D.94答案C解析由题意知:z =x 2-3xy +4y 2,则z xy =x 2-3xy +y 2xy=x y +4y x -3≥1,当且仅当x =2y 时取等号,此时z =xy =2y 2.所以x +2y -z =2y +2y -2y 2=-2y 2+4y =-2(y -1)2+2≤2.第Ⅱ卷二、填空题13.过点(3,1)作圆(x -2)2+(y -2)2=4的弦,其中最短弦的长为________.答案22解析由题意知,当弦的中点与圆心的连线与弦垂直时弦长最短,此时,点(3,1)为弦的中点,如图所示.∴AB =2BE =2BC 2-CE 2=24-2=2 2.14.在平面直角坐标系xOy 中,M x +3y -6≤0,+y -2≥0,≥0所表示的区域上一动点,则|OM |的最小值是________.答案2解析由题意知原点O 到直线x +y -2=0的距离为|OM |的最小值.所以|OM |的最小值为:22= 2.15.在平面直角坐标系xOy 中,已知OA →=(-1,t ),OB →=(2,2),若∠ABO =90°,则实数t 的值为________.答案5解析因为∠ABO =90°,即AB →⊥OB →,所以AB →·OB →=(OB →-OA →)·OB →=(3,2-t )·(2,2)=6+4-2t =0,解得:t =5.16.定义“正对数”:ln +x,0<x <1,x ,x ≥1现有四个命题:①若a >0,b >0,则ln +(a b b ln +a ;②若a >0,b >0,则ln +=ln +a +ln +b ;③若a >0,b >0,则ln ln +a -ln +b ;④若a >0,b >0,则ln +b )≤ln +a +ln +b +ln 2.其中的真命题有________.(写出所有真命题的编号)答案①③④解析①0<a b <1时(0<a <1),ln +(a b )=0=b ln +a ;a b >1时(a >1),ln +(a b )=ln a b =b ln a =b ln +a ;正确.②设a =1,b =3,则0=0+ln 3不成立,不正确;③(a >b ln a -ln b (a ,b ≥1),ln a (0<b <1≤a ),0(0<a ,b <1)(a <b ln a -ln b (a ,b ≥1),-ln b (0<a <1≤b ),0(0<a ,b <1).④(1)a +b >1,a ,b >1:ln(a +b )≤ln a +ln b +ln 2=ln 2ab 成立;(2)a +b >1,a >1,0<b <1:ln(a +b )≤ln a +ln 2=ln 2a 成立;(3)a +b >1,0<a ,b <1:ln(a +b )≤ln 2成立;(4)0<a +b <1,0<a ,b <1:0≤ln 2成立.三、解答题17.某小组共有A ,B ,C ,D ,E 五位同学,他们的身高(单位:米)及体重指标(单位:千克/米2)如下表所示:A B C D E身高 1.69 1.73 1.75 1.79 1.82体重指标19.225.118.523.320.9(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.解(1)从身高低于1.80的4名同学中任选2人,其一切可能的结果组成的基本事件有:(A ,B ),(A ,C ),(A ,D ),(B ,C ),(B ,D ),(C ,D )共6个.设“选到的2人身高都在1.78以下”为事件M ,其包括事件有3个,故P (M )=36=12.(2)从小组6名同学中任选2人,其一切可能的结果组成的基本事件有:(A ,B ),(A ,C ),(A ,D ),(A ,E ),(B ,C ),(B ,D ),(B ,E ),(C ,D ),(C ,E ),(D ,E )共10个.设“选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)”为事件N ,且事件N 包括事件有:(C ,D ),(C ,E ),(D ,E )共3个.则P (N )=310.18.设函数f (x )=32-3sin 2ωx -sin ωx cos ωx (ω>0),且y =f (x )图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间π,3π2上的最大值和最小值.解(1)f (x )=32-3sin 2ωx -sin ωx cos ωx =32-3×1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -1sin 2ωx=-ωx 依题意知2π2ω=4×π4,ω>0,所以ω=1.(2)由(1)知f (x )=-x 当π≤x ≤3π2时,5π3≤2x -π3≤8π3.所以-32≤x 1.所以-1≤f (x )≤32.故f (x )在区间π,3π2上的最大值和最小值分别为32,-1.19.如图,四棱锥P ABCD 中,AB ⊥AC ,AB ⊥PA ,AB ∥CD ,AB=2CD ,E ,F ,G ,M ,N 分别为PB ,AB ,BC ,PD ,PC 的中点.(1)求证:CF ∥平面PAD ;(2)求证:平面EFG ⊥平面EMN .证明(1)方法一取PA 的中点H ,连接EH ,DH .又E 为PB 的中点,所以EH 綊12AB .又CD 綊12AB ,所以EH 綊CD .所以四边形DCEH 是平行四边形,所以CE ∥DH .又DH ⊂平面PAD ,CE ⊄平面PAD .所以CE ∥平面PAD .方法二连接CF .因为F 为AB 的中点,所以AF =12AB .又CD =12AB ,所以AF =CD .又AF ∥CD ,所以四边形AFCD 为平行四边形.因此CF ∥AD ,又CF ⊄平面PAD ,所以CF ∥平面PAD .因为E ,F 分别为PB ,AB 的中点,所以EF ∥PA .又EF ⊄平面PAD ,所以EF ∥平面PAD .因为CF ∩EF =F ,故平面CEF ∥平面PAD .又CE ⊂平面CEF ,所以CE ∥平面PAD .(2)∵E 、F 分别为PB 、AB 的中点,∴EF ∥PA .又∵AB ⊥PA ,∴EF ⊥AB ,同理可证AB ⊥FG .又∵EF ∩FG =F ,EF ⊂平面EFG ,FG ⊂平面EFG .∴AB ⊥平面EFG .又∵M ,N 分别为PD ,PC 的中点,∴MN ∥CD ,又AB ∥CD ,∴MN ∥AB ,∴MN ⊥平面EFG .又∵MN ⊂平面EMN ,∴平面EFG ⊥平面EMN .20.设等差数列{a n }的前n 项和为S n ,且S 4=4S 2,a 2n =2a n +1.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b 1a 1+b 2a 2+…+b n a n =1-12n ,n ∈N *,求{b n }的前n 项和T n .解(1)设等差数列{a n }的首项为a 1,公差为d4=4s 2,2n =2a n +1得a 1=1,d =2所以a n =2n -1(n ∈N *).(2)由已知b 1a 1+b 2a 2+…+b n a n =1-12n ,n ∈N *①当n ≥2时,b 1a 1+b 2a 2+…+b n -1a n -1=1-12n -1②①-②得:b n a n =12n ,又当n =1时,b 1a 1=12也符合上式,所以b n a n =12n (n ∈N *).所以b n =2n -12n (n ∈N *).所以T n =b 1+b 2+b 3+…+b n =12+322+523+…+2n -12n .12T n =122+323+…+2n -32n +2n -12n +1.两式相减得:12T n =12++223+…+-2n -12n +1=32-12n -1-2n -12n +1.所以T n =3-2n +32n .21.已知函数f (x )=ax 2+bx -ln x (a ,b ∈R ).(1)设a ≥0,求f (x )的单调区间;(2)设a >0,且对任意x >0,f (x )≥f (1).试比较ln a 与-2b 的大小.解(1)f (x )的定义域为x ∈(0,+∞),f ′(x )=2ax 2+bx -1x .当a =0时,f ′(x )=bx -1x.①若b ≤0,当x >0时,f ′(x )<0恒成立,所以函数f (x )的单调递减区间是(0,+∞).②若b >0,当0<x <1b 时,f ′(x )<0,当x >1b 时,f ′(x )>0.所以函数f (x )当a >0时,由f ′(x )=0得2ax +bx -1=0.解得x 1=-b -b 2+8a 4a ,x 2=-b +b 2+8a 4a,此时x 1<0,x 2>0.当0<x <x 2时,f ′(x )<0,当x 2所以函数f (x )综上所述:当a =0,b ≤0时,函数f (x )的单调递减区间是(0,+∞).当a =0,b >0时,函数f (x )当a >0时,函数f (x )(2)由题意知:函数f (x )在x =1由(1)知,-b +b 2+8a 4a 是f (x )的惟一极小值点,故-b +b 2+8a 4a =1,整理得b =1-2a .令g (x )=2-4x +ln x ,则g ′(x )=1-4x x ,令g ′(x )>0得x =14.当0<x <14时,g ′(x )>0,g (x )单调递增;当x >14时,g ′(x )<0,g (x )单调递减;所以g (x )≤1+ln 14=1-ln 4<0.故g (a )<0,即2-4a +ln a =2b +ln a <0,即ln a <-2b .22.在平面直角坐标系xOy 中,已知椭圆C 的中心在原点O ,焦点在x 轴上,短轴长为2,离心率为22.(1)求椭圆C 的方程;(2)A ,B 为椭圆C 上满足△AOB 的面积为64的任意两点,E 为线段AB 的中点,射线OE 交椭圆C 于点P .设OP →=tOE →,求实数t 的值.解(1)设椭圆C 的方程为:x 2a 2+y 2b 21(a >b >0),=a 2-b 2,=22,=2,解得a =2,b =1,故椭圆C 的方程为x 22+y 2=1.(2)①当A ,B 两点关于x 轴对称时,设直线AB 的方程为x =m ,由题意-2<m <0或0<m <2.将x =m 代入椭圆方程得|y |=2-m 22,所以S △AOB =|m |2-m 22=64.解得m 2=32或m 2=12.(ⅰ)又OP →=tOE →=12t (OA →+OB →)=12t (2m,0)=(mt,0),又点P 在椭圆上,所以(mt )22=1.(ⅱ)由(ⅰ)(ⅱ)得t 2=4或t 2=43.又因为t >0,所以t =2或t =233.②当A ,B 两点关于x 轴不对称时,设直线AB 的方程为y =kx +n ,kx +n ,y 2=1得(1+2k 2)x 2+4knx +2n 2-2=0.设A (x 1,y 1),B (x 2,y 2),由Δ=4k 2n 2-4(1+2k 2)(2n 2-2)>0得1+2k 2>n 2.此时x 1+x 2=-4kn 1+2k 2,x 1x 2=2n 2-21+2k 2,y 1+y 2=k (x 1+x 2)+2n =2n 1+2k 2.所以|AB |=1+k 2(x 1+x 2)2-4x 1x 2=221+k 21+2k 2-n 21+2k 2.又点O 到直线AB 的距离d =|n |1+k 2.所以S △AOB =12|AB |d =12×221+k 21+2k 2-n 21+2k 2|n |1+k2.=2·1+2k 2-n 21+2k 2·|n |=64.令r =1+2k 2代入上式得:3r 2-16n 2r +16n 4=0.解得r =4n 2或r =43n 2,即1+2k 2=4n 2或1+2k 2=43n 2.又OP →=tOE →=12t (OA →+OB →)=12t (x 1+x 2,y 1+y 2)-2knt 1+2k 2,又点P 为椭圆C上一点,所以t1,即n 1+2k 2t 2=1.4n 2或1+2k 2=43n 2,2=1得t 2=4或t 2=43.又t >0,故t =2或t =233.经检验,适合题意.综合①②得t =2或t =233.。
山东省淄博市数学高三理数第二次模拟考试试卷

山东省淄博市数学高三理数第二次模拟考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2018高一下·黄冈期末) 已知x ,y∈(0,+∞),且log2x+log2y=2,则+的最小值是()A . 4B . 3C . 2D . 12. (2分)(2017·长沙模拟) 复数(2+i)i的共轭复数的虚部是()A . 2B . ﹣2C . 2iD . ﹣2i3. (2分)设,则“”是“直线与直线平行”的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件4. (2分)设函数的最小正周期为T,最大值为A,则()A . ,B . ,C . ,D . ,5. (2分)(2017·九江模拟) 在平面直角坐标系xOy中,已知双曲线C:﹣ =1(a>0,b>0)的离心率为,从C的右焦点F引渐近线的垂线,垂足为A,若△AFO的面积为1,则双曲线C的方程为()A . ﹣ =1B . ﹣y2=1C . ﹣ =1D . x2﹣ =16. (2分)一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为()A .B .C .D .7. (2分) (2016高一下·辽源期中) 两个等差数列{an}和{bn},其前n项和分别为Sn , Tn ,且,则等于()A .B .C .D .8. (2分)已知椭圆与双曲线有相同的焦点和,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为()A .B .C .D .9. (2分) (2016高二下·卢龙期末) 抛掷红、蓝两枚骰子,事件A=“红色骰子出现点数3”,事件B=“蓝色骰子出现偶数点”,则P(B|A)=()A .B .C .D .10. (2分)已知某程序框图如图所示,则该程序运行后输出的结果为()A .B .C .D .11. (2分)(2017·黑龙江模拟) 定义在R上的可导函数f(x),其导函数记为f'(x),满足f(x)+f(2﹣x)=(x﹣1)2 ,且当x≤1时,恒有f'(x)+2<x.若,则实数m的取值范围是()A . (﹣∞,1]B .C . [1,+∞)D .12. (2分)(2019高三上·衡水月考) 已知函数,若存在实数,满足,且,,,则的最小值为()A . 3B . 4C . 5D . 6二、填空题 (共4题;共4分)13. (1分)(2020·天津模拟) 在的展开式中,常数项是________.14. (1分)(2018·河南模拟) 如图,已知点,点在曲线上移动,过点作垂直轴于,若图中阴影部分的面积是四边形面积的,则点的坐标为________15. (1分)(2013·江苏理) 如图,在三棱柱A1B1C1﹣ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F﹣ADE的体积为V1 ,三棱柱A1B1C1﹣ABC的体积为V2 ,则V1:V2=________.16. (1分)(2018·荆州模拟) 设数列满足,,若使得,则正整数 ________.三、解答题 (共7题;共60分)17. (10分) (2018高二上·兰州月考) 中,角所对的边分别为 .已知,, .(1)求的值;(2)求的面积.18. (10分) (2018高二下·长春期末) 已知与之间的数据如下表:附:,,, .(1)求关于的线性回归方程;(2)完成下面的残差表:并判断(1)中线性回归方程的回归效果是否良好(若,则认为回归效果良好).19. (5分)(2019·浙江模拟) 如图,在三棱锥中,是棱的中点,,且,(Ⅰ)求证:直线平面;(Ⅱ)求二面角的正弦值.20. (10分)(2018·保定模拟) 椭圆的离心率为,且过点 . (1)求椭圆的方程;(2)设为椭圆上任一点,为其右焦点,是椭圆的左、右顶点,点满足 .①证明:为定值;②设是直线上的任一点,直线分别另交椭圆于两点,求的最小值.21. (10分) (2019高三上·桂林月考) 已知函数.(1)当时,求函数在上的最小值;(2)若,求证:.22. (5分)已知长为2的线段AB中点为C,当线段AB的两个端点A和B分别在x轴和y轴上运动时,C点的轨迹为曲线C1;(1)求曲线C1的方程;(2)直线ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.23. (10分)设Pn=(1﹣x)2n﹣1 , Qn=1﹣(2n﹣1)x+(n﹣1)(2n﹣1)x2 ,x∈R,n∈N*(1)当n≤2时,试指出Pn与Qn的大小关系;(2)当n≥3时,试比较Pn与Qn的大小,并证明你的结论.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共60分)17-1、17-2、18-1、18-2、19-1、20-1、20-2、21-1、21-2、22、答案:略23-1、23-2、。
山东省淄博市2013高三文科数学复习16《空间几何体》达标检测试卷(新人教A)
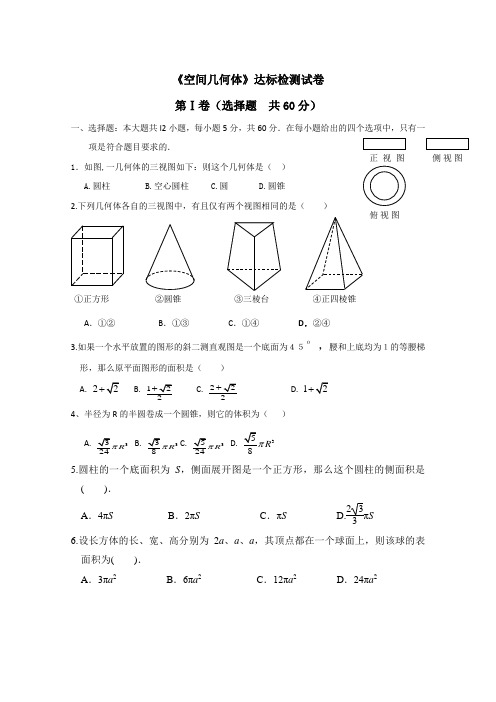
《空间几何体》达标检测试卷第Ⅰ卷(选择题共60分)一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,一几何体的三视图如下:则这个几何体是()A.圆柱B.空心圆柱C.圆D.圆锥2.下列几何体各自的三视图中,有且仅有两个视图相同的是()A.①②B.①③C.①④D.②④3.如果一个水平放置的图形的斜二测直观图是一个底面为45o,腰和上底均为1的等腰梯形,那么原平面图形的面积是()A. 2B.C.D. 14、半径为R的半圆卷成一个圆锥,则它的体积为()A. 3RB. 3RC. 3RD. 3R5.圆柱的一个底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是().A.4πS B.2πS C.πS D.233πS6.设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为().A.3πa2B.6πa2C.12πa2D.24πa2俯视图正视图侧视图①正方形②圆锥③三棱台④正四棱锥7.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( ).A .6πB .46πC .43πD .63π 8. 在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为( )9.如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12,则该几何体的俯视图可能是( ).10. 右图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是 ( ) (A)3 (B)2 (C)1 (D)011.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( )A .33523cm B .33203cm正(主)视图俯视图C .32243cm D.31603cm 12.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+ B .30+ C .56+ D .60+第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.一个高为2的圆柱,底面周长为2π,该圆柱的表面积为 14.如图,正方体1111ABCD A B C D -的棱长为1,E 为线段1B C 上的一点,则三棱锥1A DED -的体积为_____.15.已知某几何体的三视图如图所示,则该几何体的体积为____________.16.如图,在ABC 中,AB=3,BC=5,120ABC ∠=°将ABC 绕直线AB 旋转一周,则所形成的旋转体的侧面积是__________。
新课标2013届高三配套月考(二)数学试题(A卷)
2013届高三新课标数学配套月考试题二A适用地区:新课标地区考查范围:集合、逻辑、函数、导数、三角、向量、数列、不等式建议使用时间:2012年9月底本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考生作答时,将答案答在答题卡上.在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上.2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.4.保持卡面清洁,不折叠,不破损.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(2012·哈尔滨第六中学三模)已知集合{}2,0x M y y x ==>,{})2lg(2x x y x N -==,则M N 为( )A.()2,1B.()+∞,1C.[)+∞,2D.[)+∞,12. (2012·银川一中第三次月考)若b a b a >是任意实数,且、,则下列不等式成立..的是( )A .22b a > B .1<a b C .0)lg(>-b a D .1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭3.(理)[2012·辽宁卷]在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11=( )A.58B.88C.143D.176(文)[2012·辽宁卷]在等差数列{a n }中,已知a 4+a 8=16,则a 2+a 10=( ) A.12 B.16 C.20 D.244. [2012·山东卷]若ππ,42θ⎡⎤∈⎢⎥⎣⎦,sin 2θ,则sin θ=( )A.35 B.45 D.345. [2012·课标全国卷]已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=( ) A.7 B.5 C.-5 D.-7 6. [2012·山东卷]函数2sin (09)63x y x ⎛⎫=-≤≤⎪⎝⎭ππ的最大值与最小值之和为( )A.2B.0C.-1D.1-7.(理)(2012·太原三模)下列判断错误的是( ) A. “22am bm <”是”a b <”的充分不必要条件B.命题“2,10x x x ∀∈--≤R ”的否定是“ 2000,10x x x ∃∈-->R ”C.若,p q 均为假命题,则p q ∧为假命题D.若()~4,0.25B ξ,则1D ξ=(文)(2012·太原三模)下列判断正确的是( )A. 若命题p 为真命题,命题q 为假命题,则命题“p q ∧”为真命题B. 命题“若0xy =,则0x =”的否命题为“若0xy =,则0x ≠”C. “1sin 2α=”是“ 6πα=”的充分不必要条件 D. 命题“,20x x ∀∈>R ”的否定是“ 00,20x x ∃∈≤R ” 8.(2012·长春三模)函数21()3cos log 22f x x x π=--的零点个数为( ) A.2B.3C.4D.59. (2012·银川一中第三次月考)函数()sin()f x A x ωϕ=+(其中π0,2A ϕ><)的图象如图1所示,为了得到x x g 2sin )(=的图象,则只需将()f x 的图象( ) A.向右平移π6个长度单位 B.向右平移π12个长度单位 C.向左平移π6个长度单位 D.向左平移π12个长度单位 图110.(2012·郑州质检)在△ABC 中,若2···AB AB AC BA BC CA CB =++,则△ABC 是( )A.等边三角形B.锐角三角形C.钝角三角形D.直角三角形11. (2012·石家庄二模)已知函数()2,0,2,0,x f x x x ≥⎧=⎨-+<⎩则满足不等式()()232f x f x -<的x 的取值范围为( )A.B. (-3,1)C. [-3,0)D. (-3,0)12. (2012·石家庄二模)设不等式组表示的平面区域为,n n D a 表示区域D n 中整点的个数(其中整点是指横、纵坐标都是整数的点),则=( )A. 1012B. 2012C. 3021D. 4001第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卷相应位置上.) 13. [2012·课标全国卷]已知向量a ,b 夹角为45︒ ,且|a|=1,|2a -b||b|=________.AB =,则BC 的长度为________.15. [2012·课标全国卷] 设,x y 满足约束条件:,0,1,3,x y x y x y ≥⎧⎪-≥-⎨⎪+≤⎩则2z x y =-的取值范围为 .16. (2012·银川一中第三次月考)已知0,0x y >>,若2282y x m m x y+>+恒成立,则实数m 的取值范围是 .三、解答题:本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤.17.(本小题满分10分) [2012·北京卷]已知函数xx x x x f sin 2sin )cos (sin )(-=。
山东省2013届高三数学 最新模拟试题精选分类汇编1 集合 理
山东省2013届高三最新理科模拟试题精选(17套)分类汇编1:集合一、选择题 1 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)集合{}{}1,0,1,,x A B y y e x A =-==∈,则A B ⋂=( )A .{}0B .{}1C .{}0,1D .{}1,0,1-【答案】B 2 .(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)集合{}{}22(,)|,,(,)|1,,A x y y x x R B x y x y x y R ==∈=+=∈,则集合A B ⋂中元素的数为 ( )A .0B .1C .2D .无穷个 【答案】C 3 .(山东省文登市2013届高三3月二轮模拟考试数学(理))已知集合11,2A ⎧⎫=-⎨⎬⎩⎭,{}01=-=mx x B ,若B B A = ,则所有实数m 组成的集合是 ( )A .{}0,1,2-B .1,0,12⎧⎫-⎨⎬⎩⎭C .{}1,2-D .11,0,2⎧⎫-⎨⎬⎩⎭【答案】A 4 .(山东省潍坊市2013届高三第二次模拟考试数学理试题(word 版))集合{}{}|13,|4A x x B y y x =+≤==≤≤.则下列关系正确的是( )A .AB R = B .RA B ⊆C .RB A ⊆D .RRA B ⊆【答案】D5 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知全集{0,1,2,3,4,5,6}U =,集合{2,4,5}A =,{1,3,4,6}B =,则()u C A B 为( )A .{0,1,3,6}B .{0,2,4,6}C .{0,1,6}D .{1,3,6}【答案】D 6 .(山东省莱芜市莱芜四中2013届高三4月月考数学试题)已知全集U=N*,集合P={1,2,3,4,5},Q={1,2,3,6,8},则P∩(∁UQ)等于 ( ) A .{1,2,3} B .{4,5}C .{6,8}D .{1,2,3,4,5} 【答案】B 7 .(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知集合{}⎭⎬⎫⎩⎨⎧∈≥+=∈≤-=Z x x x T R x x x S ,115,,21,则T S 等于( )A .{}Z x x x ∈≤≤,30|B .{}|13,x x x Z -≤≤∈C .{}Z x x x ∈≤≤-,41|D .{}Z x x x ∈<≤-,01|【答案】A8 .(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)设全集{}9,8,7,6,5,4,3,2,1=U ,[{}3,1)(=B A U ,{}[4,2)(=B A U ,则集合B= ( ) A .{}4,3,2,1 B .{}5,4,3,2,1 C .{}9,8,7,6,5 D .{}9,8,7【答案】C 9 .(山东省莱钢高中2013届高三4月模拟检测数学理试题 )设全集,,则右图中阴影部分表示的集合为( ) ( )A .B .. D .【答案】B10.(山东省济宁市2013届高三4月联考理科数学)设全集U =R ,集合M={x |x 2+2x -3≤0),N={x |-1≤x ≤4},则M N 等于 ( ) A .{x | 1≤x ≤4} B .{x |-1≤x ≤3} C .{x |-3≤x ≤4} D .{x |-1≤x ≤1} 【答案】D 11.(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知集合2{12},{log 2}A x x B x x =-<=<,则A B =( )A .(1,3)-B .(0,4)C .(0,3)D .(1,4)-【答案】C 12.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)已知集合1A x x ,B x xm ,且A B R ,那么m 的值可以是( )A .1B .0C .1D .2【答案】DU R =(2){|21},{|ln(1)}x x A x B x y x -=<==-{|1}x x ≥{|12}x x ≤<{|01}x x <≤{|1}x x ≤13.(山东省凤城高中2013届高三4月模拟检测数学理试题 )集合{||2|2}A x x =-≤,2{|,12}B y y x x ==--≤≤,则A B =( )A .{0}B .{|0}x x ≠C .RD .∅【答案】A 14.(山东省德州市2013届高三第二次模拟考试数学(理)试题)设集合U={0,l,2,3,4,5,6},M={l,3,5},N={2,4,6},则(UM )(UN )=( )A .{0}B .{1,3,5}C .{2,4,6}D .{0,1,2,3,4,5,6}【答案】D。
2013年第二次高考诊断数学试卷
2013年第二次高考诊断数学试卷(理)试题注意事项:1.本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.回答第1卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题.每小题5分。
在每小题给出的四个选项中。
只有一项是符合题目要求的.1.已知集合A={0,1},B={ },则A B=A.{0,1} B.{0,1,一1}C.{0,1,一1,} D.{0,l,一1,一}2.若复数,则z为A.i B.一i C.2i D.1+i3.显示屏有一排7个小孔可显示0或l,若每次显示其中3个小孔,但相邻的两孔不能同时显示,则该显示屏能显示信号的种数共有A.10 B.48 C.60 D.804.已知椭圆的左焦点F1,右顶点A,上顶点∠F1BA=90°,则椭圆的离心率是A.B.C.D.5.设变量x,y满足,则戈.4+2y的最大值和最小值分别为A.1,-1 B.2,一2 C.1,一2 D.2,一16.执行右图所示的程序,输出的结果为48,对判断框中应填人的条件为A.i≥4?B.i>4?C.i≥6?D.i>6?7.已知某几何体的三视图如右,根据图中标出的尺寸,可得这个几何体的体积是A.B.C.D.8.各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是A.16 B.20 C.24 D.329.已知函数y=2sin2(则函数的最小正周期T和它的图象的一条对称轴方程是A.T=2 ,一条对称轴方程为B.T=2 ,一条对称轴方程为C.T= ,一条对称轴方程为D.T= ,一条对称轴方程为10.已知点F是双曲线的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是锐角三角形,则该双曲线的离心率e的取值范围是A.(1,+∞)B.(1,2)C.(1,1+ )D.(2,1+ )11.已知函数和在[一2,2]的图象如下图所示,给出下列四个命题:①方程有且仅有6个根;②方程有且仅有3个根;③方程有且仅有5个根;④方程有且仅有4个根.其中正确的命题个数是A.4 B.3 C.2 D.112.已知定义域为R的函数满足,且当x>2时,单调递增,如果且()()<0,则下列说法正确的是A.的值为正数B.的值为负数C.的值正负不能确定D.的值一定为零第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题一第21题为必考题。
【2013德州二模】山东省德州市2013届高三第二次模拟考试数学(文)试题 Word版含答案
山东省德州市2013届高三第二次模拟考试数学(文)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟。
注意事项:选择题为四选一题目.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上。
第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.把正确答案涂在答题卡上.1.设集合U={0,l,2,3,4,5,6},M ={l,3,5},N={2,4,6},则(U Mð)(U Nð)=A.{0} B.{1,3,5} C.{2,4,6} D.{0,1,2,3,4,5,6}2.设i为虚数单位,则复数34 12ii-++=A.-1 +2i B.1+2i C.-1-2i D.1-2i 3.在空间中,不同的直线m,n,l,不同的平面,αβ,则下列命题正确的是A.m//α,n∥α,则m∥n B.m//α,m//β,则α//βC.m⊥l,n⊥l,则m∥n D.m⊥α,m⊥β,则α//β4.已知变量x、y满足条件12xyx y≥⎧⎪≤⎨⎪-≤⎩,则x+y的最小值是A.4 B.3 C.2 D.15.已知函数f(x)=4-x2,y=g(x)是定义在R上的奇函数,当x>0时,g(x)=log2x,则函数f(x)·g(x)的大致图象为6.已知sin()4πα-=,则sin2α=A.34B.-34C.1516D.-15167.执行如图所示的程序框图,若输入n 的值为6,则输出s 的值为 A .17B .16C .10D .98.若双曲线2x m-y 2=4(m>0)的焦距为8,则它的离心率为A .3 B .2C .43 D .159.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为 A .68 B . 68.2 C .68.5D .7510.若对于定义在R 上的函数f (x ),存在常数()t t R ∈,使得f (x+t )+tf (x )=0对任意实数x 均成立,则称f (x )是t 阶回旋函数,则下面命题正确的是 A .f (x )=log a x 是0阶回旋函数 B .f (x )=sin (πx )是1阶回旋函数 C .f (x )=2x 是12-阶回旋函数 D .f (x )=x 2是1阶回旋函数11.给出下列命题:①若a ,b ∈R +,a≠b ,则a 3 +b 3>a 2b+ ab 2; ②若a ,b ∈R +,a<b ,则a m ab m b+>+;③若a ,b ,c ∈R +,则bc ac ab a b c ++≥a+b+c ; ④若3x+y=l ,则114x y+≥+ 其中正确命题的个数为A .1个B .2个C .3个D .4个12.已知f (x )为R 上的可导函数,且x ∀∈R ,均有f (x )()f x '>,则有 A .e 2013 f (-2013)<f (0),f (2013)>e 2013f (0) B .e2013f (-2013)< f (0),f (2013)<e 2013f (0) C .e 2013 f (-2013)>f (0),f (2013)>e 2013f (0) D .e 2013 f (-2013)>f (0),f (2013)<e 2013f (0)第Ⅱ卷 (共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题纸的相应位置. 13.为了解某校教师使用多媒体进行教学的情况,将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0,9), [10,19),[20,29),[30,39),[40,49)五层。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金太阳新课标资源网 wx.jtyjy.com 第 1 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 山东省淄博市沂源2013届高三复习阶段性检测 数学(文)试题
本试卷分第I卷和第II卷两部分,共5页.满分150分.考试用时120分钟,考试结束后,将试卷和答题卡一并上交. 注意事项: 1.答题前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写 在答题卡和试卷规定的位置上. 2.第1卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动, 用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上. 3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的 位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效. 4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤. 参考公式:
锥体的体积公式:13VSh,其中S是锥体的底面积,h是锥体的高.
如果事件A,B互斥,那么PABPAPB;如果事件A,B独立,那么PABPAPB.
第I卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合1,0,1,,xAByyexA,则AB=
A.0 B.1 C.0,1 D.1,0,1 2.复数11ii(i是虚数单位)的共轭复数的虚部为 A.1 B.0 C.1 D.2
3.已知等差数列na的前n项和为nS,满足1313113aSa,则 A.14 B.13 C.12 D.11 4.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是 A.1 B.2 C.3 D.4 金太阳新课标资源网 wx.jtyjy.com 第 2 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 5.函数2tan22fxxx在,上的图象大致为
6.在ABC中,“3sin2A”是“3A”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 7.如图,平行四边形ABCD中,
2,1,ABADA,点M在AB边上,且
13AMABDMDB,则等于
A.32 B.32 C.1 D.1 8.设0,5p在上随机地取值,则关于x的方程210xpx有实数根的概率为
A.15 B.25 C.35 D.45
9.已知x,y满足条件020xyxxyk(k为常数),若目标函数3zxy的最大值为8,则k= A.16 B.6 C.83 D.6 10.已知ABC中,三个内角A,B,C的对边分别为a,b,c,若ABC的面积为S,且金太阳新课标资源网 wx.jtyjy.com 第 3 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 222,tanSabcC则
等于
A.34 B.43 C.43 D.34 11.在平面直角坐标系xoy中,圆C的方程为228150xyx,若直线2ykx上至少存在一点,使得以该点为圆心,半径为1的圆与圆C有公共点,则k的最小值是 A.43 B.54 C.35 D.53
12.定义域为,ab的函数yfx的图象的两个端点为A,B,M,xyx是f图象上任意一点,其中1,1xabRONOAOB向量,若不等式MNk恒成立,则称函数,fxab在上“k阶线性近似”.若函数1
12yxx在,
上“k阶线性近似”,则实数k的取值范围为
A.0, B.1, C.322,
D.322, 第II卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分 13.执行如图所示的程序框图,若输出的结果是8,则输入的数是______.
14.若双曲线222210xyabab的左、右焦点分别为F1,F2,线段F1F2
被抛物线22ybx的焦点分成5:3两段,则此双曲线的离心率为______. 15.已知函数fx在实数集R上具有下列性质:①直线1x是函数
fx的一条对称轴;②2fxfx;③当1213xx时,
21fxfx210,xx则f(2011)
2012f、2013f从大到小的顺序为_______.
16.在如图所示的数阵中,第9行的第2个数为___________. 三、解答题:本大题共6个小题,共74分. 17.(本小题满分12分) 金太阳新课标资源网 wx.jtyjy.com 第 4 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 已知函数213sincoscos02fxxxx,其最小正周期为.2 (I)求fx的表达式; (II)将函数fx的图象向右平移8个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数ygx的图象,若关于x的方程0gxk,在区
间0,2上有且只有一个实数解,求实数k的取值范围.
18.(本小题满分12分) 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:40,50,50,60,,90,100,得到如图所示的频率分布直
方图. (I)若该校高一年级共有学生1000人,试估计成绩不低于60分的人数; (II)为了帮助学生提高数学成绩,学校决定在随机抽
取的50名学生中成立“二帮一”小组,即从成绩90,100
中选两位同学,共同帮助40,50中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙恰好被安排在同一小组的概率.
19.(本小题满分12分) 在如图所示的几何体中,ABC是边长为2的正三角形,1,AEAE平面ABC,平面BCD平面ABC,BD=CD,且.BDCD (I)AE//平面BCD; (II)平面BDE平面CDE.
20.(本小题满分12分) 等比数列....nc满足1*1104,nnnnccnNa数列的前n项和为nS,且
2log.nnac (I)求,nnaS; (II)数列1,41nnnnnbbTbS满足为数列的前n项和,是否存在正整数m,金太阳新课标资源网 wx.jtyjy.com 第 5 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 1m,使得16,,mmTTT成等比数列?若存在,求出所有m的值;若不存在,请说明理
由.
21.(本小题满分13分) 已知,Pxy为函数1lnyx图象上一点,O为坐标原点,记直线OP的斜率
kfx.
(I)若函数fx在区间1,3mm0m上存在极值,求实数m的取值范围; (II)当 1x时,不等式1tfxx恒成立,求实数t的取值范围. 22.(本小题满分13分) 已知抛物线24yx的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂
足为T),与抛物线交于不同的两点P、Q且125FPFQ. (I)求点T的横坐标0x;
(II)若以F1,F2为焦点的椭圆C过点21,2. ①求椭圆C的标准方程; ②过点F2作直线l与椭圆C交于A,B两点,设22FAFB,若2,1,TATB求的取值范围. 金太阳新课标资源网 wx.jtyjy.com 第 6 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 金太阳新课标资源网 wx.jtyjy.com
第 7 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 金太阳新课标资源网 wx.jtyjy.com
第 8 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 金太阳新课标资源网 wx.jtyjy.com
第 9 页 共 14 页 金太阳新课标资源网wx.jtyjy.com 金太阳新课标资源网 wx.jtyjy.com
第 10 页 共 14 页 金太阳新课标资源网wx.jtyjy.com
